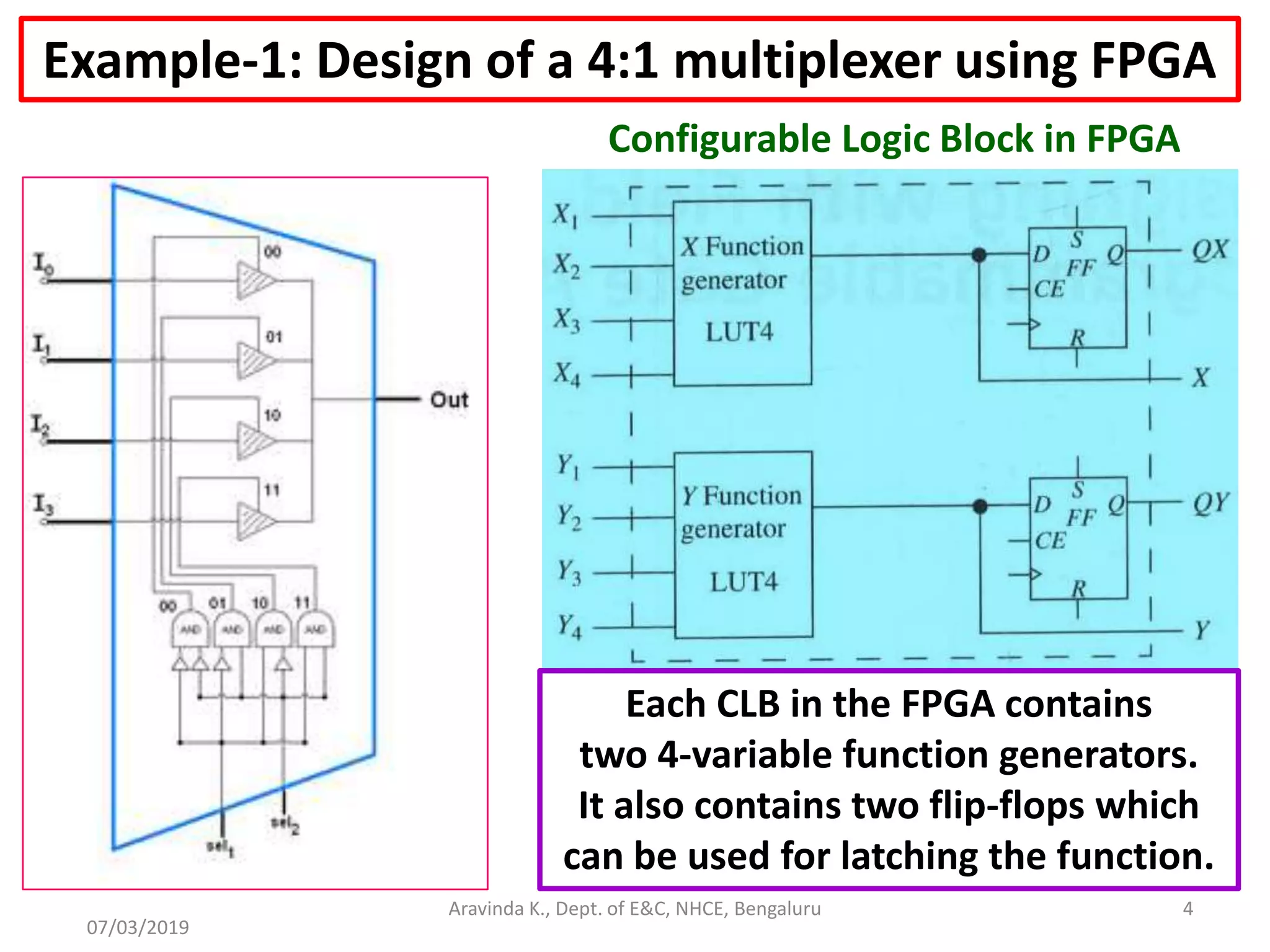
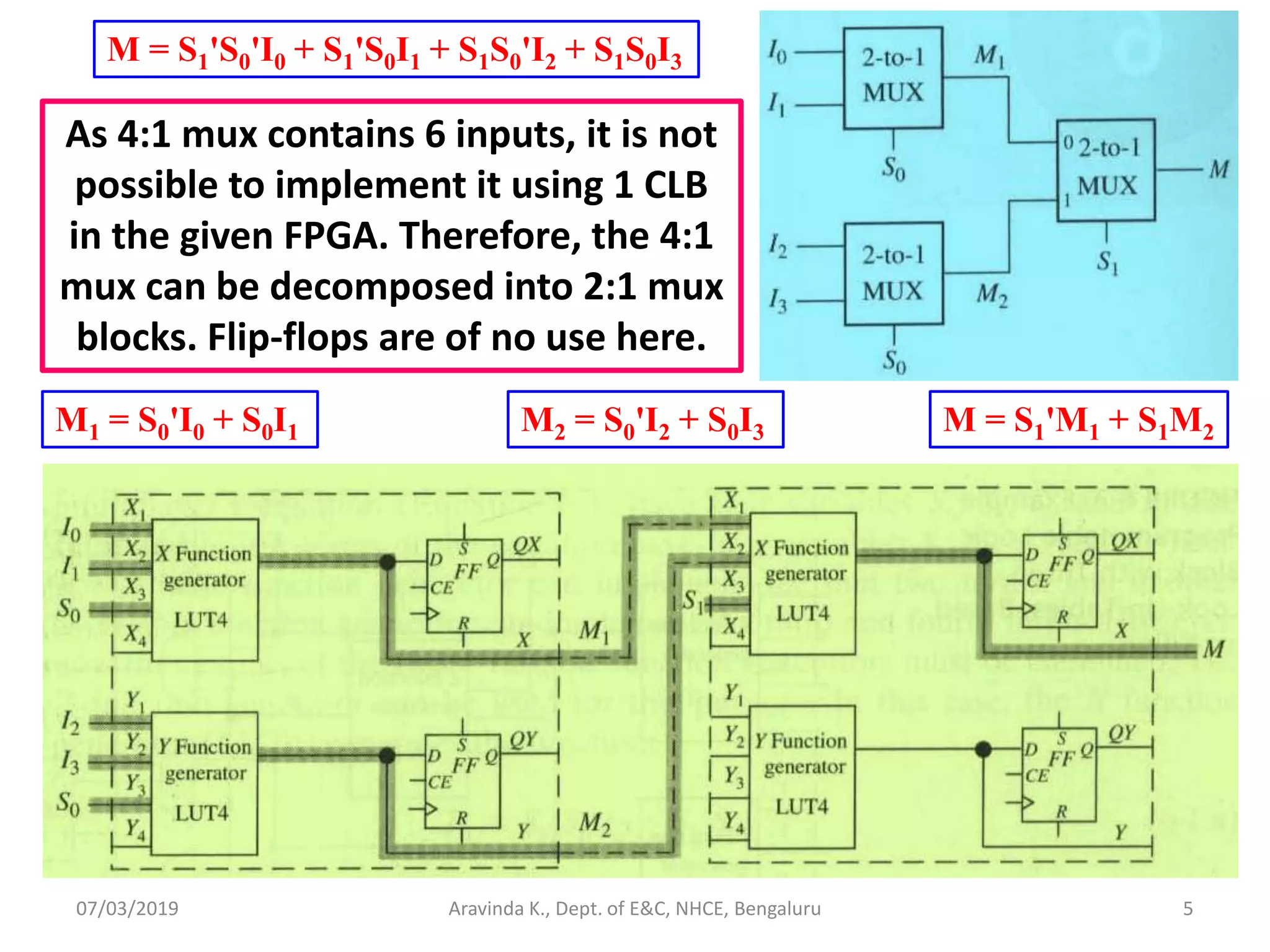
The document provides a detailed overview of FPGAs (Field Programmable Gate Arrays) and various design considerations, including the use of configurable logic blocks, LUTs (Look-Up Tables), and multiplexers for implementing digital functions. It discusses examples of designing specific components like multiplexers and shift registers, the costs of programmability, and methods for state machine implementation. Additionally, it outlines important FPGA architecture features and the associated trade-offs between programmability and hardware efficiency.














![07/03/2019 Aravinda K., Dept. of E&C, NHCE, Bengaluru 28 One method for computing the equivalent gate count for a CLB is as follows: 2:1 mux = 4 gates, 3-input XOR gate = 6 gates, 4-input XOR gate = 9 gates, Flip-flop = 7 gates, and so on. Thus, the equivalent gate count for a CLB can be obtained. The total gate count can be estimated, by multiplying the equivalent gate count with the number of CLBs in the FPGA. In general, this type of gate count is likely to be higher than the gate count of the practical circuitry that is being realized. Another method is to use the Benchmark circuits (e.g.: Benchmark suite prepared by PREP [Programmable Electronics Performance company]). For example, if an ASIC contains 2000 gates, and if an FPGA can fit 20 copies of the ASIC, with no routing between the copies, then the maximum gate count of the FPGA can be considered as 40,000.](https://image.slidesharecdn.com/sdhdlece43-m5-200302071342/75/System-design-using-HDL-Module-5-28-2048.jpg)

![07/03/2019 Aravinda K., Dept. of E&C, NHCE, Bengaluru 31 Synthesis of a ‘case’ statement module case_eg (a,b); input [1:0] a; output reg [1:0] b; always @(a) begin case (a) 0: b<=1; 1: b<=3; 2: b<=0; 3: b<=1; endcase end endmodule Synthesized circuit before optimization Logic optimization Synthesized circuit after optimization](https://image.slidesharecdn.com/sdhdlece43-m5-200302071342/75/System-design-using-HDL-Module-5-31-2048.jpg)
![07/03/2019 Aravinda K., Dept. of E&C, NHCE, Bengaluru 32 Unintentional latch creation Module latch_eg (a,b); input [1:0] a; output reg b; always @(a) begin case (a) 0: b<=1; 1: b<=0; 2: b<=1; endcase end endmodule Initial output of naïve synthesizer Optimized output of naïve synthesizer](https://image.slidesharecdn.com/sdhdlece43-m5-200302071342/75/System-design-using-HDL-Module-5-32-2048.jpg)
![07/03/2019 Aravinda K., Dept. of E&C, NHCE, Bengaluru 33 Output of optimizing synthesizer Output of naïve synthesizer Solution to eliminate latch Module latch_eg (a,b); input [1:0] a; output reg b; always @(a) begin case (a) 0: b<=1; 1: b<=0; 2: b<=1; 3: b<=0; endcase end endmodule](https://image.slidesharecdn.com/sdhdlece43-m5-200302071342/75/System-design-using-HDL-Module-5-33-2048.jpg)
![07/03/2019 Aravinda K., Dept. of E&C, NHCE, Bengaluru 34 Synthesis of ‘if’ statements if (A == 1’b1) begin nextstate <= 3; Z <= 1; end if (A == 1’b1) begin nextstate <= 3; Z <= 1; end else begin nextstate <= 2; Z <= 0; end Ambiguous code, that results in latch Unambiguous code module if_eg (A,B,C,D,E,Z); input A,B; input [2:0] C,D,E; output reg [2:0] Z; always @(A or B) begin if (A == 1’b1) Z <= C; else if (B == 1’b0) Z <= D; else Z <= E; end endmodule Synthesized output](https://image.slidesharecdn.com/sdhdlece43-m5-200302071342/75/System-design-using-HDL-Module-5-34-2048.jpg)
![07/03/2019 Aravinda K., Dept. of E&C, NHCE, Bengaluru 35 Synthesis of arithmetic components module ar_eg (clk,A,B,ge,acc,count); input clk; input [3:0] A,B; inout [3:0] acc,count; output ge; reg [3:0] acc_t, count_t; assign acc = acc_t; assign count = count_t; assign ge = (A >= B); always @(posedge clk) begin acc_t <= acc +B; count_t <= count + 1; end endmodule Synthesized output](https://image.slidesharecdn.com/sdhdlece43-m5-200302071342/75/System-design-using-HDL-Module-5-35-2048.jpg)
![07/03/2019 Aravinda K., Dept. of E&C, NHCE, Bengaluru 36 Example-7: What hardware gets resulted for the statement, assign LE = (A <= B); where A and B are 4-bit vectors? The symbol “<=” is a relational operator over here. The following statement inside the ‘always’ block, LE <= (A <= B); results in the same hardware. Example-8: What is the optimized hardware for, assign EQ3 = (A == 3); where A is 4-bit vector? A naïve synthesizer may produce a 4-bit comparator, with ‘A’ and ‘3’ as inputs. For optimization, the statement can be altered as: assign EQ3 = ~A[3]&~A[2]&A[1]&A[0];](https://image.slidesharecdn.com/sdhdlece43-m5-200302071342/75/System-design-using-HDL-Module-5-36-2048.jpg)

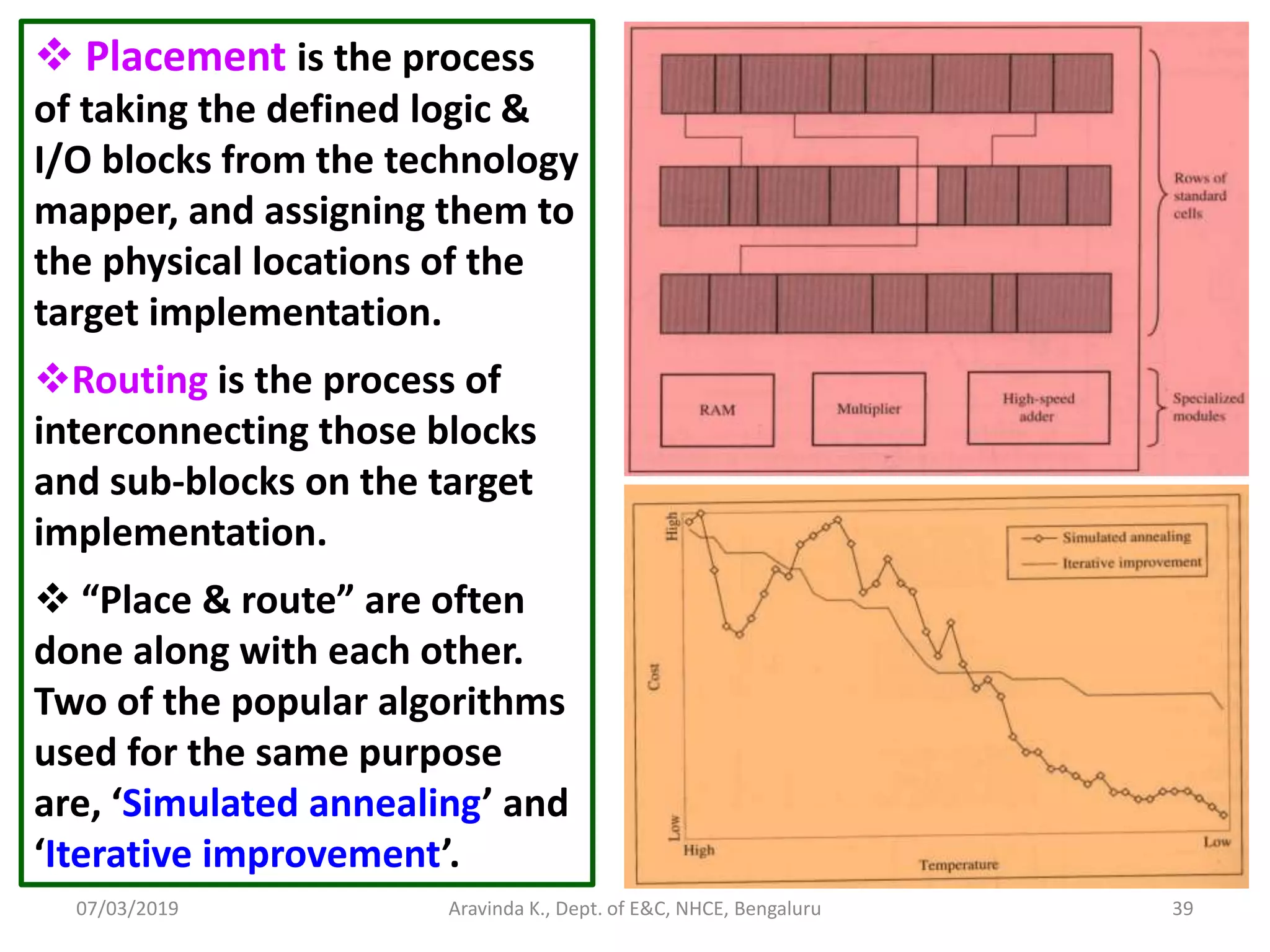
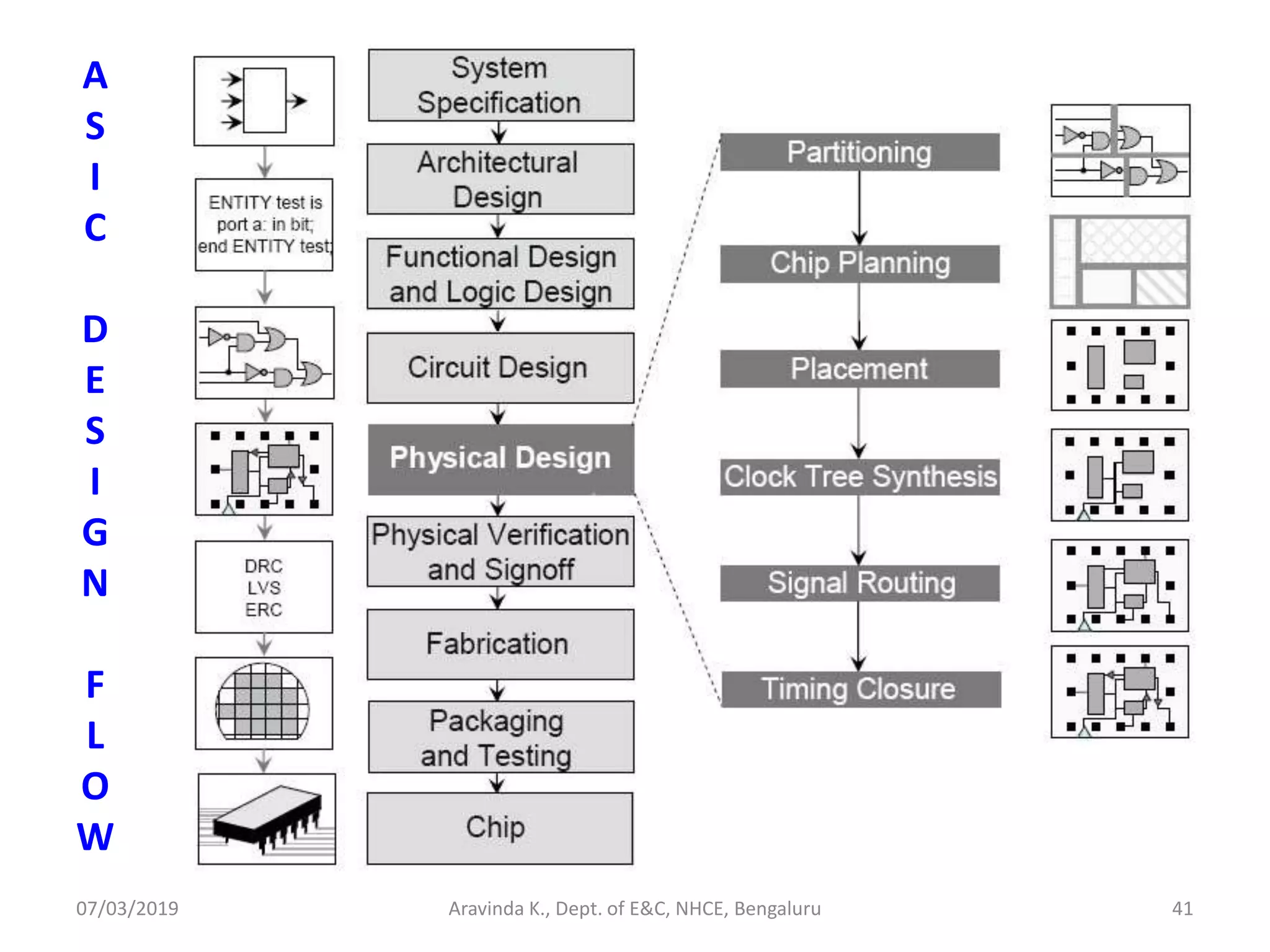
![07/03/2019 Aravinda K., Dept. of E&C, NHCE, Bengaluru 38 MAPPING, PLACEMENT AND ROUTING These are the 3 major steps that happen, to transform the design that is in the netlist form, to the appropriate target technology (MPGA, CPLD, FPGA, ASIC). Mapping is the process of translating the design into the available building blocks in the target technology. [e.g.: LUT with mux (Xilinx), Mux with gates (Microsemi)]. In other words, it is the process of binding the technology- dependent circuits of the target technology to the technology- independent circuits that are in the design. In case of FPGA, the design has to be mapped into muxes, LUTs etc. In case of ASIC, the design has to be mapped into the standard cells that are available in the library (e.g.: logic gates, muxes, decoders, encoders, comparators, counters etc.)](https://image.slidesharecdn.com/sdhdlece43-m5-200302071342/75/System-design-using-HDL-Module-5-38-2048.jpg)