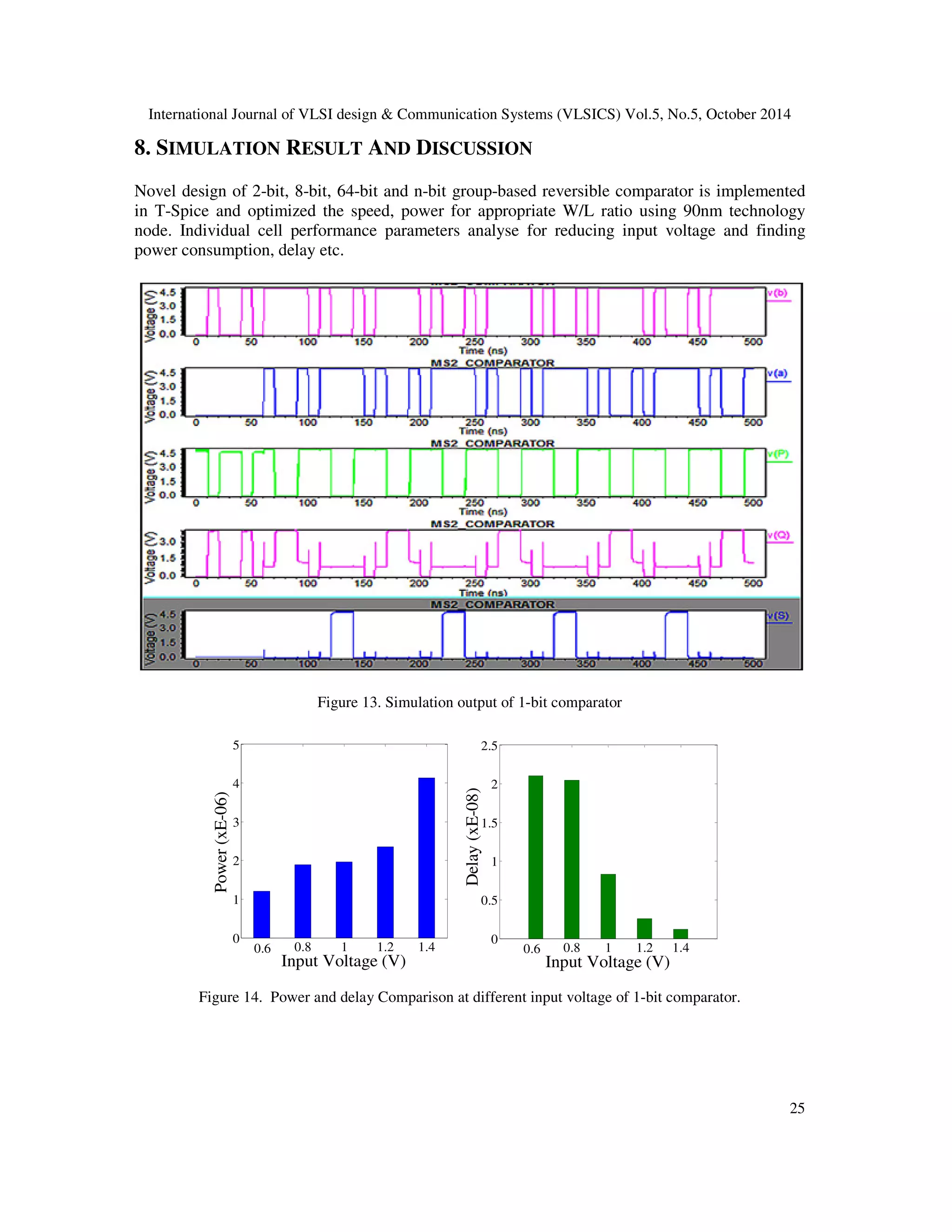
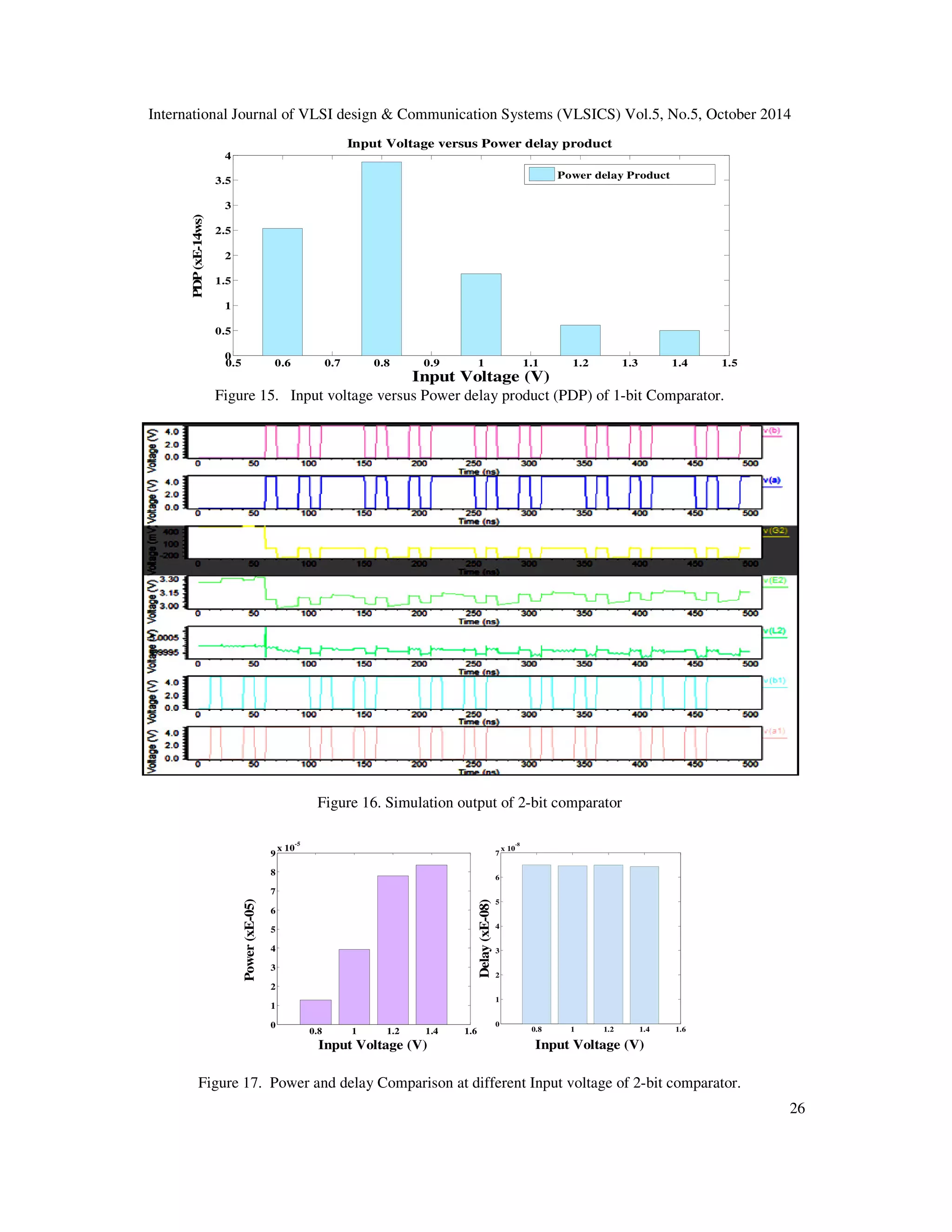
The document presents a novel 4x4 reversible gate called the inventive gate, which is used to construct various group-based reversible comparators and an n-to-2n decoder, emphasizing low power consumption in VLSI systems. The paper details the implementation, design parameters, and benefits of the inventive gate, demonstrating its versatility in logical operations and efficiency compared to existing designs. Additionally, it discusses potential applications and setups for n-bit reversible comparators in digital circuit design.
![International Journal of VLSI design & Communication Systems (VLSICS) Vol.5, No.5, October 2014 EVOLUTION OF STRUCTURE OF SOME BINARY GROUP-BASED N-BIT COMPARATOR, N-TO-2N DECODER BY REVERSIBLE TECHNIQUE Neeraj Kumar Misra1, Subodh Wairya2 and Vinod Kumar Singh3 Department of Electronics Engineering, Institute of Engineering and Technology, Lucknow, India ABSTRACT Reversible logic has attracted substantial interest due to its low power consumption which is the main concern of low power VLSI systems. In this paper, a novel 4x4 reversible gate called inventive gate has been introduced and using this gate 1-bit, 2-bit, 8-bit, 32-bit and n-bit group-based reversible comparator have been constructed with low value of reversible parameters. The MOS transistor realizations of 1-bit, 2- bit, and 8-bit of reversible comparator are also presented and finding power, delay and power delay product (PDP) with appropriate aspect ratio W/L. Novel inventive gate has the ability to use as an n-to-2n decoder. Different novel reversible circuit design style is compared with the existing ones. The relative results shows that the novel reversible gate wide utility, group-based reversible comparator outperforms the present style in terms of number of gates, garbage outputs and constant input. KEYWORDS Reversible Logic, Inventive Gate, Garbage Output, Constant input, Full subtractor, n-bit reversible comparator, Reversible decoder etc. 1. INTRODUCTION In low power VLSI systems planning of power is one of important aspects. According to Landauer [1] in 1960 demonstrate that single bit of information loss generate at least KT ln2 J/K of energy where K is the Boltzmann constant (1.38x10-23 J/K) and T is the absolute temperature. Reversible circuits are totally different from irreversible circuits. In reversible logic no bits is loss the circuit that doesn't loss information is reversible. C.H Bennet [2] in 1973 proves that KT ln2 joule of energy wouldn't be dissipated if the reversible circuit consist of reversible gates only. Thus reversible logic operations do not loss information and dissipate less heat also as power. Thus reversible logic is probably going to be in demand in high speed power aware circuits. A reversible circuit planning has following important attributes Garbage output, number of reversible gates, constant input all should be minimum for efficient reversible circuits. Comparator has wide applications in Analog and digital circuits, Analog to digital (A/D) converters, Level shifter, and communication system etc. It compares the 2-number of several DOI : 10.5121/vlsic.2014.5502 9](https://image.slidesharecdn.com/5514vlsi02-141111011632-conversion-gate02/75/Evolution-of-Structure-of-Some-Binary-Group-Based-N-Bit-Compartor-N-To-2N-Decoder-by-Reversible-Technique-1-2048.jpg)
![International Journal of VLSI design & Communication Systems (VLSICS) Vol.5, No.5, October 2014 bits. In this paper introduce group-based n-bit reversible comparator [6,9,11] and n-to-2n reversible decoder with low value of reversible parameters with the help of lemmas. This paper is organised with the following sections: Section 2 and 3 discuss basic definition of reversible logic and parameter optimization taken; Section 4 discuss the past work; Section 5 discuss the utility and design issue of novel 4x4 inventive gate; Section 6 Planning of low value style reversible comparator subsection of 6.1 introduce novel 1-bit comparator cell, subsection 6.2 and 6.3 is novel match, larger and smaller comparator cell design; Subsection 6.4, 6.5, 6.6. 6.7 for 2-bit, 8-bit, 32-bit and n- bit group-based reversible comparator design respectively; Section 7 Implement all comparator cell in MOS transistor with minimum MOS transistor count. Section 8 categories as simulation result of comparator. Finally, the paper is concluded and future work with Section 9. 10 2. BASIC DEFINITIONS OF REVERSIBLE LOGIC In this section, we introduce the essential definitions of reversible logic which are relevant with this research work. Definition 2.1 A reversible gate is a Z - input and Z - output that generate a unique output pattern for each possible input pattern. Definition 2.2 In Reversible logic output and input is equal in number. Unwanted output is called garbage output it should be minimum as possible and fan-out is not allowed. 3. PARAMETER OPTIMIZED FOR DESIGNING EFFICIENT REVERSIBLE CIRCUITS The main challenge of designing efficient reversible circuits is to optimize the different reversible parameters which result the circuit design is costly. The most necessary parameters which have dominant in efficient reversible logic circuits are: 3.1 Garbage output Unutilized or unwanted output of reversible circuit is called garbage output. It should be kept minimum as possible. 3.2 Constant Input Constant bits are additional inputs that are not part of the original specification. These bits are added in hopes to reduce the circuit complexity or realize a reversible function. They come in the form of a constant logic 1 or 0. It is ideal to keep in minimal. 3.3 Few Reversible gates utilized In this subsection, we present few reversible gates that are used to design for planning different types of reversible circuit. First TR (3×3) utilize input (A, B, C) and carry output (P=A, Q=A⊗B, R=AB’⊗C, Second BME gate(4X4) utilize input (A, B, C, D) and carry output (P=A,](https://image.slidesharecdn.com/5514vlsi02-141111011632-conversion-gate02/75/Evolution-of-Structure-of-Some-Binary-Group-Based-N-Bit-Compartor-N-To-2N-Decoder-by-Reversible-Technique-2-2048.jpg)
![International Journal of VLSI design & Communication Systems (VLSICS) Vol.5, No.5, October 2014 Q=AB⊗C, R=AD⊗C) and S=A’B⊗C⊗D, Third Feynman gate (FG) 2x2 utilize input (A, B ) and carry output (P=A, Q=A⊗B), Fourth Peres gate (PG) 3x3 utilize input (A, B, C) and carry output (P=A, Q=A⊗B, R=AB⊗C) 11 3.4 Flexibility Flexibility refers to the universality of reversible logic gate in realizing more logical function. 4. PAST WORK In 2010, Himanshu thapliyal et.al [17] design a reversible 8-bit and 64-bit tree-based comparator using TR Gate that has the latency of O(log2(n)).But this approach is not suitable for low value of reversible parameter and not extended for n-bit reversible comparator. Furthermore another comparator design by Rangaraju H Ga [7, 8] in 2011 has shows that design has input circuit as first stage and 1-Bit comparator cell as second stage and so on. This idea is extend for n-bit reversible comparator design but it is not sufficient to optimizing the reversible parameter. In 2011, Nagamani et.al. [21] Design a reversible 1-bit reversible comparator with low value of reversible parameter but this idea is not extended for n-bit comparator. In 2013, Ri-gui Zhou et.al. [5] design a novel 4-bit reversible comparator. It is mentioned in paper further possibilities of reducing the number of reversible gates, constant input and garbage output in the area of reversible comparator design. They proposed new gate and using this gate form various gate AND, OR, XNOR, NOT, FA, FS but not form gate NAND, NOR. For increasing order of comparator, gate increase in higher order and complexity of design increases and also garbage outputs means performance of comparator degrade. In 2013, Hafiz Md. Hasan babu et.al. [4] design compact n-bit reversible comparator. Its design is efficient because it reduce complexity of design. Approach is sufficient and proposed various theorem and lemma for calculating n-bit reversible parameter number of gate, total delay, power. They proposed two new gate BJS and HLN. These gate form OR, AND, XOR and NOT Operation but not form FA, FS, NAND and NOR Operation. For showing expertise of reversible gate we work on this and proposed Universal gate called Inventive Gate. It’s performing all logical operation NAND, NOR, AND, OR, HA, HS, FA and FS and also form efficient group-based n-bit reversible comparator and n-to-2n bit decoder with low value of reversible parameters. 5. UTILITY AND DESIGN ISSUES OF FRESHLY PROJECTED 4X4 INVENTIVE GATE In this section, a new 4 x 4 reversible gates called Inventive gate, is proposed. The block representation of inventive gate is shown in Figure 1.The corresponding truth table shown in Table 1. And subsequent four logical configuration is presented P=(a⊗b⊗c), Q=[(a⊗b)⊗d]c+b(a⊗d), R=(c'b'+d)a'+bc and S=b’d’(a+c)+d(b+a’c’) of inventive gate. It is shown from the truth table that the attainable output pattern can be uniquely determined.](https://image.slidesharecdn.com/5514vlsi02-141111011632-conversion-gate02/75/Evolution-of-Structure-of-Some-Binary-Group-Based-N-Bit-Compartor-N-To-2N-Decoder-by-Reversible-Technique-3-2048.jpg)

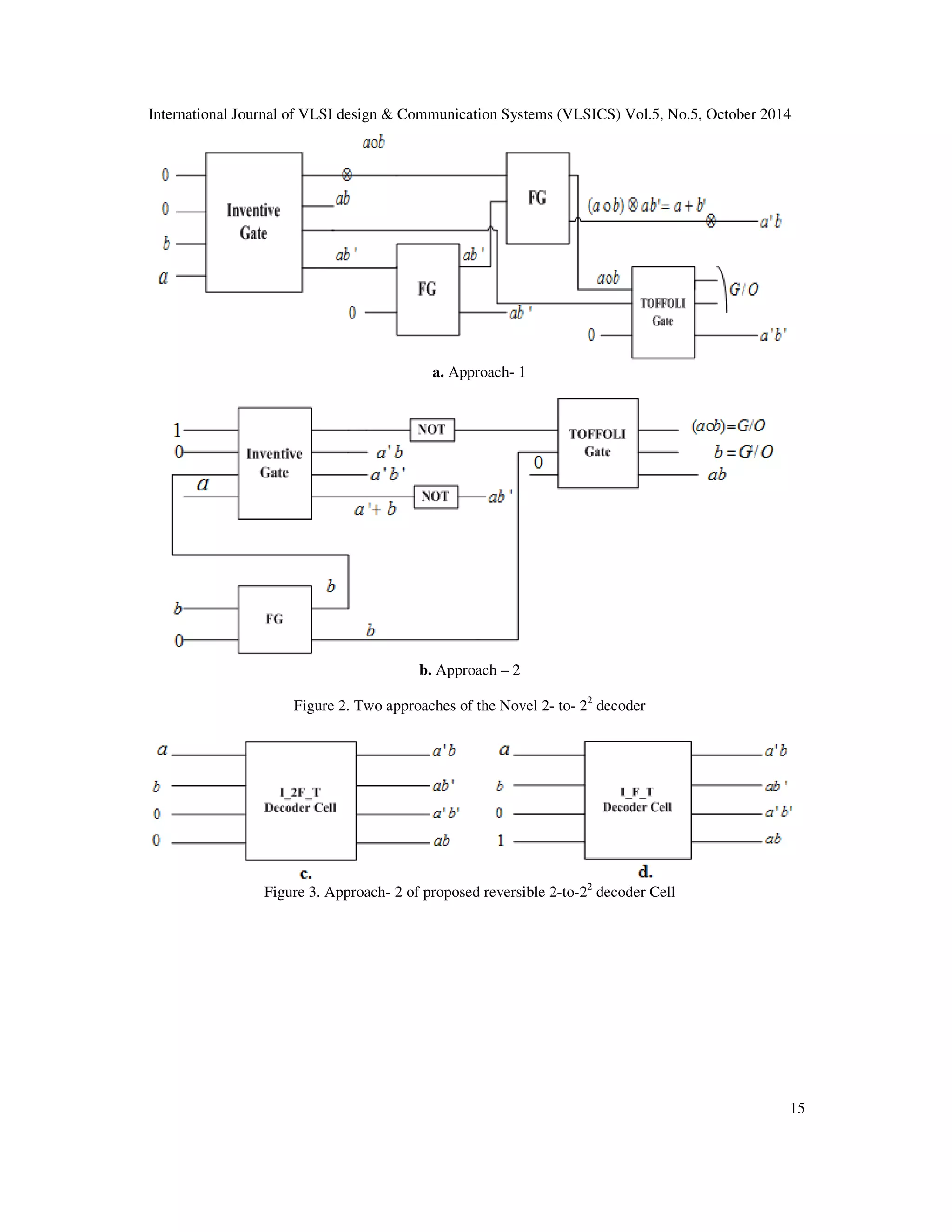
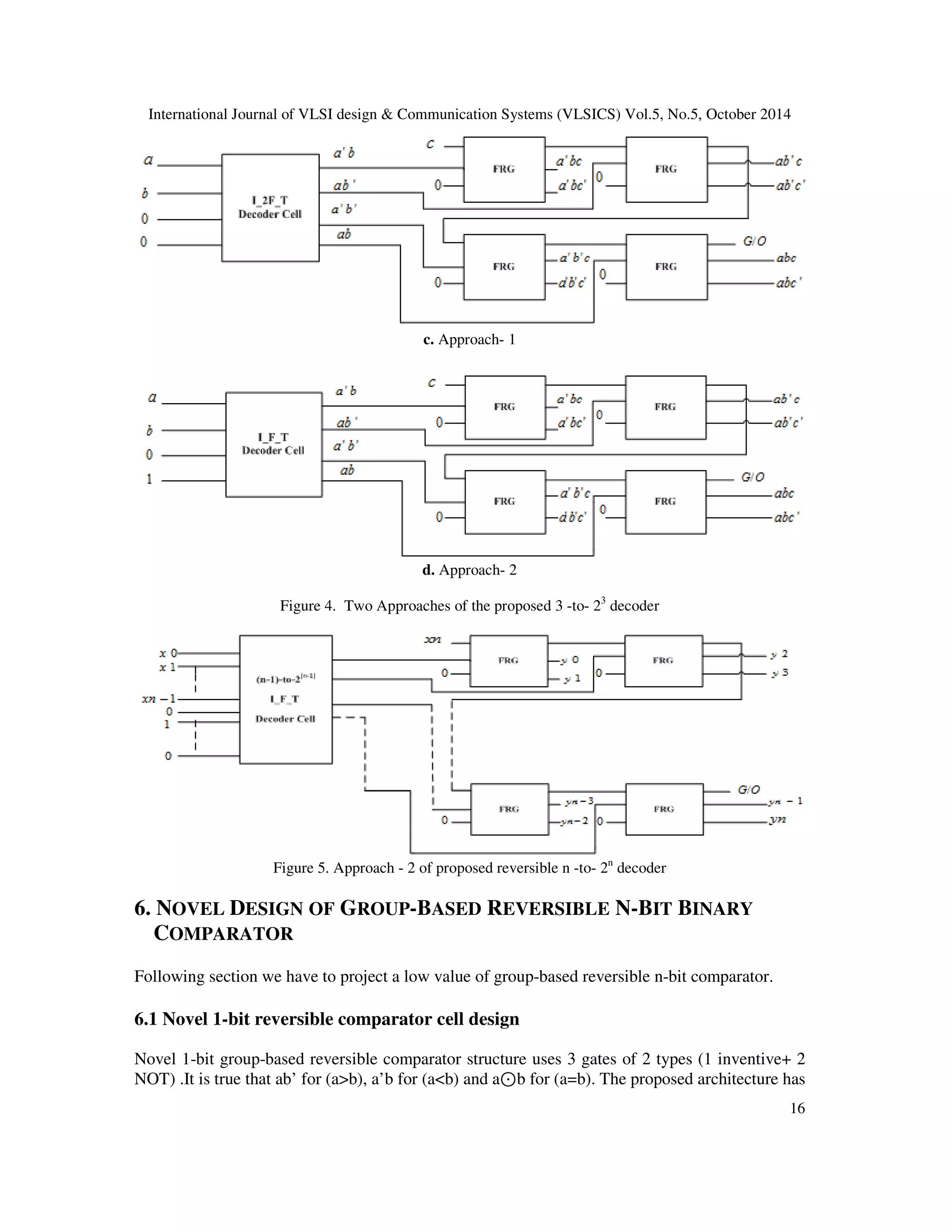
![International Journal of VLSI design & Communication Systems (VLSICS) Vol.5, No.5, October 2014 13 Fig c. NOR gate Implementation Fig d. XNOR, AND gates Implementation Fig e. Half adder Implementation Fig f. Half substractor Implementation Fig g. Full adder Implementation Fig h. Full substractor Implementation 5.2. Utility-2 of Reversible inventive gate as Reversible n-to-2n decoder In this section we show the utility-2 of Inventive gate. It performs the operation of Reversible 2- to-22 decoder it consists of two approaches named approach - 1 and approach - 2. Approach- 1 of 2-to-22 decoder generate 2 garbage output and number of gate count is 5. Whereas the Approach - 2 generate 2 garbage output but reduces number of gate count is 4 as shown in Figure 2 (b). And also implement of 3-to-23 decoder (Approach 2) generate 3 garbage output and number of gate count 7 as shown in Figure 4 .Decoder [3,11,14] are widely used in applications like information multiplexing, 7 segment show and memory addressing. 5.2.1 Reversible 2-to-22 decoder and 3-to-23 decoder Planning of Reversible 2-to-22 decoder is shown in Figure 2(b). It consists of (1 inventive gate+ 2NOT+ 1 FG+ 1TG) types of gates. It has two input marked a, b apply to inventive gate and Feynman gate (FG) respectively obtained output is passed to TG and gives output is (ab) other output of decoder is (a' b), (a b') and (a' b'). Completed cell of 2-to-22 decoder are named as I_F_T decoder cell. These cell are utilize for designing 3-to-23 decoder as shown in Figure 4. Lemma 5.2.1.1 An n-to-2n reversible decoder (Approach 1) may be accomplished by a minimum of 2n + 2 reversible gates, where n is that the range of bits and n 2 Proof. We ensure the above statement by mathematical induction.](https://image.slidesharecdn.com/5514vlsi02-141111011632-conversion-gate02/75/Evolution-of-Structure-of-Some-Binary-Group-Based-N-Bit-Compartor-N-To-2N-Decoder-by-Reversible-Technique-5-2048.jpg)


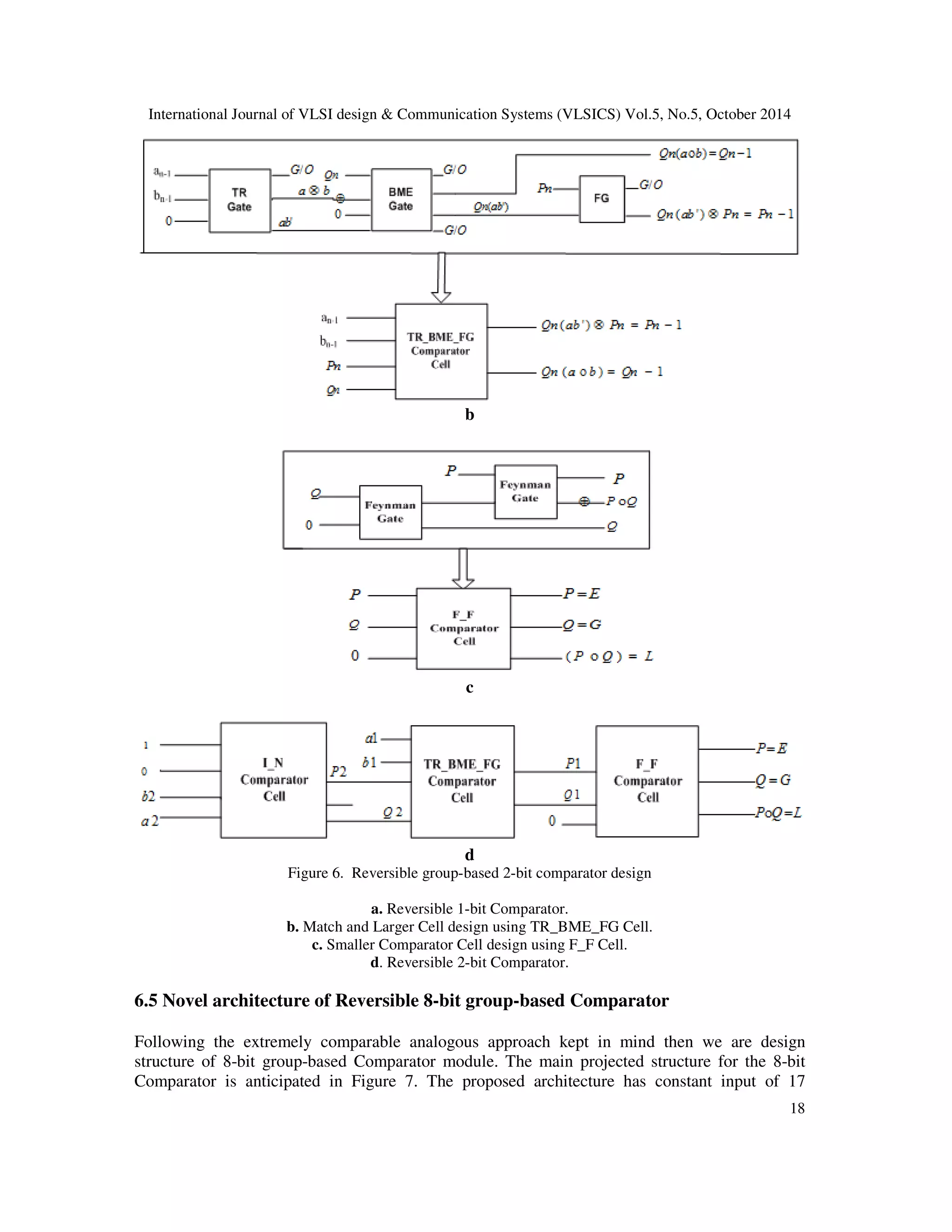




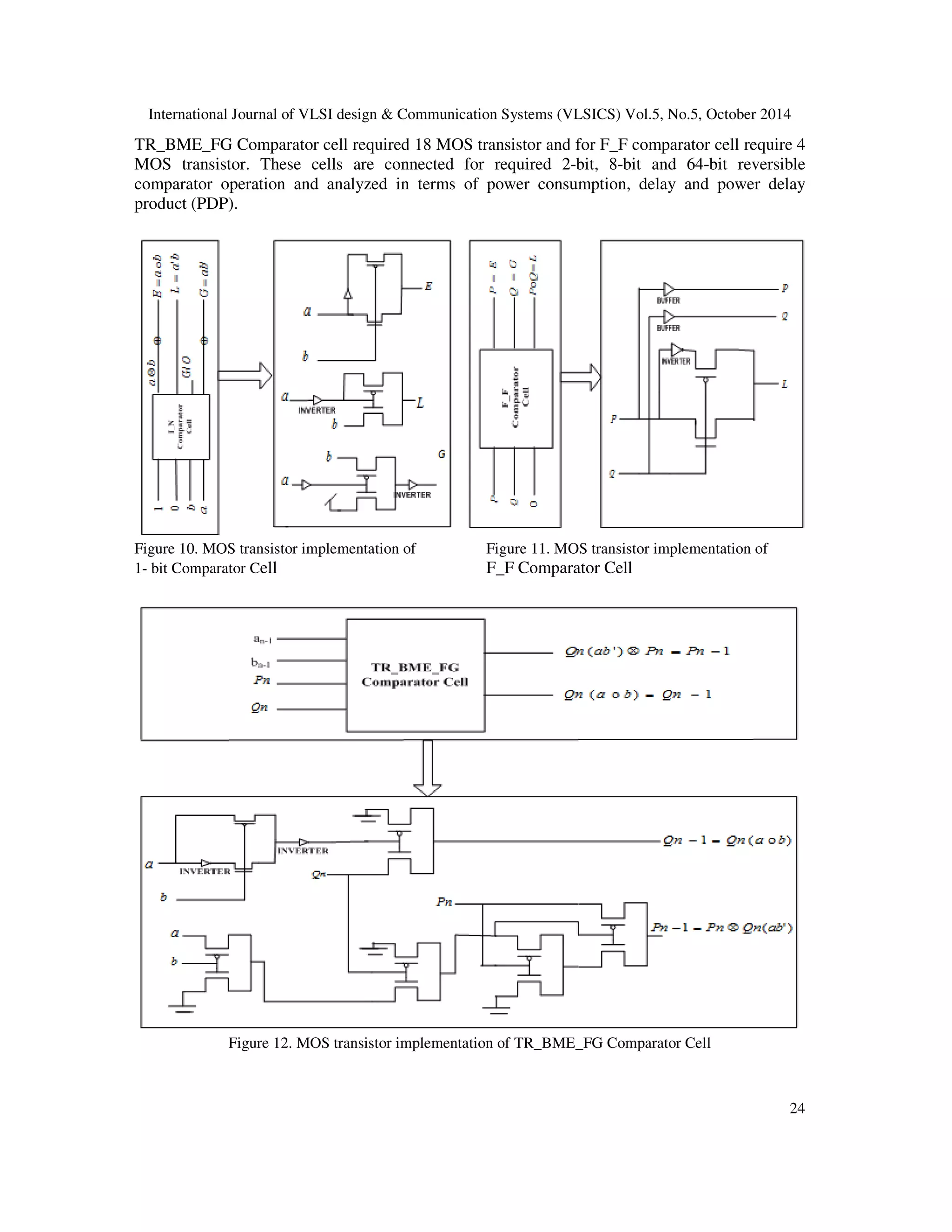
![International Journal of VLSI design Communication Systems (VLSICS) Vol.5, No.5, October 2014 Algorithm- 2 Reversible group-based n-bit comparator *Design a n-bit reversible binary comparator when (n 2) with minimum number of gates and Else Yn[1] = Pyn = 1 End if Step 2. For TR_BME_FG and F_F Comparator cell, Level of input and output are considered 23 garbage output. Begin Step 1. Pick up I_N comparator cell and pick input Xn and output Yn for two n-bit number Xn[1] = an //nth input of an Xn[2] = bn //nth input of bn Xn[3] = 0 Xn[4] = 1 If Xn[1] Xn[2] then Yn[2] = Ryn=1 Else if Xn[1] Xn[2] then Yn[4] = Qyn=1 to be Yn and Yn-1 respectively Loop For j = n - 1 to 1 Pick up TR_BME_FG Comparator cell WJ If j = n-1 then WJ[1] = Xn[4] = QYn WJ[2] = Xn[1] = PYn WJ[3] = bn-1 WJ[4] = an-1 Else WJ[1] = WJ-1[2] = QYn-1 WJ[2] = WJ-1[1] = PYn-1 WJ[3] = aj //(n-1)th input of an WJ[4] = bj //(n-1)th input of bn End if End loop Step 3. Pick up F_F Comparator cell and pick input V and output Z V[1]= W[1] V[2] = W[2] V[3] = 0 Z[1] = W[1] Z[2] = [W[1]⊗ W[2]]⊗ 1 Z[3] = W[2] End 7. MOS TRANSISTOR IMPLEMENTATION OF DIFFERENT COMPARATOR CELL In this section implement different comparator cell in MOS transistor with minimum MOS transistor count. MOS transistor implementations of 2-bit comparator uses 14 MOS transistors,](https://image.slidesharecdn.com/5514vlsi02-141111011632-conversion-gate02/75/Evolution-of-Structure-of-Some-Binary-Group-Based-N-Bit-Compartor-N-To-2N-Decoder-by-Reversible-Technique-15-2048.jpg)
![International Journal of VLSI design Communication Systems (VLSICS) Vol.5, No.5, October 2014 10 8 6 4 2 Maximum Power and Delay Variation(s) versus Channel Length Variation(u) Maximum Power variation (xE-05) Maximum Delay variation (xE-08) 1 2 4 6 8 27 1 0.8 0.6 0.4 0.2 0 x 10 -12 0.7 0.8 0.9 1 1.1 1.2 1.3 1.4 1.5 Input Voltage (V) PDP (xE-13) Figure 18. Input voltage versus Power delay product (PDP) of 2-bit Comparator. Channel Length Variation (nm) Figure 19. Channel Length Variation versus power and delay of 2-bit Comparator Table 2. Comparison between anticipated and existing in terms of expertise of reversible gate RGate Gate can be used as n-bit comparator Single Gate can be used as Full subtractor Gate can be used as n-to-2n decoder Anticipated Inventive Gate Y Y Y Available Circuit [4] Y N N Available Circuit [3] N N Y Available Circuit [12] N N N Available Circuit [13] N N N Available Circuit [15] N N N Available Circuit [6] Y N N Available Circuit [5] Y Y N](https://image.slidesharecdn.com/5514vlsi02-141111011632-conversion-gate02/75/Evolution-of-Structure-of-Some-Binary-Group-Based-N-Bit-Compartor-N-To-2N-Decoder-by-Reversible-Technique-19-2048.jpg)
![International Journal of VLSI design Communication Systems (VLSICS) Vol.5, No.5, October 2014 Table 3. Comparison between anticipated and existing style comparator in terms of NOG, GO, CI, power 28 and delay Methods NOG GO CI Power (μW) Delay (ns) Anticipated work 6+4(n-1) 1+4(n-1) 1+2n NOG-number of gate, GO-Garbage output, CI-Constant input Table 4 Comparison between anticipated and existing style Comparator in terms of garbage output and constant input (85.81n – 78.98) (115.010n – 100.854) Thaplial et al. [17] 9n (6n −6) -- (268.23n −239.2) {0.23 x log2(n) + 0.1} Vudadha et al. [18] (4n −2) (5n −4) -- (122.36n −60.36) {0.09*log2(n) + 0.2} Rangaraju et al. [7 ] (7n −4) (5n −4) -- (182.53n +76.55) (0.2n − 0.16) Hafiz Md. Hasan Babu [ 4] 3n (4n-3) 3 (117.76n −32.94) (0.15n − 0.03)](https://image.slidesharecdn.com/5514vlsi02-141111011632-conversion-gate02/75/Evolution-of-Structure-of-Some-Binary-Group-Based-N-Bit-Compartor-N-To-2N-Decoder-by-Reversible-Technique-20-2048.jpg)
![International Journal of VLSI design Communication Systems (VLSICS) Vol.5, No.5, October 2014 29 9. CONCLUSION AND FUTURE WORK This paper is mainly focused on novel design of the reversible 4x4 inventive Gate. It utilized as 1-bit, 2-bit, 8-bit, 32-bit and n-bit group-based binary comparator and n-to-2n decoder. Moreover, the low value styles of reversible parameter have been established for the proposed circuits. For example, and n-to-2n decoder uses at least 2n + 1 reversible gates and its n garbage output: an n-bit comparator utilize 6+4 (n - 1) number of reversible gate, 1+4 (n-1) garbage output. The proposed group- based comparator achieves the improvement of 19.87% in terms of garbage output and 31.57% in terms of constant input over the existing one [7]. Simulation of the novel comparator circuits have shown that it works correctly and finding parameter power and delay. The proposed circuits will be useful for implementing the ALU and control unit of processor. ACKNOWLEDGMENT Authors would like to acknowledge Research Cum Teaching Fellowship through TEQIP-II provide by World Bank for the financial support for this work. REFERENCES [1] J R.Landauer, “Irreversibility and Heat Generation in the Computational Process”, IBM Journal of Research and Development, pp: 183-191, 1961. [2] C H Bennett, “Logical Reversibility of Computation,” IBM Journal of Research and Development, vol. 17, no. 6, pp. 525-532,November 1973. [3] Lafifa Jamal, Md. Masbaul Alam, Hafiz Md. Hasan Babu “An efficient approach to design a reversible control unit of a processor” Elsevier Sustainable Computing: Informatics and Systems pp: 286-294, 2013 [4] Hafiz Md. Hasan Babu, Nazir Saleheen, Lafifa Jamal, Sheikh Muhammad Sarwar,Tsutomu Sasao Approach to design a compact reversible low power binary comparator IET Computers Digital Techniques Vol. 8, Iss. 3, pp. 129–139 doi: 10.1049/iet-cdt.2013.0066, 2014 [5] Ri-gui Zhou, Man-qun Zhang, QianWu •Yan-cheng Li Optimization Approaches for Designing a Novel 4-Bit Reversible Comparator Springer International jounal of theoretical physics DOI 10.1007/s10773-012-1360-y pp:559-575, 2013 [6] Farah Sharmin, Rajib Kumar Mitra, Rashida Hasan, Anisur Rahman Low cost reversible signed comparator International Journal of VLSI design Communication Systems” Vol.4, No.5,pp:19- 33,2013 [7] Rangaraju H G, Vinayak Hegdeb, Raja K B, Muralidhara K N Design of Efficient Reversible Binary Comparator Elsevier International Conference on Communication Technology and System Design Procedia Engineering pp:897-904, 2012 [8] Rangaraju, H.G., Hegde, V., Raja, K.B., Muralidhara, K.N. “Design of low power reversible binary comparator”. Proc. Engineering (ScienceDirect), 2011 [9] Bahram Dehghan, Abdolreza Roozbeh, Jafar Zare Design of Low Power Comparator Using DG Gate Scientific research ciruits and systems doi.org/10.4236/cs.2013.51002pp: 7-12, 2014 [10] Pallavi Mall , A.G.Rao, H.P.Shukla Novel Design of Four-Bit Reversible Numerical Comparator International Journal of Advanced Research in Computer and Communication Engineering Vol. 2, Issue 4 pp:1808-1807, 2013 [11] Neeta Pandey, Nalin Dadhich, Mohd. Zubair Talha Realization of 2-to-4 reversible decoder and its applications International Conference on Signal Processing and Integrated Networks (SPIN) pp:349- 353,2014 [12] Md. M. H Azad Khan, “Design of Full-adder With Reversible Gates”,International Conference on Computer and Information Technology,Dhaka, Bangladesh, 2002, pp. 515-519](https://image.slidesharecdn.com/5514vlsi02-141111011632-conversion-gate02/75/Evolution-of-Structure-of-Some-Binary-Group-Based-N-Bit-Compartor-N-To-2N-Decoder-by-Reversible-Technique-21-2048.jpg)
![International Journal of VLSI design Communication Systems (VLSICS) Vol.5, No.5, October 2014 [13] Hafiz Md. Hasan Babu, Md. Rafiqul Islam, Syed Mostahed Ali Chowdhury and Ahsan Raja Chowdhury ,“Reversible Logic Synthesis for Minimization of Full Adder Circuit”, Proceedings of the EuroMicro Symposium on Digital System Design(DSD’03), 3-5 September 2003, 30 [14] Neeraj Kumar Misra, Subodh Wairya, Vinod Kumar Singh “Preternatural Low-Power Reversible Decoder Design in 90 nm Technology Node” International Journal of Scientific Engineering Research, Volume 5, Issue 6, pp: 969-978, June 2014 [15] J.W. Bruce, M.A. Thornton,L. Shivakumariah, P.S. Kokate and X.Li, Efficient Adder Circuits Based on a Conservative Logic Gate, Proceedings of the IEEE Computer Society Annual Symposium on VLSI(ISVLSI'02),April 2002, Pittsburgh, PA, USA, pp 83-88. [16] Lafifa Jamal, Md. Masbaul Alam Polash On the Compact Designs of Low Power Reversible Decoders and Sequential Circuits Springer LNCS7373, pp. 281–288, 2012. [17] Himanshu Thapliyal, Nagarajan Ranganathan and Ryan Ferreira Design of a Comparator Tree Based on Reversible Logic 10th IEEE International Conference on Nanotechnology Joint Symposium with Nano Korea pp:1113-1116, 2010 [18] Vudadha, C.Phaneendra, P.S.,Sreehari,V.Ahmed,S.E.Muthukrishnan, N.M.Srinivas “Design of prefix-based Optimal reversible comparator” IEEE Computer Society Annual Symp. On VLSI pp. 201–206 [19] Nagamani, A.N., Jayashree, H.V., Bhagyalakshmi, H.R.: ‘Novel low power comparator design using reversible logic gates’, Indian J. Comput. Sci. Eng.vol 2, (4), pp. 566–574, 2011 [20] Morrison, M., Lewandowski, M., Ranganathan “Design of a tree-based comparator and memory unit based on a novel reversible logic structure” IEEE Computer Society Annual Symp. on VLSI, pp. 331–336, 2012 [21] Neeraj Kumar Misra, Subodh Wairya, Vinod Kumar Singh “An Inventive Design of 4*4 Bit Reversible NS Gate” IEEE International Conference on Recent Advances and Innovation in Engineering (ICRAIE-2014), pp: 1-6, 2014 doi no. 10.1109/ICRAIE.2014.6909323](https://image.slidesharecdn.com/5514vlsi02-141111011632-conversion-gate02/75/Evolution-of-Structure-of-Some-Binary-Group-Based-N-Bit-Compartor-N-To-2N-Decoder-by-Reversible-Technique-22-2048.jpg)