Downloaded 2,600 times





















K-means clustering is an algorithm that groups data points into k number of clusters based on their similarity. It works by randomly selecting k data points as initial cluster centroids and then assigning each remaining point to the closest centroid. It then recalculates the centroids and reassigns points in an iterative process until centroids stabilize. While efficient, k-means clustering has weaknesses in that it requires specifying k, can get stuck in local optima, and is not suitable for non-convex shaped clusters or noisy data.
























Introduction of the K-means clustering algorithm presented by Kasun Ranga Wijeweera.
Clustering organizes data into classes with high intra-class and low inter-class similarities. It emphasizes subjective natural groupings, illustrated with examples.
Definition of distance measures to understand dissimilarity between objects in clustering.
Consideration of data points and clusters to illustrate the fundamental goal of clustering.
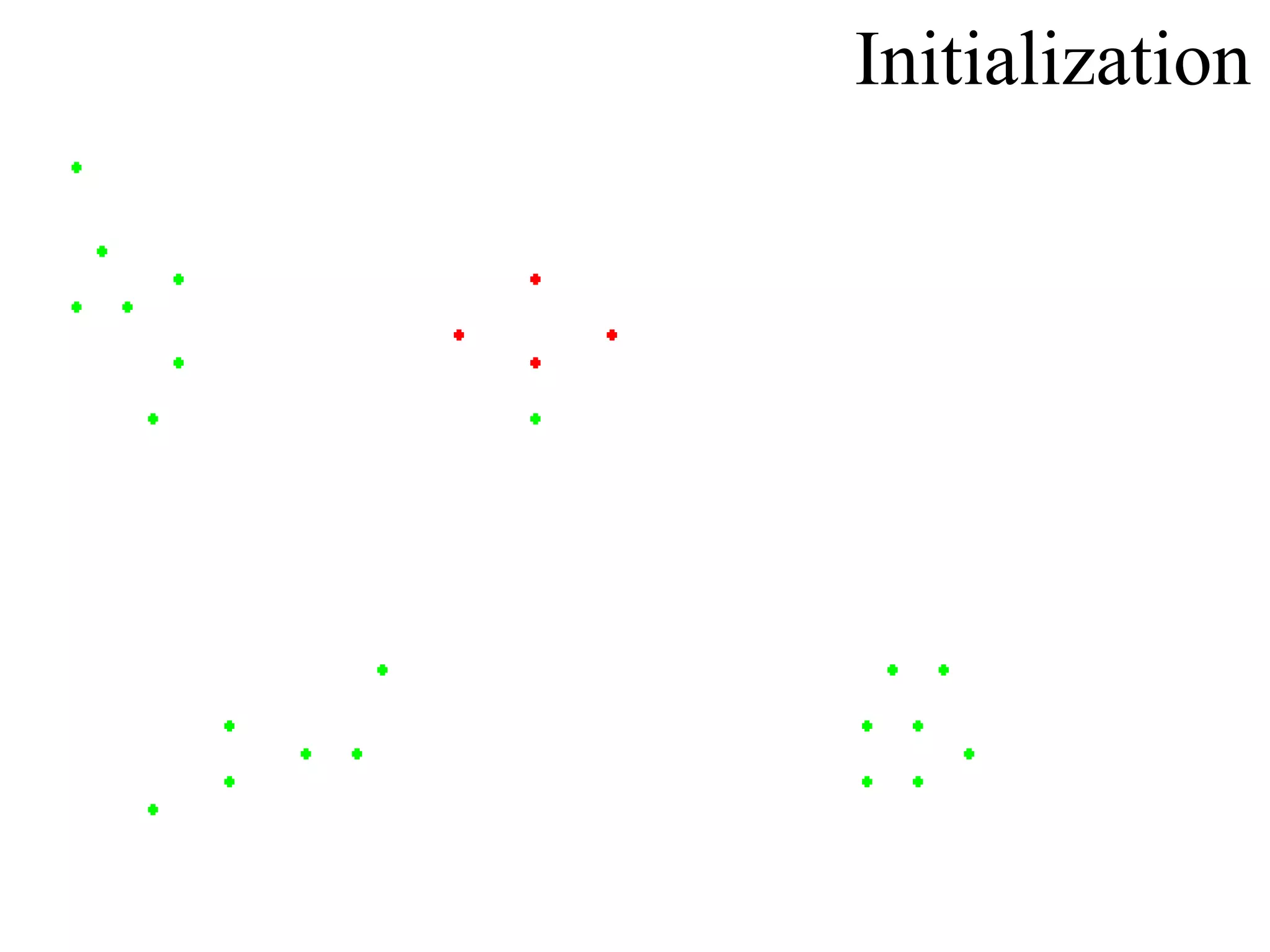
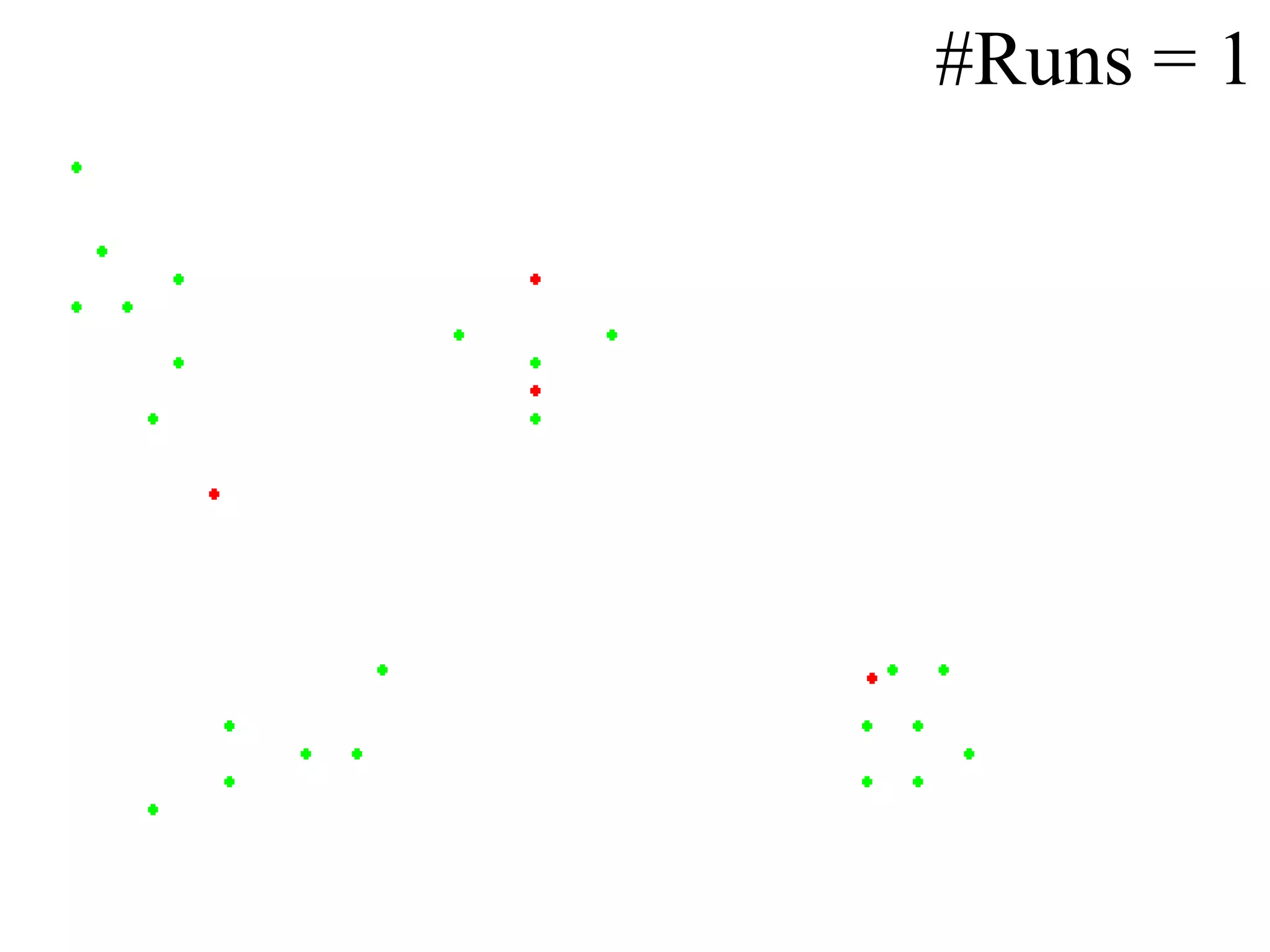
Details on the K-means algorithm including the steps to assign data points to clusters and calculate centroids until convergence.
Illustrations of the data points and multiple runs of the K-means process to display the algorithm's execution.
Applications of the K-means method including Optical Character Recognition, Biometrics, Diagnostic Systems, and Military Applications.
Strengths and weaknesses of K-means clustering, highlighting efficiency, local optimal issues, and limitations with specific data types.
Open floor for any questions related to the K-means clustering presentation.
Final thanks for the audience's attention during the presentation.