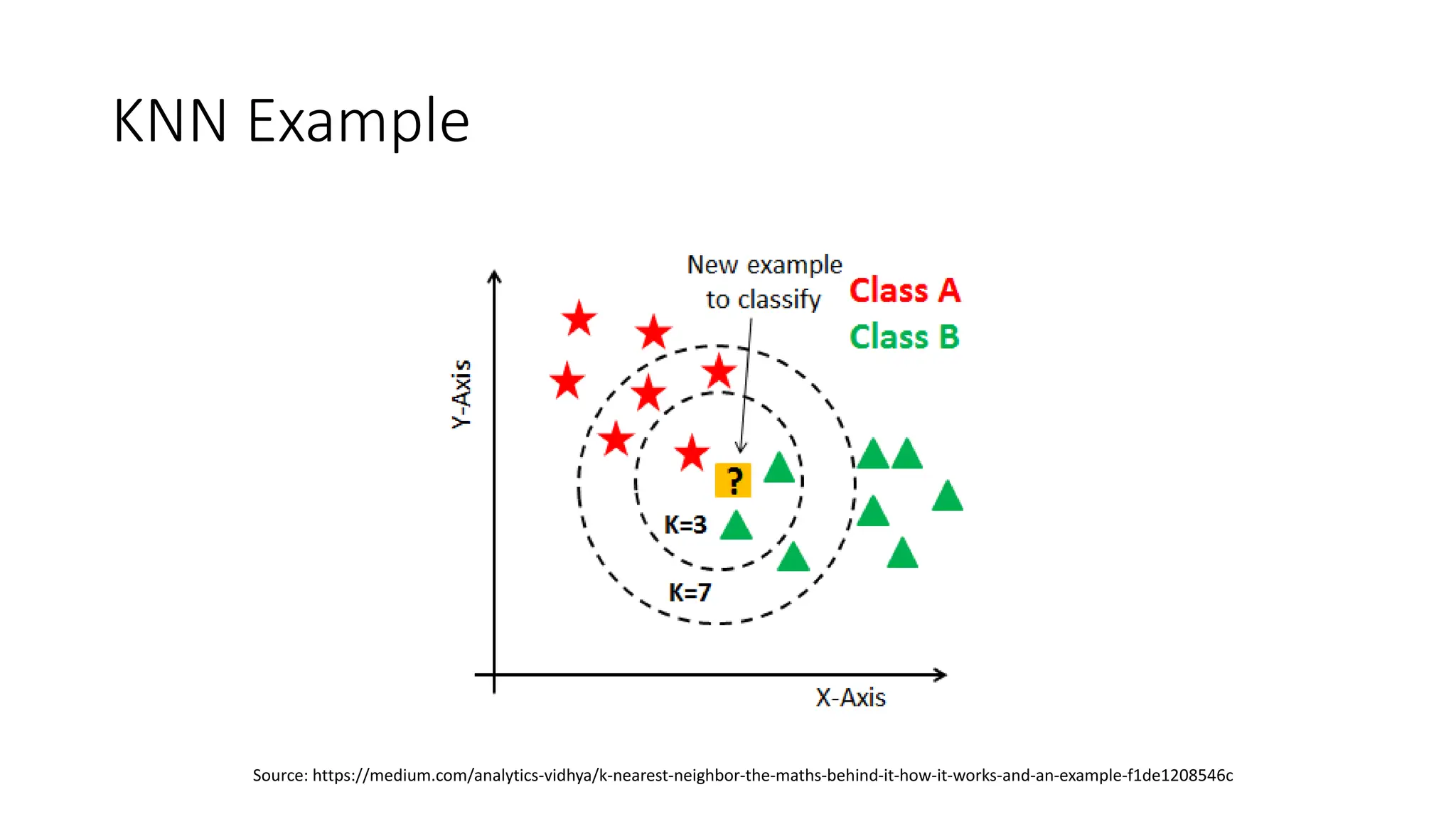
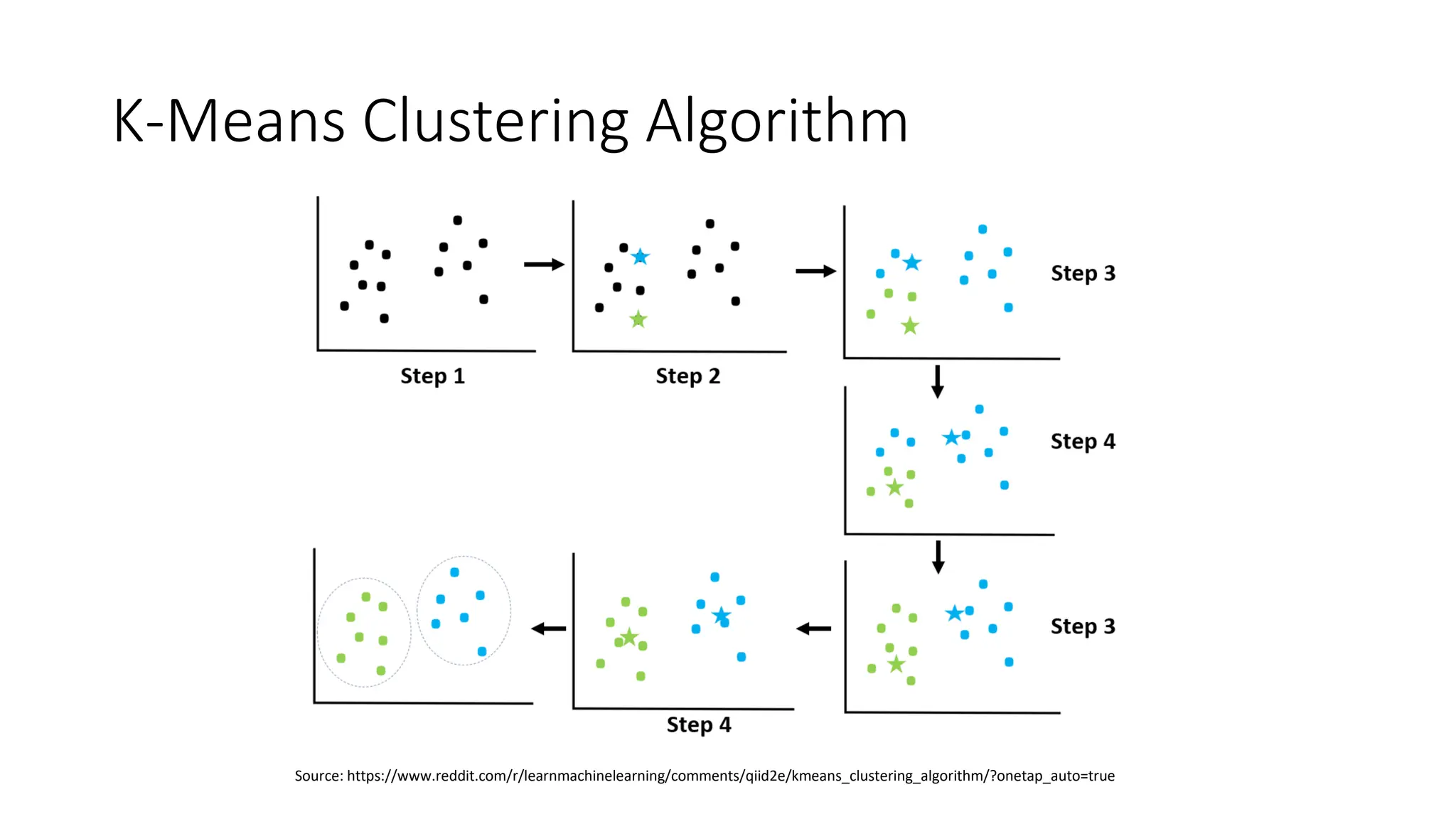
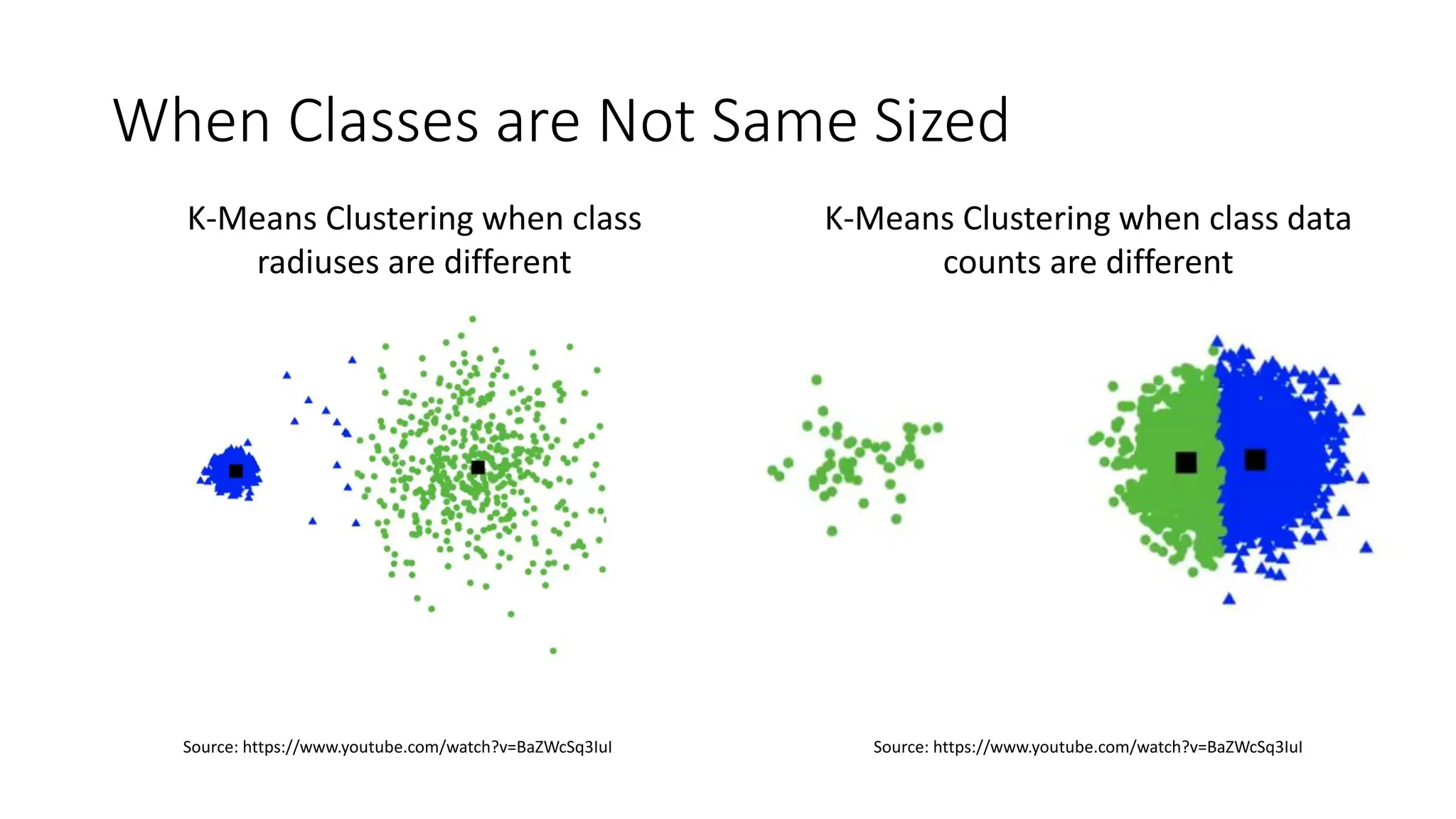
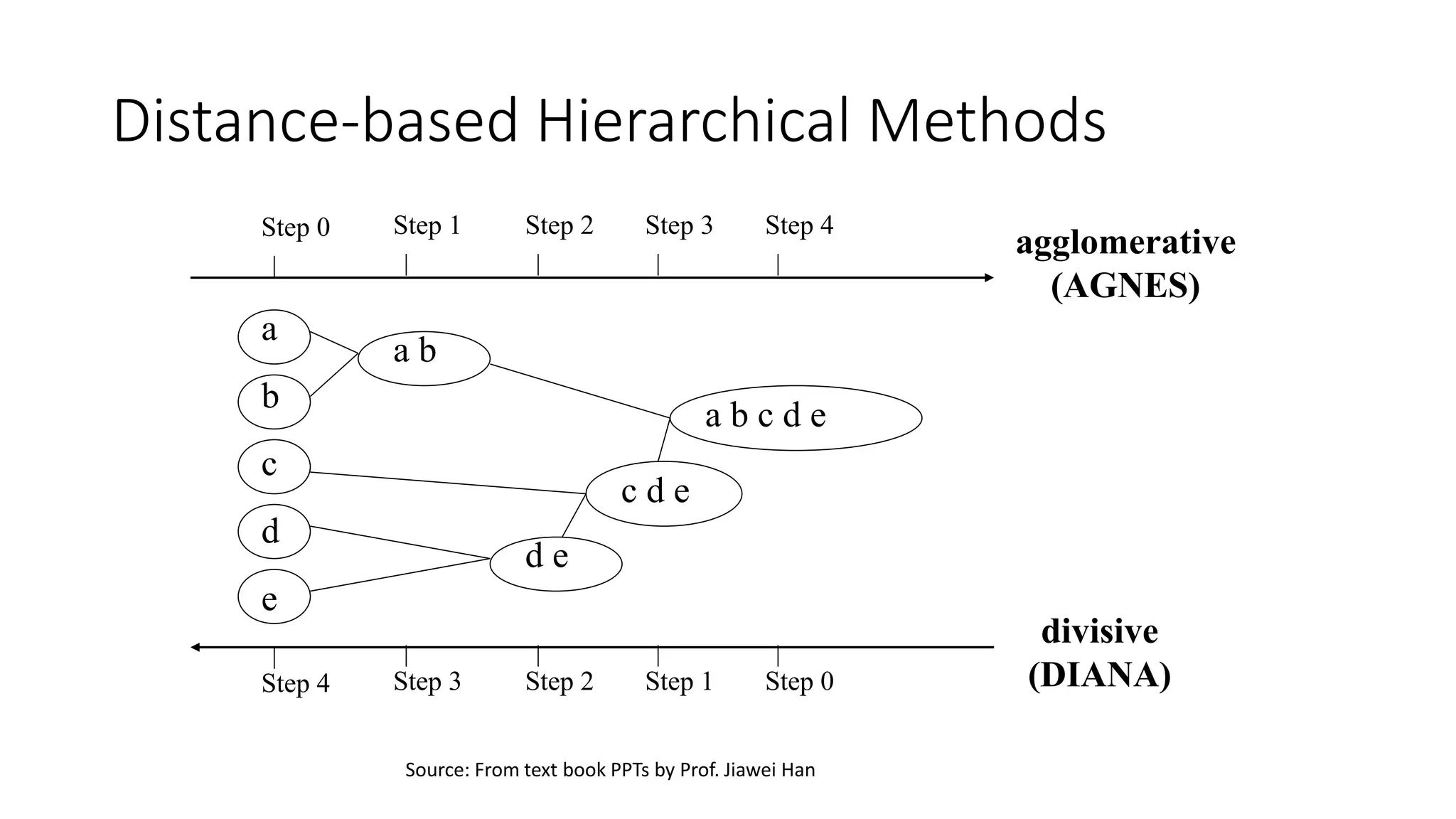
The document discusses key concepts in statistical and machine learning, focusing on the k-nearest neighbors (KNN) algorithm and clustering methods. It explains the Minkowski distance used for measuring distances between data points and describes KNN as a lazy algorithm for classification and regression. Additionally, it covers unsupervised learning, the types of clustering algorithms, their properties, limitations, and evaluation metrics for clustering quality.