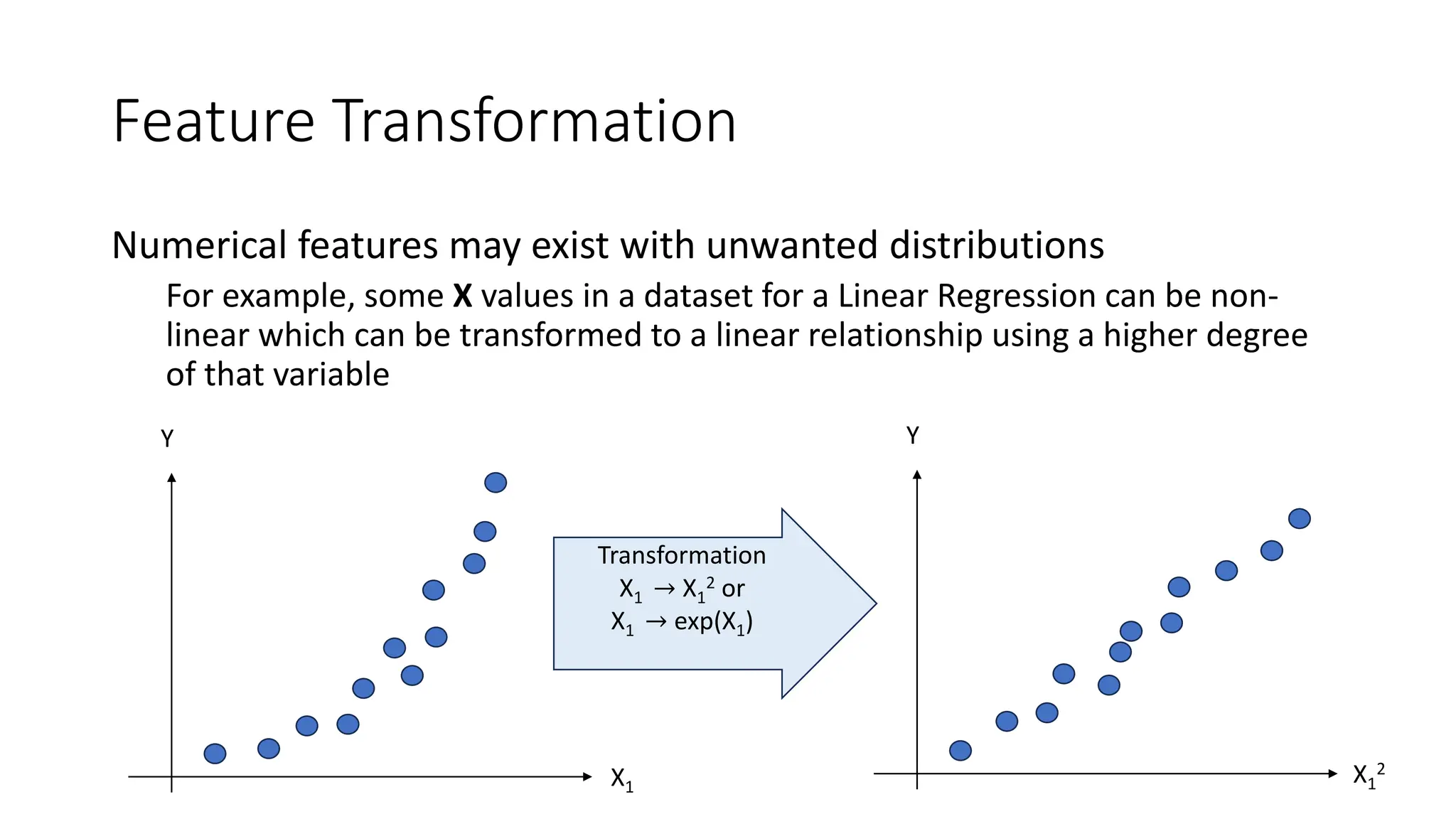
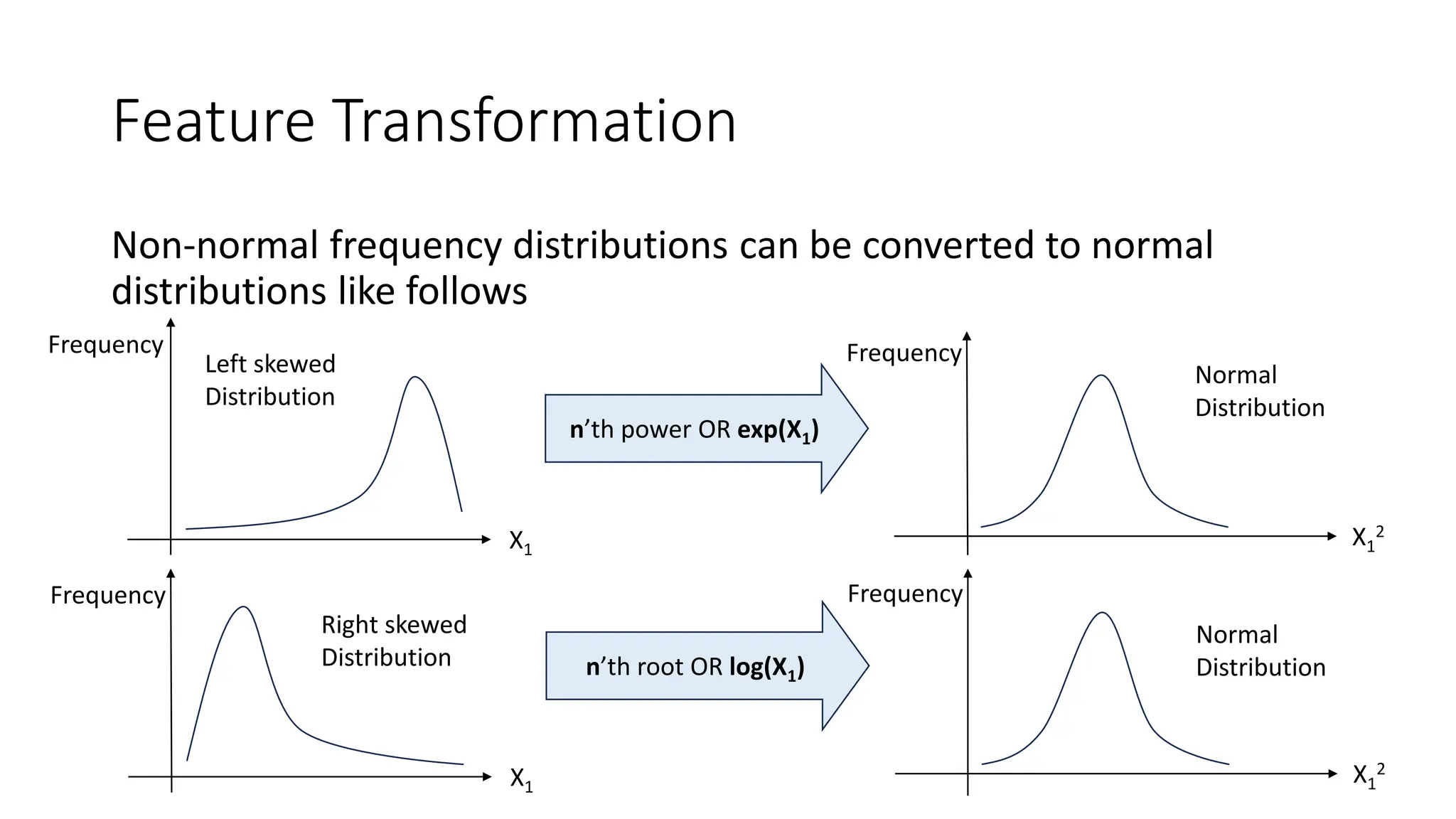
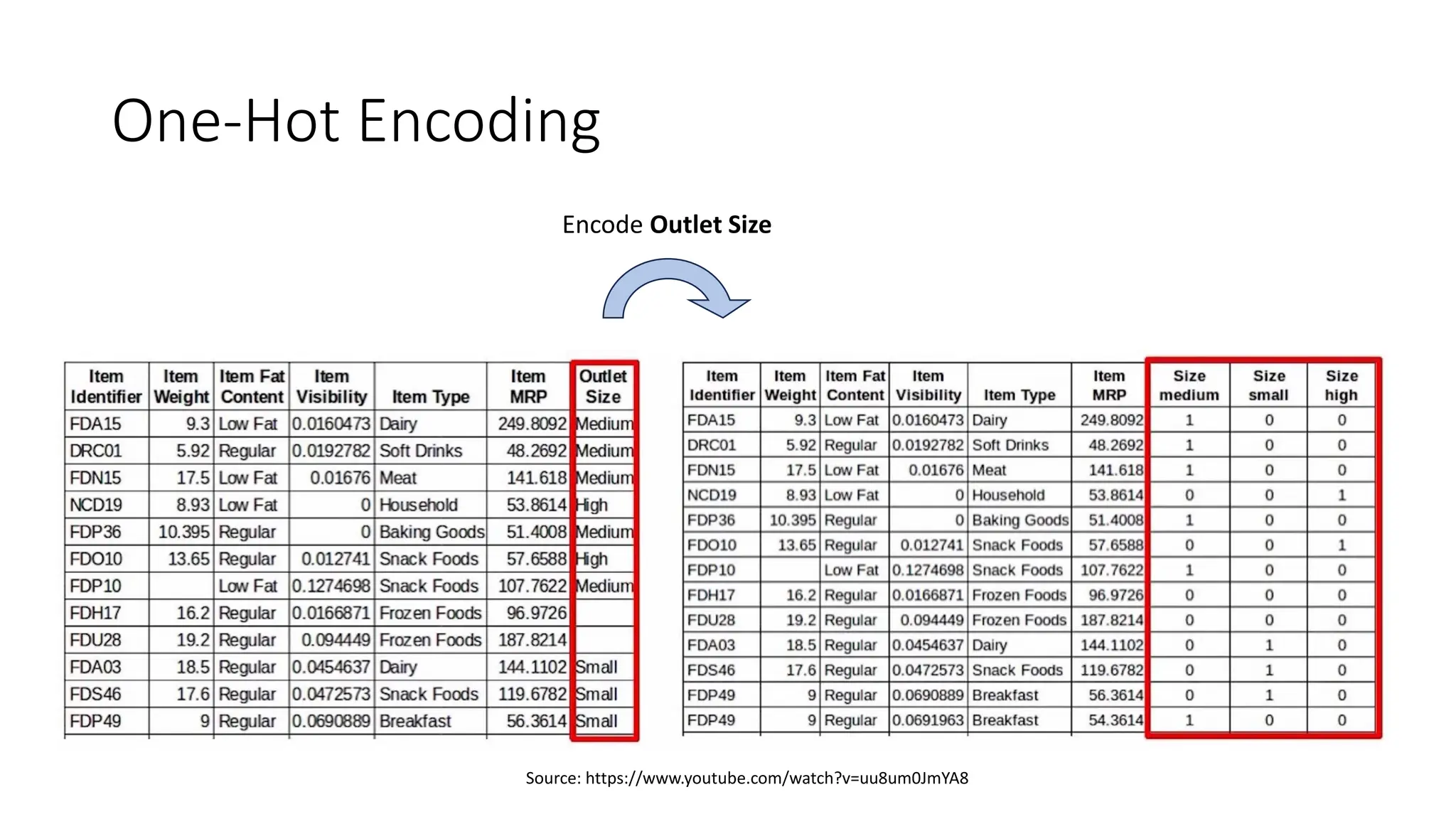
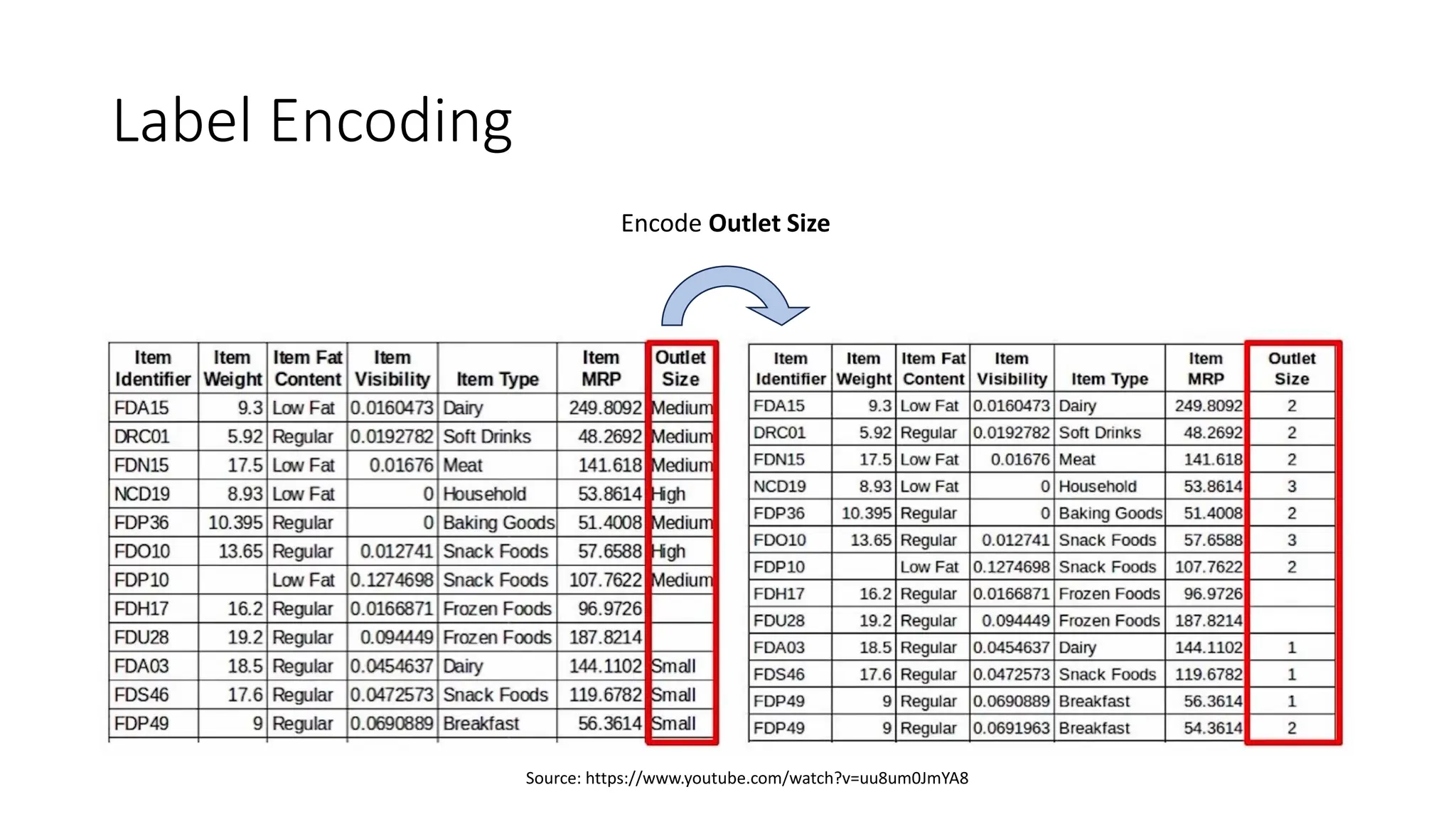
The document discusses feature engineering and optimization in machine learning, highlighting the importance of high-quality features for improving model accuracy. It covers feature selection techniques, including forward selection and backward elimination, as well as transformation, encoding, scaling of features, and handling missing data. Additionally, the document emphasizes the significance of feature generation and domain knowledge in enhancing model performance.