Intro to MATLAB and K-mean algorithm

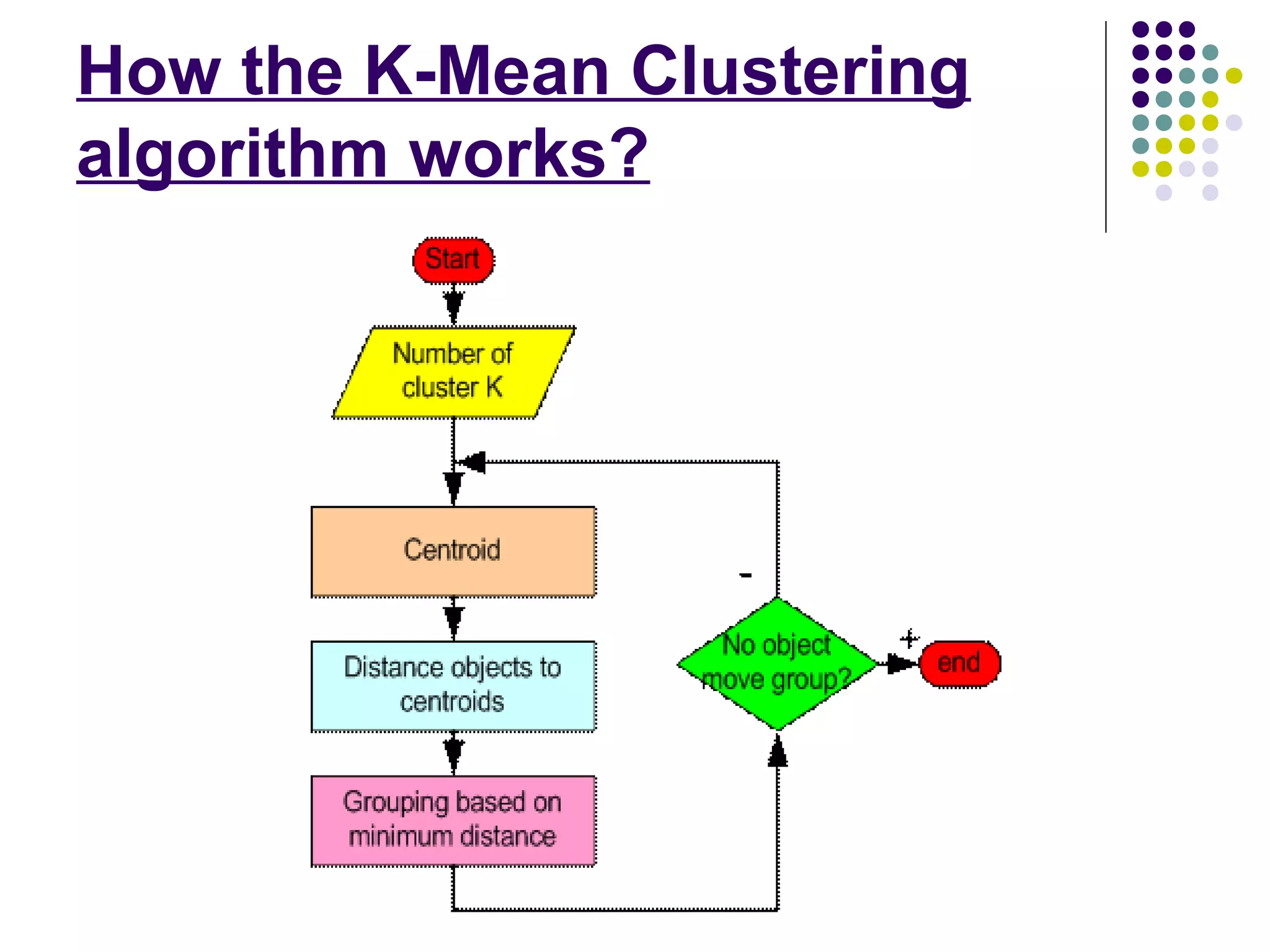
 MATLAB (Matrix Laboratory) [1]  MATLAB(matrix laboratory) is a multi-paradigm numerical computing environment and fourth-generation programming language.  Developed by Math Works, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages, including C, C++, Java and Fortran. MATLAB

 MATLAB (Matrix Laboratory) [2]  Although MATLAB is intended primarily for numerical computing, an option al toolbox uses the MuPAD symbolic engine, allowing access to symbolic computing capabilities. An additional package, Simulink, adds graphical multi-domain simulation and Model-Based Design for dynamic and embedded systems.  In 2004, MATLAB had around one million users across industry and academia. MATLAB users come from various backgrounds of engineering, science, and economics. MATLAB is widely used in academic and research institutions as well as industrial enterprises. MATLAB

 Commands  >>433.12*15.7  ans=6.8000e+003  MATLAB spits out the answer to our query conveniently named ans.  This is a variable or symbolic name that can be used to represent the value later.  >>x=5*6  X=30 MATLAB

 Commands  To write the multiplication ab, in MATLAB we type a*b  For division, the quantity a÷b is typed as a/b. This type of division is referred to as right division.  MATLAB also allows another way to enter division, called left division. We can enter the quantity by a typing the slash mark used for division in the opposite way, that is, we use a back slash instead of a forward slash ab MATLAB

 Commands  Exponentiation a to the power b is entered in the following way a ^ b  Finally, addition and subtraction are entered in the usual way  a + b  a –b MATLAB

 Commands  Individual matrix and vector entries can be referenced with indices inside parentheses. For example, A(2,3) denotes the entry in the second row, third column of matrix A.  A=[123;456;-179]  A(2,3)  Create a column vector, x, with:  x=[321]’  Or equivalently:  x=[3;2;1] MATLAB

 Commands  The relational operators in MATLAB are:  < less than  > greater than  <= less than or equal  >= greater than or equal  == equal  ~= not equal  Note that = is used in an assignment statement whereas == is a relational operator. MATLAB

 Commands  Logical operators:  Relational operators may be connected by logical operators:  & and  | or  ~ not  && short-circuit and  || short-circuit or MATLAB

 Commands  Inner product or dot product  .* Array multiply:  X.*Y denotes element-by-element multiplication. X and Y must have the same dimensions unless one is a scalar.  * Matrix multiply:  X*Y is the matrix product of X and Y. Any scalar (a 1-by- 1 matrix) may multiply anything. Otherwise, the number of columns of X must equal the number of rows of Y. MATLAB

 Commands  /Slash or right matrix divide:  A/B is the matrix division of B into A, which is roughly the same as A*INV(B), except it is computed in a different way. More precisely, A/B = (B'A')'.  Backslash or left matrix divide:  AB is the matrix division of A into B, which is roughly the same as INV(A)*B, except it is computed in a different way. If A is an N-by-N matrix and B is a column vector with N components, or a matrix with several such columns, then X=AB is the solution to the equation singular MATLAB

 Commands  To divide Matrices, element-by-element, the following formula is useful A./B  A = [2 4 6 8]; B = [2 2 3 1];  C = A./B  % C = [1 2 2 8]  Array left division is indicated by writing C = A.B (this is the same as C = B./A):  C = A.B  % C = [1.0000 0.5000 0.5000 0.125] MATLAB

 Commands  fix()  fix(X) rounds the elements of X to the nearest integers towards zero.  >> fix(5.5)  ans =  5  >> fix(5.9)  ans =  5 MATLAB

 Commands  rand()  rand():returns an n-by-n matrix containing pseudo random values drawn from the standard uniform distribution on the open interval(0,1).  >> n = rand(1,10)  n =0.1576 0.9706 0.9572 0.4854 0.8003 0.1419 0.4218 0.9157 0.7922 0.9595  >> n = fix(10*rand(1,10))  n =8 9 1 9 6 0 2 5 9 9 MATLAB

 Commands  Question: Simulate the outcomes of 1000 biased coin tosses with p[Head] = 0.3  Solution:  n = 1000;  randomNumber= rand(n,1);  Heads = randomNumber<= 0.3;  totalNumberOfHeads= sum(Heads);  probabilityOfHeads= totalNumberOfHeads/n; MATLAB

 Commands  Plot(x,y) plot the graph between x and y.  X and y are the vectors of same lengths.  >>X=1:10  >>y=11:20  >> plot(x,y) MATLAB

 Commands  Two or more than two graphs plot on at same time with hold on function  x=-5:5  y=x.*x  plot(x,y)  hold on  a=1:5  b=1:5  plot(a,b) MATLAB

INTRODUCTION- What is clustering?  Clustering is the classification of objects into different groups, or more precisely, the partitioning of a data set into subsets (clusters), so that the data in each subset (ideally) share some common trait - often according to some defined distance measure.

Common Distance measures:  Distance measure will determine how the similarity of two elements is calculated and it will influence the shape of the clusters. They include: 1. The Euclidean distance (also called 2-norm distance) is given by: 2. The Manhattan distance (also called taxicab norm or 1- norm) is given by:

K-MEANS CLUSTERING  The k-means algorithm is an algorithm to cluster n objects based on attributes into k partitions, where k < n.

K-MEANS CLUSTERING  Simply speaking k-means clustering is an algorithm to classify or to group the objects based on attributes/features into K number of group.  K is positive integer number.  The grouping is done by minimizing the sum of squares of distances between data and the corresponding cluster centroid.

How the K-Mean Clustering algorithm works?

 Step 1: Begin with a decision on the value of k = number of clusters .  Step 2: Put any initial partition that classifies the data into k clusters. You may assign the training samples randomly,or systematically as the following: 1.Take the first k training sample as single- element clusters 2. Assign each of the remaining (N-k) training sample to the cluster with the nearest centroid. After each assignment, recompute the centroid of the gaining cluster.

 Step 3: Take each sample in sequence and compute its distance from the centroid of each of the clusters. If a sample is not currently in the cluster with the closest centroid, switch this sample to that cluster and update the centroid of the cluster gaining the new sample and the cluster losing the sample.  Step 4 . Repeat step 3 until convergence is achieved, that is until a pass through the training sample causes no new assignments.

Applications of K-Mean Clustering  It is relatively efficient and fast. It computes result at O(tkn), where n is number of objects or points, k is number of clusters and t is number of iterations.  k-means clustering can be applied to machine learning or data mining  Used on acoustic data in speech understanding to convert waveforms into one of k categories (known as Vector Quantization or Image Segmentation).  Also used for choosing color palettes on old fashioned graphical display devices and Image Quantization.

Intro to MATLAB and K-mean algorithm

Intro to MATLAB and K-mean algorithm

More Related Content

What's hot

Viewers also liked

Similar to Intro to MATLAB and K-mean algorithm

Recently uploaded

Intro to MATLAB and K-mean algorithm

Editor's Notes