MATLAB : Introduction , Features , Display Windows, Syntax, Operators, Graph Plot

MATLAB ANAMIKA KUMARI ASSISTANT PROFESSOR AMITY SCHOOL OF ENGINEERING & TECHNOLOGY

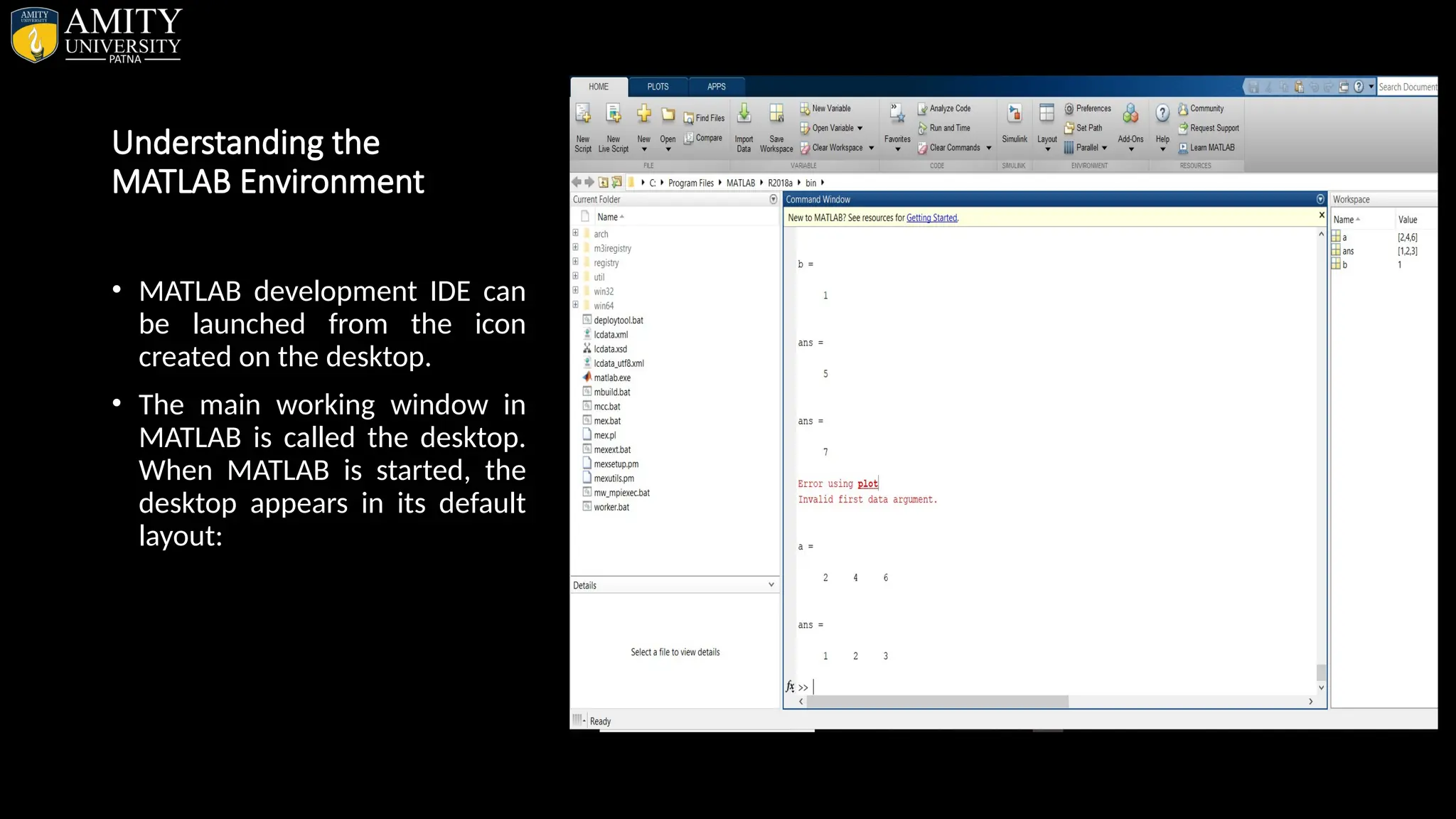
Introduction to MATLAB • MATLAB (MATrix LABoratory) is a fourth-generation high-level programming language and interactive environment for numerical computation, visualization and programming. • MATLAB is developed by MathWorks. • It allows matrix manipulations; plotting of functions and data; implementation of algorithms; creation of user interfaces; interfacing with programs written in other languages, including C, C++, Java, and FORTRAN; analyze data; develop algorithms; and create models and applications. • It has numerous built-in commands and math functions that help you in mathematical calculations, generating plots, and performing numerical methods.

Uses of MATLAB MATLAB is widely used as a computational tool in science and engineering encompassing the fields of physics, chemistry, math and all engineering streams. It is used in a range of applications including: • Signal processing and Communications • Image and video Processing • Control systems • Test and measurement • Computational finance • Computational biology • Algorithm development • Data acquisition • Modeling, simulation, and prototyping • Data analysis, exploration, and visualization • Scientific and engineering graphics • Application development, including graphical user interface building

Features of MATLAB • It is a high-level language for numerical computation, visualization and application development. • It also provides an interactive environment for iterative exploration, design and problem solving. • It provides vast library of mathematical functions for linear algebra, statistics, Fourier analysis, filtering, optimization, numerical integration and solving ordinary differential equations. • It provides built-in graphics for visualizing data and tools for creating custom plots. • MATLAB's programming interface gives development tools for improving code quality, maintainability, and maximizing performance.

Understanding the MATLAB Environment • MATLAB development IDE can be launched from the icon created on the desktop. • The main working window in MATLAB is called the desktop. When MATLAB is started, the desktop appears in its default layout:

Layout of MATLAB R2013a Command Window Workspace Command History Current Folder

MATLAB has four windows 1. Command Window : All the commands are entered in command window. 2. Workspace : Workspace contains all the variable and details of same entered in command window. 3. Command History : Command history shows all the command entered in command window. 4. Current folder : After saving the file i.e., .m, .mat, .mex files are saved in current folder. We can change the path of current folder.

MATLAB has three display windows. 1. Command window 2. A graphics window which is used to display plots and graphs. 3. An editor window which is used to create and modify M- files. M-files are files that contain a program or script of MATLAB commands. • If a semicolon (;) is typed at the end of a command the output of the command is not displayed. • When percent symbol (%) is typed in the beginning of a line, the line is designated as a comment.

BASIC SYNTAX • MATLAB environment behaves like a super- complex calculator. You can enter commands at the >> command prompt. • MATLAB is an interpreted environment. In other words, you give a command and MATLAB executes it right away.

Hands on Practice Example # 1 Type a valid expression, for example, And press ENTER When you click the Execute button, or type Ctrl+E, MATLAB executes it immediately and the result returned is: 5+5 ans = 10

Example #2 Let us take up few more examples: When you click the Execute button, or type Ctrl+E, MATLAB executes it immediately and the result returned is: 3 ^ 2 % 3 raised to the power of 2 ans = 9

Example #3 Let us take up few more examples: When you click the Execute button, or type Ctrl+E, MATLAB executes it immediately and the result returned is: sin(pi /2) % sine of angle 90 ans = 1

Example #4 Let us take up few more examples: When you click the Execute button, or type Ctrl+E, MATLAB executes it immediately and the result returned is: (MATLAB provides some special expressions for some mathematical symbols, like pi for π, Inf for ∞, i (and j) for √-1 etc. Nan stands for 'not a number’.) 7/0 % Divide by zero ans = Inf warning: division by zero

Use of Semicolon (;) in MATLAB • Semicolon (;) indicates end of statement. However, if you want to suppress and hide the MATLAB output for an expression, add a semicolon after the expression. For example, When you click the Execute button, or type Ctrl+E, MATLAB executes it immediately and the result returned is: x = 3; y = x + 5 y = 8

Adding Comments The percent symbol (%) is used for indicating a comment line. For example, • You can also write a block of comments using the block comment operators % { and % }. The MATLAB editor includes tools and context menu items to help you add, remove, or change the format of comments. x = 9 % assign the value 9 to x

Commonly used Operators and Special Characters • MATLAB supports the following commonly used operators and special characters: Operator Purpose + Plus; addition operator. - Minus; subtraction operator. * Scalar and matrix multiplication operator. .* Array multiplication operator. ^ Scalar and matrix exponentiation operator. .^ Array exponentiation operator. Left-division operator. / Right-division operator.

Commonly used Operators and Special Characters (Cont.) Operator Purpose . Array left-division operator. ./ Array right-division operator. : Colon; generates regularly spaced elements and represents an entire row or column. ( ) Parentheses; encloses function arguments and array indices; overrides precedence. [ ] Brackets; enclosures array elements. . Decimal point. … Ellipsis; line-continuation operator , Comma; separates statements and elements in a row ; Semicolon; separates columns and suppresses display. % Percent sign; designates a comment and specifies formatting. = Assignment operator.

Naming Variables • Variable names consist of a letter followed by any number of letters, digits or underscore. • MATLAB is case-sensitive. • Variable names can be of any length, however, MATLAB uses only first N characters, where N is given by the function namelengthmax.

Saving Your Work • The save command is used for saving all the variables in the workspace, as a file with .mat extension, in the current directory. For example, You can reload the file anytime later using the load command. save myfile load myfile

On-line help Command Description Help Lists topic on which help is available helpwin Opens the interactive help window helpdesk Opens the web browser based help facility. help topic Provides help on topic. lookfor string Lists help topics containing string. demo Runs the demo program.

Exercise • Find the addition of two numbers in which one number is present in a variable name a. •

Experiment No. 1 Creating a One and Two- Dimensional Array (Row / Column Vector) (Matrix of given size) then, (A). Performing Arithmetic Operations -Addition, Subtraction, Multiplication and Exponentiation. (B). Performing Matrix operations -Inverse, Transpose, Rank with PLOTS

MATRIX Referencing the Element of Matrix

Creating Sub-Matrix part of Matrix

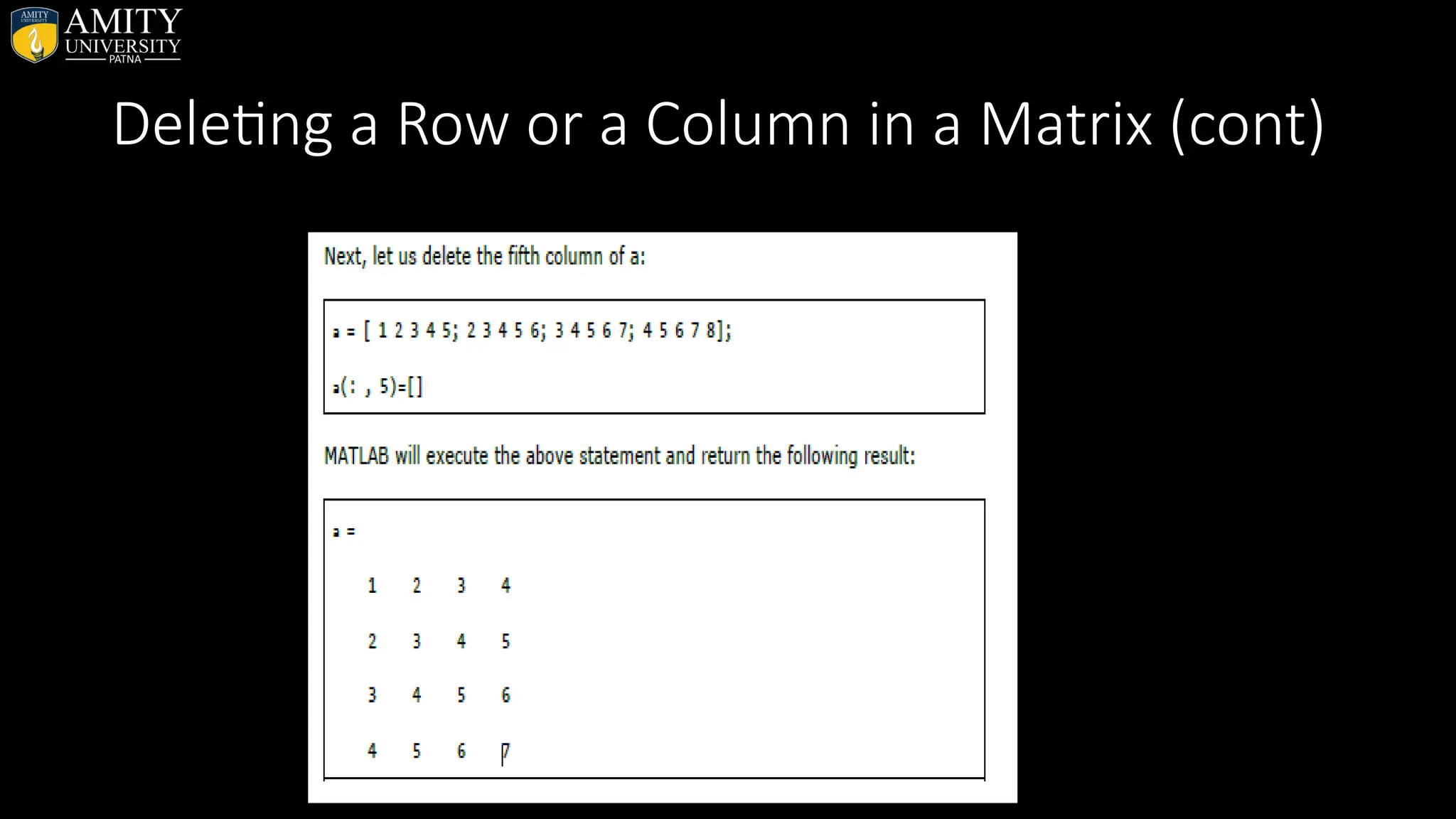
Deleting a Row or a Column in a Matrix • You can delete an entire row or column of a matrix by assigning an empty set of square braces [] to that row or column. Basically, [] denotes an empty array. • For example, let us delete the fourth row of a: a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]; a( 4 , : ) = [] MATLAB will execute the above statement and return the following result: a = 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7

Deleting a Row or a Column in a Matrix (cont)

Deleting a Row or a Column in a Matrix (cont.)

Matrix Operations The following basic and commonly used matrix operations: • Addition and Subtraction of Matrices • Division of Matrices • Scalar Operations of Matrices • Transpose of a Matrix • Concatenating Matrices • Matrix Multiplication • Determinant of a Matrix • Inverse of a Matrix

Addition and Subtraction of Matrices

Division (Left, Right) of Matrix • You can divide two matrices using left () or right (/) division operators. • Both the operand matrices must have the same number of rows and columns.

Scalar Operations of Matrices • When you add, subtract, multiply or divide a matrix by a number, this is called the scalar operation. • Scalar operations produce a new matrix with same number of rows and columns with each element of the original matrix added to, subtracted from, multiplied by or divided by the number.

Transpose of a Matrix • The transpose operation switches the rows and columns in a matrix. It is represented by a single quote(').

Matrix Multiplication • Consider two matrices A and B. If A is an m x n matrix and B is an n x p matrix, they could be multiplied together to produce an m x n matrix C. Matrix multiplication is possible only if the number of columns n in A is equal to the number of rows n in B. • In matrix multiplication, the elements of the rows in the first matrix are multiplied with corresponding columns in the second matrix. • Each element in the (i, j)th position, in the resulting matrix C, is the summation of the products of elements in ith row of first matrix with the corresponding element in the jth column of the second matrix. • Matrix multiplication in MATLAB is performed by using the * operator.

Determinant of a Matrix • Determinant of a matrix is calculated using the det function of MATLAB. Determinant of a matrix A is given by det(A).

Rank of matrix Syntax • k = rank(A) • Examples

Inverse of a Matrix • The inverse of a matrix A is denoted by A−1 such that the following relationship holds: The inverse of a matrix does not always exist. If the determinant of the matrix is zero, then the inverse does not exist and the matrix is singular. Inverse of a matrix in MATLAB is calculated using the inv function. Inverse of a matrix A is given by inv(A).

PLOT: Create 2-D Graph and Customize Lines This example shows how to create a simple line graph. • Use the linspace function to define x as a vector of 100 linearly spaced values between 0 and 2pi. x = linspace(0,2*pi,100); • Define y as the sine function evaluated at the values in x. y = sin(x); • Plot y versus the corresponding values in x figure plot(x,y)

This example shows how to create a graph in a new figure window, instead of plotting into the current figure. • Define x and y. • x = linspace(0,2*pi,25); • y = sin(x); • Create a stairstep plot of y versus x. Open a new figure window using the figure command. If you do not open a new figure window, then by default, MATLAB® clears existing graphs and plots into the current figure. • figure % new figure window • stairs(x,y)

Colors, Line Styles, and Markers • To change the line color, line style, and marker type, add a line specification input argument to the x,y pair. For example, 'g:*' plots a green dotted line with star markers. You can omit one or more options from the line specification, such as 'g:' for a green dotted line with no markers. To change just the line style, specify only a line style option, such as '--' for a dashed line. • For more information, see the LineSpec input argument for plot. • Specify Line Style • Open Live Script • This example shows how to create a plot using a dashed line. Add the optional line specification, '--', to the x,y pair. • x = linspace(0,2*pi,100); • y = sin(x); • figure • plot(x,y,'--')

Specify Line Style and Color • This example shows how to specify the line styles and line colors for a plot. • Plot a sine wave with a green dashed line using '--g'. Plot a second sine wave with a red dotted line using ':r'. The elements of the line specification can appear in any order. • x = linspace(0,2*pi,100); • y1 = sin(x); • y2 = sin(x-pi/4); • figure • plot(x,y1,'--g',x,y2,':r')

ARRAYS • Arrays are Set of Elements having same data type or we can Say that Arrays are Collection of Elements having same name and same data type. • All variables of all data types in MATLAB are multidimensional arrays. • A vector is a one-dimensional array and a matrix is a two-dimensional array. • Two Dimensional Array or the Matrix • The Two Dimensional array is used for representing the elements of the array in the form of the rows and columns and these are used for representing the Matrix A Two Dimensional Array uses the two subscripts for declaring the elements of the Array • “Like this int a[3][3]” • This is the Example of the Two Dimensional Array In this first 3 represents the total number of Rows and the Second Elements Represents the Total number of Columns The Total Number of elements are judge by Multiplying the Numbers of Rows * Number of Columns. In the above array the Total Number of elements

Special Arrays in MATLAB • In this section, we will discuss some functions that create some special arrays. For all these functions, a single argument creates a square array, double arguments create rectangular array. • The zeros() function creates an array of all zeros: • For example:

The ones() function creates an array of all ones:

Multidimensional Arrays • A multidimensional array in MATLAB® is an array with more than two dimensions. In a matrix, the two dimensions are represented by rows and columns. • Each element is defined by two subscripts, the row index and the column index. Multidimensional arrays are an extension of 2-D matrices and use additional subscripts for indexing. A 3-D array, for example, uses three subscripts. The first two are just like a matrix, but the third dimension represents pages or sheets of elements.

Multidimensional Arrays • An array having more than two dimensions is called a multidimensional array in MATLAB. Multidimensional arrays in MATLAB are an extension of the normal two-dimensional matrix. • Generally to generate a multidimensional array, we first create a two-dimensional array and extend it. • For example, let's create a two-dimensional array a.

We can also use the cat() function to build multidimensional arrays. It concatenates a list of arrays along a specified dimension: Syntax for the cat() function is: B = cat(3,A,[3 2 1; 0 9 8; 5 3 7])

Array Functions . MATLAB provides the following functions to sort, rotate, permute, reshape, or shift array contents. • Function Purpose • length Length of vector or largest array dimension • ndims Number of array dimensions • numel Number of array elements • size Array dimensions • iscolumn Determines whether input is column vector • isempty Determines whether array is empty • ismatrix Determines whether input is matrix • isrow Determines whether input is row vector • isscalar Determines whether input is scalar • isvector Determines whether input is vector • blkdiag Constructs block diagonal matrix from input arguments • circshift Shifts array circularly • ctranspose Complex conjugate transpose

Examples The following examples illustrate some of the functions mentioned above. • Length, Dimension and Number of elements: • Create a script file and type the following code into it:

Concatenating Matrice • You can concatenate two matrices to create a larger matrix. The pair of square brackets '[]' is the concatenation operator. • MATLAB allows two types of concatenations: • Horizontal concatenation • Vertical concatenation • When you concatenate two matrices by separating those using commas, they are just appended horizontally. It is called horizontal concatenation. • Alternatively, if you concatenate two matrices by separating those using semicolons, they are appended vertically. It is called vertical concatenation.

When you run the file, it displays the following result:

Sorting Arrays • Create a script file and type the following code into it:

Reshape • Reshape array collapse all in page • Syntax • B = reshape(A,sz) • B = reshape(A,sz1,...,szN) EXAMPLE • h=[2 3 4 5;8 1 2 0;6 9 3 7] • g=reshape(h,6,2)

Rotating of Matrix • SYNTAX : • rot90 %Rotates matrix 90 degrees • EXAMPLE: • i=rot90(g)

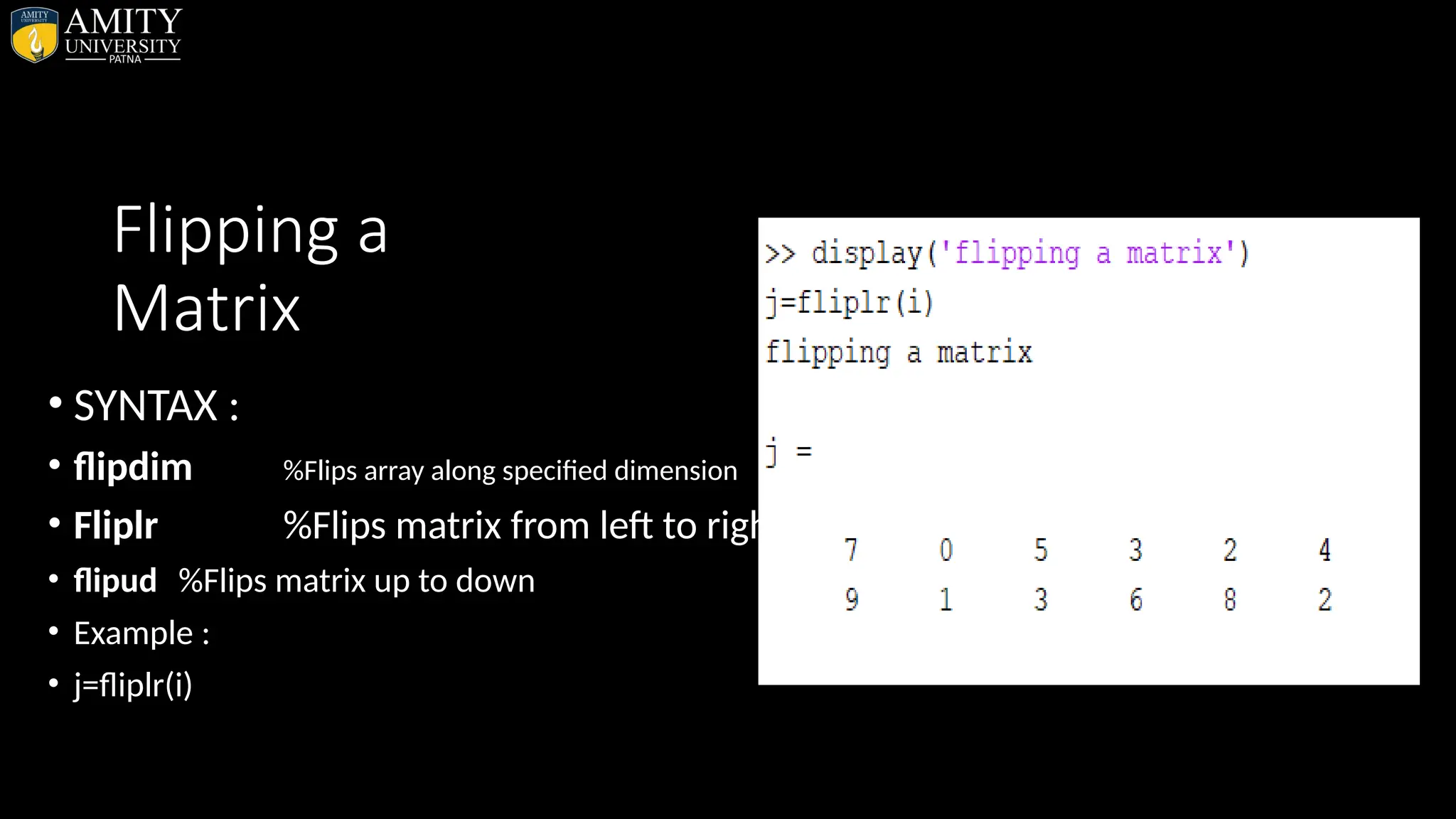
Flipping a Matrix • SYNTAX : • flipdim %Flips array along specified dimension • Fliplr %Flips matrix from left to right • flipud %Flips matrix up to down • Example : • j=fliplr(i)

Shifting the Matrix • Circular Shifting of the Array Elements: • Create a script file and type the following code into it: • a = [1 2 3; 4 5 6; 7 8 9] % the original array a • b = circshift(a,1) % circular shift first dimension values down by 1. • c = circshift(a,[1 -1]) % circular shift first dimension values % down by 1 • % and second dimension values to the left % by 1.

It displays the following result:

Relational Operators • Relational operators for arrays perform element-by-element comparisons between two arrays and return a logical array of the same size, with elements set to logical 1 (true) where the relation is true and elements set to logical 0 (false) where it is not.

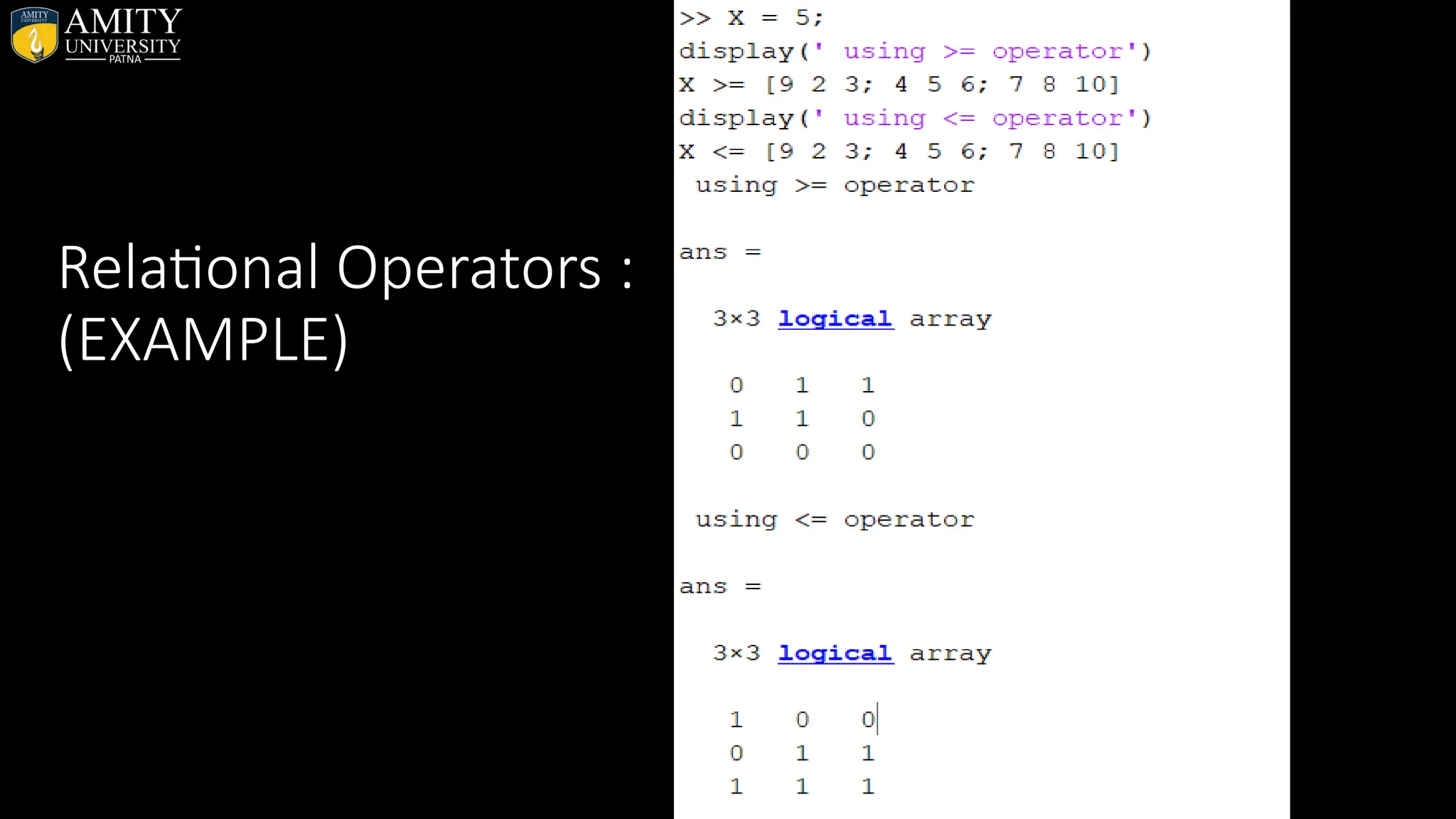
Relational Operators : (EXAMPLE)

Logical Operators • MATLAB offers two types of logical operators and functions: • Element-wise - These operators operate on corresponding elements of logical arrays. • Short-circuit - These operators operate on scalar and logical expressions. • Element-wise logical operators operate element-by-element on logical arrays. The symbols &, |, and ~ are the logical array operators AND, OR, and NOT. • Short-circuit logical operators allow short-circuiting on logical operations. The symbols && and || are the logical short-circuit operators AND and OR.

Functions for Logical Operations Function • and(A, B) • not(A) • or(A, B) • xor(A, B) • all(A) %Determine if all array elements of array A are nonzero or true.

EXPERIMENT NO. 2 • AIM: Performing Matrix Manipulations - Concatenating, Indexing, Sorting, Shifting, Reshaping, Resizing and Flipping about a Vertical Axis / Horizontal Axis; Creating Arrays X & Y of given size (1 x N) and Performing (A). Relational Operations - >, <, ==, <=, >=, ~= (B). Logical Operations - ~, &, |, XOR

ADDING VALUES IN A VECTOR >> sum = 0; for i = 1:5 sum = sum+i; end display(sum) OUTPUT sum = 15

CHECKING THE SUM CHECK SUM: >> A = [1 2 3 4 5] OUTPUT A = 1 2 3 4 5 >> B = sum(A) OUTPUT B = 15

RUNNING SUM Program: >> sum = 0; >> for i = 1:5 sum = sum+i; display(sum) end OUTPUT : sum = 1 sum = 3 sum = 6 sum = 10 sum = 15

Cumulative sum • Syntax –CUMSUM • Find the cumulative sum of the integers from 1 to 5. The element B(2) is the sum of A(1) and A(2), while B(5) is the sum of elements A(1) through A(5). Eg: >> A = [1 2 3 4 5] A = 1 2 3 4 5 >> B = cumsum(A) B = 1 3 6 10 15

Rand() Function: (Random) • The rand() function creates an array of uniformly distributed random numbers on (0,1): • For example: • MATLAB will execute the above statement and return the following result:

Adding a Values in Vector: >> sum = 0; for i = 1:5 sum = sum+i; end display(sum) OUTPUT sum = 15

CHECK SUM: • >> A = [1 2 3 4 5] OUTPUT A = 1 2 3 4 5 >> B = sum(A) OUTPUT B = 15

CHECK RUNNING SUM: >> sum = 0; >> for i = 1:5 sum = sum+i; display(sum) end OUTPUT sum = 1 sum = 3 sum = 6 sum = 10 sum = 15

CHECK CUMSUM: • >> A = [1 2 3 4 5] OUTPUT A = 1 2 3 4 5 >> B = cumsum(A) OUTPUT B = 1 3 6 10 15

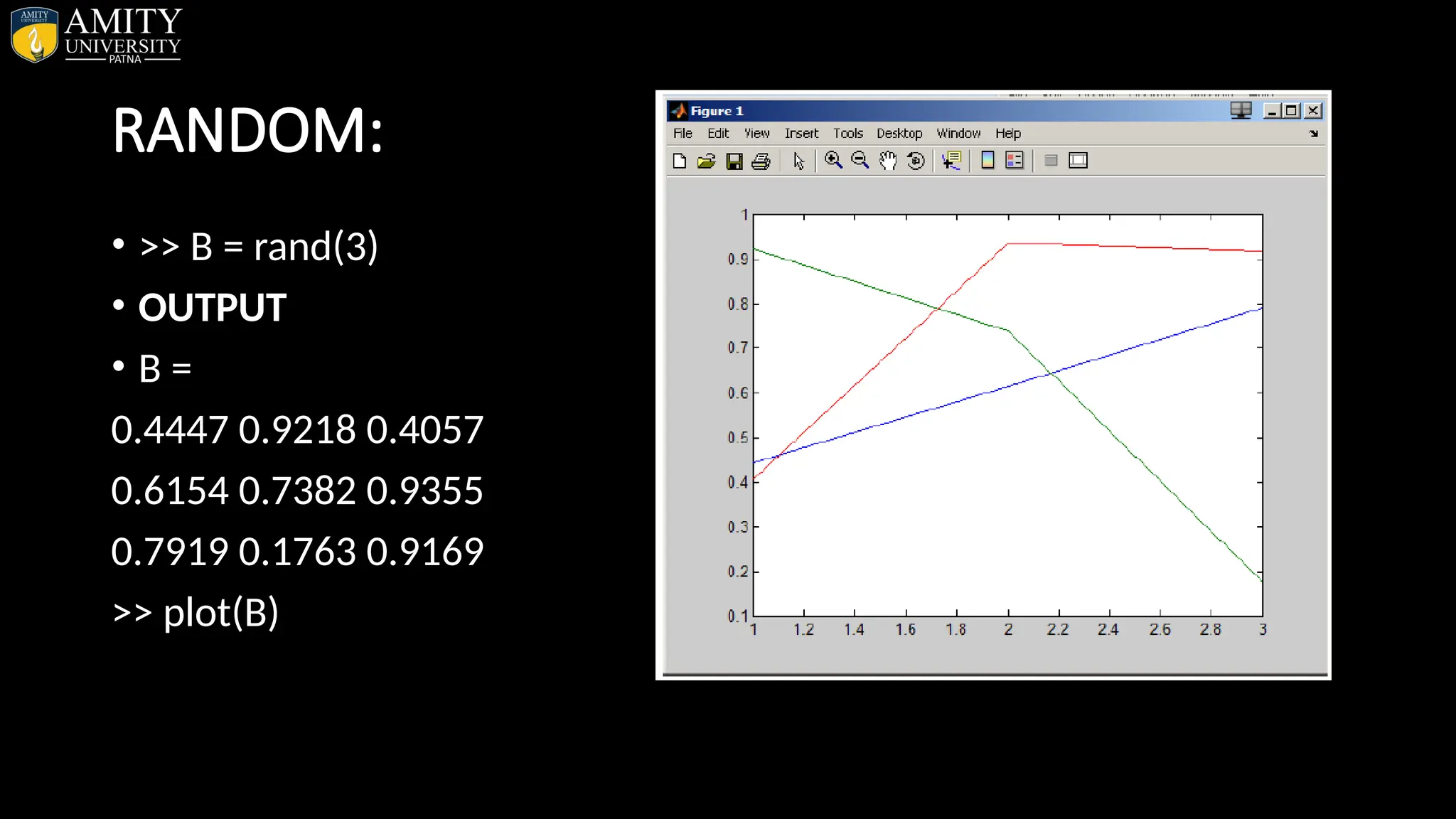
RANDOM: • >> B = rand(3) • OUTPUT • B = 0.4447 0.9218 0.4057 0.6154 0.7382 0.9355 0.7919 0.1763 0.9169 >> plot(B)

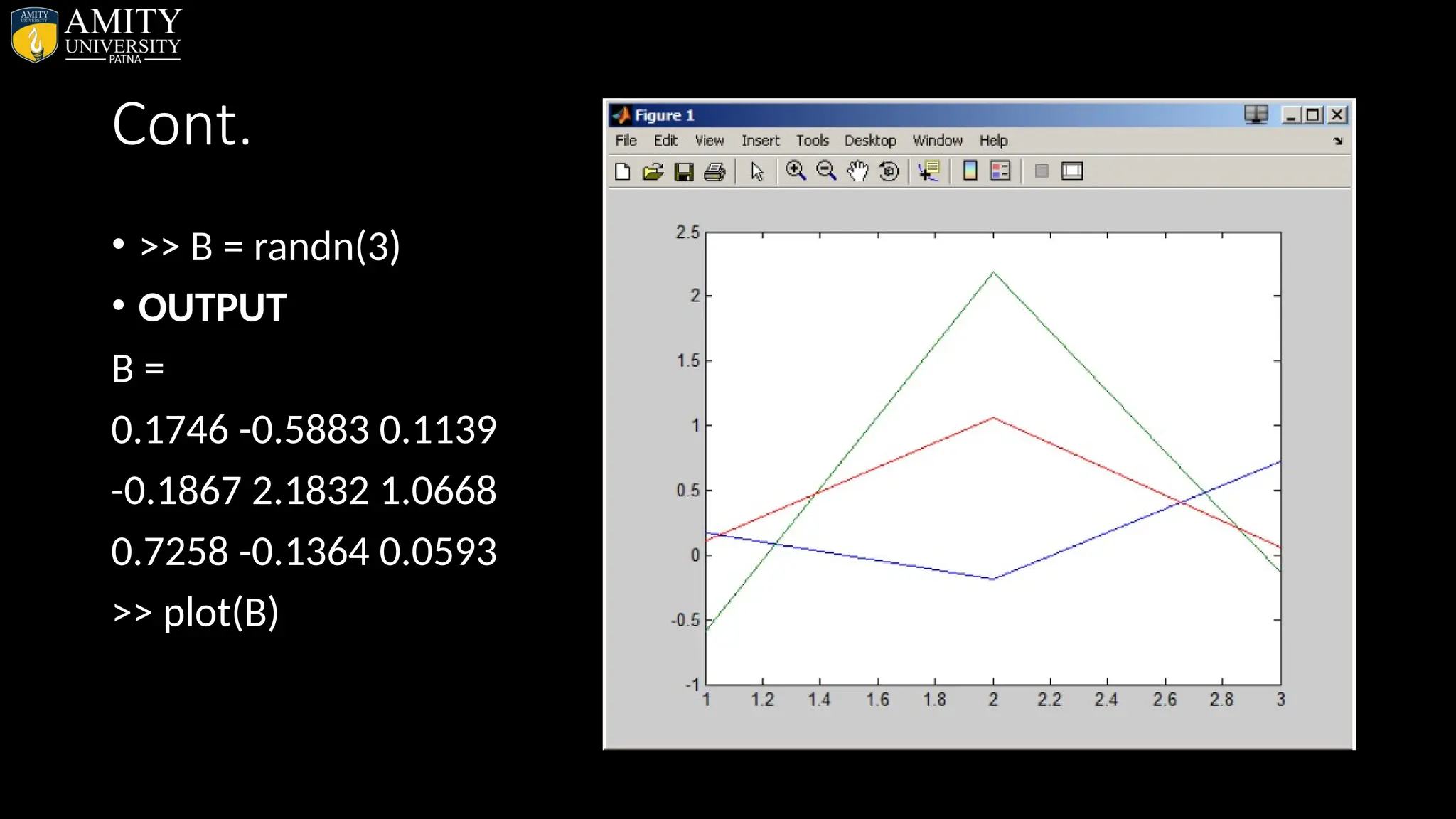
Cont. • >> B = randn(3) • OUTPUT B = 0.1746 -0.5883 0.1139 -0.1867 2.1832 1.0668 0.7258 -0.1364 0.0593 >> plot(B)

Rounding to the nearest integer value using Round, Floor, Ceil and Fix functions • round(A) : Round to nearest integer • ceil(A) : Round toward positive infinity; rounds the elements of A to the nearest integers greater than or equal to A. • fix(A) : Round toward nearest zero • floor(A) : Round toward negative infinity; rounds the elements of A to the nearest integers less than or equal to A.

Examples with syntax (Rounding Functions) • 1. ROUND >>round(3.67) • OUTPUT ans = 4 • 2. FLOOR >>floor(3.67) • OUTPUT ans = 3 • 3. CEIL >>ceil(3.67) • OUTPUT ans = 4 • 4. FIX >>a = [1.88 2.05 9.54 8.5] • OUTPUT • a = 1.8800 2.0500 9.5400 8.5000 >>fix(a) • ans = 1 2 9 8

Derivatives of Exponential, Logarithmic, and Trigonometric Functions

TRIGONOMETRIC FUNCTIONS • 1. sin(t) >> x=(0:0.01:2*pi); >> y=sin(x); >>plot(x,y); 2. cos(t) >> x=(0:0.01:2*pi); >> y=cos(x); >>plot(x,y);

3. cosec(t) >> x=(0:0.01:2*pi); >> y=csc(x); >>plot(x,y); • 4. sec(t) • >> x=(0:0.01:2*pi); • >> y=sec (x); • >>plot(x,y);

• 5. tan(t) >> x=(0:0.01:2*pi); >> y=sin(x); >>plot(x,y); • 6. cot(t) >> x=(0:0.01:2*pi); >> y=cot(x); >>plot(x,y);

LOGARITHMIC FUNCTIONS • 1. log(t) >> x=(0:0.01:20) >> plot(log(x)) Warning: Log of zero 2. log10(t) >> x=(0.01:0.01:20) >> plot(log(x))

Exponential function • Exponential function is an elementary function that operates element-wise on arrays. • Its domain also includes complex numbers • Y = exp(X) returns the exponential for each element of X.

Example : (Exp. #5) • Creating a vector X with elements, Xn = (-1)^n+1/(2n-1) and Adding up 100 elements of the vector, X; • And, plotting the functions; over the interval 0 < x < 4 (by choosing appropriate mesh values for x to obtain smooth curves), on a Rectangular Plot 1. x, 2. x^3, 3. exp, 4. exp(x^2)

Solution: • Adding up to 100 elements >> n = 1:100; x = ( (-1).^(n+1) ) ./ (2*n - 1); y = sum(x) • x plot(x(1,1:4))

Cont. • x3 • a=x.^3; • plot(a(1,1:4)) • Exp(x) • b=exp(x) • plot(b(1,1:4)) • Exp(n2) • c=exp(x.^2); • plot(c(1,1:4))

Plotting with Graphical Enhancements

MATLAB PROGRAM:- (Generating a Sinusoidal Signal ) Generating a Sinusoidal Signal of a given frequency with Titling, Labeling, Adding Text, Adding Legends, Printing Text in Greek Letters, Plotting as Multiple and Subplot. Time scale the generated signal for different values. t=-0.25:0.0001:0.25; f1=3; y1=sin(2*pi*f1*t); y2=sin(2*pi*f1*2*t); y3=sin(2*pi*f1*4*t); y4=sin(2*pi*f1*0.25*t); y5=sin(2*pi*f1*0.625*t); plot(t,y1,'k',t,y2,'g',t,y3,'b',t,y4,'m',t,y5,'r') xlabel('Time(-0.2 < x < 0)') ylabel(' Amplitude (sine values)') title('Graph of sine waves having different time value') legend('y1','y2','y3','y4','y5')

Graph Editing : (with help of figure properties)

First, Second and third Order Ordinary Differential Equation using Built-in Functions and plot. Syntax: dsolve (Ordinary differential equation and system solver )

Procedure Of Solving Diff. Equations • STEP 1: Before using dsolve, create the symbolic function for which you want to solve an ordinary differential equation. Use sym or syms to create a symbolic function. For example, create a function y(x): • syms y(x) • STEP 2: specify initial or boundary conditions, use additional equations. (If you do not specify initial or boundary conditions, the solutions will contain integration constants, such as C1, C2, and so on. )

First Order Diff. Equation • >> y = dsolve('Dy = y*x','x’); -----------------Equation • >> y = dsolve('Dy = y*x','y(1) = 1','x’); • >> x = linspace(0,1,20); • >> z = eval(vectorize(y)); • >> plot(x,z); Equation Initialization With Respect to X

Second Order Diff. Equation • >> eq1 = 'D2y + 8*Dy + 2*y = cos(x)’; -----------------Equation • >> inits2 = 'y(0)=0, Dy(0)=1'; -----------------Intialization • >> y = dsolve(eq1,inits2,'x'); • >> x = linspace(0,1,20); • >> z = eval(vectorize(y)); • >> plot(x,z); Equation Initialization With Respect to X SYNTAX

Third Order Diff. Equation • >> eq1 = 'D3y + 3*D2y + Dy = cos(x)'; • >> inits2 = 'y(0)=0, Dy(0)=1,D2y(0)=3'; • >> y = dsolve(eq1,inits2,'x'); • >> x = linspace(0,1,20); • >> z = eval(vectorize(y)); • >> plot(x,z);

Script with a request for input • Input Funtion: • x = input (prompt) displays the text in prompt and waits for the user to input a value and press the Return key. The user can enter expressions, like pi/4 or rand(3), and can use variables in the workspace. • • If the user presses the Return key without entering anything, then input returns an empty matrix. • • If the user enters an invalid expression at the prompt, then MATLAB® displays the relevant error message, and then redisplays the prompt. • Example: • str = input(prompt,'s') returns the entered text as a string, without evaluating the input as an expression.

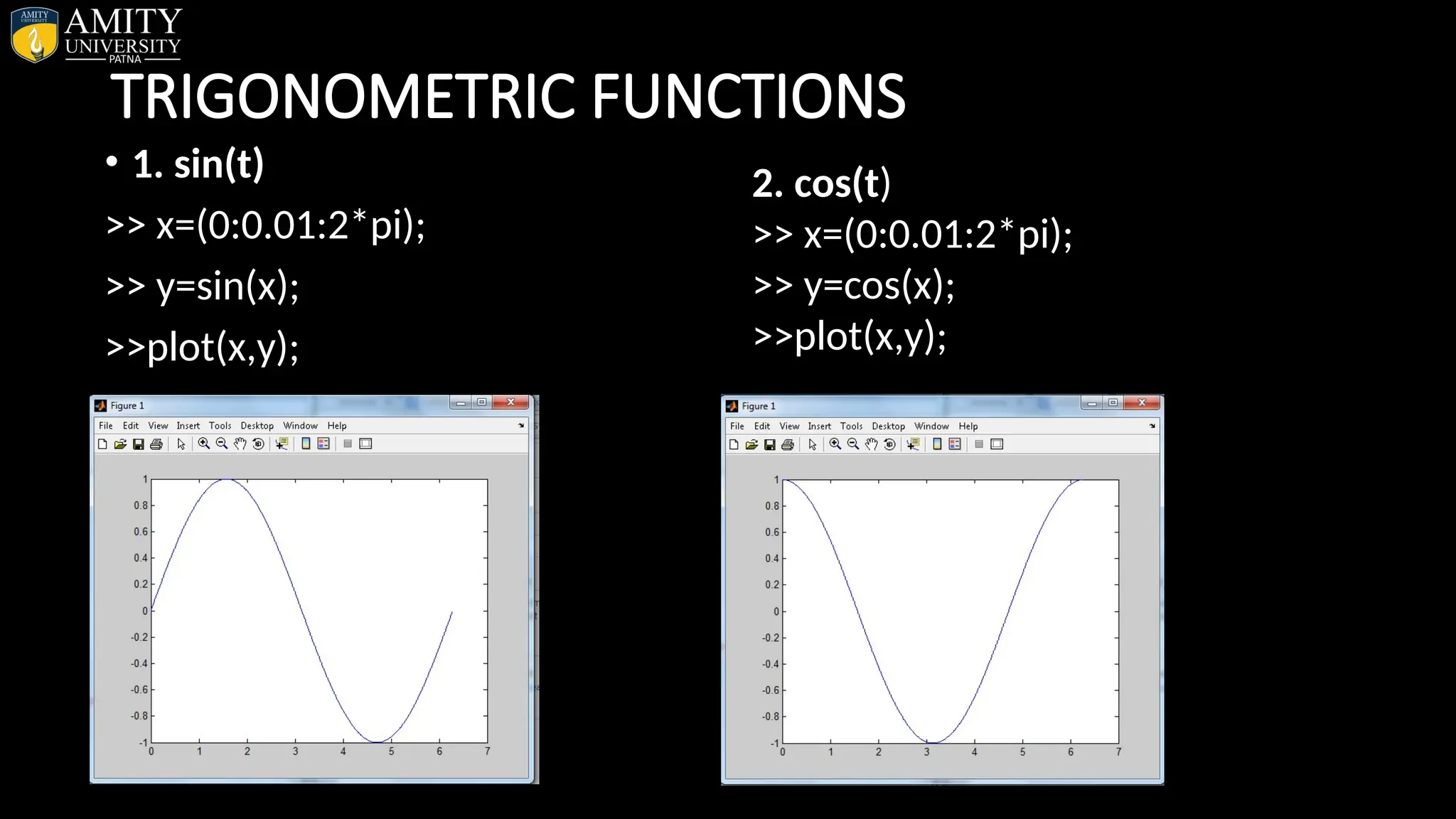
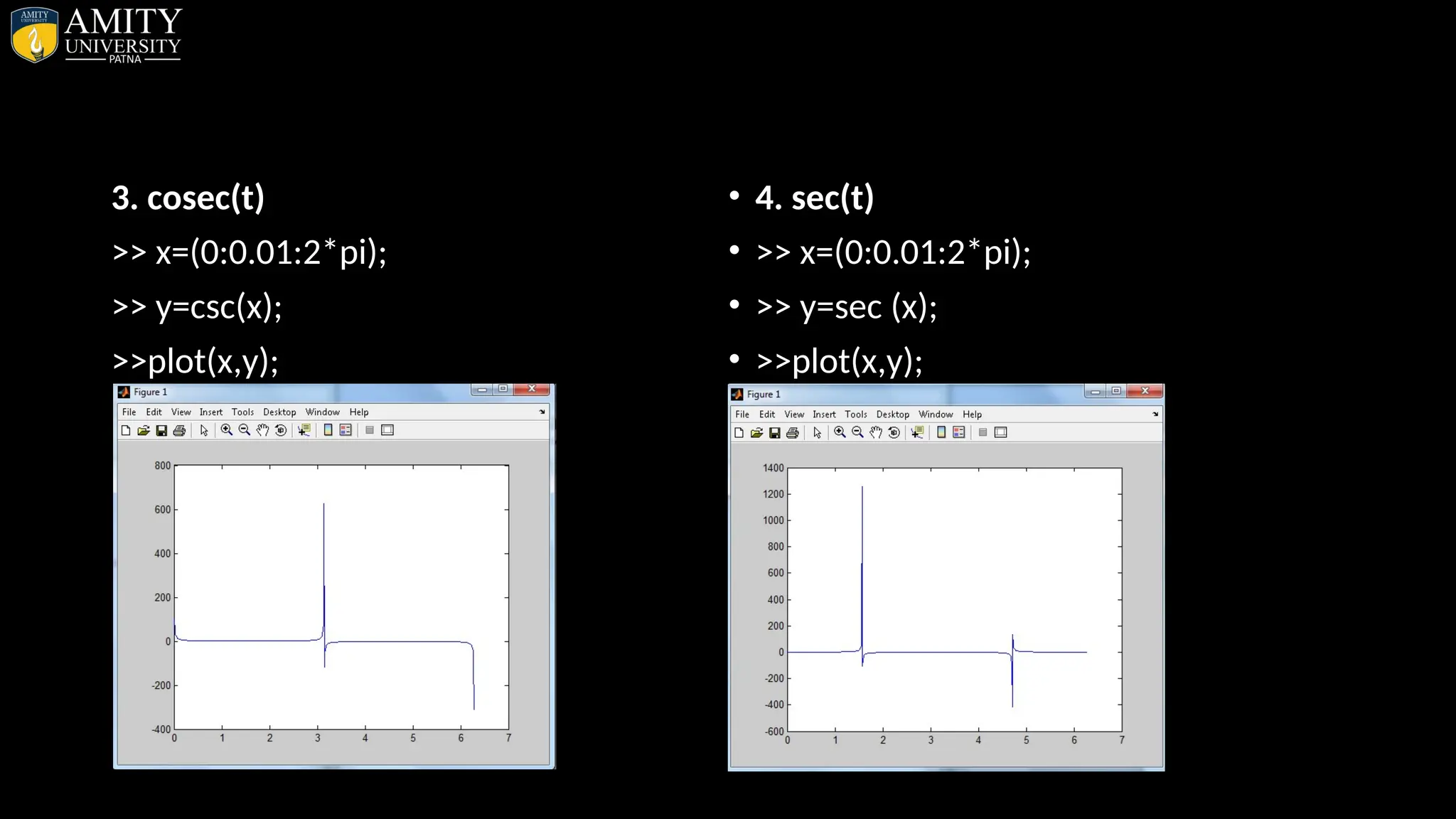
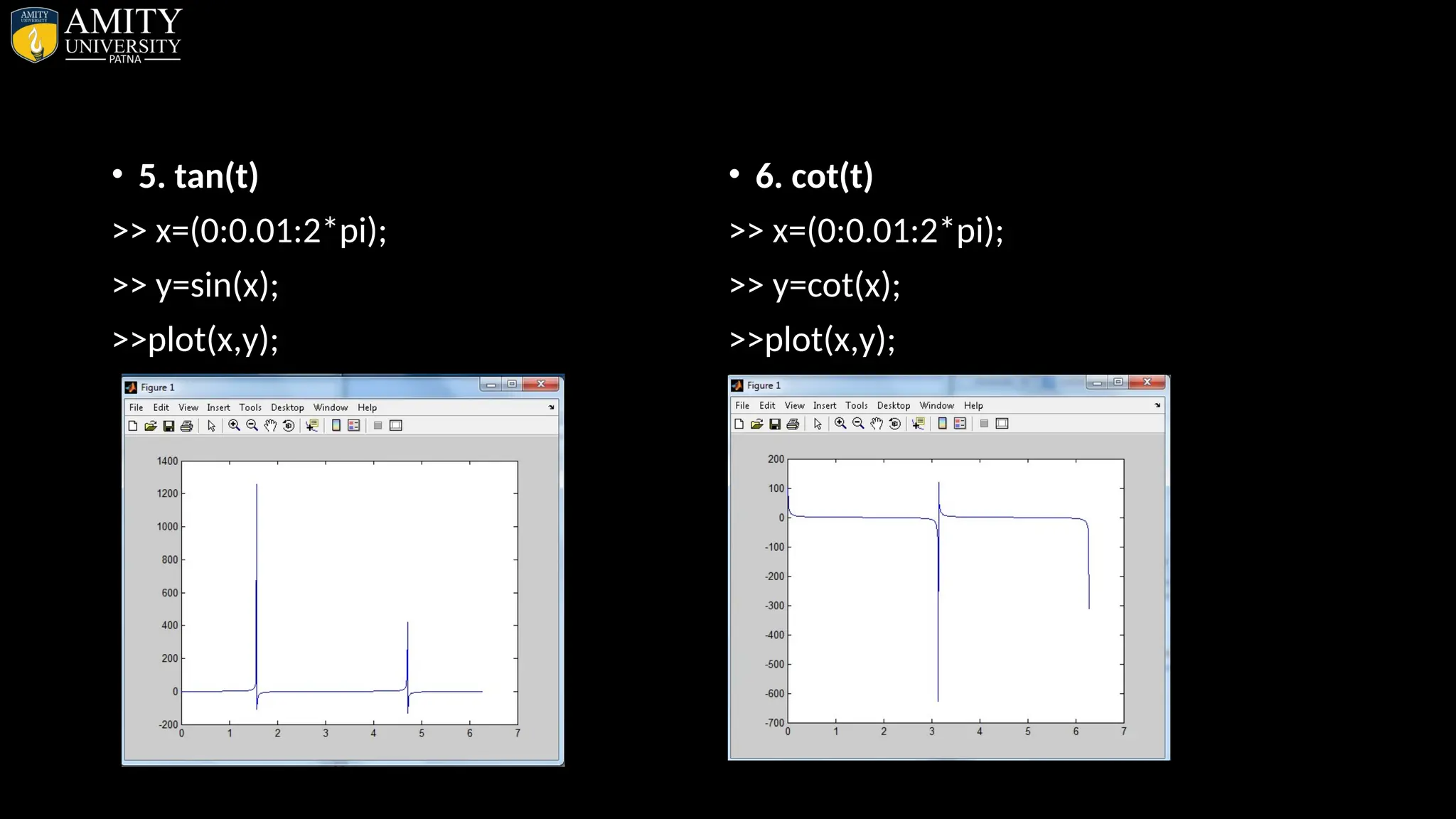
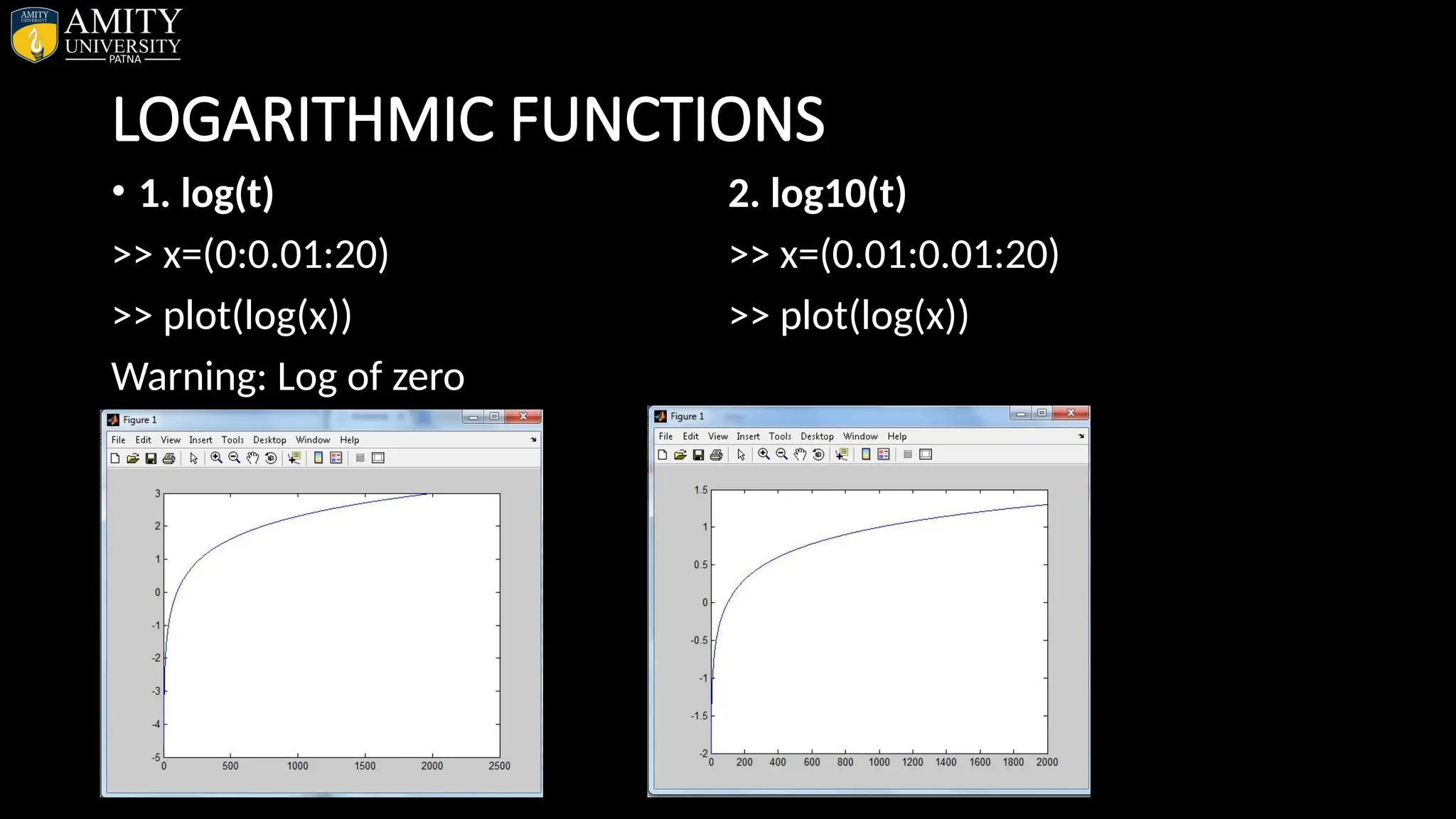
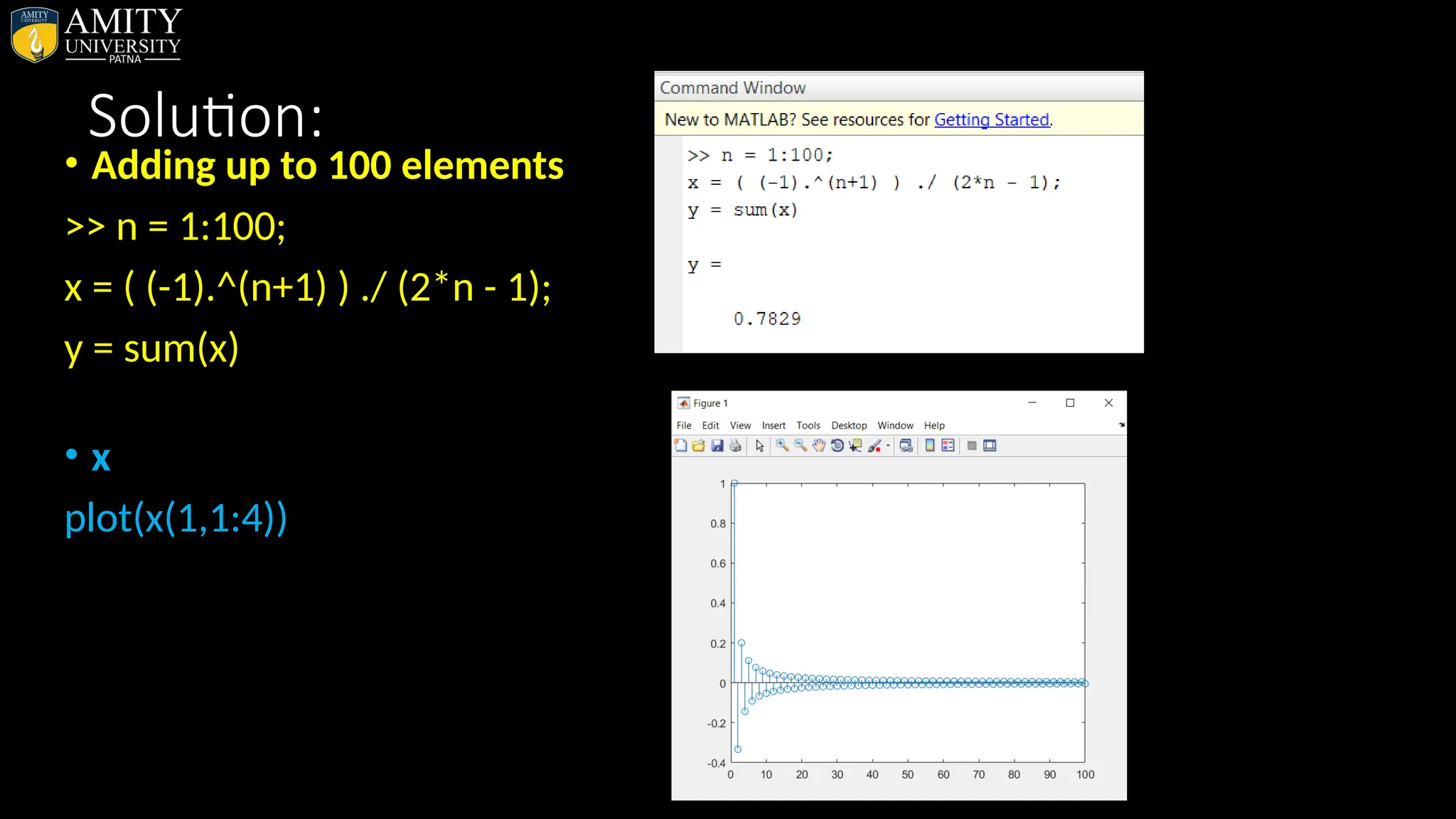
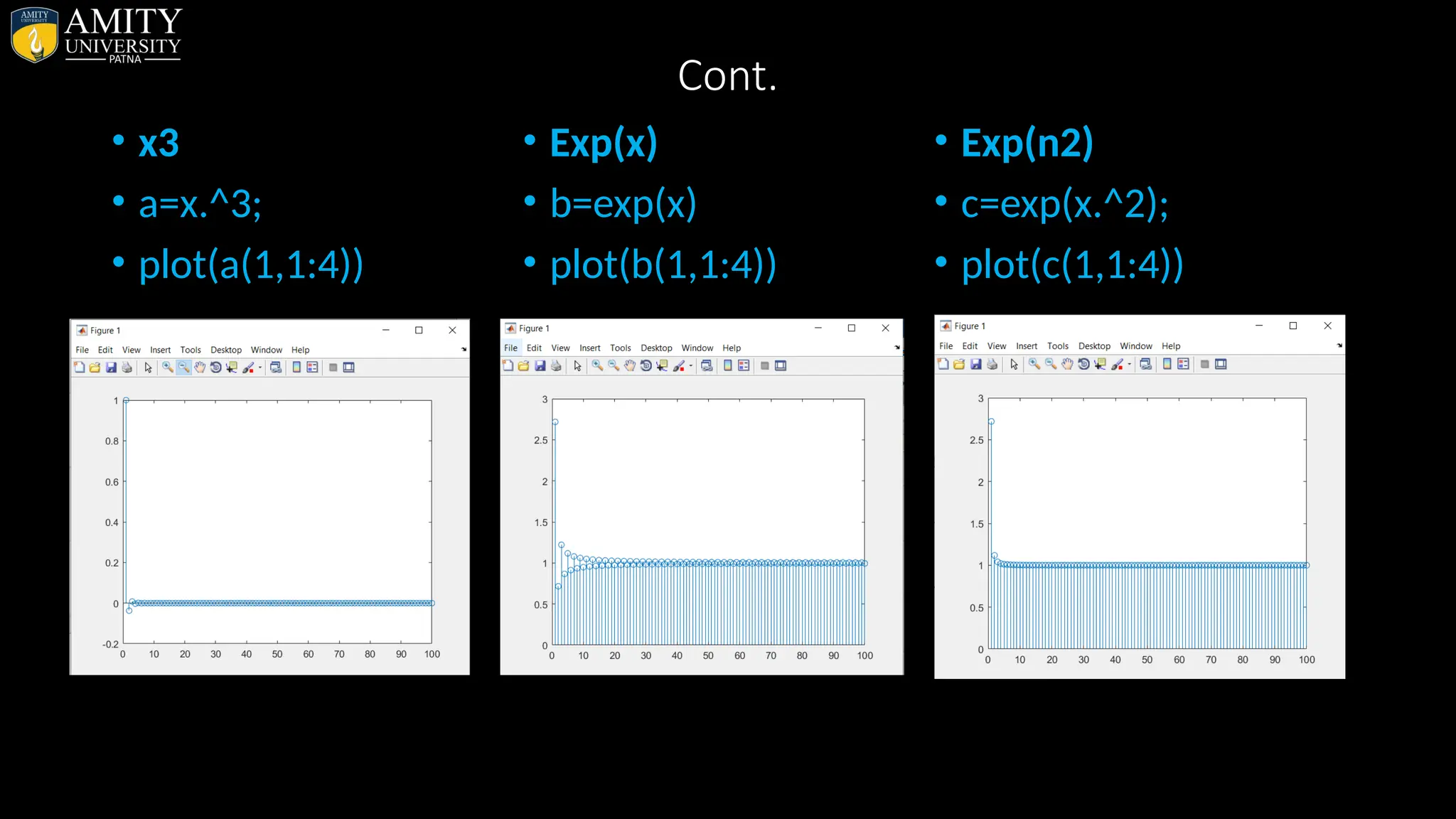
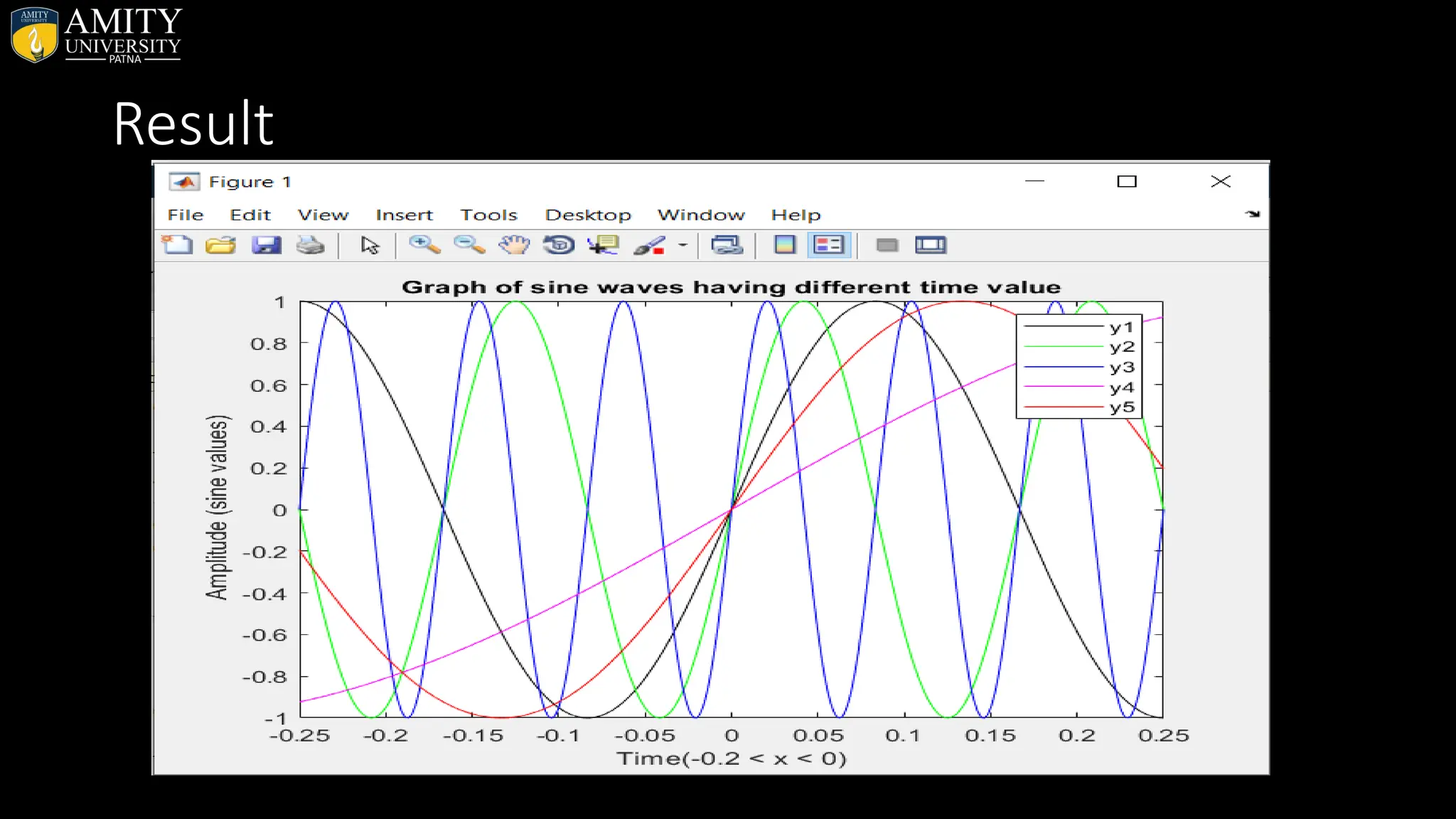
If, Else, Else If Statements: • if expression, statements, end evaluates an expression, and executes a group of statements when the expression is true. An expression is true when its result is nonempty and contains only nonzero elements (logical or real numeric). Otherwise, the expression is false. • The elseif and else blocks are optional. The statements execute only if previous expressions in the if...end block are false. An if block can include multiple elseif blocks. Syntax if expression statements elseif expression statements else statements end

MATLAB PROGRAM:- • %Writing brief Scripts starting each Script with a request for input(using input) to Evaluate the function h(T) using if-else statement, where, h(T) = (T – 10) for 0 < T < 100 = (0.45 T + 900) for T > 100. Exercise: Testing the Scripts written using A). T = 5, h = -5 and B). T = 110, h =949.5%

Program: T=input('enter the value:') if(T>0 & T<100) h=(T-10) elseif(T>100) h=(0.45*T+900) else disp('Enter a number greater than 0'); end • COMMAND WINDOW RESULT:- >>enter the value:5 T = 5 h = -5 >> enter the value:110 T = 110 h = 949.5000

t=0:0.1:10; y=sin(t); z = sin(t) + sin(3*t)/3 + sin(5*t)/5 + sin(7*t)/7 + sin(9*t)/9; plot(t,y,t,z); legend('Sine wave','Square wave') title('Generating square wave from sum of sine waves') xlabel('Time period') ylabel('Amplitude') %Generating a Square Wave from sum of Sine Waves of certain Amplitude and Frequencies.%

Basic 2D and 3D plots Contour Plots A contour plot displays isolines of matrix Z. Label the contour lines using clabel. contour(X,Y,Z), contour(X,Y,Z,n), and contour(X,Y,Z,v) draw contour plots of Z using X and Y to determine the x and y values. • If X and Y are vectors, then length(X) must equal size(Z,2) and length(Y) must equal size(Z,1). The vectors must be strictly increasing or strictly decreasing and cannot contain any repeated values. • If X and Y are matrices, then their sizes must equal the size of Z. Typically, you should set X and Y so that the columns are strictly increasing or strictly decreasing and the rows are uniform (or the rows are strictly increasing or strictly decreasing and the columns are uniform). If X or Y is irregularly spaced, then contour calculates contours using a regularly spaced contour grid, and then transforms the data to X or Y. contour3 creates a 3-D contour plot of a surface defined on a rectangular grid. contour3(X,Y,Z), contour3(X,Y,Z,n), and contour3(X,Y,Z,v) draw contour plots of Z using X and Y to determine the x and y values. • If X and Y are vectors, then length(X) must equal size(Z,2) and length(Y) must equal size(Z,1). The vectors must be strictly increasing or strictly decreasing and cannot contain any repeated values. • If X and Y are matrices, then their sizes must equal the size of Z. Typically, you should set X and Y so that the columns are strictly increasing or strictly decreasing and the rows are uniform (or the rows are strictly increasing or strictly decreasing and the columns are uniform). If X or Y is irregularly spaced, then contour3 calculates contours using a regularly spaced contour grid, and then transforms the data to X or Y.

Bar Graph Plot bar(y) creates a bar graph with one bar for each element in y. If y is a matrix, then bar groups the bars according to the rows in y. bar3 draws a three-dimensional bar graph. bar3(Y) draws a three-dimensional bar chart, where each element in Y corresponds to one bar. When Y is a vector, the x-axis scale ranges from 1 to length(Y). When Y is a matrix, the x-axis scale ranges from 1 to size(Y,1) and the elements in each row are grouped together.

• Pie Chart Plot • pie(X) draws a pie chart using the data in X. Each slice of the pie chart represents an element in X. • • If sum(X) ≤ 1, then the values in X directly specify the areas of the pie slices. pie draws only a partial pie if sum(X) < 1. • • If sum(X) > 1, then pie normalizes the values by X/sum(X) to determine the area of each slice of the pie. • • If X is of data type categorical, the slices correspond to categories. The area of each slice is the number of elements in the category divided by the number of elements in X. • pie3(X) draws a three-dimensional pie chart using the data in X. Each element in X is represented as a slice in the pie chart. • • If sum(X) ≤ 1, then the values in X directly specify the area of the pie slices. pie3 draws only a partial pie ifsum(X) < 1. • • If the sum of the elements in X is greater than one, then pie3 normalizes the values by X/sum(X) to determine the area of each slice of the pie.

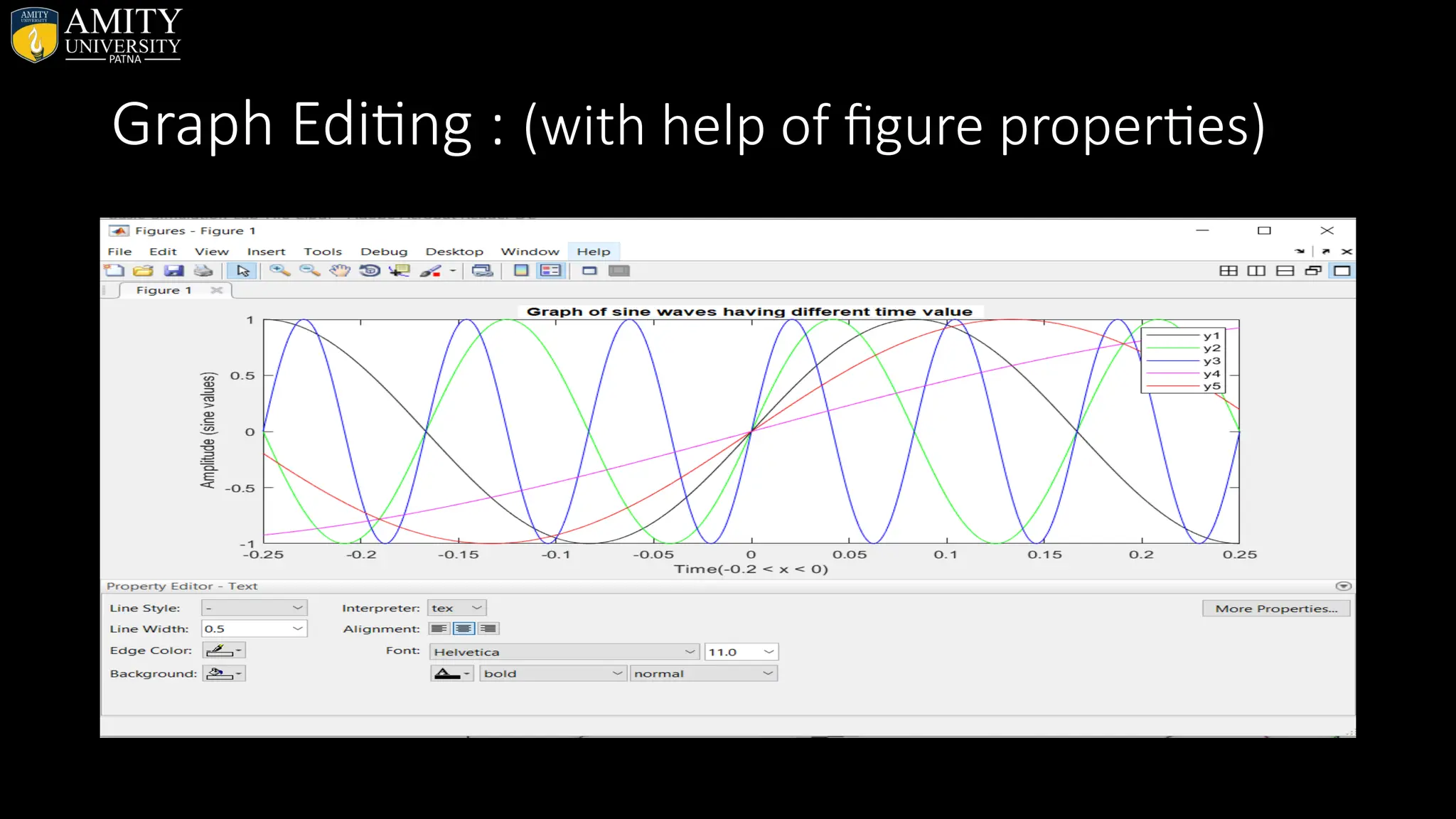
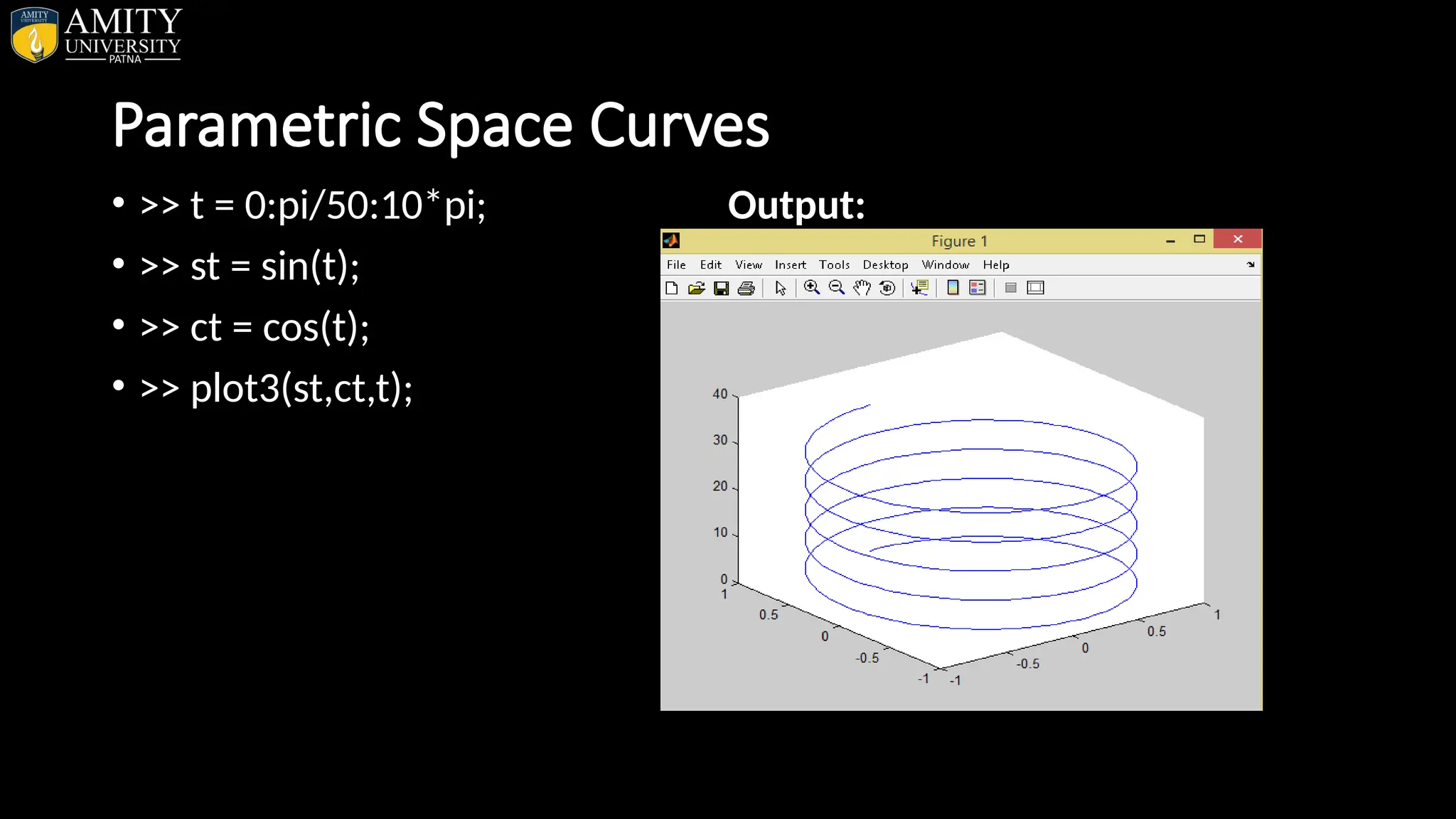
• Sphere Plot • The sphere function generates the x-, y-, and z-coordinates of a unit sphere for use with surf and mesh. • sphere generates a sphere consisting of 20-by-20 faces. • sphere(n) draws a surf plot of an n-by-n sphere in the current figure. • [X,Y,Z] = sphere(n) returns the coordinates of a sphere in three matrices that are (n+1)-by-(n+1) in size. You draw the sphere with surf(X,Y,Z) or mesh(X,Y,Z).

• Line Plots • The plot3 function displays a three-dimensional plot of a set of data points. • plot3(X1,Y1,Z1,...), where X1, Y1, Z1 are vectors or matrices, plots one or more lines in three-dimensional space through the points whose coordinates are the elements of X1, Y1, and Z1.

• Polygon Plots • The fill function creates colored polygons. • fill(X,Y,C) creates filled polygons from the data in X and Y with vertex color specified by C. C is a vector or matrix used as an index into the colormap. If C is a row vector, length(C) must equal size(X,2) and size(Y,2); if C is a column vector, length(C) must equal size(X,1) and size(Y,1). If necessary, fill closes the polygon by connecting the last vertex to the first. • The fill3 function creates flat-shaded and Gouraud-shaded polygons. • fill3(X,Y,Z,C) fills three-dimensional polygons. X, Y, and Z triplets specify the polygon vertices. If X, Y, or Z is a matrix, fill3 creates n polygons, where n is the number of columns in the matrix. fill3 closes the polygons by connecting the last vertex to the first when necessary.

• Cylinder Plot • cylinder generates x-, y-, and z-coordinates of a unit cylinder. You can draw the cylindrical object using surf ormesh, or draw it immediately by not providing output arguments. • [X,Y,Z] = cylinder returns the x-, y-, and z-coordinates of a cylinder with a radius equal to 1. The cylinder has 20 equally spaced points around its circumference.

Parametric Space Curves • >> t = 0:pi/50:10*pi; • >> st = sin(t); • >> ct = cos(t); • >> plot3(st,ct,t); Output:

3-D Contour Lines • >>x = -2:0.25:2; • >>[X,Y] = meshgrid(x); • >>Z = X.*exp(-X.^2-Y.^2); • >>contour3(X,Y,Z,30) • Output:

Pie Chart & Bar Chart • >> x = [1,2,3,4,5,6,7,8]; • >> pie(x); • Output: • >> z = magic(5); • >> b = bar3(z); • Output:

MATLAB : Introduction , Features , Display Windows, Syntax, Operators, Graph Plot

More Related Content

Similar to MATLAB : Introduction , Features , Display Windows, Syntax, Operators, Graph Plot

Recently uploaded

MATLAB : Introduction , Features , Display Windows, Syntax, Operators, Graph Plot