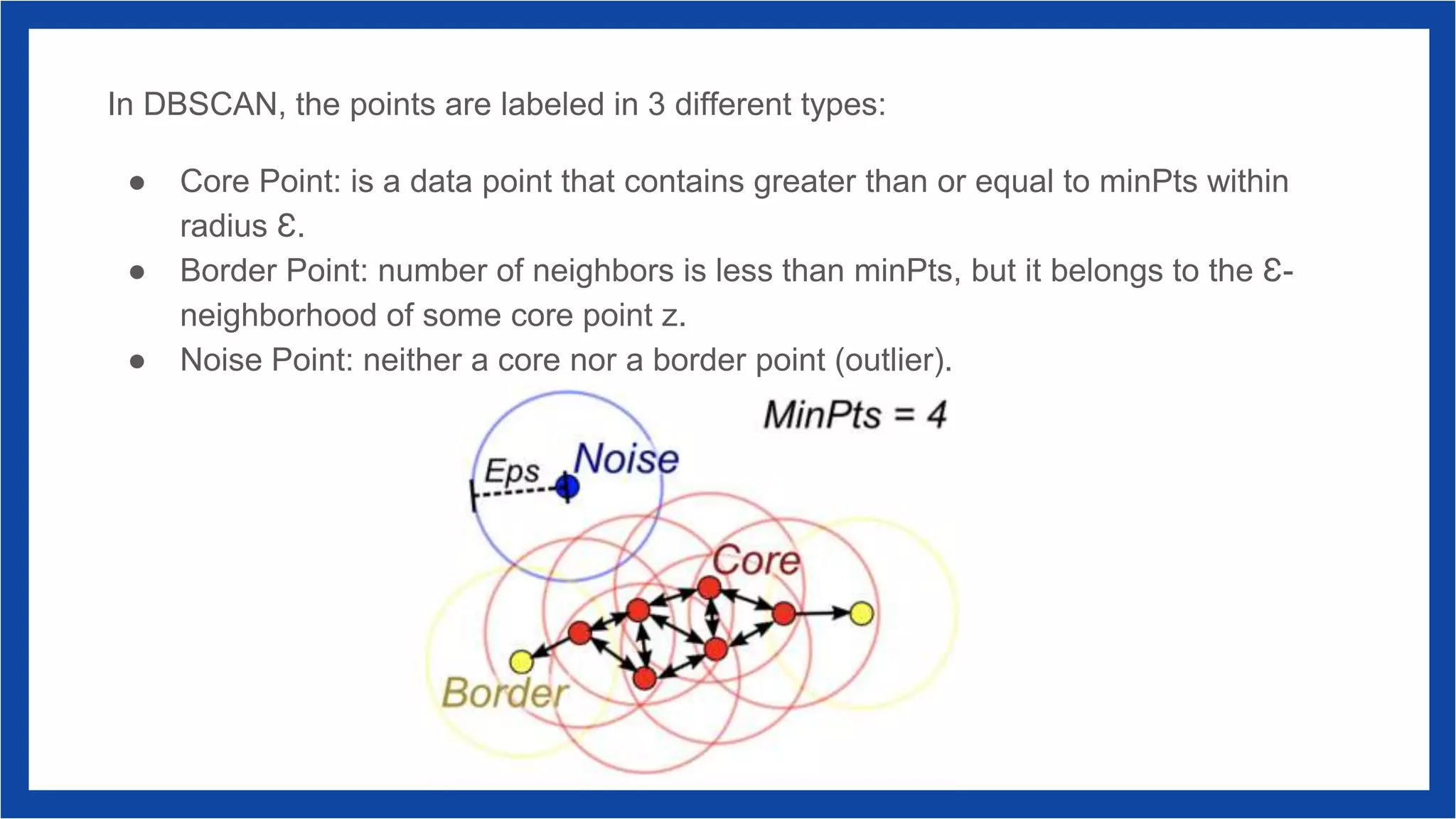
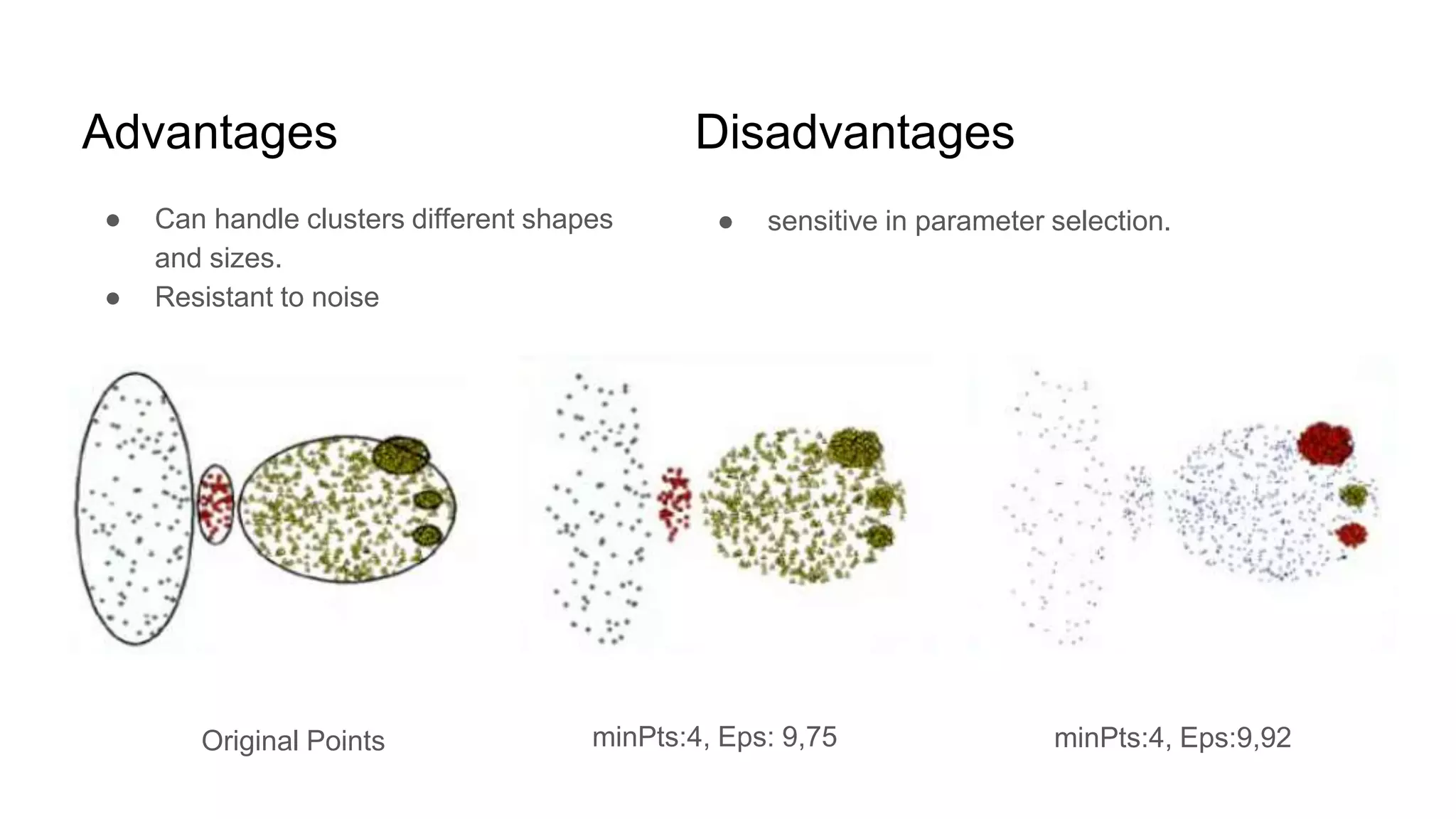
DBSCAN is a density-based clustering algorithm that groups data points based on their density, effectively handling arbitrary cluster shapes and noise. It operates by identifying core points, border points, and noise points, requiring two parameters: eps (the neighborhood radius) and minpts (minimum points required for a core point). While DBSCAN is robust against noise and flexible with cluster shapes, it is sensitive to the selection of its parameters.