Relational Model in dbms & sql database

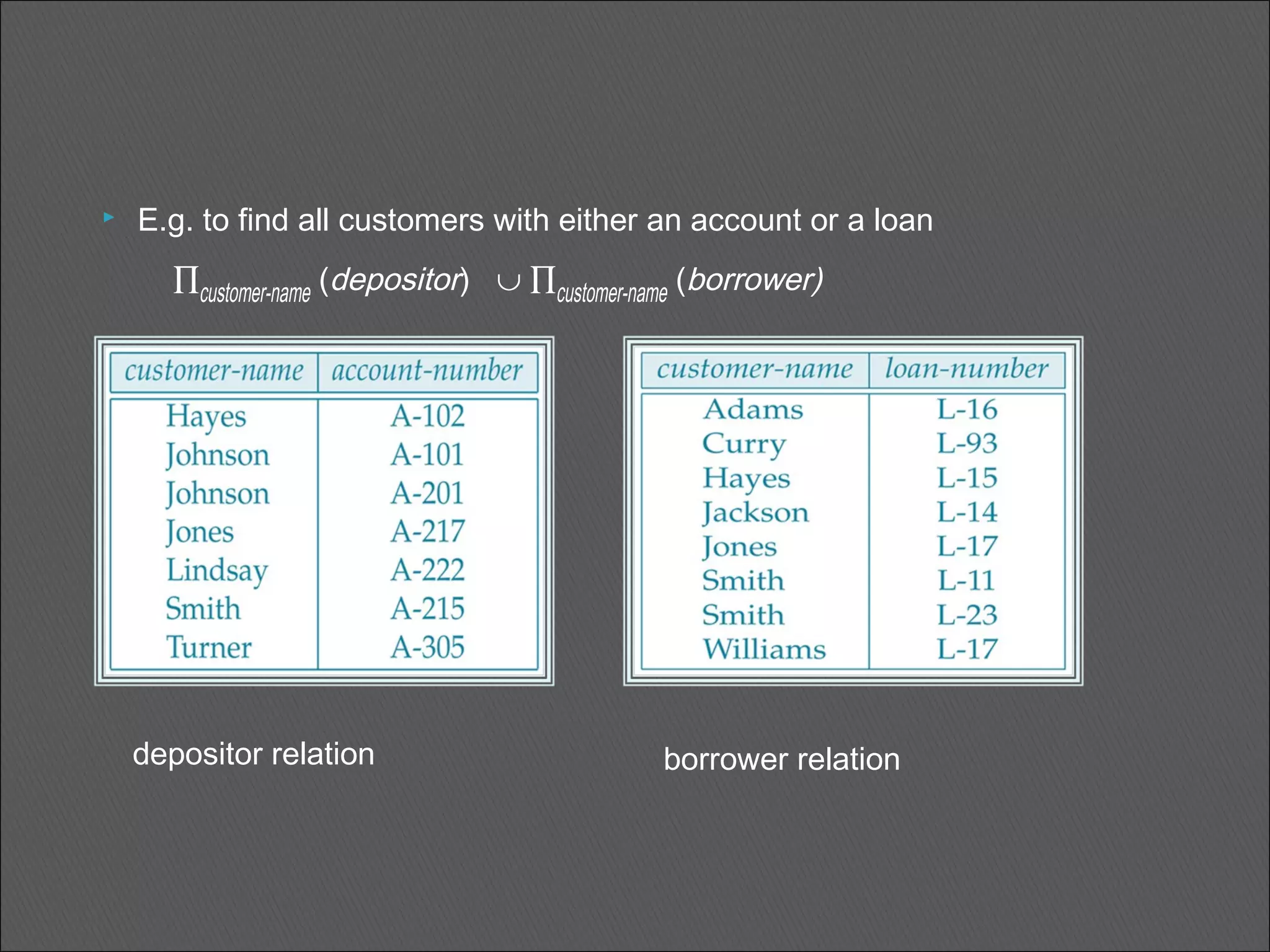
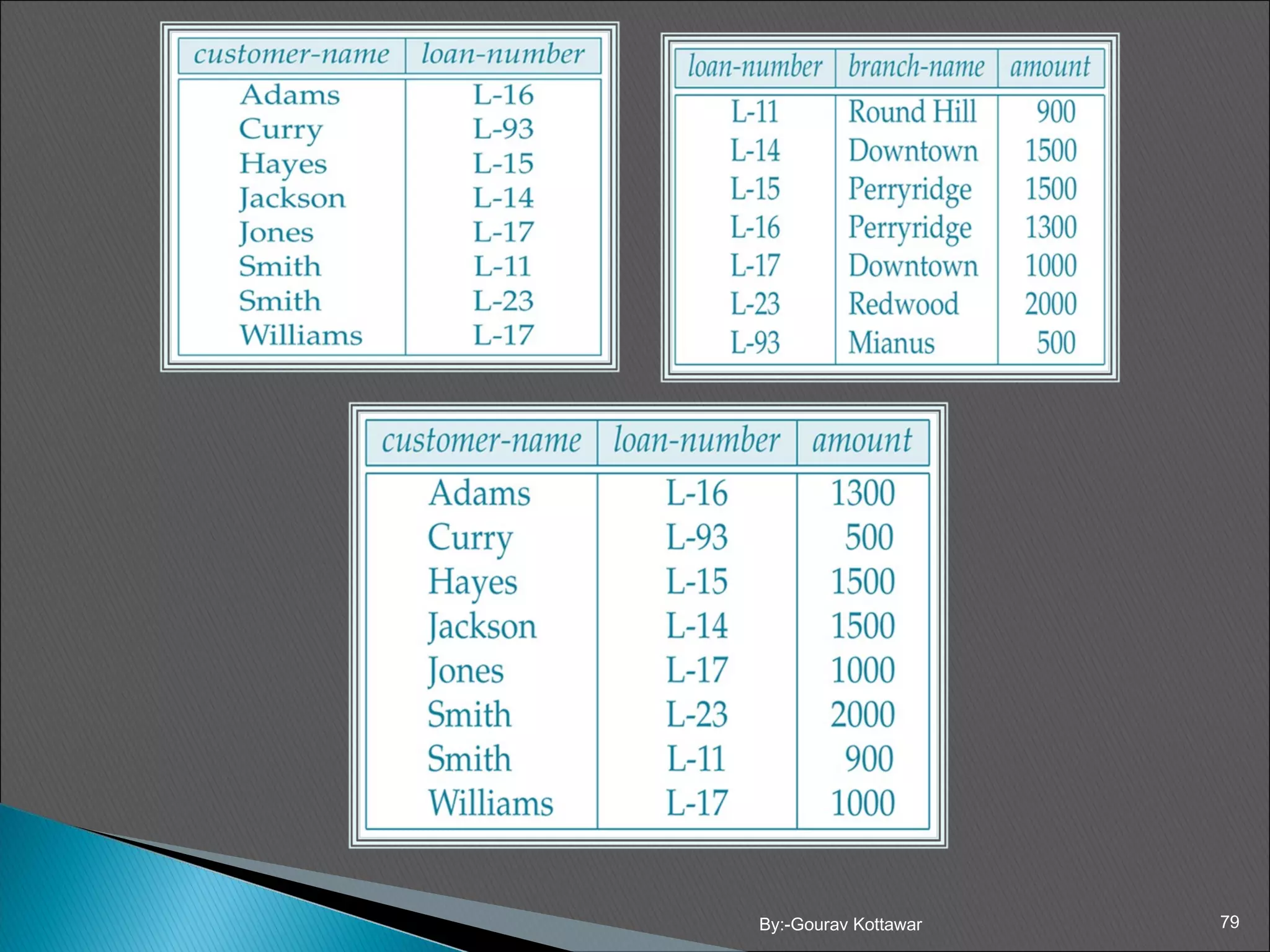
 Codd’s rules  Relational data model & relational algebra  Relational model concept  Relational model constraints  Relational Algebra  Relational database language  Data definition in SQL, Views and  Queries in SQL, Specifying constraints and Indexes in SQL, Specifying constraints management systems,Oracle , Ingres/SQL Server / My SQL

 Codd's Rules can be divided into 5 functional areas – ◦ Foundation Rules ◦ Structural Rules ◦ Integrity Rules ◦ Data Manipulation Rules ◦ Data Independence Rules 5By:-Gourav Kottawar

 Foundation Rules (Rules 0 & 12)  Rule 0 –  Any system claimed to be a RDBMS must be able to manage databases entirely through its relational capabilities. ◦ All data definition & manipulation must be able to be done through relational operations. 6By:-Gourav Kottawar

 Rule 12 – Non subversion Rule -  If a RDBMS has a low level (record at a time) language, that low level language cannot be used to subvert or bypass the integrity rules & constraints expressed in the higher-level relational language. ◦ All database access must be controlled through the DBMS so that the integrity of the database cannot be compromised without the knowledge of the user or the DBA.  This does not prohibit use of record at a time languages e.g. PL/SQL  E.g C++ (oracle coding) should not bypass constraints 7By:-Gourav Kottawar

 Structural Rules (Rules 1 & 6) ◦ The fundamental structural construct is the table. ◦ Codd states that an RDBMS must support tables, domains, primary & foreign keys. ◦ Each table should have a primary key. 8By:-Gourav Kottawar

 Rule 1 -  All info in a RDB is represented explicitly at the logical level in exactly one way - by values in a table. ◦ ALL info even the Metadata held in the system catalogue MUST be stored as relations(tables) & manipulated in the same way as data. 9By:-Gourav Kottawar

 Rule 6 - View Updating –  All views that are theoretically updatable are updatable by the system. (Primary key should be specified in creating views ) ◦ Not really implemented yet by any available system. ◦ (As if one column of view is shared by two users it is not possible to update even if the view is updatable) 10By:-Gourav Kottawar

 Rule 10 - Integrity independence -  Integrity constraints specific to a particular RDB MUST be definable in the relational data sublanguage(SQL) & storable in the DB, NOT the application program. ◦ This gives the advantage of centralized control & enforcement 11By:-Gourav Kottawar

 Integrity Rules (Rules 3 & 10) ◦ Integrity should be maintained by the DBMS not the application.  Rule 3 - Systematic treatment of null values -  Null values are supported for representation of 'missing' & inapplicable information in a systematic way & independent of data type. 12By:-Gourav Kottawar

 Data Manipulation Rules (Rule 2, 4, 5 & 7)  User should be able to manipulate the 'Logical View' of the data with no need for knowledge of how it is Physically stored or accessed.  Rule 2 - Guaranteed Access -  Each & every datum in an RDB is guaranteed to be logically accessible by a combination of table name, primary key value & column name. 13By:-Gourav Kottawar

 Rule 4 - Dynamic on-line Catalog based on relational model  The DB description (metadata) is represented at logical level in thesame way as ordinary data, so that same relational language can be used to interrogate the metadata as regular data. ◦ System & other data stored & manipulated in the same way. ◦ User accounts, set of privileges, user constraints all the info should get stored in table form & also can be viewed with the usual SQL commands 14By:-Gourav Kottawar

 Rule 5 - Comprehensive Data Sublanguage (SQL) -  RDBMS may support many languages & modes of use, but there must be at least ONE language whose statements can express ALL of the following – ◦ Data Definition ◦ View Definition ◦ Data manipulation (interactive & via program) ◦ Integrity constraints ◦ Authorization ◦ Transaction boundaries (begin, commit & rollback)  1992 - ISO standard for SQL provides all these functions 15By:-Gourav Kottawar

 Rule 7 - High-level insert, update & delete -  Capability of handling a base table or view as a single operand applies not only to data retrieval but also to insert, update & delete operations. 16By:-Gourav Kottawar

 Data Independence Rules (Rules 8, 9, 11)  These rules protect users & application developers from having to change the applications following any low-level reorganisation of the DB. 17By:-Gourav Kottawar

Rule 8 - Physical Data Independence -  Application Programs & Terminal Activities remain logically unimpaired whenever any changes are made either to the storage organisation or access methods. Rule 9 - Logical Data Independence -  Appn Progs & Terminal Acts remain logically unimpaired when information-preserving changes of any kind that theoretically permit unimpairment are made to the base tables. 18By:-Gourav Kottawar

 Rule 11 - Distribution Independence - ◦ This means that an Application Program that accesses the DBMS on a single computer should also work ,without modification, even if the data is moved from one computer to another in a network environment.  The user should 'see' one centralised DB whether data is located on one or more computers. ◦ This rule does not say that to be fully Relational the DBMS must support distributed DB's but that if it does the query must remain the same. 19By:-Gourav Kottawar

 Collection of tables with each table assigned a unique name  A table is a collection of relationships , hence there is correspondence between the concept of table & the mathematical concept of relation  A row in a table represents a relationship among a set of values called as tuple.  In relational model a table is termed as relation  E.g consider account table with three columns branch-name , account-number, balance 21By:-Gourav Kottawar

 Mathematics define a relation to be a subset of a Cartesian product of a list of domains  This definition corresponds almost exactly with our definition of table  The In general a relation or table will be a subset of the set of all possible rows D1×D2 ×D3  In general , a table of n attributes must be a subset of  D1 × D2 ×…………. × Dn-1 × Dn 22By:-Gourav Kottawar

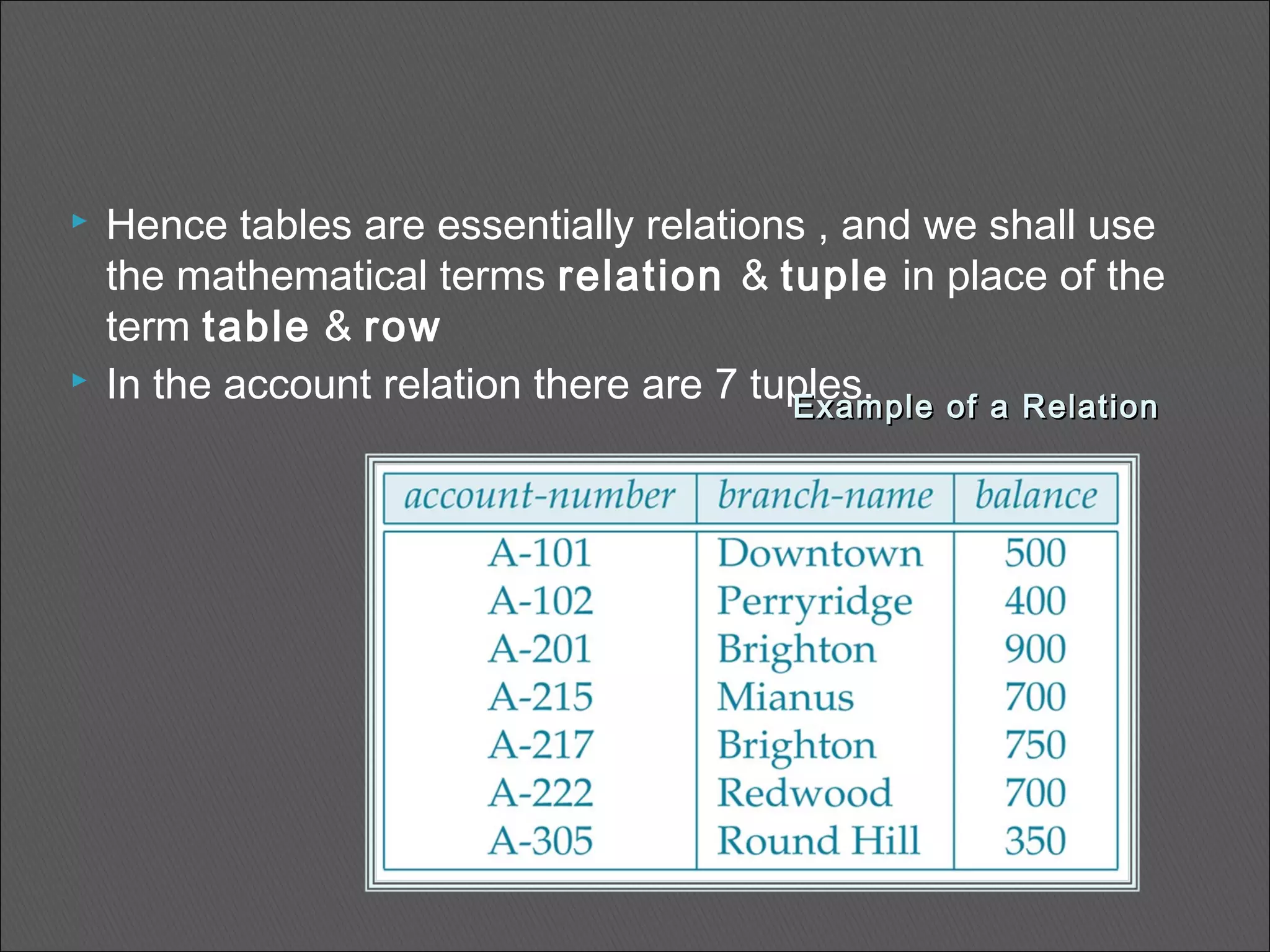
 Hence tables are essentially relations , and we shall use the mathematical terms relation & tuple in place of the term table & row  In the account relation there are 7 tuples.Example of a RelationExample of a Relation

 Let the tuple variable be “t” which refer to the first tuple of the relation.  We use the notation “t[branch-name]” to denote the value of t on the branch-name attribute.  Thus , t [branch-name]=“Downtown,” & t[account- number]=“A-101” , t[balance]=500. 24By:-Gourav Kottawar

 Relational Data Model consists of three basic components: ◦ A set of domains and a set of relations ◦ Operations on relations ◦ Integrity rules RDBMS DBMS Attribute Column Domain Column Type Tuple Row Attribute Value Column Value 25By:-Gourav Kottawar

A1 A2 A3 ... An a1 a2 a3 an b1 b2 a3 cn a1 c3 b3 bn . . . x1 v2 d3 wn Set theoretic Domain — set of values assigned to attributes like a data type int , char Relation- subset of cartesian product of one or more domains FINITE only; empty set allowed Tuples = rows of a relation. Cardinality = number of tuples for each domain Relation as table Rows = tuples Columns = components Names of columns = attributes REL (A1,A2,...,An) C a r d i n a l i t y Attributes Tuple 26By:-Gourav Kottawar

 We must differentiate between the database schema and a database instance.  The concept of relation schema corresponds to the programming language notion of type definition.  Example of type definition in ‘C++’ language  Class stud {  int rollno;  char name[20];  char addr[20];  getdata();  putdata();  }  It is convenient to give a name to a relation schema , just as we give names to type definitions in programming language. 28By:-Gourav Kottawar

 Logical schema: ◦ Students(sid: string, name: string, login: string, age: integer, gpa:real) ◦ Faculty(fid:string, fname:string, sal:real) ◦ Courses(cid: string, cname:string, credits:integer) ◦ Enrolled(sid:string, cid:string, grade:string)  Physical schema: ◦ Relations stored as unordered files. ◦ Index on first column of Students.  External Schema (View): ◦ Course_info(cid:string,fname:string, enrollment:integer) Database Schema 29By:-Gourav Kottawar

 Consider a relation account. We use Account-schema to denote relation schema for relation account.  Thus , ◦ Account-schema = (branch-name, account- number, balance)  We denote the fact that account is a relation on Account- schema by ◦ account (Account-schema)  In general , a relation schema comprises a list of attributes and their corresponding domains. account relation

 The concept of relation instance corresponds to the programming language notion of a value of a variable.  The value of a variable may change with time , similarly the relation instance may change with time when relation is updated.  Example of a relation instance:  Consider customer relation , the schema for that relation is ◦ Customer-schema = (customer-name, customer-street, customer-city) customer relation

 The current values (relation instance) of a relation are specified by a table  An element t of r is a tuple, represented by a row in a table Jones Smith Curry Lindsay customer-name Main North North Park customer-street Harrison Rye Rye Pittsfield customer-city customer attributes (or columns) tuples (or rows) 32By:-Gourav Kottawar

Name Address Telephone Bob 123 Main St 555-1234 Bob 128 Main St 555-1235 Pat 123 Main St 555-1235 Harry 456 Main St 555-2221 Sally 456 Main St 555-2221 Sally 456 Main St 555-2223 Pat 12 State St 555-1235 33By:-Gourav Kottawar

 Order of tuples is irrelevant (tuples may be stored in an random order)  E.g. account relation with unordered tuples 34By:-Gourav Kottawar

 A database consists of multiple relations  Information about an enterprise is broken up into parts, with each relation storing one part of the information E.g.: account : stores information about accounts deposits : stores information about which customer owns which account customer : stores information about customers  Storing all information as a single relation such as bank(account-number, balance, customer- name, ..) results in repetition of information (e.g. two customers own an account) ◦ the need for null values (e.g. represent a customer without an account) 35By:-Gourav Kottawar

 There are various restrictions on data that can be specified on a relational database schema in the form of constraints.  These include domain constraints , key constraints , entity integrity & referential integrity constraints.  Other types of constraints , called data dependencies which include functional dependencies & multivalued dependencies are used mainly for database design by normalization. 41By:-Gourav Kottawar

 Domain constraints: attribute must be an atomic value  The data types associated with domains typically include standard numeric data types for integers (such as short-integer , integer, long-integer) and real numbers (float & double-precision float).  Characters , fixed length strings and variable length strings are also available, as are date, time, timestamp, and money data types. 42By:-Gourav Kottawar

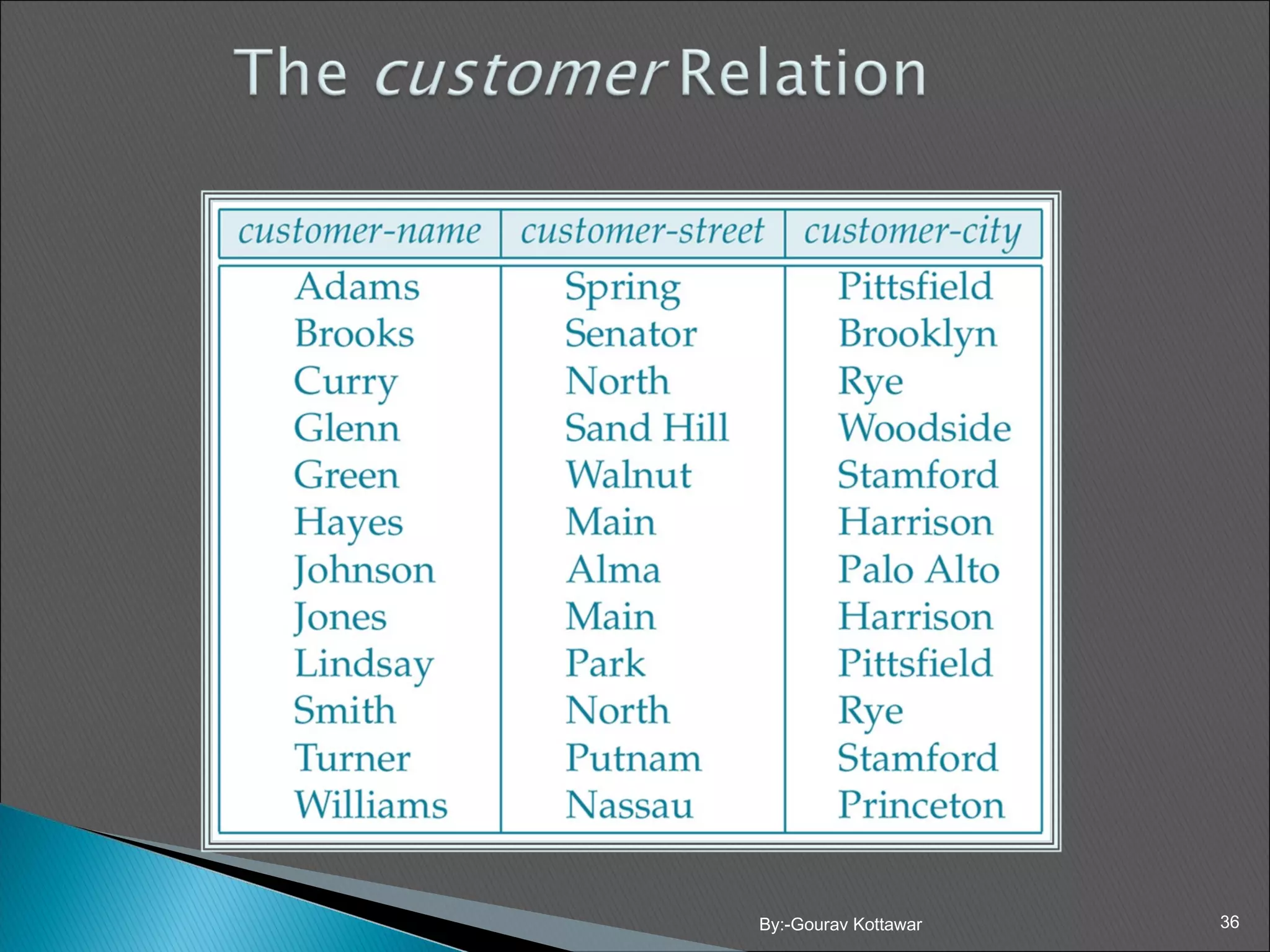
 Key Constraints: A relation is defined as a set of tuples. By definition all elements of a set are distinct; hence all tuples in a relation must also be distinct.  This means that no two tuples can have the same combination of values for all their attributes.  Suppose we form a superkey with combination of some set of attributes. Then the value of the superkey of one tuple should not be same as that of the value of superkey of second tuple. ◦ i.e t1[SK] = t2[SK]  A super key SK specifies a uniqueness constraint that no two distinct tuples in a relation can have same value for SK. 43By:-Gourav Kottawar

 A key is determined from the meaning of the attributes , and the property is time-invariant; it must continue to hold when we insert new tuples in the relation.  Another constraint on attributes specifies whether null values are or are not permitted.  For e.g if every STUDENT tuple must have a valid ,non-null value for the Name attribute, then Name of STUDENT is constrained to be NOT NULL. 44By:-Gourav Kottawar

 Entity Integrity: Entity integrity rule is concerned with primary key values. Primary key does not allow null values.  Example: If the E_id is consisting a null value then it means that the employee whose information is stored in that tuple does not exist at all in the company. Therefore, it is great loss to that employee as he is working in the company but database is not able to search any info about him as his tuple is not given any key. 45By:-Gourav Kottawar

 This contradicts the requirements for a primary key. id Name 101 103 104 107 110 112 Jones Smith Lory Evan Drew Smith (a) (b) id Name 101 @ 104 107 110 @ @ Jones Smith Lory Evan Drew Lory Smith 46By:-Gourav Kottawar

 Entity Integrity constraint (rule) states that If attribute A of relation r(R) is a prime attribute of r(R), then A cannot accept null values.  Referential Integrity: The referential integrity constraint is specified between two relations and is used to maintain the consistency among tuples of the two relations.  Informally , the referential integrity constraint states that a tuple in one relation that refers to another relation must refer to an existing tuple in that relation. 47By:-Gourav Kottawar

 For e.g consider two relations Department & Employee EMPLOYEE FNAME LNAME ADDRESS EMP-ID DNO John Smith Castle 1001 5 Ramesh Narayan Berry 1002 5 James Borg Dallas 1003 1 Ahmad Jabbar Stone 1004 4 DEPARTME NT DNAME DNUMBER MGRSSN MGRSTARTDATE Research 5 333 1988-05-22 Administration 4 987 1995-01-01 Headquarters 1 888 1981-06-19 48By:-Gourav Kottawar

 The attribute DNO of employee gives the department number for which each employee works; hence, its value in every EMPLOYEE tuple must match the DNUMBER value of some tuple in the DEPARTMENT relation.  To define referential integrity more formally , we must define the concept of a foreign key.  The conditions for a foreign key , given below, specify a referential integrity constraint between the two relation schemas R1 & R2. 49By:-Gourav Kottawar

 Referential integrity is very important. Because the foreign key is used as a surrogate for another entity, the rule enforces the existence of a tuple for the relation corresponding to the instance of the referred entity.  The integrity rule also implicitly defines the possible actions that could be taken whenever updates , insertions, and deletions are made  If we delete a tuple that is a target of a foreign key reference , then three explicit possibilities exist to maintain the database integrity: 51By:-Gourav Kottawar

◦ All tuples that contain references to the deleted tuple should also be deleted. This option is referred to as domino or cascading deletion, since one deletion leads to another. ◦ A tuple which is referred by other tuples in the database cannot be deleted. ◦ If the tuple is deleted , to avoid the domino effect , the pertinent foreign key attributes of all referencing tuples are set to null. 52By:-Gourav Kottawar

 Hence Referential Integrity rule states that Given two relations R & S , suppose R refers to the relation S via a set of attributes that forms the primary key of S & this set of attributes forms a foreign key in R. Then the value of the foreign key in a tuple in R must either be equal to the primary key of a tuple of S or be entirely null. 53By:-Gourav Kottawar

 Relational algebra is a Procedural query language.  It consists of set of operations that take one or two relations as input and produce a new relation as their result.  Six basic operators ◦ select ◦ project ◦ union ◦ set difference ◦ Cartesian product ◦ rename 54By:-Gourav Kottawar

 The select operation selects tuples that satisfy a given predicate.  We use lowercase Greek letter sigma (σ) to denote selection, the predicate appears as subscript to σ.  The argument relation is given in parenthesis following the σ.  E.g Suppose we want to find all tuples where the branch-name is= Perryridge σbranch-name = “Perryridge” (loan) Loan relation

 Notation: ∏A1, A2, …, Ak (r) where A1, A2 are attribute names and r is a relation name.  The result is defined as the relation of k columns obtained by erasing the columns that are not listed  Duplicate rows removed from result, since relations are sets  E.g. The query to list all loan numbers & the amount of the loan can be wrtiten as: ◦ ∏loan-number,amount (loan)

 Relation r: A B C 10 20 30 40 1 1 1 2 A C α α β β 1 1 1 2 = A C α β β 1 1 2 • ∏A,C (r) α α β β 58By:-Gourav Kottawar

 Notation: r ∪ s  Defined as: r ∪ s = {t | t ∈ r or t ∈ s}  For r ∪ s to be valid. 1. r, s must have the same arity (same number of attributes) 2. The attribute domains must be compatible (e.g., 2nd column of r deals with the same type of values as does th2nd column of s)

 E.g. to find all customers with either an account or a loan ∏customer-name (depositor) ∪ ∏customer-name (borrower) depositor relation borrower relation

 Notation r – s  Defined as: r – s = {t | t ∈ r and t ∉ s}  Set difference operation , denoted by – , allows us to find tuples that are in one relation but are not in another.  The expression r – s results in a relation containing those tuples in r but not in s. (common tuples are eliminated)  Set differences must be taken between compatible relations. ◦ r and s must have the same arity ◦ attribute domains of r and s must be compatible 62By:-Gourav Kottawar

 Suppose we want to find all customers of the bank with an account but no loan, we write ∏customer-name (depositor) – ∏customer-name (borrower) depositor relation borrower relation

 Notation r x s  Allows us to combine information from any two relations. It is the concatenation of tuples belonging to the two relations.  A new resultant relation schema is created consisting of all possible combinations of the tuples. 65By:-Gourav Kottawar

 Select Operation : This operation is used to select rows from a table (relation) that specifies a given logic, which is called as a predicate. The predicate is a user defined condition to select rows of user's choice.  Project Operation : If the user is interested in selecting the values of a few attributes, rather than selection all attributes of the Table (Relation), then one should go for PROJECT Operation  PROJECT eliminates columns while SELECT eliminates rows. 68By:-Gourav Kottawar

 SELECT is used to obtain a subset of the tuples of a relation that satisfy a select condition.  For example, find all employees born after 1st Jan 1950:  SELECTdob '01/JAN/1950'(employee) Relational PROJECT  The PROJECT operation is used to select a subset of the attributes of a relation by specifying the names of the required attributes.  For example, to get a list of all employees surnames and employee numbers:  PROJECTsurname,empno(employee) 69By:-Gourav Kottawar

 Find all loans of over $1200 Find the loan number for each loan of an amount greater than $1200 σamount > 1200 (loan) ∏ loan-number (σamount > 1200 (loan)) 71By:-Gourav Kottawar

We define additional operations that do not add any power to the relational algebra, but that simplify common queries.  Set intersection  Natural join  Division  Assignment 74By:-Gourav Kottawar

 Notation: r ∩ s  Defined as:  r ∩ s ={ t | t ∈ r and t ∈ s }  Assume: ◦ r, s have the same arity ◦ attributes of r and s are compatible  Thus ,set intersection is not a fundamental operation and does not add any power to the relational algebra. 75By:-Gourav Kottawar

 Notation: r s r join s  The natural join is a binary operation that allows us to combine certain selections & a Cartesian product into one operation.  It forms a Cartesian product of its two arguments , performs selection forcing equality on those attributes that appear in both relation schemas , and finally removes duplicate attributes.  Join is basically the Cartesian product of the relations followed by selection operation.  Let r and s be relations on schemas R and S respectively. The n, r s is a relation on schema R ∪ S obtained as follows:  r s = ∏ R U S (σ r.A1= s.A1 ^r.A2=s.A2^…^r. An = s. An rxs) where R S= {A1,A2,……,An} ∩ 77By:-Gourav Kottawar

 E.g find the names of all customers who have a loan at the bank , and find the amount of the loan.  Using natural join the query can be expressed as : ◦ ∏customer-name,loan-number,amount( borrower loan) borrower loan

 The content of the database may be modified using the following operations: ◦ Deletion ◦ Insertion ◦ Updation  All these operations are expressed using the assignment operator. 82By:-Gourav Kottawar

 A delete request is expressed similarly to a query, except instead of displaying tuples to the user, the selected tuples are removed from the database.  Can delete only whole tuples; cannot delete values on only particular attributes  A deletion is expressed in relational algebra by: r ← r – E where r is a relation and E is a relational algebra query. 83By:-Gourav Kottawar

 Delete all account records in the Perryridge branch. Delete all loan records with amount in the range of 0 to 50 loan ← loan – σ amount ≥ 0 and amount ≤ 50 (loan) account ← account – σ branch-name = “Perryridge” (account) 84By:-Gourav Kottawar

 To insert data into a relation, we either: ◦ specify a tuple to be inserted ◦ write a query whose result is a set of tuples to be inserted  in relational algebra, an insertion is expressed by: r ← r ∪ E where r is a relation and E is a relational algebra expression.  The insertion of a single tuple is expressed by letting E be a constant relation containing one tuple. 85By:-Gourav Kottawar

 Insert information in the database specifying that Smith has $1200 in account A-973 at the Perryridge branch. account ← account ∪ {(“Perryridge”, A-973, 1200)} depositor ← depositor ∪ {(“Smith”, A-973)} 86By:-Gourav Kottawar

 A mechanism to change a value in a tuple without changing all values in the tuple  Use the generalized projection operator to do this task r ← ∏ F1, F2, …, FI, (r)  Each Fi is either ◦ the ith attribute of r, if the ith attribute is not updated, or, ◦ if the attribute is to be updated Fi is an expression, involving only constants and the attributes of r, which gives the new value for the attribute 87By:-Gourav Kottawar

Relational Model in dbms & sql database

More Related Content

What's hot

Viewers also liked

Similar to Relational Model in dbms & sql database

More from gourav kottawar

Recently uploaded

Relational Model in dbms & sql database

Editor's Notes