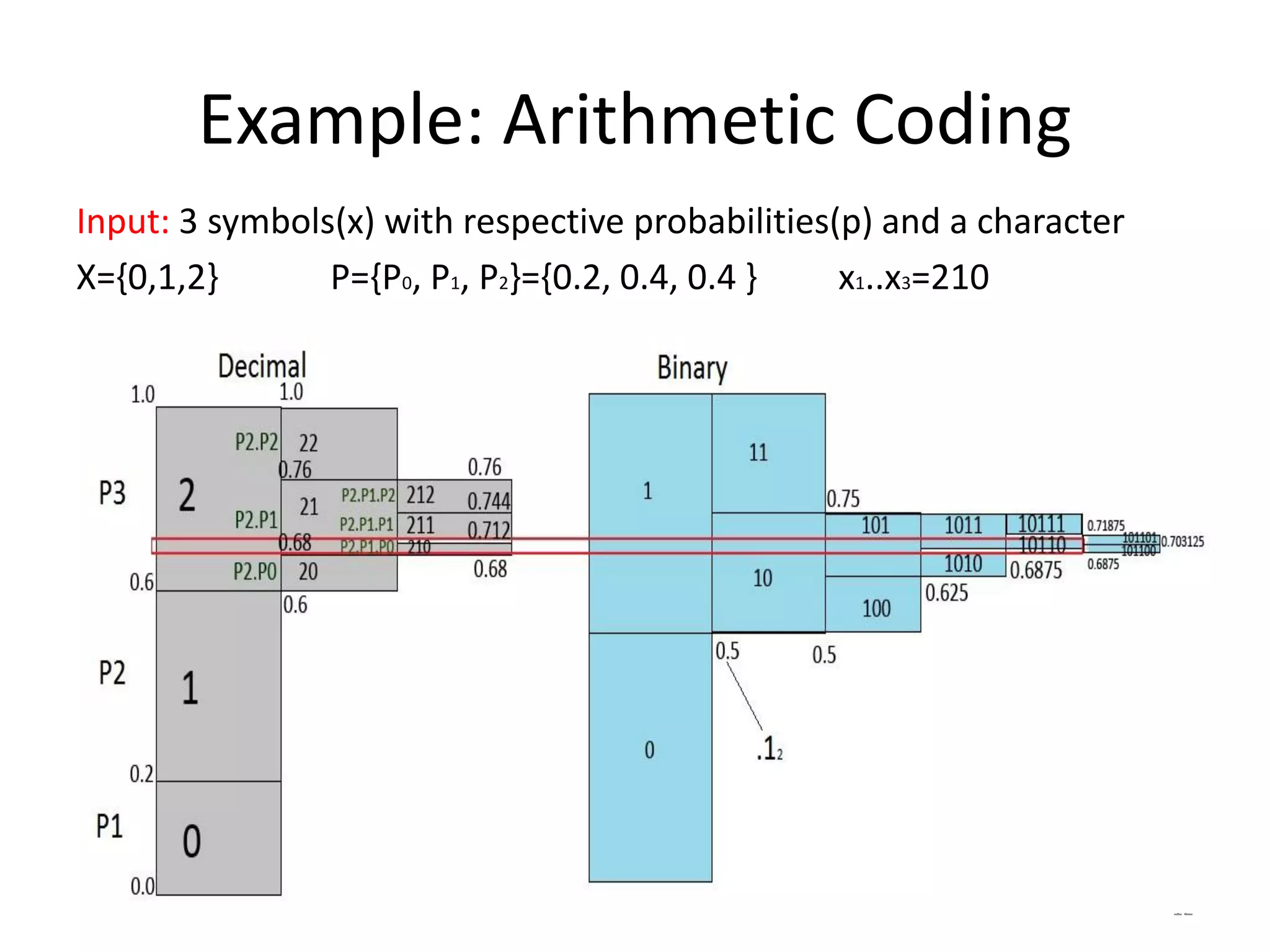
Huffman coding and arithmetic coding are analyzed for complexity. Huffman coding assigns variable length codes to symbols based on probability and has O(N2) complexity. Arithmetic coding encodes the entire message as a fraction between 0 and 1 by dividing intervals based on symbol probability and has better O(N log n) complexity. Arithmetic coding compresses data more efficiently with fewer bits per symbol and has lower complexity than Huffman coding asymptotically.








![Huffman Coding Complexity analysis • Huffman algorithm is based on greedy approach to get the optimal result(code length). • Using the pseudo code: • Running Time Function: T(n)= N[n+ log(2n-1)]+ Sn • Complexity: O(N ) 9 2](https://image.slidesharecdn.com/performanceanalysisofhuffmanandarithmeticcodingcompression-150819042135-lva1-app6892/75/Huffman-and-Arithmetic-coding-Performance-analysis-9-2048.jpg)



![Arithmetic Coding Complexity analysis Running time Function: T(n)=N[log n+ a]+ Sn N Number of input symbols n current number of unique symbols S Time to maintain internal data structure Complexity: O(N log n) 14](https://image.slidesharecdn.com/performanceanalysisofhuffmanandarithmeticcodingcompression-150819042135-lva1-app6892/75/Huffman-and-Arithmetic-coding-Performance-analysis-14-2048.jpg)


