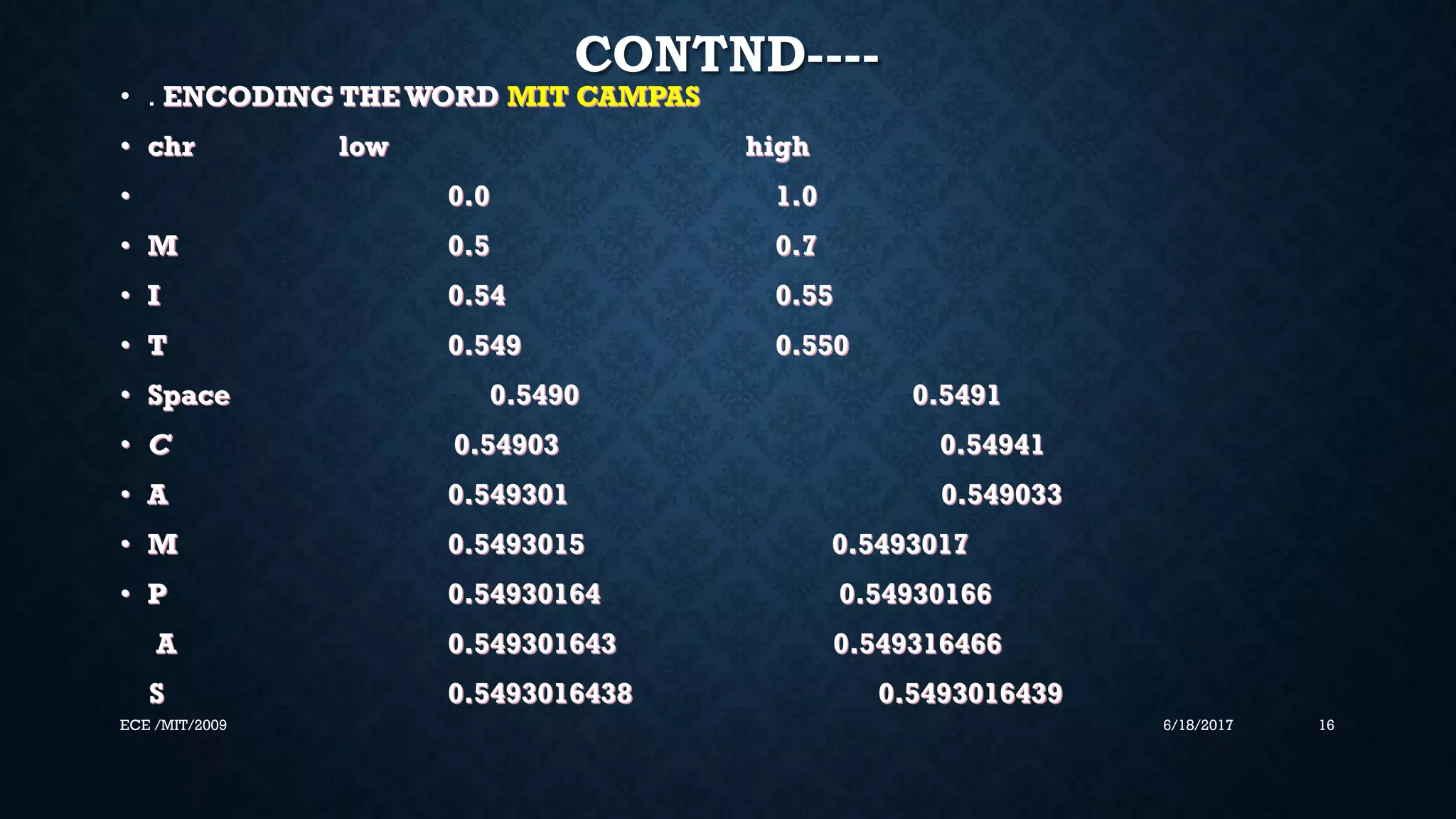
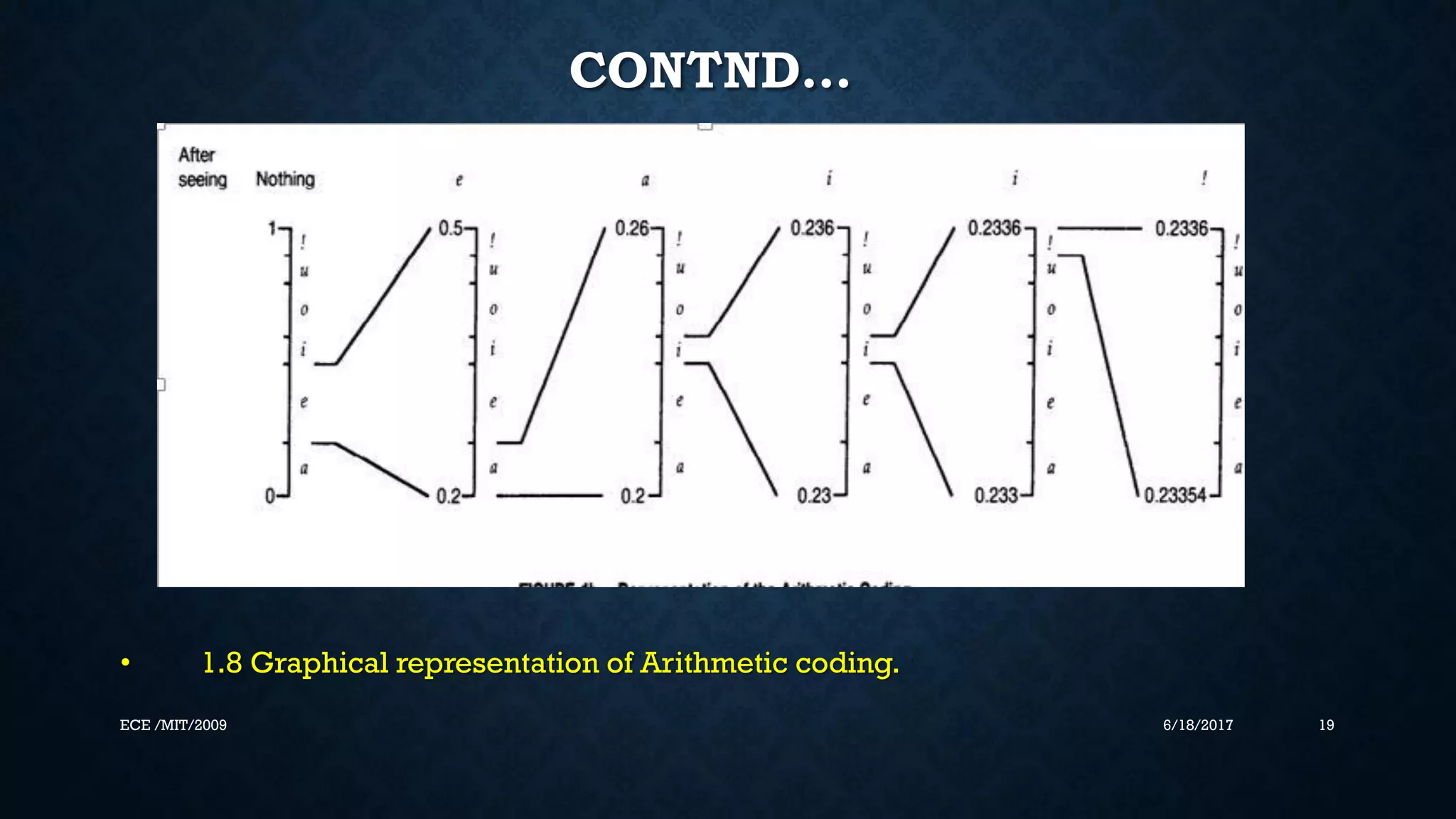
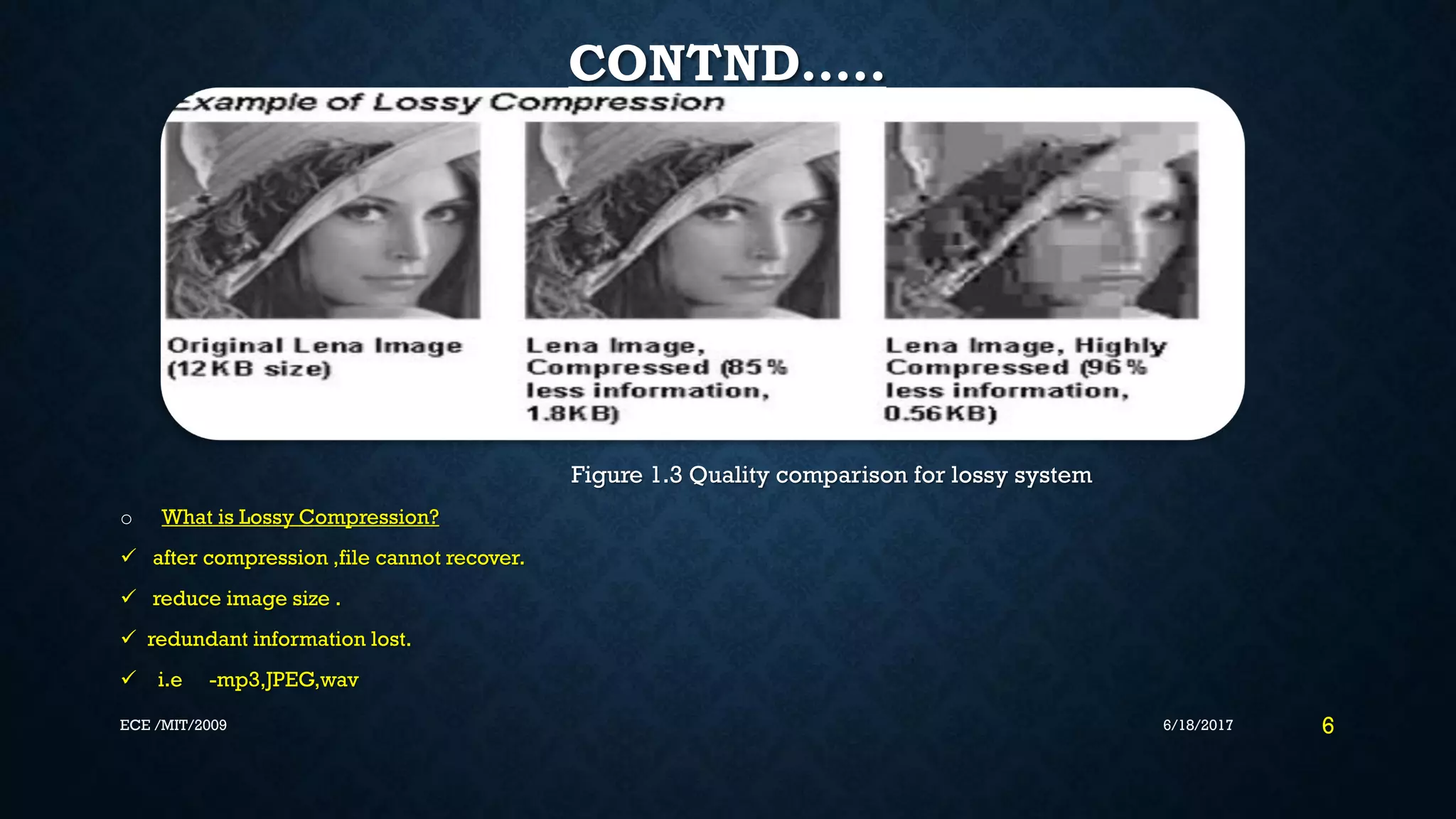
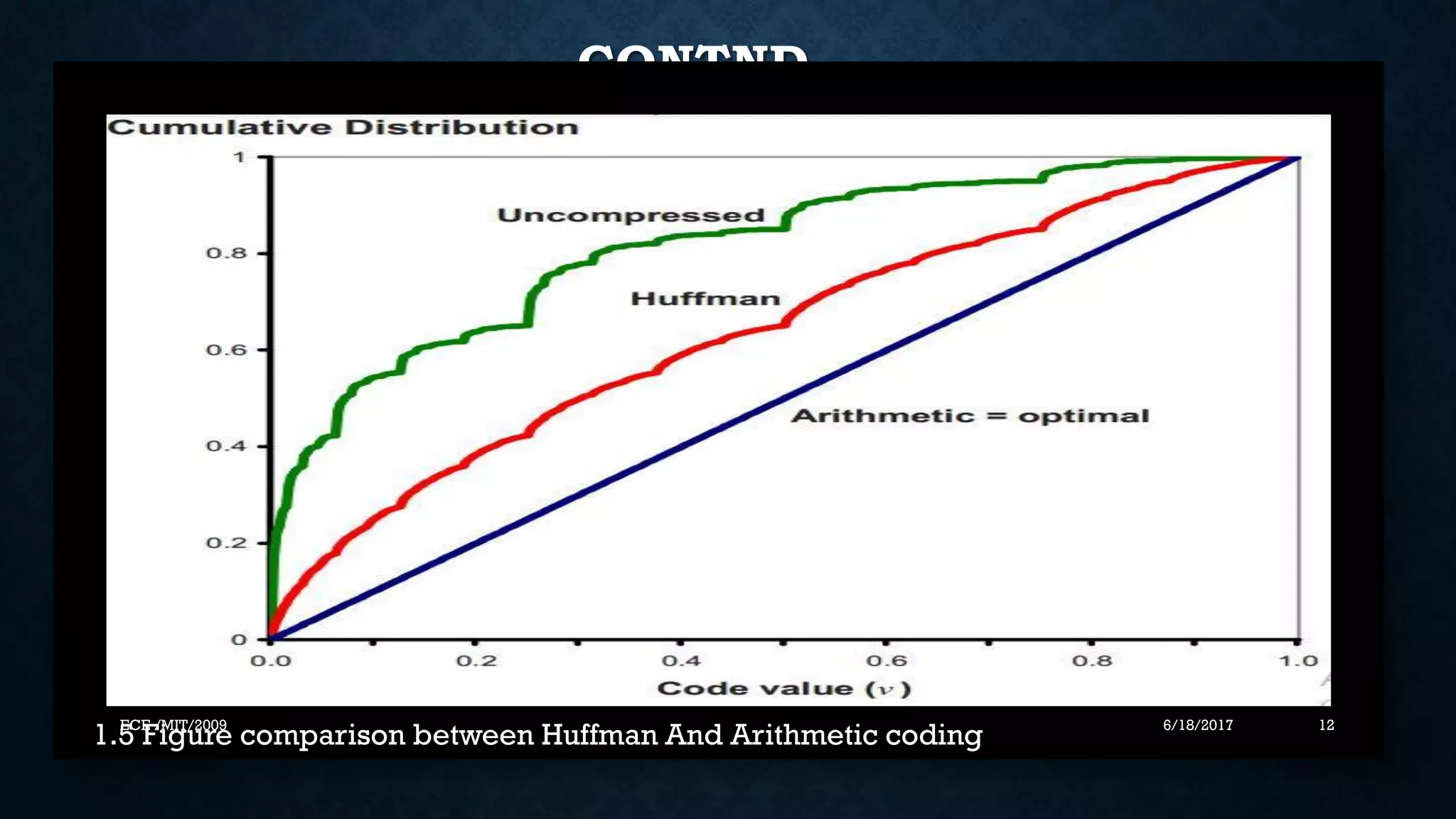
This document discusses arithmetic coding, a lossless data compression technique. It begins with an overview of source coding and commonly used compression algorithms like Huffman coding and run-length encoding. It then describes problems with Huffman coding like less efficiency and flexibility. Arithmetic coding is presented as an alternative with better compression ratios and adaptiveness. The document proceeds to explain the encoding and decoding process of arithmetic coding through assigning probabilities to symbols and mapping them to ranges within 0 to 1. It provides examples and figures to illustrate the technique. In summary, arithmetic coding achieves better compression than Huffman coding by producing a single codeword rather than multiple codewords.










![4.ARITHMETIC ENCODING STEPS • To code symbol s ,where symbols are numbered from 1 to n and symbol I has the probability pr[i]; • low bound = 𝑖=0𝑝𝑟 𝑠−1 [𝑖] • High bound = 𝑖=0𝑝𝑟 𝑠−1 [𝑖] • Range=high-low • Low=low + range *(low bound) • High=low + range *(high bound) 6/18/2017 13ECE /MIT/2009](https://image.slidesharecdn.com/arithmeticcoding-170618164546/75/Arithmetic-coding-13-2048.jpg)