Unit 3 Arithmetic Coding

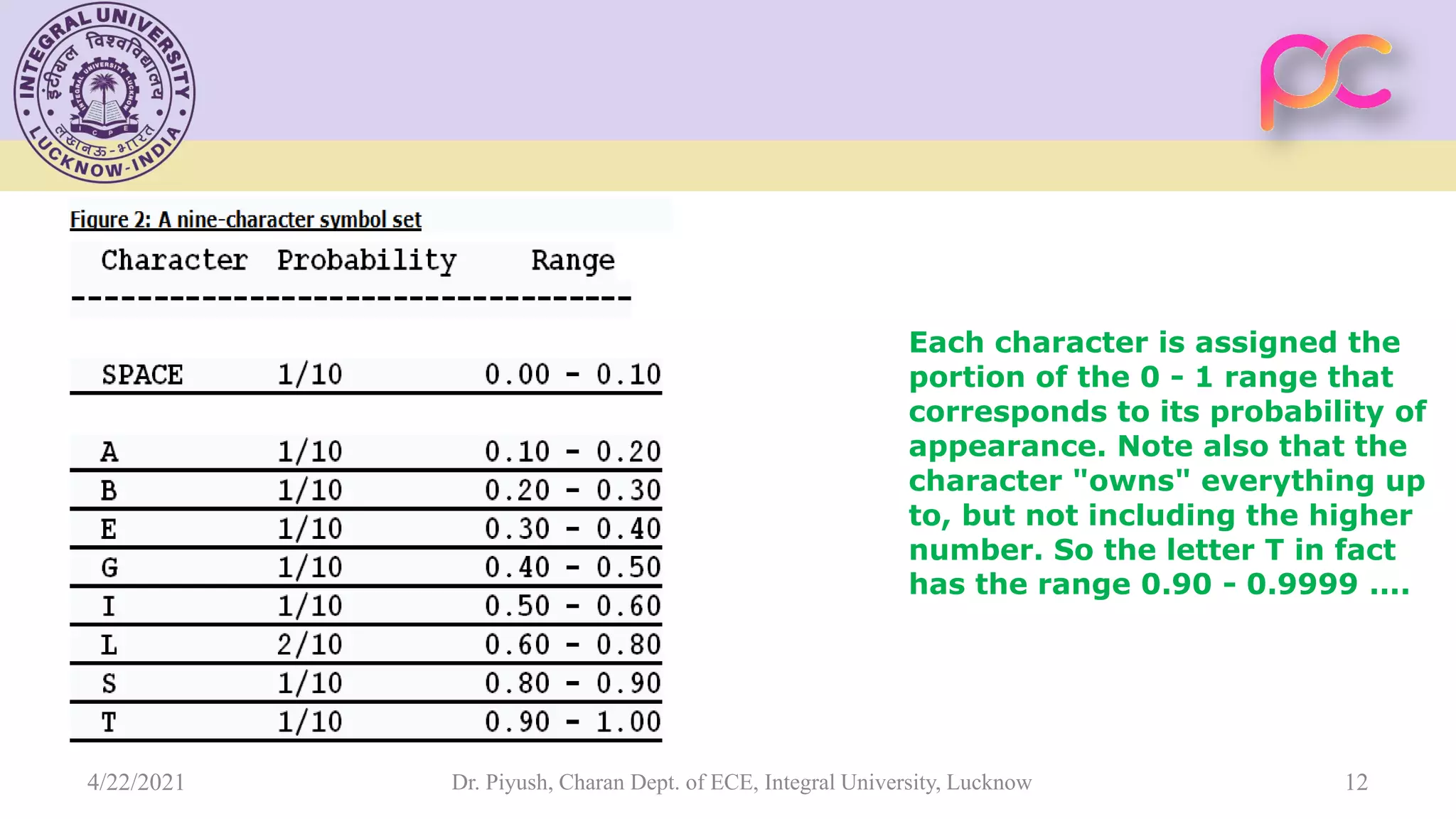
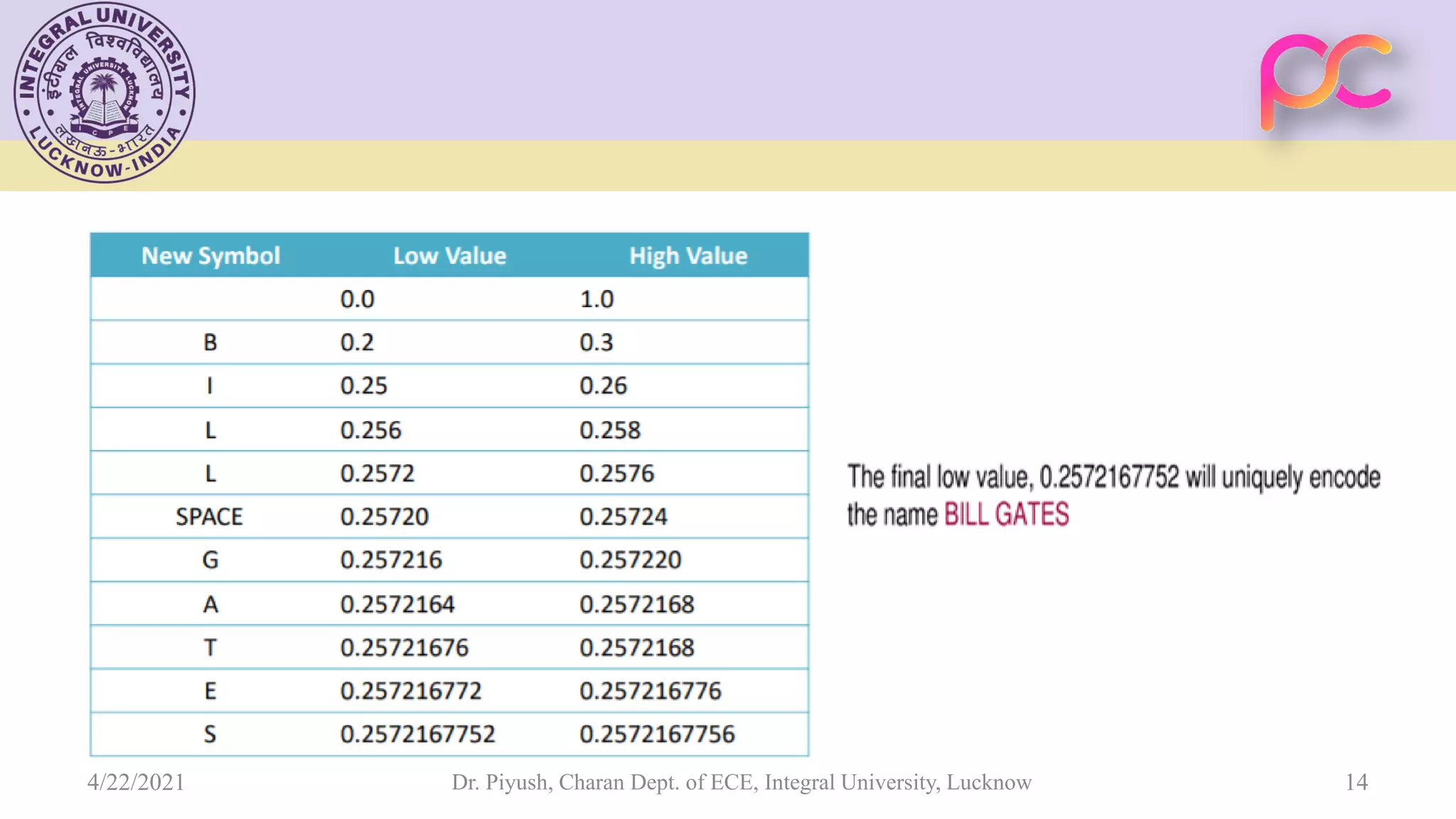
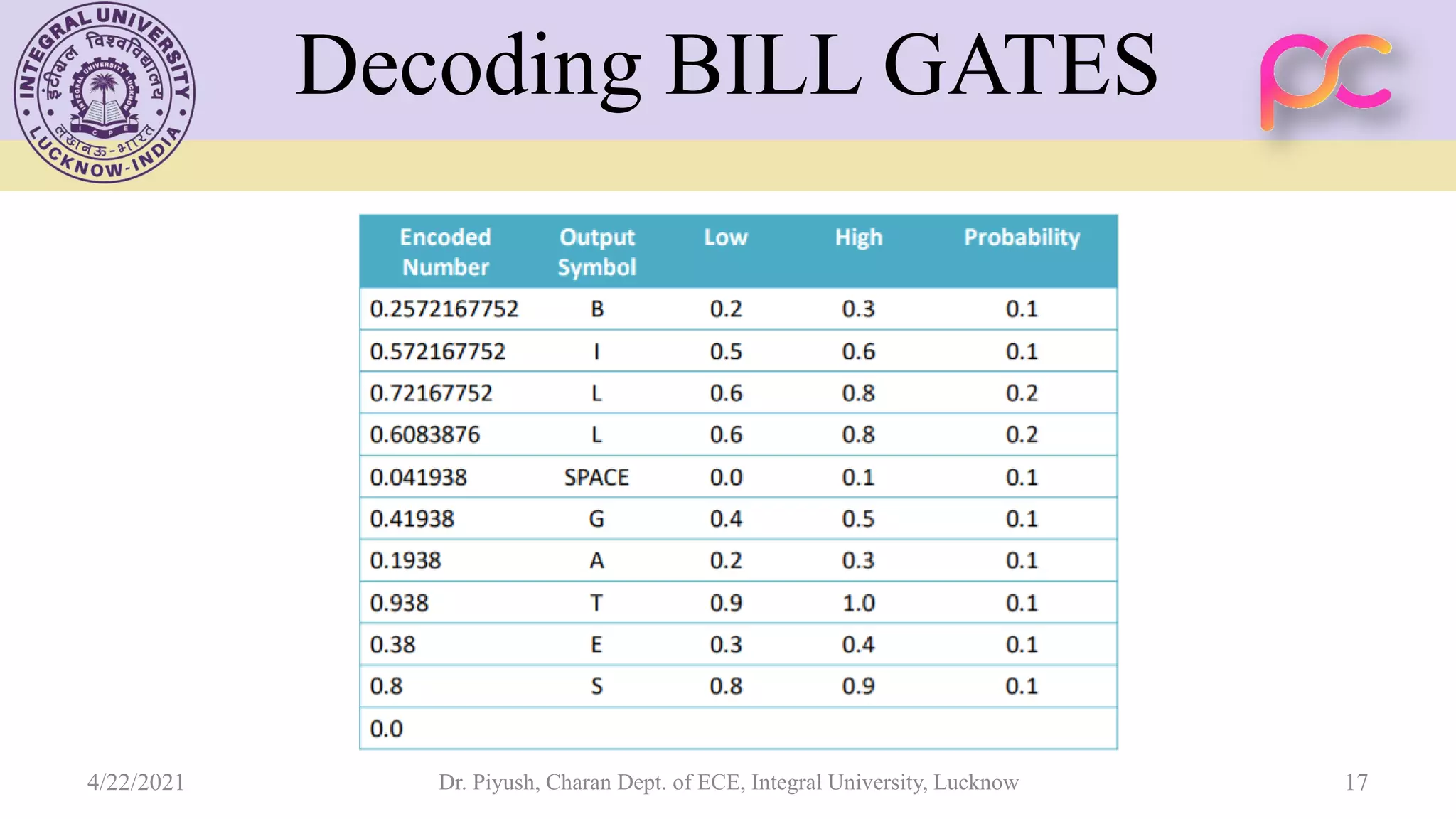
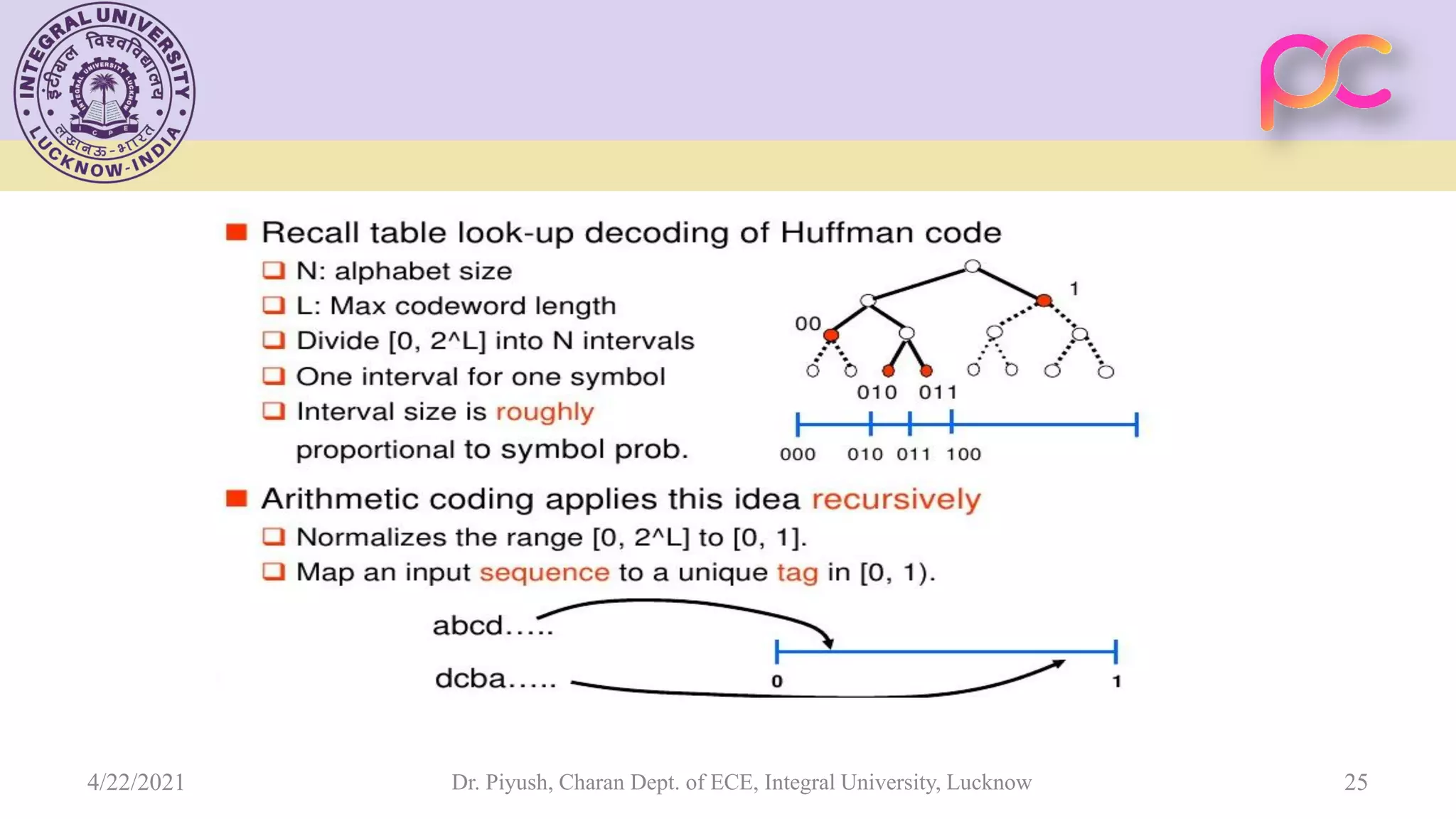
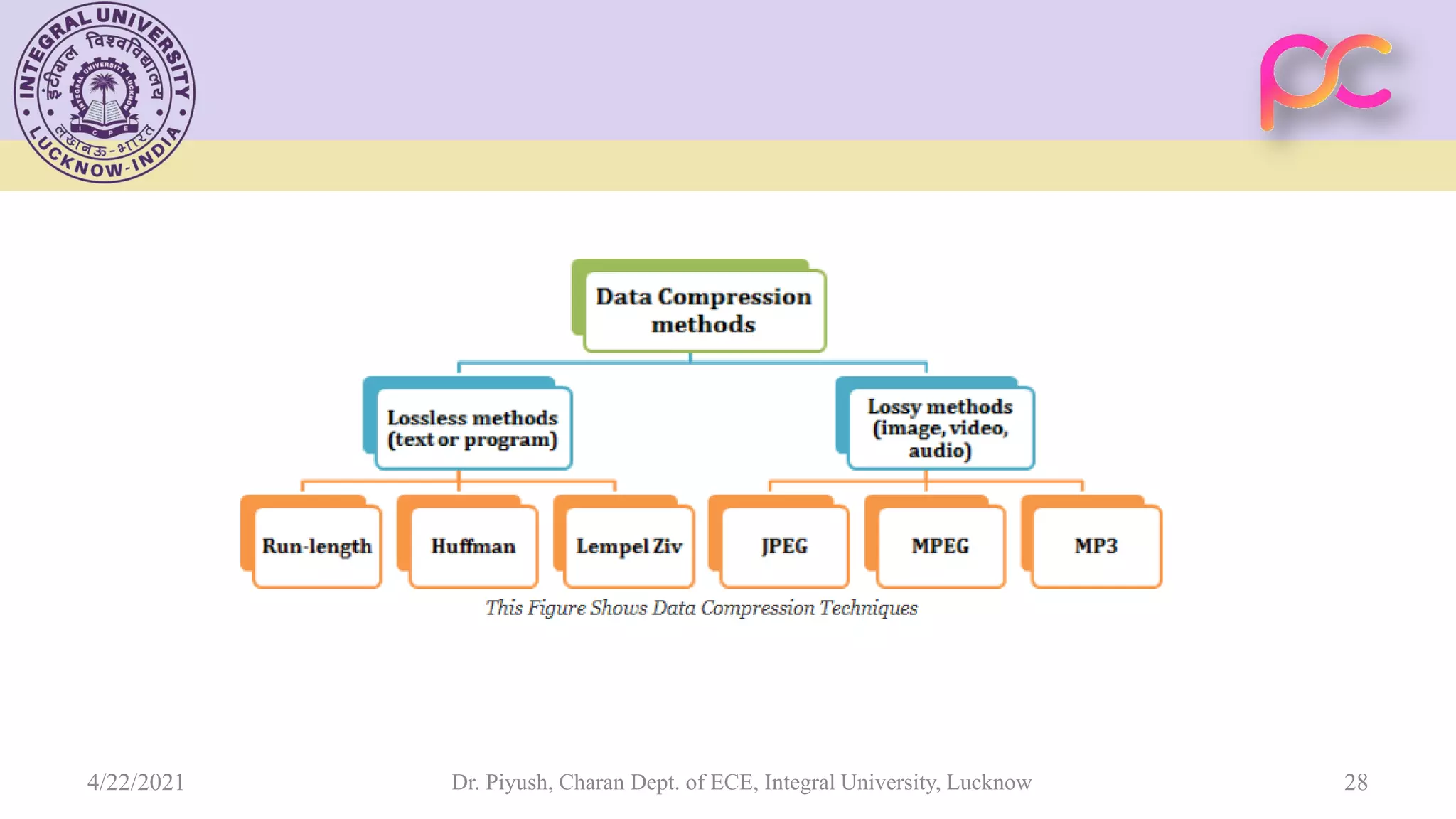
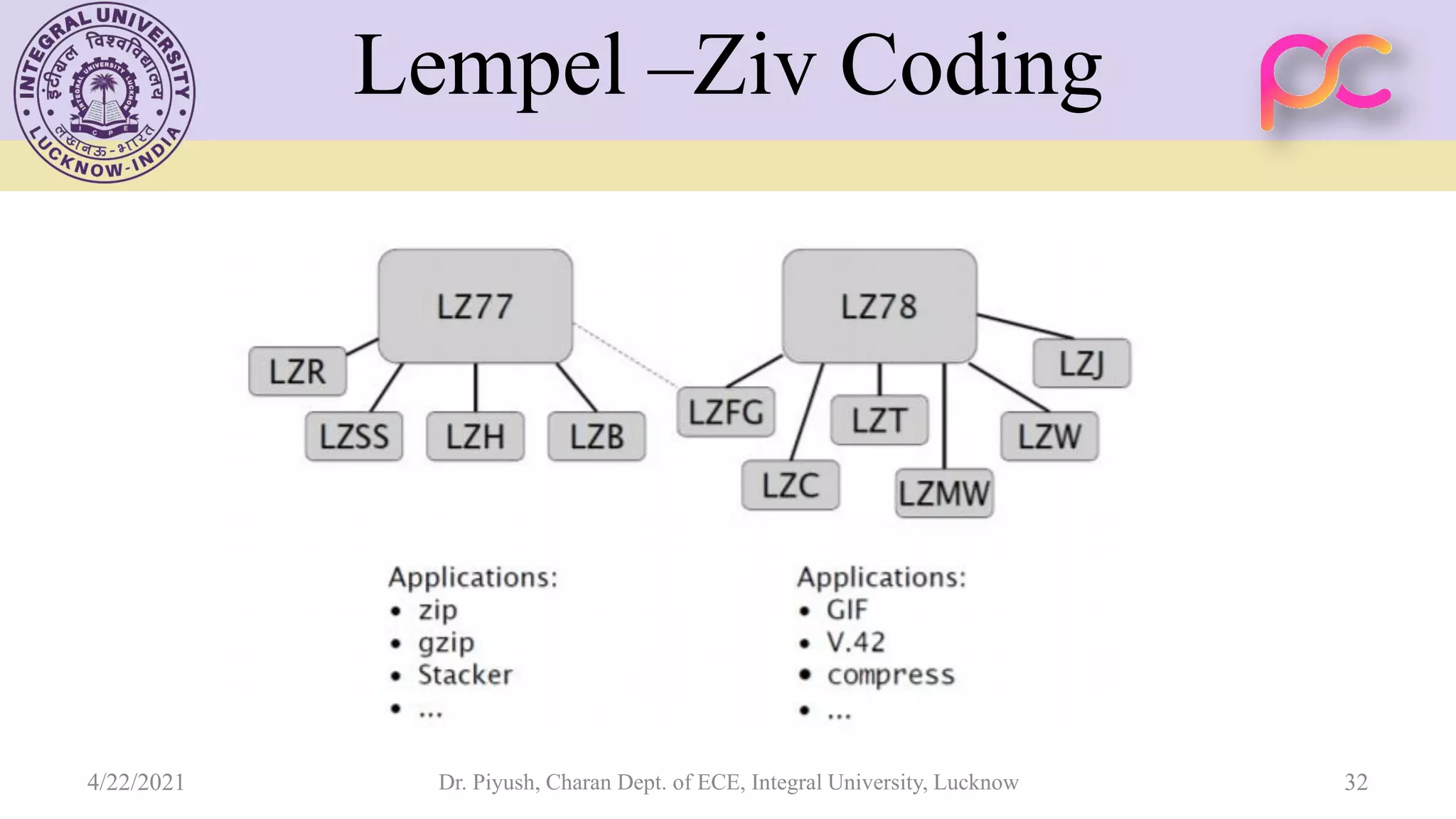
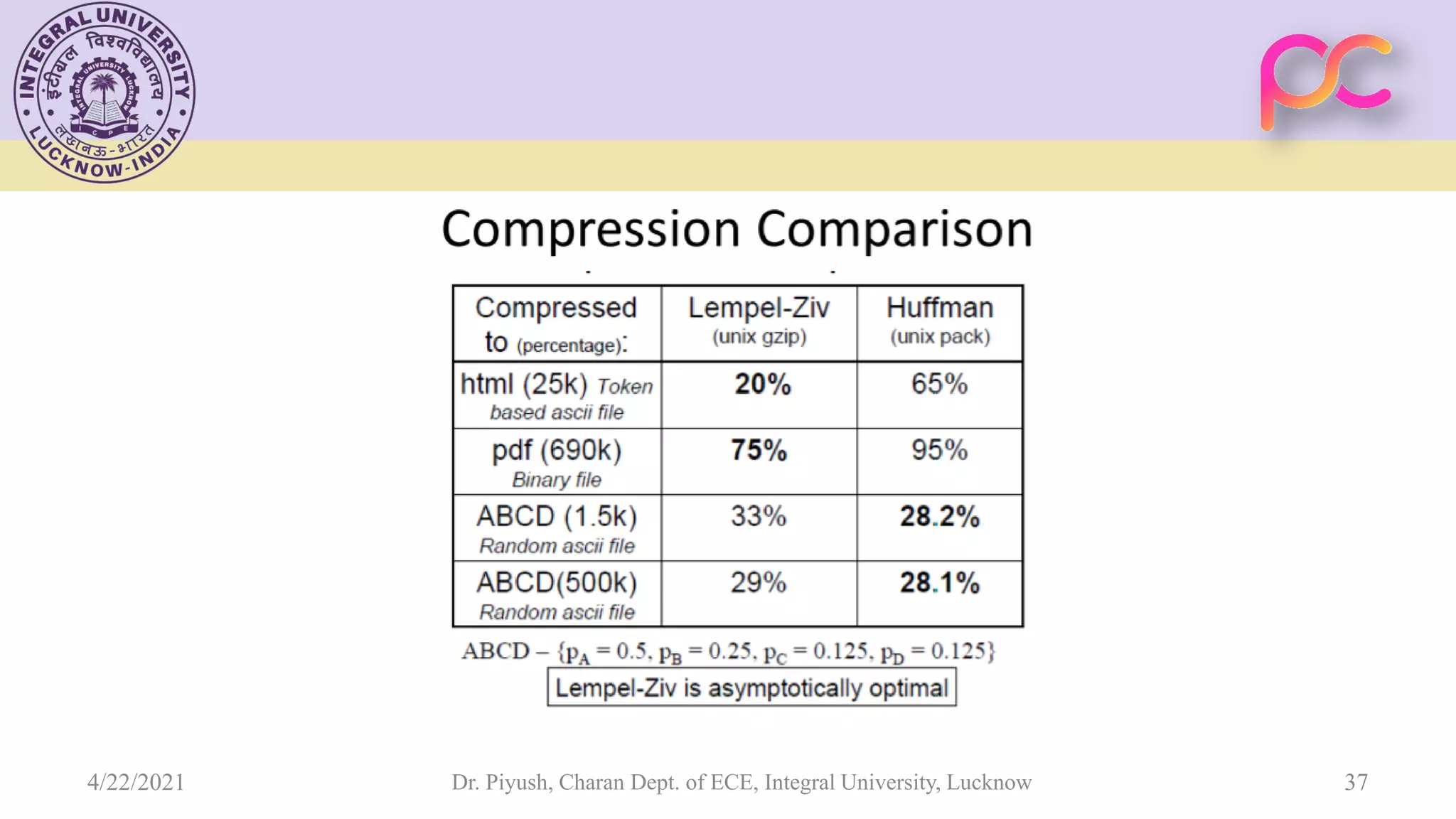
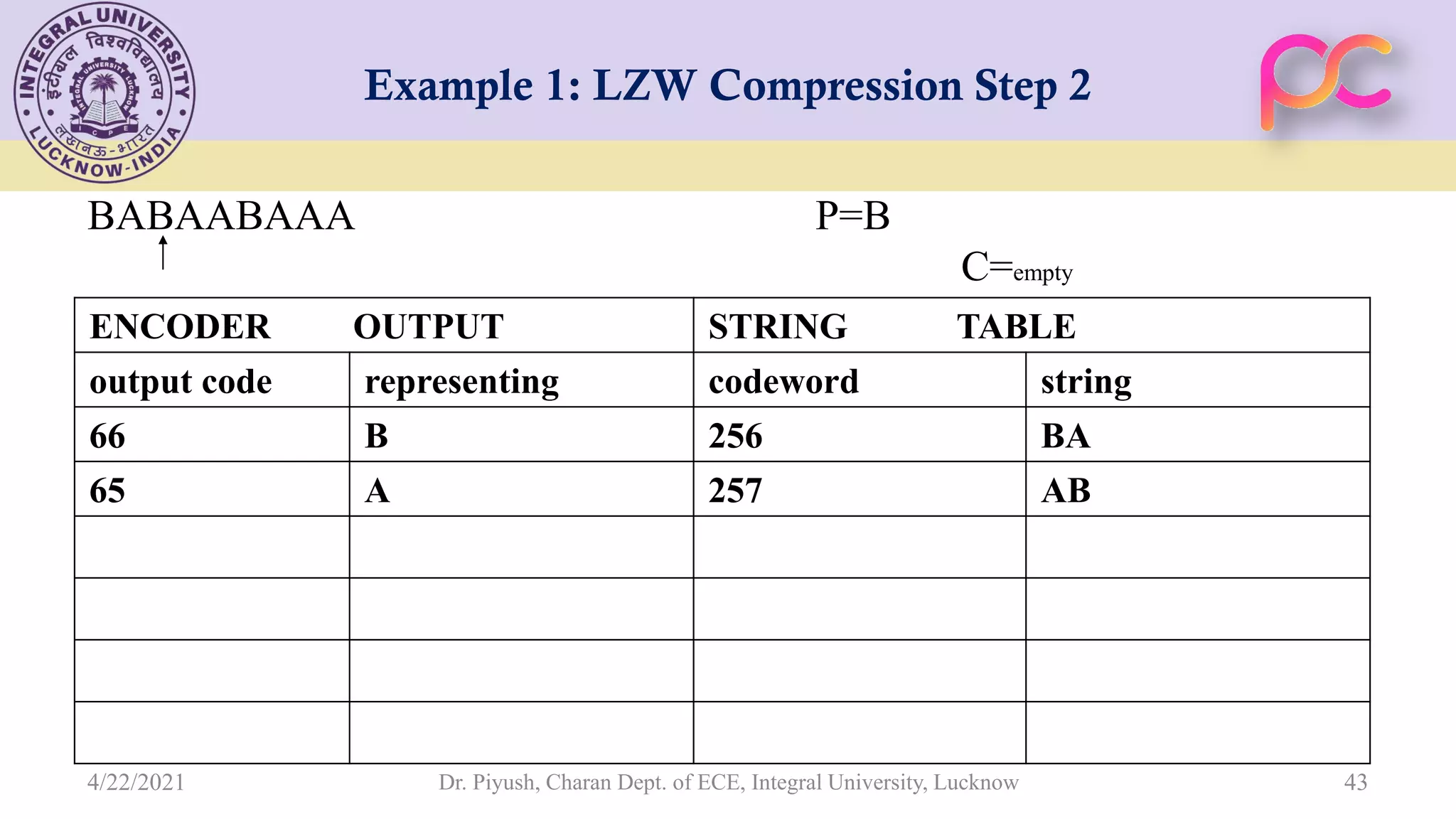
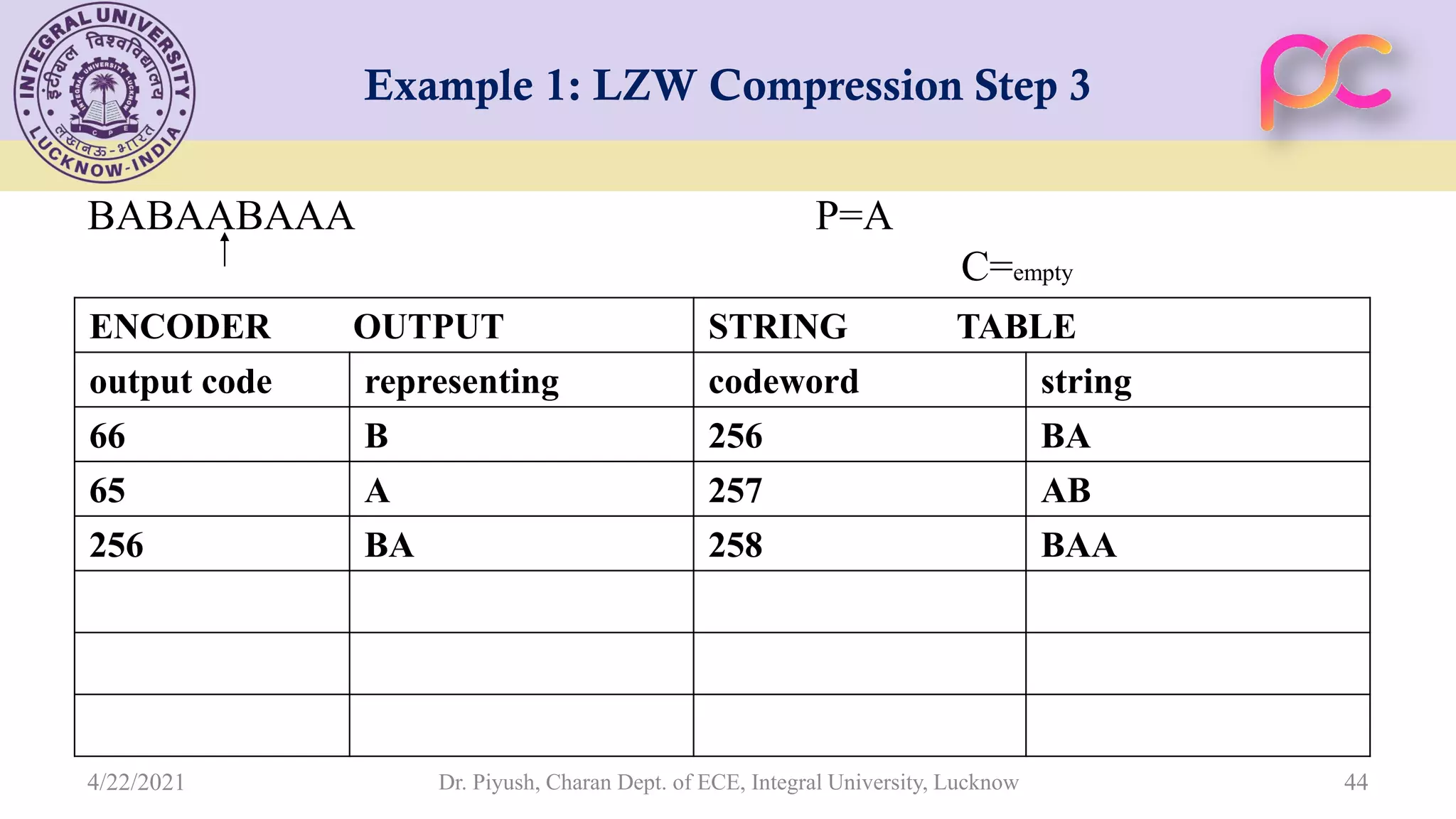
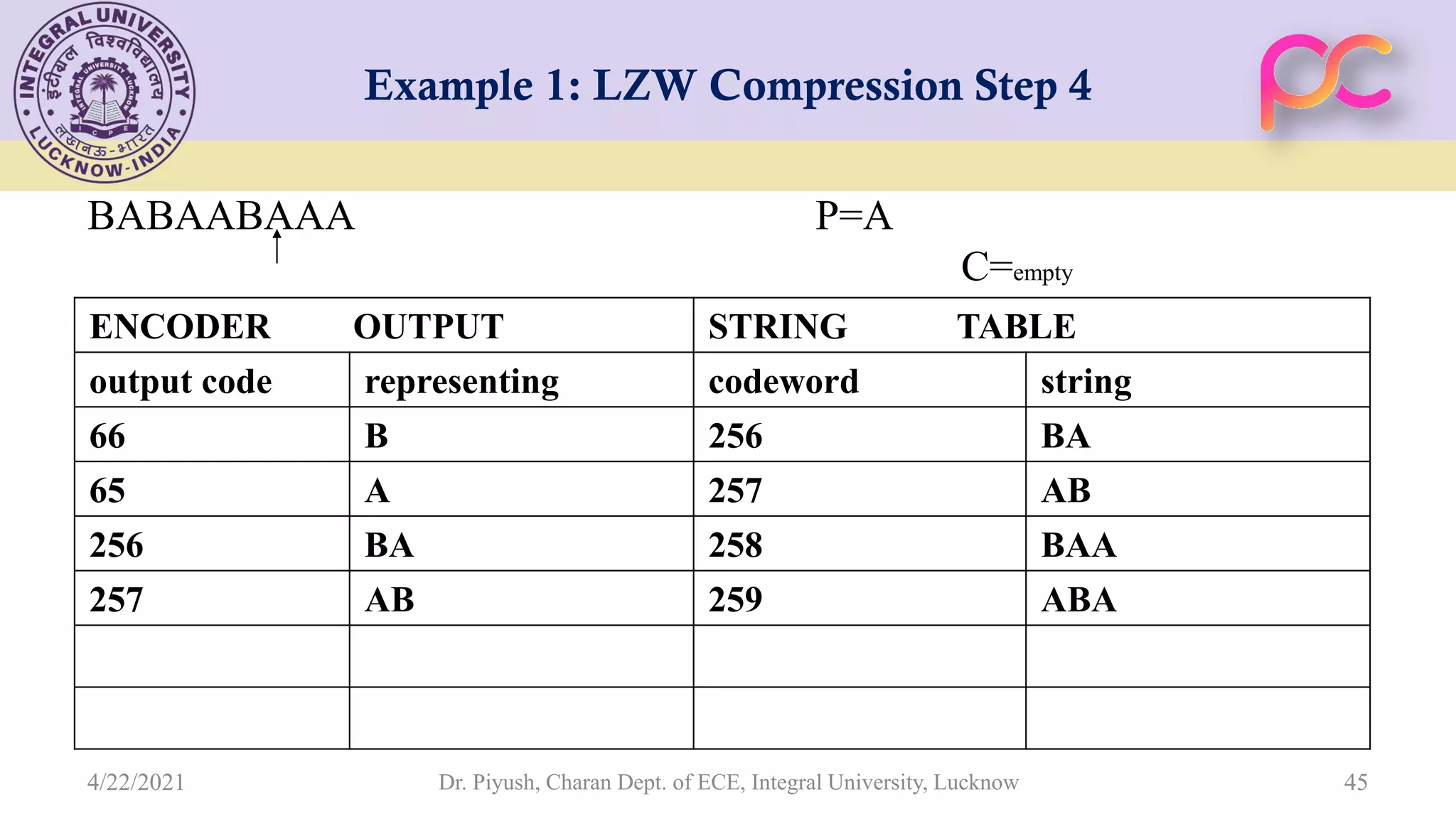
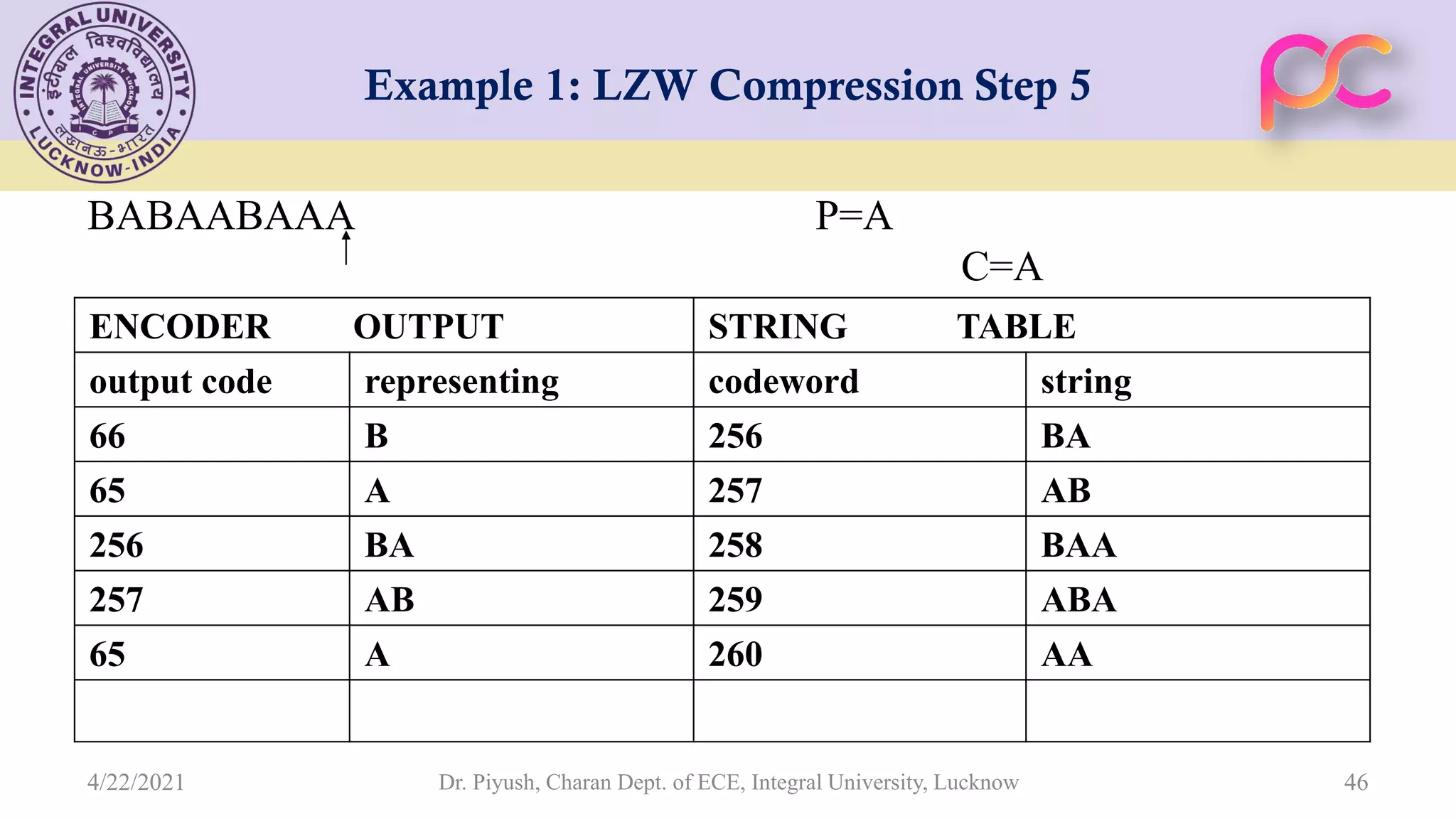
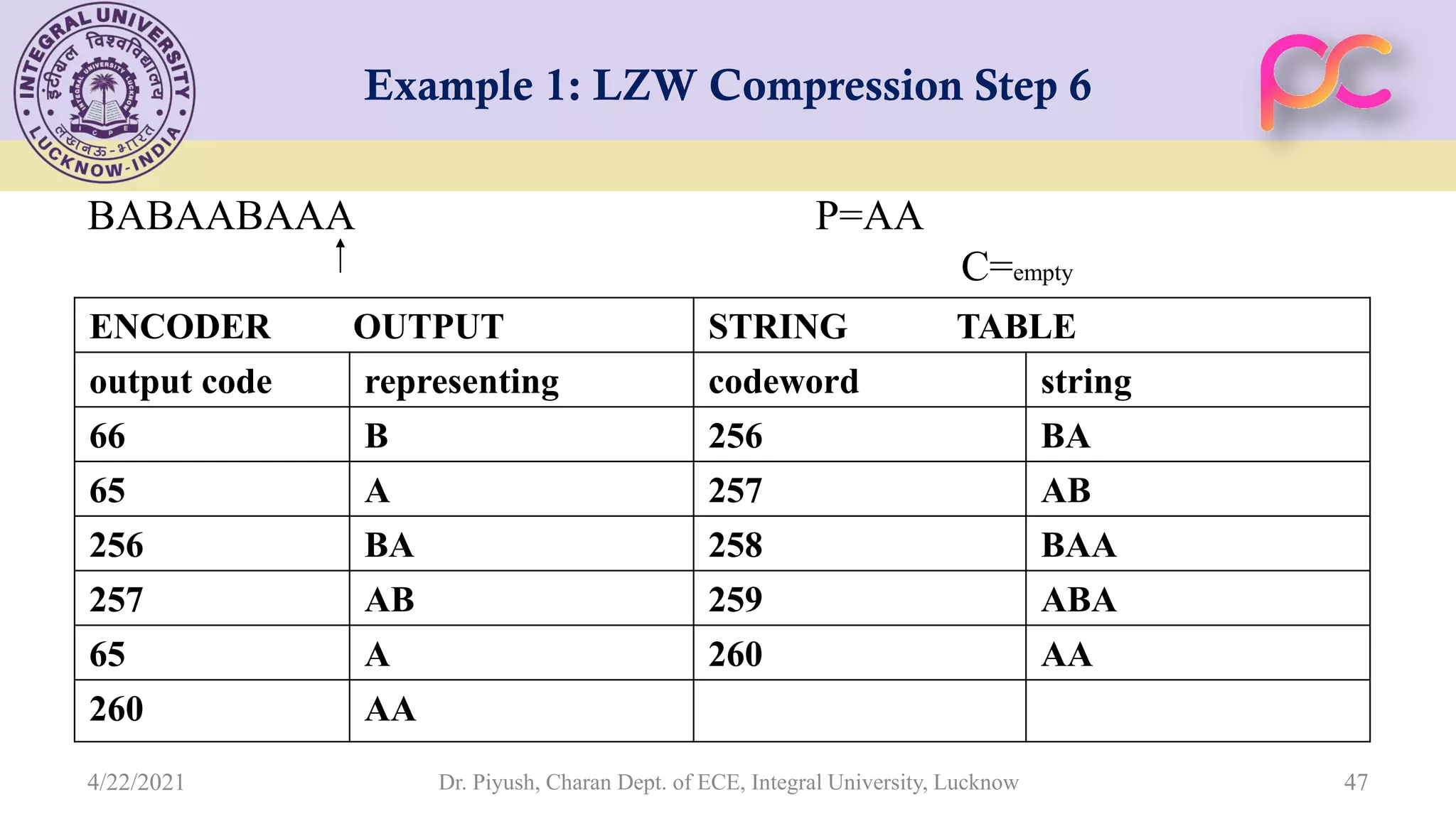
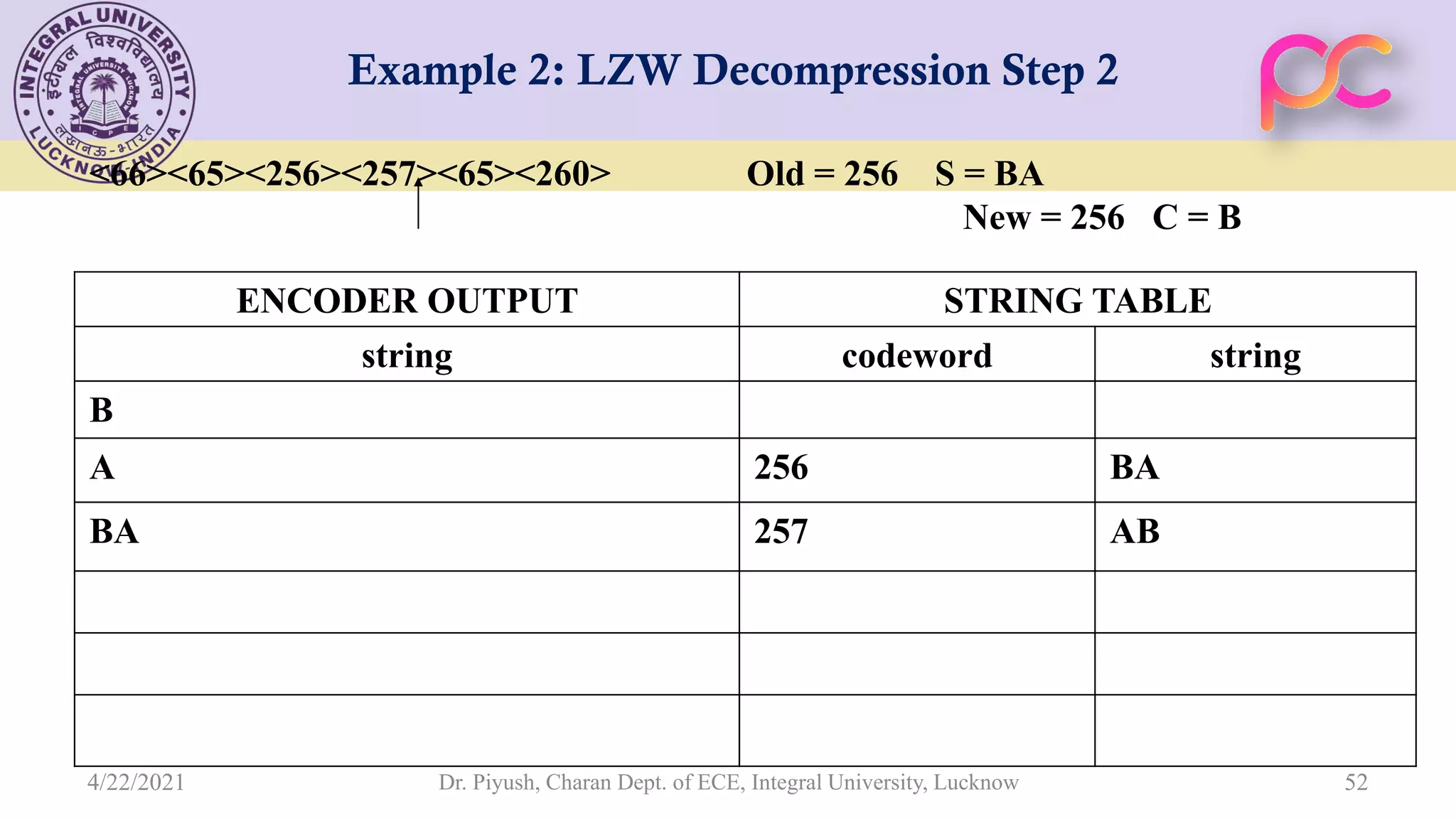
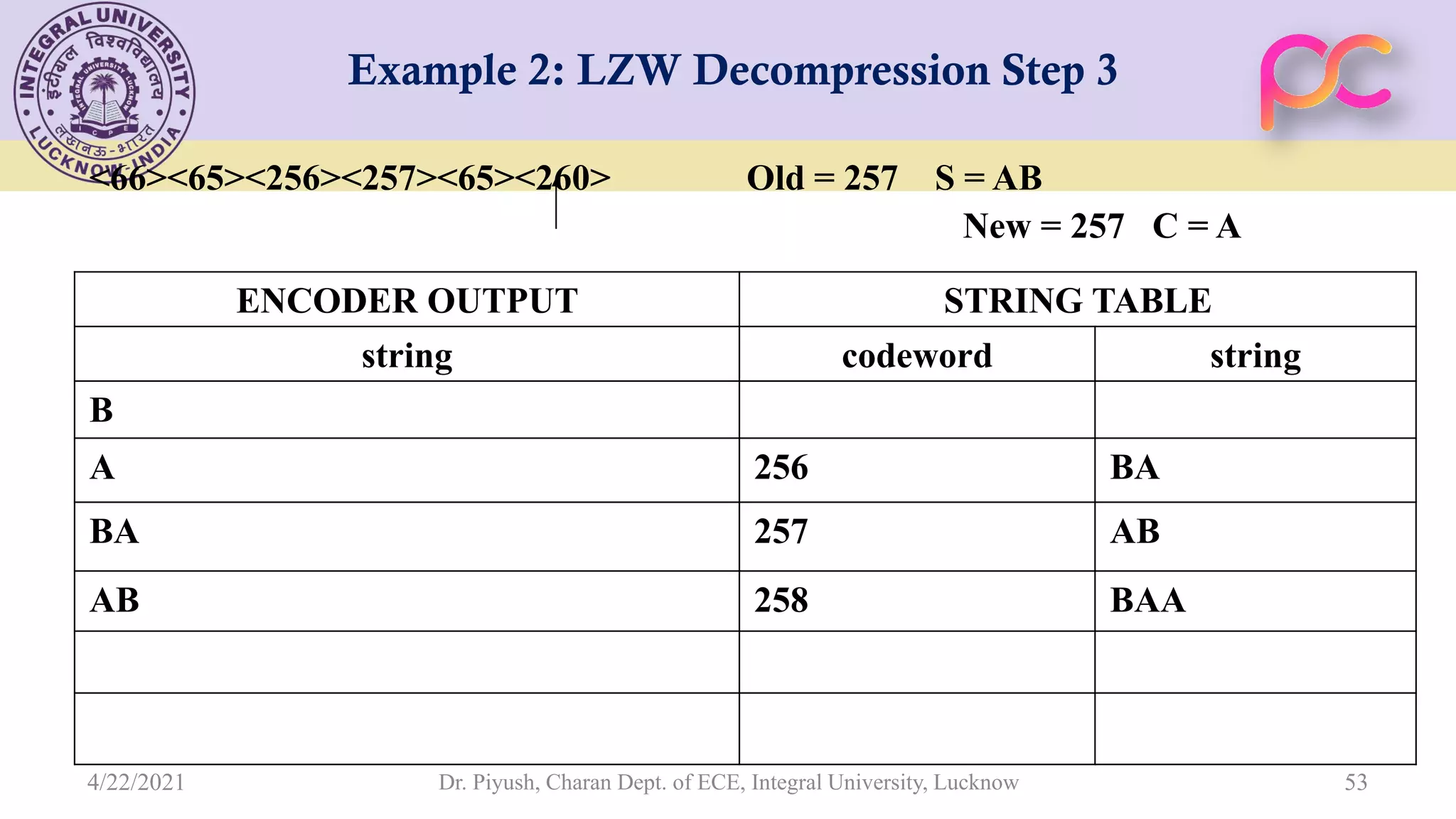
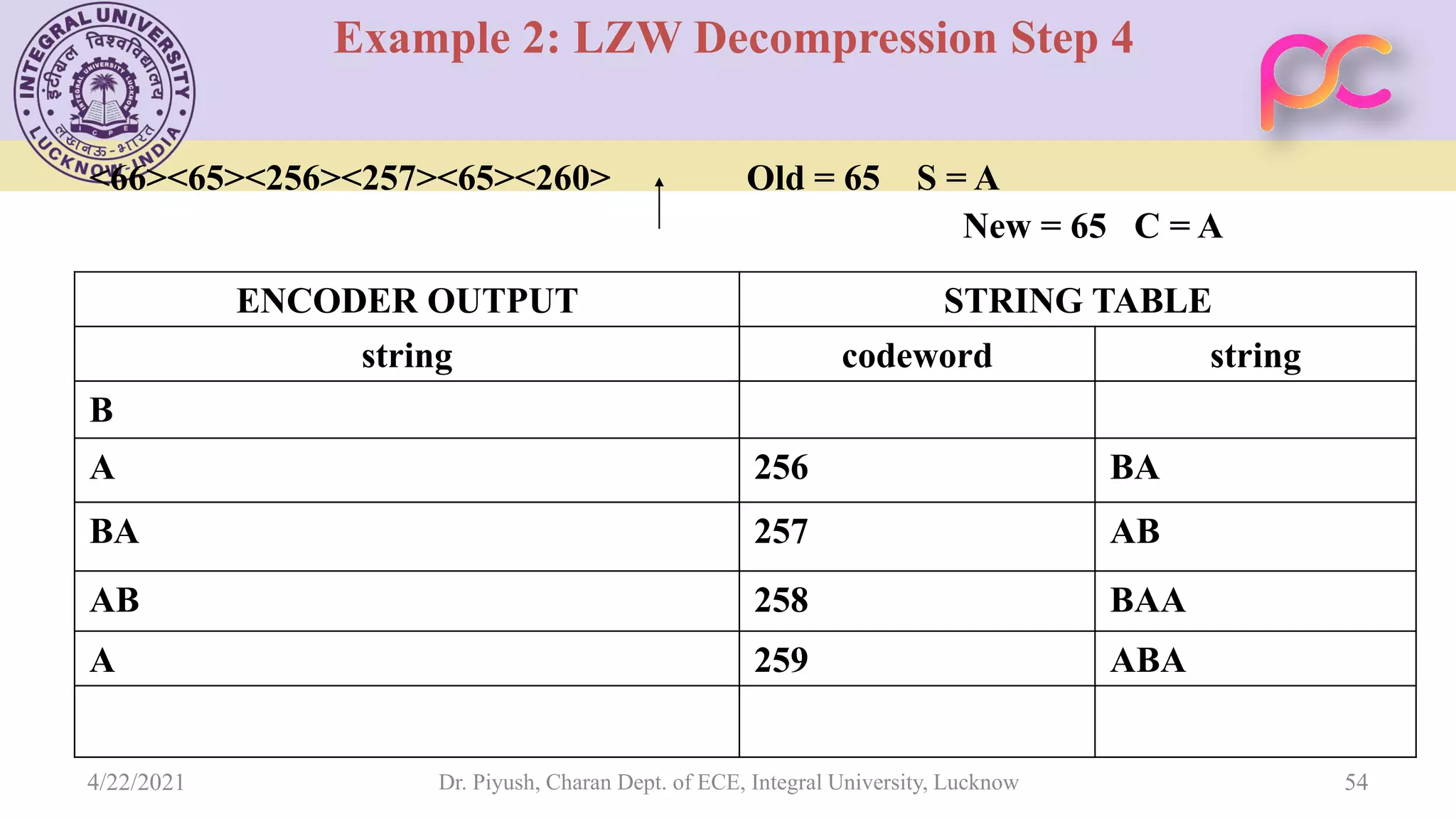
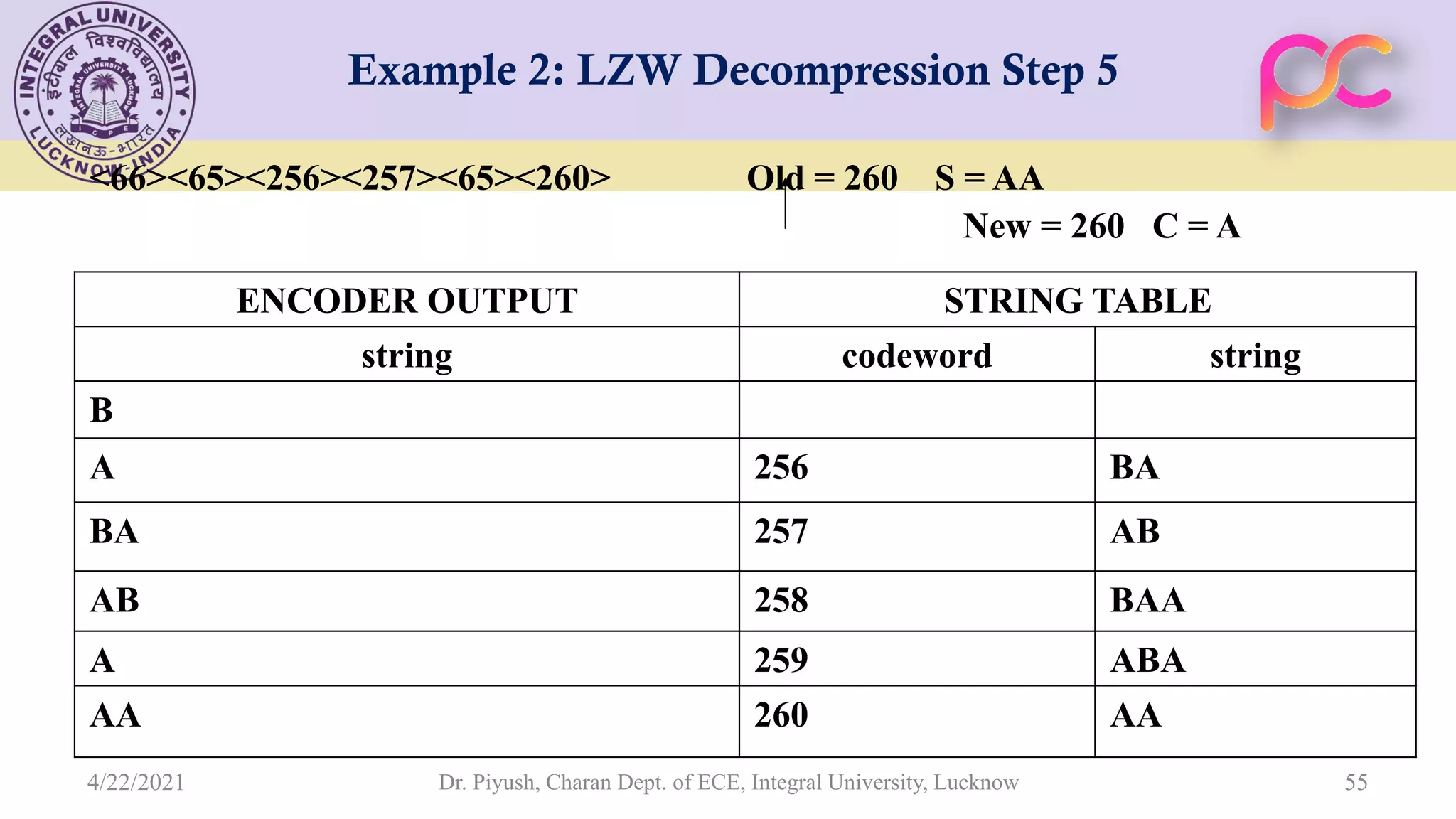
Lecture Notes on Arithmetic Coding for Open Educational Resource on Data Compression(CA209) by Dr. Piyush Charan Assistant Professor Department of Electronics and Communication Engg. Integral University, Lucknow This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.

UNIT-III Syllabus • Arithmetic Coding: Coding a sequence, • Generating a Binary code, • Comparison of Arithmetic and Huffman coding. • Dictionary Techniques: Introduction, Static Dictionary: • Diagram Coding, Adaptive Dictionary: • The LZ77 Approach, The LZ78 Approach. • Applications: File Compression, Image Compression • Lossless Image Compression: Multi-resolution Approaches. • Context Based Compression: Dynamic Markov Compression. 4/22/2021 Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 2

 Coding rate is the average number of bits used to represent a symbol from a source.  For a given probability model, the entropy is the lowest rate at which the source can be coded.  Huffman coding will generate whose rate is within p_max + 0. 086  Therefore, in Huffman coding, when the alphabet size is large, the amount of deviation from the entropy is quite small, and vice versa.  One solution for this problem is blocking in Huffman coding. In which, it is more efficient to generate codewords for groups or sequences of symbols rather than to generate a separate codeword for each symbol in a sequence.  In order to find the Huffman coding for a sequence of length m, we need codewords for all possible sequences of length m.  This causes an exponential growth in the size of the code book. Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 3 4/22/2021

 We need a way of assigning codewords to particular sequences with out having to generate a codes for all sequences of that length.  Rather than separating the input into component symbols and replacing each with a code, arithmetic encodes the entire message with a number (tag).  Firstly, a unique identifier or tag is generated for a sequence. Secondly, this tag is then given a unique binary code. • Entropy encoding • Lossless data compression • Variable length coding Arithmetic Coding 4/22/2021 Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 4

Arithmetic Coding  Arithmetic coding is based on the concept of interval subdividing. – In arithmetic coding a source ensemble is represented by an interval between 0 and 1 on the real number line. – Each symbol of the ensemble narrows this interval. – As the interval becomes smaller, the number of bits needed to specify it grows – Arithmetic coding assumes an explicit probabilistic model of the source. – It uses the probabilities of the source messages to successively narrow the interval used to represent the ensemble.  A high probability message narrows the interval less than a low probability message, so that high probability messages contribute fewer bits to the coded ensemble. 4/22/2021 Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 5

 Assume we know the probabilities of each symbol of the data source,  we can allocate to each symbol an interval with width proportional to its probability, and each of the intervals does not overlap with others.  This can be done if we use the cumulative probabilities as the two ends of each interval.  Therefore, the two ends of each symbol x amount to Q[x-1] and Q[x].  Symbol x is said to own the range [Q[x-1], Q[x]). Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 6 4/22/2021

4/22/2021 Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 7  We begin with the interval [0, 1) and subdivide the interval iteratively.  For each symbol entered, the current interval is divided according to the probabilities of the alphabet.  The interval corresponding to the symbol is picked as the interval to be further proceeded with.  The procedure continues until all symbols in the message have been processed.  Since each symbol's interval does not overlap with others, for each possible message there is a unique interval assigned.  We can represent the message with the interval's two ends [L, H). In fact, taking any single value in the interval as the encoded code is enough, and usually the left end L is selected.

Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 8 4/22/2021

Once the character probabilities are known, the individual symbols need to be assigned a range along a "probability line," which is nominally 0 to 1. It doesn't matter which characters are assigned which segment of the range, as long as it is done in the same manner by both the encoder and the decoder. The nine-character symbol set used here would look like Figure 2. Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 11 4/22/2021

Each character is assigned the portion of the 0 - 1 range that corresponds to its probability of appearance. Note also that the character "owns" everything up to, but not including the higher number. So the letter T in fact has the range 0.90 - 0.9999 .... Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 12 4/22/2021

After the first character is encoded, we also know that the range for our output number is bounded by the low and high numbers. During the rest of the encoding process, each new symbol to be encoded will further restrict the possible range of the output number. The next character to be encoded, I, owns the range 0.50 through 0.60. If this was the first number in our message, we would set these as our low- and high-range values. But I is the second character; therefore, we say that I owns the range corresponding to 0.50 - 0.60 in the new subrange of 0.2 - 0.3. This means that the new encoded number will have to fall somewhere in the 50 to 60th percentile of the currently established range. Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 13 4/22/2021

Binary Codeword 4/22/2021 Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 15

Decoding Algorithm 4/22/2021 Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 16

Decoding BILL GATES 4/22/2021 Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 17

Huffman vs. Arithmetic Codes 4/22/2021 Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 19

Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 21 4/22/2021 Huffman vs. Arithmetic Codes

Arithmetic Coding Huffman Coding Does not need the probability distribution Need a probability distribution No need to keep and send codeword table Need to store the codeword table Decompression speed is slow Decompression speed is Fast Compression Speed is low Compression speed is Fast Compression ratio is very good Compression ratio is poor No compressed pattern matching Compressed pattern matching Fractional codeword length Minimum codeword length is 1 bit Does not produce Prefix code Produce Prefix code Comparison of Arithmetic vs. Huffman Coding 4/22/2021 Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 24

 each symbol or group of symbols is encoded with a variable length code, according to some probability distribution.  based on the use of a dictionary, which can be static or dynamic, and they code each symbol or group of symbols with an element of the dictionary. Huffman Dynamic Markov Compression Lempel-Ziv-Welch Lossless Compression Techniques 4/22/2021 Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 29

Lempel-Ziv-Welch (LZW) Created by Abraham Lempel, Jacob Ziv, and Terry Welch. It was published by Welch in 1984as an improved implementation of the LZ78 algorithm, published by Lempel and Ziv in 1978 universal adaptative1 lossless data compression algorithm builds a translation table (also called dictionary) from the text being compressed the string translation table maps the message strings to fixed-length codes 1 The coding scheme used for the kth character of a message is based on the characteristics of the preceding k − 1 characters in the message Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 30 4/22/2021

Dictionary Based Techniques 4/22/2021 Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 31

Lempel –Ziv Coding 4/22/2021 Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 32

Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 33 4/22/2021 Lempel –Ziv Coding

Lempel-Ziv-Welch (LZW) Compression Algorithm  As mentioned earlier, static coding schemes require some knowledge about the data before encoding takes place.  Universal coding schemes, like LZW, do not require advance knowledge and can build such knowledge on-the-fly.  LZW is the foremost technique for general purpose data compression due to its simplicity and versatility.  It is the basis of many PC utilities that claim to “double the capacity of your hard drive”  LZW compression uses a code table, with 4096 as a common choice for the number of table entries. Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 38 4/22/2021

LZW (cont'd)  Codes 0-255 in the code table are always assigned to represent single bytes from the input file.  When encoding begins the code table contains only the first 256 entries, with the remainder of the table being blanks.  Compression is achieved by using codes 256 through 4095 to represent sequences of bytes.  As the encoding continues, LZW identifies repeated sequences in the data, and adds them to the code table.  Decoding is achieved by taking each code from the compressed file, and translating it through the code table to find what character or characters it represents. Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 39 4/22/2021

LZW Encoding Algorithm 1 Initialize table with single character strings 2 P = first input character 3 WHILE not end of input stream 4 C = next input character 5 IF P + C is in the string table 6 P = P + C 7 ELSE 8 output the code for P 9 add P + C to the string table 10 P = C 11 END WHILE 12 output code for P Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 40 4/22/2021

Example 1: Compression using LZW Example 1: Use the LZW algorithm to compress the string BABAABAAA Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 41 4/22/2021

Example 1: LZW Compression Step 1 BABAABAAA P=A C=empty Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 42 STRING TABLE ENCODER OUTPUT string codeword representing output code BA 256 B 66 4/22/2021

Example 1: LZW Compression Step 2 BABAABAAA P=B C=empty Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 43 STRING TABLE ENCODER OUTPUT string codeword representing output code BA 256 B 66 AB 257 A 65 4/22/2021

Example 1: LZW Compression Step 3 BABAABAAA P=A C=empty Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 44 STRING TABLE ENCODER OUTPUT string codeword representing output code BA 256 B 66 AB 257 A 65 BAA 258 BA 256 4/22/2021

Example 1: LZW Compression Step 4 BABAABAAA P=A C=empty Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 45 STRING TABLE ENCODER OUTPUT string codeword representing output code BA 256 B 66 AB 257 A 65 BAA 258 BA 256 ABA 259 AB 257 4/22/2021

Example 1: LZW Compression Step 5 BABAABAAA P=A C=A Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 46 STRING TABLE ENCODER OUTPUT string codeword representing output code BA 256 B 66 AB 257 A 65 BAA 258 BA 256 ABA 259 AB 257 AA 260 A 65 4/22/2021

Example 1: LZW Compression Step 6 BABAABAAA P=AA C=empty Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 47 STRING TABLE ENCODER OUTPUT string codeword representing output code BA 256 B 66 AB 257 A 65 BAA 258 BA 256 ABA 259 AB 257 AA 260 A 65 AA 260 4/22/2021

LZW Decompression  The LZW decompressor creates the same string table during decompression.  It starts with the first 256 table entries initialized to single characters.  The string table is updated for each character in the input stream, except the first one.  Decoding achieved by reading codes and translating them through the code table being built. Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 48 4/22/2021

LZW Decompression Algorithm 1 Initialize table with single character strings 2 OLD = first input code 3 output translation of OLD 4 WHILE not end of input stream 5 NEW = next input code 6 IF NEW is not in the string table 7 S = translation of OLD 8 S = S + C 9 ELSE 10 S = translation of NEW 11 output S 12 C = first character of S 13 OLD + C to the string table 14 OLD = NEW 15 ENDWHILE Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 49 4/22/2021

Example 2: LZW Decompression 1 Example 2: Use LZW to decompress the output sequence of Example 1: <66><65><256><257><65><260>. Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 50 4/22/2021

Example 2: LZW Decompression Step 1 <66><65><256><257><65><260> Old = 65 S = A New = 66 C = A Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 51 STRING TABLE ENCODER OUTPUT string codeword string B BA 256 A 4/22/2021

Example 2: LZW Decompression Step 2 <66><65><256><257><65><260> Old = 256 S = BA New = 256 C = B Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 52 STRING TABLE ENCODER OUTPUT string codeword string B BA 256 A AB 257 BA 4/22/2021

Example 2: LZW Decompression Step 3 <66><65><256><257><65><260> Old = 257 S = AB New = 257 C = A Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 53 STRING TABLE ENCODER OUTPUT string codeword string B BA 256 A AB 257 BA BAA 258 AB 4/22/2021

Example 2: LZW Decompression Step 4 <66><65><256><257><65><260> Old = 65 S = A New = 65 C = A Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 54 STRING TABLE ENCODER OUTPUT string codeword string B BA 256 A AB 257 BA BAA 258 AB ABA 259 A 4/22/2021

Example 2: LZW Decompression Step 5 <66><65><256><257><65><260> Old = 260 S = AA New = 260 C = A Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 55 STRING TABLE ENCODER OUTPUT string codeword string B BA 256 A AB 257 BA BAA 258 AB ABA 259 A AA 260 AA 4/22/2021

LZW: Some Notes  This algorithm compresses repetitive sequences of data well.  Since the codewords are 12 bits, any single encoded character will expand the data size rather than reduce it.  In this example, 72 bits are represented with 72 bits of data. After a reasonable string table is built, compression improves dramatically.  Advantages of LZW over Huffman:  LZW requires no prior information about the input data stream.  LZW can compress the input stream in one single pass.  Another advantage of LZW its simplicity, allowing fast execution. Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 56 4/22/2021

LZW: Limitations  What happens when the dictionary gets too large (i.e., when all the 4096 locations have been used)?  Here are some options usually implemented:  Simply forget about adding any more entries and use the table as is.  Throw the dictionary away when it reaches a certain size.  Throw the dictionary away when it is no longer effective at compression.  Clear entries 256-4095 and start building the dictionary again.  Some clever schemes rebuild a string table from the last N input characters. Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 57 4/22/2021

Lossless Image Compression: Multi-resolution Approaches. Image compression is a type of data compression applied to digital images, to reduce their cost for storage or transmission. Image compression may be lossy or lossless. Lossless compression is preferred for archival purposes and often for medical imaging, technical drawings, clip art, or comics. Methods for lossless compression: Run-length encoding – used in default method in PCX and as one of possible in BMP, TGA, TIFF Area image compression Predictive coding – used in DPCM Entropy encoding – the two most common entropy encoding techniques are arithmetic coding and Huffman coding Adaptive dictionary algorithms such as LZW – used in GIF and TIFF DEFLATE – used in PNG, MNG, and TIFF Chain codes Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 58 4/22/2021

Context Based Compression: Dynamic Markov Compression.  developed by Gordon Cormack and Nigel Horspool (1987)  adaptative lossless data compression algorithm  based on the modelization of the binary source to be encoded by means of a Markov chain, which describes the transition probabilities between the symbol “0” and the symbol “1”  the built model is used to predict the future bit of a message. The predicted bit is then coded using arithmetic coding Dynamic Markov compression (DMC) is a lossless data compression algorithm developed by Gordon Cormack and Nigel Horspool.It uses predictive arithmetic coding similar to prediction by partial matching (PPM), except that the input is predicted one bit at a time (rather than one byte at a time). DMC has a good compression ratio and moderate speed, similar to PPM, but requires somewhat more memory and is not widely implemented. Dynamic Markov Compression is an obscure form of compression that uses Markov chains to model the patterns represented in a file. Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 59 4/22/2021

Each circle represents a state, and each arrow represents a transition. In this example, we have two states, raining and sunny, a perfect representation of true weather. Each state has two possible transitions, it can transition to itself again or it can transition to another state. The likelihood of each transition is defined by a percentage representing the probability that the transition occurs. Now let’s say it’s sunny and we’re following this model. According to the model there’s a 50% chance it’s sunny again tomorrow or a 50% chance it’s rainy tomorrow. If it becomes rainy, then there’s a 25% chance it’s rainy the day after that or a 75% chance it’s sunny the day after that. Dr. Piyush, Charan Dept. of ECE, Integral University, Lucknow 60 4/22/2021

Unit 3 Arithmetic Coding

More Related Content

What's hot

Similar to Unit 3 Arithmetic Coding

More from Dr Piyush Charan

Recently uploaded

Unit 3 Arithmetic Coding