Mohamed Loey, profile picture
Uploaded byMohamed Loey
5,267 views

Algorithms Lecture 7: Graph Algorithms

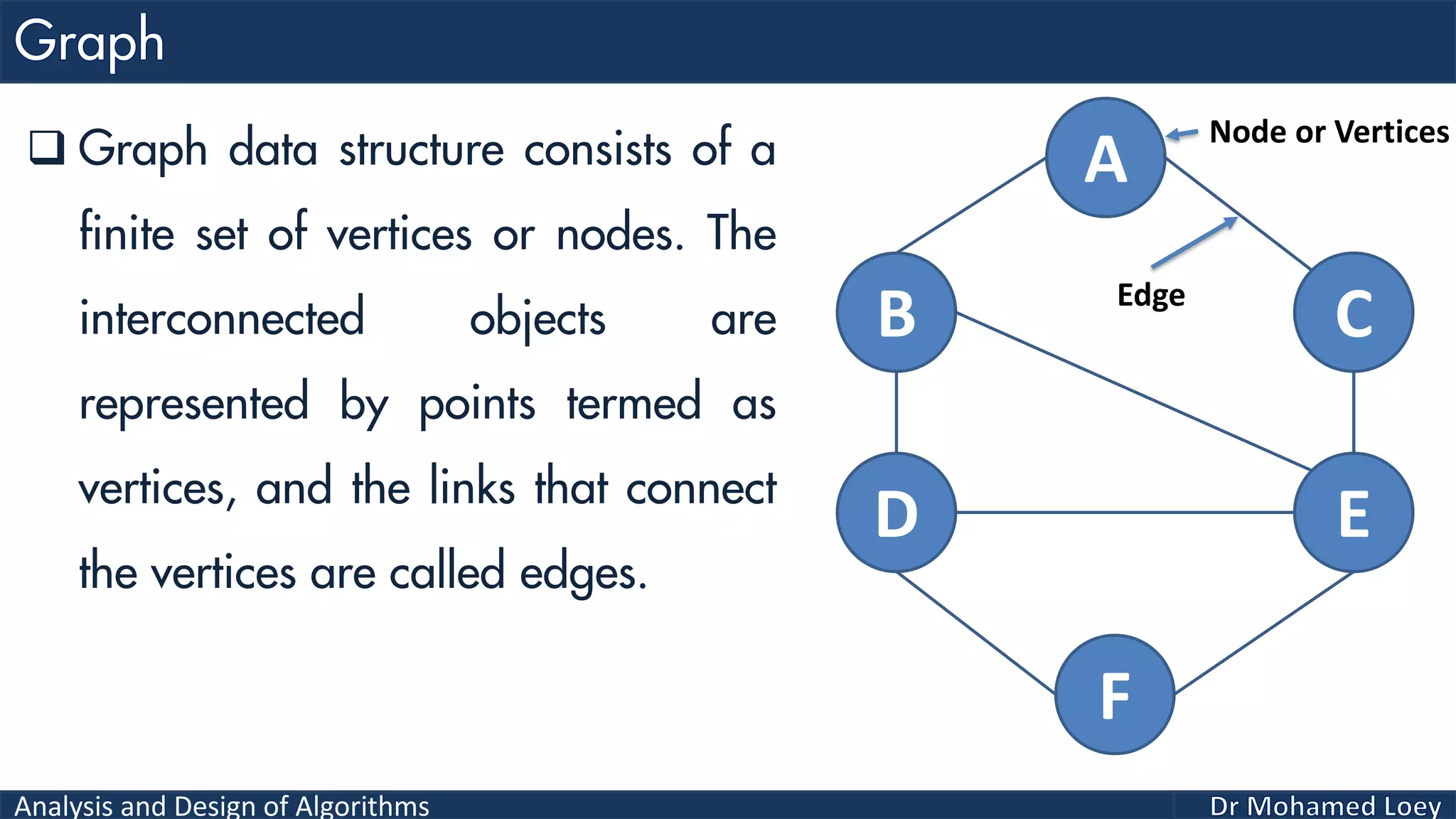
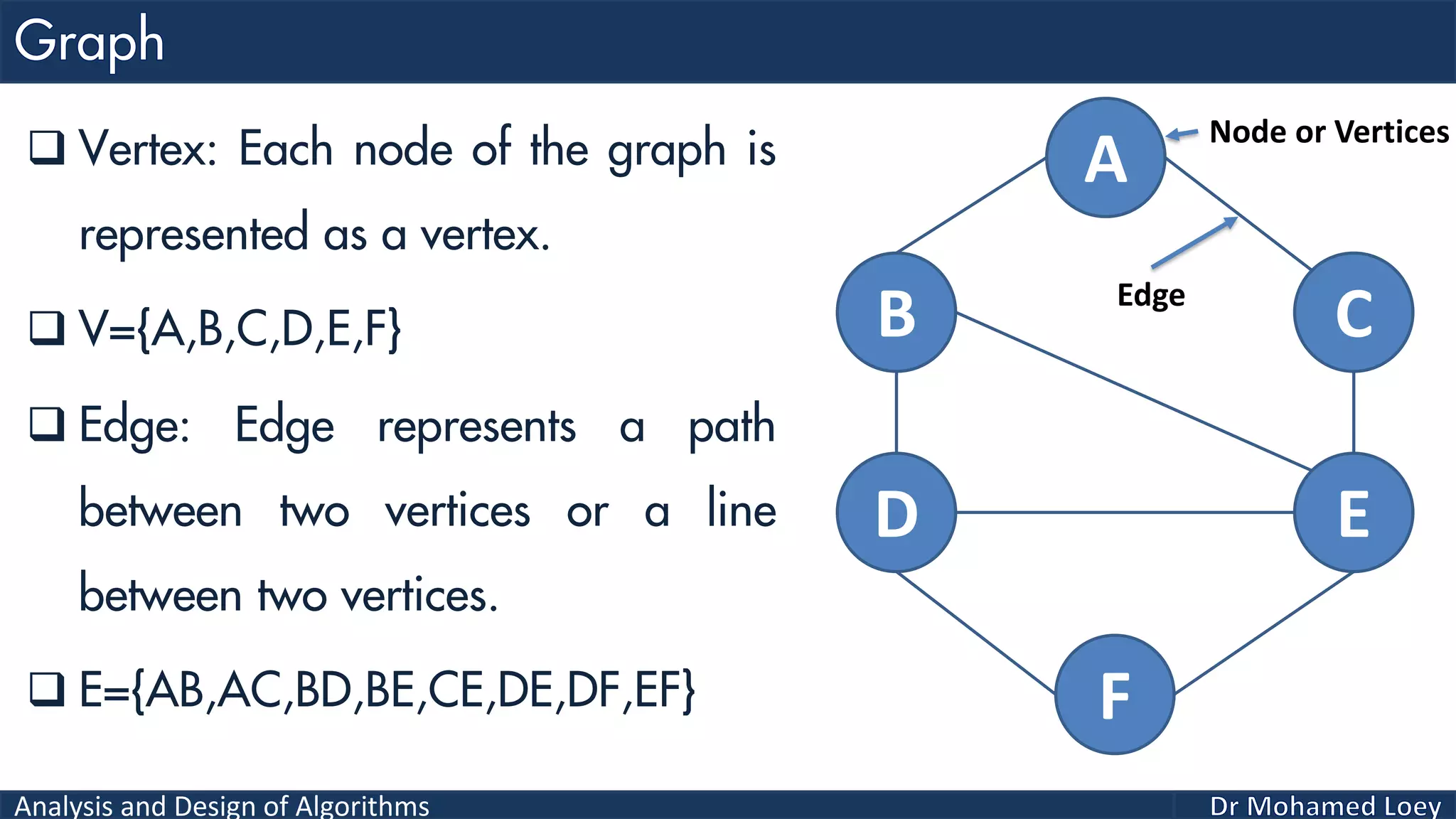
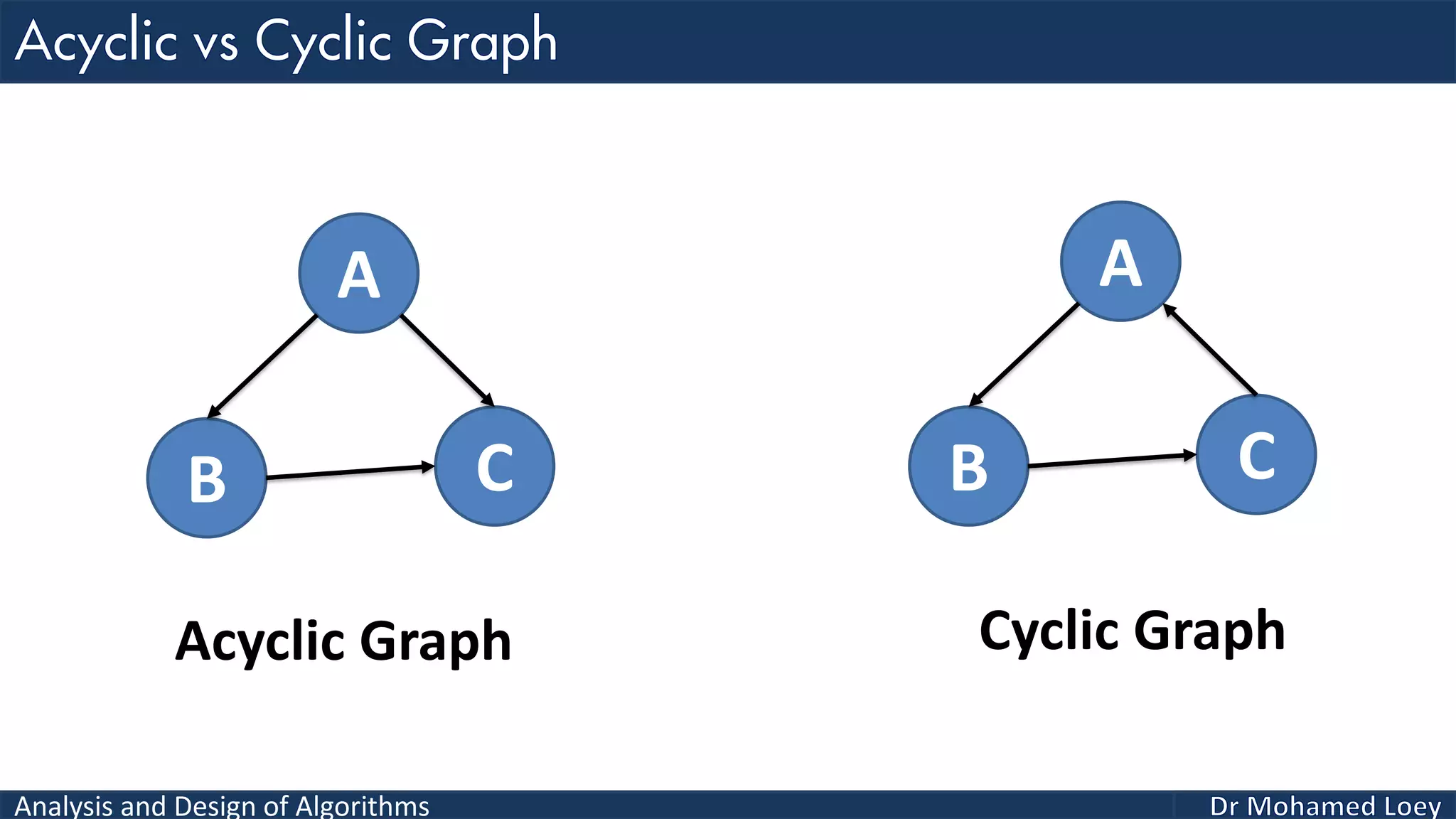
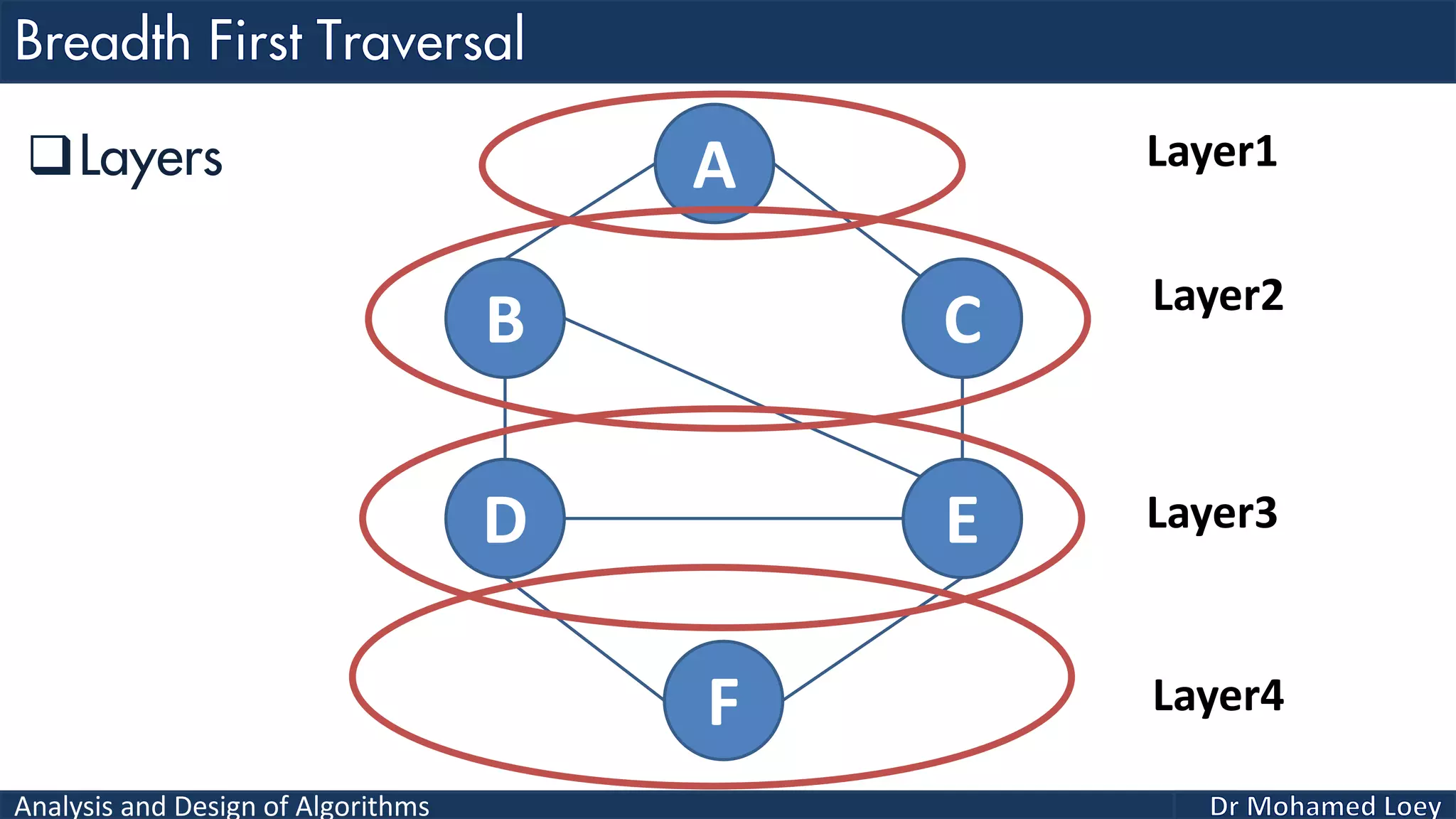
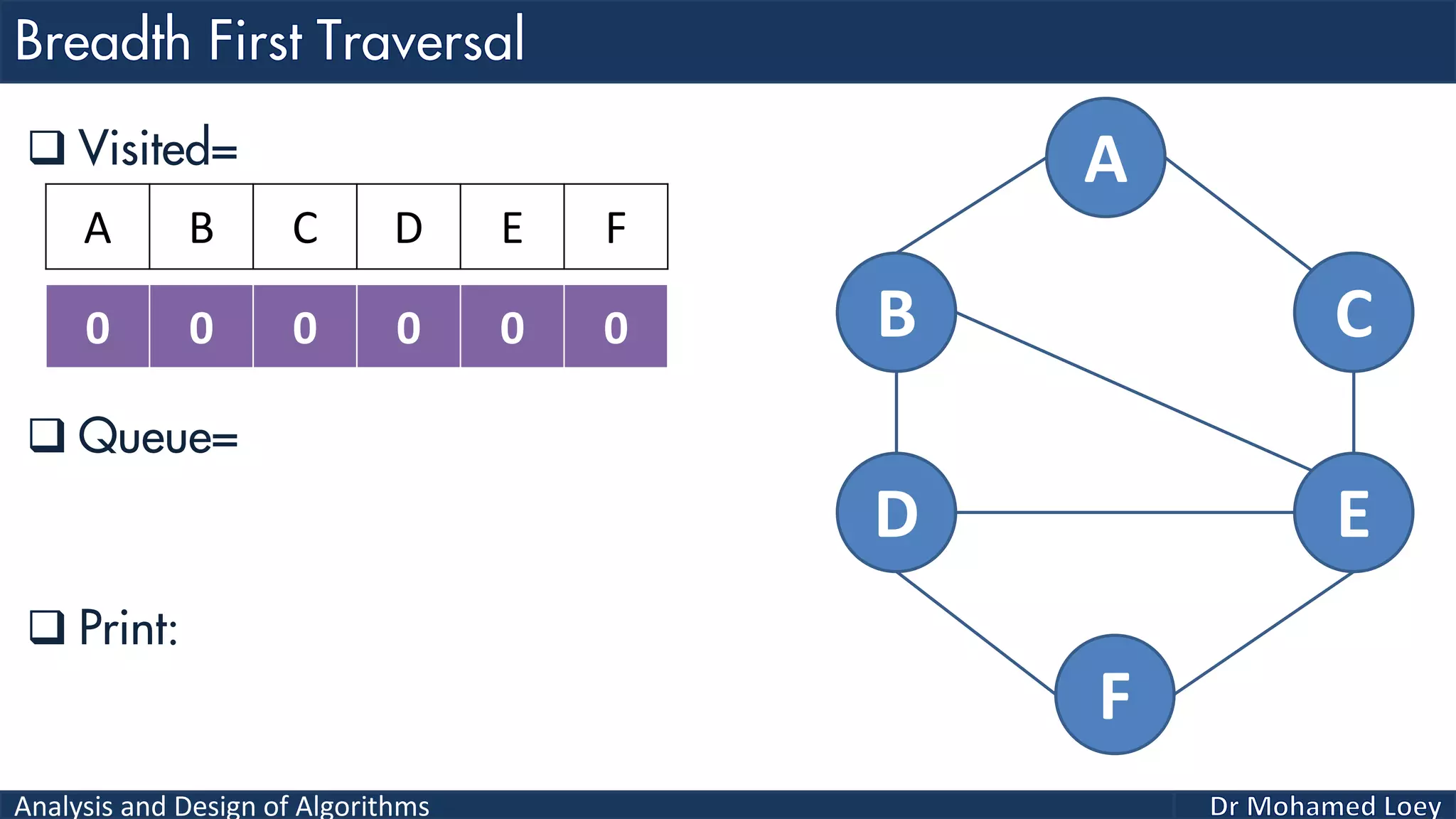
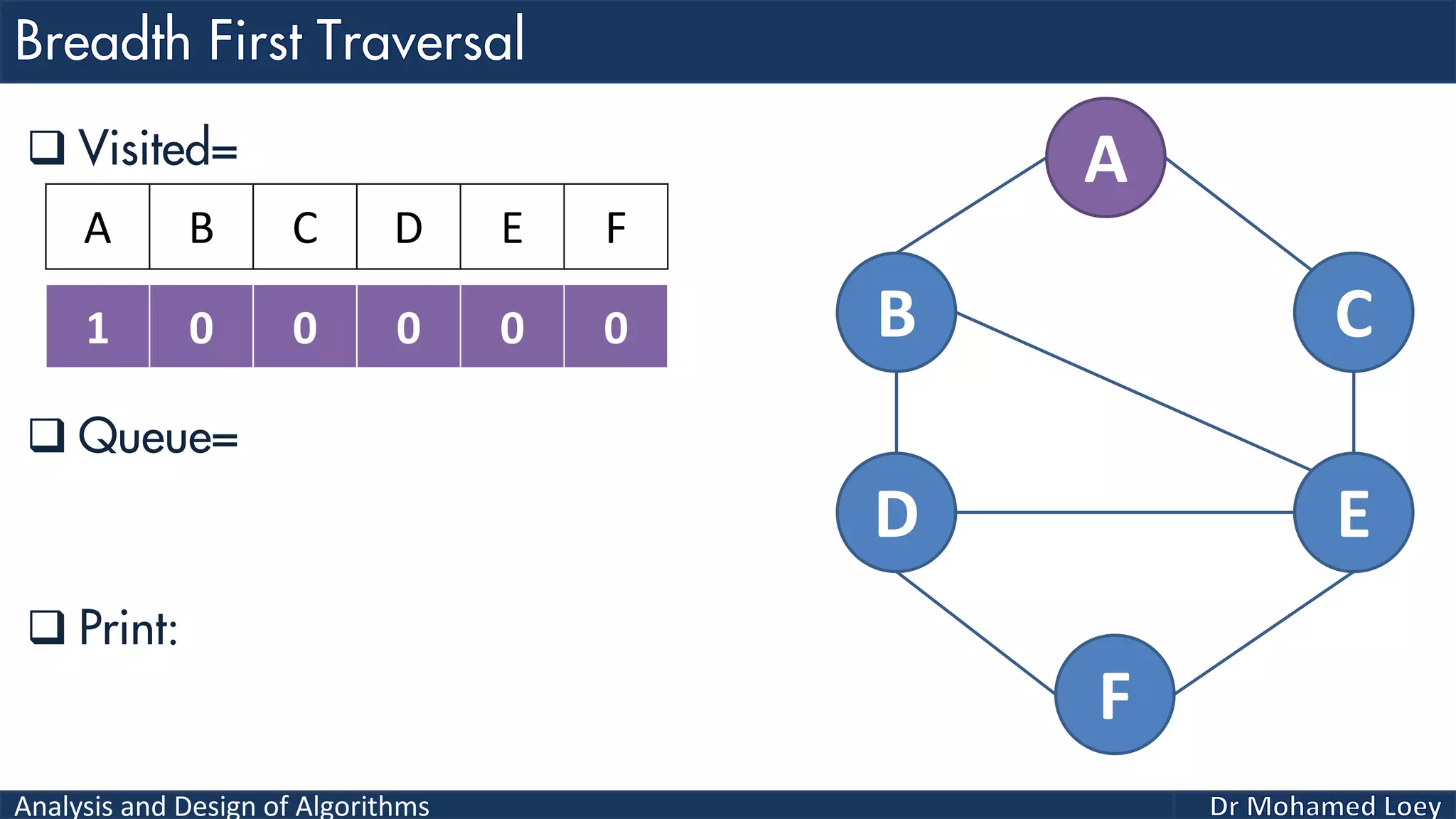
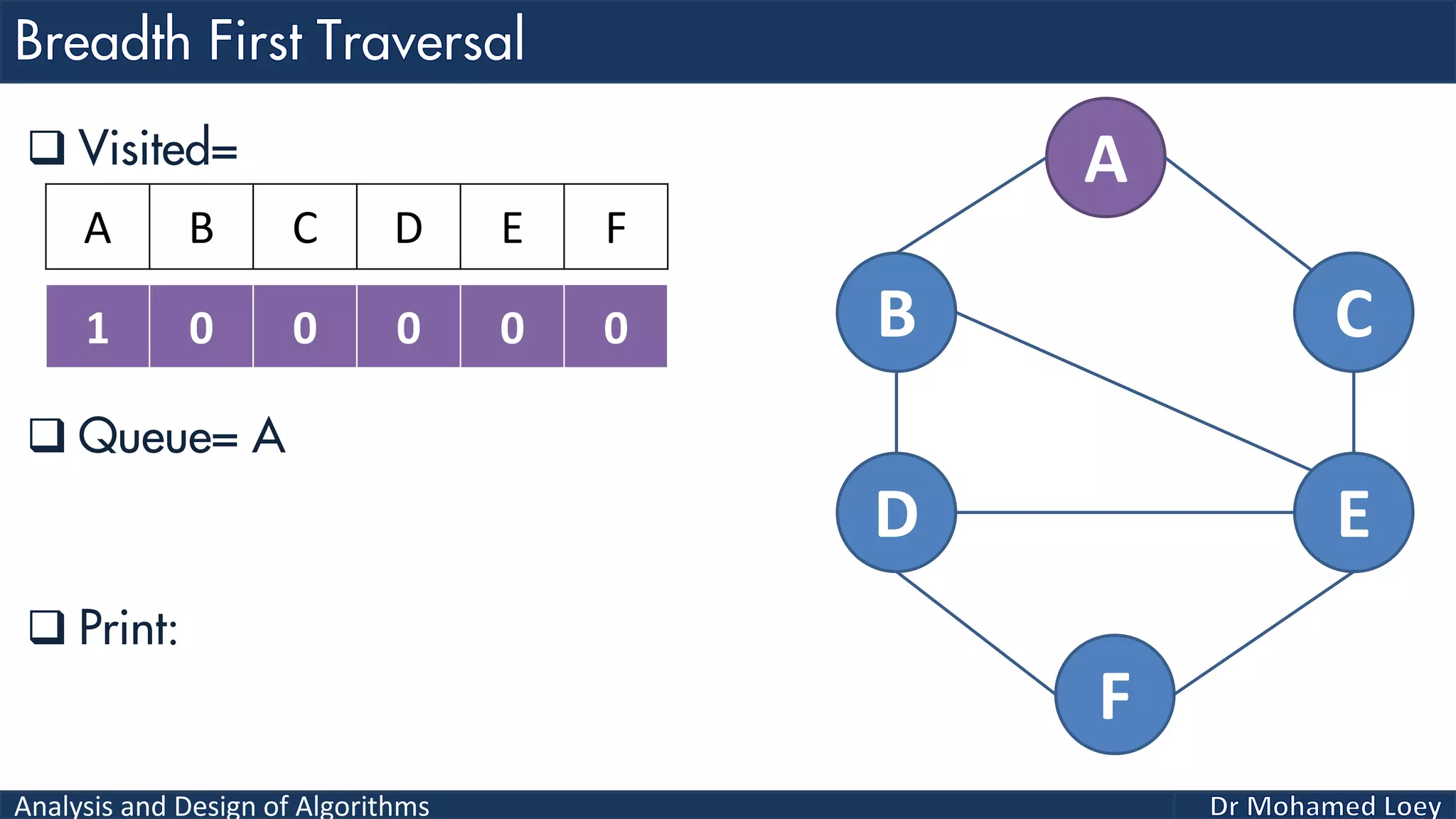
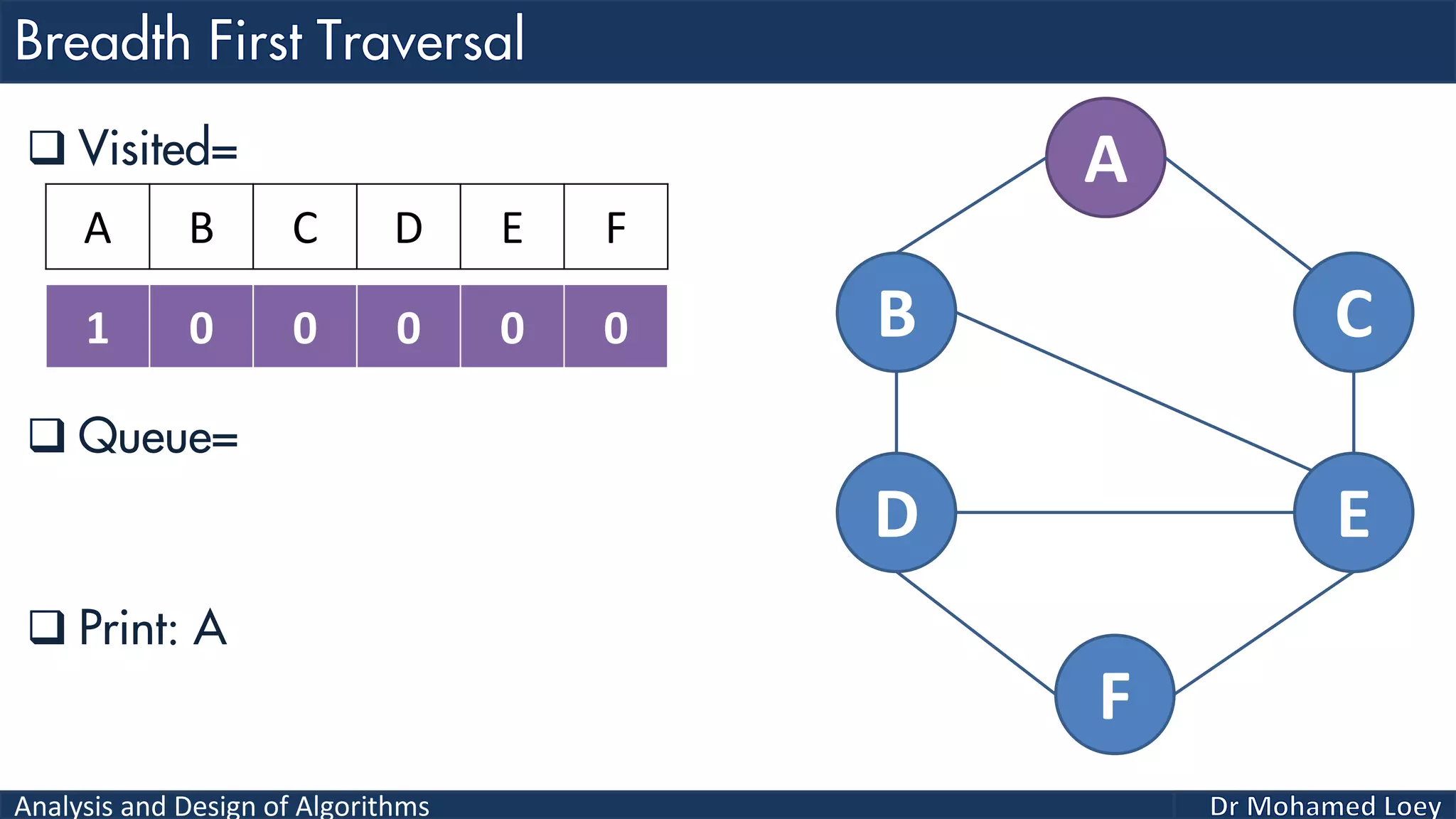
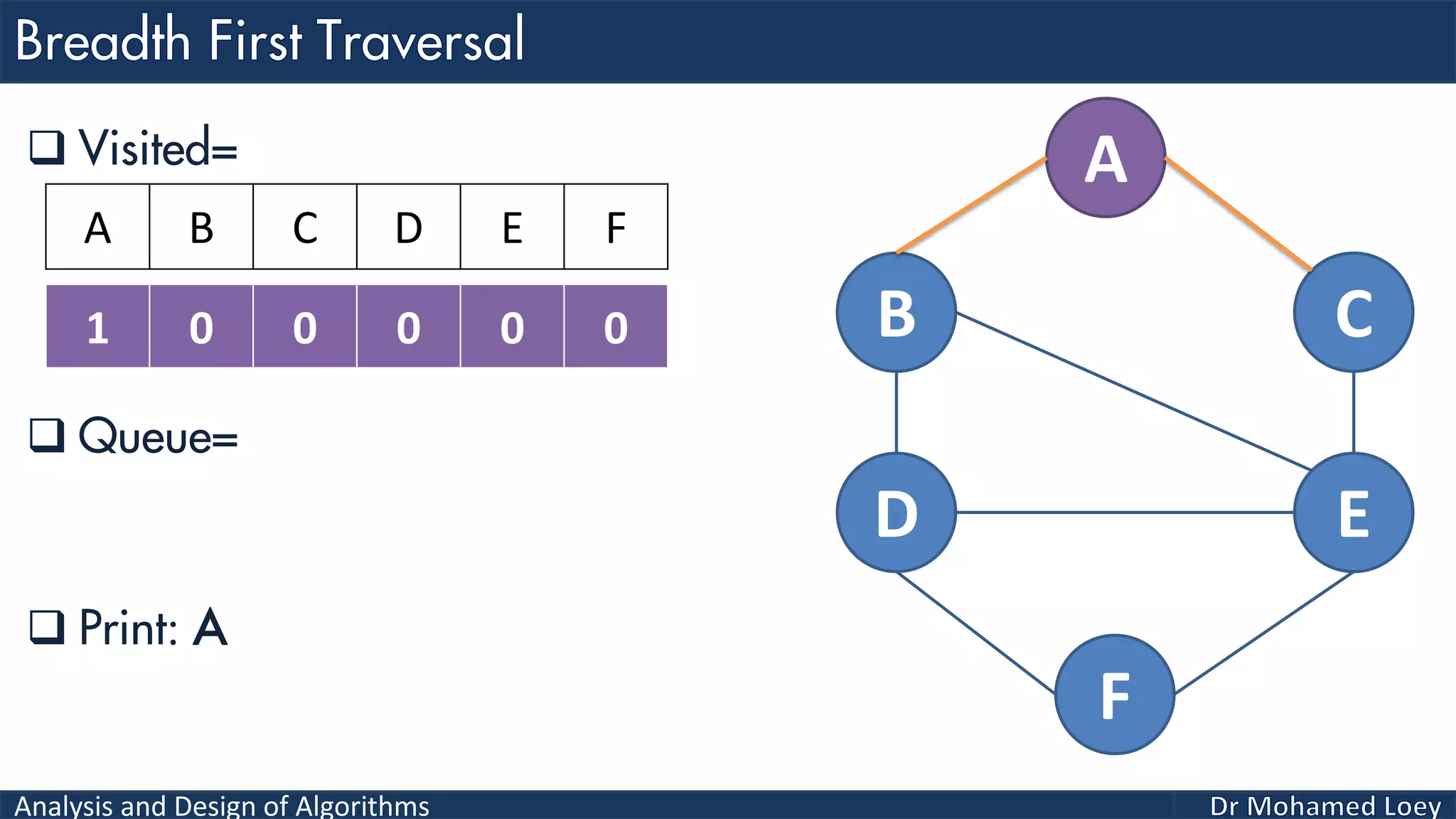
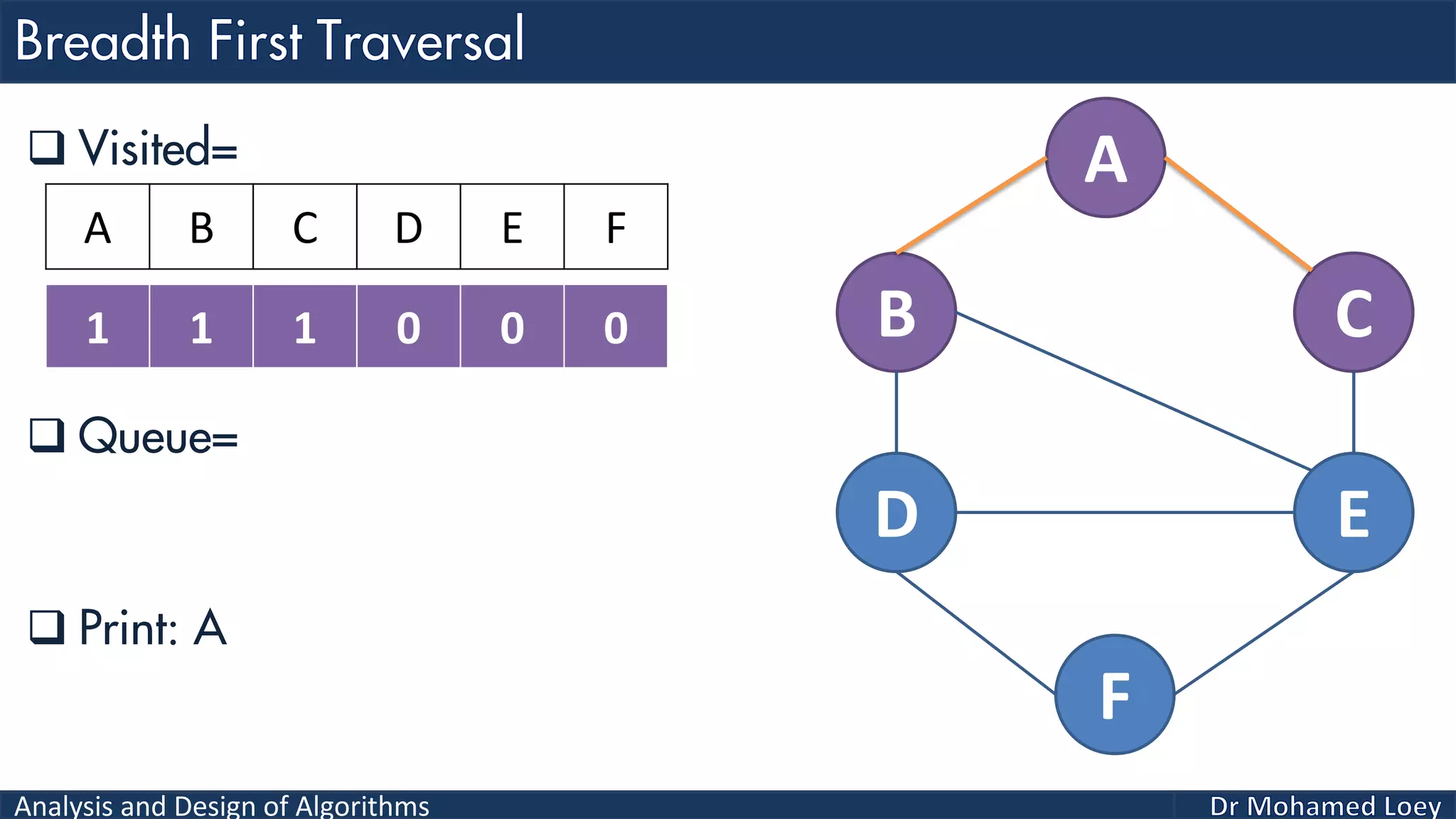
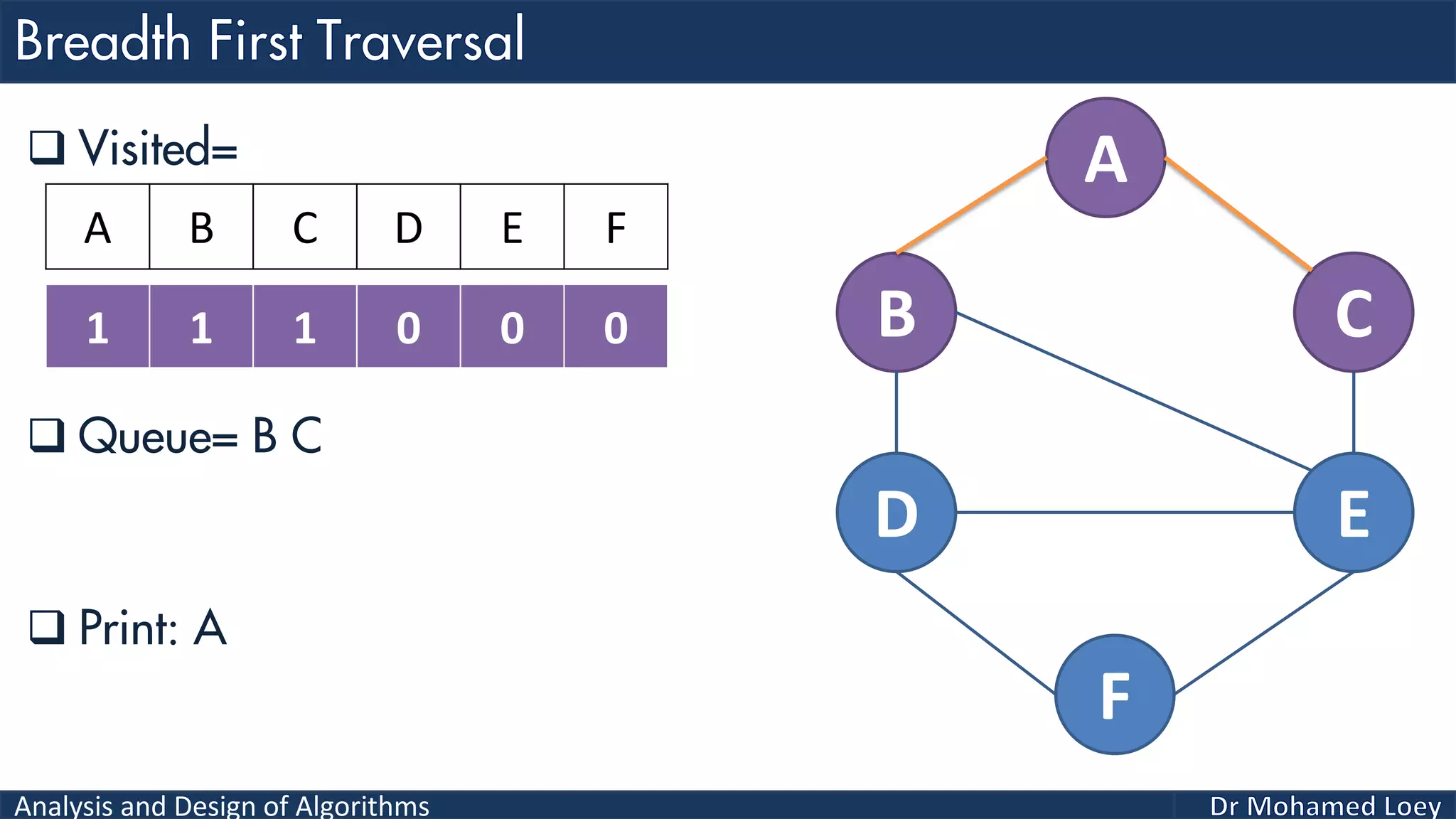
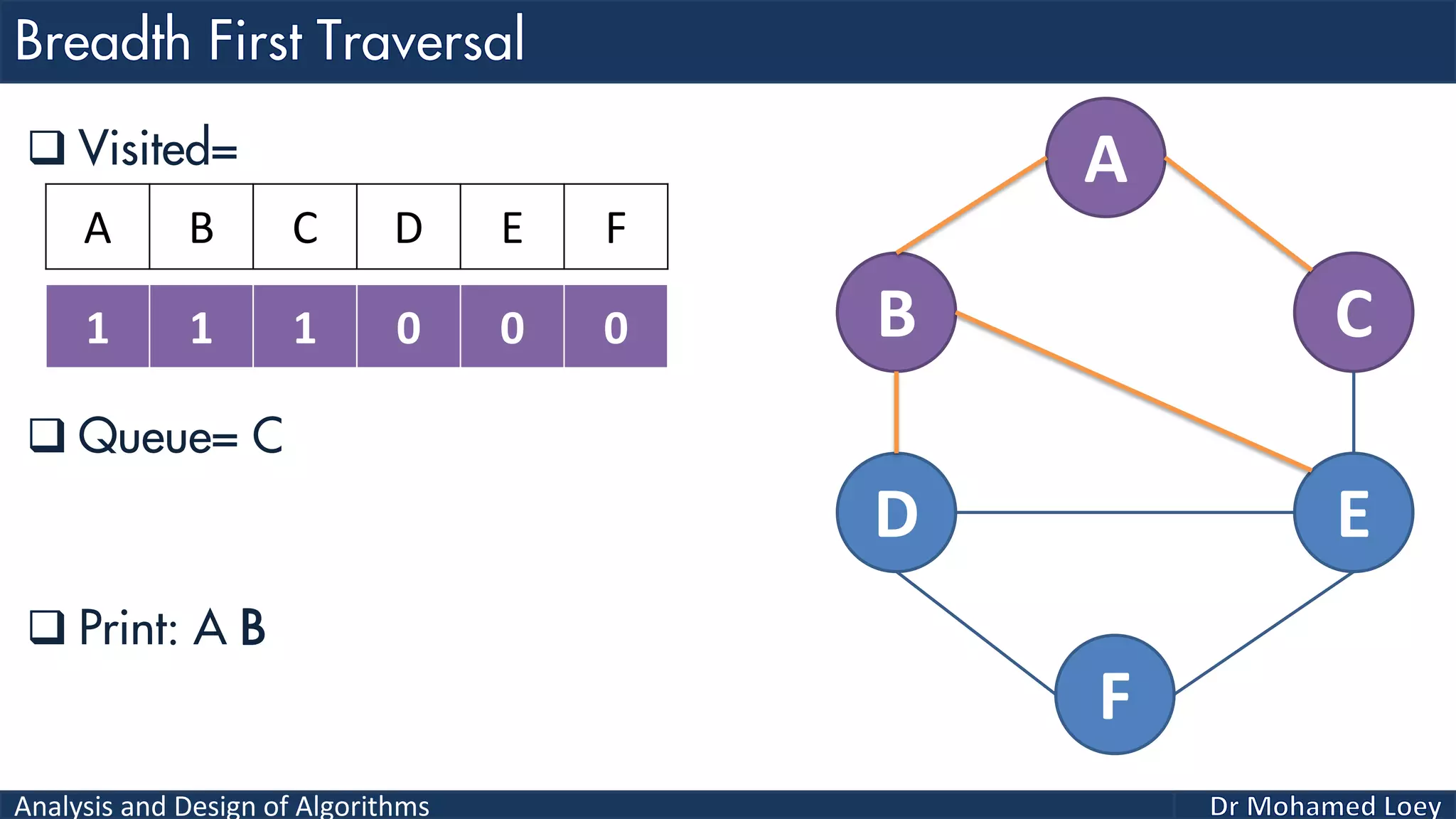
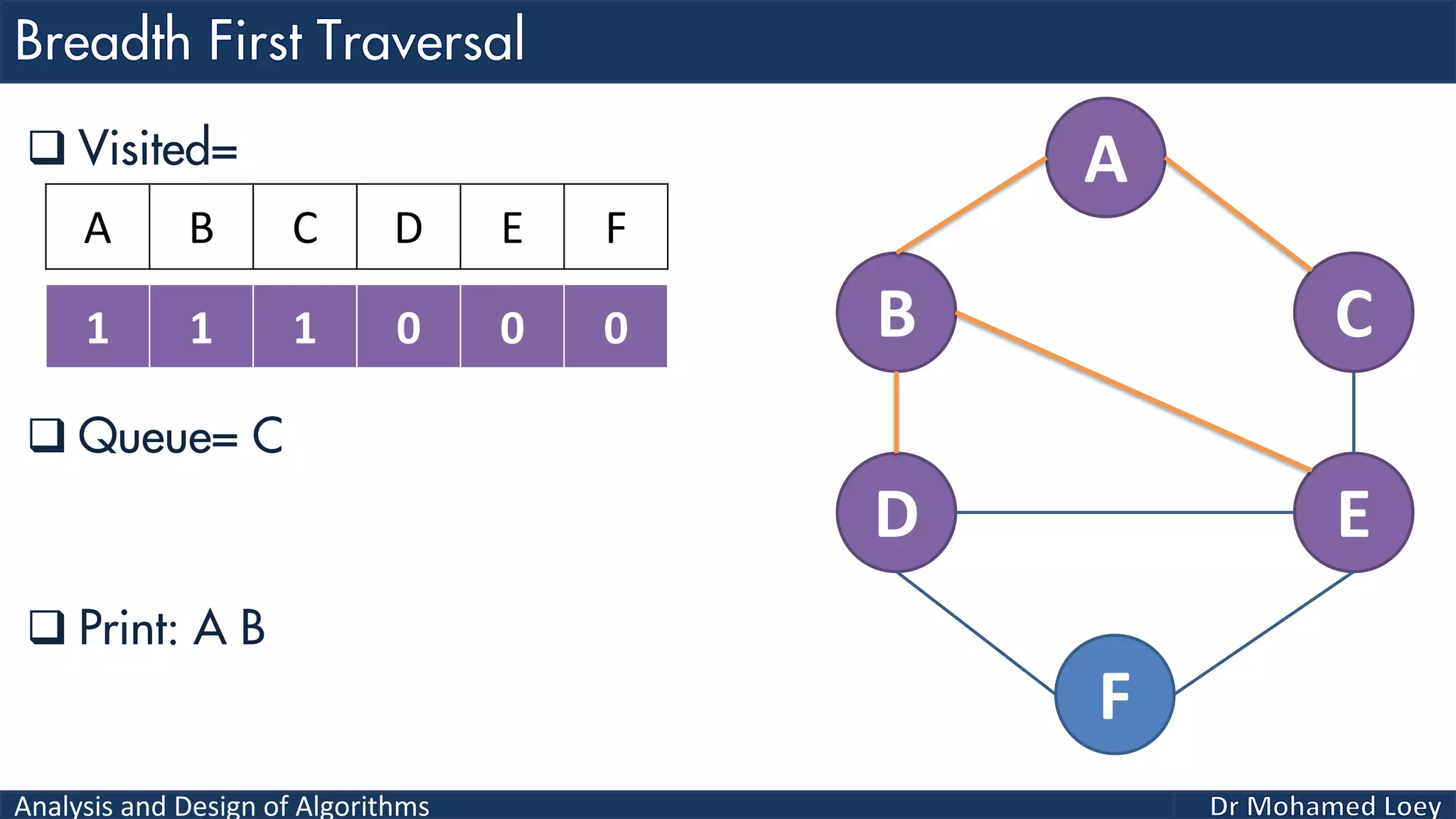
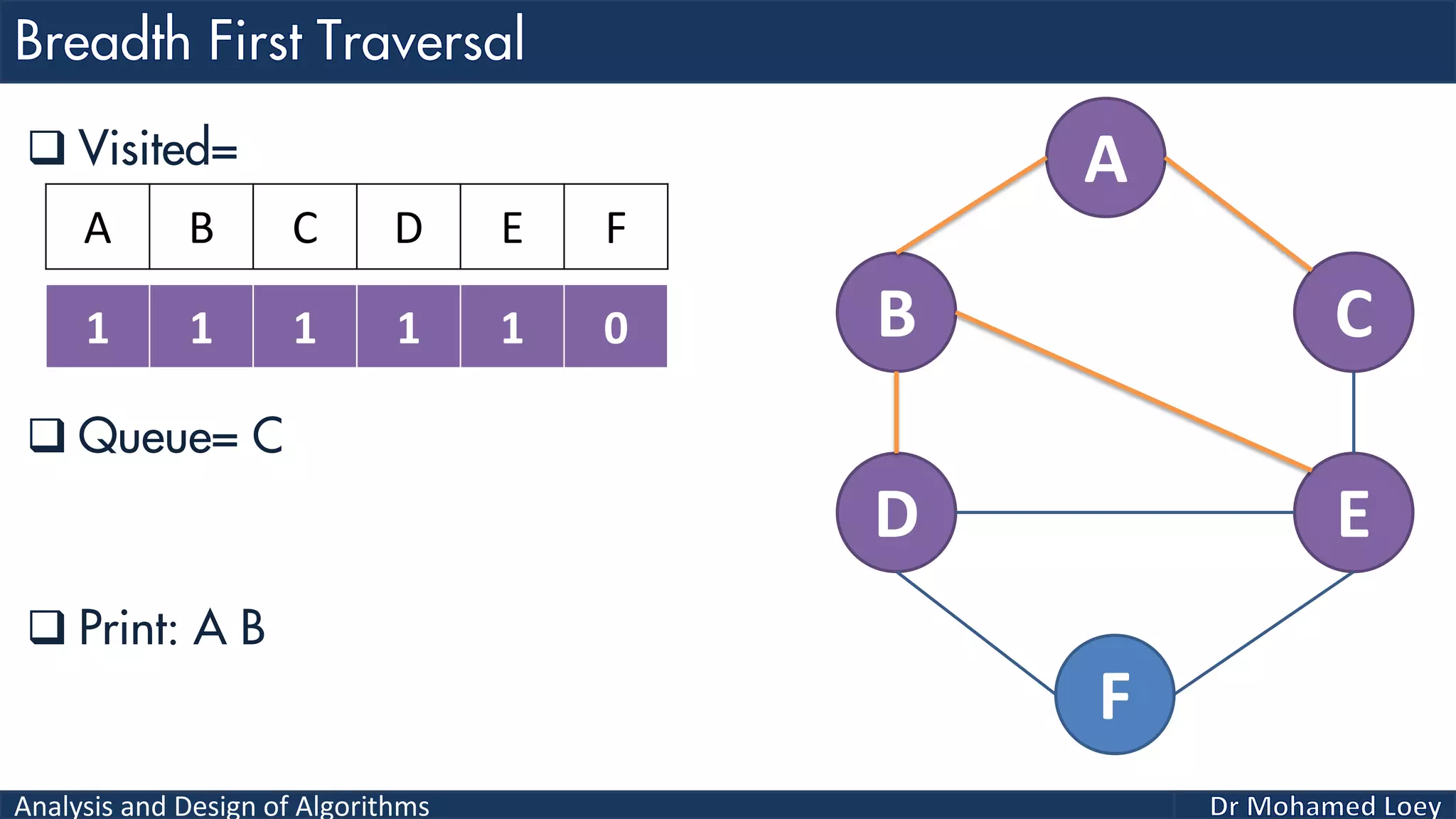
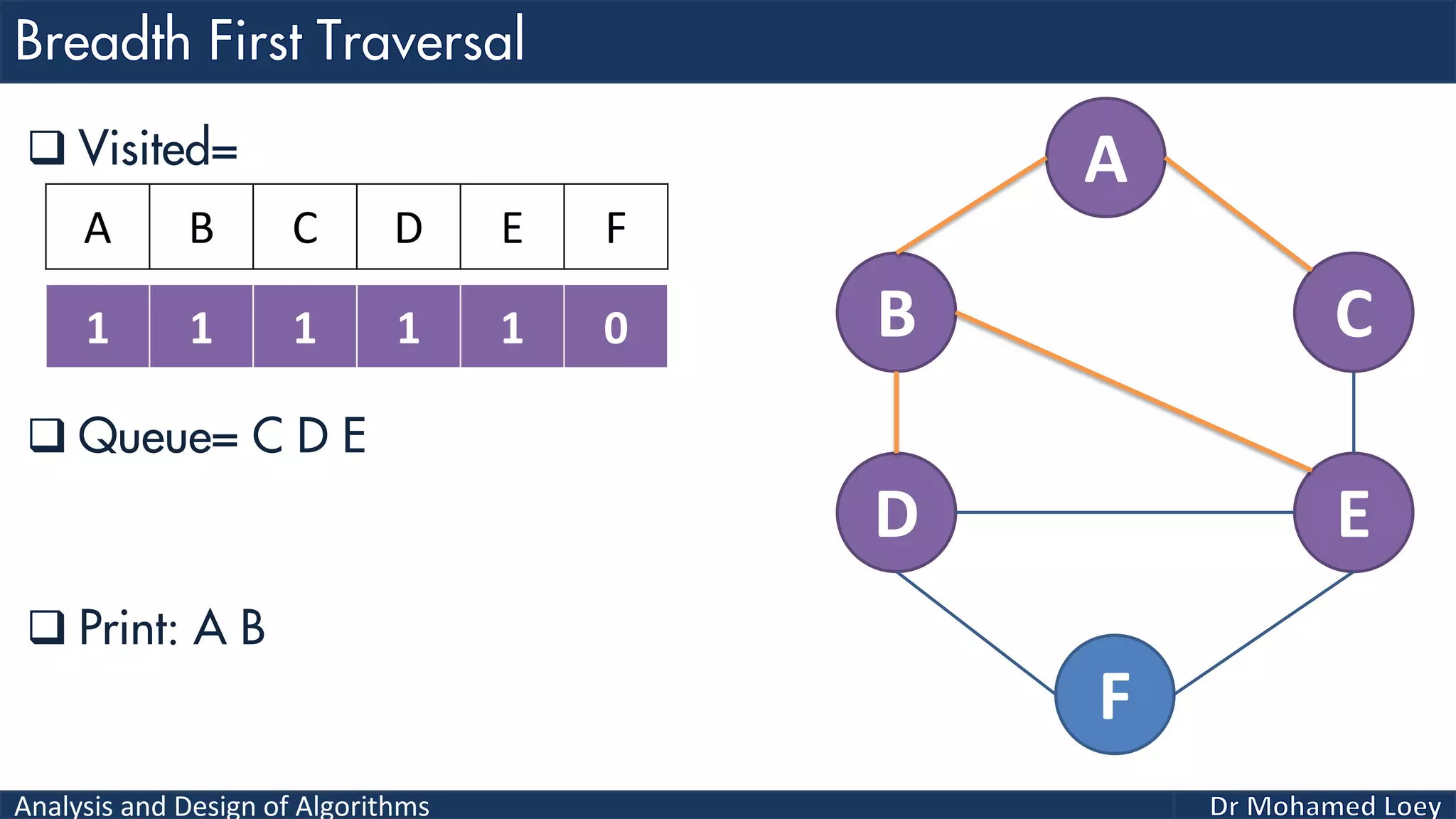
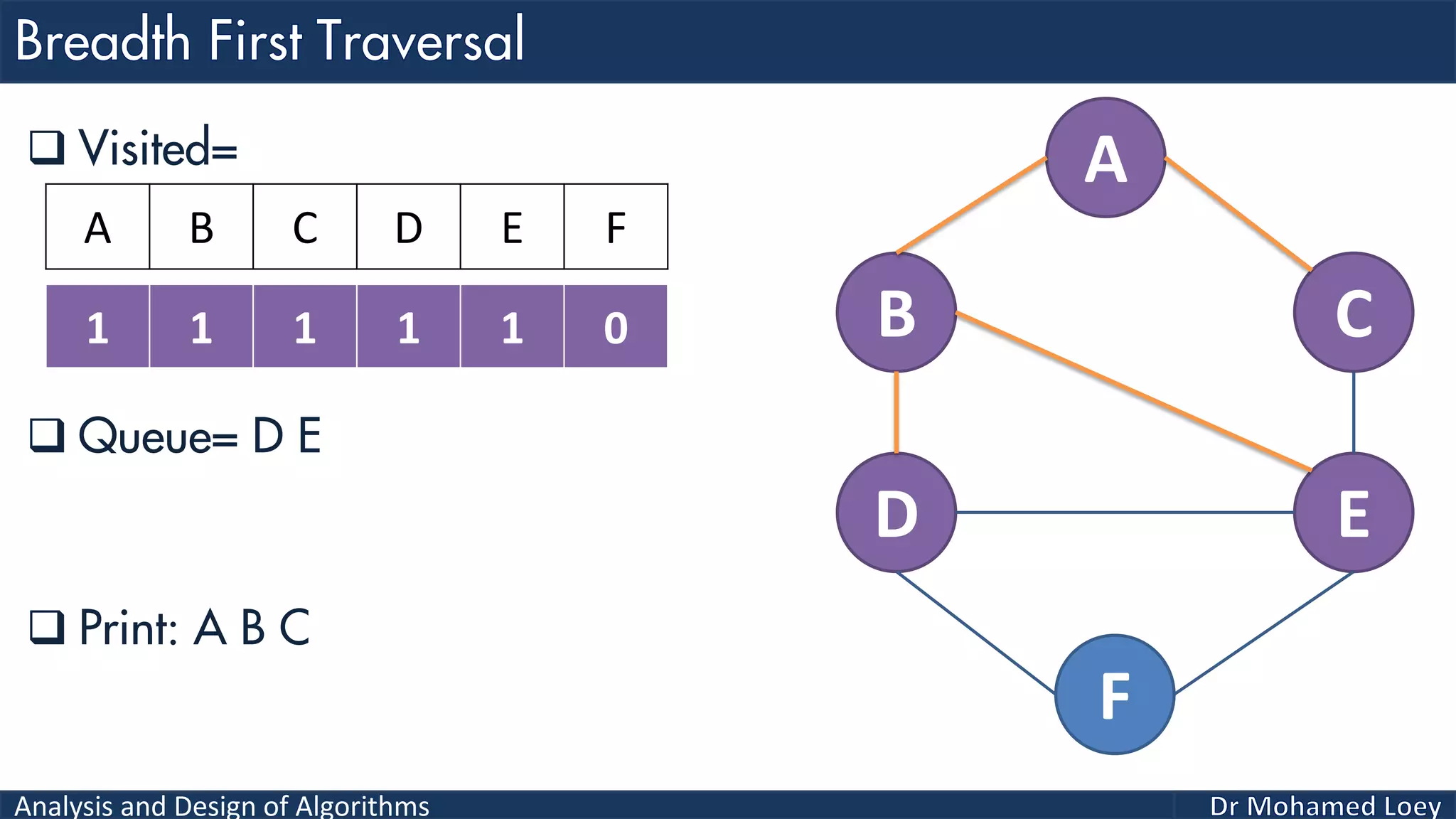
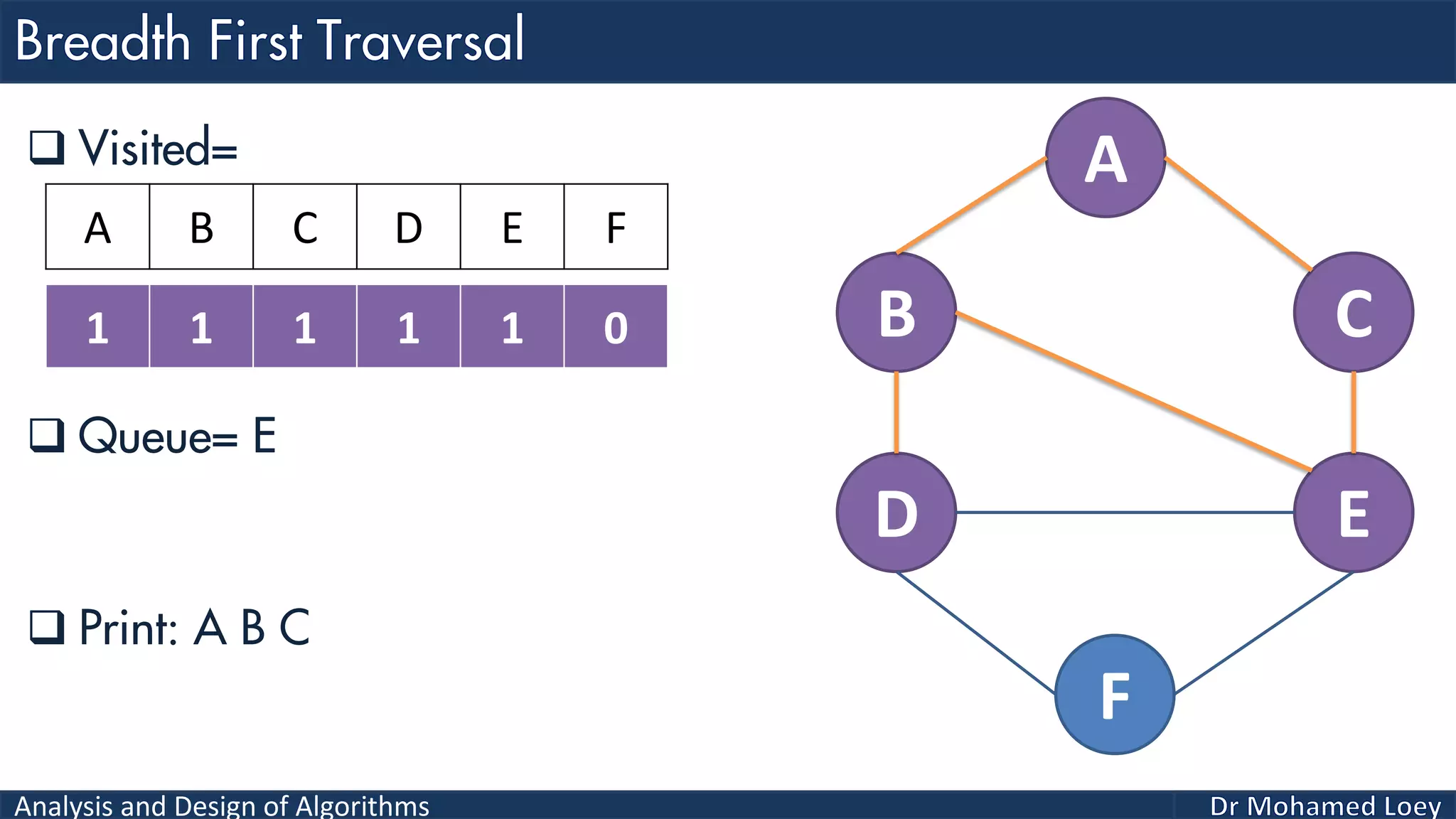
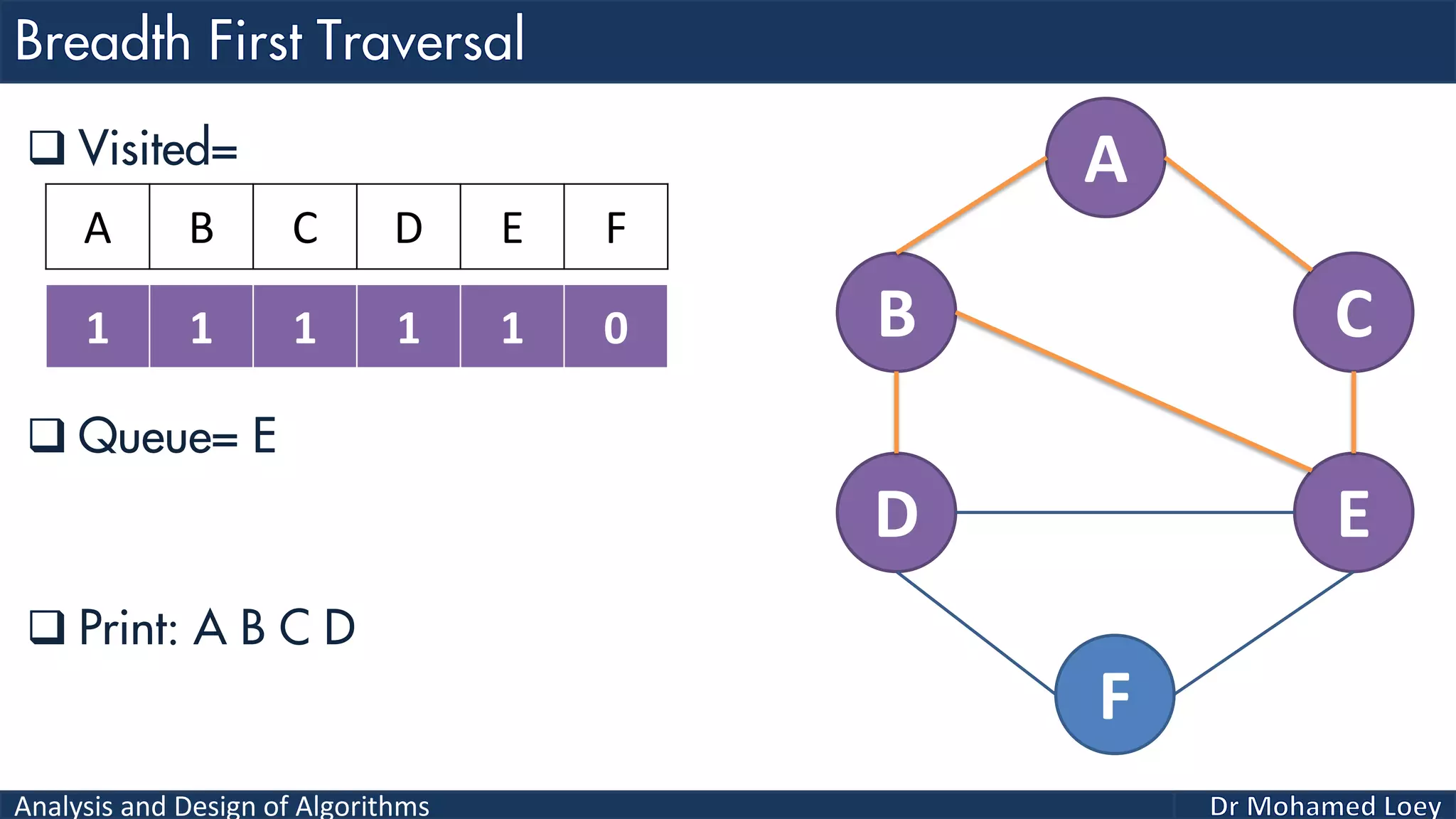
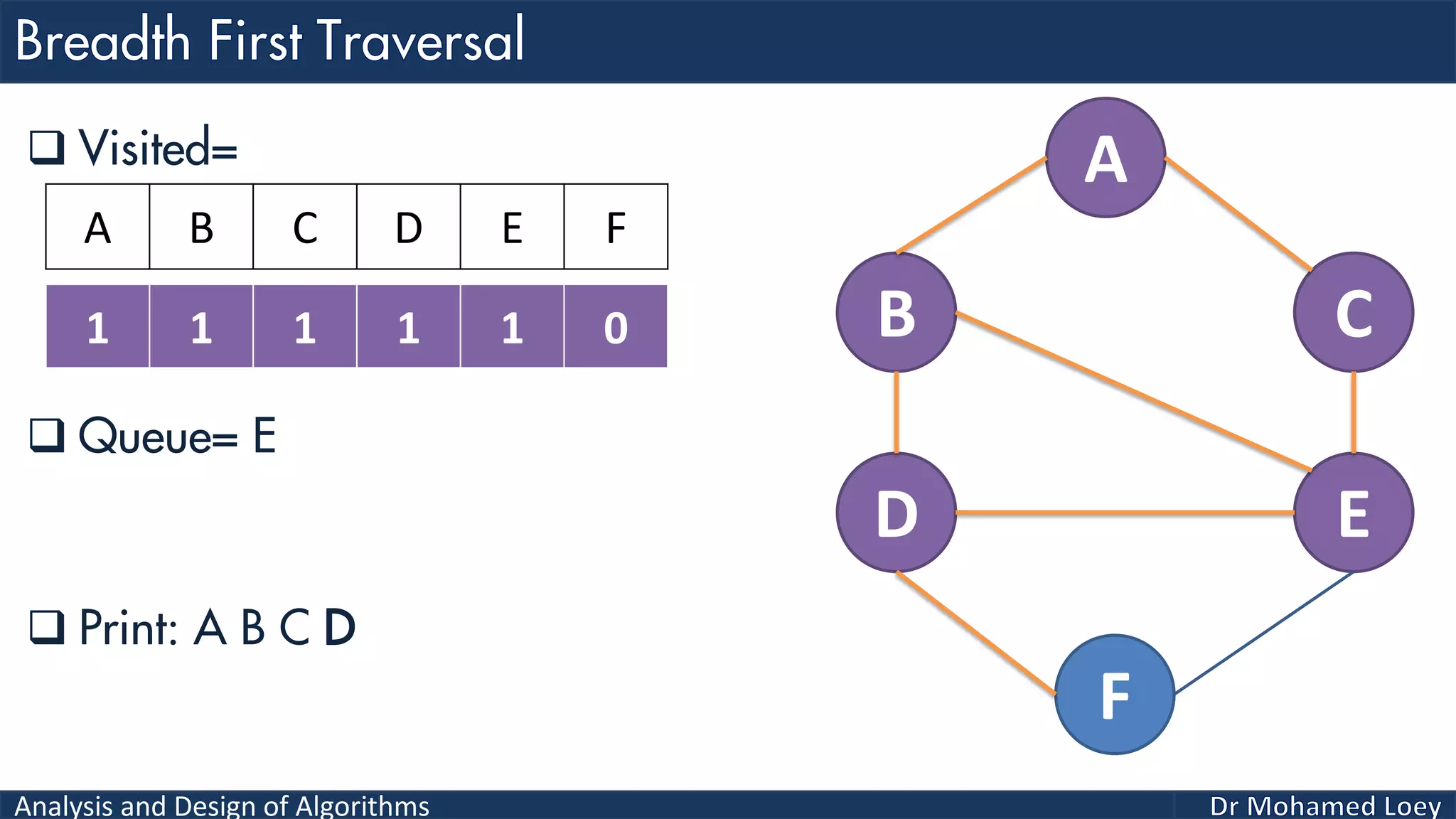
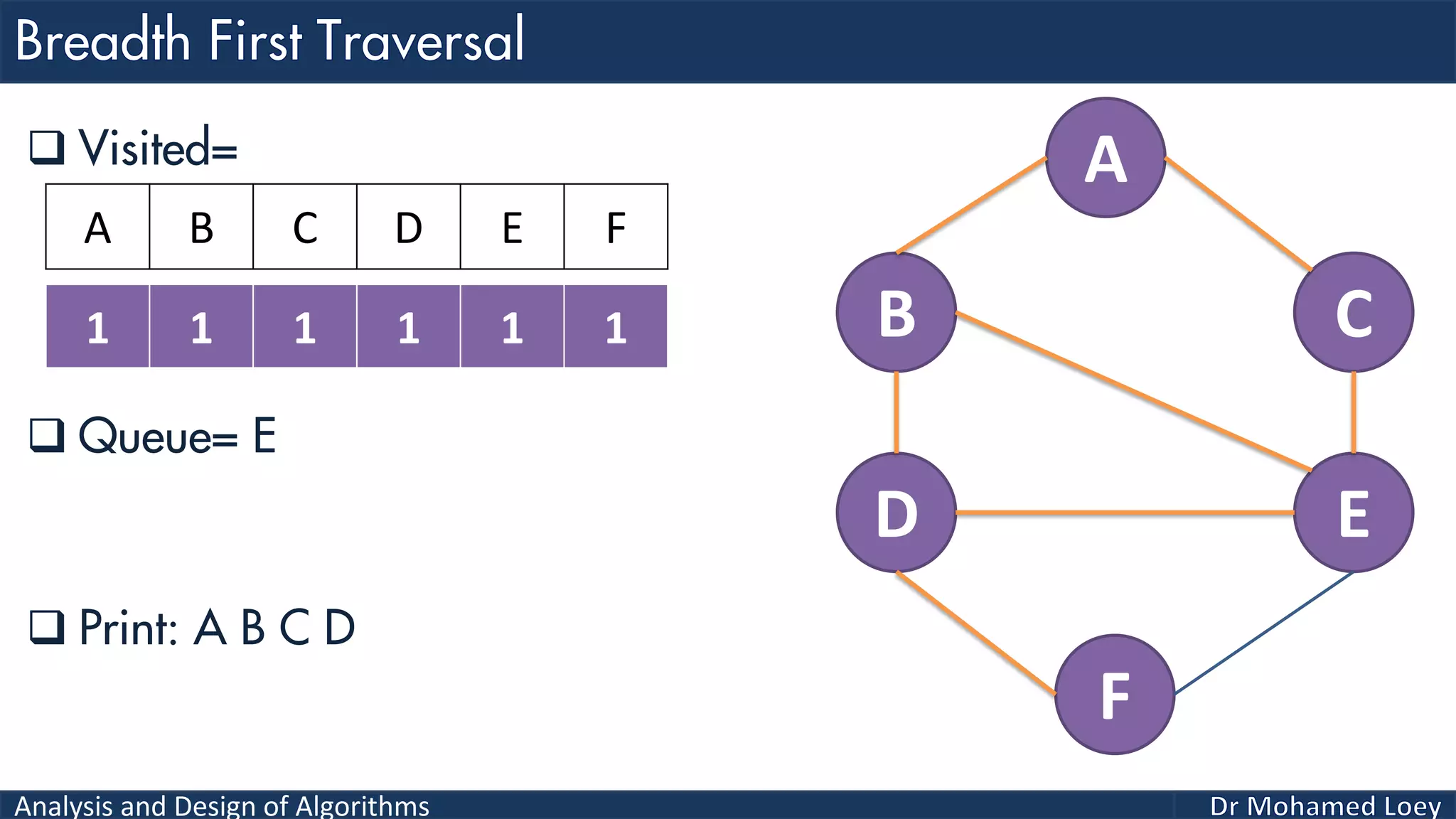
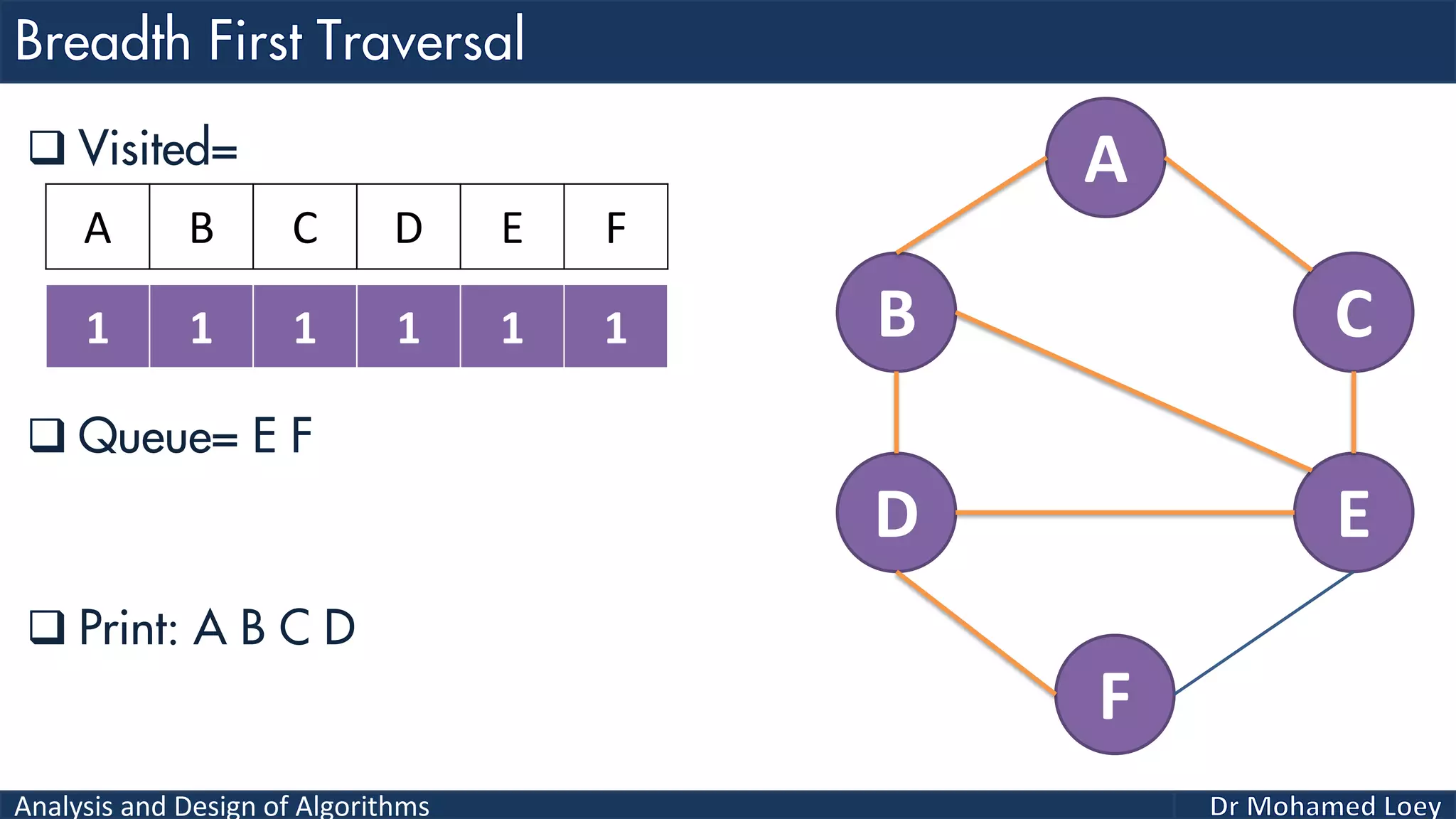
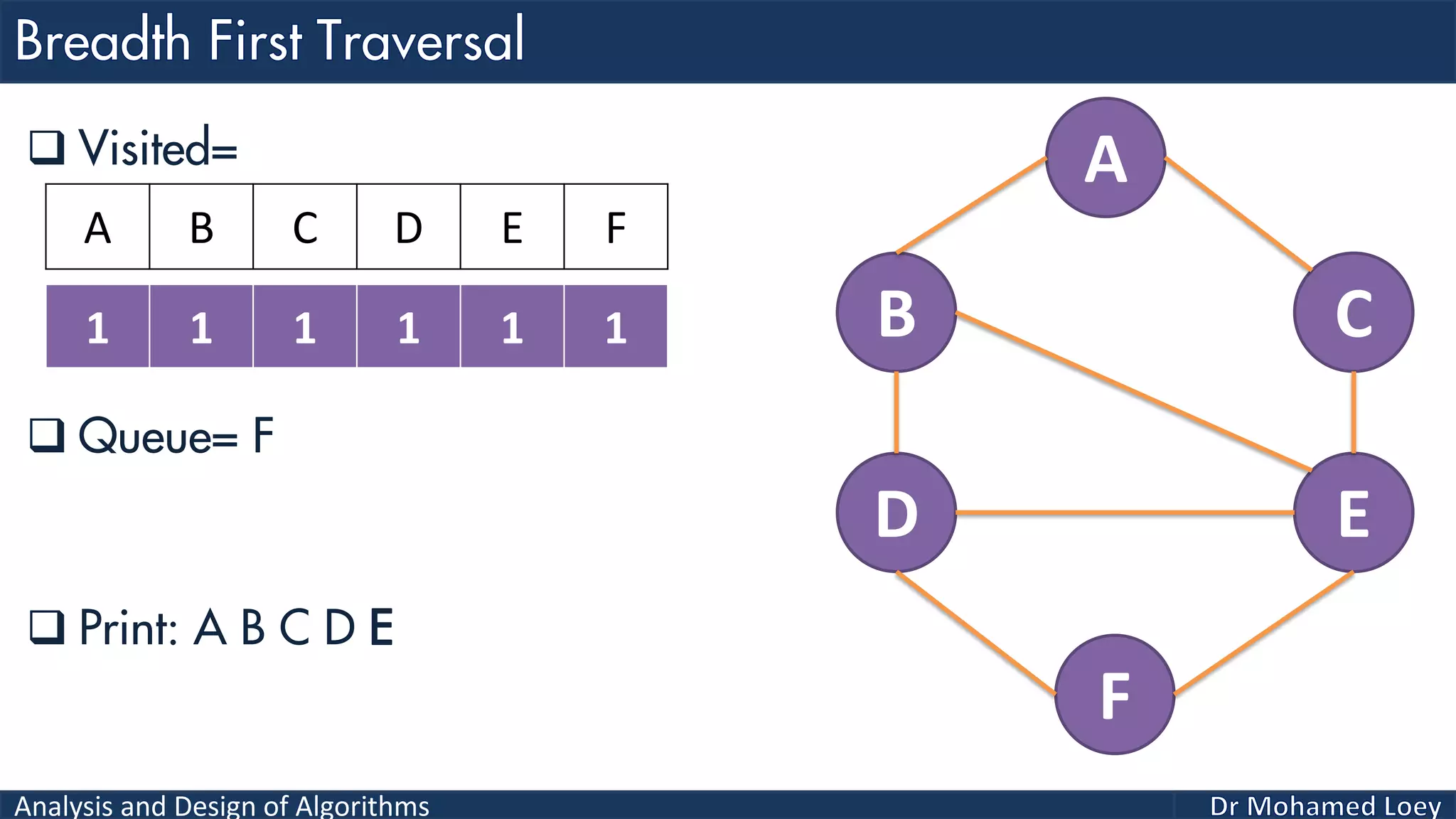
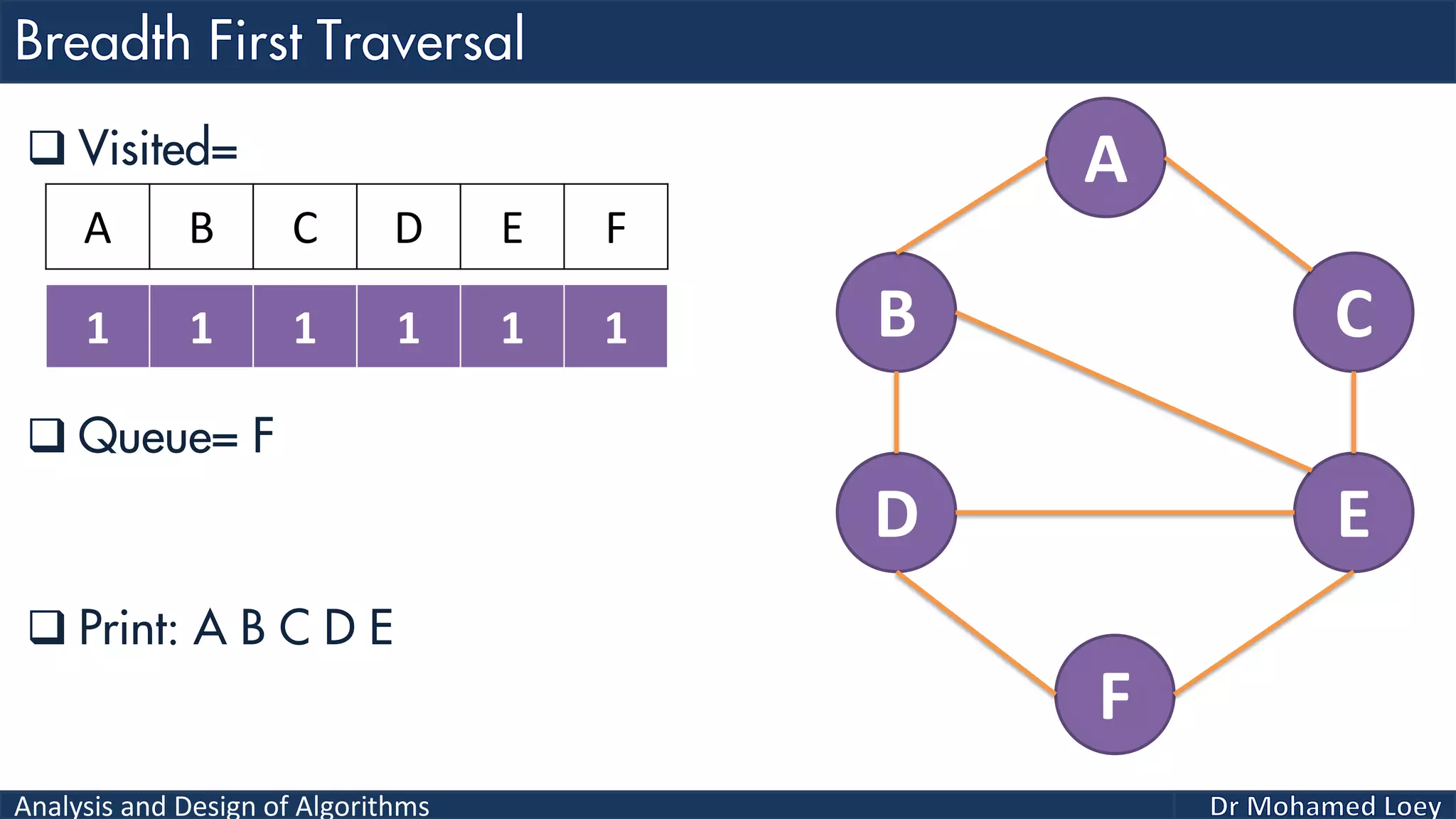
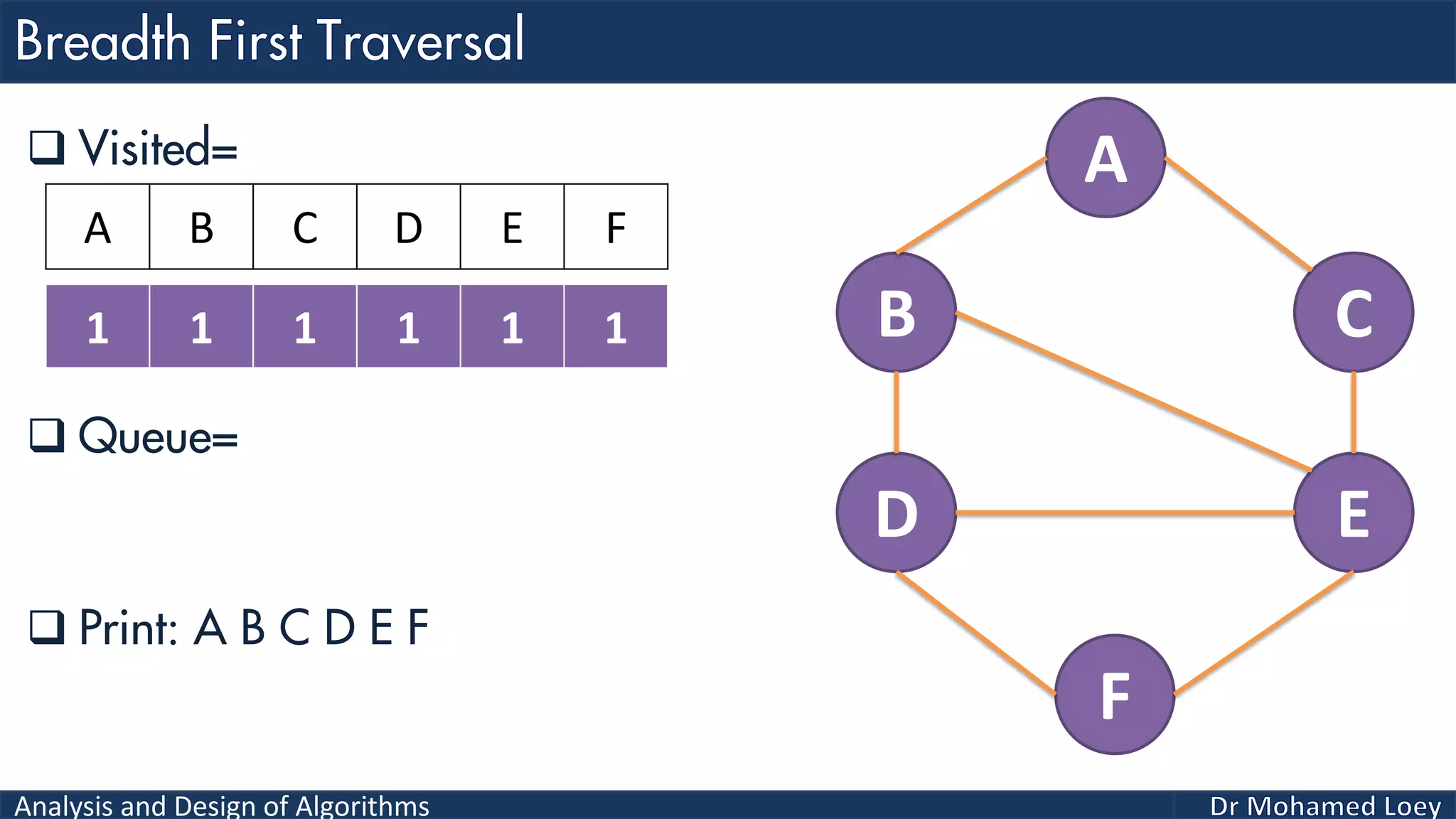
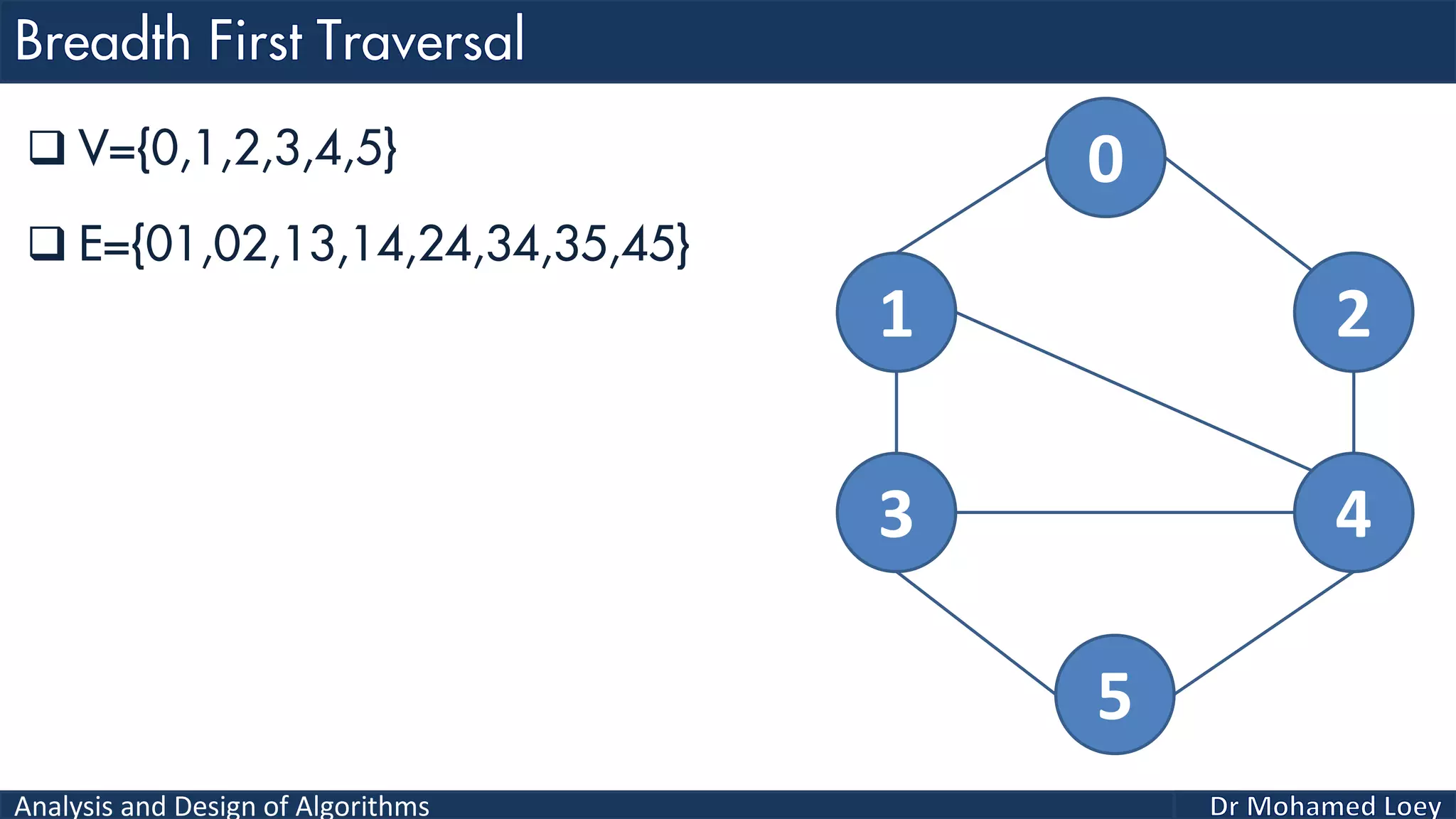
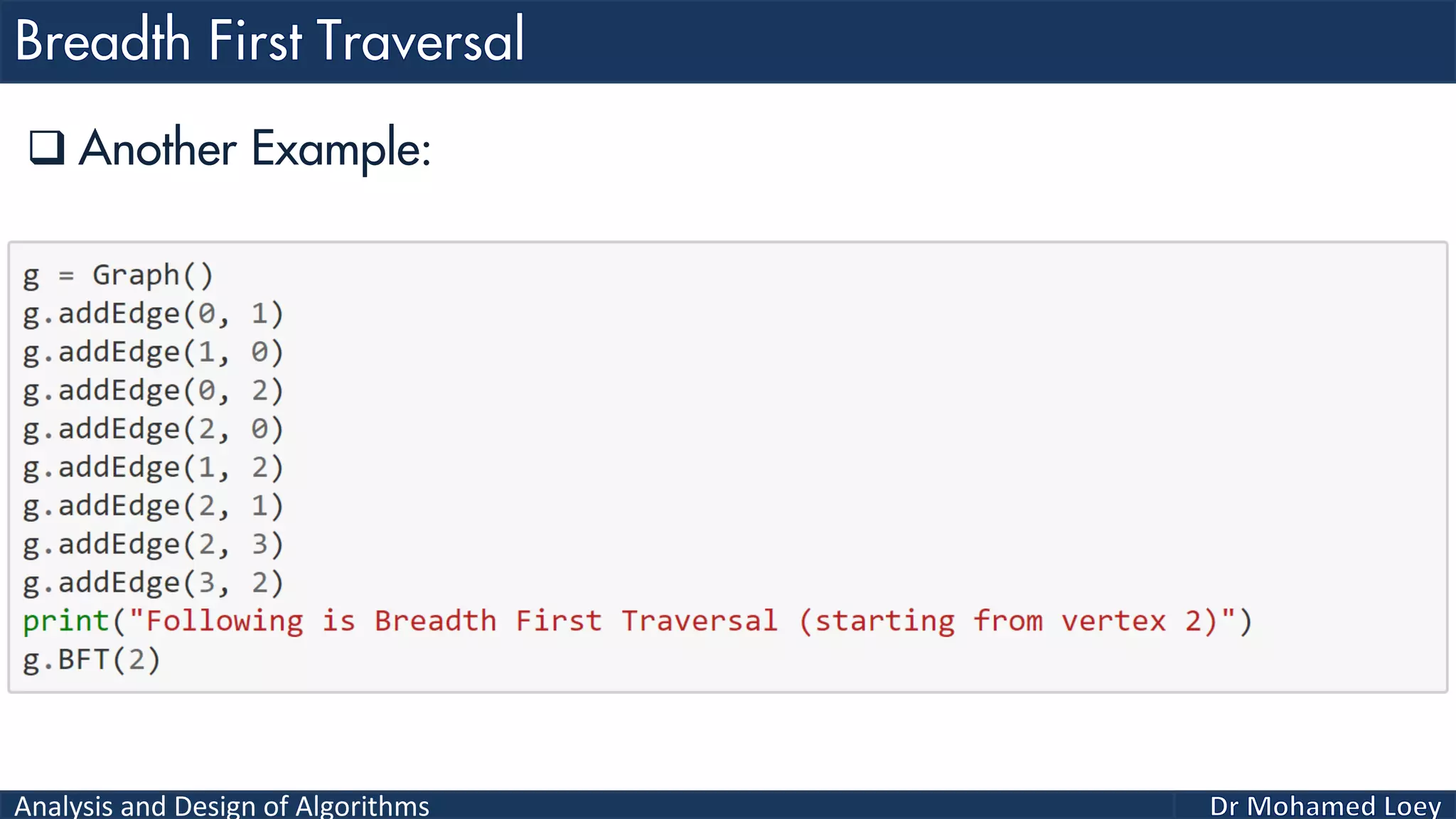
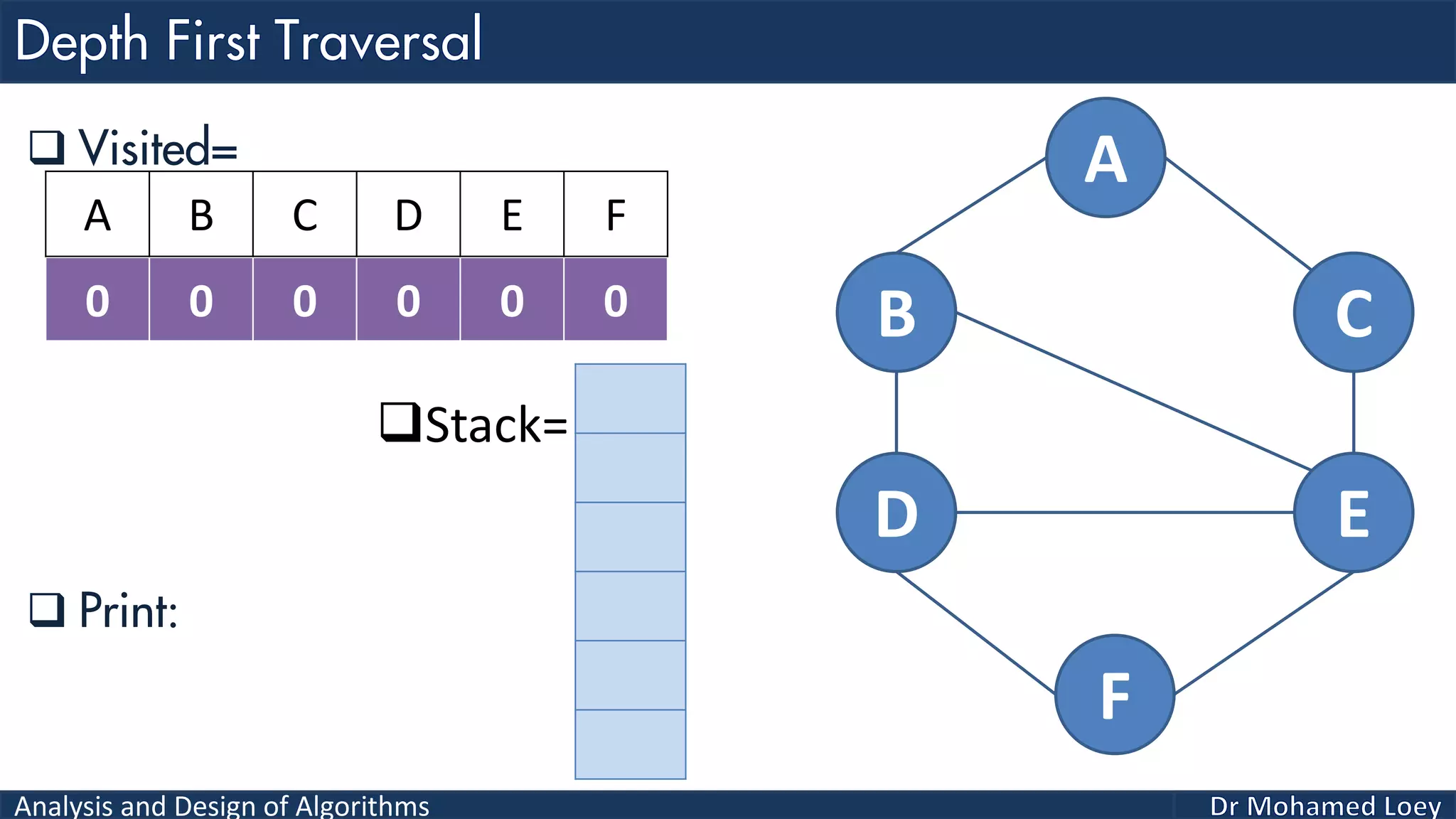
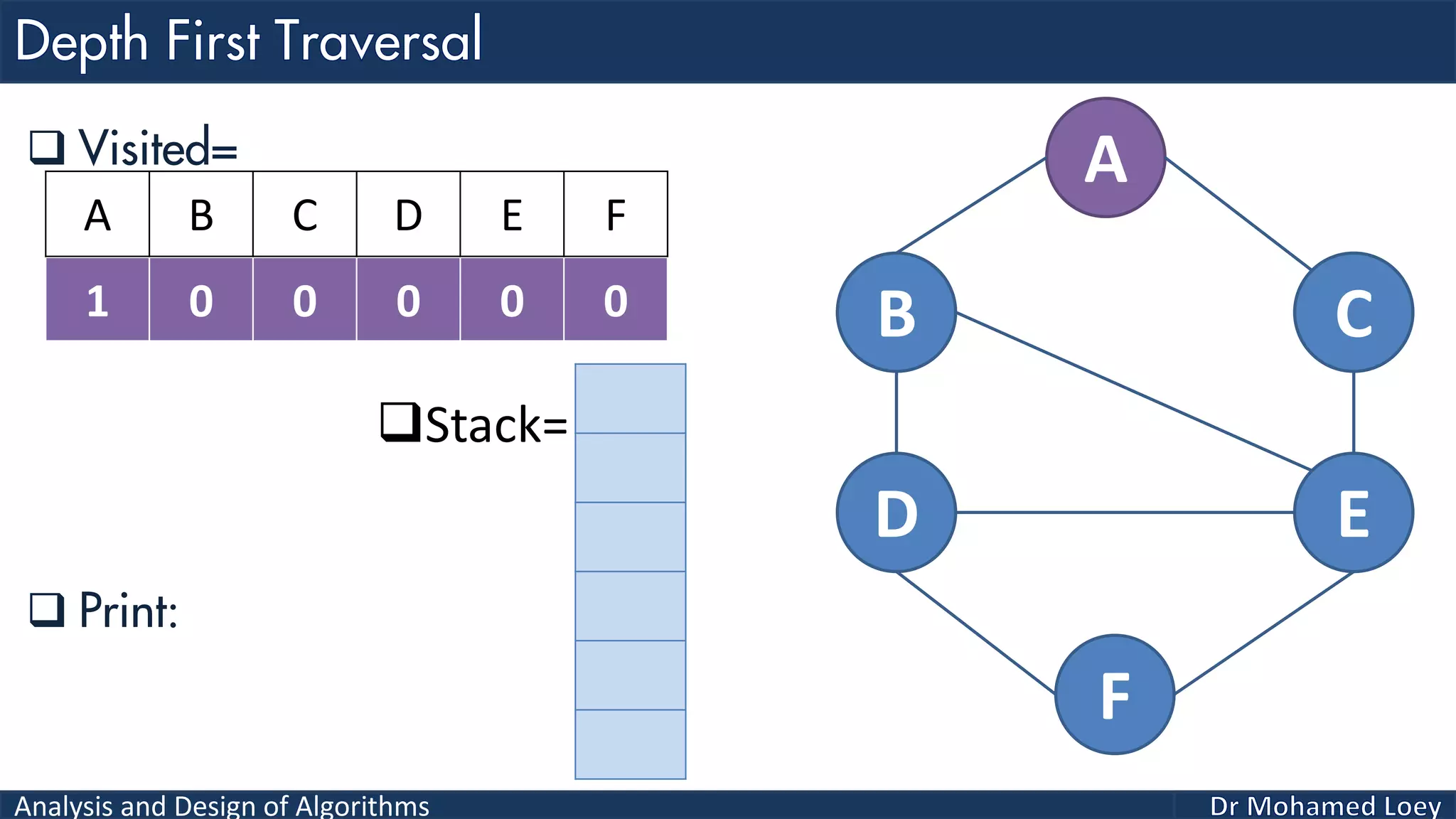
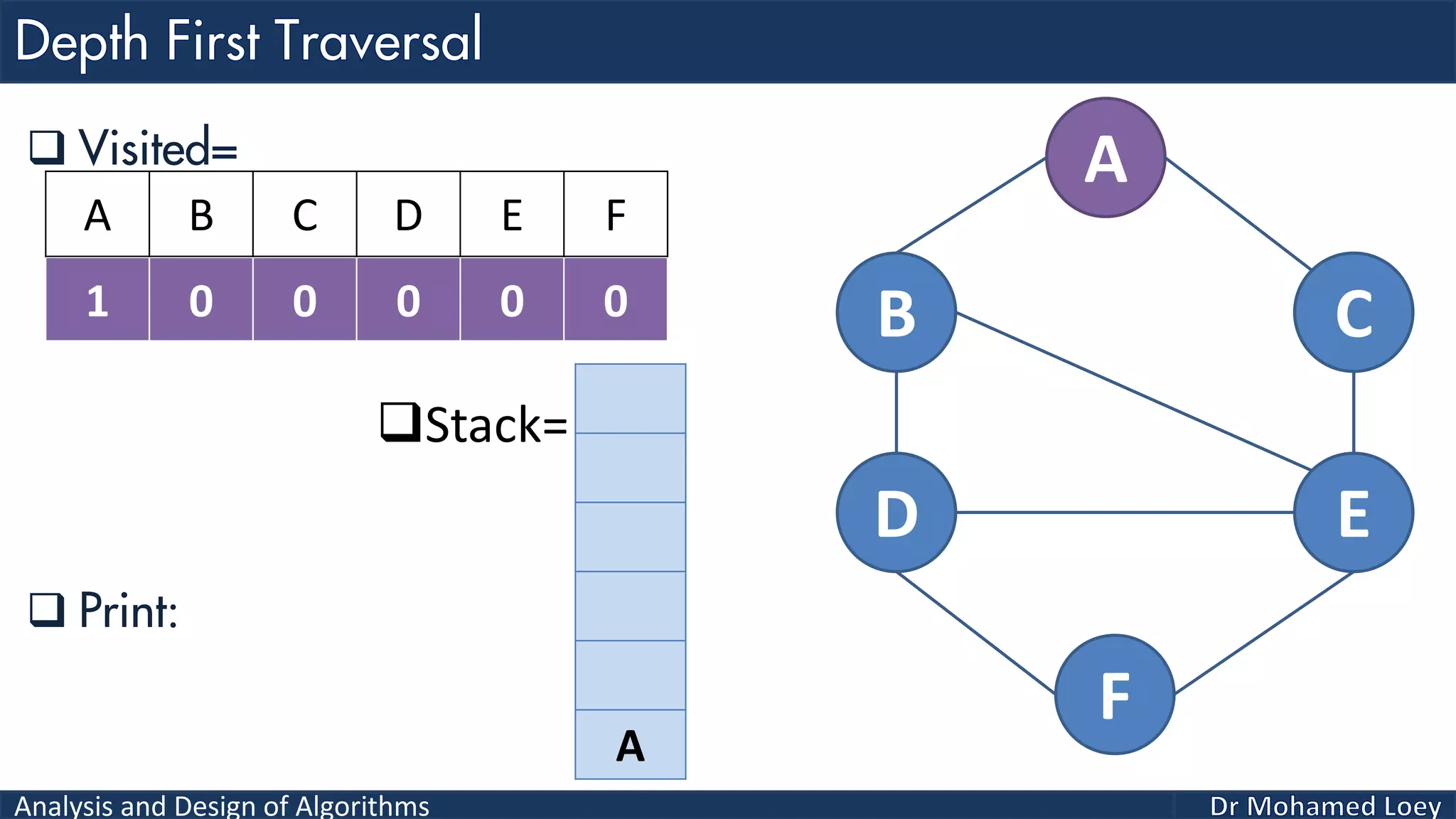
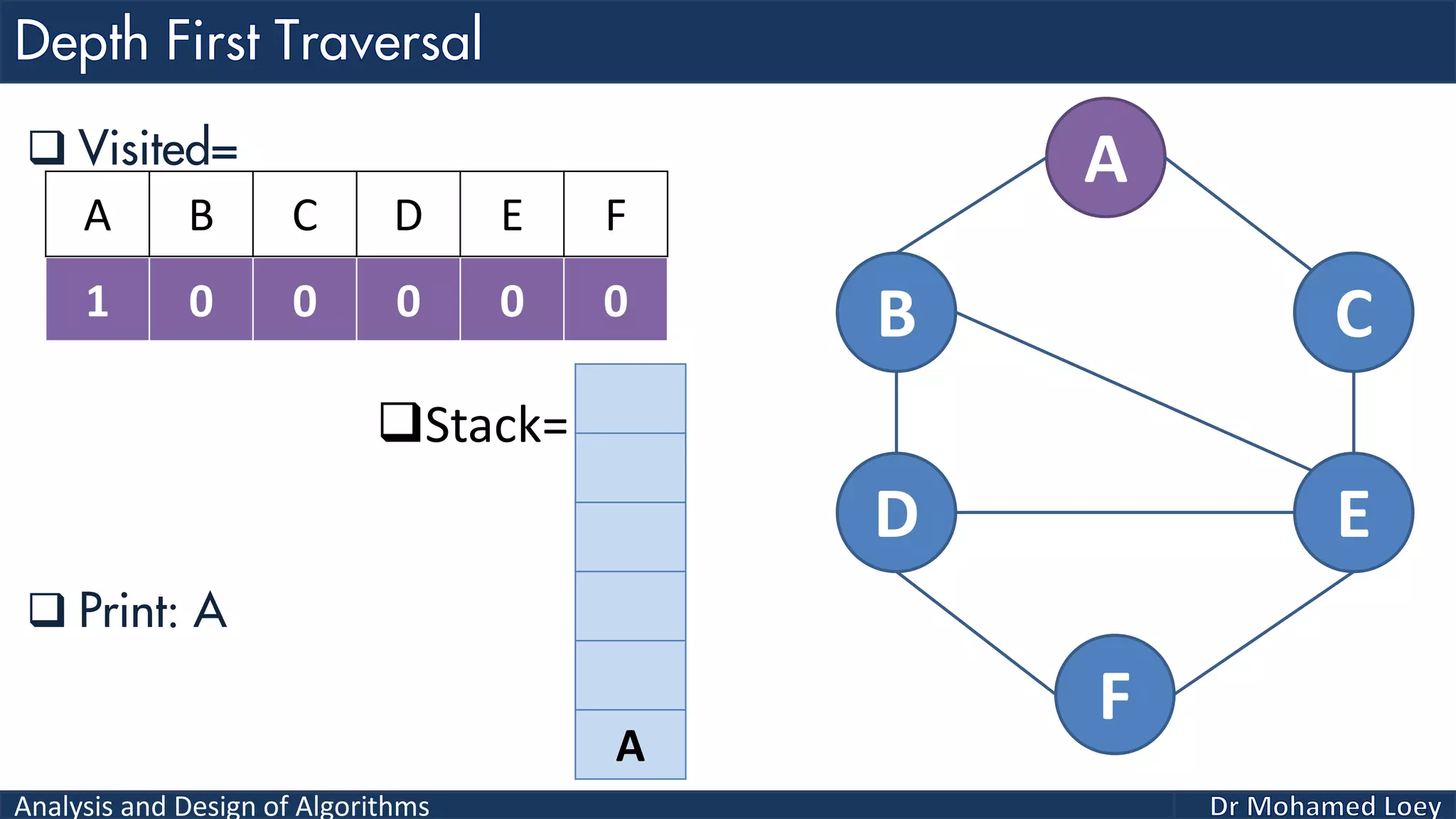
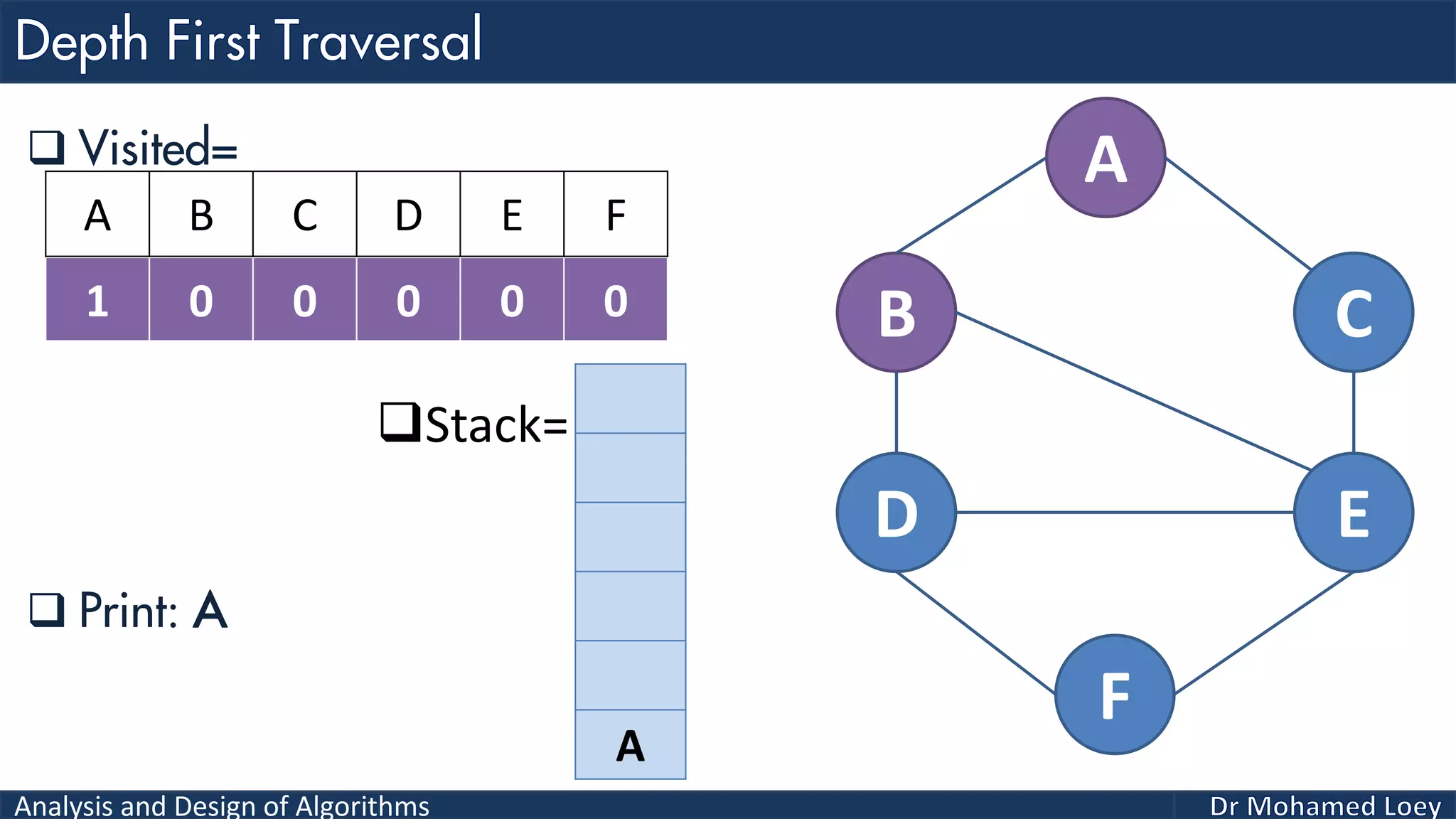
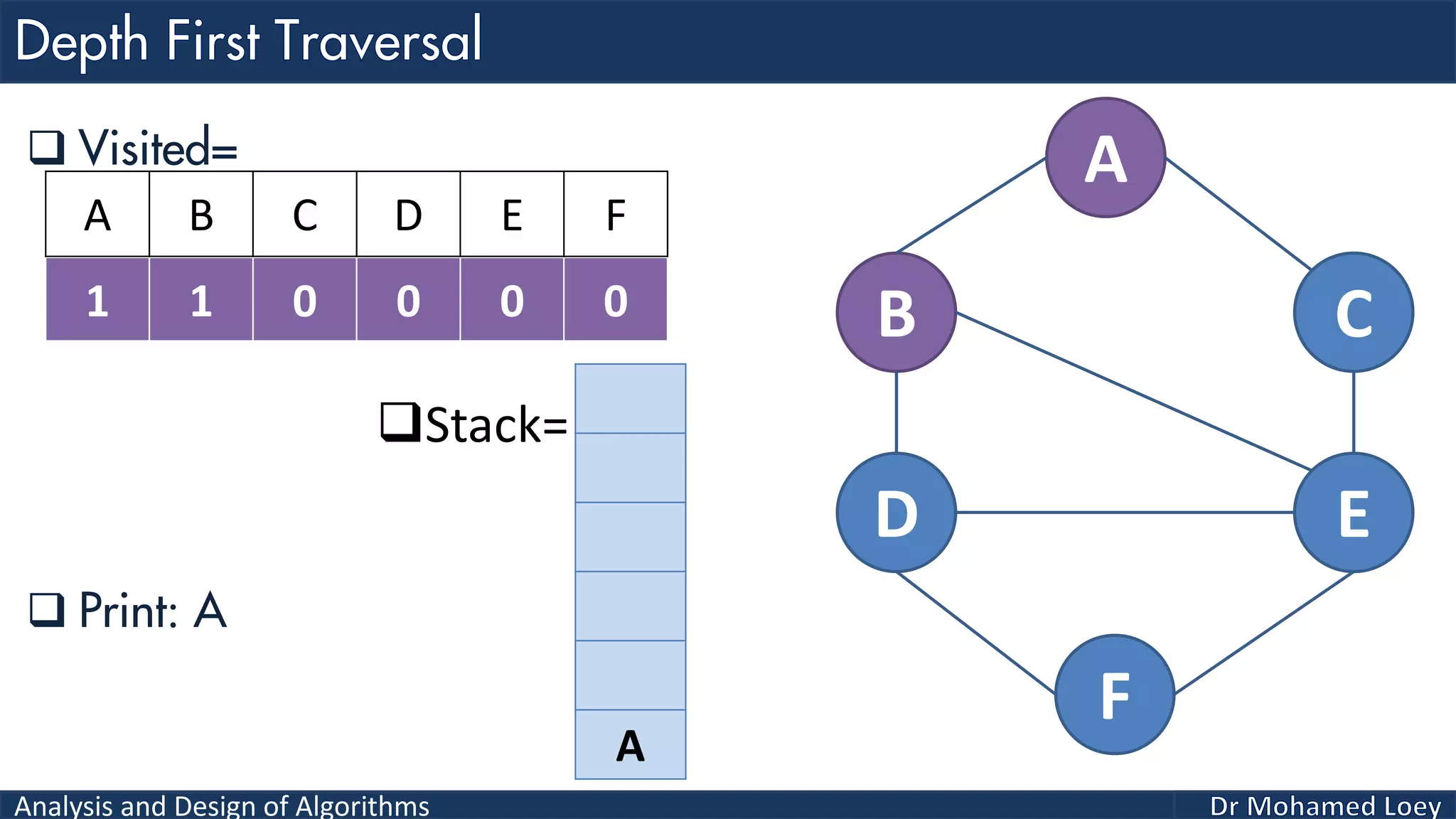
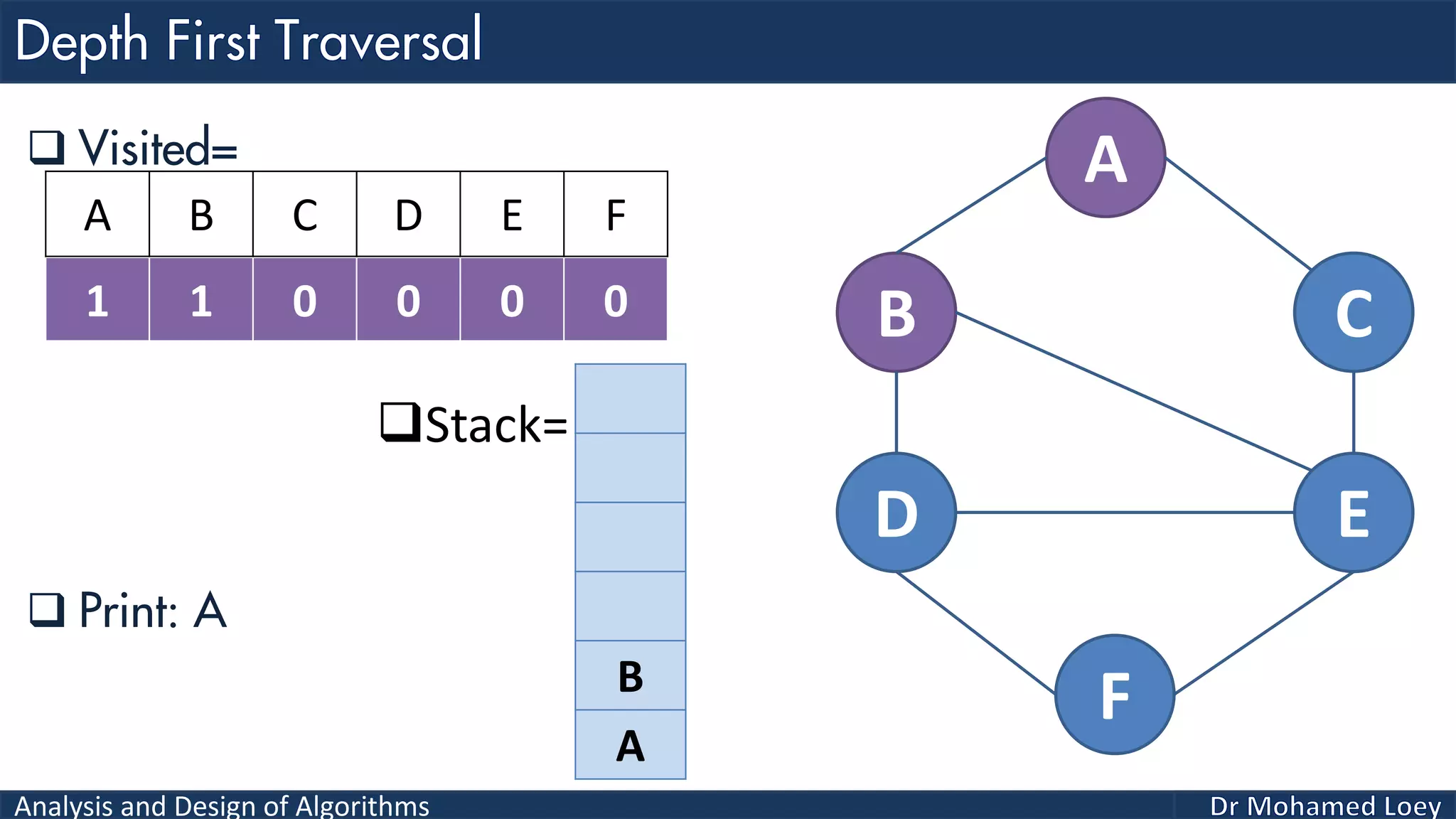
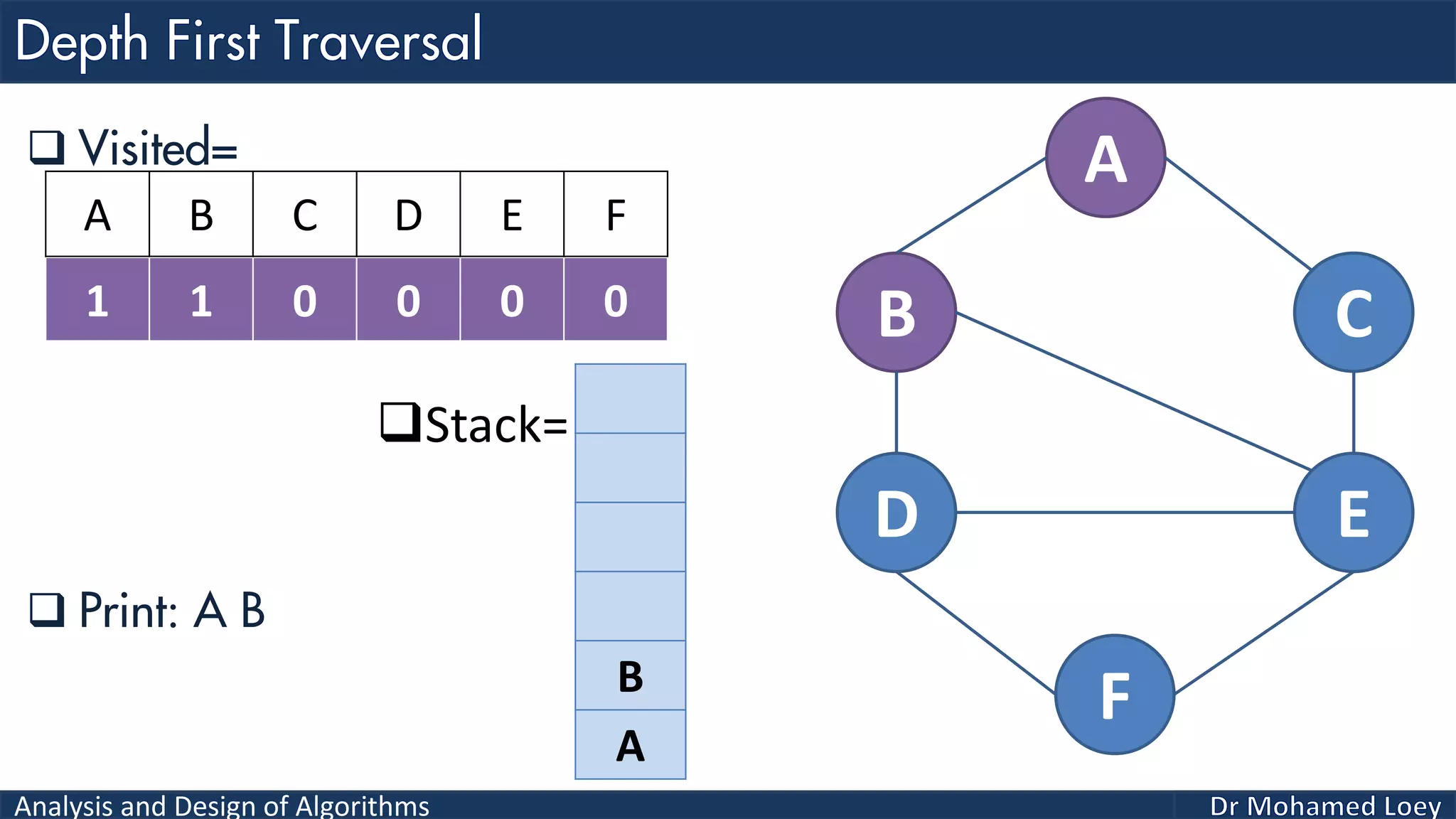
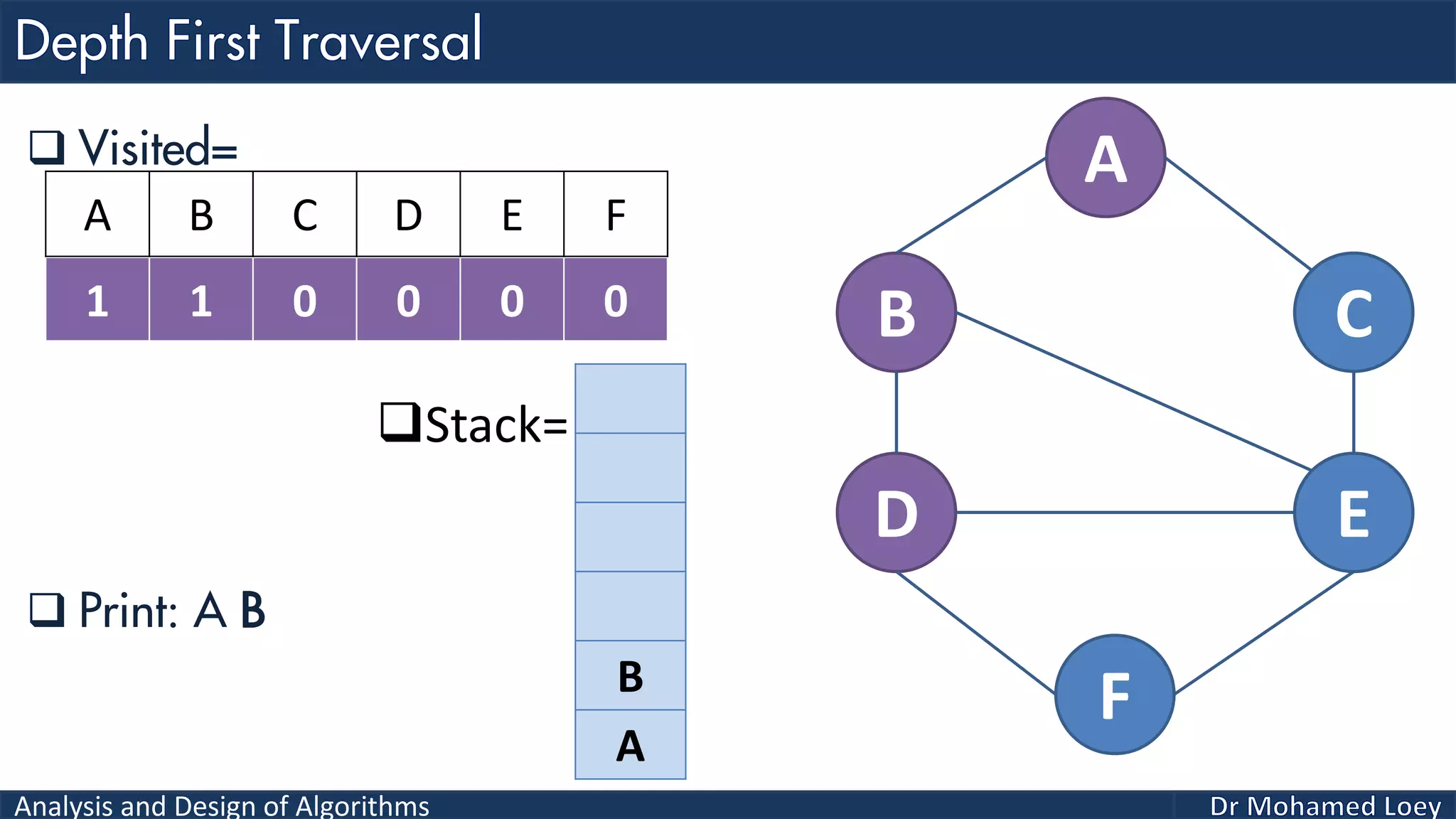
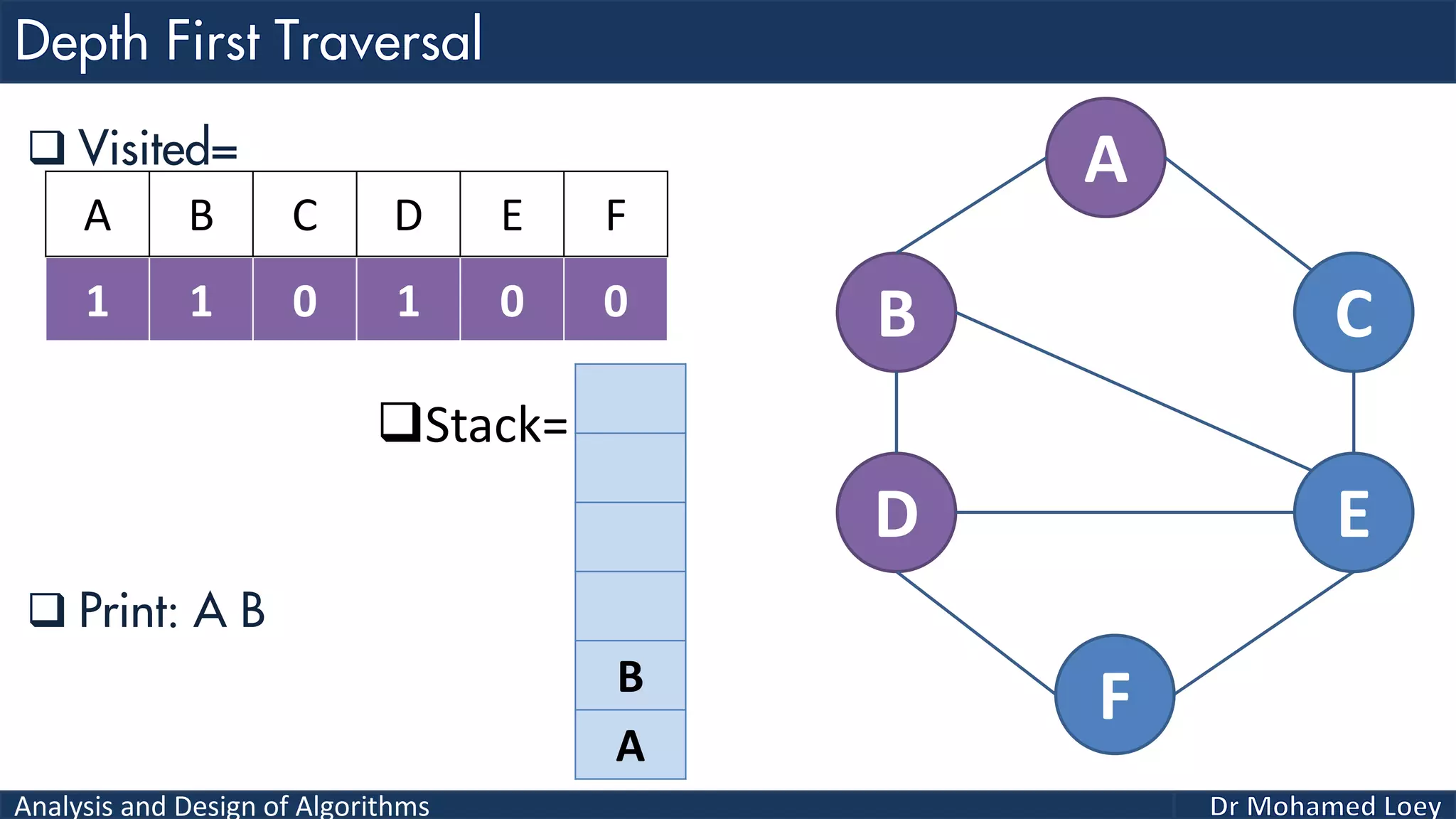
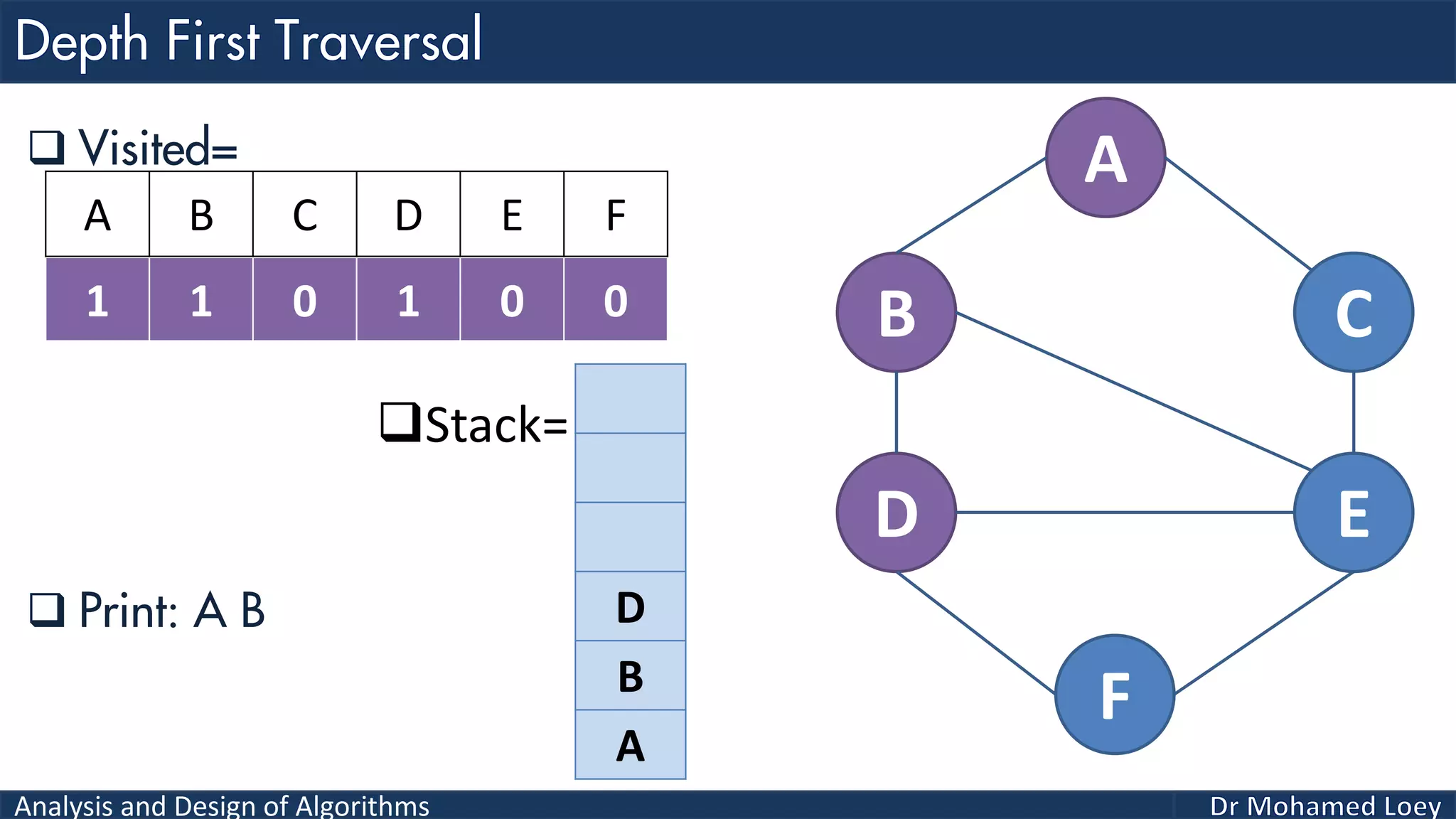
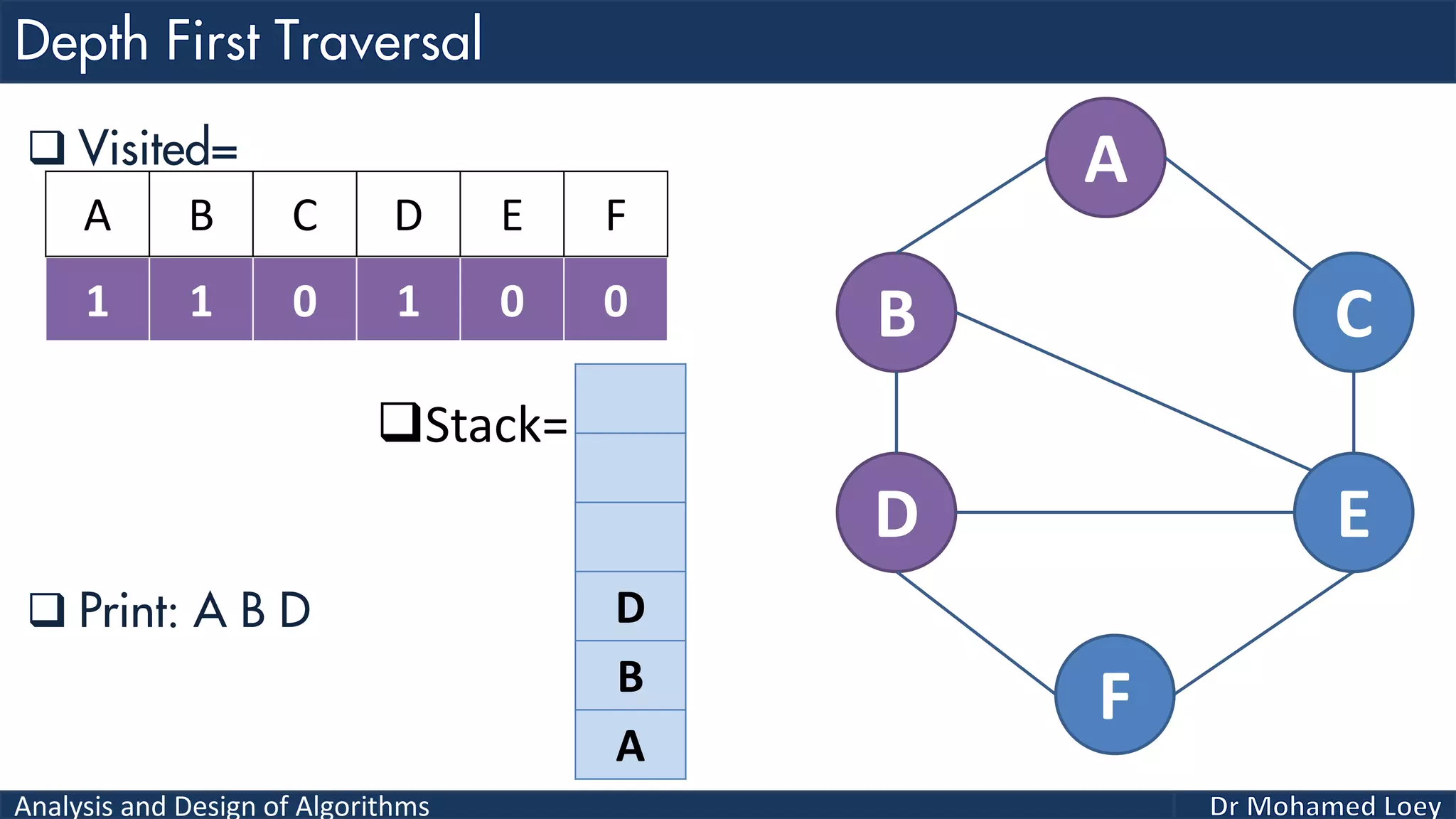
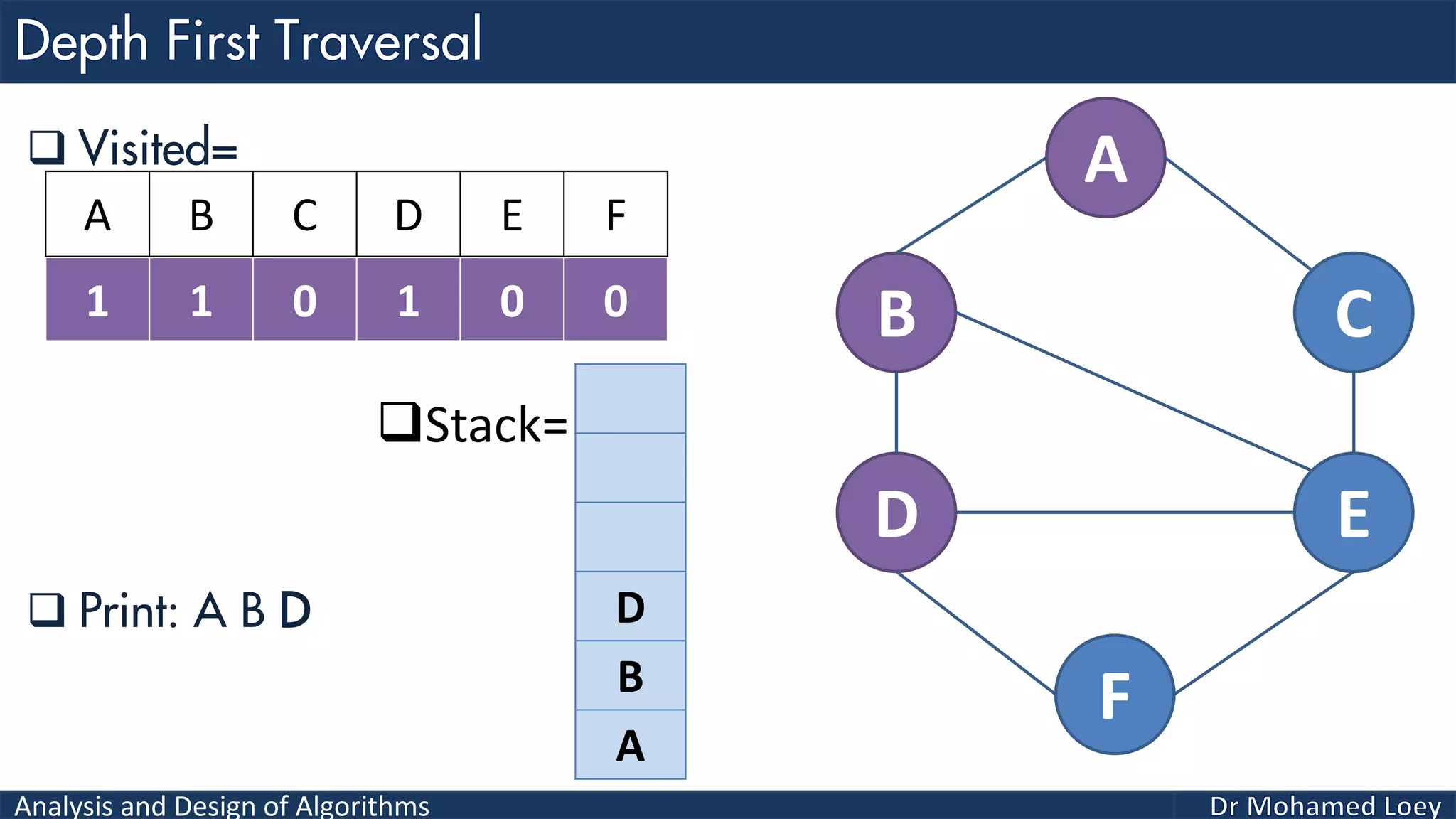
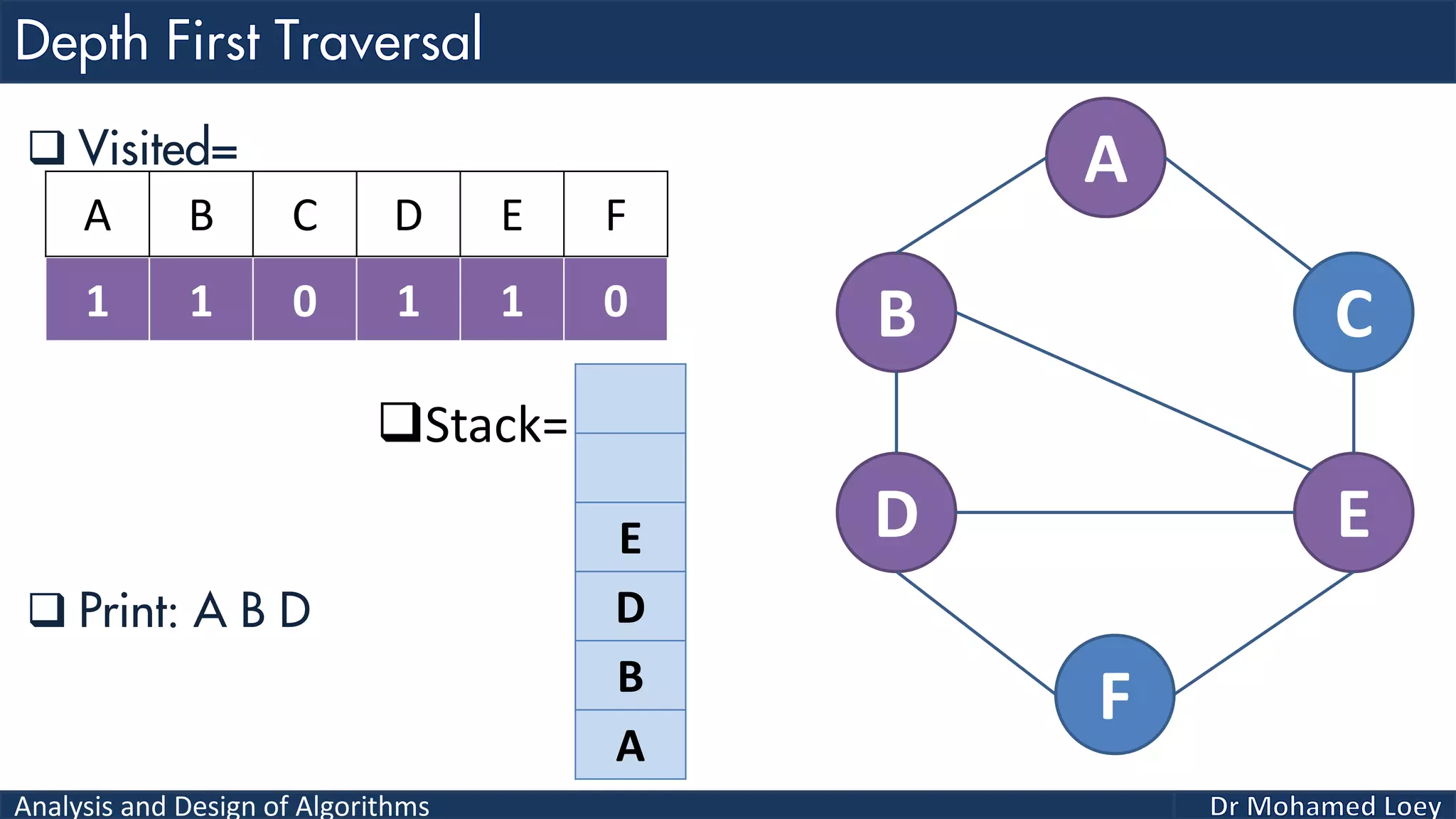
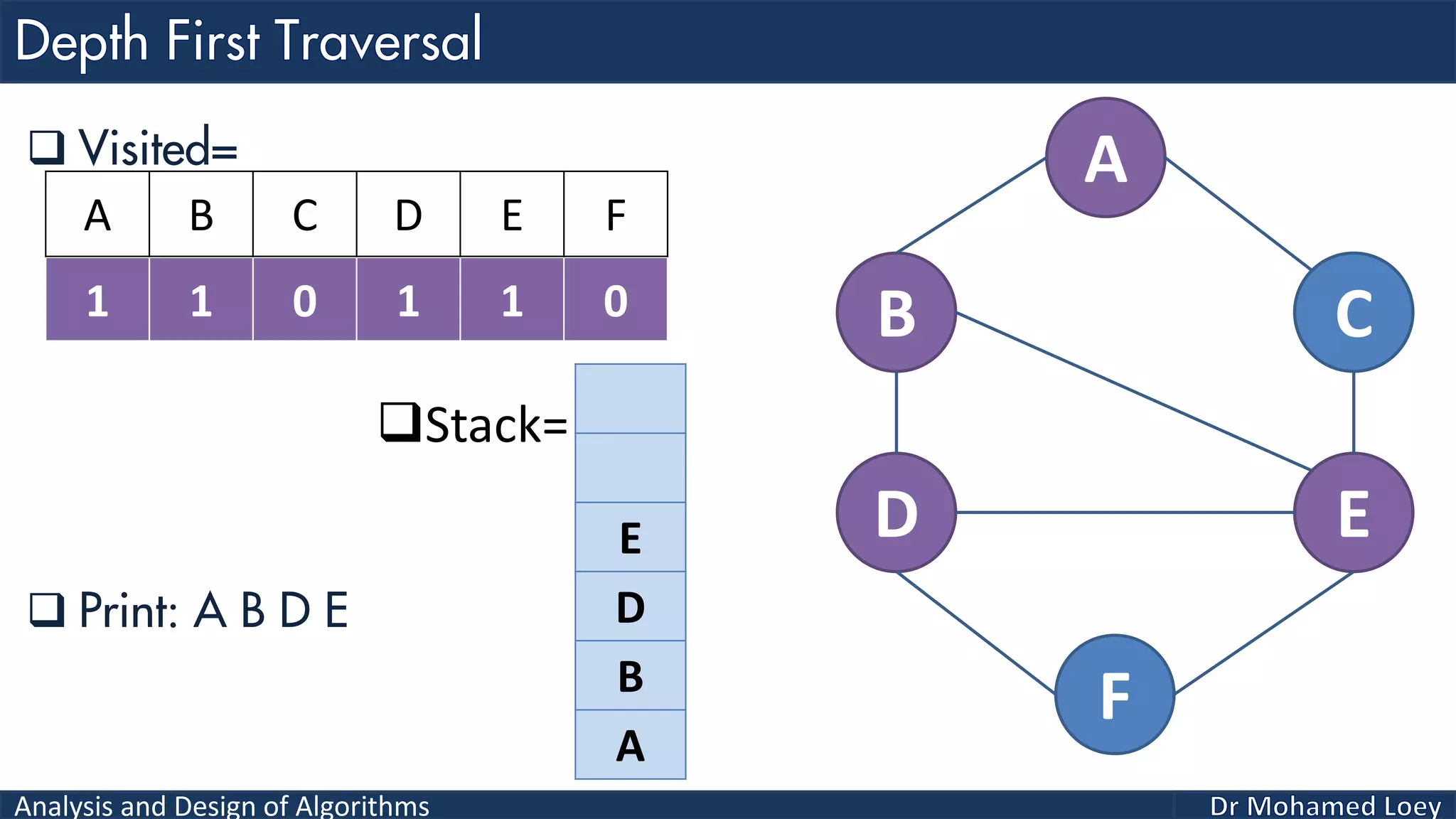
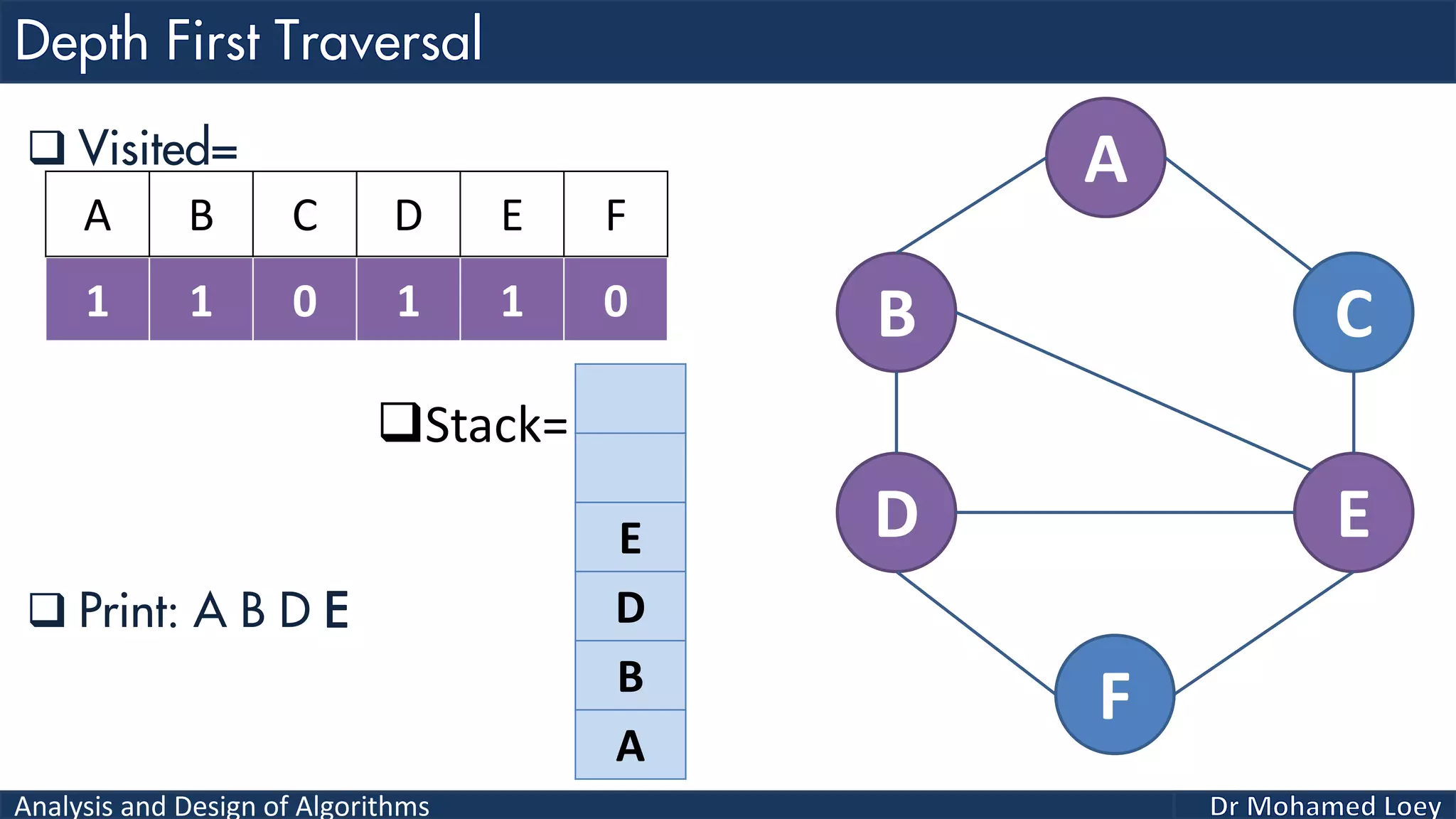
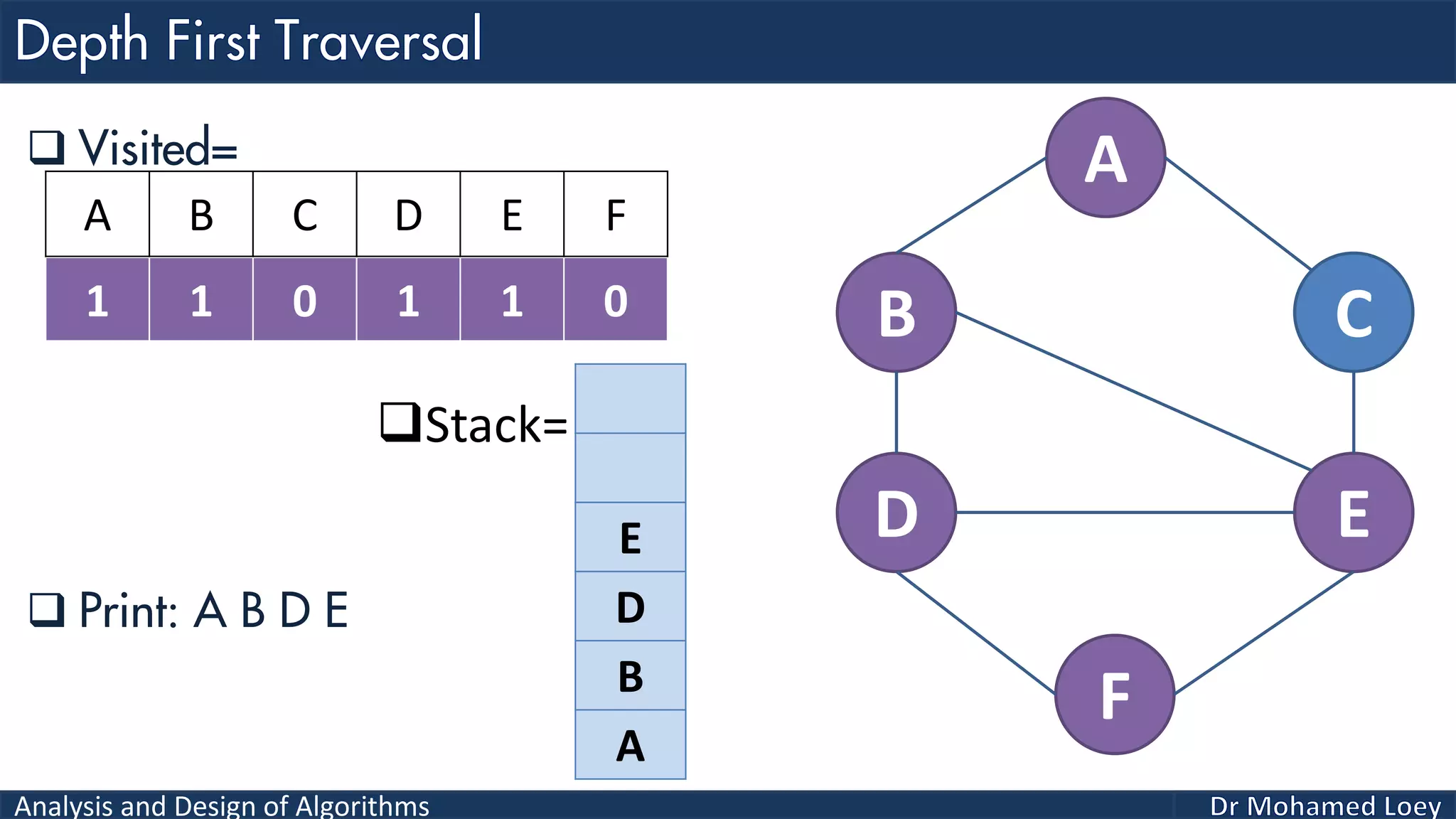
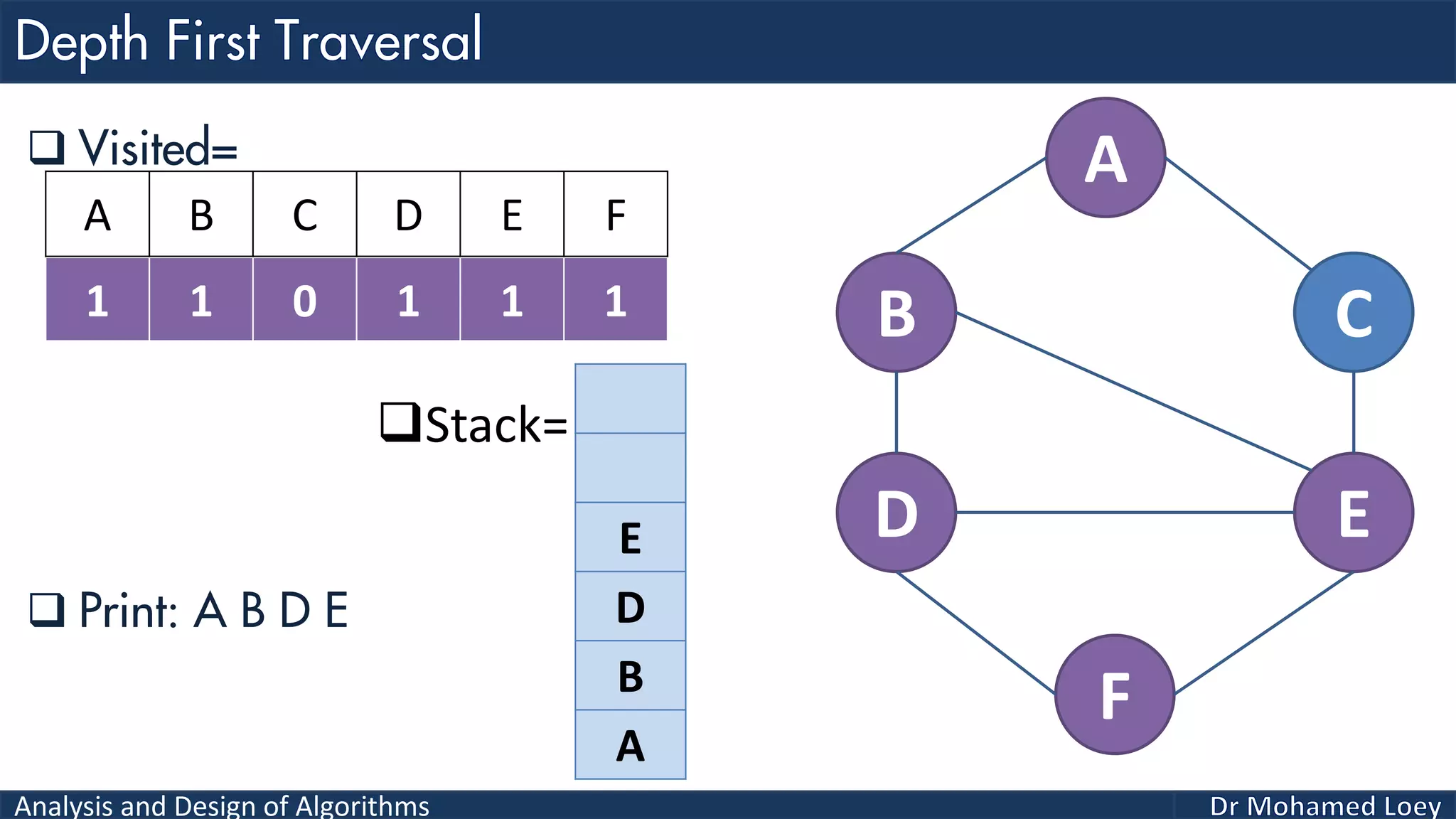
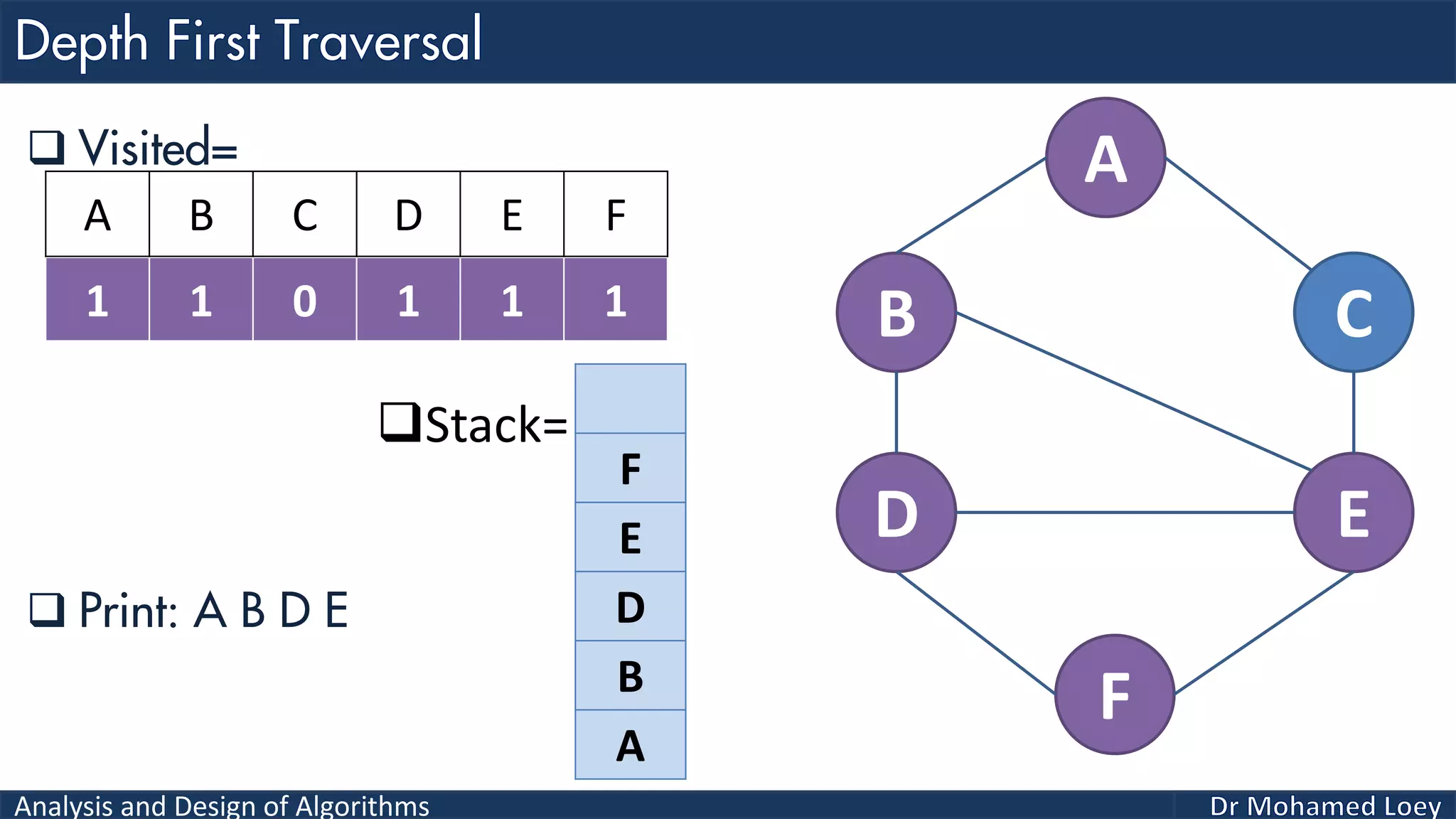
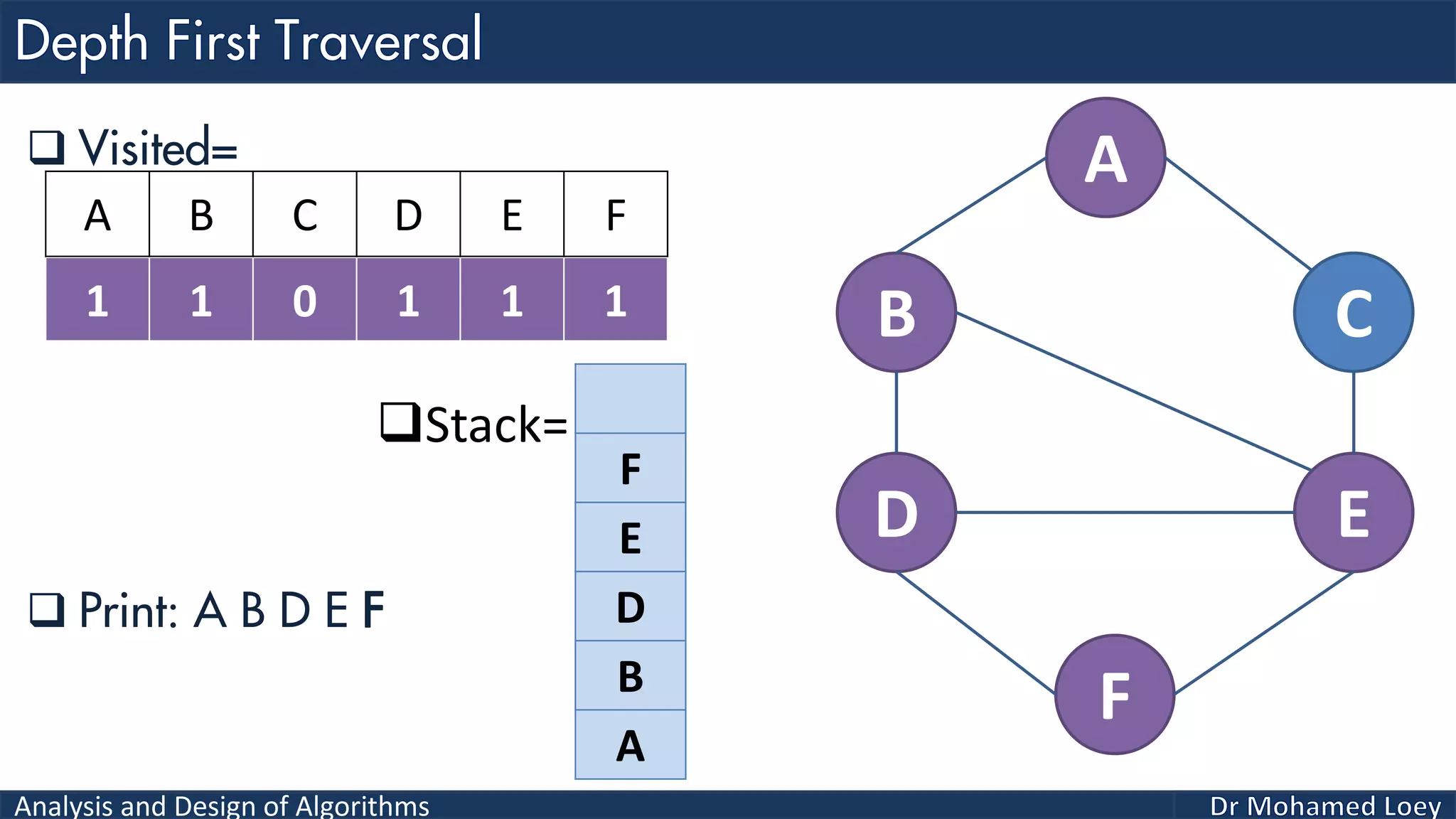
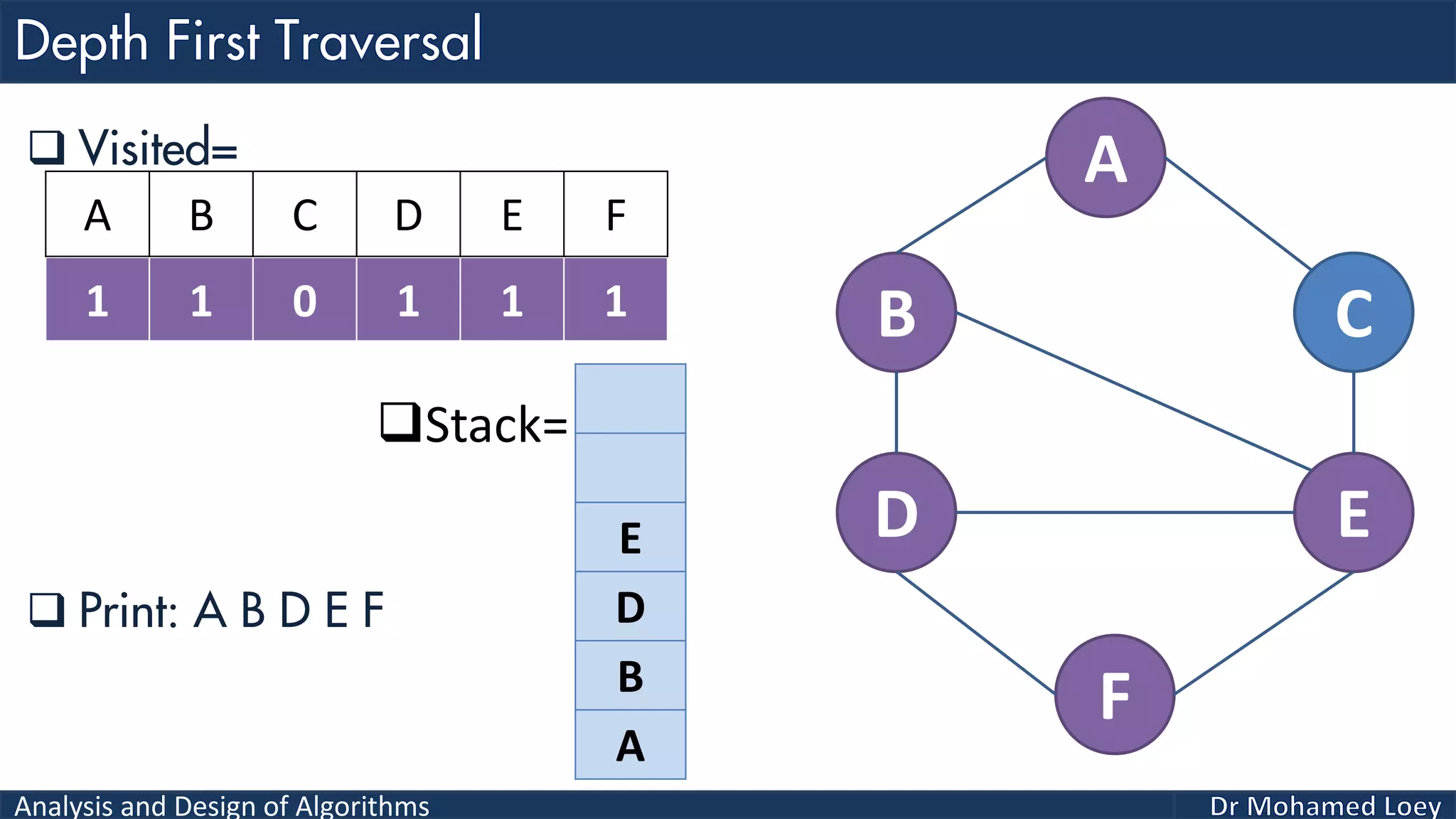
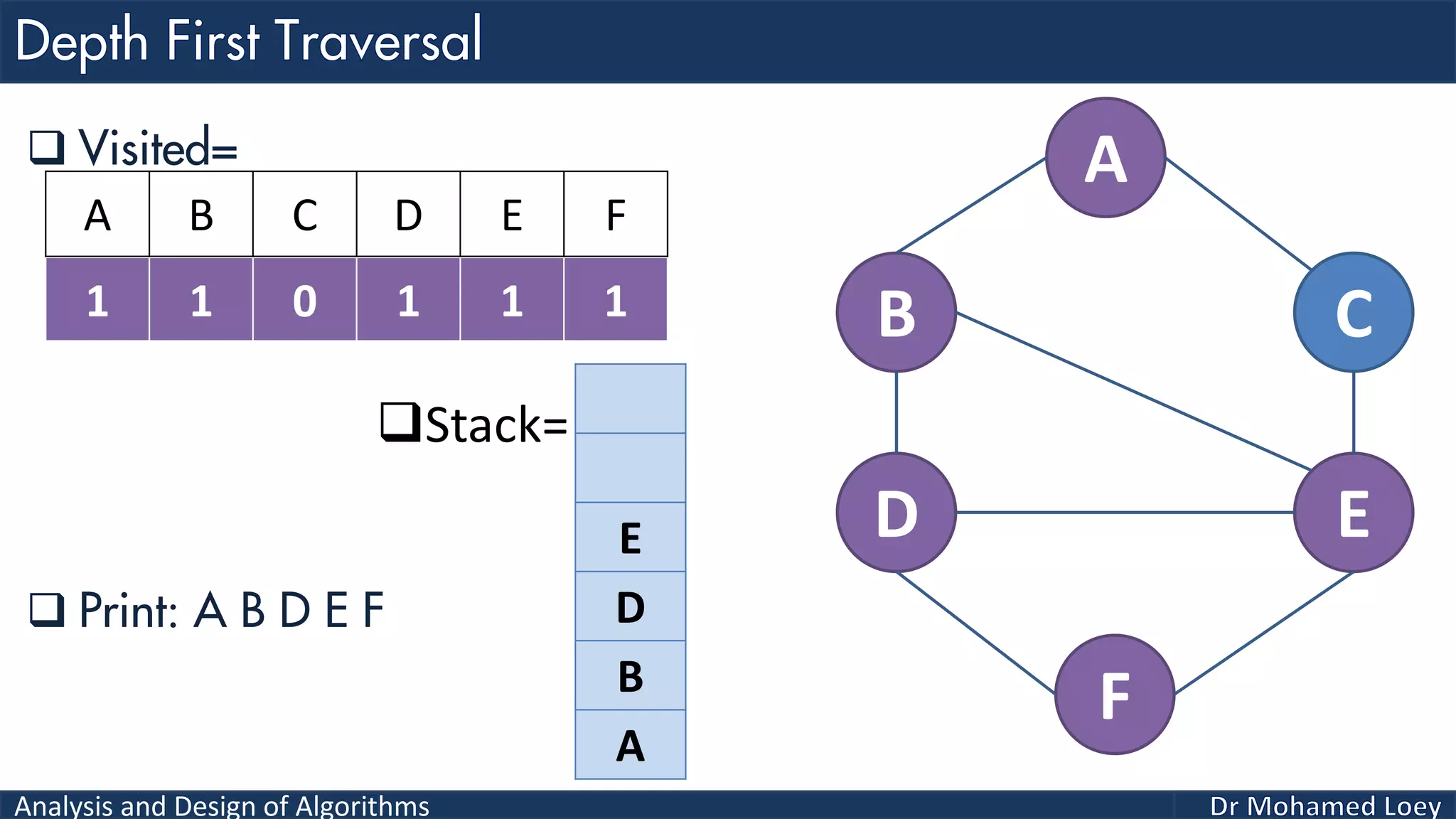
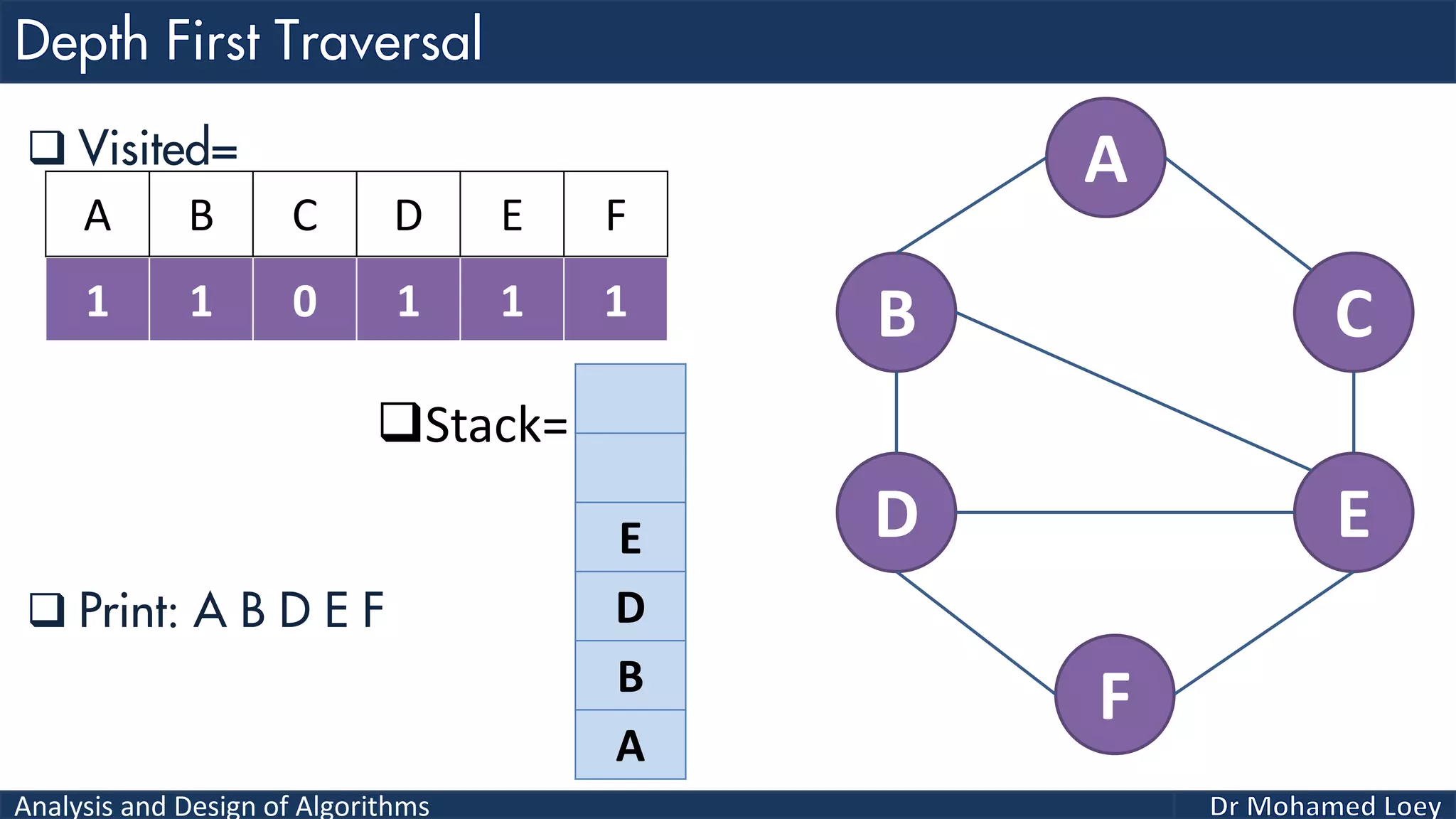
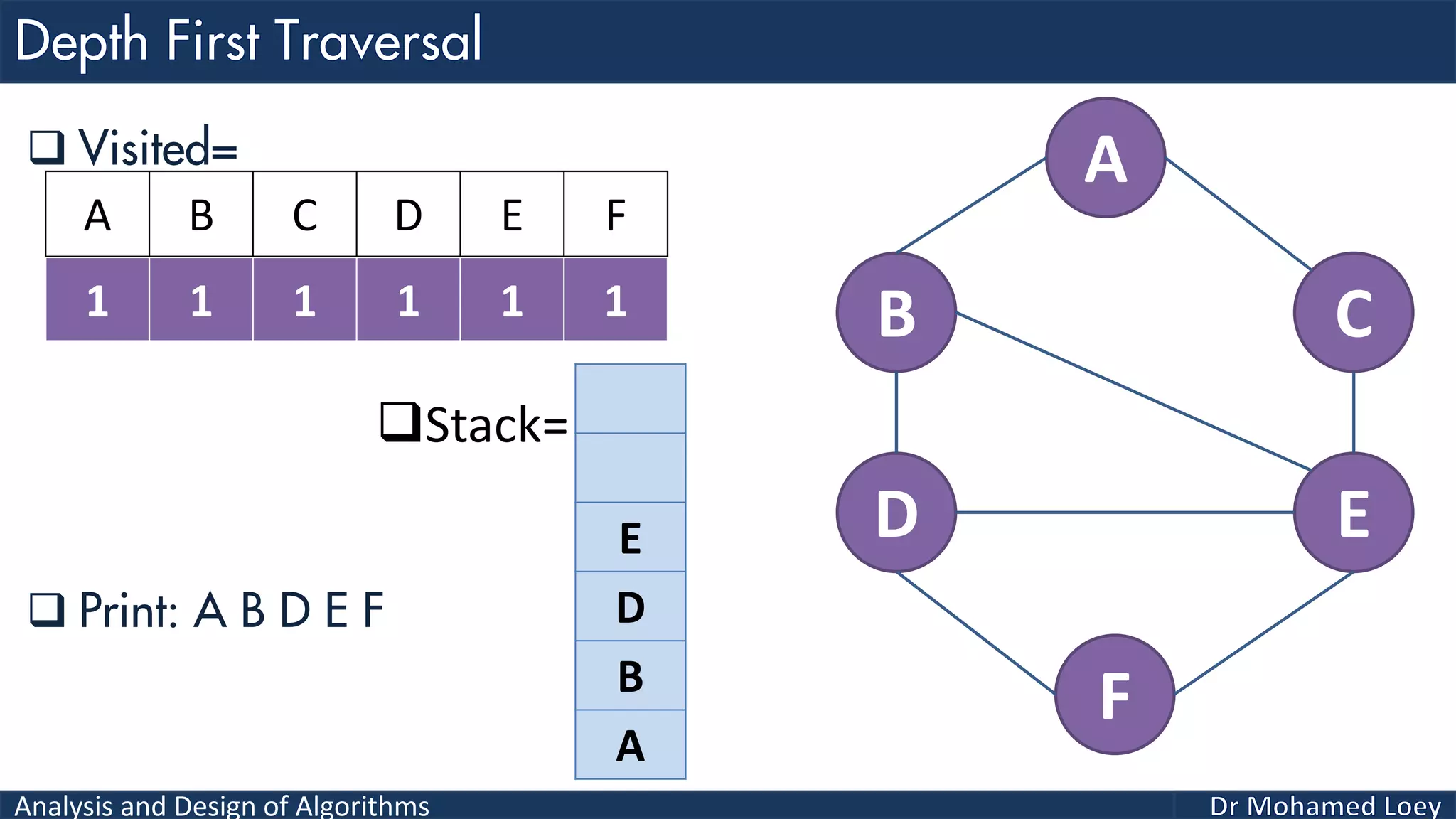
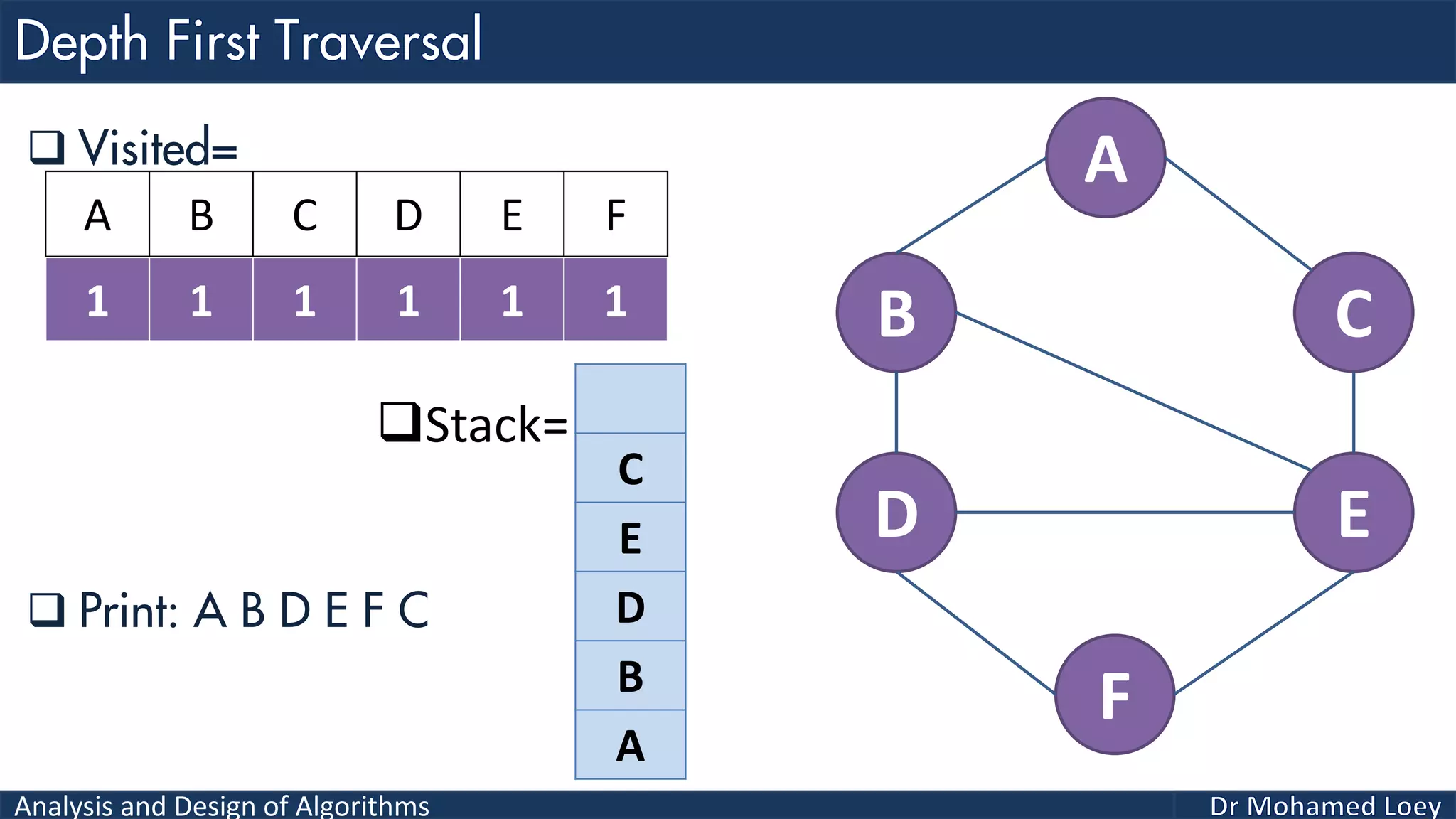
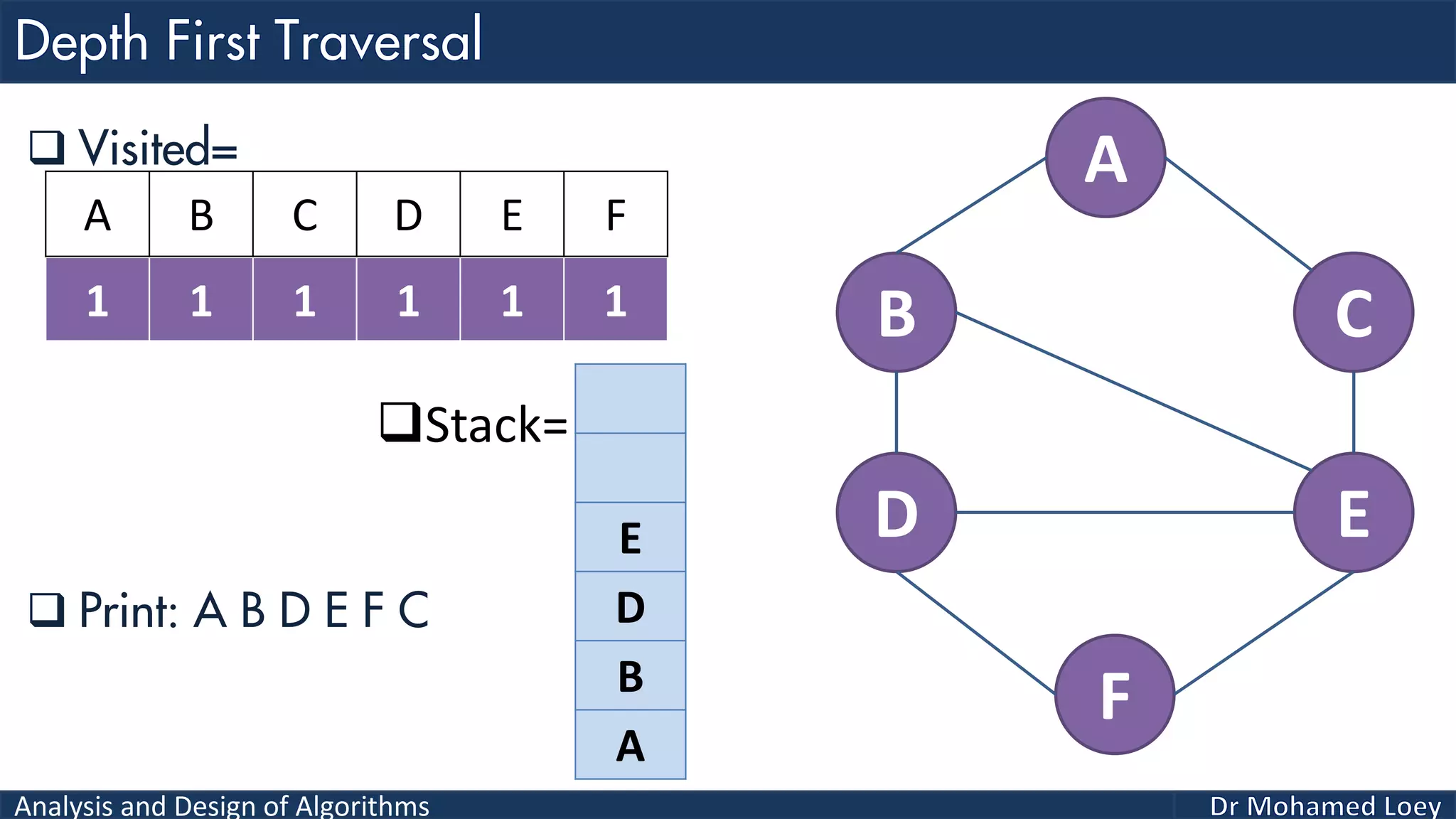
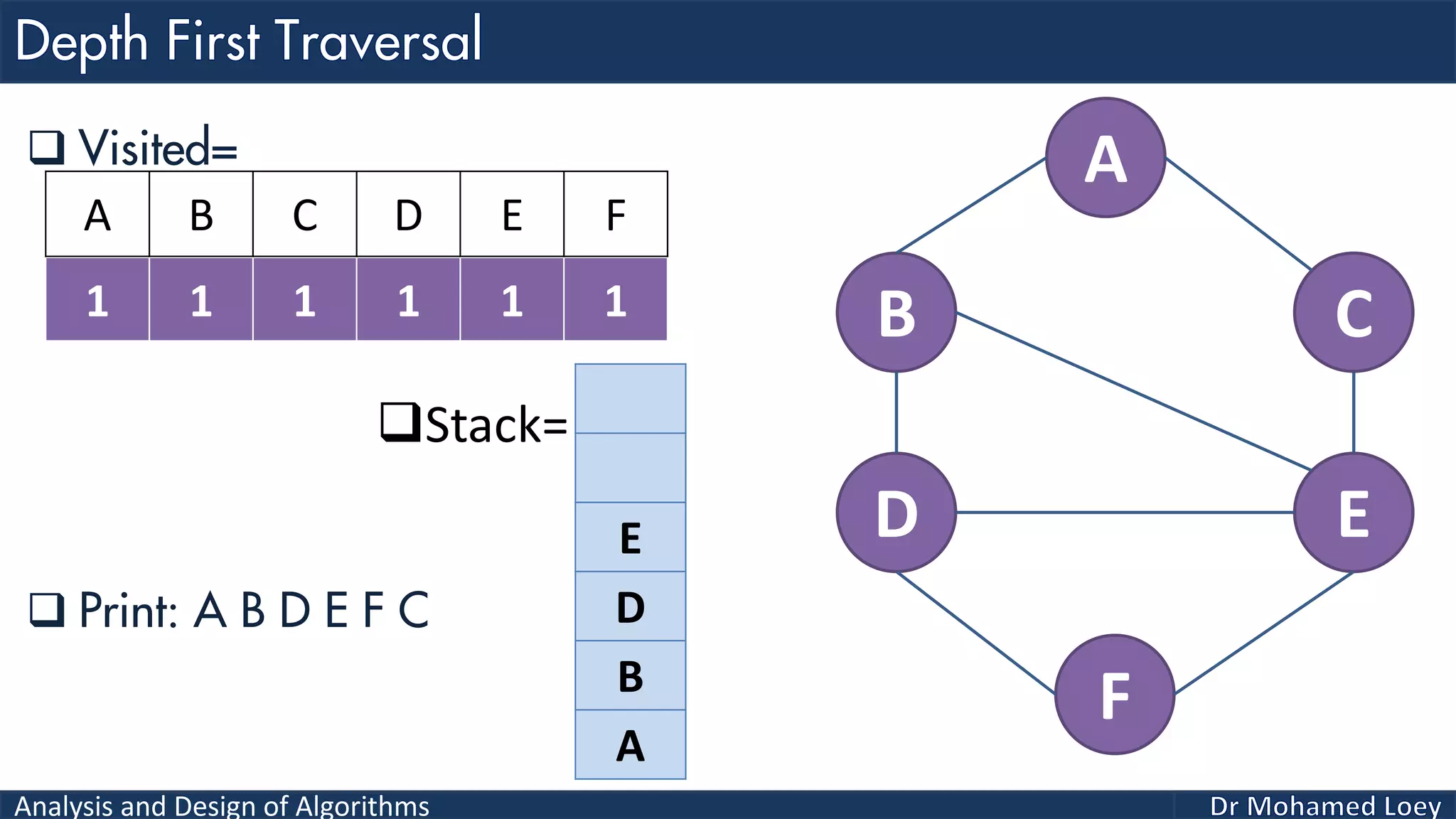
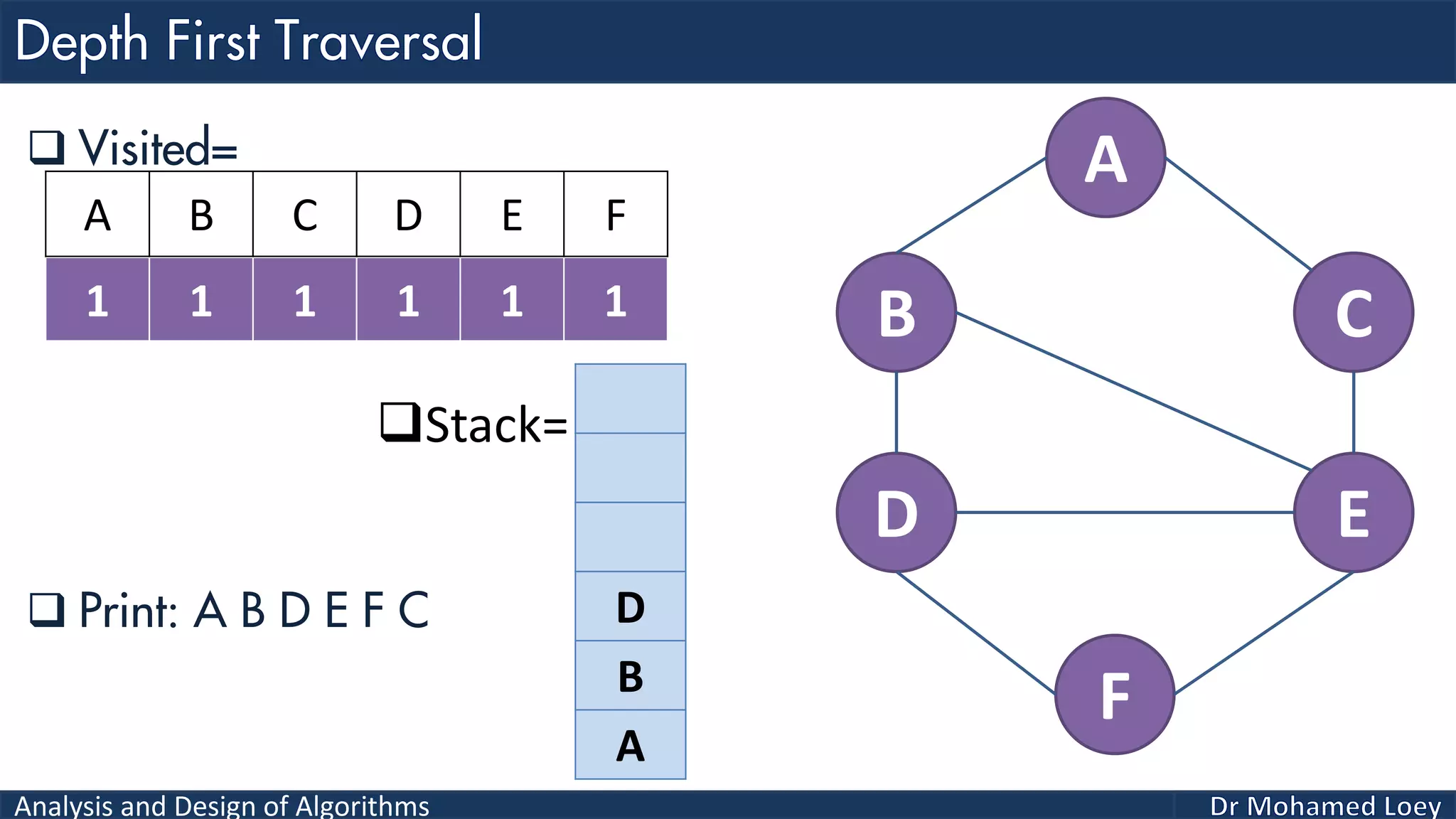
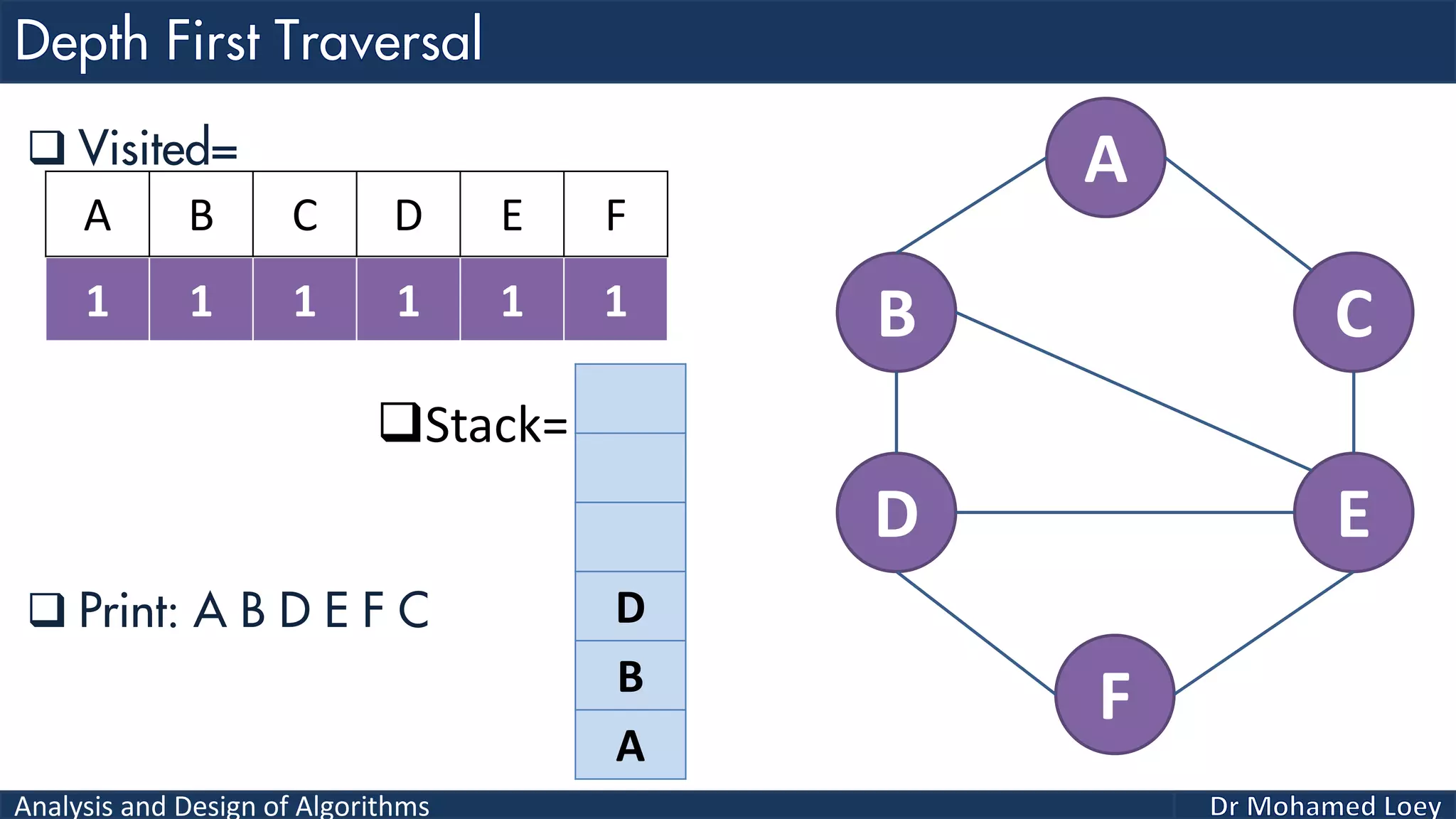
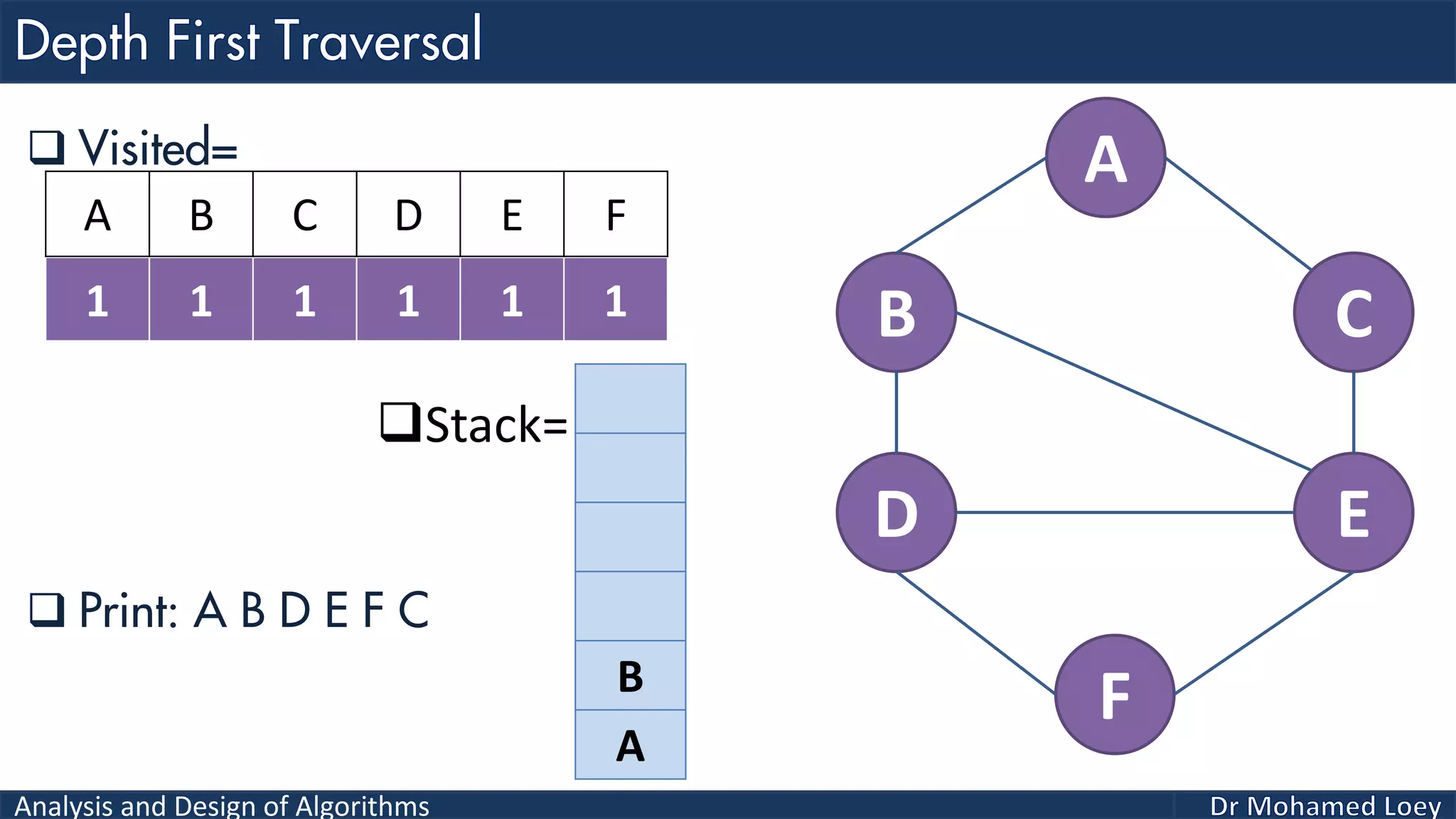
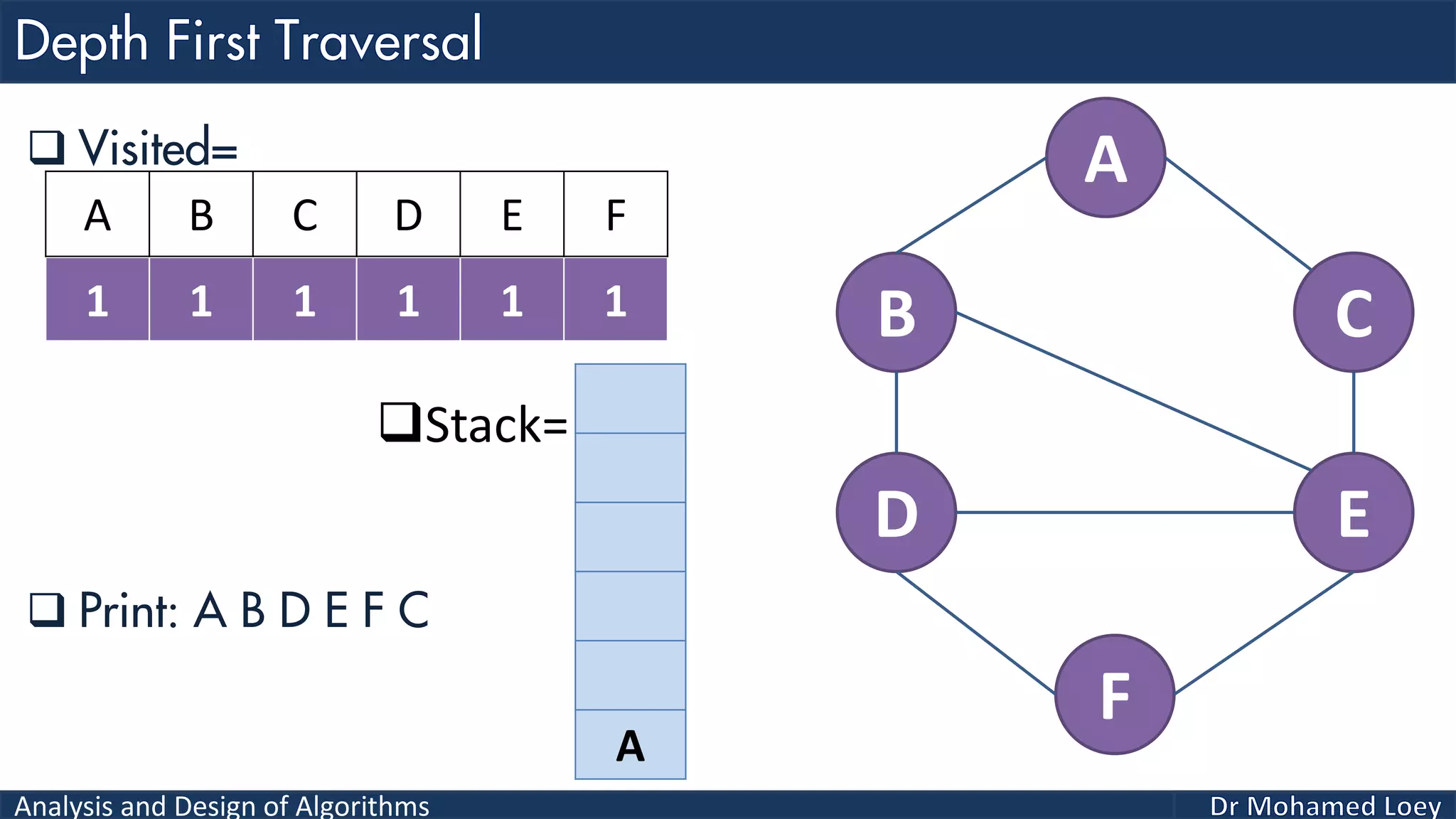
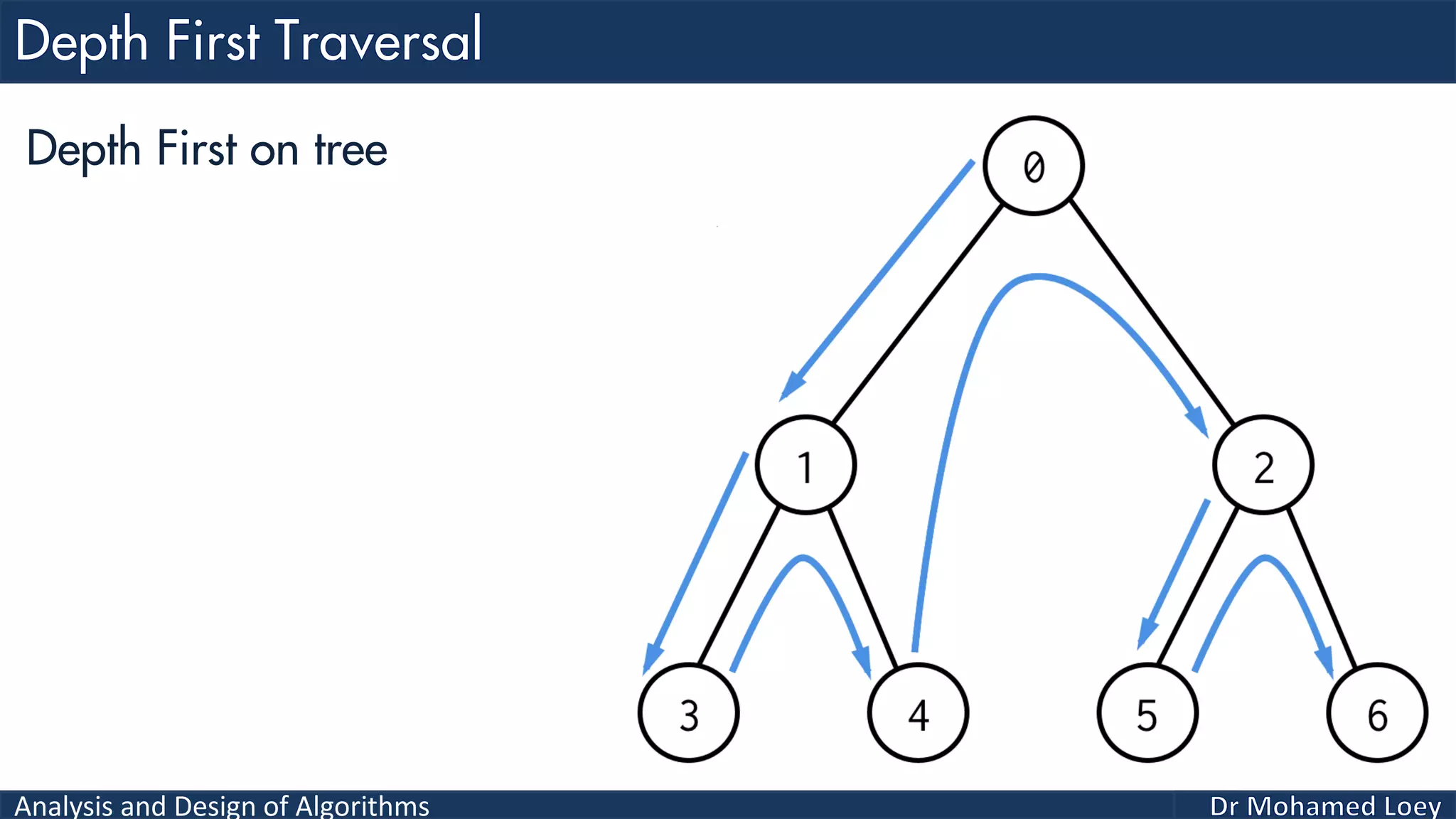
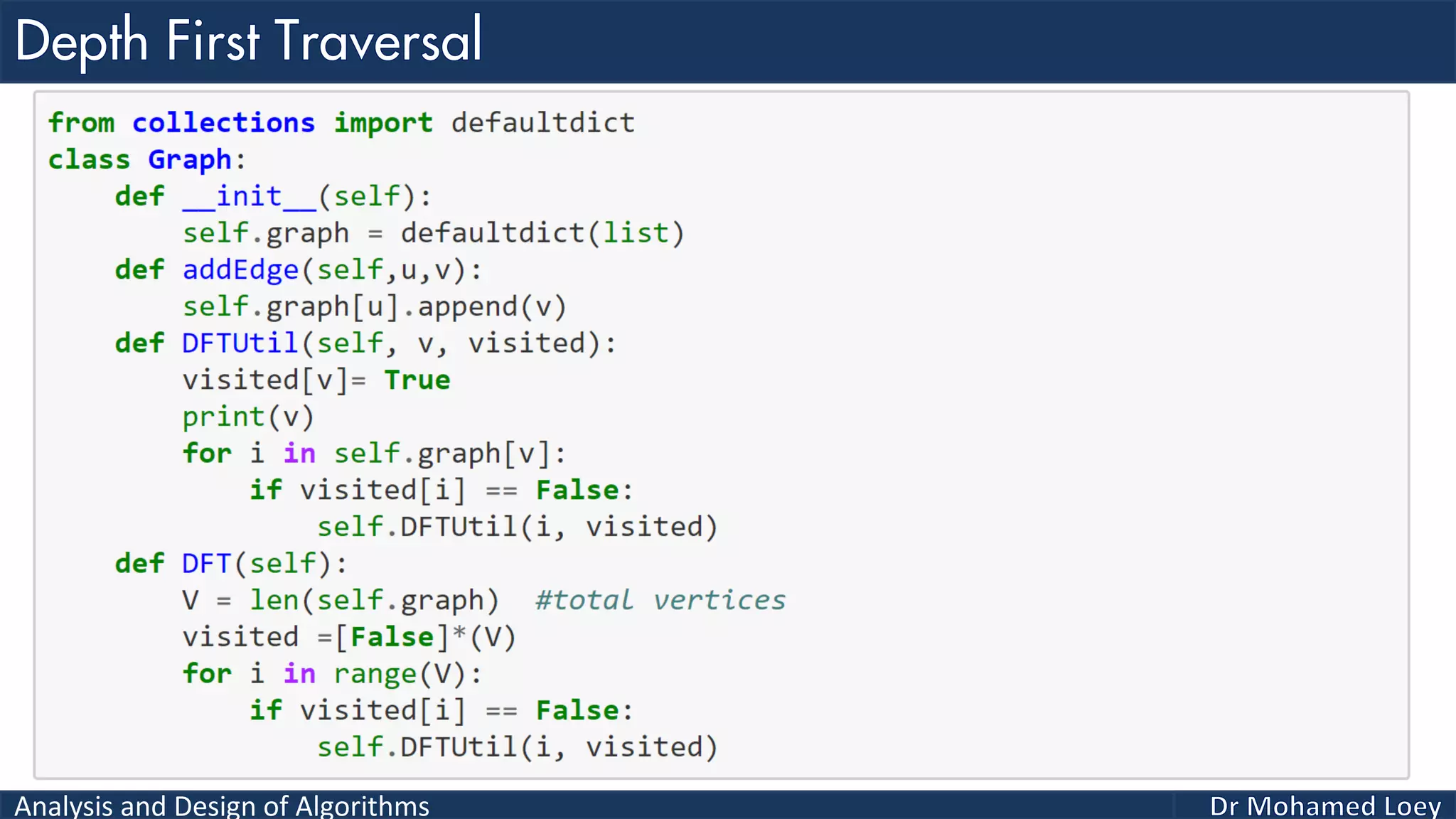
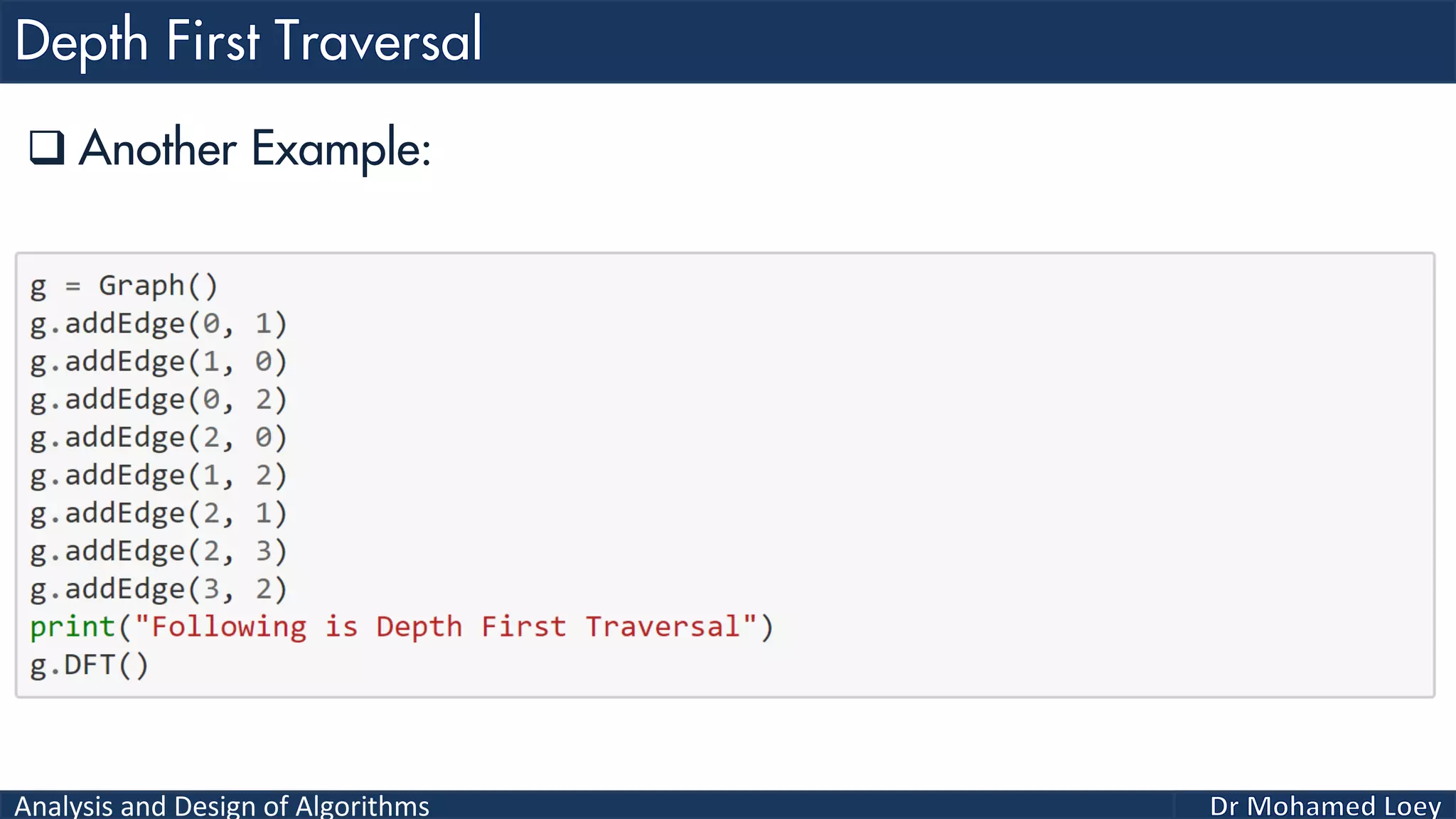
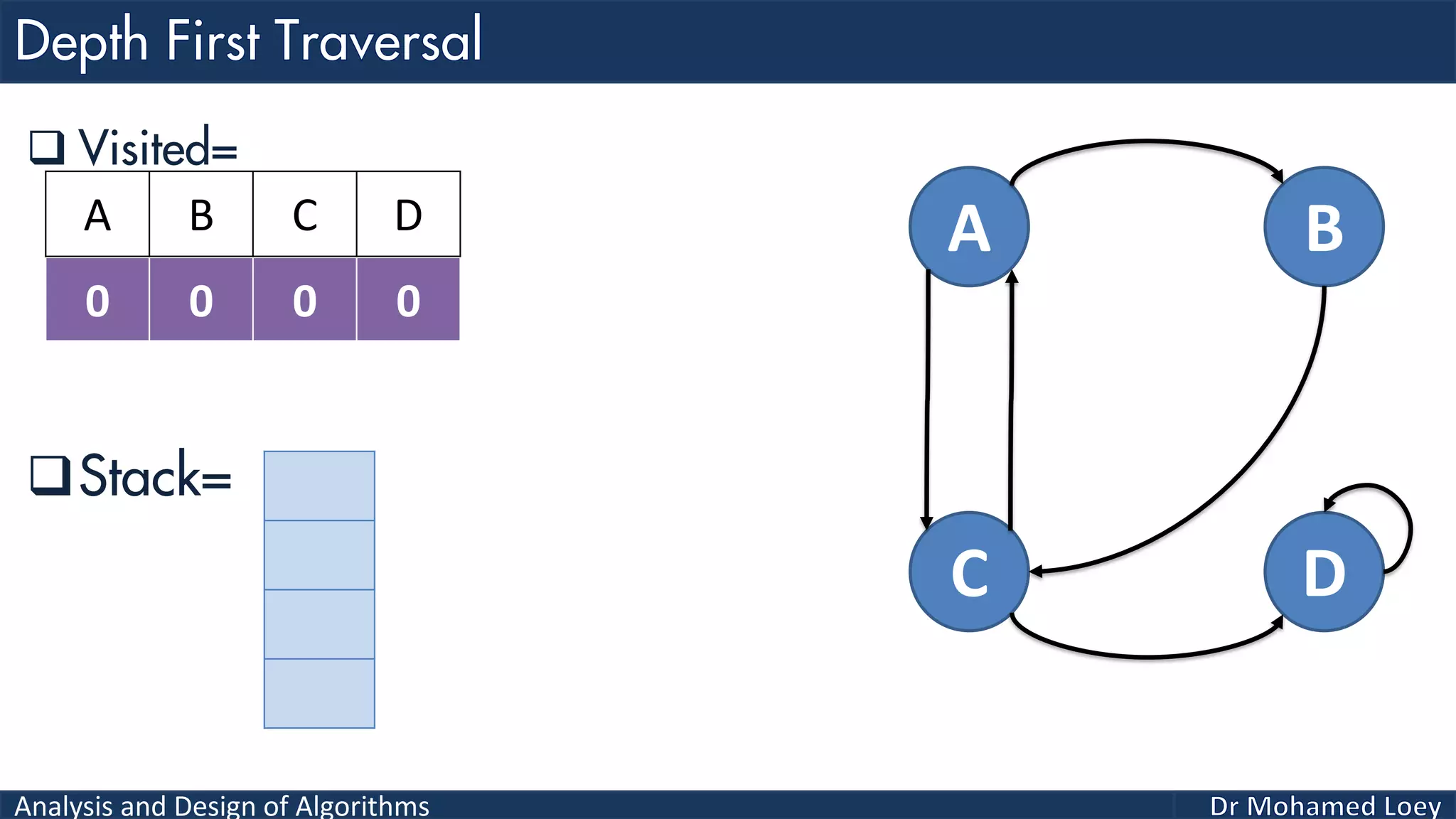
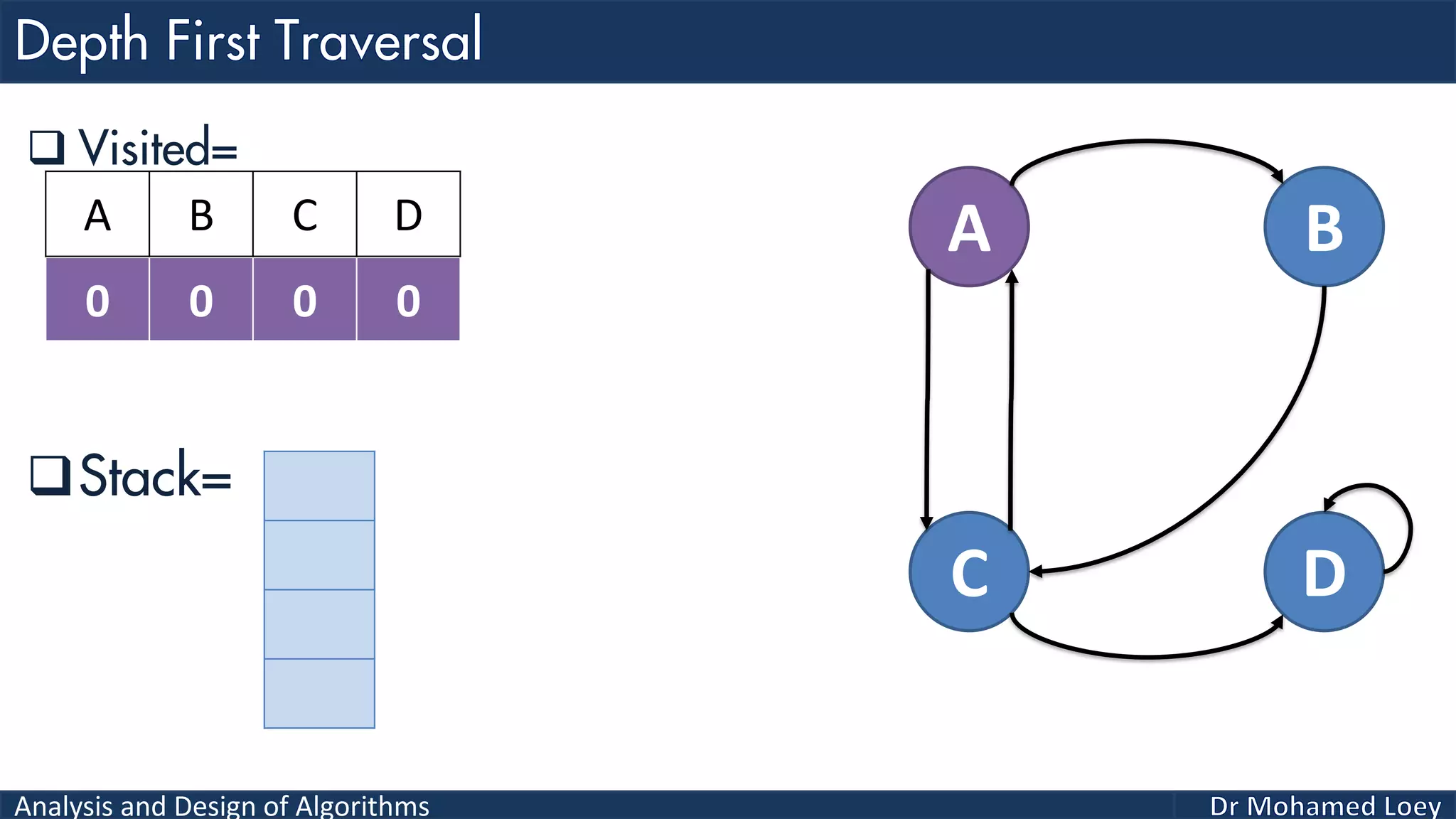
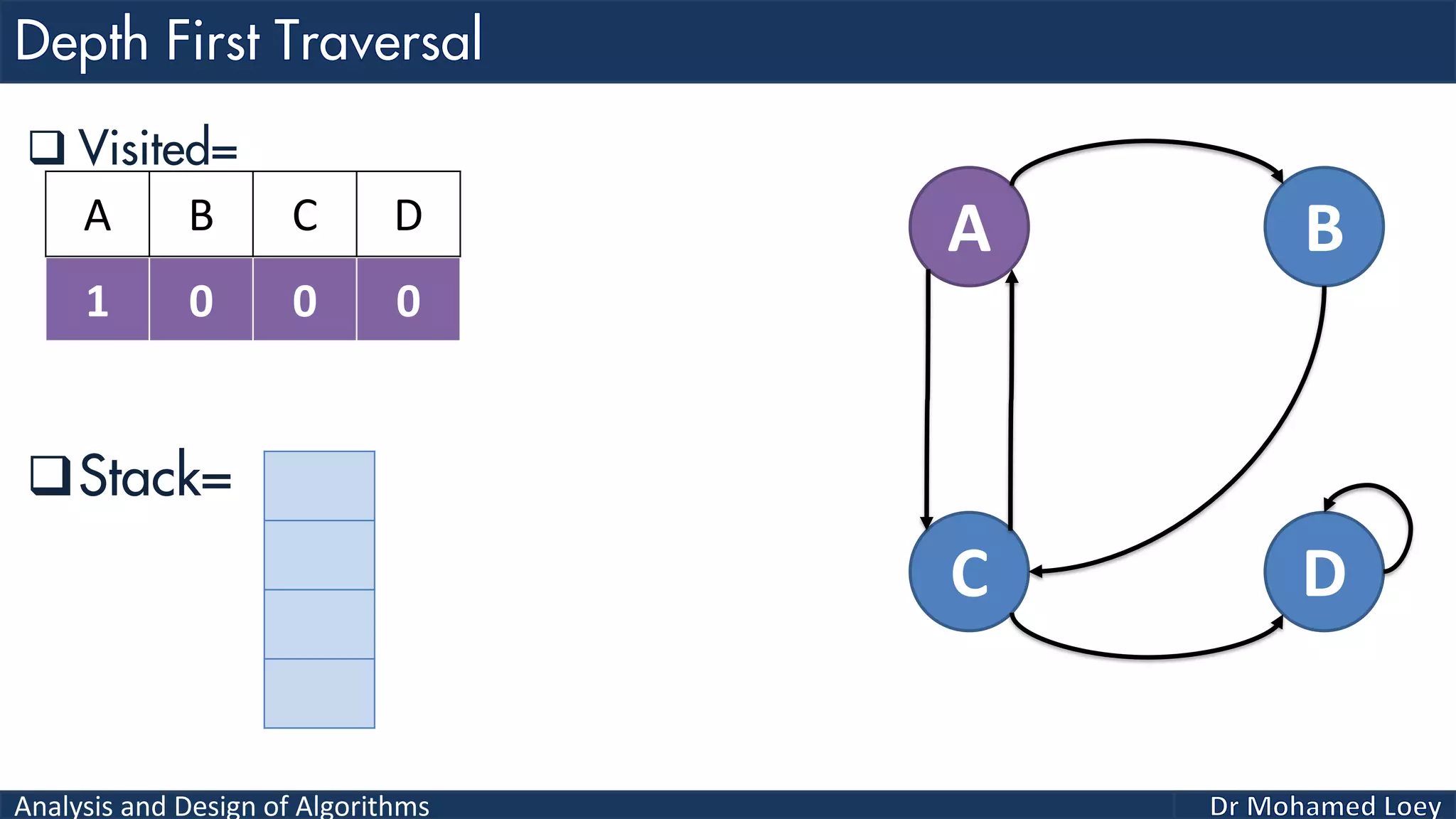
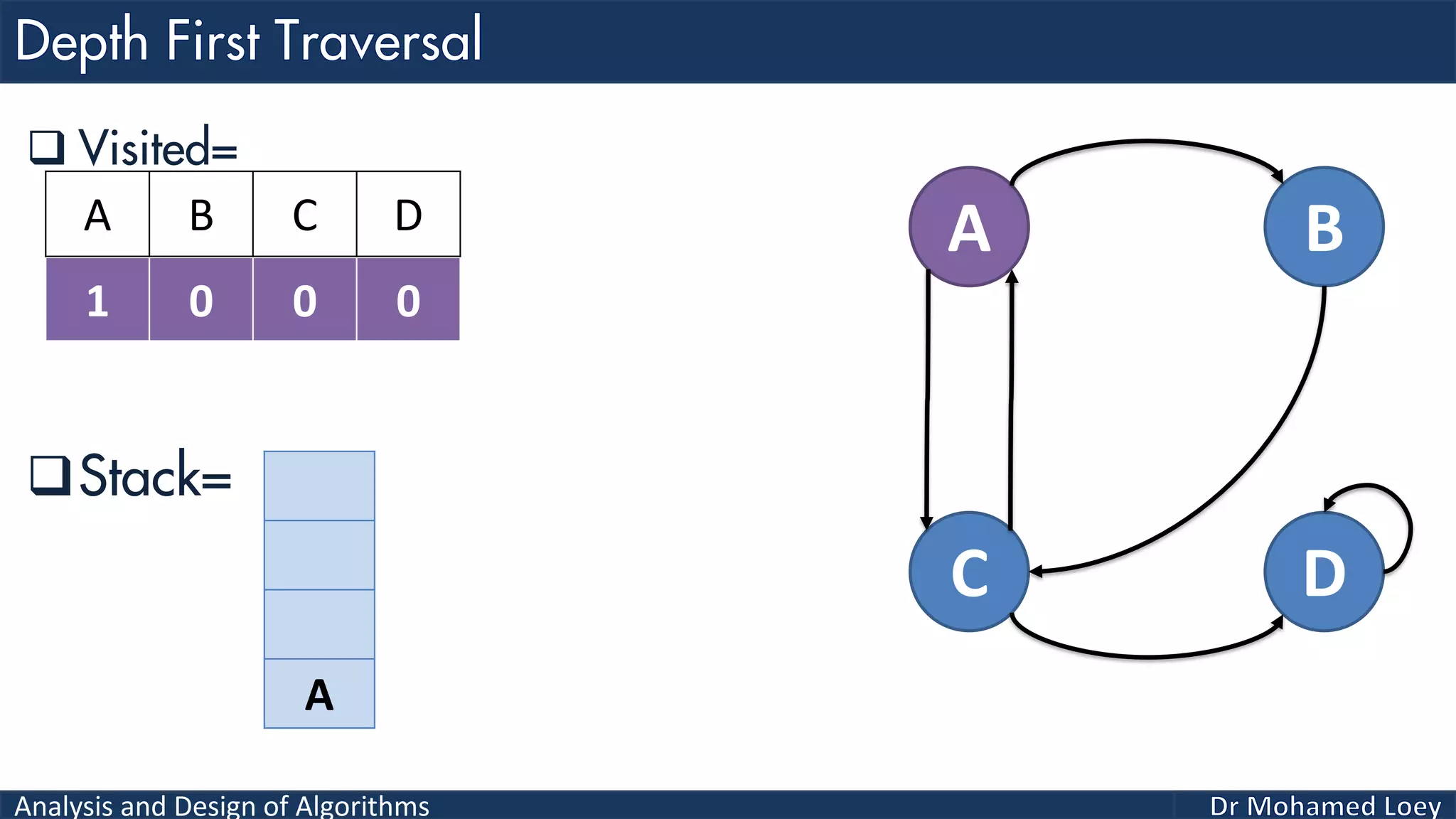
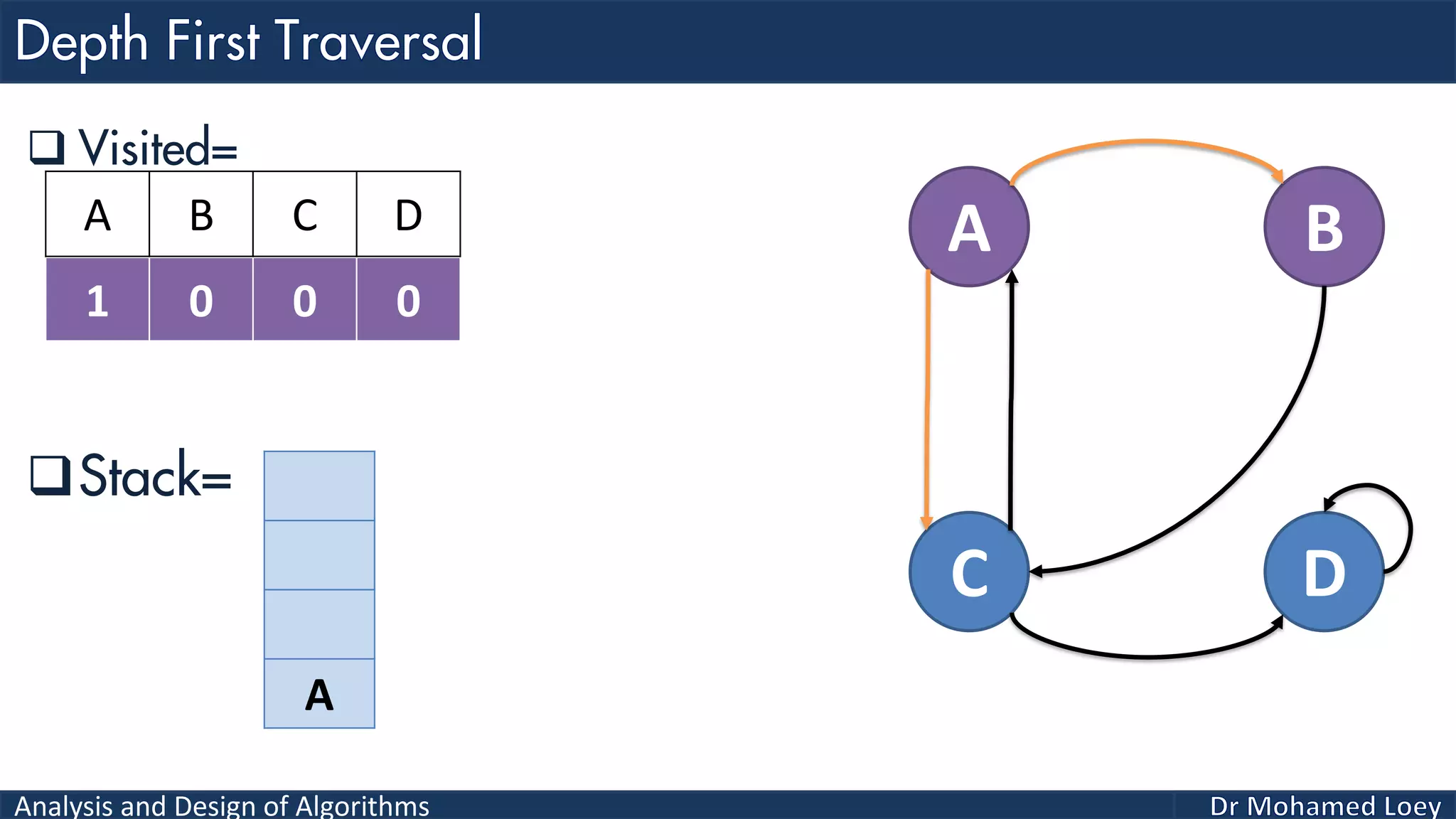
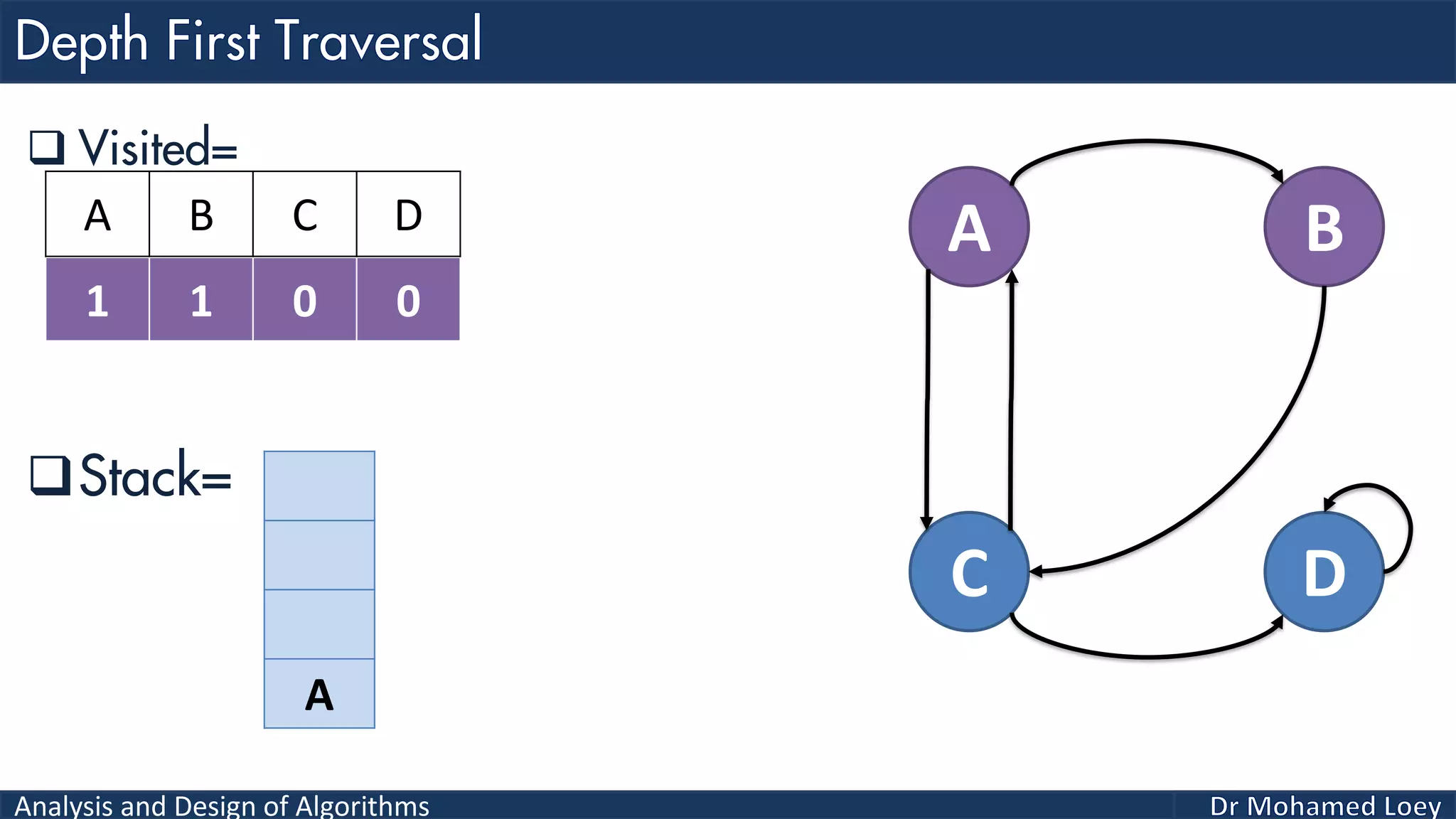
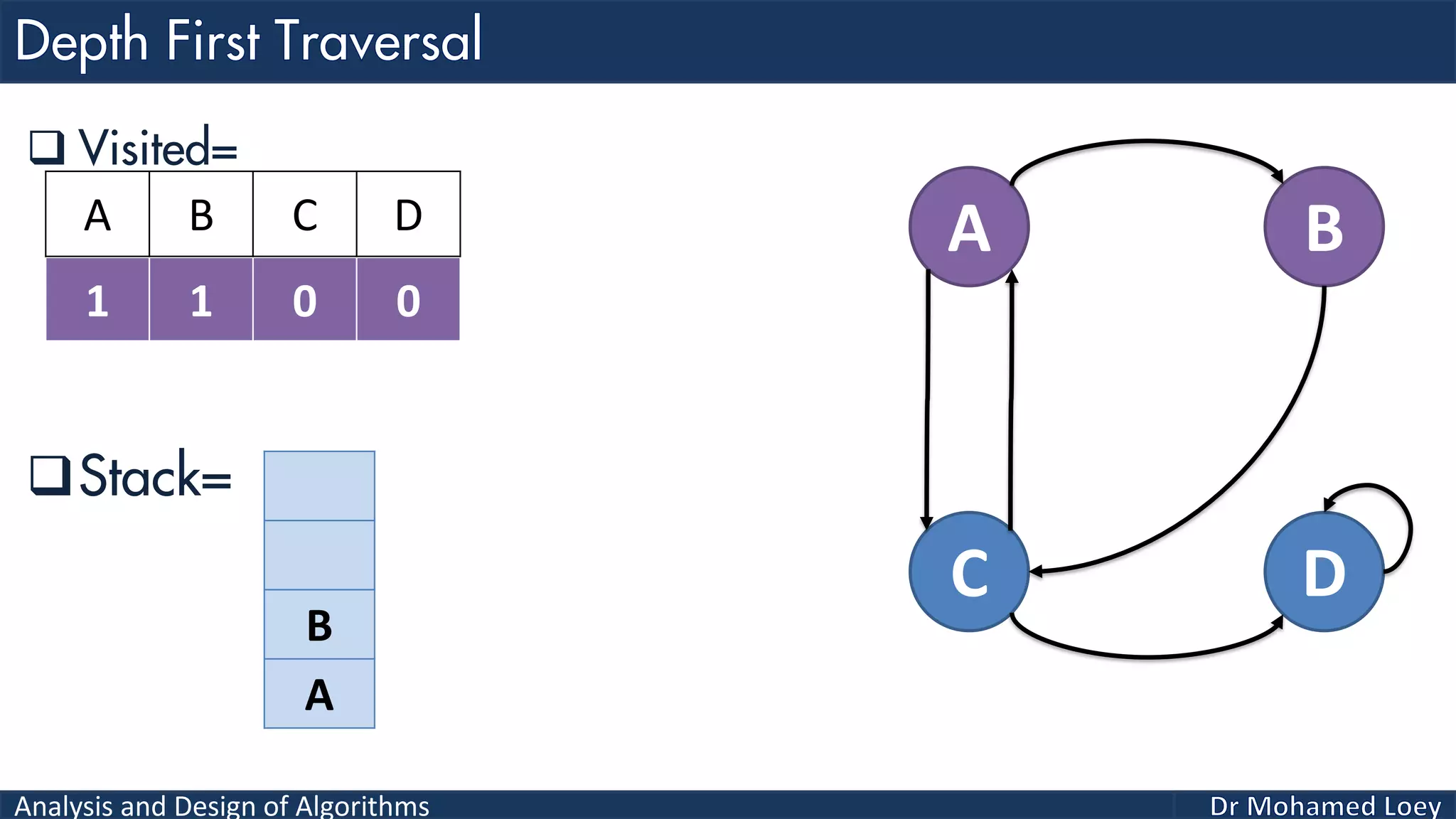
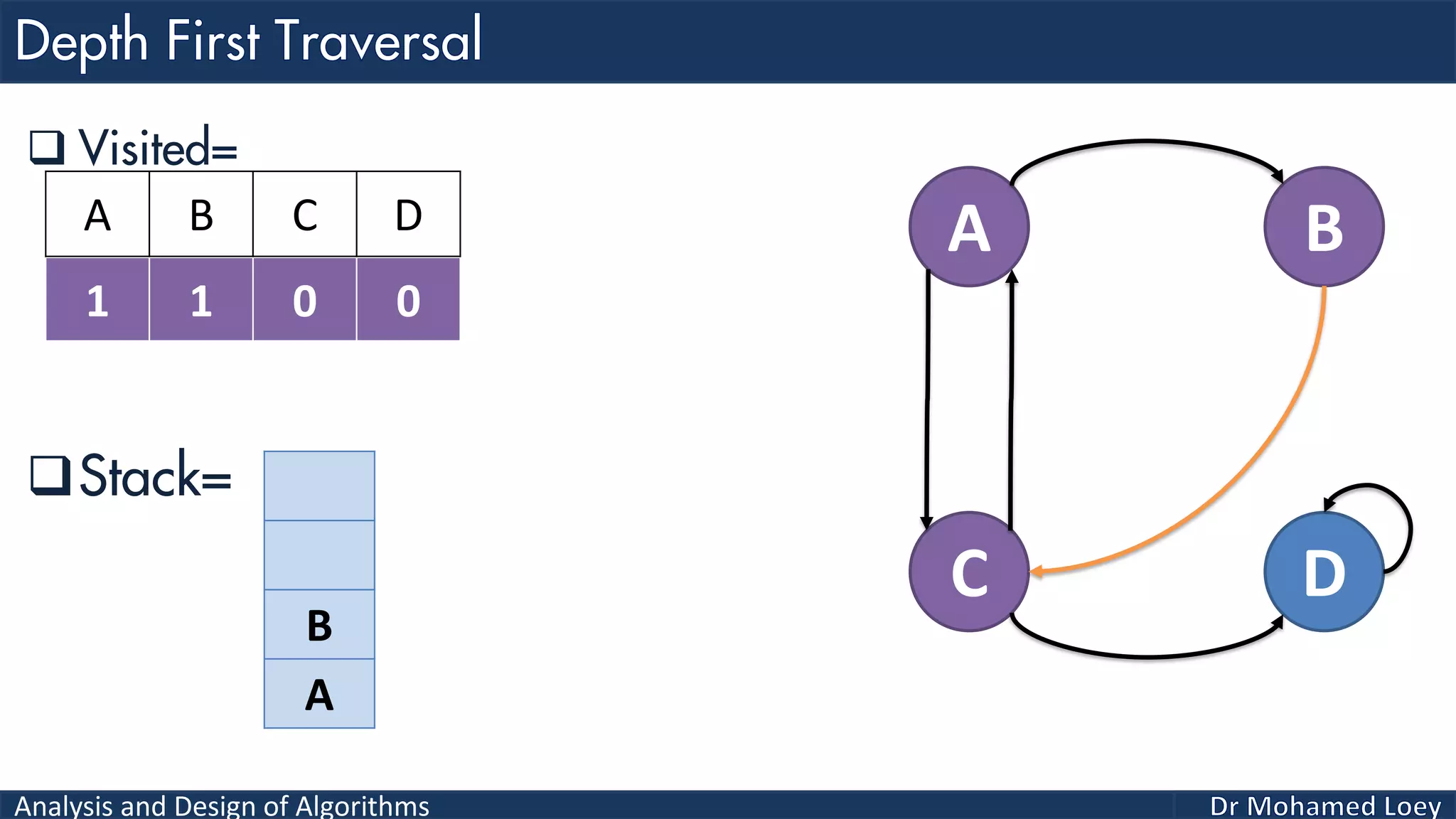
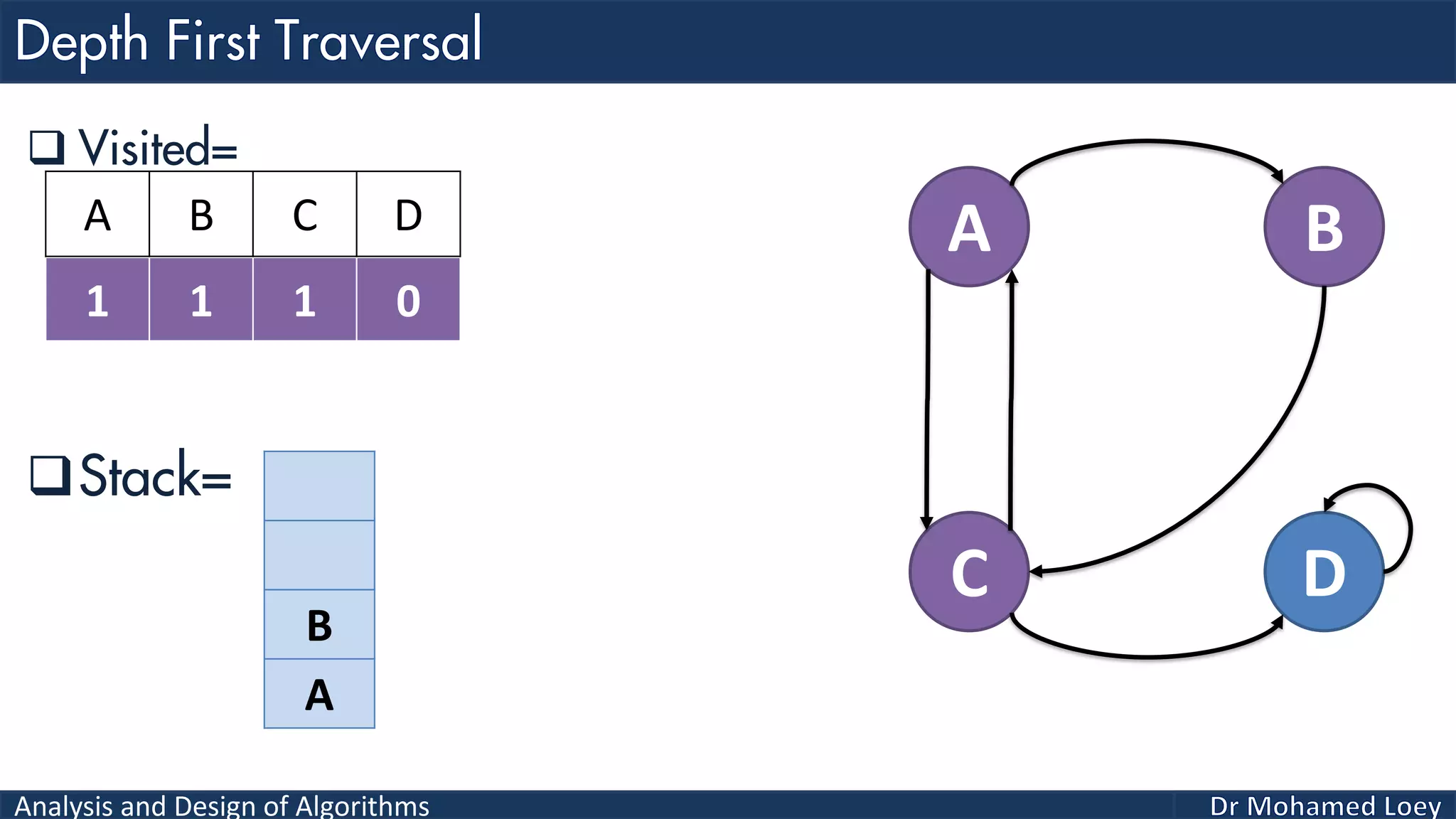
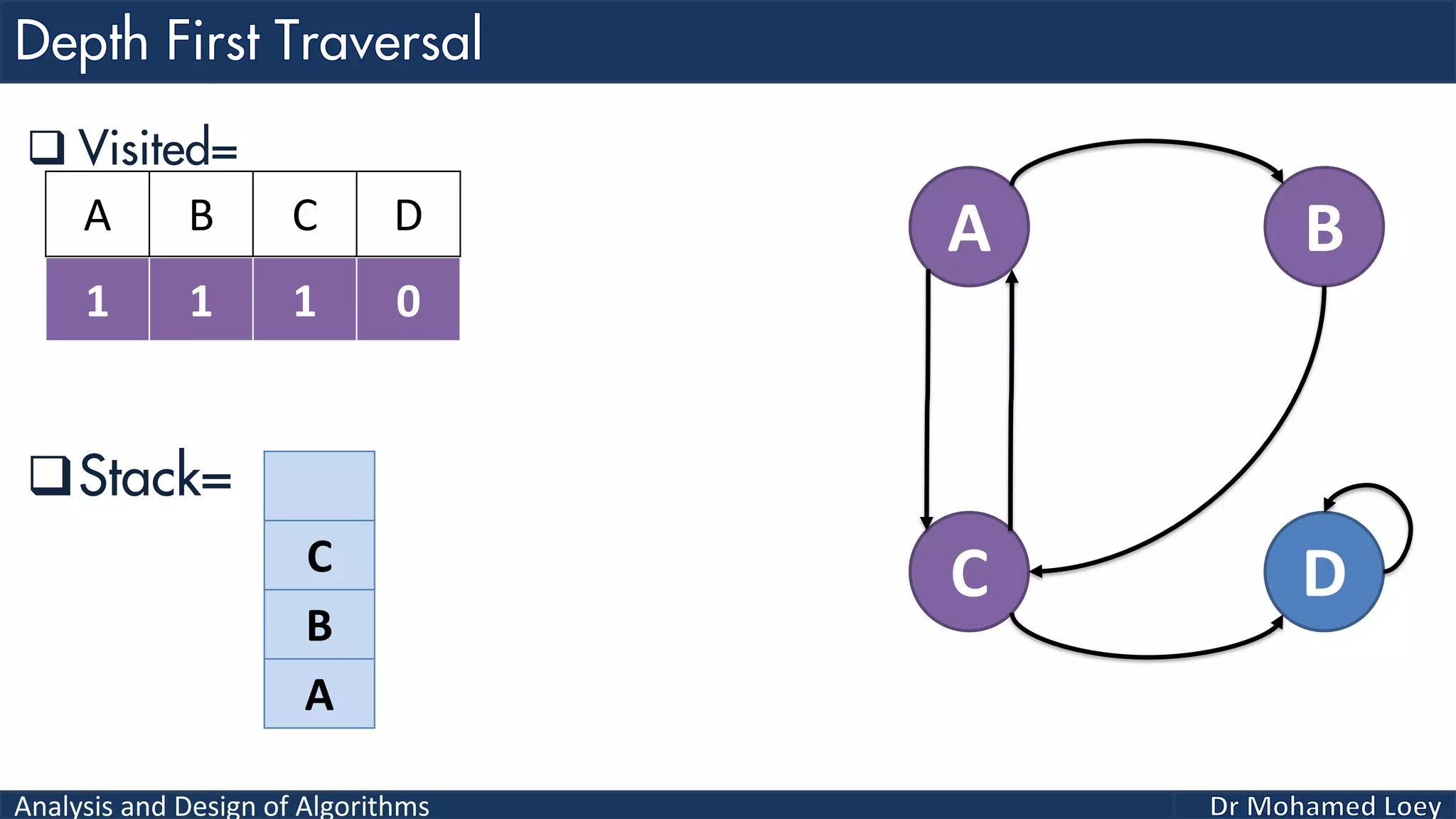
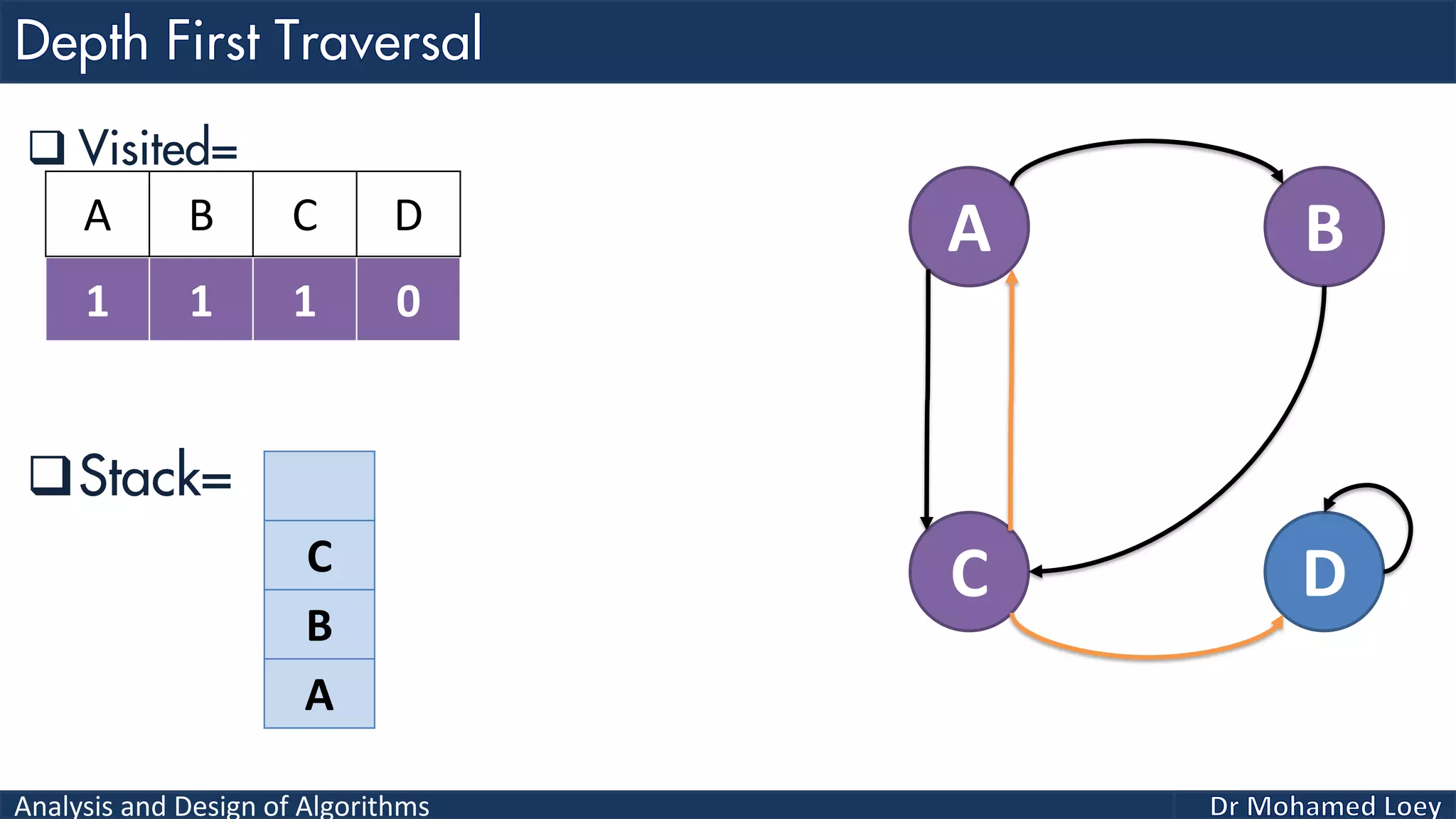
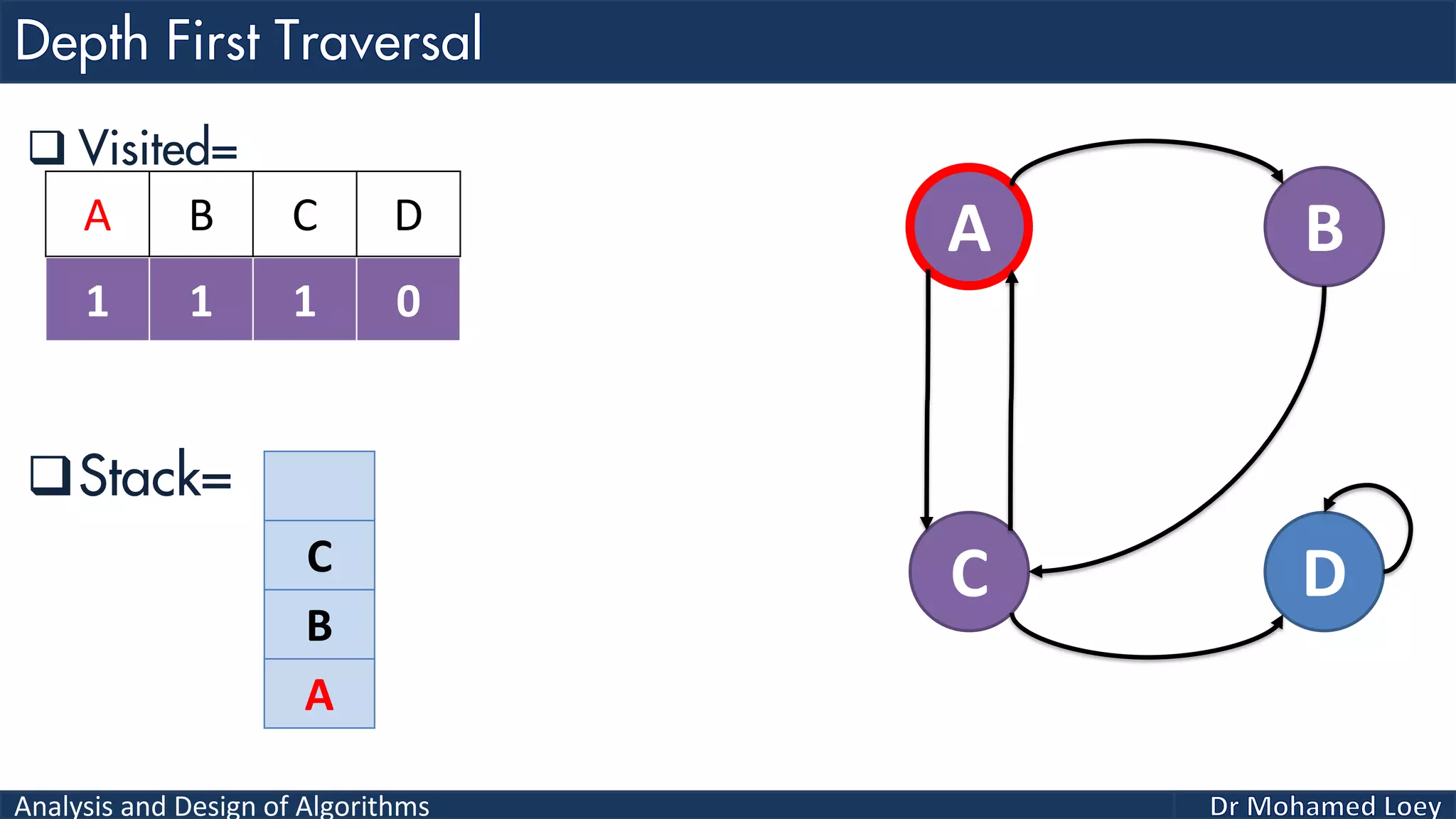
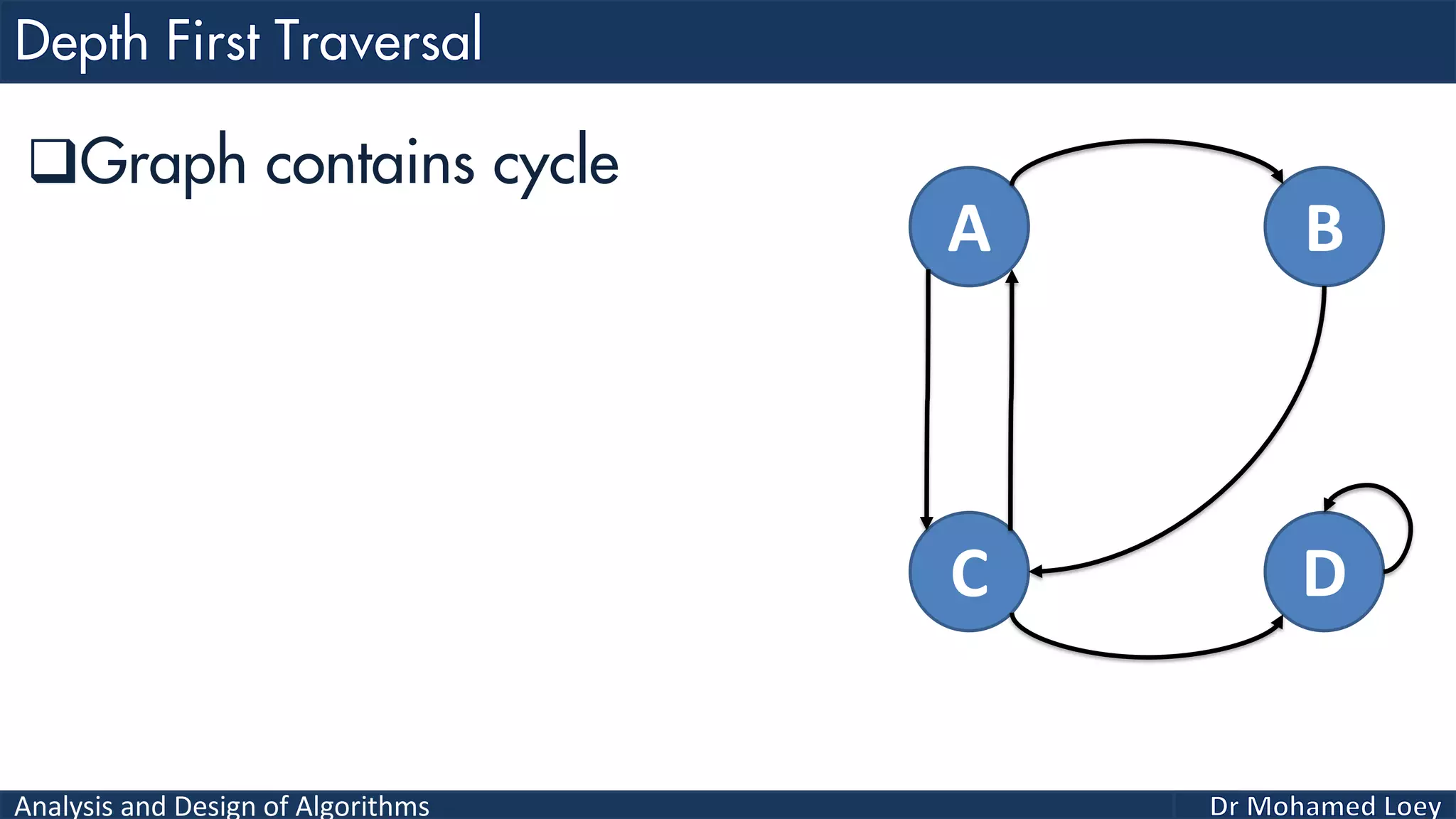
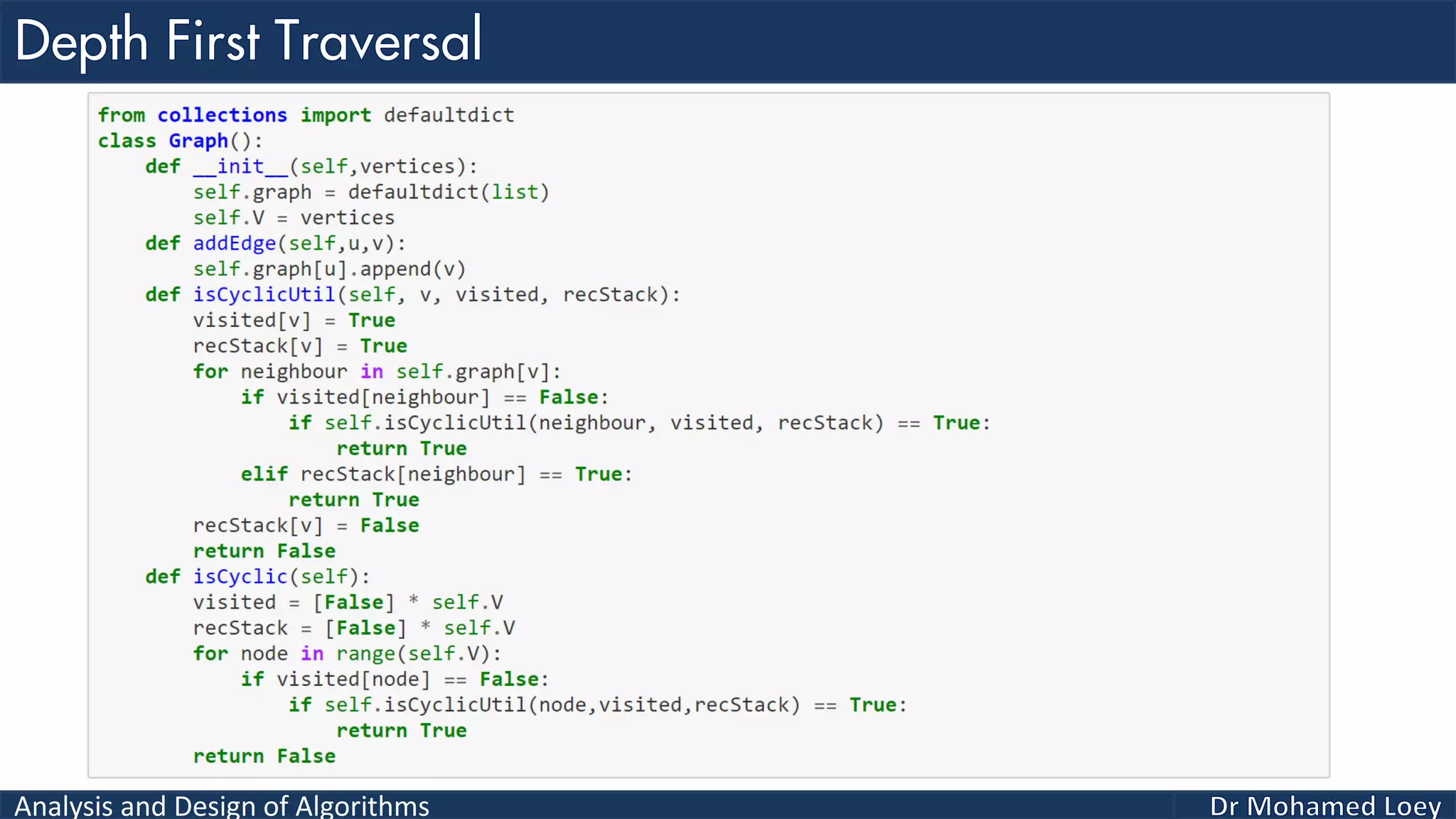
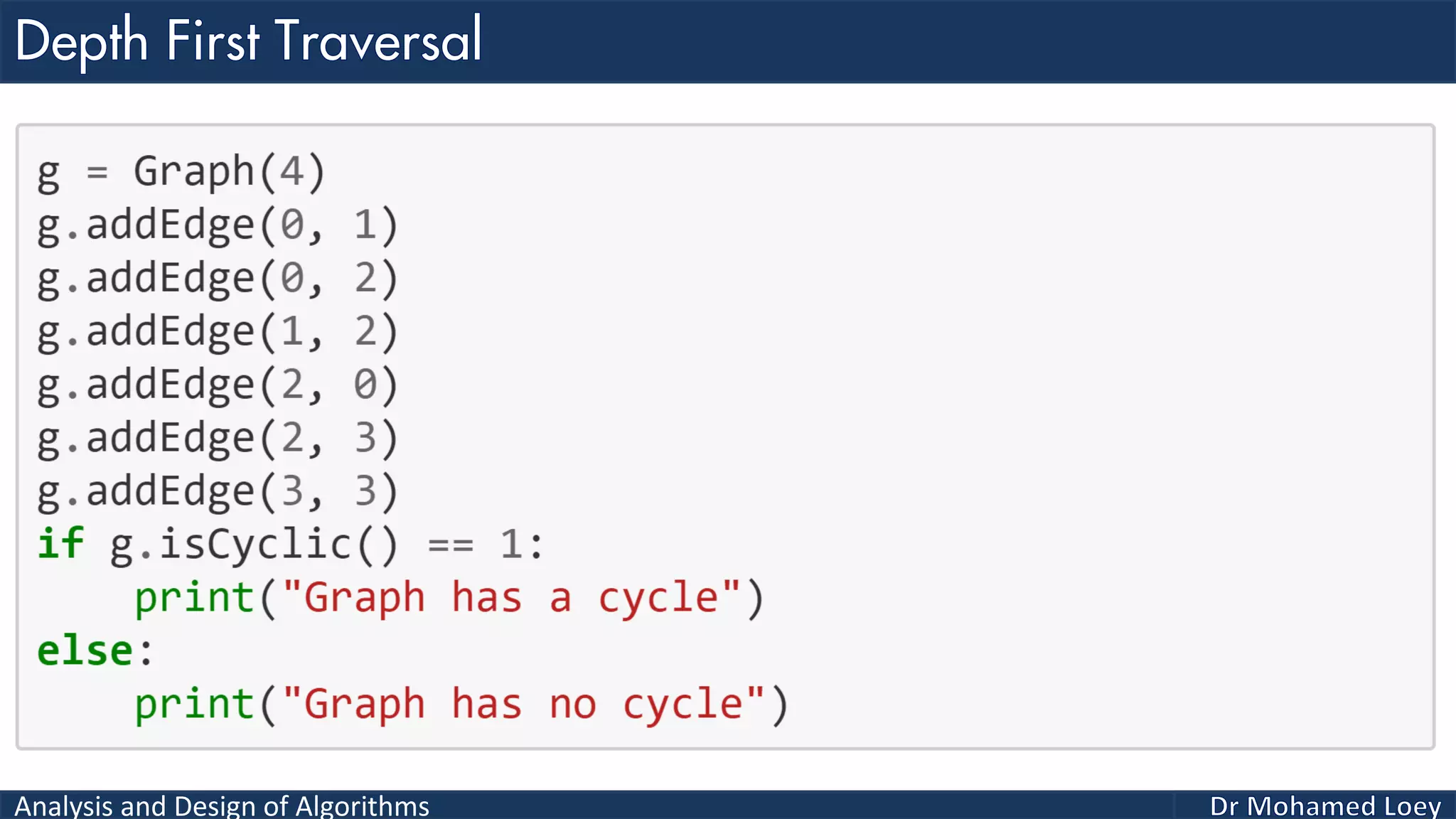
The document provides a comprehensive analysis and design of algorithms related to graph theory, focusing on concepts such as directed and undirected graphs, acyclic and cyclic graphs, and techniques for graph traversal including breadth-first and depth-first search methods. It explains the significance of vertices and edges, the operations of searching and traversing nodes, and includes examples illustrating the application of these concepts. Additionally, it addresses cycle detection in directed graphs using depth-first traversal.

Downloaded 275 times
1 / 103
2 / 103
3 / 103
Most read
4 / 103
5 / 103
6 / 103
7 / 103
8 / 103
9 / 103
10 / 103
Most read
11 / 103
12 / 103
13 / 103
14 / 103
15 / 103
16 / 103
17 / 103
Most read
18 / 103
19 / 103
20 / 103
21 / 103
22 / 103
23 / 103
24 / 103
25 / 103
26 / 103
27 / 103
28 / 103
29 / 103
30 / 103
31 / 103
32 / 103
33 / 103
34 / 103
35 / 103
36 / 103
37 / 103
38 / 103
39 / 103
40 / 103
41 / 103
42 / 103
43 / 103
44 / 103
45 / 103
46 / 103
47 / 103
48 / 103
49 / 103
50 / 103
51 / 103
52 / 103
53 / 103
54 / 103
55 / 103
56 / 103
57 / 103
58 / 103
59 / 103
60 / 103
61 / 103
62 / 103
63 / 103
64 / 103
65 / 103
66 / 103
67 / 103
68 / 103
69 / 103
70 / 103
71 / 103
72 / 103
73 / 103
74 / 103
75 / 103
76 / 103
77 / 103
78 / 103
79 / 103
80 / 103
81 / 103
82 / 103
83 / 103
84 / 103
85 / 103
86 / 103
87 / 103
88 / 103
89 / 103
90 / 103
91 / 103
92 / 103
93 / 103
94 / 103
95 / 103
96 / 103
97 / 103
98 / 103
99 / 103
100 / 103
101 / 103
102 / 103
103 / 103
Analysis and Design of Algorithms Graph Algorithms
Analysis and Design of Algorithms Graph Directed vs Undirected Graph Acyclic vs Cyclic Graph Backedge Search vs Traversal Breadth First Traversal Depth First Traversal Detect Cycle in a Directed Graph
Analysis and Design of Algorithms  Graph data structure consists of a finite set of vertices or nodes. The interconnected objects are represented by points termed as vertices, and the links that connect the vertices are called edges. A B C D E F Node or Vertices Edge
Analysis and Design of Algorithms  Vertex: Each node of the graph is represented as a vertex.  V={A,B,C,D,E,F}  Edge: Edge represents a path between two vertices or a line between two vertices.  E={AB,AC,BD,BE,CE,DE,DF,EF} A B C D E F Node or Vertices Edge
Analysis and Design of Algorithms A B C A B C Directed Graph Undirected Graph
Analysis and Design of Algorithms A B C Acyclic Graph Cyclic Graph A B C
Analysis and Design of Algorithms Backedge is an edge that is from node to itself (selfloop), or one to its ancestor. A B A
Analysis and Design of Algorithms Search: Look for a given node Traversal: Always visit all nodes
Analysis and Design of Algorithms Breadth First Traversal
Analysis and Design of Algorithms Breadth First Traversal (BFT) algorithm traverses all nodes on graph in a breadthward motion and uses a queue to remember to get the next vertex.
Analysis and Design of Algorithms Layers A B C D E F Layer1 Layer2 Layer3 Layer4
Analysis and Design of Algorithms  Visited=  Queue=  Print: A B C D E F 0 0 0 0 0 0 A B C D E F
Analysis and Design of Algorithms  Visited=  Queue=  Print: A B C D E F 1 0 0 0 0 0 A B C D E F
Analysis and Design of Algorithms  Visited=  Queue= A  Print: A B C D E F 1 0 0 0 0 0 A B C D E F
Analysis and Design of Algorithms  Visited=  Queue=  Print: A A B C D E F 1 0 0 0 0 0 A B C D E F
Analysis and Design of Algorithms  Visited=  Queue=  Print: A A B C D E F 1 0 0 0 0 0 A B C D E F
Analysis and Design of Algorithms  Visited=  Queue=  Print: A A B C D E F 1 0 0 0 0 0 A B C D E F
Analysis and Design of Algorithms  Visited=  Queue=  Print: A A B C D E F 1 1 1 0 0 0 A B C D E F
Analysis and Design of Algorithms  Visited=  Queue= B C  Print: A A B C D E F 1 1 1 0 0 0 A B C D E F
Analysis and Design of Algorithms  Visited=  Queue= C  Print: A B A B C D E F 1 1 1 0 0 0 A B C D E F
Analysis and Design of Algorithms  Visited=  Queue= C  Print: A B A B C D E F 1 1 1 0 0 0 A B C D E F
Analysis and Design of Algorithms  Visited=  Queue= C  Print: A B A B C D E F 1 1 1 0 0 0 A B C D E F
Analysis and Design of Algorithms  Visited=  Queue= C  Print: A B A B C D E F 1 1 1 1 1 0 A B C D E F
Analysis and Design of Algorithms  Visited=  Queue= C D E  Print: A B A B C D E F 1 1 1 1 1 0 A B C D E F
Analysis and Design of Algorithms  Visited=  Queue= D E  Print: A B C A B C D E F 1 1 1 1 1 0 A B C D E F
Analysis and Design of Algorithms  Visited=  Queue= D E  Print: A B C A B C D E F 1 1 1 1 1 0 A B C D E F
Analysis and Design of Algorithms  Visited=  Queue= E  Print: A B C A B C D E F 1 1 1 1 1 0 A B C D E F
Analysis and Design of Algorithms  Visited=  Queue= E  Print: A B C D A B C D E F 1 1 1 1 1 0 A B C D E F
Analysis and Design of Algorithms  Visited=  Queue= E  Print: A B C D A B C D E F 1 1 1 1 1 0 A B C D E F
Analysis and Design of Algorithms  Visited=  Queue= E  Print: A B C D A B C D E F 1 1 1 1 1 1 A B C D E F
Analysis and Design of Algorithms  Visited=  Queue= E F  Print: A B C D A B C D E F 1 1 1 1 1 1 A B C D E F
Analysis and Design of Algorithms  Visited=  Queue= F  Print: A B C D E A B C D E F 1 1 1 1 1 1 A B C D E F
Analysis and Design of Algorithms  Visited=  Queue= F  Print: A B C D E A B C D E F 1 1 1 1 1 1 A B C D E F
Analysis and Design of Algorithms  Visited=  Queue= F  Print: A B C D E A B C D E F 1 1 1 1 1 1 A B C D E F
Analysis and Design of Algorithms  Visited=  Queue=  Print: A B C D E A B C D E F 1 1 1 1 1 1 A B C D E F
Analysis and Design of Algorithms  Visited=  Queue=  Print: A B C D E F A B C D E F 1 1 1 1 1 1 A B C D E F
Analysis and Design of Algorithms Breadth First on Tree
Analysis and Design of Algorithms
Analysis and Design of Algorithms  V={0,1,2,3,4,5}  E={01,02,13,14,24,34,35,45} 0 1 2 3 4 5
Analysis and Design of Algorithms
Analysis and Design of Algorithms  Another Example:
Analysis and Design of Algorithms Depth First Traversal
Analysis and Design of Algorithms Depth First Traversal (DFT) algorithm traverses a graph in a depthward motion and uses a stack to remember to get the next vertex to start a search.
Analysis and Design of Algorithms depthward motion A B C D E F
Analysis and Design of Algorithms  Visited= Stack=  Print: A B C D E F 0 0 0 0 0 0 A B C D E F
Analysis and Design of Algorithms  Visited= Stack=  Print: A B C D E F 0 0 0 0 0 0 A B C D E F
Analysis and Design of Algorithms  Visited= Stack=  Print: A B C D E F 1 0 0 0 0 0 A B C D E F
Analysis and Design of Algorithms  Visited= Stack=  Print: A B C D E F 1 0 0 0 0 0 A B C D E F A
Analysis and Design of Algorithms  Visited= Stack=  Print: A A B C D E F 1 0 0 0 0 0 A B C D E F A
Analysis and Design of Algorithms  Visited= Stack=  Print: A A B C D E F 1 0 0 0 0 0 A B C D E F A
Analysis and Design of Algorithms  Visited= Stack=  Print: A A B C D E F 1 1 0 0 0 0 A B C D E F A
Analysis and Design of Algorithms  Visited= Stack=  Print: A A B C D E F 1 1 0 0 0 0 A B C D E F B A
Analysis and Design of Algorithms  Visited= Stack=  Print: A B A B C D E F 1 1 0 0 0 0 A B C D E F B A
Analysis and Design of Algorithms  Visited= Stack=  Print: A B A B C D E F 1 1 0 0 0 0 A B C D E F B A
Analysis and Design of Algorithms  Visited= Stack=  Print: A B A B C D E F 1 1 0 1 0 0 A B C D E F B A
Analysis and Design of Algorithms  Visited= Stack=  Print: A B A B C D E F 1 1 0 1 0 0 A B C D E F D B A
Analysis and Design of Algorithms  Visited= Stack=  Print: A B D A B C D E F 1 1 0 1 0 0 A B C D E F D B A
Analysis and Design of Algorithms  Visited= Stack=  Print: A B D A B C D E F 1 1 0 1 0 0 A B C D E F D B A
Analysis and Design of Algorithms  Visited= Stack=  Print: A B D A B C D E F 1 1 0 1 0 0 A B C D E F D B A
Analysis and Design of Algorithms  Visited= Stack=  Print: A B D A B C D E F 1 1 0 1 1 0 A B C D E F D B A
Analysis and Design of Algorithms  Visited= Stack=  Print: A B D A B C D E F 1 1 0 1 1 0 A B C D E F E D B A
Analysis and Design of Algorithms  Visited= Stack=  Print: A B D E A B C D E F 1 1 0 1 1 0 A B C D E F E D B A
Analysis and Design of Algorithms  Visited= Stack=  Print: A B D E A B C D E F 1 1 0 1 1 0 A B C D E F E D B A
Analysis and Design of Algorithms  Visited= Stack=  Print: A B D E A B C D E F 1 1 0 1 1 0 A B C D E F E D B A
Analysis and Design of Algorithms  Visited= Stack=  Print: A B D E A B C D E F 1 1 0 1 1 1 A B C D E F E D B A
Analysis and Design of Algorithms  Visited= Stack=  Print: A B D E A B C D E F 1 1 0 1 1 1 A B C D E F F E D B A
Analysis and Design of Algorithms  Visited= Stack=  Print: A B D E F A B C D E F 1 1 0 1 1 1 A B C D E F F E D B A
Analysis and Design of Algorithms  Visited= Stack=  Print: A B D E F A B C D E F 1 1 0 1 1 1 A B C D E F E D B A
Analysis and Design of Algorithms  Visited= Stack=  Print: A B D E F A B C D E F 1 1 0 1 1 1 A B C D E F E D B A
Analysis and Design of Algorithms  Visited= Stack=  Print: A B D E F A B C D E F 1 1 0 1 1 1 A B C D E F E D B A
Analysis and Design of Algorithms  Visited= Stack=  Print: A B D E F A B C D E F 1 1 1 1 1 1 A B C D E F E D B A
Analysis and Design of Algorithms  Visited= Stack=  Print: A B D E F C A B C D E F 1 1 1 1 1 1 A B C D E F C E D B A
Analysis and Design of Algorithms  Visited= Stack=  Print: A B D E F C A B C D E F 1 1 1 1 1 1 A B C D E F E D B A
Analysis and Design of Algorithms  Visited= Stack=  Print: A B D E F C A B C D E F 1 1 1 1 1 1 A B C D E F E D B A
Analysis and Design of Algorithms  Visited= Stack=  Print: A B D E F C A B C D E F 1 1 1 1 1 1 A B C D E F D B A
Analysis and Design of Algorithms  Visited= Stack=  Print: A B D E F C A B C D E F 1 1 1 1 1 1 A B C D E F D B A
Analysis and Design of Algorithms  Visited= Stack=  Print: A B D E F C A B C D E F 1 1 1 1 1 1 A B C D E F B A
Analysis and Design of Algorithms  Visited= Stack=  Print: A B D E F C A B C D E F 1 1 1 1 1 1 A B C D E F A
Analysis and Design of Algorithms  Visited= Stack=  Print: A B D E F C A B C D E F 1 1 1 1 1 1 A B C D E F
Analysis and Design of Algorithms Depth First on tree
Analysis and Design of Algorithms
Analysis and Design of Algorithms  V={0,1,2,3,4,5}  E={01,02,13,14,24,34,35,45} 0 1 2 3 4 5
Analysis and Design of Algorithms
Analysis and Design of Algorithms  Another Example:
Analysis and Design of Algorithms Given a directed graph, check whether the graph contains a cycle or not. Your function should return true if the given graph contains at least one cycle, else return false.
Analysis and Design of Algorithms Depth First Traversal can be used to detect cycle in a Graph. There is a cycle in a graph only if there is a back edge present in the graph.
Analysis and Design of Algorithms  Visited= Stack= A C B D 0 0 0 0 A B C D
Analysis and Design of Algorithms  Visited= Stack= A C B D 0 0 0 0 A B C D
Analysis and Design of Algorithms  Visited= Stack= A C B D 1 0 0 0 A B C D
Analysis and Design of Algorithms  Visited= Stack= A C B D 1 0 0 0 A B C D A
Analysis and Design of Algorithms  Visited= Stack= A C B D 1 0 0 0 A B C D A
Analysis and Design of Algorithms  Visited= Stack= A C B D 1 1 0 0 A B C D A
Analysis and Design of Algorithms  Visited= Stack= A C B D 1 1 0 0 A B C D B A
Analysis and Design of Algorithms  Visited= Stack= A C B D 1 1 0 0 A B C D B A
Analysis and Design of Algorithms  Visited= Stack= A C B D 1 1 1 0 A B C D B A
Analysis and Design of Algorithms  Visited= Stack= A C B D 1 1 1 0 A B C D C B A
Analysis and Design of Algorithms  Visited= Stack= A C B D 1 1 1 0 A B C D C B A
Analysis and Design of Algorithms  Visited= Stack= A C B D 1 1 1 0 A B C D C B A
Analysis and Design of Algorithms Graph contains cycle A C B D
Analysis and Design of Algorithms
Analysis and Design of Algorithms
Analysis and Design of Algorithms facebook.com/mloey mohamedloey@gmail.com twitter.com/mloey linkedin.com/in/mloey mloey@fci.bu.edu.eg mloey.github.io
Analysis and Design of Algorithms www.YourCompany.com © 2020 Companyname PowerPoint Business Theme. All Rights Reserved. THANKS FOR YOUR TIME

More Related Content

PDF
Algorithms Lecture 3: Analysis of Algorithms II
byMohamed Loey
 
PDF
Algorithms Lecture 5: Sorting Algorithms II
byMohamed Loey
 
PDF
Algorithms Lecture 2: Analysis of Algorithms I
byMohamed Loey
 
PPT
Design and Analysis of Algorithms
bySwapnil Agrawal
 
PPT
ANALYSIS-AND-DESIGN-OF-ALGORITHM.ppt
byDaveCalapis3
 
PPT
DESIGN AND ANALYSIS OF ALGORITHMS
byGayathri Gaayu
 
PPT
Asymptotic notations
byEhtisham Ali
 
PPTX
Analysis of algorithm
byRajendra Dangwal
 
Algorithms Lecture 3: Analysis of Algorithms II
byMohamed Loey
 
Algorithms Lecture 5: Sorting Algorithms II
byMohamed Loey
 
Algorithms Lecture 2: Analysis of Algorithms I
byMohamed Loey
 
Design and Analysis of Algorithms
bySwapnil Agrawal
 
ANALYSIS-AND-DESIGN-OF-ALGORITHM.ppt
byDaveCalapis3
 
DESIGN AND ANALYSIS OF ALGORITHMS
byGayathri Gaayu
 
Asymptotic notations
byEhtisham Ali
 
Analysis of algorithm
byRajendra Dangwal
 

What's hot

PDF
Algorithms Lecture 4: Sorting Algorithms I
byMohamed Loey
 
PPTX
Asymptotic Notation
byProtap Mondal
 
PPTX
Greedy algorithms
bysandeep54552
 
PDF
A* Search Algorithm
byvikas dhakane
 
PPT
Hashing PPT
bySaurabh Kumar
 
PPT
Unit 1 chapter 1 Design and Analysis of Algorithms
byP. Subathra Kishore, KAMARAJ College of Engineering and Technology, Madurai
 
PPTX
Brute force method
bypriyankabhansali217
 
PPTX
Hashing
byAmar Jukuntla
 
PPTX
Informed and Uninformed search Strategies
byAmey Kerkar
 
PPTX
Dijkstra's algorithm presentation
bySubid Biswas
 
PPTX
Graph coloring using backtracking
byshashidharPapishetty
 
PPT
Spanning trees
byShareb Ismaeel
 
PPTX
Problem solving in Artificial Intelligence.pptx
bykitsenthilkumarcse
 
PPTX
B and B+ tree
byAshish Arun
 
PPTX
Data Structure and Algorithms.pptx
bySyed Zaid Irshad
 
PPTX
0 1 knapsack using branch and bound
byAbhishek Singh
 
PPTX
heap Sort Algorithm
byLemia Algmri
 
PPT
Dinive conquer algorithm
byMohd Arif
 
PDF
Introduction to Algorithms Complexity Analysis
byDr. Pankaj Agarwal
 
PPT
Algorithm analysis
bysumitbardhan
 
Algorithms Lecture 4: Sorting Algorithms I
byMohamed Loey
 
Asymptotic Notation
byProtap Mondal
 
Greedy algorithms
bysandeep54552
 
A* Search Algorithm
byvikas dhakane
 
Hashing PPT
bySaurabh Kumar
 
Unit 1 chapter 1 Design and Analysis of Algorithms
byP. Subathra Kishore, KAMARAJ College of Engineering and Technology, Madurai
 
Brute force method
bypriyankabhansali217
 
Hashing
byAmar Jukuntla
 
Informed and Uninformed search Strategies
byAmey Kerkar
 
Dijkstra's algorithm presentation
bySubid Biswas
 
Graph coloring using backtracking
byshashidharPapishetty
 
Spanning trees
byShareb Ismaeel
 
Problem solving in Artificial Intelligence.pptx
bykitsenthilkumarcse
 
B and B+ tree
byAshish Arun
 
Data Structure and Algorithms.pptx
bySyed Zaid Irshad
 
0 1 knapsack using branch and bound
byAbhishek Singh
 
heap Sort Algorithm
byLemia Algmri
 
Dinive conquer algorithm
byMohd Arif
 
Introduction to Algorithms Complexity Analysis
byDr. Pankaj Agarwal
 
Algorithm analysis
bysumitbardhan
 

Similar to Algorithms Lecture 7: Graph Algorithms

PDF
Design and Analysis Algorithms.pdf
byHarshNagda5
 
PPTX
Array Data StructureData StructureData Structure.pptx
bymenukam354
 
PPT
l01-intro (3).ppt
byssuser15a62a
 
PPTX
CS8451 DAA Unit-I.pptx
byBolliniNivas
 
PPT
Types of Algorithms.ppt
byALIZAIB KHAN
 
PPTX
Algorithms : Introduction and Analysis
byDhrumil Patel
 
PDF
Lec01-Algorithems - Introduction and Overview.pdf
byMAJDABDALLAH3
 
PPT
UNIT-1-PPT-DESIGN AND ANALYSIS OF ALGORITHMS
byramalakshmikaliappan
 
PPT
UNIT-1-PPTS-DAA INTRO WITH DIVIDE AND CONQUER
bySalini P
 
PPT
UNIT 1- Design Analysis of algorithms and its working
byBobby Pra A
 
PPT
UNIT-1-PPTS-DAA_INTRODUCTION_TO_DAA_GH.ppt
bysravansonga007
 
PDF
DAA Notes.pdf
bySauravPawar14
 
PPT
Day 1 Chapter 1 Unit 1
byP. Subathra Kishore, KAMARAJ College of Engineering and Technology, Madurai
 
PPT
Introduction to Design Algorithm And Analysis.ppt
byBhargaviDalal4
 
PPT
UNIT-1-PPTS-DAA.ppt
bySamridhiGulati4
 
PPT
UNIT-1-PPTS-DAA.ppt
byracha49
 
PDF
1. Introduction to Algorithms, Specification of Algorithm, Complexity.pdf
byNetraBansal3
 
PPT
L01 intro-daa - ppt1
bysankaran L
 
PDF
Data Structure - Lecture 1 - Introduction.pdf
bydonotreply20
 
PDF
ADA complete notes
byVinay Kumar C
 
Design and Analysis Algorithms.pdf
byHarshNagda5
 
Array Data StructureData StructureData Structure.pptx
bymenukam354
 
l01-intro (3).ppt
byssuser15a62a
 
CS8451 DAA Unit-I.pptx
byBolliniNivas
 
Types of Algorithms.ppt
byALIZAIB KHAN
 
Algorithms : Introduction and Analysis
byDhrumil Patel
 
Lec01-Algorithems - Introduction and Overview.pdf
byMAJDABDALLAH3
 
UNIT-1-PPT-DESIGN AND ANALYSIS OF ALGORITHMS
byramalakshmikaliappan
 
UNIT-1-PPTS-DAA INTRO WITH DIVIDE AND CONQUER
bySalini P
 
UNIT 1- Design Analysis of algorithms and its working
byBobby Pra A
 
UNIT-1-PPTS-DAA_INTRODUCTION_TO_DAA_GH.ppt
bysravansonga007
 
DAA Notes.pdf
bySauravPawar14
 
Day 1 Chapter 1 Unit 1
byP. Subathra Kishore, KAMARAJ College of Engineering and Technology, Madurai
 
Introduction to Design Algorithm And Analysis.ppt
byBhargaviDalal4
 
UNIT-1-PPTS-DAA.ppt
bySamridhiGulati4
 
UNIT-1-PPTS-DAA.ppt
byracha49
 
1. Introduction to Algorithms, Specification of Algorithm, Complexity.pdf
byNetraBansal3
 
L01 intro-daa - ppt1
bysankaran L
 
Data Structure - Lecture 1 - Introduction.pdf
bydonotreply20
 
ADA complete notes
byVinay Kumar C
 

More from Mohamed Loey

PDF
Lecture 6: Deep Learning Applications
byMohamed Loey
 
PDF
Lecture 5: Convolutional Neural Network Models
byMohamed Loey
 
PDF
Lecture 4: Deep Learning Frameworks
byMohamed Loey
 
PDF
Lecture 4: How it Works: Convolutional Neural Networks
byMohamed Loey
 
PPTX
Lecture 3: Convolutional Neural Networks
byMohamed Loey
 
PDF
Lecture 2: Artificial Neural Network
byMohamed Loey
 
PDF
Lecture 1: Deep Learning for Computer Vision
byMohamed Loey
 
PDF
Design of an Intelligent System for Improving Classification of Cancer Diseases
byMohamed Loey
 
PDF
Computer Security - CCNA Security - Lecture 2
byMohamed Loey
 
PDF
Computer Security - CCNA Security - Lecture 1
byMohamed Loey
 
PDF
Algorithms Lecture 8: Pattern Algorithms
byMohamed Loey
 
PDF
Algorithms Lecture 6: Searching Algorithms
byMohamed Loey
 
PDF
Algorithms Lecture 1: Introduction to Algorithms
byMohamed Loey
 
PDF
Convolutional Neural Network Models - Deep Learning
byMohamed Loey
 
PDF
Deep Learning - Overview of my work II
byMohamed Loey
 
PDF
Computer Security Lecture 7: RSA
byMohamed Loey
 
PDF
Computer Security Lecture 5: Simplified Advanced Encryption Standard
byMohamed Loey
 
PDF
Computer Security Lecture 4.1: DES Supplementary Material
byMohamed Loey
 
PDF
PMP Lecture 4: Project Integration Management
byMohamed Loey
 
PDF
Computer Security Lecture 4: Block Ciphers and the Data Encryption Standard
byMohamed Loey
 
Lecture 6: Deep Learning Applications
byMohamed Loey
 
Lecture 5: Convolutional Neural Network Models
byMohamed Loey
 
Lecture 4: Deep Learning Frameworks
byMohamed Loey
 
Lecture 4: How it Works: Convolutional Neural Networks
byMohamed Loey
 
Lecture 3: Convolutional Neural Networks
byMohamed Loey
 
Lecture 2: Artificial Neural Network
byMohamed Loey
 
Lecture 1: Deep Learning for Computer Vision
byMohamed Loey
 
Design of an Intelligent System for Improving Classification of Cancer Diseases
byMohamed Loey
 
Computer Security - CCNA Security - Lecture 2
byMohamed Loey
 
Computer Security - CCNA Security - Lecture 1
byMohamed Loey
 
Algorithms Lecture 8: Pattern Algorithms
byMohamed Loey
 
Algorithms Lecture 6: Searching Algorithms
byMohamed Loey
 
Algorithms Lecture 1: Introduction to Algorithms
byMohamed Loey
 
Convolutional Neural Network Models - Deep Learning
byMohamed Loey
 
Deep Learning - Overview of my work II
byMohamed Loey
 
Computer Security Lecture 7: RSA
byMohamed Loey
 
Computer Security Lecture 5: Simplified Advanced Encryption Standard
byMohamed Loey
 
Computer Security Lecture 4.1: DES Supplementary Material
byMohamed Loey
 
PMP Lecture 4: Project Integration Management
byMohamed Loey
 
Computer Security Lecture 4: Block Ciphers and the Data Encryption Standard
byMohamed Loey
 

Recently uploaded

PPTX
Eyeball presentation ocular anatomy.pptx
byanmols3059
 
PPTX
STAND UP activity - Future .
byJohanes MAKUB
 
PDF
ENTHIRAN THE ROBOT (2010) QUIZ | THE QUIZ CLUB OF PSGCAS | A PSGCAS QC SLIDES...
byQuiz Club of PSG College of Arts & Science
 
PDF
BÀI TẬP TEST BỔ TRỢ THEO TỪNG CHỦ ĐỀ CỦA TỪNG UNIT KÈM BÀI TẬP NGHE - TIẾNG A...
byNguyen Thanh Tu Collection
 
PPTX
maxiosocialis quiz for class 7b.ppt.pptx
byKARTHIKKALESH1
 
PPTX
How to Manage Pricelist in Odoo 18 Sales
byCeline George
 
PPTX
THIS IS MY TESTING SLIDESHARE POWERPOINT
byiammrhaywood
 
PDF
Presentation: Open Pedagogy for Open EdTech
byRobert Reuter
 
PPTX
Alkali and Alkaline Earth Metals - Brief Description.pptx
byManarat International University
 
PPTX
"Aspergillus: Habitat, Structure, Reproduction and Life Cycle"
byRohit Jirobe
 
PDF
Coal and Types of Coal MCWs and Assertion Reason Questions.pdf
byAkashDTejwani
 
PPTX
Shock, AHN - I, Medical Surgical Nursing
byAbhijeet Mahale
 
PPTX
ENG PPT W6Q2 day 1 sequencing events.pptx
byalma66979
 
PDF
Cornea anatomy ppt eyeball cornea. ..pdf
byanmols3059
 
PPTX
KS-3-ARAL-READING-PLUS-WEEK-1- powerpoint
byELMAGARALZA1
 
PPTX
Challenges and Opportunities of integrating indigenous knowledge of Performi...
byvidhinagar3
 
PPTX
Year 11 Information Evening - Tuesday 30th September 2025
byWestHatch
 
PPTX
GOAL Method in Interviewing - Method.pptx
bysreelakshmyvaishnav
 
PPTX
ARAL-Reading Plus Progression Plan and IDF (BRIDGE Framework) FINAL.pptx
byNorjanaOttoMedalMada
 
PPTX
FORK Method in Interview Techniques.pptx
bysreelakshmyvaishnav
 
Eyeball presentation ocular anatomy.pptx
byanmols3059
 
STAND UP activity - Future .
byJohanes MAKUB
 
ENTHIRAN THE ROBOT (2010) QUIZ | THE QUIZ CLUB OF PSGCAS | A PSGCAS QC SLIDES...
byQuiz Club of PSG College of Arts & Science
 
BÀI TẬP TEST BỔ TRỢ THEO TỪNG CHỦ ĐỀ CỦA TỪNG UNIT KÈM BÀI TẬP NGHE - TIẾNG A...
byNguyen Thanh Tu Collection
 
maxiosocialis quiz for class 7b.ppt.pptx
byKARTHIKKALESH1
 
How to Manage Pricelist in Odoo 18 Sales
byCeline George
 
THIS IS MY TESTING SLIDESHARE POWERPOINT
byiammrhaywood
 
Presentation: Open Pedagogy for Open EdTech
byRobert Reuter
 
Alkali and Alkaline Earth Metals - Brief Description.pptx
byManarat International University
 
"Aspergillus: Habitat, Structure, Reproduction and Life Cycle"
byRohit Jirobe
 
Coal and Types of Coal MCWs and Assertion Reason Questions.pdf
byAkashDTejwani
 
Shock, AHN - I, Medical Surgical Nursing
byAbhijeet Mahale
 
ENG PPT W6Q2 day 1 sequencing events.pptx
byalma66979
 
Cornea anatomy ppt eyeball cornea. ..pdf
byanmols3059
 
KS-3-ARAL-READING-PLUS-WEEK-1- powerpoint
byELMAGARALZA1
 
Challenges and Opportunities of integrating indigenous knowledge of Performi...
byvidhinagar3
 
Year 11 Information Evening - Tuesday 30th September 2025
byWestHatch
 
GOAL Method in Interviewing - Method.pptx
bysreelakshmyvaishnav
 
ARAL-Reading Plus Progression Plan and IDF (BRIDGE Framework) FINAL.pptx
byNorjanaOttoMedalMada
 
FORK Method in Interview Techniques.pptx
bysreelakshmyvaishnav
 

Algorithms Lecture 7: Graph Algorithms

  • 1.
    Analysis and Designof Algorithms Graph Algorithms
  • 2.
    Analysis and Designof Algorithms Graph Directed vs Undirected Graph Acyclic vs Cyclic Graph Backedge Search vs Traversal Breadth First Traversal Depth First Traversal Detect Cycle in a Directed Graph
  • 3.
    Analysis and Designof Algorithms  Graph data structure consists of a finite set of vertices or nodes. The interconnected objects are represented by points termed as vertices, and the links that connect the vertices are called edges. A B C D E F Node or Vertices Edge
  • 4.
    Analysis and Designof Algorithms  Vertex: Each node of the graph is represented as a vertex.  V={A,B,C,D,E,F}  Edge: Edge represents a path between two vertices or a line between two vertices.  E={AB,AC,BD,BE,CE,DE,DF,EF} A B C D E F Node or Vertices Edge
  • 5.
    Analysis and Designof Algorithms A B C A B C Directed Graph Undirected Graph
  • 6.
    Analysis and Designof Algorithms A B C Acyclic Graph Cyclic Graph A B C
  • 7.
    Analysis and Designof Algorithms Backedge is an edge that is from node to itself (selfloop), or one to its ancestor. A B A
  • 8.
    Analysis and Designof Algorithms Search: Look for a given node Traversal: Always visit all nodes
  • 9.
    Analysis and Designof Algorithms Breadth First Traversal
  • 10.
    Analysis and Designof Algorithms Breadth First Traversal (BFT) algorithm traverses all nodes on graph in a breadthward motion and uses a queue to remember to get the next vertex.
  • 11.
    Analysis and Designof Algorithms Layers A B C D E F Layer1 Layer2 Layer3 Layer4
  • 12.
    Analysis and Designof Algorithms  Visited=  Queue=  Print: A B C D E F 0 0 0 0 0 0 A B C D E F
  • 13.
    Analysis and Designof Algorithms  Visited=  Queue=  Print: A B C D E F 1 0 0 0 0 0 A B C D E F
  • 14.
    Analysis and Designof Algorithms  Visited=  Queue= A  Print: A B C D E F 1 0 0 0 0 0 A B C D E F
  • 15.
    Analysis and Designof Algorithms  Visited=  Queue=  Print: A A B C D E F 1 0 0 0 0 0 A B C D E F
  • 16.
    Analysis and Designof Algorithms  Visited=  Queue=  Print: A A B C D E F 1 0 0 0 0 0 A B C D E F
  • 17.
    Analysis and Designof Algorithms  Visited=  Queue=  Print: A A B C D E F 1 0 0 0 0 0 A B C D E F
  • 18.
    Analysis and Designof Algorithms  Visited=  Queue=  Print: A A B C D E F 1 1 1 0 0 0 A B C D E F
  • 19.
    Analysis and Designof Algorithms  Visited=  Queue= B C  Print: A A B C D E F 1 1 1 0 0 0 A B C D E F
  • 20.
    Analysis and Designof Algorithms  Visited=  Queue= C  Print: A B A B C D E F 1 1 1 0 0 0 A B C D E F
  • 21.
    Analysis and Designof Algorithms  Visited=  Queue= C  Print: A B A B C D E F 1 1 1 0 0 0 A B C D E F
  • 22.
    Analysis and Designof Algorithms  Visited=  Queue= C  Print: A B A B C D E F 1 1 1 0 0 0 A B C D E F
  • 23.
    Analysis and Designof Algorithms  Visited=  Queue= C  Print: A B A B C D E F 1 1 1 1 1 0 A B C D E F
  • 24.
    Analysis and Designof Algorithms  Visited=  Queue= C D E  Print: A B A B C D E F 1 1 1 1 1 0 A B C D E F
  • 25.
    Analysis and Designof Algorithms  Visited=  Queue= D E  Print: A B C A B C D E F 1 1 1 1 1 0 A B C D E F
  • 26.
    Analysis and Designof Algorithms  Visited=  Queue= D E  Print: A B C A B C D E F 1 1 1 1 1 0 A B C D E F
  • 27.
    Analysis and Designof Algorithms  Visited=  Queue= E  Print: A B C A B C D E F 1 1 1 1 1 0 A B C D E F
  • 28.
    Analysis and Designof Algorithms  Visited=  Queue= E  Print: A B C D A B C D E F 1 1 1 1 1 0 A B C D E F
  • 29.
    Analysis and Designof Algorithms  Visited=  Queue= E  Print: A B C D A B C D E F 1 1 1 1 1 0 A B C D E F
  • 30.
    Analysis and Designof Algorithms  Visited=  Queue= E  Print: A B C D A B C D E F 1 1 1 1 1 1 A B C D E F
  • 31.
    Analysis and Designof Algorithms  Visited=  Queue= E F  Print: A B C D A B C D E F 1 1 1 1 1 1 A B C D E F
  • 32.
    Analysis and Designof Algorithms  Visited=  Queue= F  Print: A B C D E A B C D E F 1 1 1 1 1 1 A B C D E F
  • 33.
    Analysis and Designof Algorithms  Visited=  Queue= F  Print: A B C D E A B C D E F 1 1 1 1 1 1 A B C D E F
  • 34.
    Analysis and Designof Algorithms  Visited=  Queue= F  Print: A B C D E A B C D E F 1 1 1 1 1 1 A B C D E F
  • 35.
    Analysis and Designof Algorithms  Visited=  Queue=  Print: A B C D E A B C D E F 1 1 1 1 1 1 A B C D E F
  • 36.
    Analysis and Designof Algorithms  Visited=  Queue=  Print: A B C D E F A B C D E F 1 1 1 1 1 1 A B C D E F
  • 37.
    Analysis and Designof Algorithms Breadth First on Tree
  • 38.
    Analysis and Designof Algorithms
  • 39.
    Analysis and Designof Algorithms  V={0,1,2,3,4,5}  E={01,02,13,14,24,34,35,45} 0 1 2 3 4 5
  • 40.
    Analysis and Designof Algorithms
  • 41.
    Analysis and Designof Algorithms  Another Example:
  • 42.
    Analysis and Designof Algorithms Depth First Traversal
  • 43.
    Analysis and Designof Algorithms Depth First Traversal (DFT) algorithm traverses a graph in a depthward motion and uses a stack to remember to get the next vertex to start a search.
  • 44.
    Analysis and Designof Algorithms depthward motion A B C D E F
  • 45.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B C D E F 0 0 0 0 0 0 A B C D E F
  • 46.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B C D E F 0 0 0 0 0 0 A B C D E F
  • 47.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B C D E F 1 0 0 0 0 0 A B C D E F
  • 48.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B C D E F 1 0 0 0 0 0 A B C D E F A
  • 49.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A A B C D E F 1 0 0 0 0 0 A B C D E F A
  • 50.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A A B C D E F 1 0 0 0 0 0 A B C D E F A
  • 51.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A A B C D E F 1 1 0 0 0 0 A B C D E F A
  • 52.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A A B C D E F 1 1 0 0 0 0 A B C D E F B A
  • 53.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B A B C D E F 1 1 0 0 0 0 A B C D E F B A
  • 54.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B A B C D E F 1 1 0 0 0 0 A B C D E F B A
  • 55.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B A B C D E F 1 1 0 1 0 0 A B C D E F B A
  • 56.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B A B C D E F 1 1 0 1 0 0 A B C D E F D B A
  • 57.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B D A B C D E F 1 1 0 1 0 0 A B C D E F D B A
  • 58.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B D A B C D E F 1 1 0 1 0 0 A B C D E F D B A
  • 59.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B D A B C D E F 1 1 0 1 0 0 A B C D E F D B A
  • 60.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B D A B C D E F 1 1 0 1 1 0 A B C D E F D B A
  • 61.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B D A B C D E F 1 1 0 1 1 0 A B C D E F E D B A
  • 62.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B D E A B C D E F 1 1 0 1 1 0 A B C D E F E D B A
  • 63.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B D E A B C D E F 1 1 0 1 1 0 A B C D E F E D B A
  • 64.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B D E A B C D E F 1 1 0 1 1 0 A B C D E F E D B A
  • 65.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B D E A B C D E F 1 1 0 1 1 1 A B C D E F E D B A
  • 66.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B D E A B C D E F 1 1 0 1 1 1 A B C D E F F E D B A
  • 67.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B D E F A B C D E F 1 1 0 1 1 1 A B C D E F F E D B A
  • 68.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B D E F A B C D E F 1 1 0 1 1 1 A B C D E F E D B A
  • 69.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B D E F A B C D E F 1 1 0 1 1 1 A B C D E F E D B A
  • 70.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B D E F A B C D E F 1 1 0 1 1 1 A B C D E F E D B A
  • 71.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B D E F A B C D E F 1 1 1 1 1 1 A B C D E F E D B A
  • 72.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B D E F C A B C D E F 1 1 1 1 1 1 A B C D E F C E D B A
  • 73.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B D E F C A B C D E F 1 1 1 1 1 1 A B C D E F E D B A
  • 74.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B D E F C A B C D E F 1 1 1 1 1 1 A B C D E F E D B A
  • 75.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B D E F C A B C D E F 1 1 1 1 1 1 A B C D E F D B A
  • 76.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B D E F C A B C D E F 1 1 1 1 1 1 A B C D E F D B A
  • 77.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B D E F C A B C D E F 1 1 1 1 1 1 A B C D E F B A
  • 78.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B D E F C A B C D E F 1 1 1 1 1 1 A B C D E F A
  • 79.
    Analysis and Designof Algorithms  Visited= Stack=  Print: A B D E F C A B C D E F 1 1 1 1 1 1 A B C D E F
  • 80.
    Analysis and Designof Algorithms Depth First on tree
  • 81.
    Analysis and Designof Algorithms
  • 82.
    Analysis and Designof Algorithms  V={0,1,2,3,4,5}  E={01,02,13,14,24,34,35,45} 0 1 2 3 4 5
  • 83.
    Analysis and Designof Algorithms
  • 84.
    Analysis and Designof Algorithms  Another Example:
  • 85.
    Analysis and Designof Algorithms Given a directed graph, check whether the graph contains a cycle or not. Your function should return true if the given graph contains at least one cycle, else return false.
  • 86.
    Analysis and Designof Algorithms Depth First Traversal can be used to detect cycle in a Graph. There is a cycle in a graph only if there is a back edge present in the graph.
  • 87.
    Analysis and Designof Algorithms  Visited= Stack= A C B D 0 0 0 0 A B C D
  • 88.
    Analysis and Designof Algorithms  Visited= Stack= A C B D 0 0 0 0 A B C D
  • 89.
    Analysis and Designof Algorithms  Visited= Stack= A C B D 1 0 0 0 A B C D
  • 90.
    Analysis and Designof Algorithms  Visited= Stack= A C B D 1 0 0 0 A B C D A
  • 91.
    Analysis and Designof Algorithms  Visited= Stack= A C B D 1 0 0 0 A B C D A
  • 92.
    Analysis and Designof Algorithms  Visited= Stack= A C B D 1 1 0 0 A B C D A
  • 93.
    Analysis and Designof Algorithms  Visited= Stack= A C B D 1 1 0 0 A B C D B A
  • 94.
    Analysis and Designof Algorithms  Visited= Stack= A C B D 1 1 0 0 A B C D B A
  • 95.
    Analysis and Designof Algorithms  Visited= Stack= A C B D 1 1 1 0 A B C D B A
  • 96.
    Analysis and Designof Algorithms  Visited= Stack= A C B D 1 1 1 0 A B C D C B A
  • 97.
    Analysis and Designof Algorithms  Visited= Stack= A C B D 1 1 1 0 A B C D C B A
  • 98.
    Analysis and Designof Algorithms  Visited= Stack= A C B D 1 1 1 0 A B C D C B A
  • 99.
    Analysis and Designof Algorithms Graph contains cycle A C B D
  • 100.
    Analysis and Designof Algorithms
  • 101.
    Analysis and Designof Algorithms
  • 102.
    Analysis and Designof Algorithms facebook.com/mloey mohamedloey@gmail.com twitter.com/mloey linkedin.com/in/mloey mloey@fci.bu.edu.eg mloey.github.io
  • 103.
    Analysis and Designof Algorithms www.YourCompany.com © 2020 Companyname PowerPoint Business Theme. All Rights Reserved. THANKS FOR YOUR TIME