Introduction to Design Algorithm And Analysis.ppt

CMR ENGINEERING COLLEGE DEPARTMENT OF CSE (Cyber security) SUBJECT: DESIGN AND ANALYSIS OF ALGORITHMS III B.TECH I- SEM By M.Amrutha Assistant Professor CSE-Cyber security

UNIT – I INTRODUCTION: Algorithm, Performance Analysis-Space complexity, Time complexity, Asymptotic Notations- Big oh notation, Omega notation, Theta notation and Little oh notation. Divide and conquer: General method, applications-Binary search, Quick sort, Merge sort, Stassen's matrix multiplication. UNIT – II Disjoint Sets: Disjoint set operations, union and find algorithms Backtracking: General method, applications, n-queen’s problem, sum of subsets problem, graph coloring SYLLABUS

UNIT - III Dynamic Programming: General method, applications- Optimal binary search trees, 0/1 knapsack problem, All pairs shortest path problem, Traveling sales person problem, Reliability design. UNIT – IV Greedy method: General method, applications-Job sequencing with deadlines, knapsack problem, Minimum cost spanning trees, Single source shortest path problem.

UNIT - V Branch and Bound: General method, applications - Travelling sales person problem, 0/1 knapsack problem - LC Branch and Bound solution, FIFO Branch and Bound solution. NP-Hard and NP-Complete problems: Basic concepts, non deterministic algorithms, NP - Hard and NP-Complete classes, Cook’s theorem. TEXT BOOKS 1. Fundamentals of Computer Algorithms, Ellis Horowitz, Satraj Sahni and Rajasekharan,3rd Edition University Press.

REFERENCES  Design and Analysis of Algorithms, Aho, Ullman and, Pearson education.  Introduction to Algorithms, second edition, T.H. Coremen, C.E Leiserson, R.L.Rivest and C. Stien, PHI Pvt . Ltd./Pearson Education.  Algorithm Design; Foundations, Analysis and Internet Examples, M.T. Goodrich and R. Tamassia, John Wiley and sons.

INTRODUCTION The word algorithm comes from the name of the person author -Abu Jafar Mohammed Ibn Musa Al khowarizmi who wrote A text book entitled-”Algorithmi de numero indorum” Now term” Algorithmi ”in the title of the book led to the term Algorithm. An algorithm is an effective method for finding out the solution for a given problem. It is a sequence of instruction That conveys the method to address a problem Algorithm : Step by step procedure to solve a computational problem is called Algorithm. or An Algorithm is a step-by-step plan for a computational procedure that possibly begins with an input and yields an output value in a finite number of steps in order to solve a particular problem.

INTRODUCTION  An algorithm is a set of steps of operations to solve a problem performing calculation, data processing, and automated reasoning tasks.  An algorithm is an efficient method that can be expressed within finite amount of Time and space.  The important aspects of algorithm design include creating an efficient algorithm to solve a problem in an efficient way using minimum time and space.  To solve a problem, different approaches can be followed. Some of them can be efficient with respect to time consumption, whereas other approaches may be memory efficient.

PROPERTIES OF ALGORITHM TO EVALUATE AN ALGORITHM WE HAVE TO SATISFY THE FOLLOWING CRITERIA: 1.INPUT: The Algorithm should be given zero or more input. 2.OUTPUT: At least one quantity is produced. For each input the algorithm produced value from specific task. 3.DEFINITENESS: Each instruction is clear and unambiguous. 4.FINITENESS: If we trace out the instructions of an algorithm, then for all cases, the algorithm terminates after a finite number of steps. 5.EFFECTIVENESS: Every instruction must very basic so that it can be carried out, in principle, by a person using only pencil & paper.

ALGORITHM (CONTD…)  A well-defined computational procedure that takes some value, or set of values, as input and produces some value, or set of values, as output.  Written in a pseudo code which can be implemented in the language of programmer’s choice. PSEUDO CODE: A notation resembling a simplified programming language, used in program design.

How To Write an Algorithm Step-1:start Step-1: start Step-2:Read a,b,c Step-2: Read a,b,c Step-3:if a>b Step-3:if a>b then go to step 4 if a>c otherwise go to step 5 print a is largest Step-4:if a>c then else print a is largest otherwise if b>c print c is largest print b is largest Step-5: if b>c then else print b is largest otherwise print c is largest print c is largest Step-4 : stop step-6: stop

Differences Algorithm Program 1.At design phase 1.At Implementation phase 2.Natural language 2.written in any programming language 3.Person should have 3.Programmer Domain knowledge 4.Analyze 4.Testing

Algorithm can be described (Represent) in four ways. 1.Natural language like English: When this way is chooses, care should be taken, we should ensure that each & every statement is definite. (no ambiguity) 2. Graphic representation called flowchart: This method will work well when the algorithm is small& simple. 3. Pseudo-code Method: In this method, we should typically describe algorithms as program, which resembles language like Pascal & Algol(Algorithmic Language). 4.Programming Language: we have to use programming language to write algorithms like C, C++,JAVA etc. ALGORITHM SPECIFICATION

PSEUDO-CODE CONVENTIONS 1. Comments begin with // and continue until the end of line. 2. Blocks are indicated with matching braces { and }. 3. An identifier begins with a letter. The data types of variables are not explicitly declared. node= record { data type 1 data 1; data type n data n; node *link; } 4. There are two Boolean values TRUE and FALSE. Logical Operators AND, OR, NOT Relational Operators <, <=,>,>=, =, !=

5. Assignment of values to variables is done using the assignment statement. <Variable>:= <expression>; 6. Compound data types can be formed with records. Here is an example, Node. Record { data type – 1 data-1; . . . data type – n data – n; node * link; } Here link is a pointer to the record type node. Individual data items of a record can be accessed with  and period.

Contd… 7. The following looping statements are employed. For, while and repeat-until While Loop: While < condition > do { <statement-1> .. .. <statement-n> } For Loop: For variable: = value-1 to value-2 step step do { <statement-1> . . . <statement-n> }

repeat-until: repeat <statement-1> . . . <statement-n> until<condition> 8. A conditional statement has the following forms.  If <condition> then <statement>  If <condition> then <statement-1> Else <statement-1>

Case statement: Case { : <condition-1> : <statement-1> . . . : <condition-n> : <statement-n> : else : <statement-n+1> } 9. Input and output are done using the instructions read & write. No format is used to specify the size of input or output quantities

10. There is only one type of procedure: Algorithm, the heading takes the form, Algorithm Name (Parameter lists) consider an example, the following algorithm fields & returns the maximum of n given numbers: 1. algorithm Max(A,n) 2. // A is an array of size n 3. { 4. Result := A[1]; 5. for i:= 2 to n do 6. if A[i] > Result then 7. Result :=A[i]; 8. return Result; 9. } Contd…

Issue in the study of algorithm 1. How to create an algorithm. 2. How to validate an algorithm. 3. How to analyses an algorithm 4. How to test a program. 1 .How to create an algorithm: To create an algorithm we have following design technique a) Divide & Conquer b) Greedy method c) Dynamic Programming d) Branch & Bound e) Backtracking

2.How to validate an algorithm: Once an algorithm is created it is necessary to show that it computes the correct output for all possible legal input , this process is called algorithm validation. 3.How to analyses an algorithm: Analysis of an algorithm or performance analysis refers to task of determining how much computing Time & storage algorithms required. a) Computing time-Time complexity: Frequency or Step count method b) Storage space- To calculate space complexity we have to use number of input used in algorithms. 4.How to test the program: Program is nothing but an expression for the algorithm using any programming language. To test a program we need following a) Debugging: It is processes of executing programs on sample data sets to determine whether faulty results occur & if so correct them. b) Profiling or performance measurement is the process of executing a correct program on data set and measuring the time & space it takes to compute the result.

ANALYSIS OF ALGORITHM PRIORI POSTERIORI 1.Done priori to run algorithm 1.Analysis after running on a specific system it on system. 2.Hardware independent 2.Dependent on hardware 3.Approximate analysis 3.Actual statistics of an algorithm 4.Dependent on no of time 4.They do not do posteriori statements are executed analysis

Problem: Suppose there are 60 students in the class. How will you calculate the number of absentees in the class? Pseudo Approach 1.Initialize a variable called as Count to zero, absent to zero, total to 60 2.FOR EACH Student PRESENT DO the following: Increase the Count by One 3.Then Subtract Count from total and store the result in absent 4.Display the number of absent students

Problem: Suppose there are 60 students in the class. How will you calculate the number of absentees in the class? Algorithmic Approach: 1.Count <- 0, absent <- 0, total <- 60 2.REPEAT till all students counted Count <- Count + 1 3.absent <- total - Count 4.Print "Number absent is:" , absent

Need of Algorithm 1. To understand the basic idea of the problem. 2. To find an approach to solve the problem. 3. To improve the efficiency of existing techniques. 4. To understand the basic principles of designing the algorithms. To compare the performance of the algorithm with respect to other techniques. 6. It is the best method of description without describing the implementation detail. 7. The Algorithm gives a clear description of requirements and goal of the problem to the designer. 8. A good design can produce a good solution. 9. To understand the flow of the problem.

PERFORMANCE ANALYSIS Performance Analysis: An algorithm is said to be efficient and fast if it take less time to execute and consumes less memory space at run time is called Performance Analysis. 1. SPACE COMPLEXITY: The space complexity of an algorithm is the amount of Memory Space required by an algorithm during course of execution is called space complexity .There are three types of space a) Instruction space :executable program b) Data space: Required to store all the constant and variable data space. c) Environment: It is required to store environment information needed to resume the suspended space. 2. TIME COMPLEXITY: The time complexity of an algorithm is the total amount of time required by an algorithm to complete its execution.

Space complexity Now there are two types of space complexity a) Constant space complexity b) Linear(variable)space complexity

1.Constant space complexity: A fixed amount of space for all the input values. Example : int square(int a) { return a*a; } Here algorithm requires fixed amount of space for all the input values.

2.Linear space complexity: The space needed for algorithm is based on size. Size of the variable ‘n’ = 1 word Array of a values = n word Loop variable = 1 word Sum variable = 1 word Example: int sum(int A[],int n) { n int sum=0,i; 1 for (i=0;i<n;i++) 1 Sum=sum+A[i]; 1 Return sum; } Ans : 1+n+1+1 = n+3 words

Examples: 1.Algorithm sum(a,,b,c) { a=10; a-1 b=20; b-1 c=a+b; c-1 } s(p)=c+sp 3+0=3 0(n)=3

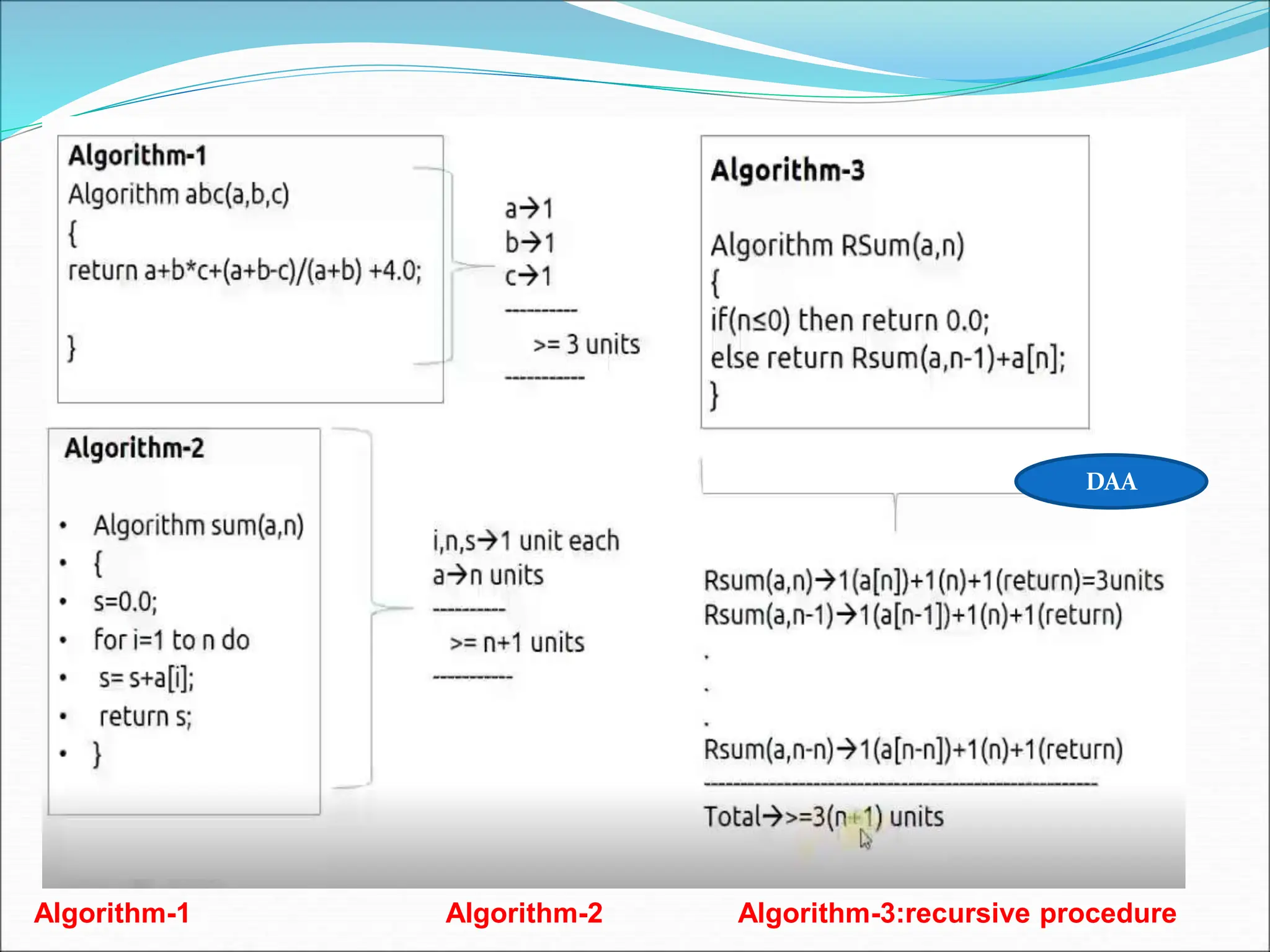
2. algorithm sum(a,n) { total-=0; - 1 Fori=1 to n do -1,1 Total=total+a[i]--n Return total

DAA Algorithm-1 Algorithm-2 Algorithm-3:recursive procedure

1.Constant time complexity : If a program required fixed amount of time for all input values is called Constant time complexity . Example : int sum(int a , int b) { return a+b; }

2.Linear time complexity: If the input values are increased then the time complexity will changes.  comments = 0 step Assignment statement= 1 step condition statement= 1 step  loop condition for n times = n+1 steps  body of the loop = n steps

Example : int sum(int A[],int n) { int sum=0,i; for (i=0;i<n;i++) sum=sum+A[i]; return sum; cost repetation total 1 1 1 1+1+1 1+(n+1)+n 2n+2 2 n 2n 1 1 1 4n+4

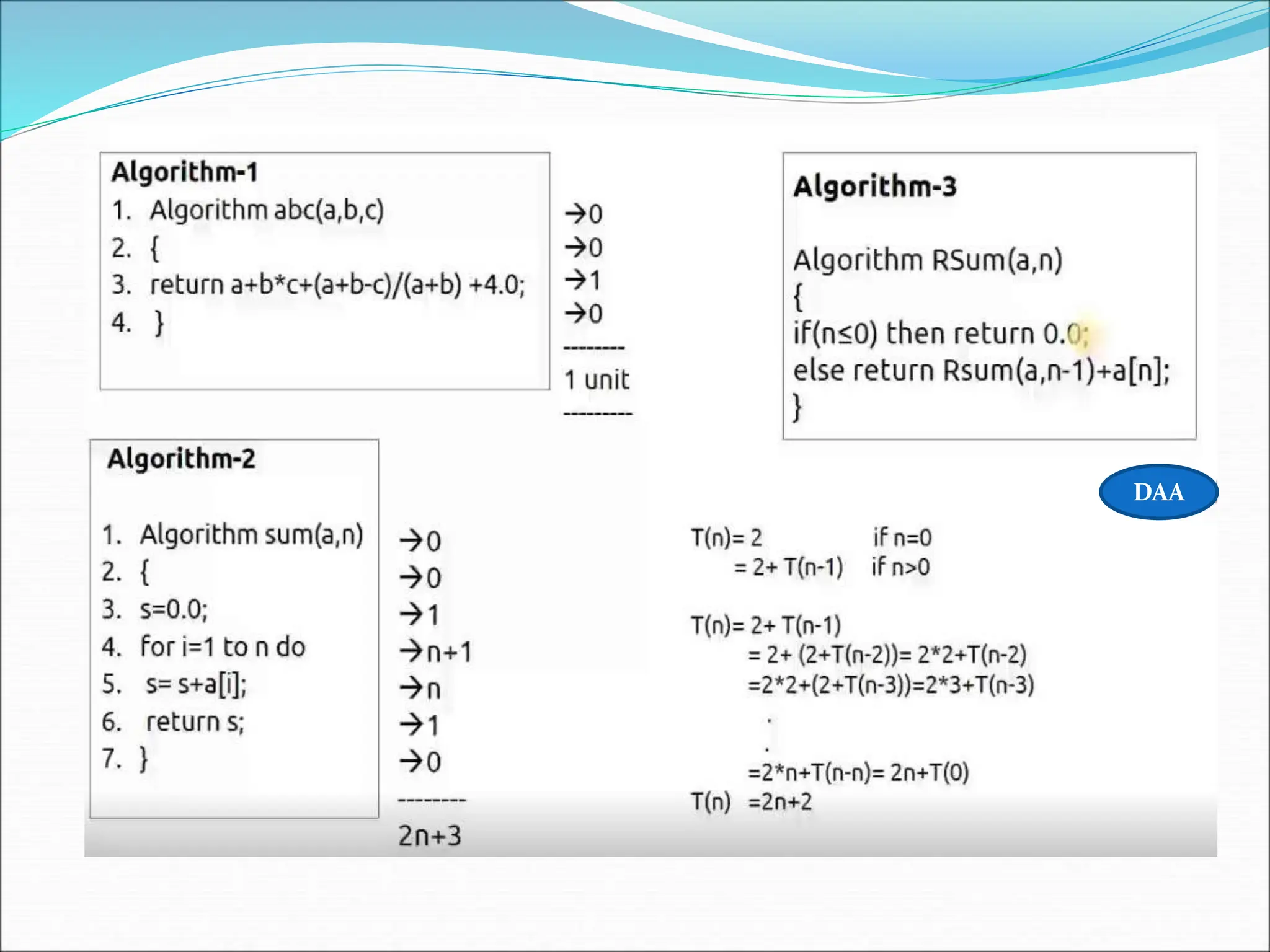
Statement S/e Frequency Total 1. Algorithm Sum(a,n) 0 - 0 2.{ 0 - 0 3. S=0.0; 1 1 1 4. for i=1 to n do 1 n+1 n+1 5. s=s+a[I]; 1 n n 6. return s; 1 1 1 7. } 0 - 0 Total 2n+3 The time T(p) taken by a program P is the sum of the compile time and the run time(execution time) TIME COMPLEXITY

KINDS OF ANALYSIS 1.Worst-case: (usually) • T(n) = maximum time of algorithm on any input of size n. 2.Average-case: (sometimes) • T(n) = expected time of algorithm over all inputs of size n. • Need assumption of statistical distribution of inputs. 3.Best-case: • T(n) = minimum time of algorithm on any input of size n. COMPLEXITY: Complexity refers to the rate at which the storage time grows as a function of the problem size

Analysis of an Algorithm The goal of analysis of an algorithm is to compare algorithm in running time and also Memory management. Running time of an algorithm depends on how long it takes a computer to run the lines of code of the algorithm. Running time of an algorithm depends on 1.Speed of computer 2.Programming language 3.Compiler and translator Examples: binary search, linear search

ASYMPTOTIC ANALYSIS:  Expressing the complexity in term of its relationship to know function. This type analysis is called asymptotic analysis. The main idea of Asymptotic analysis is to have a measure of efficiency of an algorithm , that doesn’t depends on 1.Machine constants. 2.Doesn’t require algorithm to be implemented. 3.Time taken by program to be prepare.

ASYMPTOTIC NOTATION ASYMPTOTIC NOTATION: The mathematical way of representing the Time complexity. The notation we use to describe the asymptotic running time of an algorithm are defined in terms of functions whose domains are the set of natural numbers. Definition : It is the way to describe the behavior of functions in the limit or without bounds. Asymptotic growth: The rate at which the function grows… “growth rate” is the complexity of the function or the amount of resource it takes up to compute. Growth rate Time +memory

Classification of growth 1.Growing with the same rate. 2. Growing with the slower rate. 3.Growing with the faster rate.

They are 3 asymptotic notations are mostly used to represent time complexity of algorithm. 1.Big oh (O)notation 2.Big omega (Ω) notation 3.Theta(Θ) notation 4.Little oh notation 5.Little omega(Ω) notation

1.Big oh (O)notation 1.Big oh (O)notation : Asymptotic “less than”(slower rate).This notation mainly represent upper bound of algorithm run time. Big oh (O)notation is useful to calculate maximum amount of time of execution. By using Big-oh notation we have to calculate worst case time complexity. Formula : f(n)<=c g(n) n>=n0 , c>0 ,n0 >=1 Definition: Let f(n) ,g(n) be two non negative (positive) function now the f(n)=O(g(n)) if there exist two positive constant c,n0 such that f(n)<= c.g(n) for all value of n>0 & c>0

1.Big O-notation  For a given function , we denote by the set of functions  We use O-notation to give an asymptotic upper bound of a function, to within a constant factor.  means that there existes some constant c s.t. is always for large enough n. ) (n g )) ( ( n g O           0 0 all for ) ( ) ( 0 s.t. and constants positive exist there : ) ( )) ( ( n n n cg n f n c n f n g O )) ( ( ) ( n g O n f  ) (n cg  ) (n f

Examples Example : f(n)=2n +3 & g(n)= n Formula : f(n)<=c g(n) n>=n0 , c>0 ,n0 >=1 f(n)=2n+3 & g(n)=n Now 3n+2<=c.n 3n+2<=4.n Put the value of n =1 5<=4 false N=2 8<=8 true now n0>2 For all value of n>2 & c=4 now f(n)<= c.g(n) 3n+2<=4n for all value of n>2 Above condition is satisfied this notation takes maximum amount of time to execute .so that it is called worst case complexity.

2.Ω-Omega notation Ω-Omega notation : Asymptotic “greater than”(faster rate). It represent Lower bound of algorithm run time. By using Big Omega notation we can calculate minimum amount of time. We can say that it is best case time complexity. Formula : f(n)>=c g(n) n>=n0 , c>0 ,n0 >=1 where c is constant, n is function Lower bound Best case

Ω-Omega notation  For a given function , we denote by the set of functions  We use Ω-notation to give an asymptotic lower bound on a function, to within a constant factor.  means that there exists some constant c s.t. is always for large enough n. ) (n g )) ( ( n g             0 0 all for ) ( ) ( 0 s.t. and constants positive exist there : ) ( )) ( ( n n n f n cg n c n f n g )) ( ( ) ( n g n f   ) (n f ) (n cg 

Examples Example : f(n)=3n +2 Formula : f(n)>=c g(n) n>=n0 , c>0 ,n0 >=1 f(n)=3n+2 3n+2>=1*n, c=1 put the value of n=1 n=1 5>=1 true n0>=1 for all value of n It means that f(n)= Ω g(n).

3. -Theta notation Theta (Θ) notation : Asymptotic “Equality”(same rate). It represent average bond of algorithm running time. By using theta notation we can calculate average amount of time. So it called average case time complexity of algorithm. Formula : c1 g(n)<=f(n)<=c2 g(n) where c is constant, n is function Average bound 

-Theta notation  For a given function , we denote by the set of functions  A function belongs to the set if there exist positive constants and such that it can be “sand- wiched” between and or sufficienly large n.  means that there exists some constant c1 and c2 s.t. for large enough n. ) (n g )) ( ( n g              0 2 1 0 2 1 all for ) ( ) ( ) ( c 0 s.t. and , , constants positive exist there : ) ( )) ( ( n n n g c n f n g n c c n f n g ) (n f )) ( ( n g  1 c 2 c ) ( 1 n g c ) ( 2 n g c Θ )) ( ( ) ( n g n f   ) ( ) ( ) ( 2 1 n g c n f n g c  

Examples Example : f(n)=3n+2 Formula : c1 g(n)<=f(n)<=c2 g(n) f(n)=2n+3 1*n<=3n+2<=4*n now put the value of n=1 we get 1<=5<=4 false n=2 we get 2<=8<=8 true n=3 we get 3<=11<=12 true Now all value of n>=2 it is true above condition is satisfied.

4.Little oh notation  Little o notation is used to describe an upper bound that cannot be tight. In other words, loose upper bound of f(n). Slower growth rate f(n) grows slower than g(n)  Let f(n) and g(n) are the functions that map positive real numbers. We can say that the function f(n) is o(g(n)) if for any real positive constant c, there exists an integer constant n0 ≤ 1 such that f(n) > 0.

Using mathematical relation, we can say that f(n) = o(g(n)) means, if Example on little o asymptotic notation: 1.If f(n) = n2 and g(n) = n3 then check whether f(n) = o(g(n)) or not.

The result is 0, and it satisfies the equation mentioned above. So we can say that f(n) = o(g(n)). Sol:

5.Little omega(ω) notation  Another asymptotic notation is little omega notation. it is denoted by (ω).  Little omega (ω) notation is used to describe a loose lower bound of f(n).  Faster growth rate  F(n) grows faster than g(n) ∞  If ∞ Formally stated as f(n)=ωg(n)

Example of asymptotic notation Problem:-Find upper bond ,lower bond & tight bond range for functions: f(n)= 2n+5 Solution:-Let us given that f(n)= 2n+5 , now g(n)= n lower bond=2n, upper bond =3n, tight bond=2n For Big –oh notation(O):- according to definition f(n)<=cg(n) for Big oh we use upper bond so f(n)=2n+5, g(n)=n and c=3 according to definition 2n+5<=3n Put n=1 7<=3 false Put n=2 9<=6 false Put n=3 14<=9 false Put n=4 13<=12 false Put n=5 15<=15 true now for all value of n>=5 above condition is satisfied. C=3 n>=5

2. Big - omega notation :- f(n)>=c.g(n) we know that this Notation is lower bond notation so c=2 Let f(n)=2n+5 & g(n)=2.n Now 2n+5>=c.g(n); 2n+5>=2n put n=1 We get 7>=2 true for all value of n>=1,c=2 condition is satisfied. 3. Theta notation :- according to definition c1.g(n)<=f(n)<=c2.g

ANALYSIS OF INSERTION-SORT(CONTD.) •The worst case: The array is reverse sorted (tj =j for j=2,3, ...,n). ) 1 2 / ) 1 ( ( ) 1 ( ) ( 5 2 1       n n c n c n c n T ) 1 ( ) 2 / ) 1 ( ( ) 2 / ) 1 ( ( 8 7 6       n c n n c n n c n c c c c c c c n c c c ) 2 / 2 / 2 / ( ) 2 / 2 / 2 / ( 8 7 6 5 4 2 1 2 7 6 5           2 ) 1 ( 1     n n j n j c bn an n T    2 ) (

 A randomized algorithm is an algorithm that employs a degree of randomness as part of its logic.  The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random bits.  An algorithm that uses random numbers to decide what to do next anywhere in its logic is called Randomized Algorithm..  Example: Quick sort RANDOMIZED ALGORITHMS

Select: pick an arbitrary element x in S to be the pivot. Partition: rearrange elements so that elements with value less than x go to List L to the left of x and elements with value greater than x go to the List R to the right of x. Recursion: recursively sort the lists L and R. QUICK SORT

DIVIDE AND CONQUER  Given a function to compute on ‘n’ inputs the divide-and-conquer strategy suggests splitting the inputs into ‘k’ distinct subsets, 1<k<=n, yielding ‘k’ sub problems.  These sub problems must be solved, and then a method must be found to combine sub solutions into a solution of the whole.  If the sub problems are still relatively large, then the divide-and- conquer strategy can possibly be reapplied.

 If the problem p and the size is n , sub problems are n1, n2 ….nk, respectively, then the computing time of D And C is described by the recurrence relation.  T(n)= { g(n) n small  T(n1)+T(n2)+……………+T(nk)+f(n);  otherwise. “Where T(n) is the time for D And C on any I/p of size n.  g(n) is the time of compute the answer directly for small I/p s. f(n) is the time for dividing P & combining the solution to sub problems.

DIVIDE AND CONQUER :GENERAL METHOD 1. Algorithm D And C(P) 2. { 3. if small(P) then return S(P); 4. else 5. { 6. divide P into smaller instances 7. P1, P2… Pk, k>=1; 8. Apply D And C to each of these sub problems; 9. return combine (D And C(P1), D And C(P2),…….,D And C(Pk)); 10. } 11. }

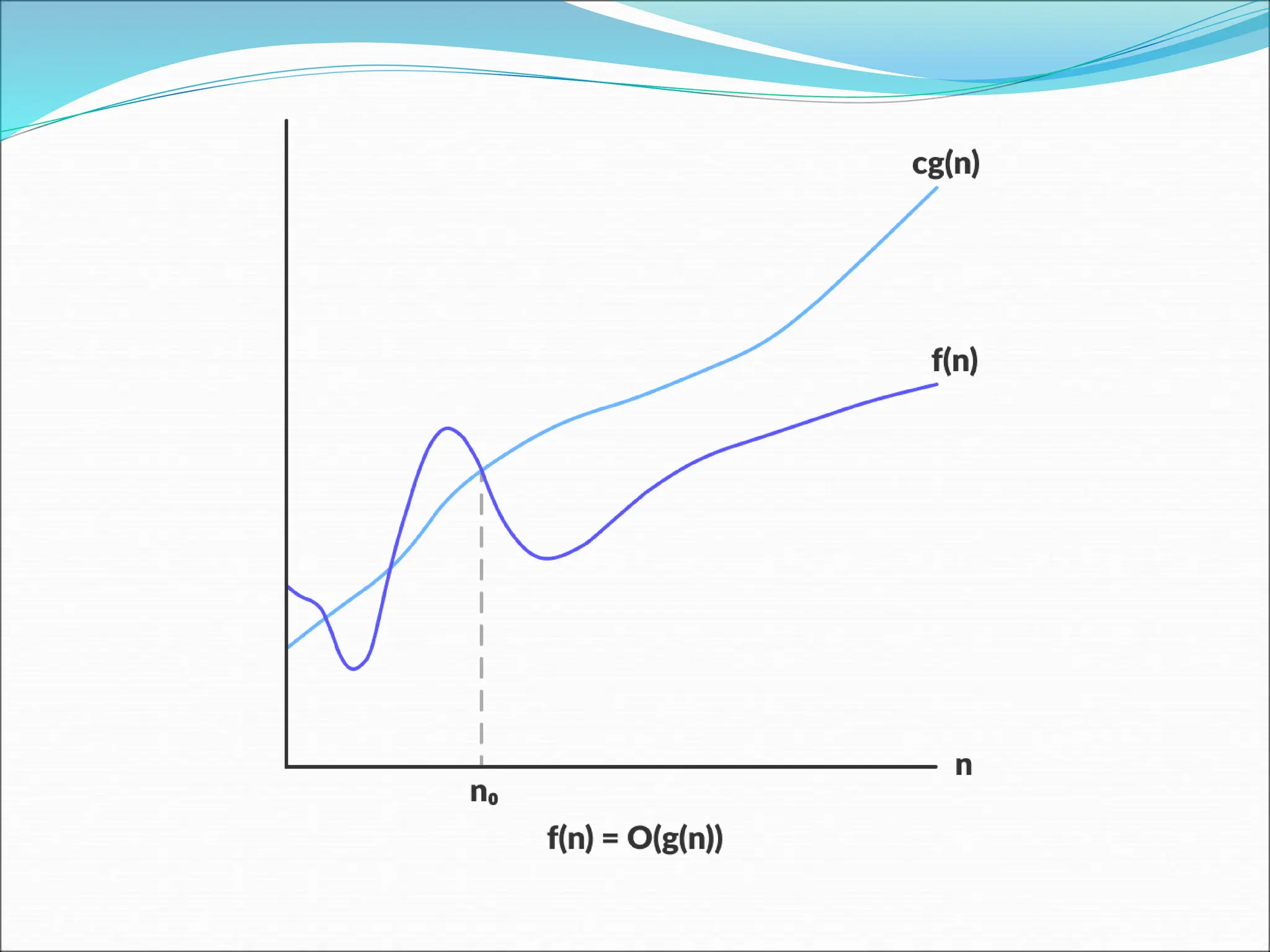
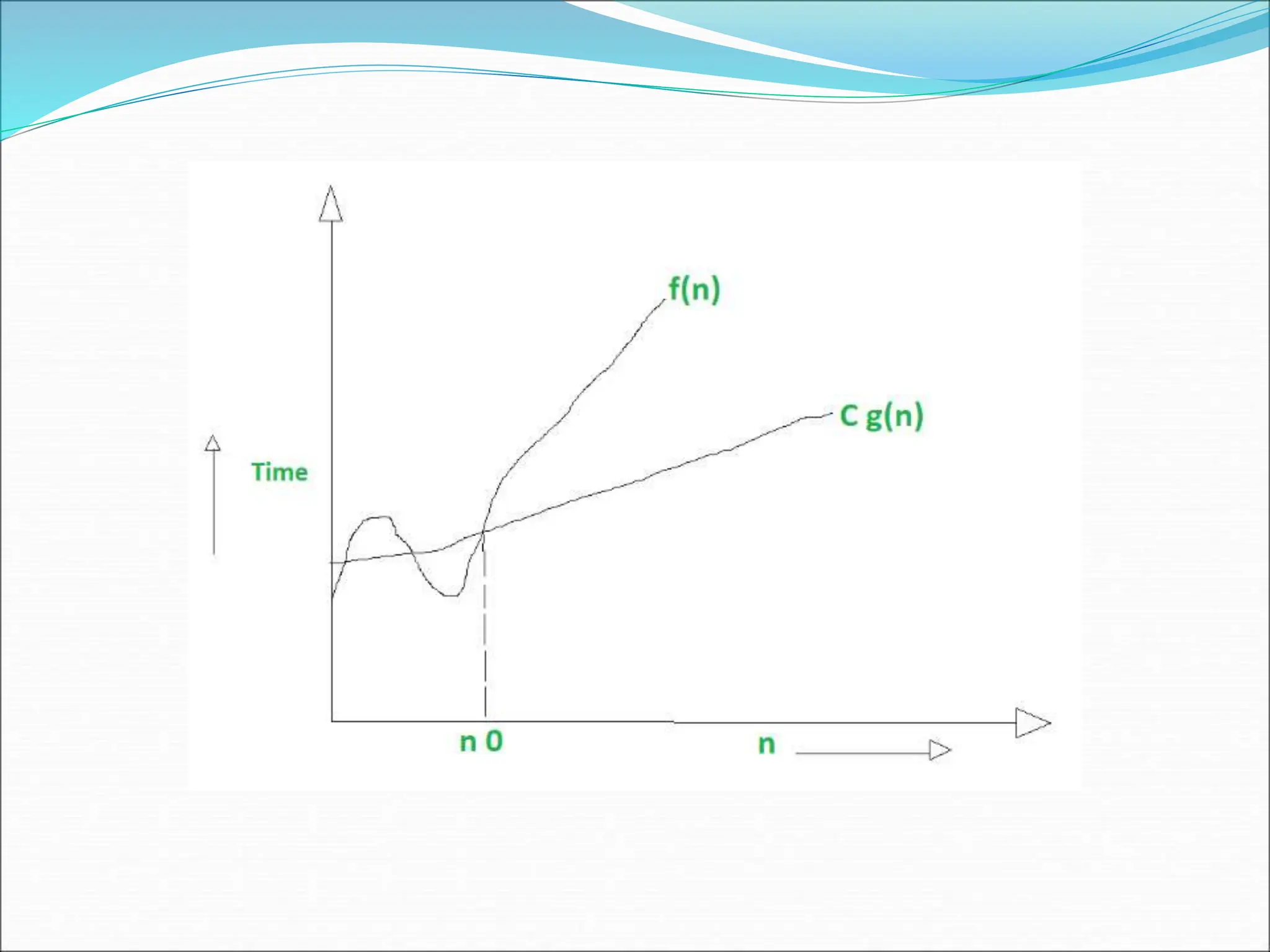
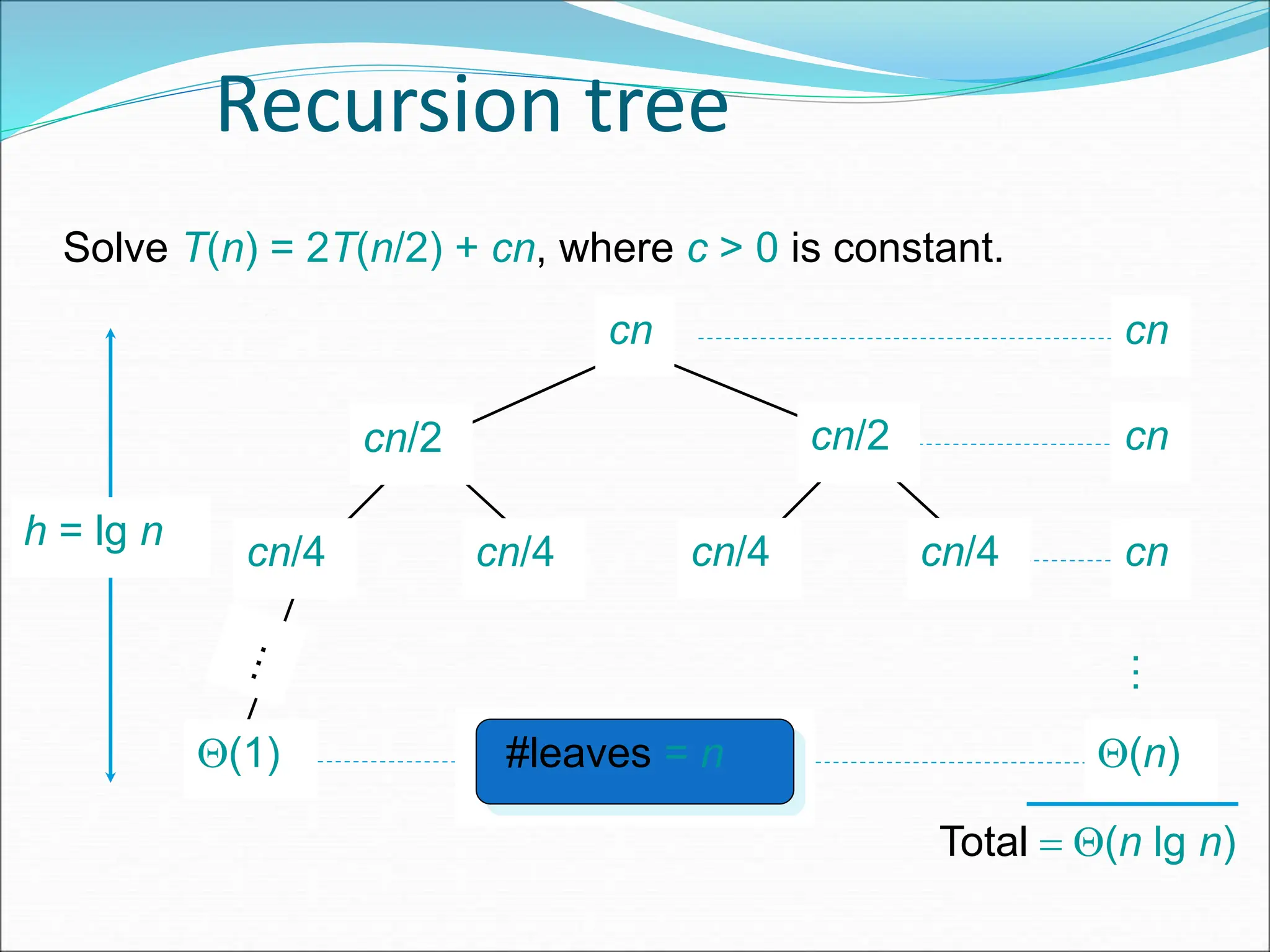
EXAMPLE Consider the case in which a=2 and b=2. Let T(1)=2 & f(n)=n. We have, T(n) = 2T(n/2)+n 2[2T(n/2/2)+n/2]+n [4T(n/4)+n]+n 4T(n/4)+2n 4[2T(n/4/2)+n/4]+2n 4[2T(n/8)+n/4]+2n 8T(n/8)+n+2n 8T(n/8)+3n

23T(n/23)+3n By using substitution method Let n=2k K=logn 2 K=3 2kT(n/n)+3n nT(1)+3N 2n+kn 2n+nlogn Time complexity is O(nlogn)

APPLICATIONS 1. Binary Search is a searching algorithm. In each step, the algorithm compares the input element x with the value of the middle element in array. If the values match, return the index of middle. Otherwise, if x is less than the middle element, then the algorithm recurs for left side of middle element, else recurs for right side of middle element.

2.Quick sort is a sorting algorithm. The algorithm picks a pivot element, rearranges the array elements in such a way that all elements smaller than the picked pivot element move to left side of pivot, and all greater elements move to right side. Finally, the algorithm recursively sorts the sub arrays on left and right of pivot element. 3.Merge Sort is also a sorting algorithm. The algorithm divides the array in two halves, recursively sorts them and finally merges the two sorted halves.

1. Algorithm Bin search(a,n,x) 2. // Given an array a[1:n] of elements in non-decreasing 3. //order, n>=0,determine whether x is present and 4. // if so, return j such that x=a[j]; else return 0. 5. { 6. low:=1; high:=n; 7. while (low<=high) do 8. { 9. mid:=[(low+high)/2]; 10. if (x<a[mid]) then high; 11. else if(x>a[mid]) then 12. low=mid+1; 13. else return mid; 14. } 15. return 0; } BINARY SEARCH

EXAMPLE 1) Let us select the 14 entries. –15,6,0,7,9,23,54,82,101,112,125,131,142,151. Place them in a[1:14] and simulate the steps Binsearch goes through as it searches for different values of x. Only the variables low, high & mid need to be traced as we simulate the algorithm. We try the following values for x: 151, -14 and 9. for 2 successful searches & 1 unsuccessful search.

X=151 low high mid 1 14 7 8 14 11 12 14 13 14 14 14 Found x=-14 low high mid 1 14 7 1 6 3 1 2 1 2 2 2 2 1 Not found x=9 low high mid 1 14 7 1 6 3 4 6 5 Found Table. Shows the traces of Bin search on these 3 steps.

 Another application of Divide and conquer is merge sort.  Given a sequence of n elements a[1],…,a[n] the general idea is to imagine then split into 2 sets a[1],…..,a[n/2] and a[[n/2]+1],….a[n].  Each set is individually sorted, and the resulting sorted sequences are merged to produce a single sorted sequence of n elements.  Thus, we have another ideal example of the divide-and-conquer strategy in which the splitting is into 2 equal-sized sets & the combining operation is the merging of 2 sorted sets into one. MERGE SORT

ALGORITHM FOR MERGE SORT  Algorithm MergeSort(low,high)  //a[low:high] is a global array to be sorted  //Small(P) is true if there is only one element  //to sort. In this case the list is already sorted.  {  if (low<high) then //if there are more than one element  {  //Divide P into subproblems  //find where to split the set  mid = [(low+high)/2];  //solve the subproblems.  mergesort (low,mid);  mergesort(mid+1,high); //combine the solutions .  merge(low,mid,high);  }  }

Algorithm: Merging 2 sorted subarrays using auxiliary storage. 1. Algorithm merge(low,mid,high) 2. /*a[low:high] is a global array containing two sorted subsets in a[low:mid] and in a[mid+1:high].The goal is to merge these 2 sets into a single set residing in a[low:high].b[] is an auxiliary global array. */ 3. { 4. h=low; I=low; j=mid+1; 5. while ((h<=mid) and (j<=high)) do { 6. if (a[h]<=a[j]) then { 7. b[I]=a[h]; 8. h = h+1; } 9. else { 10.b[I]= a[j]; 11.j=j+1; } 12.I=I+1; } 13.if (h>mid) then 14.for k=j to high do { 15.b[I]=a[k]; 16.I=I+1; 17.} 18.else 19.for k=h to mid do 20.{ 21.b[I]=a[k]; 22.I=I+1; } 23.for k=low to high do a[k] = b[k]; }

 Consider the array of 10 elements a[1:10] =(310, 285, 179, 652, 351, 423, 861, 254, 450, 520) Algorithm Mergesort begins by splitting a[] into 2 sub arrays each of size five (a[1:5] and a[6:10]).  The elements in a[1:5] are then split into 2 sub arrays of size 3 (a[1:3] ) and 2(a[4:5])  Then the items in a [1:3] are split into sub arrays of size 2 a[1:2] & one(a[3:3])  The 2 values in a[1:2] are split to find time into one-element sub arrays and now the merging begins. EXAMPLE

Recursion tree Solve T(n) = 2T(n/2) + cn, where c > 0 is constant. cn cn/4 cn/4 cn/4 cn/4 cn/2 cn/2 (1) h = lg n cn cn cn #leaves = n (n) Total  (n lg n) …

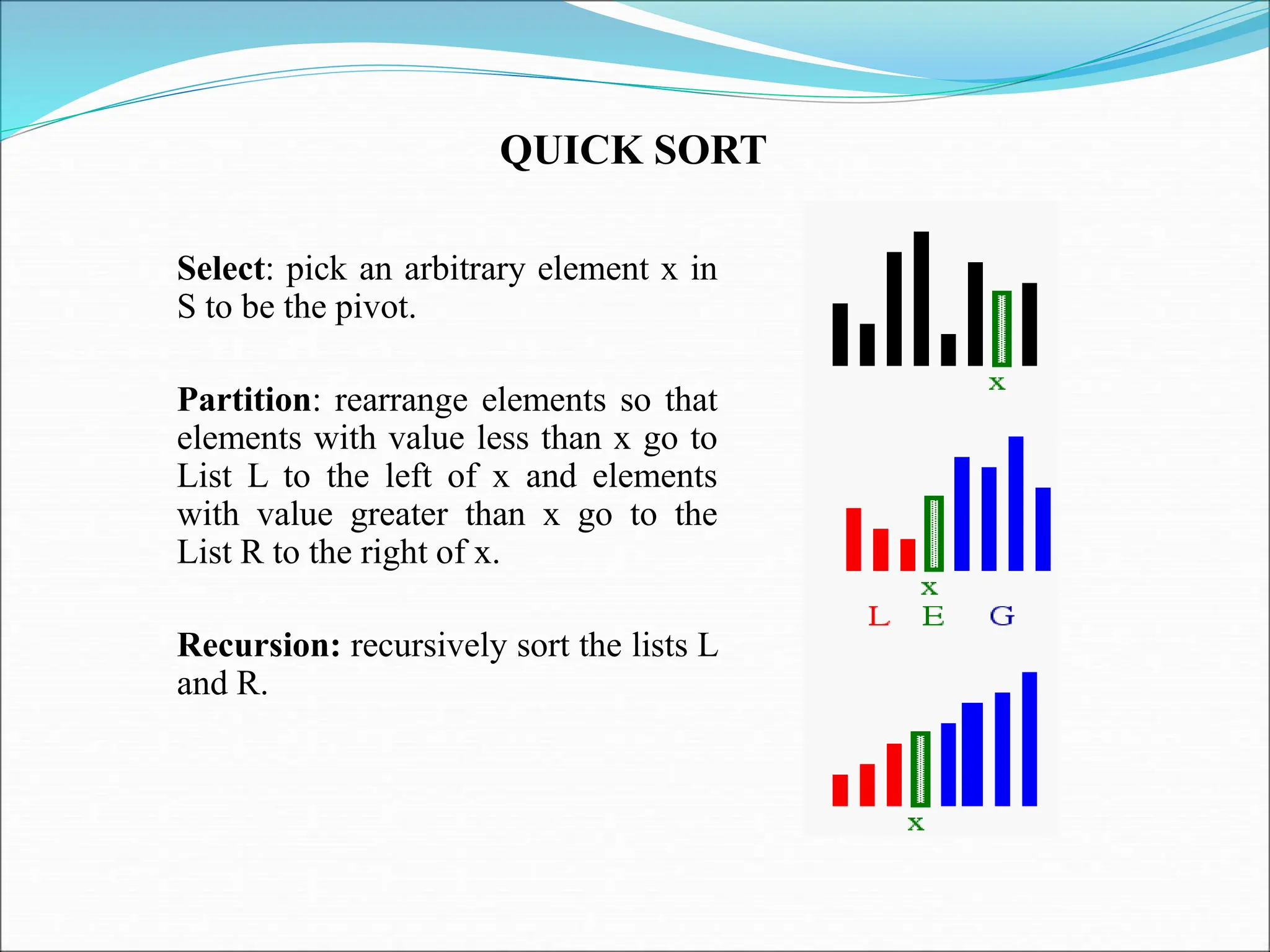
 In Quick sort, the division into 2 sub arrays is made so that the sorted sub arrays do not need to be merged later.  This is accomplished by rearranging the elements in a[1:n] such that a[I]<=a[j] for all I between 1 & n and all j between (m+1) & n for some m, 1<=m<=n.  Thus the elements in a[1:m] & a[m+1:n] can be independently sorted.  No merge is needed. This rearranging is referred to as partitioning. QUICK SORT

1. Algorithm: Partition the array a[m:p-1] about a[m] 2. Algorithm Partition(a,m,p) 3. /*within a[m],a[m+1],…..,a[p-1] the elements are rearranged in such a manner that if initially t=a[m],then after completion a[q]=t for some q between m and 4. p-1,a[k]<=t for m<=k<q, and a[k]>=t for q<k<p. q is returned Set a[p]=infinite. */ 5. { 6. v=a[m];I=m;j=p; 7. repeat 8. { 9. repeat 10. I=I+1; 11. until(a[I]>=v); 12. repeat 13. j=j-1; 14. until(a[j]<=v); 15. if (I<j) then interchange(a,i.j); 16. }until(I>=j); 17. a[m]=a[j]; a[j]=v; 18. retun j; 19. } 20. Algorithm Interchange(a,I,j) //Exchange a[I] with a[j] 21. { 22. p=a[I]; 23. a[I]=a[j]; 24. a[j]=p; 25. }

 Algorithm: Sorting by Partitioning  Algorithm Quicksort(p,q)  //Sort the elements a[p],….a[q] which resides  //is the global array a[1:n] into ascending //order; a[n+1] is considered to be defined  // and must be >= all the elements in a[1:n]  {  if(p<q) then // If there are more than one element  {  // divide p into 2 subproblems  j=partition(a,p,q+1);  //‟j‟ is the position of the partitioning element.  //solve the subproblems.  quicksort(p,j-1);  quicksort(j+1,q);  //There is no need for combining solution.  }  }

1. www.mit.edu 2. www.soe.stanford.edu 3. www.grad.gatech.edu 4. www.gsas.harward.edu 5. www.eng.ufl.edu 6. www.iitk.ac.in 7. www.iitd.ernet.in 8. www.ieee.org 9. www.ntpel.com 10. WWW.JNTUWORLD.COM 11. www.firstrankers.com 12. www. studentgalaxi.blogspot.com WEBSITES

TEXT BOOKS 1. Fundamentals of Computer Algorithms, Ellis Horowitz,Satraj Sahni and Rajasekharam,Galgotia publications pvt. Ltd. 2. Algorithm Design: Foundations, Analysis and Internet examples, M.T.Goodrich and R.Tomassia,John wiley and sons. SUGGESTED BOOKS

1. Introduction to Algorithms, secondedition,T.H.Cormen,C.E.Leiserson, R.L.Rivest,and C.Stein,PHI Pvt. Ltd./ Pearson Education 2. Introduction to Design and Analysis of Algorithms A strategic approach, R.C.T.Lee, S.S.Tseng, R.C.Chang and T.Tsai, Mc Graw Hill. 3. Data structures and Algorithm Analysis in C++, Allen Weiss, Second edition, Pearson education. REFERENCES

Introduction to Design Algorithm And Analysis.ppt

More Related Content

What's hot

Similar to Introduction to Design Algorithm And Analysis.ppt

Recently uploaded

In this document

Introduction to Design Algorithm And Analysis.ppt