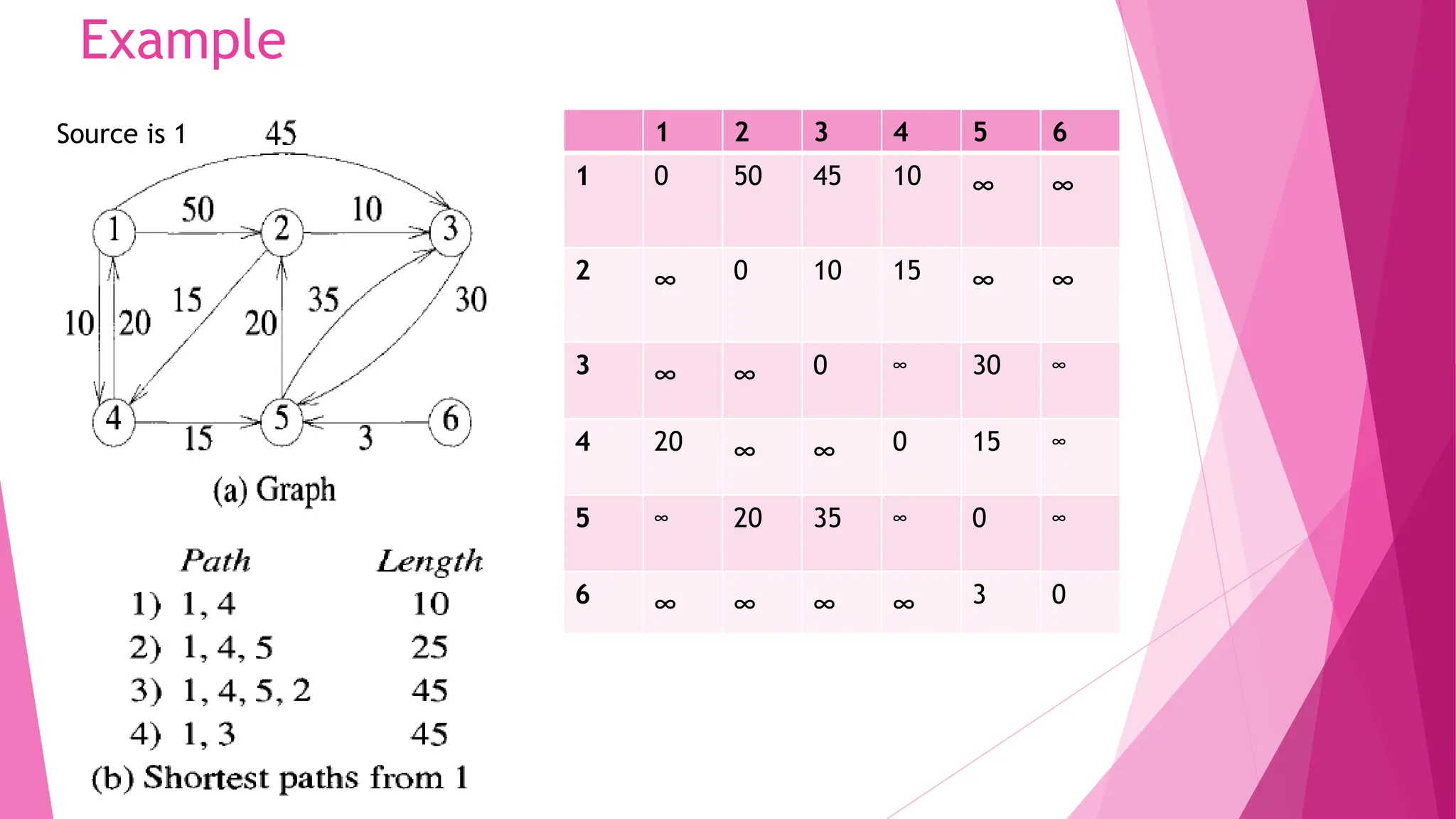
The document outlines various algorithm design techniques, including divide and conquer, greedy methods, and their applications to specific problems such as finding maximum and minimum values, the knapsack problem, job sequencing with deadlines, and the optimal merge pattern for files. It discusses the control abstraction of these techniques, recurrence relations for running time, and provides examples to illustrate how these algorithms can be implemented. Additionally, it covers the analysis of these algorithms in terms of computational efficiency and complexity.







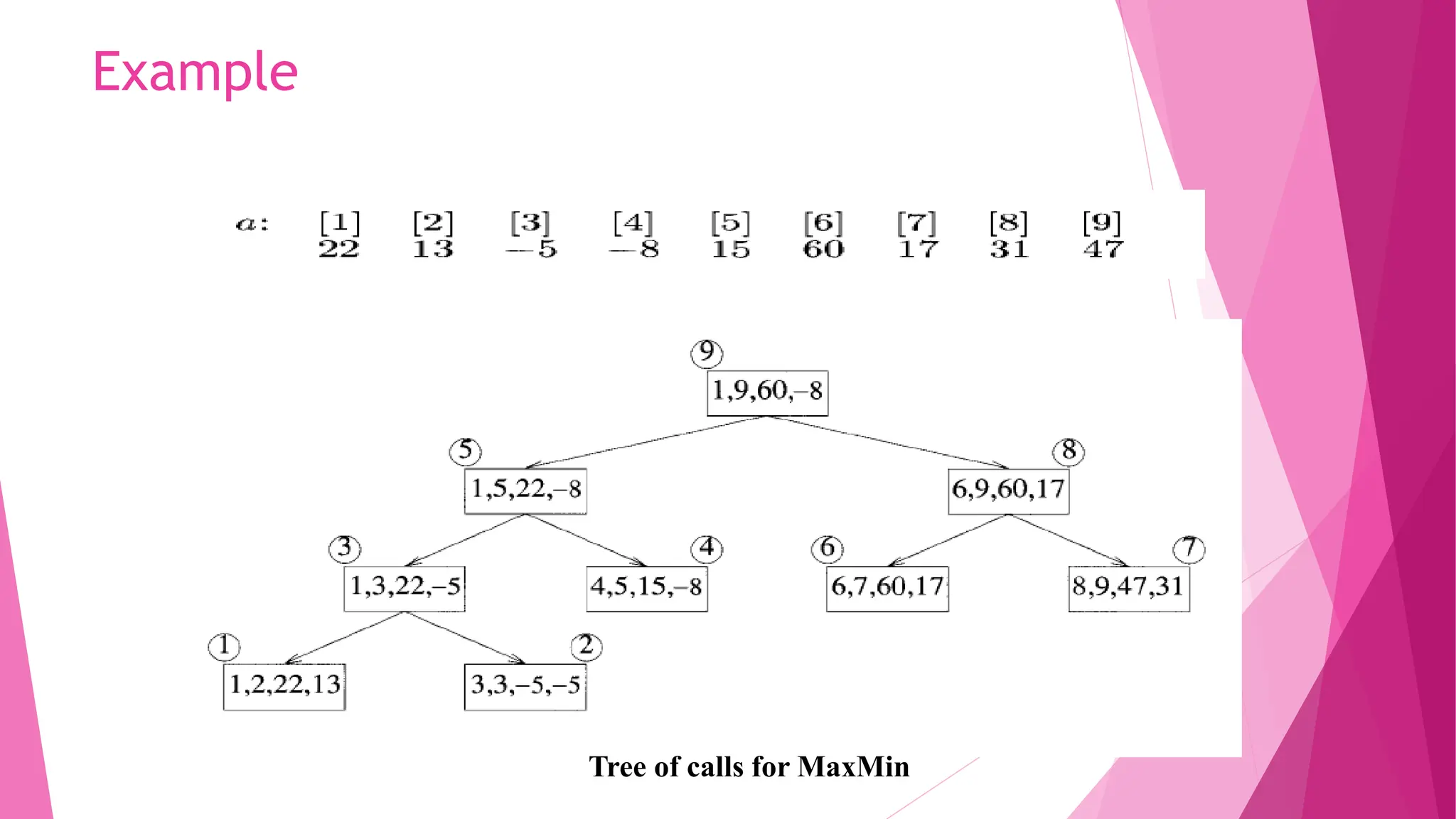
![Divide and Conquer Approach Let P = (n,a[i],...,a[j]) denote an arbitrary instance of the problem. Here n is the number of elements in the list a[i],...a[j]and we are interested in finding the maximum and minimum of this list. Let Small(P) be true when n <2. In this case, the maximum and minimum are a[i] if n = 1. If n = 2, the problem can be solved by making one comparison. If the list has more than two elements, P has to be divided into smaller instances. After having divided P into two smaller subproblems we can solve them by recursively invoking the same divide-and-conquer algorithm. When the maxima and minima of these subproblems are determined, the two maxima are compared and the two minima are compared to achieve the solution for the entire set.](https://image.slidesharecdn.com/algorithmdesigntechiquesi-240611063143-1148155f/75/Algorithm-Design-Techiques-divide-and-conquer-8-2048.jpg)

















![Algorithm Algorithm optimalMerge(files, n) { for i:=1 to n do{ for j:=i+1 to n do{ if (files[i] > files[j]) { temp = files[i]; files[i] = files[j]; files[j] = temp; } } } cost := 0; while (n > 1) { // Merge the smallest two files mergedFileSize = files[1] + files[2]; cost:= cost + mergedFileSize; // Replace the first file with the merged file size files[1]: = mergedFileSize; // Shift the remaining files to the left for i := 1 to n-1 do { files[i]:= files[i + 1]; } n--; // Reduce the number of files // Sort the files again for i:=1 to n do { for j:=i+1 to n do { if (files[i] > files[j]) { temp := files[i]; files[i] := files[j]; files[j] := temp; } } } } return cost; }](https://image.slidesharecdn.com/algorithmdesigntechiquesi-240611063143-1148155f/75/Algorithm-Design-Techiques-divide-and-conquer-27-2048.jpg)