Design and analysis of algorithm devide and conquer

Divide and Conquer Algorithm • Divide and Conquer Algorithm is a problem-solving technique used to solve problems by dividing the main problem into sub problems, solving them individually and then merging them to find solution to the original problem. • Working of Divide and Conquer Algorithm: • Divide and Conquer Algorithm can be divided into three steps: Divide, Conquer and Merge . • Divide and Conquer algorithm consists of a dispute using the following three steps. • Divide the original problem into a set of subproblems. • Conquer: Solve every subproblem individually, recursively. • Combine: Put together the solutions of the subproblems to get the solution to the whole problem.

• Divide: • Break down the original problem into smaller sub problems. • Each sub problem should represent a part of the overall problem. • The goal is to divide the problem until no further division is possible. • 2. Conquer: • Solve each of the smaller sub problems individually. • If a sub problem is small enough (often referred to as the “base case”), we solve it directly without further recursion. • The goal is to find solutions for these sub problems independently. • 3. Merge: • Combine the sub-problems to get the final solution of the whole problem. • Once the smaller sub problems are solved, we recursively combine their solutions to get the solution of larger problem. • The goal is to formulate a solution for the original problem by merging the results from the sub problems.

• Characteristics of Divide and Conquer Algorithm: • Divide and Conquer Algorithm involves breaking down a problem into smaller, more manageable parts, solving each part individually, and then combining the solutions to solve the original problem. The characteristics of Divide and Conquer Algorithm are: • Dividing the Problem: The first step is to break the problem into smaller, more manageable subproblems. This division can be done recursively until the subproblems become simple enough to solve directly. • Independence of Subproblems: Each subproblem should be independent of the others, meaning that solving one subproblem does not depend on the solution of another. This allows for parallel processing or concurrent execution of subproblems, which can lead to efficiency gains. • Conquering Each Subproblem: Once divided, the subproblems are solved individually. This may involve applying the same divide and conquer approach recursively until the subproblems become simple enough to solve directly, or it may involve applying a different algorithm or technique. • Combining Solutions: After solving the subproblems, their solutions are combined to obtain the solution to the original problem. This combination step should be relatively efficient and straightforward, as the solutions to the subproblems should be designed to fit together seamlessly.

• Applications of Divide and Conquer Approach: • Binary Search. • Quick sort. • Merge Sort • Strassen's Algorithm.

Binary Search Algorithm – • This search algorithm works on the principle of divide and conquer, since it divides the array into half before searching. For this algorithm to work properly, the data collection should be in the sorted form. • Binary search looks for a particular key value by comparing the middle most item of the collection. If a match occurs, then the index of item is returned. But if the middle item has a value greater than the key value, the right sub-array of the middle item is searched. Otherwise, the left sub-array is searched. This process continues recursively until the size of a subarray reduces to zero.

• Binary Search Algorithm • Binary Search algorithm is an interval searching method that performs the searching in intervals only. The input taken by the binary search algorithm must always be in a sorted array since it divides the array into subarrays based on the greater or lower values. The algorithm follows the procedure below − • Step 1 − Select the middle item in the array and compare it with the key value to be searched. If it is matched, return the position of the median. • Step 2 − If it does not match the key value, check if the key value is either greater than or less than the median value. • Step 3 − If the key is greater, perform the search in the right sub-array; but if the key is lower than the median value, perform the search in the left sub-array. • Step 4 − Repeat Steps 1, 2 and 3 iteratively, until the size of sub-array becomes 1. • Step 5 − If the key value does not exist in the array, then the algorithm returns an unsuccessful search.

Quick Sort • QuickSort is a sorting algorithm based on the Divide and Conquer that picks an element as a pivot and partitions the given array around the picked pivot by placing the pivot in its correct position in the sorted array. • It is an algorithm of Divide & Conquer type. • Divide: Rearrange the elements and split arrays into two subarrays and an element in between search that each element in left sub array is less than or equal to the average element and each element in the right sub- array is larger than the middle element. • Conquer: Recursively, sort two sub arrays. • Combine: Combine the already sorted array.

• How does QuickSort Algorithm work? • There are mainly three steps in the algorithm. 1. Choose a pivot 2. Partition the array around pivot. After partition, it is ensured that all elements are smaller than all right and we get index of the end point of smaller elements. The left and right may not be sorted individually. 3. Recursively call for the two partitioned left and right subarrays. 4. We stop recursion when there is only one element is left.

Greedy Algorithm • The greedy method is one of the strategies like Divide and conquer used to solve the problems. This method is used for solving optimization problems. An optimization problem is a problem that demands either maximum or minimum results. Let's understand through some terms. • It is not an algorithm, but it is a technique. The main function of this approach is that the decision is taken on the basis of the currently available information. Whatever the current information is present, the decision is made without worrying about the effect of the current decision in future.

• This technique is basically used to determine the feasible solution that may or may not be optimal. The feasible solution is a subset that satisfies the given criteria. The optimal solution is the solution which is the best and the most favorable solution in the subset. • In the case of feasible, if more than one solution satisfies the given criteria then those solutions will be considered as the feasible, whereas the optimal solution is the best solution among all the solutions.

• Let's understand through an example. • Suppose there is a problem 'P'. I want to travel from A to B shown as below: • P : A → B • The problem is that we have to travel this journey from A to B. There are various solutions to go from A to B. We can go from A to B by walk, car, bike, train, aeroplane, etc. There is a constraint in the journey that we have to travel this journey within 12 hrs. If I go by train or aeroplane then only, I can cover this distance within 12 hrs. There are many solutions to this problem but there are only two solutions that satisfy the constraint.

• If we say that we have to cover the journey at the minimum cost. This means that we have to travel this distance as minimum as possible, so this problem is known as a minimization problem. Till now, we have two feasible solutions, i.e., one by train and another one by air. Since travelling by train will lead to the minimum cost so it is an optimal solution. An optimal solution is also the feasible solution, but providing the best result so that solution is the optimal solution with the minimum cost. There would be only one optimal solution. • The problem that requires either minimum or maximum result then that problem is known as an optimization problem. Greedy method is one of the strategies used for solving the optimization problems.

Fractional Knapsack Problem • The fractional knapsack problem is also one of the techniques which are used to solve the knapsack problem. In fractional knapsack, the items are broken in order to maximize the profit. The problem in which we break the item is known as a Fractional knapsack problem. • There are basically three approaches to solve the problem: • The first approach is to select the item based on the maximum profit. • The second approach is to select the item based on the minimum weight. • The third approach is to calculate the ratio of profit/weight.

• A spanning tree is a subset of an undirected Graph that has all the vertices connected by minimum number of edges. • If all the vertices are connected in a graph, then there exists at least one spanning tree. In a graph, there may exist more than one spanning tree. • Properties • A spanning tree does not have any cycle. • Any vertex can be reached from any other vertex.

• Minimum Spanning Tree • A Minimum Spanning Tree (MST) is a subset of edges of a connected weighted undirected graph that connects all the vertices together with the minimum possible total edge weight. To derive an MST, Prim’s algorithm or Kruskal’s algorithm can be used. • As we have discussed, one graph may have more than one spanning tree. If there are n number of vertices, the spanning tree should have − number of edges. In this 𝒏 𝟏 context, if each edge of the graph is associated with a weight and there exists more than one spanning tree, we need to find the minimum spanning tree of the graph.

• In the above graph, we have shown a spanning tree though it’s not the minimum spanning tree. The cost of this spanning tree is (5 + 7 + 3 + 3 + 5 + 8 + 3 + 4) = 38.

Kruskal’s Minimal Spanning Tree Algorithm • Kruskal's minimal spanning tree algorithm is one of the efficient methods to find the minimum spanning tree of a graph. • A minimum spanning tree is a subgraph that connects all the vertices present in the main graph with the least possible edges and minimum cost (sum of the weights assigned to each edge). • The algorithm first starts from the forest – which is defined as a subgraph containing only vertices of the main graph – of the graph, adding the least cost edges later until the minimum spanning tree is created without forming cycles in the graph. • Kruskal's Algorithm • The inputs taken by the kruskal’s algorithm are the graph G {V, E}, where V is the set of vertices and E is the set of edges, and the source vertex S and the minimum spanning tree of graph G is obtained as an output.

Examples Construct a minimum spanning tree using kruskal’s algorithm for the graph given below

• As the first step, sort all the edges in the given graph in an ascending order and store the values in an array. • Edge B→D, 5 • A→B, 6 • C→F , 9 • F→E , 10 • B→C , 11 • G→F , 12 • A→G, 15 • C→D, 17 • D→E, 22 • C→G, 25

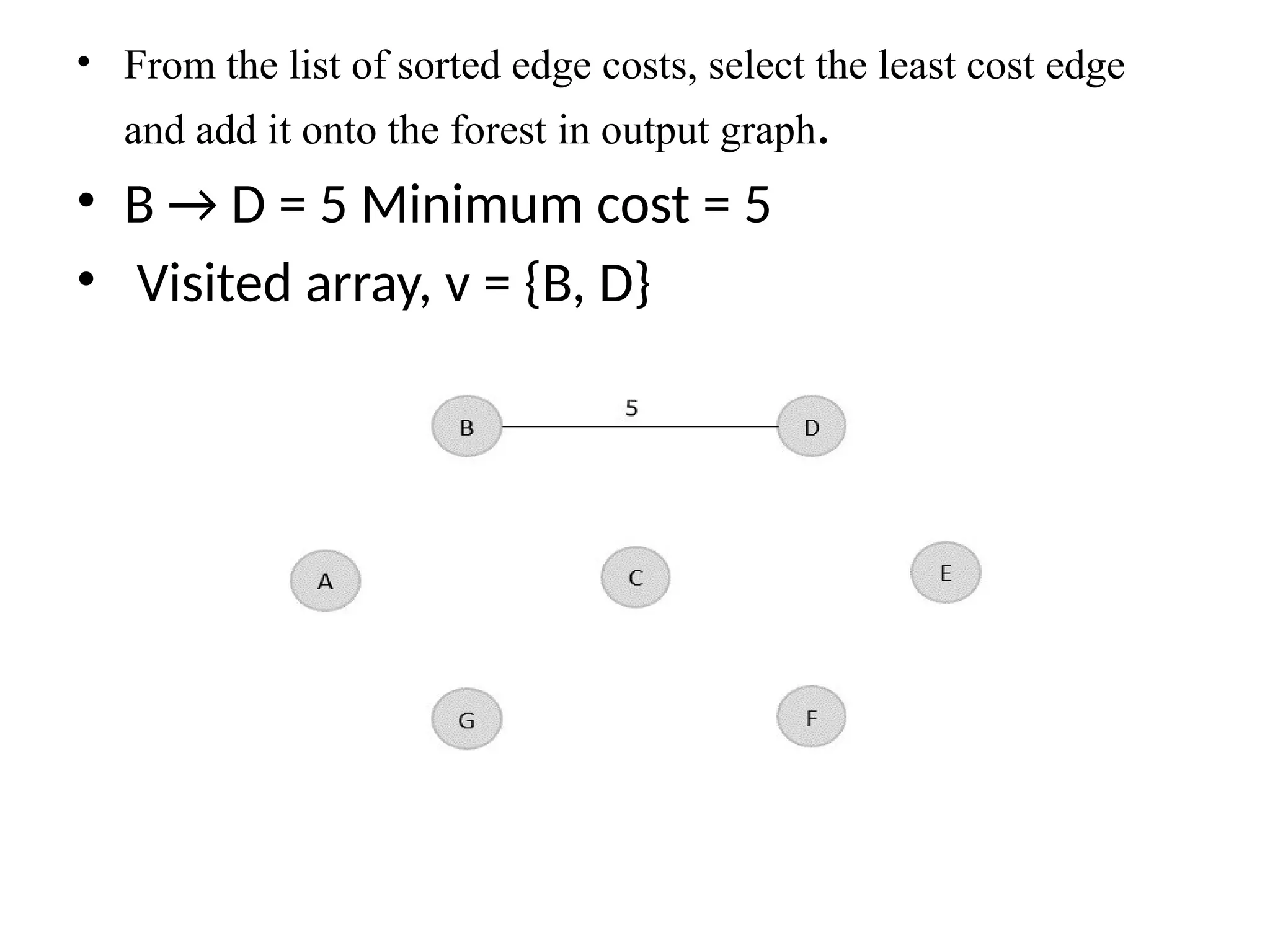
• From the list of sorted edge costs, select the least cost edge and add it onto the forest in output graph. • B → D = 5 Minimum cost = 5 • Visited array, v = {B, D}

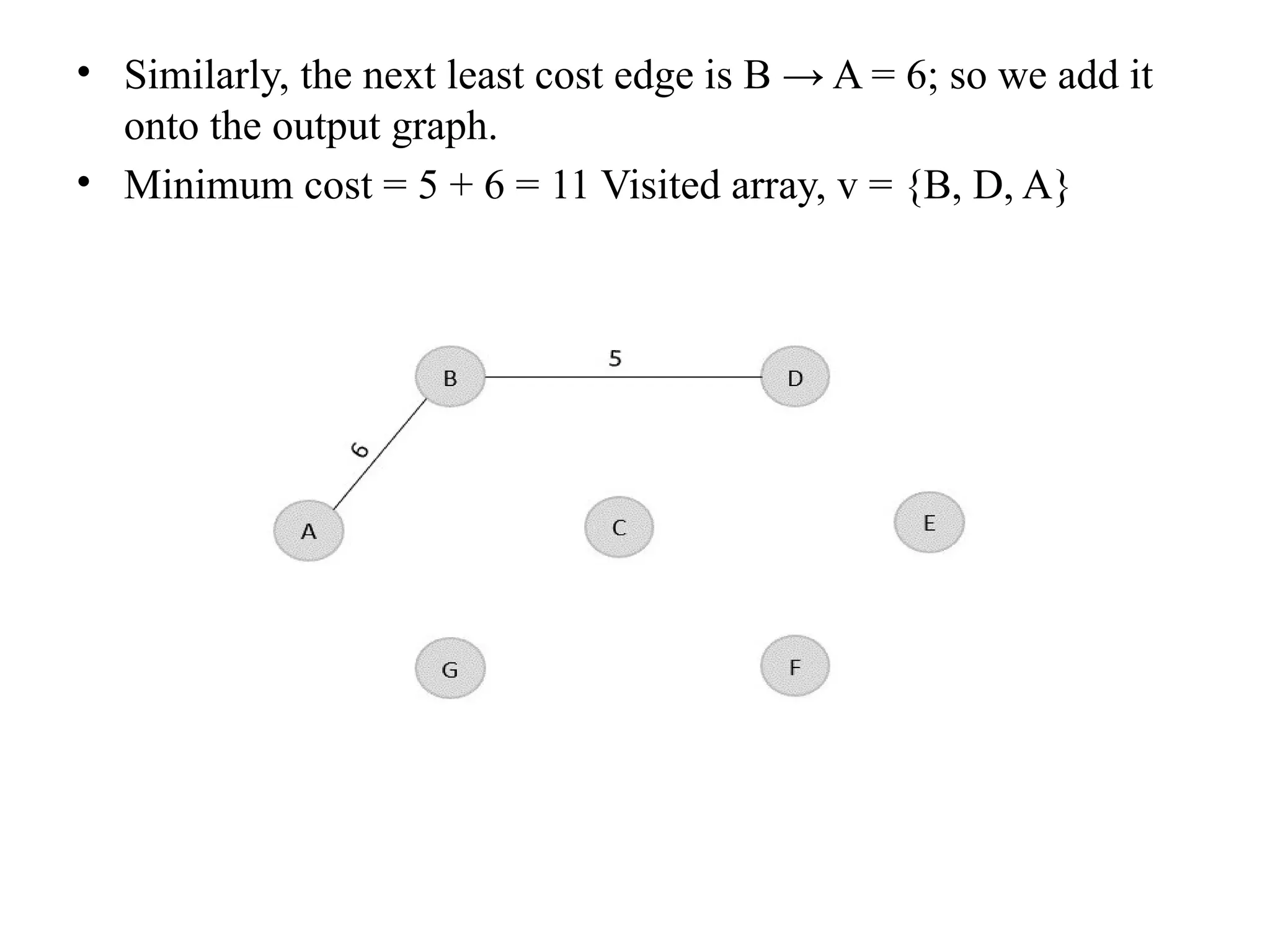
• Similarly, the next least cost edge is B → A = 6; so we add it onto the output graph. • Minimum cost = 5 + 6 = 11 Visited array, v = {B, D, A}

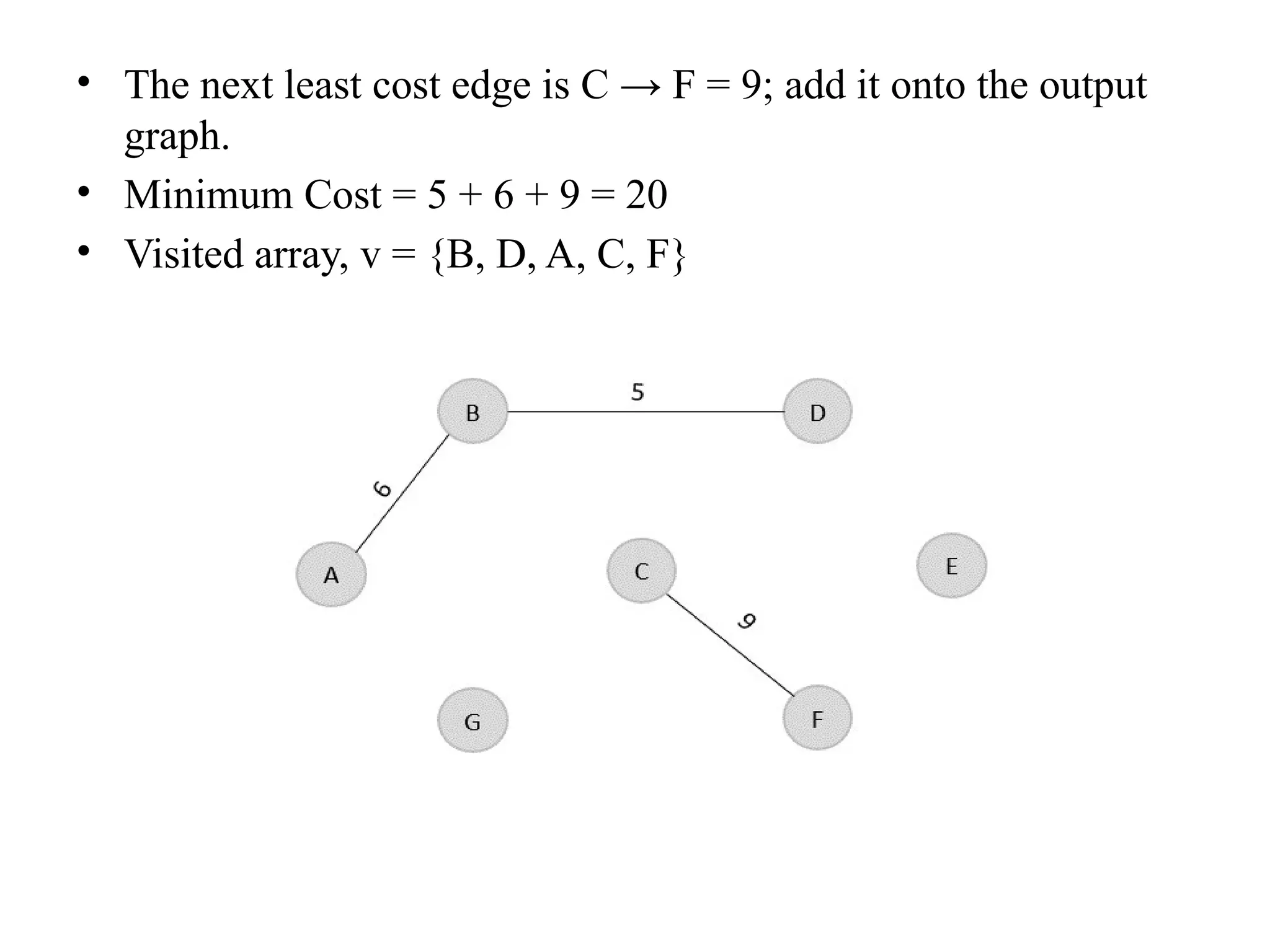
• The next least cost edge is C → F = 9; add it onto the output graph. • Minimum Cost = 5 + 6 + 9 = 20 • Visited array, v = {B, D, A, C, F}

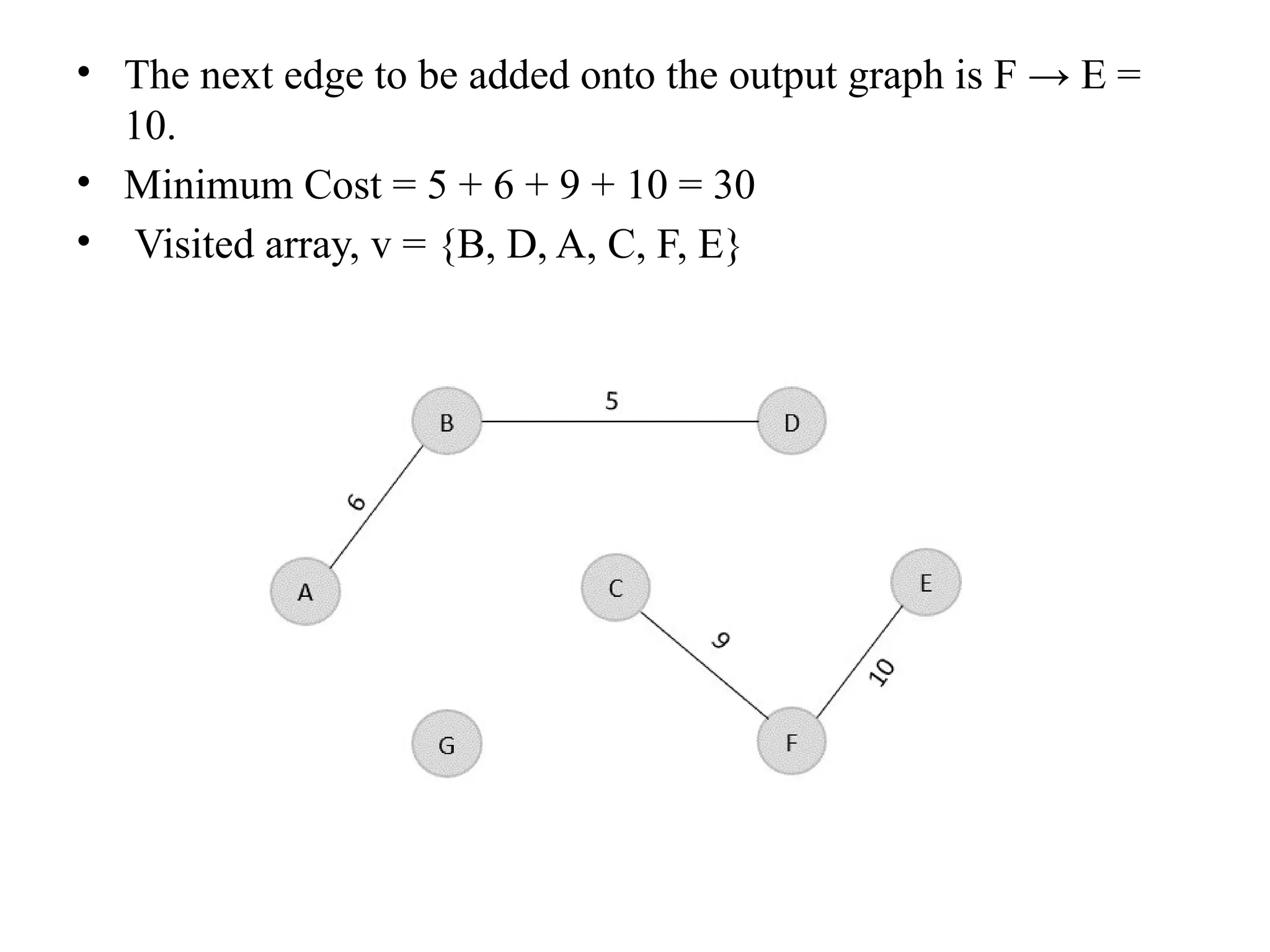
• The next edge to be added onto the output graph is F → E = 10. • Minimum Cost = 5 + 6 + 9 + 10 = 30 • Visited array, v = {B, D, A, C, F, E}

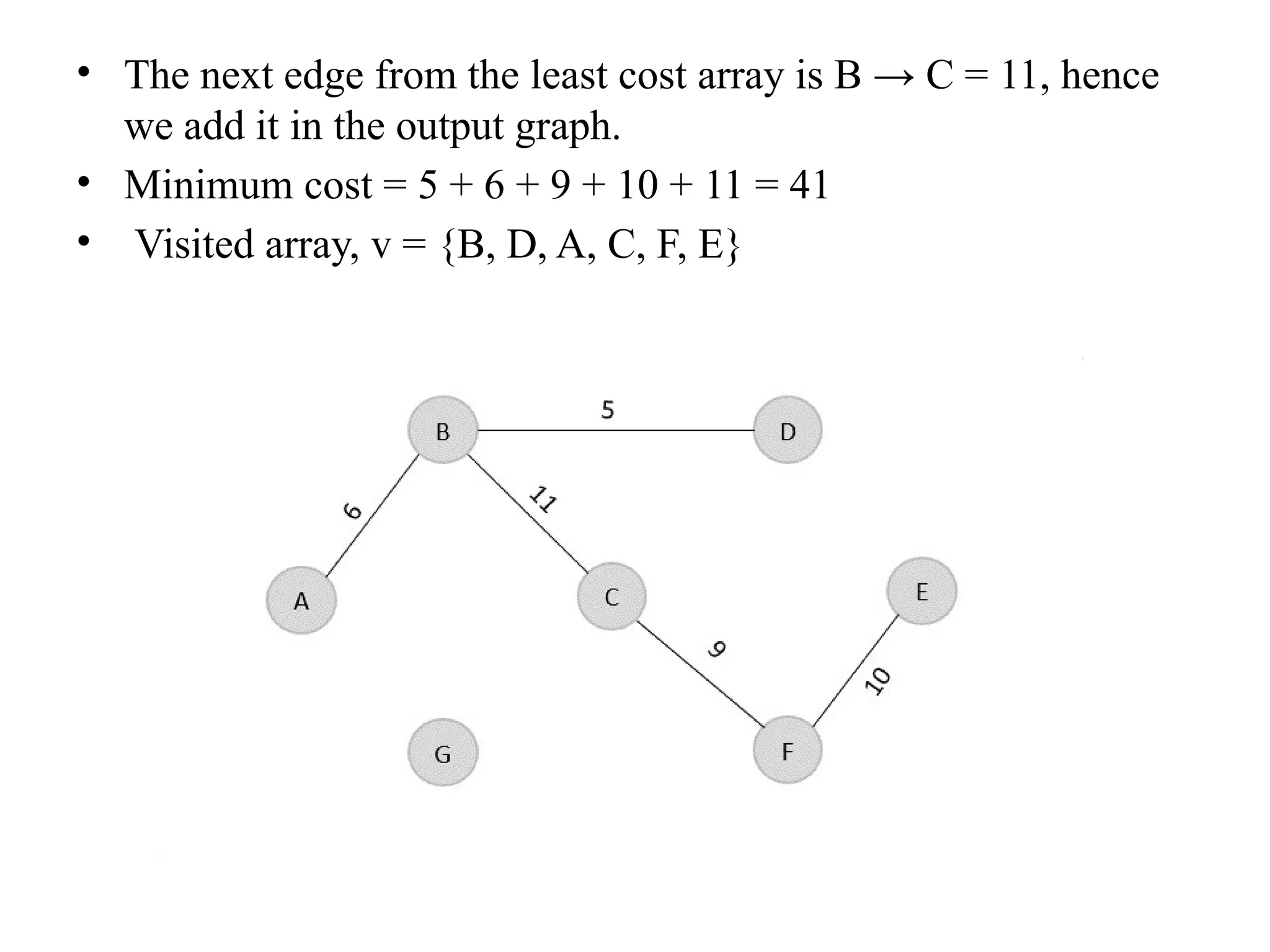
• The next edge from the least cost array is B → C = 11, hence we add it in the output graph. • Minimum cost = 5 + 6 + 9 + 10 + 11 = 41 • Visited array, v = {B, D, A, C, F, E}

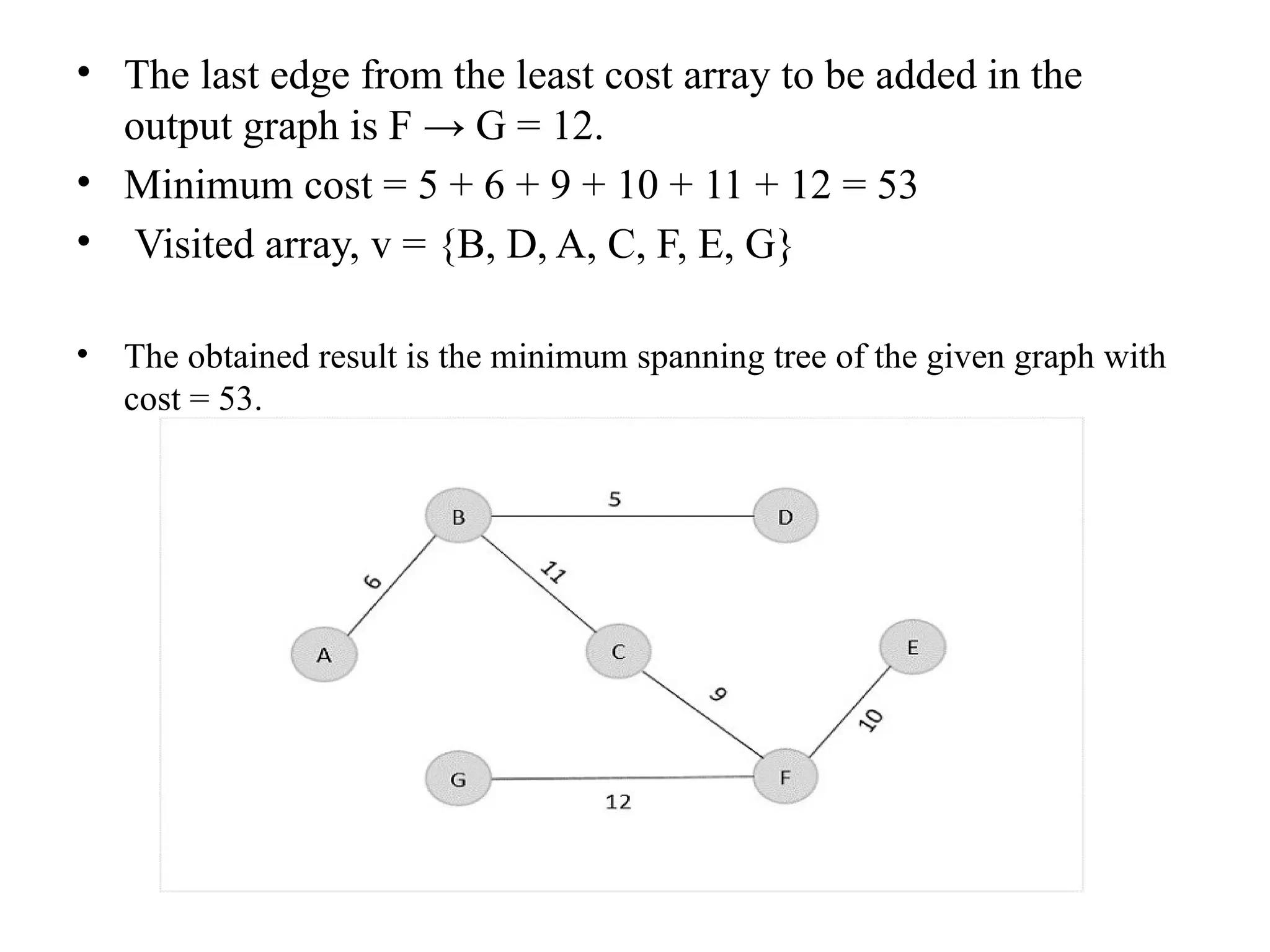
• The last edge from the least cost array to be added in the output graph is F → G = 12. • Minimum cost = 5 + 6 + 9 + 10 + 11 + 12 = 53 • Visited array, v = {B, D, A, C, F, E, G} • The obtained result is the minimum spanning tree of the given graph with cost = 53.

Prims algorithm • Prim's Algorithm is a greedy algorithm that is used to find the minimum spanning tree from a graph. Prim's algorithm finds the subset of edges that includes every vertex of the graph such that the sum of the weights of the edges can be minimized. • Prim's algorithm starts with the single node and explores all the adjacent nodes with all the connecting edges at every step. The edges with the minimal weights causing no cycles in the graph got selected. • How does the prim's algorithm work? • Prim's algorithm is a greedy algorithm that starts from one vertex and continue to add the edges with the smallest weight until the goal is reached. The steps to implement the prim's algorithm are given as follows - • .

• First, we have to initialize an MST with the randomly chosen vertex. • Now, we have to find all the edges that connect the tree in the above step with the new vertices. From the edges found, select the minimum edge and add it to the tree. • Repeat step 2 until the minimum spanning tree is formed.

• Step 1 - First, we have to choose a vertex from the above graph. Let's choose B. • Step 2 - Now, we have to choose and add the shortest edge from vertex B. There are two edges from vertex B that are B to C with weight 10 and edge B to D with weight 4. Among the edges, the edge BD has the minimum weight. So, add it to the MST.

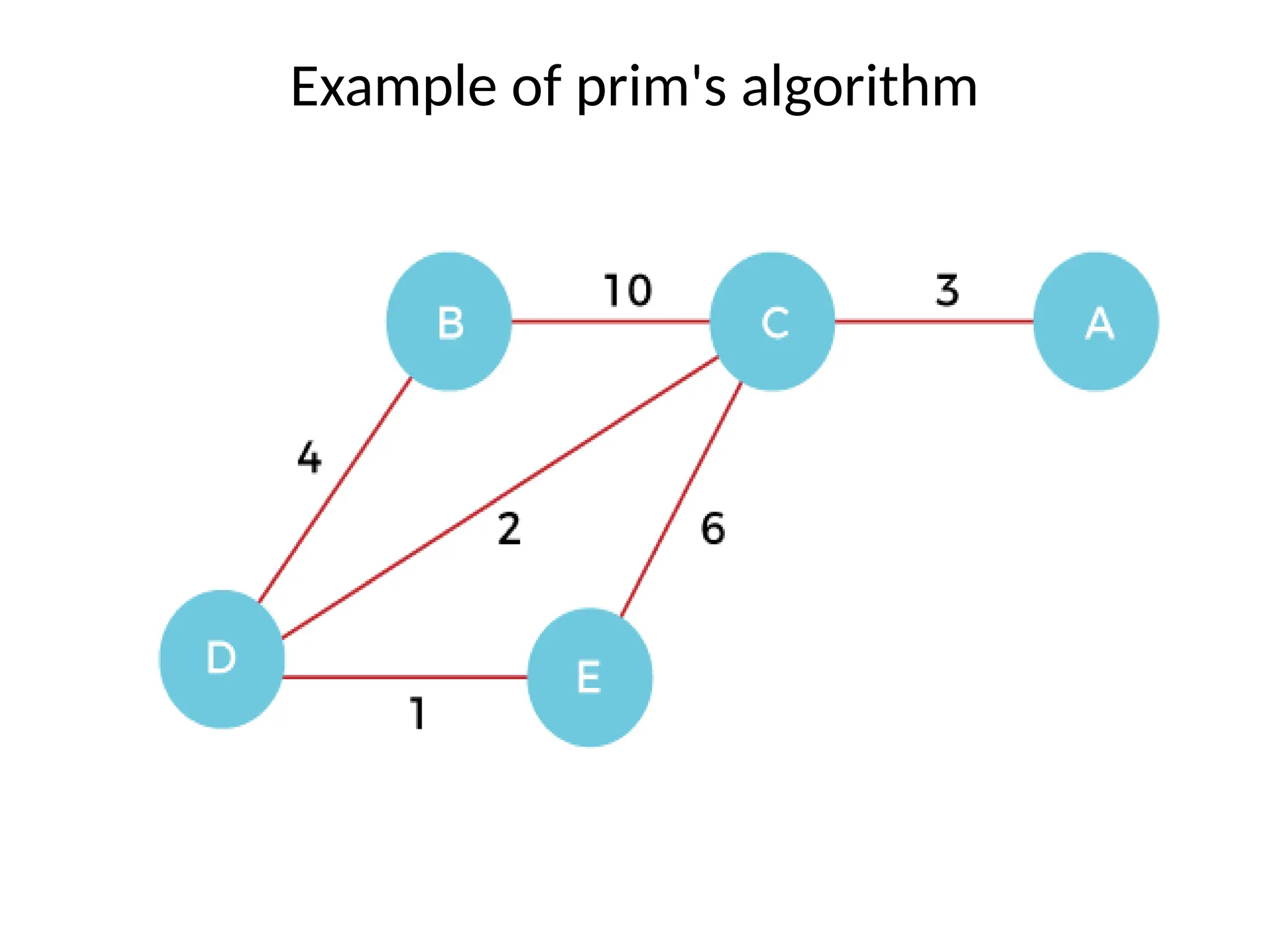
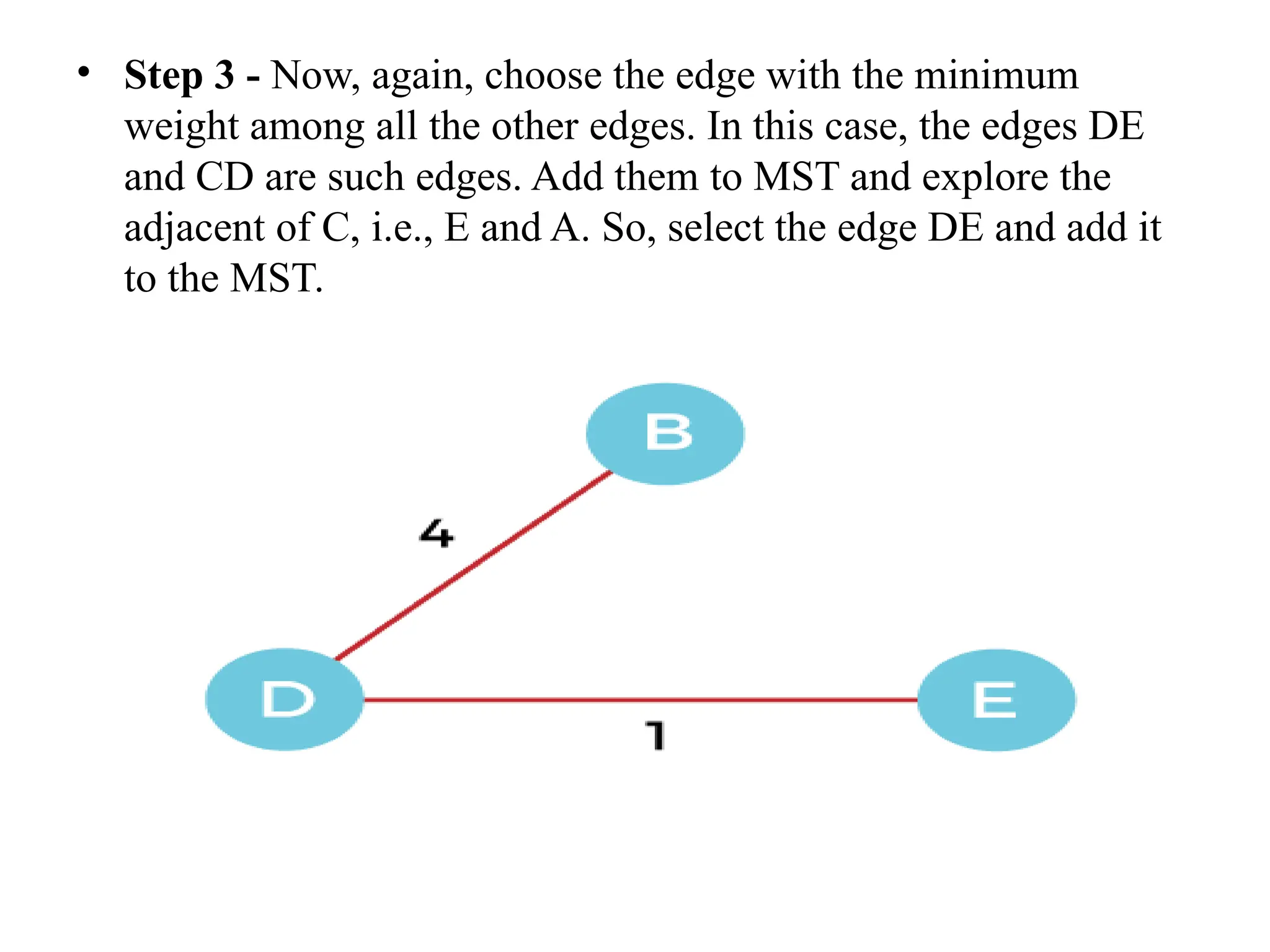
• Step 3 - Now, again, choose the edge with the minimum weight among all the other edges. In this case, the edges DE and CD are such edges. Add them to MST and explore the adjacent of C, i.e., E and A. So, select the edge DE and add it to the MST.

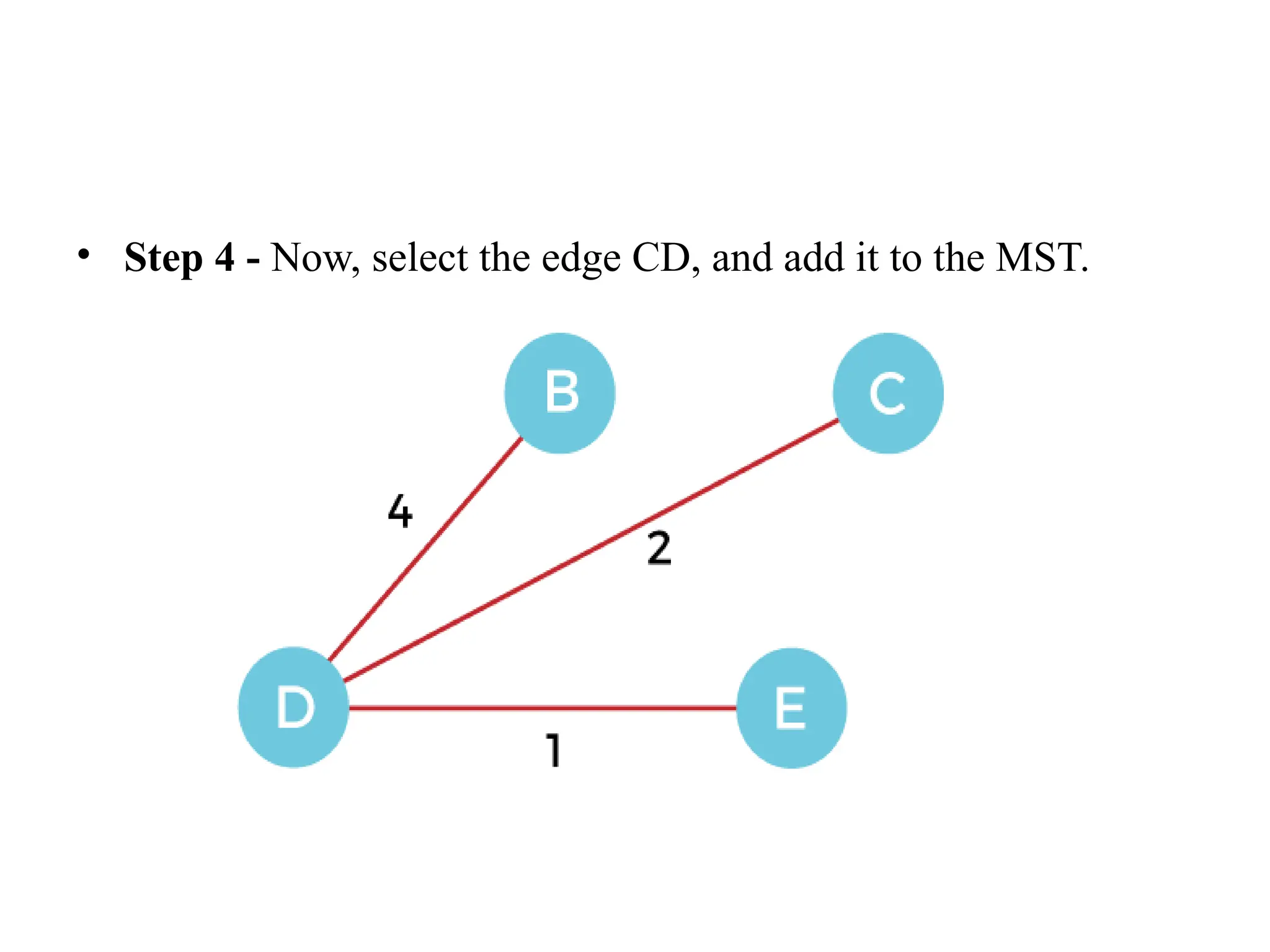
• Step 4 - Now, select the edge CD, and add it to the MST.

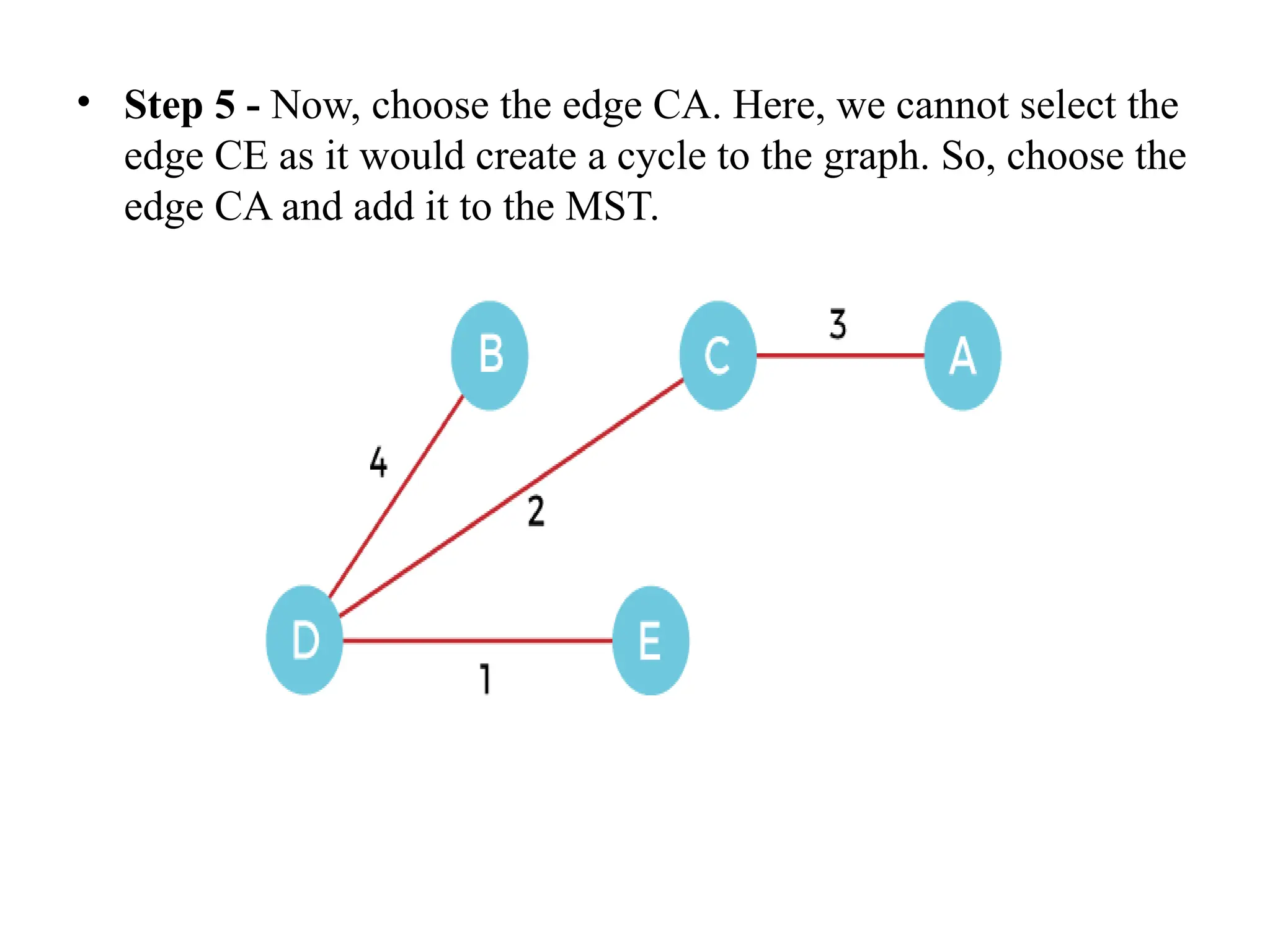
• Step 5 - Now, choose the edge CA. Here, we cannot select the edge CE as it would create a cycle to the graph. So, choose the edge CA and add it to the MST.

• So, the graph produced in step 5 is the minimum spanning tree of the given graph. The cost of the MST is given below – • Cost of MST = 4 + 2 + 1 + 3 = 10 units. • Algorithm • Step 1: Select a starting vertex • Step 2: Repeat Steps 3 and 4 until there are fringe vertices (least cost path) • Step 3: Select an edge 'e' connecting the tree vertex and fringe vertex that ha s minimum weight • Step 4: Add the selected edge and the vertex to the minimum spanning tree T • [END OF LOOP] • Step 5: EXIT

• A • / • 1 3 • / • B---2---C • Start with vertex A. Add edges (A-B) and (A-C) to the priority queue. Select edge (A-B) as it has the smallest weight (1). Now the MST includes A and B. Update the priority queue to include edge (B-C) with weight 2.Select edge (B-C) (smallest weight now) and add C to the MST. Now all vertices are included, and the MST is formed.

• example of time complexity of prims • To illustrate the time complexity of Prim's algorithm, let’s analyze it using both an adjacency matrix and an adjacency list with a priority queue. • 1. Using an Adjacency Matrix • Time Complexity: OV2 • Initialization: Initializing the distance array and setting the first vertex takes O(V) • Finding the Minimum Edge: For each vertex, we scan the entire row of the matrix to find the minimum edge connecting the MST to a vertex outside the MST. This requires O(V) or each of the V vertices.

• Thus, the overall complexity is: • O(V) +O V2 = O (V2 • Example with Adjacency Matrix • Consider a graph with 4 vertices: • A • / • 1 3 • / • B---2---C • / • 4 5 • / • D

• The adjacency matrix would look like this: • A B C D • A [ 0, 1, 3, ∞ ] • B [ 1, 0, 2, 4 ] • C [ 3, 2, 0, 5 ] • D [ ∞, 4, 5, 0 ] • If we have 4 vertices (A, B, C, D), the algorithm will run in O (42 = O (16)

• Using an Adjacency List and Priority Queue • Time Complexity: • O(ElogV) • Initialization: Initializing the priority queue takes • O(V) • Main Loop: For each of the E edges, inserting and extracting from the priority queue takes • O(logV) • The overall complexity is: • O(V+O(ElogV =O(ElogV)

• Example with Adjacency List • Using the same graph above, let’s consider the adjacency list representation: • A: [(B, 1), (C, 3)] • B: [(A, 1), (C, 2), (D, 4)] • C: [(A, 3), (B, 2), (D, 5)] • D: [(B, 4), (C, 5)]

• If we have 4 vertices and 5 edges, the algorithm will run in: • O(5log⁡ 4)= O(5×2) =O(10) • Summary • Using Adjacency Matrix: O(V2 ) – suitable for dense graphs • Using Adjacency List with Priority Queue: O(Elog⁡ V) more efficient for sparse graphs. • In practice, using the adjacency list with a priority queue is generally more efficient for larger graphs, especially when the number of edges E is significantly less than V2 .

Dijkstra’s Algorithm: • is a popular algorithms for solving many single-source shortest path problems having non-negative edge weight in the graphs i.e., it is to find the shortest distance between two vertices on a graph. • It starts at the source vertex and iteratively selects the unvisited vertex with the smallest tentative distance from the source. It then visits the neighbors of this vertex and updates their tentative distances if a shorter path is found. This process continues until the destination vertex is reached, or all reachable vertices have been visited.

• Algorithm for Dijkstra’s Algorithm: • Mark the source node with a current distance of 0 and the rest with infinity. • Set the non-visited node with the smallest current distance as the current node. • For each neighbor, N of the current node adds the current distance of the adjacent node with the weight of the edge connecting 0->1. If it is smaller than the current distance of Node, set it as the new current distance of N. • Mark the current node 1 as visited. • Go to step 2 if there are any nodes are unvisited.

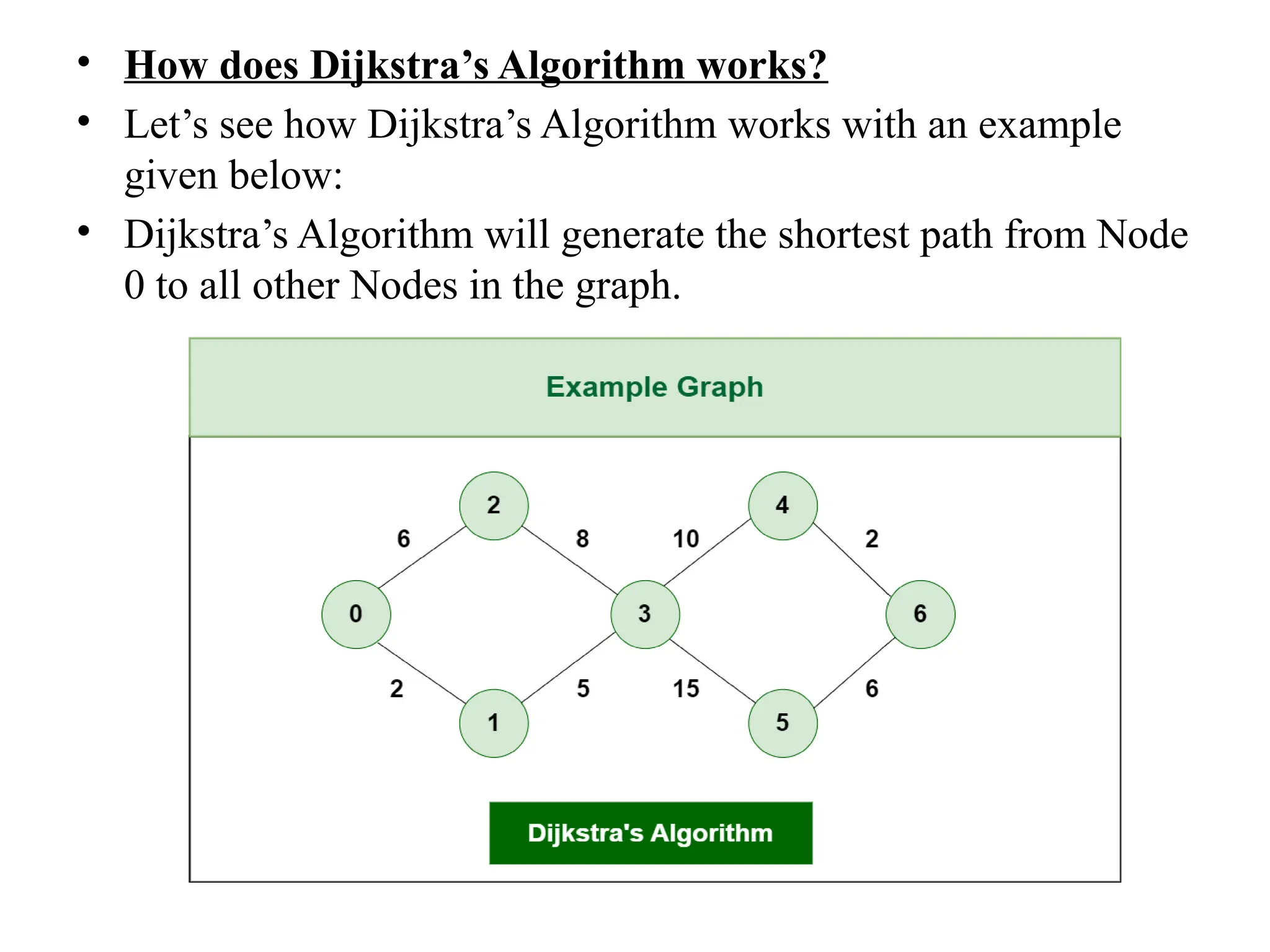
• How does Dijkstra’s Algorithm works? • Let’s see how Dijkstra’s Algorithm works with an example given below: • Dijkstra’s Algorithm will generate the shortest path from Node 0 to all other Nodes in the graph.

• The algorithm will generate the shortest path from node 0 to all the other nodes in the graph. • For this graph, we will assume that the weight of the edges represents the distance between two nodes. • As, we can see we have the shortest path from, Node 0 to Node 1, from Node 0 to Node 2, from Node 0 to Node 3, from Node 0 to Node 4, from Node 0 to Node 6. • Initially we have a set of resources given below : • The Distance from the source node to itself is 0. In this example the source node is 0. • The distance from the source node to all other node is unknown so we mark all of them as infinity. • Example: 0 -> 0, 1-> ∞,2-> ∞,3-> ∞,4-> ∞,5-> ∞,6-> ∞.

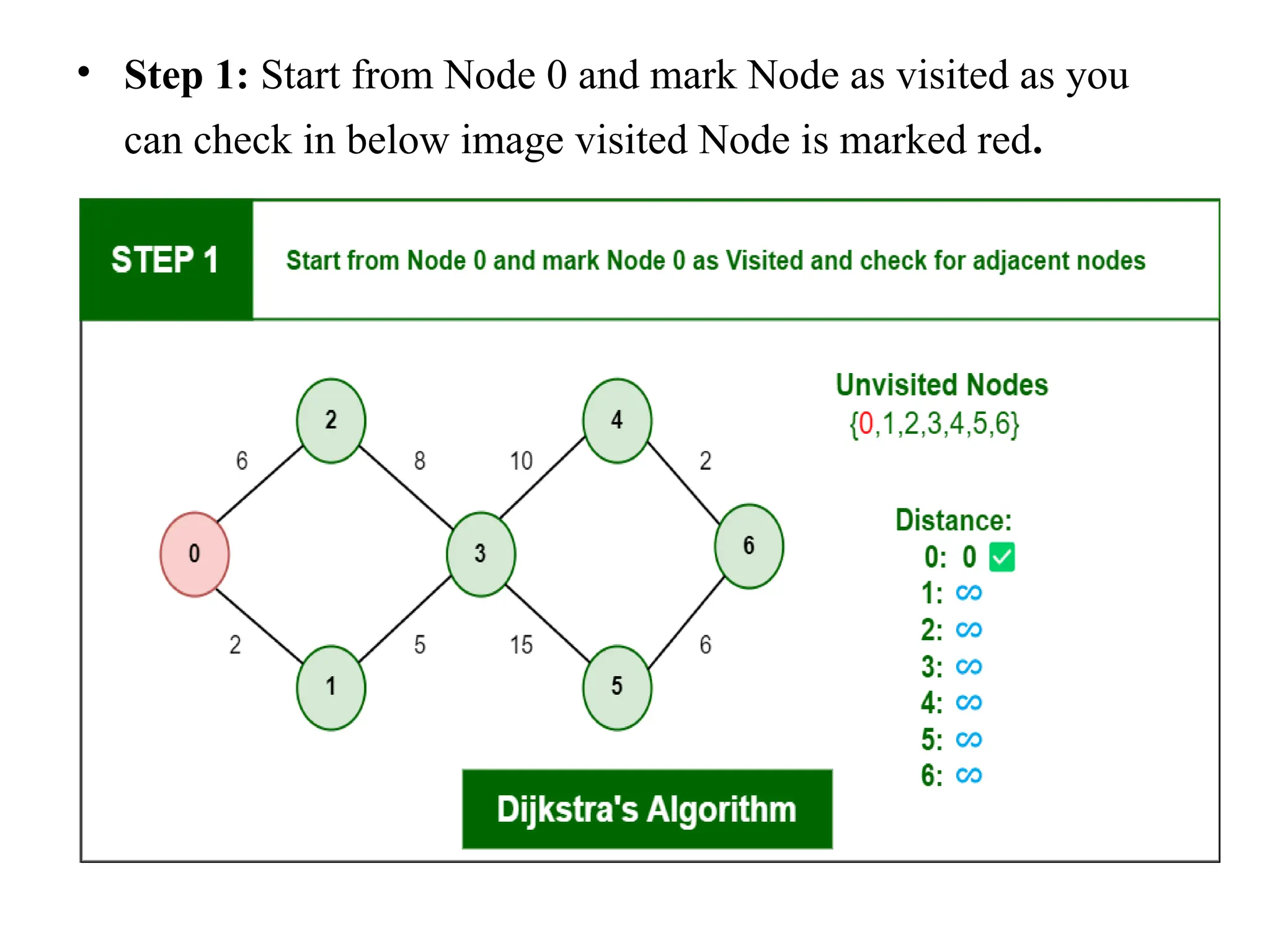
• Step 1: Start from Node 0 and mark Node as visited as you can check in below image visited Node is marked red.

• Step 2: Check for adjacent Nodes, Now we have to choices (Either choose Node1 with distance 2 or either choose Node 2 with distance 6 ) and choose Node with minimum distance. In this step Node 1 is Minimum distance adjacent Node, so marked it as visited and add up the distance. • Distance: Node 0 -> Node 1 = 2

• Step 3: Then Move Forward and check for adjacent Node which is Node 3, so marked it as visited and add up the distance, Now the distance will be: • Distance: Node 0 -> Node 1 -> Node 3 = 2 + 5 = 7

• Step 4: Again we have two choices for adjacent Nodes (Either we can choose Node 4 with distance 10 or either we can choose Node 5 with distance 15) so choose Node with minimum distance. In this step Node 4 is Minimum distance adjacent Node, so marked it as visited and add up the distance. • Distance: Node 0 -> Node 1 -> Node 3 -> Node 4 = 2 + 5 + 10 = 17

• Step 5: Again, Move Forward and check for adjacent Node which is Node 6, so marked it as visited and add up the distance, Now the distance will be: • Distance: Node 0 -> Node 1 -> Node 3 -> Node 4 -> Node 6 = 2 + 5 + 10 + 2 = 19

• So, the Shortest Distance from the Source Vertex is 19 which is optimal one

• C program for implementing binary search looks great! It correctly defines the binary search function using an iterative approach and demonstrates how to use it in the main function. Here’s a brief overview of how the code works: • Function Definition: The binarySearch function takes an array, the left and right indices, and the key to search for. It performs the binary search by repeatedly dividing the search interval in half. • Midpoint Calculation: The midpoint is calculated to avoid potential overflow. If the key matches the element at the midpoint, it returns the index. If the key is greater than the midpoint value, it narrows the search to the right half; otherwise, it narrows to the left half. • Looping Until Found or Exhausted: The loop continues until the left index exceeds the right index, indicating that the key is not present. • Main Function: It initializes an array and searches for a specified key, printing the result.

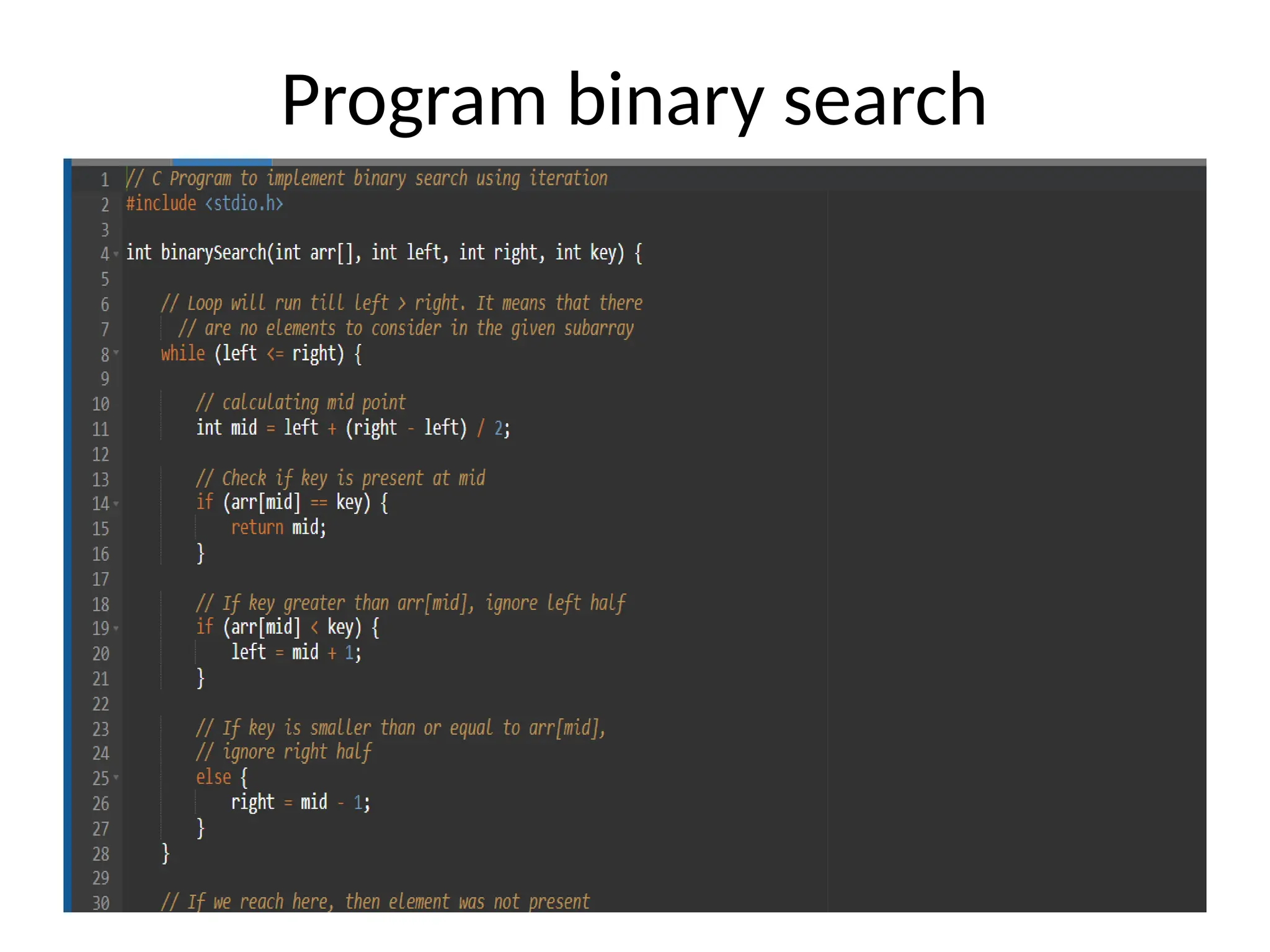
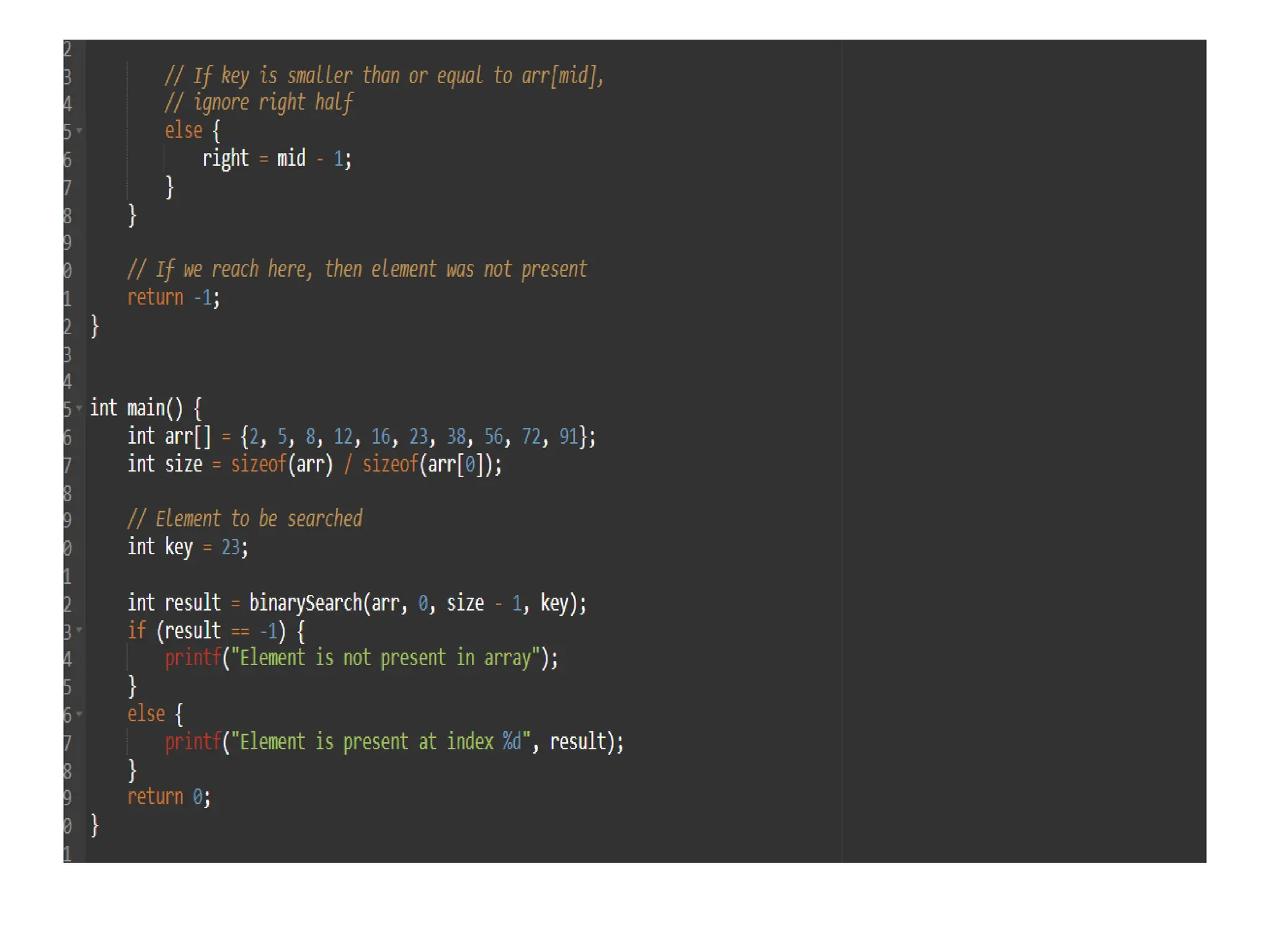
• #include <stdio.h> • This line includes the standard input-output library, which allows the program to use functions like printf() and scanf(). • int binarySearch(int arr[], int left, int right, int key) { • This line defines the function binarySearch, which takes four parameters:arr[]: The sorted array where the search will be performed. • left: The starting index of the subarray. • right: The ending index of the subarray. • key: The value to search for.

• while (left <= right) { • This begins a loop that continues as long as the left index is less than or equal to the right index. If left exceeds right, it means the element is not present in the array. • int mid = left + (right - left) / 2; • This calculates the midpoint index of the current subarray. The formula left + (right - left) / 2 prevents overflow that could occur if left and right are large.

• if (arr[mid] == key) { return mid; } • This checks if the element at the midpoint index is equal to the key. If it is, the function returns the index mid, indicating that the key has been found. • if (arr[mid] < key) { left = mid + 1; } • If the element at mid is less than the key, it means the key must be in the right half of the array. Therefore, the left index is updated to mid + 1, effectively ignoring the left half.

• else { right = mid - 1; } • If the element at mid is greater than the key, the key must be in the left half. The right index is updated to mid - 1, ignoring the right half. • } • This closes the while loop. If the loop exits without finding the key, it means the element is not present. • return -1; } • If the key is not found in the array, the function returns -1 to indicate this.

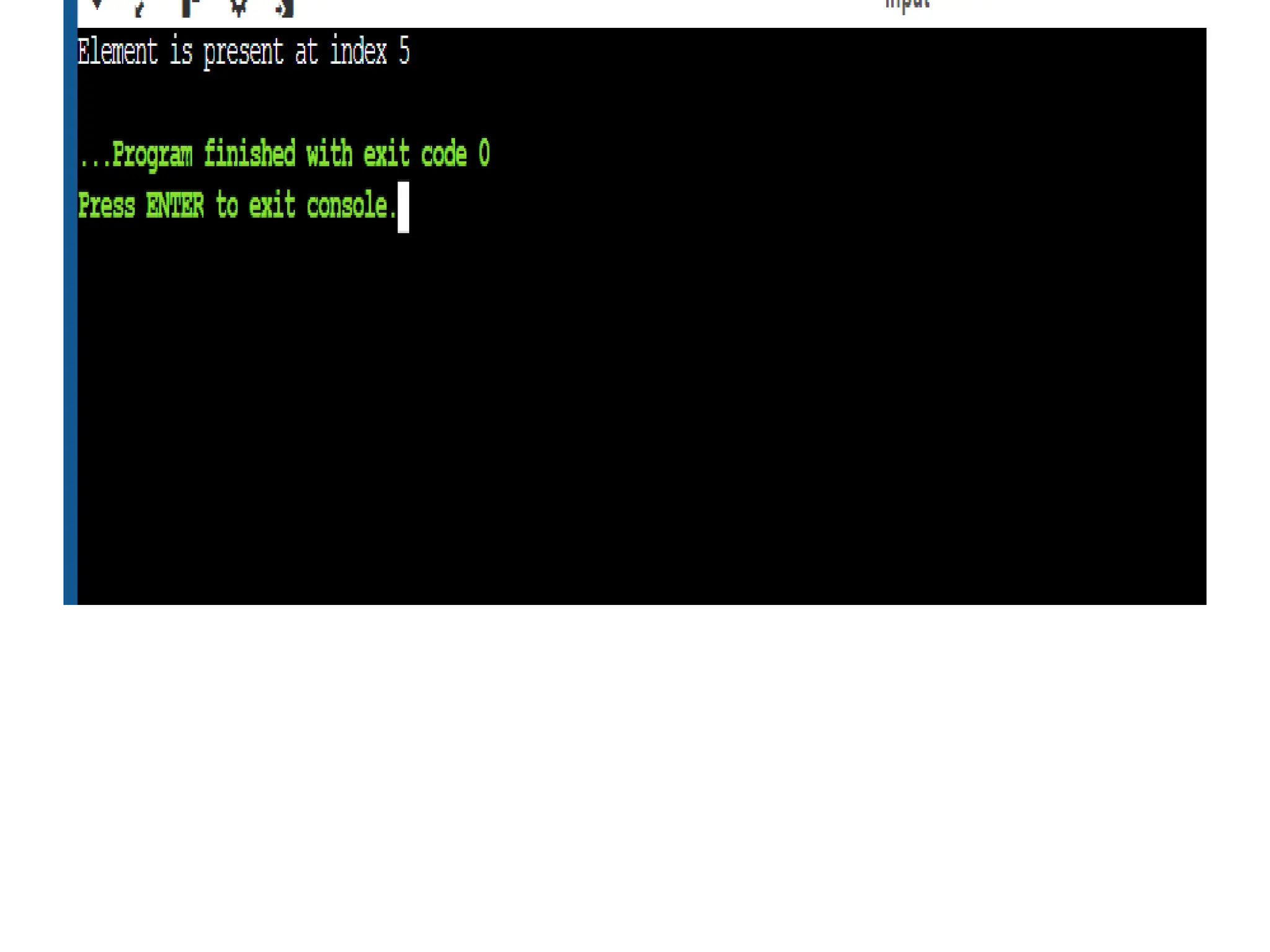
• int main() { • This defines the main function, which is the entry point of the program. • int arr[] = {2, 5, 8, 12, 16, 23, 38, 56, 72, 91}; • An array of integers is defined. This is the sorted array where the binary search will be performed. • int size = sizeof(arr) / sizeof(arr[0]); • This calculates the size of the array by dividing the total size of the array by the size of a single element. • int key = 23; • This initializes the key variable with the value to be searched in the array. • int result = binarySearch(arr, 0, size - 1, key); • This calls the binarySearch function, passing the array, the left index (0), the right index (size - 1), and the key. The result (the index of the found element or -1) is stored in the variable result.

• if (result == -1) { printf("Element is not present in array"); } • This checks if the result is -1. If it is, it prints a message indicating that the element is not present in the array. • else { printf("Element is present at index %d", result); } • If the result is not -1, it prints the index where the element was found. • return 0; • }

Design and analysis of algorithm devide and conquer

More Related Content

Similar to Design and analysis of algorithm devide and conquer

Recently uploaded

Design and analysis of algorithm devide and conquer