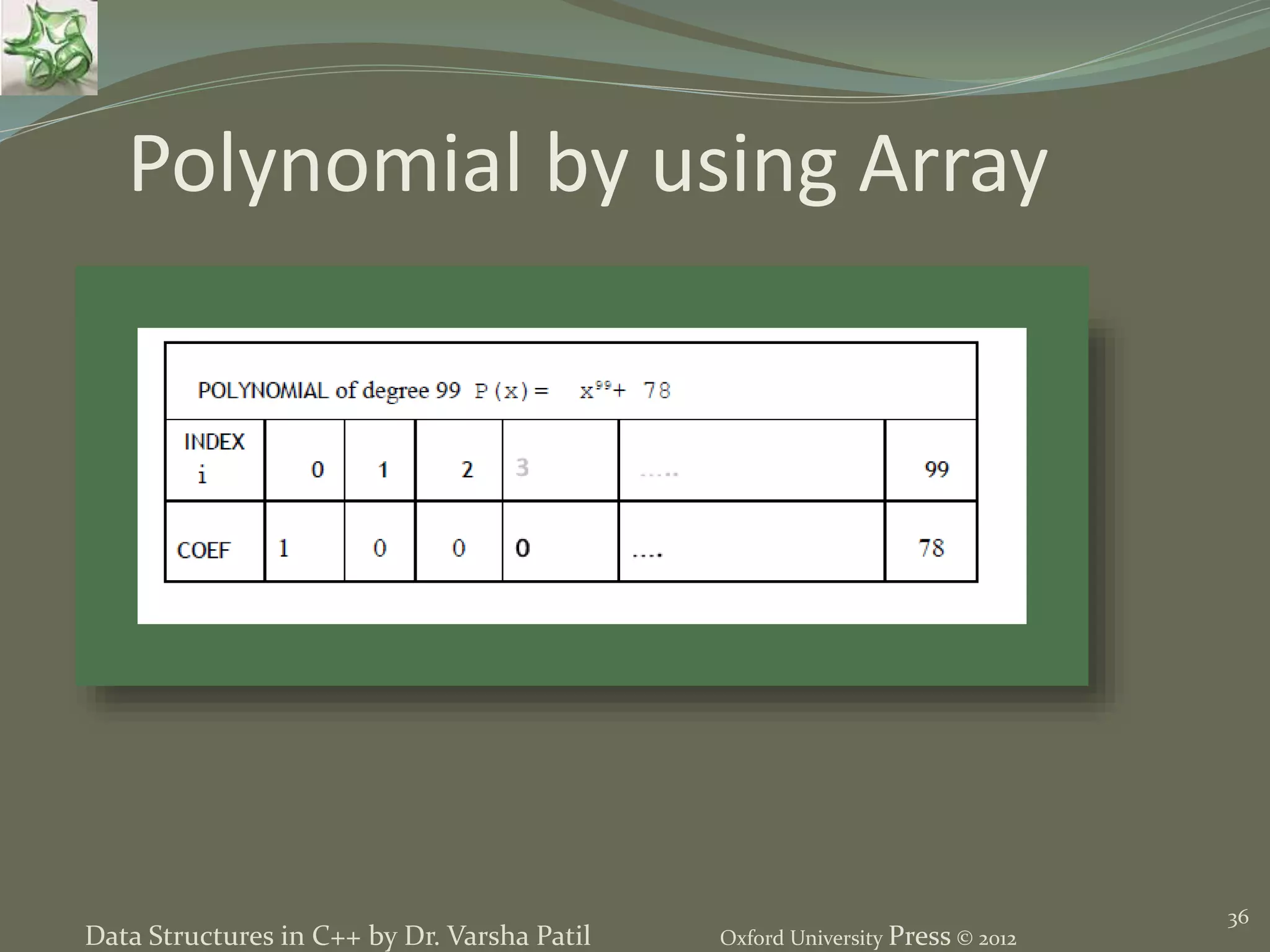
This document discusses arrays and ordered lists as linear data structures. It describes arrays as a collection of homogeneous data elements that allow direct access via indexes. The key properties of arrays include sequential storage of elements, random access, and calculation of element addresses based on base address and offsets. The document also covers array implementation in C++, one-dimensional and two-dimensional arrays, row-major and column-major representations, and the use of arrays to represent polynomials, strings and sparse matrices. Finally, it provides a brief introduction to ordered lists and their representation as linear data structures.




![Oxford University Press © 2012Data Structures Using C++ by Dr Varsha Patil An array is a finite ordered collection of homogeneous data elements which provides direct access (or random access) to any of its elements. An array as a data structure is defined as a set of pairs (index, value) such that with each index a value is associated. index — indicates the location of an element in an array. value - indicates the actual value of that data element. Declaration of an array in ‘C++’: int Array_A[20]; 5](https://image.slidesharecdn.com/2lineardatastructureusingarraysppt-150824111020-lva1-app6892/75/2-Linear-Data-Structure-Using-Arrays-Data-Structures-using-C-by-Varsha-Patil-5-2048.jpg)
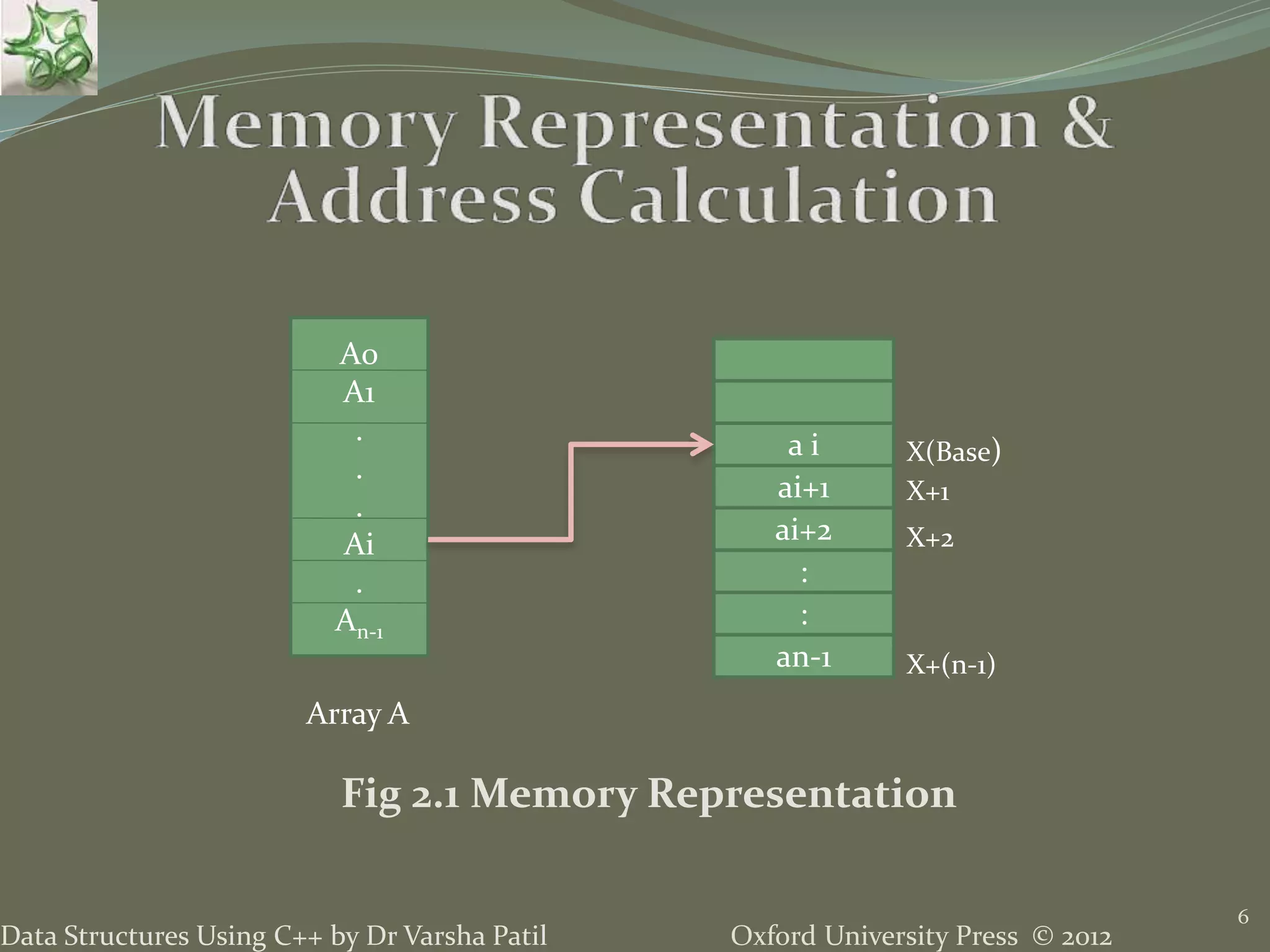





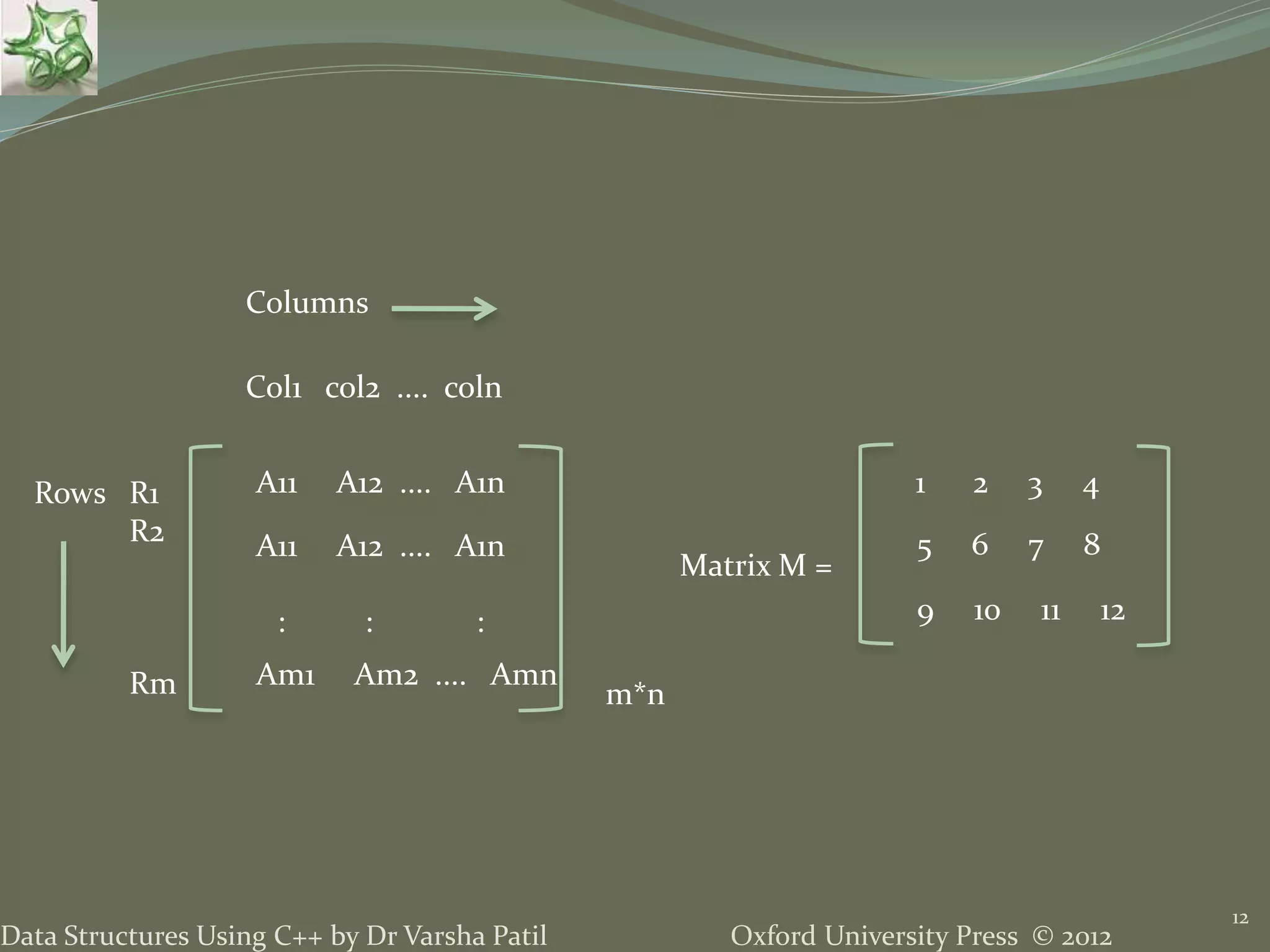


![15 The address of the element of the ith row and the jth column for matrix of size m x n can be calculated as: Addr(A[i][j]) = Base Address+ Offset = Base Address + (number of rows placed before ith row * size of row) * (Size of Element) + (number of elements placed before in jth element in ith row)* size of element As row indexing starts from 0, i indicate number of rows before the ith row here and similarly for j. For Element Size = 1 the address is Address of A[i][j]= Base + (i * n ) + j Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012](https://image.slidesharecdn.com/2lineardatastructureusingarraysppt-150824111020-lva1-app6892/75/2-Linear-Data-Structure-Using-Arrays-Data-Structures-using-C-by-Varsha-Patil-15-2048.jpg)
![16 In general, Addr[i][j] = ((i–LB1) * (UB2 – LB2 + 1) * size) + ((j– LB2) * size) where number of rows placed before ith row = (i – LB1) where LB1 is the lower bound of the first dimension. Size of row = (number of elements in row) * (size of element)Memory Locations The number of elements in a row = (UB2 – LB2 + 1) where UB2 and LB2 are upper and lower bounds of the second dimension. Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012](https://image.slidesharecdn.com/2lineardatastructureusingarraysppt-150824111020-lva1-app6892/75/2-Linear-Data-Structure-Using-Arrays-Data-Structures-using-C-by-Varsha-Patil-16-2048.jpg)

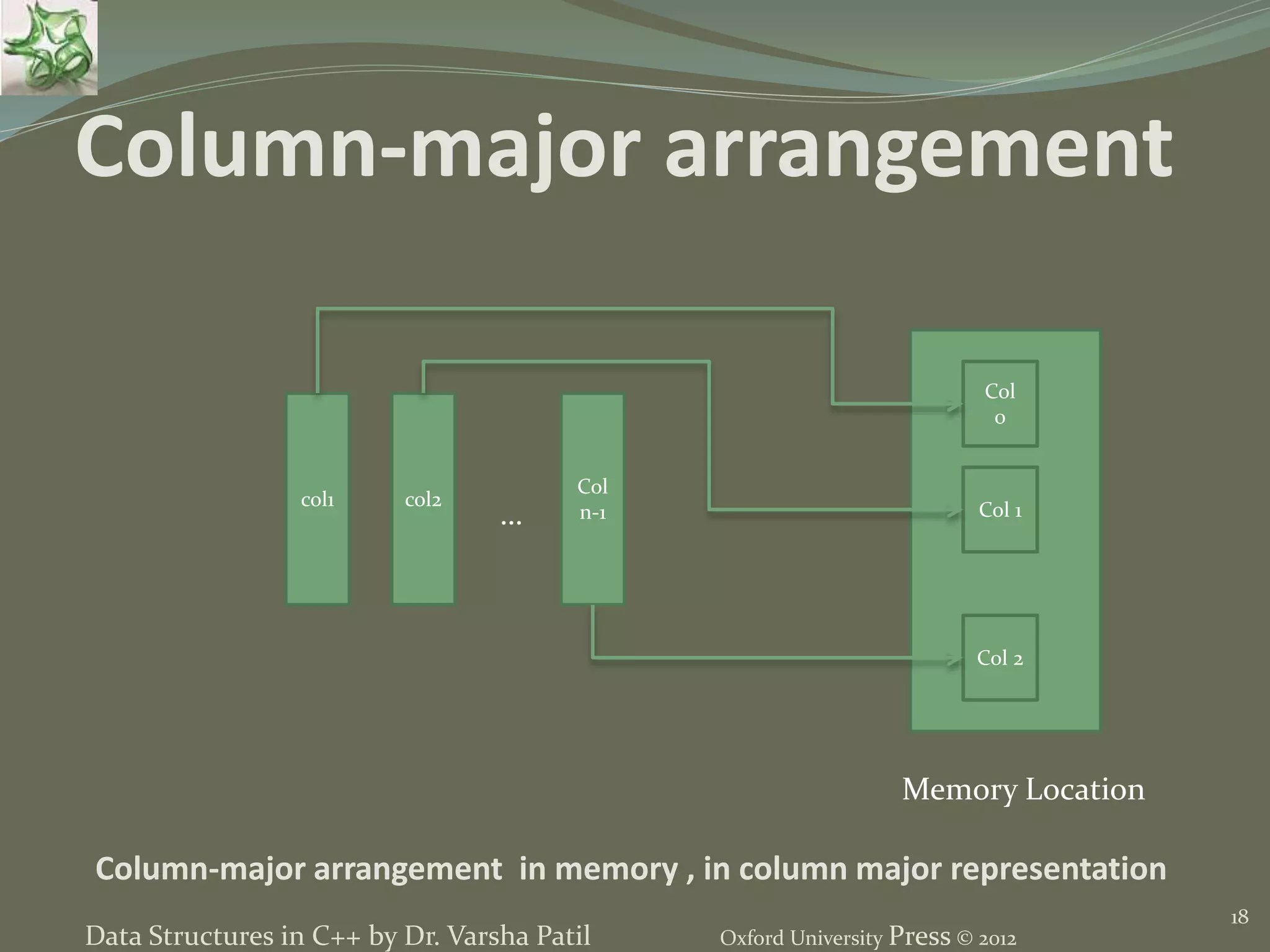
![19 The address of A[i][j] is computed as Addr(A[i][j]) = Base Address+ Offset= Base Address + (number of columns placed before jth column * size of column) * (Size of Element) + (number of elements placed before in ith element in ith row)* size of element For Element_Size = 1 the address is Address of A[i][j] for column major arrangement = Base + (j * m ) + I In general, for column-major arrangement; address of the element of the jth row and the jth column therefore is Addr (A[i][j] = ((j – LB2) * (UB1 – LB1 + 1) * size) + ((i –LB1) * size) Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012](https://image.slidesharecdn.com/2lineardatastructureusingarraysppt-150824111020-lva1-app6892/75/2-Linear-Data-Structure-Using-Arrays-Data-Structures-using-C-by-Varsha-Patil-19-2048.jpg)
![20 Example 2.1: Consider an integer array, int A[3][4] in C++. If the base address is 1050, find the address of the element A[2] [3] with row-major and column-major representation of the array. For C++, lower bound of index is 0 and we have m=3, n=4, and Base= 1050. Let us compute address of element A [2][3] using the address computation formula 1. Row-Major Representation: Address of A [2][3] = Base + (i * n ) + j = 1050 + (2 * 4) + 3 = 1061 Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012](https://image.slidesharecdn.com/2lineardatastructureusingarraysppt-150824111020-lva1-app6892/75/2-Linear-Data-Structure-Using-Arrays-Data-Structures-using-C-by-Varsha-Patil-20-2048.jpg)

![22 2. Column-Major Representation: Address of A [2][3] = Base + (j * m ) + i = 1050 + (3 * 3) + 2 = 1050 + 11 = 1061 Here the address of the element is same because it is the last member of last row and last column. Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012](https://image.slidesharecdn.com/2lineardatastructureusingarraysppt-150824111020-lva1-app6892/75/2-Linear-Data-Structure-Using-Arrays-Data-Structures-using-C-by-Varsha-Patil-22-2048.jpg)




![27 Three dimensions row-major arrangement (i*m2*m3) elements A[0][m2][m3] A[1][m2][m3] A[i][m2][m3] A[m1-1][m2] Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012](https://image.slidesharecdn.com/2lineardatastructureusingarraysppt-150824111020-lva1-app6892/75/2-Linear-Data-Structure-Using-Arrays-Data-Structures-using-C-by-Varsha-Patil-27-2048.jpg)
![28 The address of A[i][j][k] is computed as Addr of A[i][j][k] = X + i * m2 * m3 + j * m3 + k By generalizing this we get the address of A[i1][i2][i3] … [ in] in n- dimensional array A[m1][m2][m3]. ….[ mn ] Consider the address of A [0][0][0]…..[0] is X then the address of A [i][0][0]….[0] = X + (i1 * m2 * m3 * - - -- - * mn ) and Address of A [i1][i2] …. [0] = X + (i1 * m2 * m3 * - -- - *mn ) + (i2 * m3 * m4 *--- * mn) Continuing in a similar way, address of A[i1][i2][i3]- - - -[ in] will be Address of A[i1][i2][i3]----[ in] = X + (i1 * m2 * m3 * - - -- - * mn) + (i2 * m3 * m4 *--- - - * mn )+(i3 * m4 * m5--- * mn + (i4 * m5 * m6-- - - - * mn +…….+ in = Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012](https://image.slidesharecdn.com/2lineardatastructureusingarraysppt-150824111020-lva1-app6892/75/2-Linear-Data-Structure-Using-Arrays-Data-Structures-using-C-by-Varsha-Patil-28-2048.jpg)






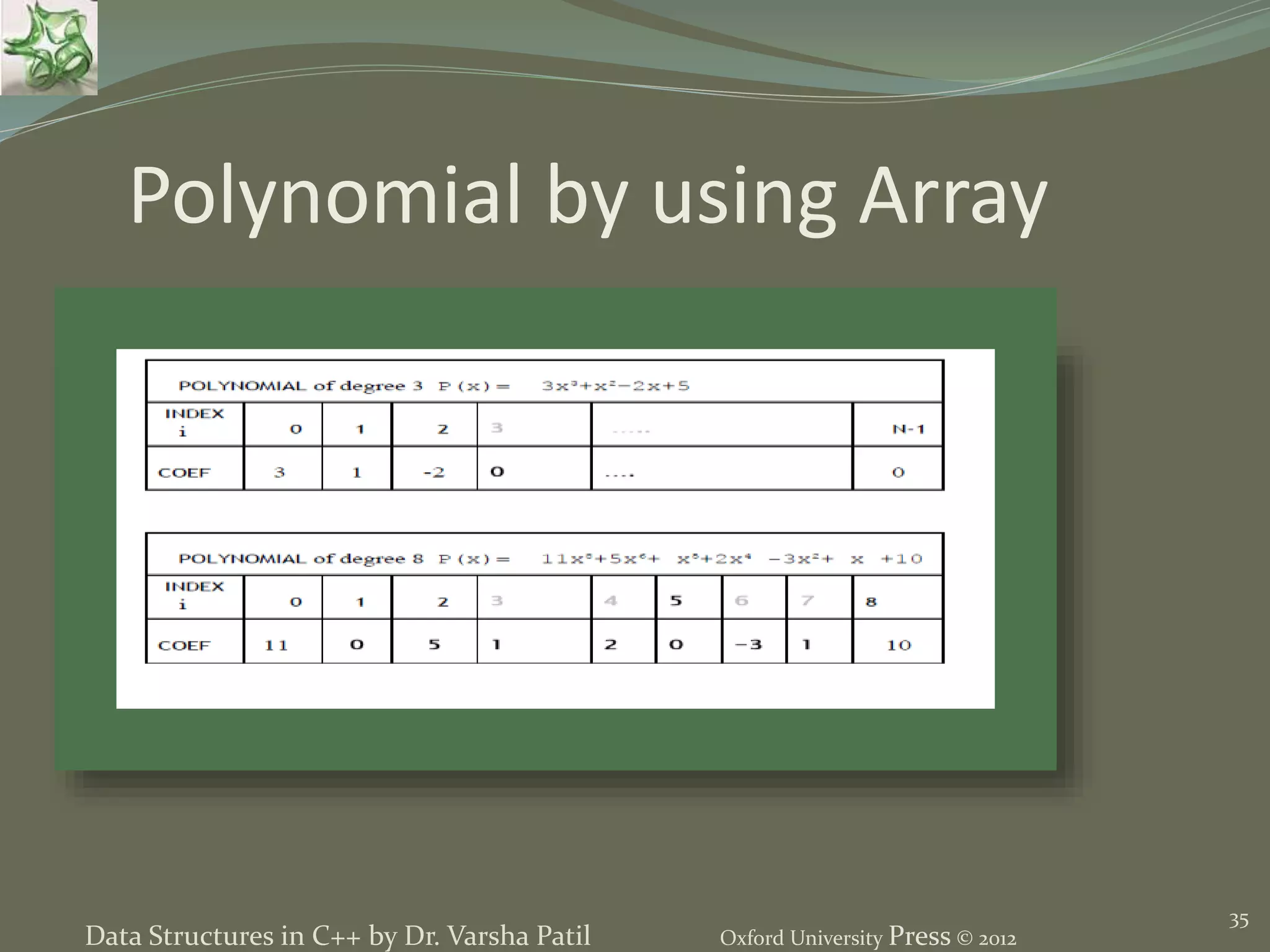


![39 AN ARRAY FOR FREQUENCY COUNT We can use array to store the number of times a particular element occurs in any sequence. Such occurrence of particular element is known as frequency count. void Frequency_Count ( int Freq[10 ], int A [ 100]) { int i; for ( i=0;i<10;i++) Freq[i]=0; for ( i=0;i<100;i++) Freq[A[i] ++; } Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012](https://image.slidesharecdn.com/2lineardatastructureusingarraysppt-150824111020-lva1-app6892/75/2-Linear-Data-Structure-Using-Arrays-Data-Structures-using-C-by-Varsha-Patil-39-2048.jpg)










![50 Basically a string is stored as a sequence of characters in one- dimensional character array say A. char A[10] ="STRING" ; Each string is terminated by a special character that is null character ‘0’. This null character indicates the end or termination of each string. Data Structures in C++ by Dr. Varsha Patil Oxford University Press © 2012](https://image.slidesharecdn.com/2lineardatastructureusingarraysppt-150824111020-lva1-app6892/75/2-Linear-Data-Structure-Using-Arrays-Data-Structures-using-C-by-Varsha-Patil-50-2048.jpg)





