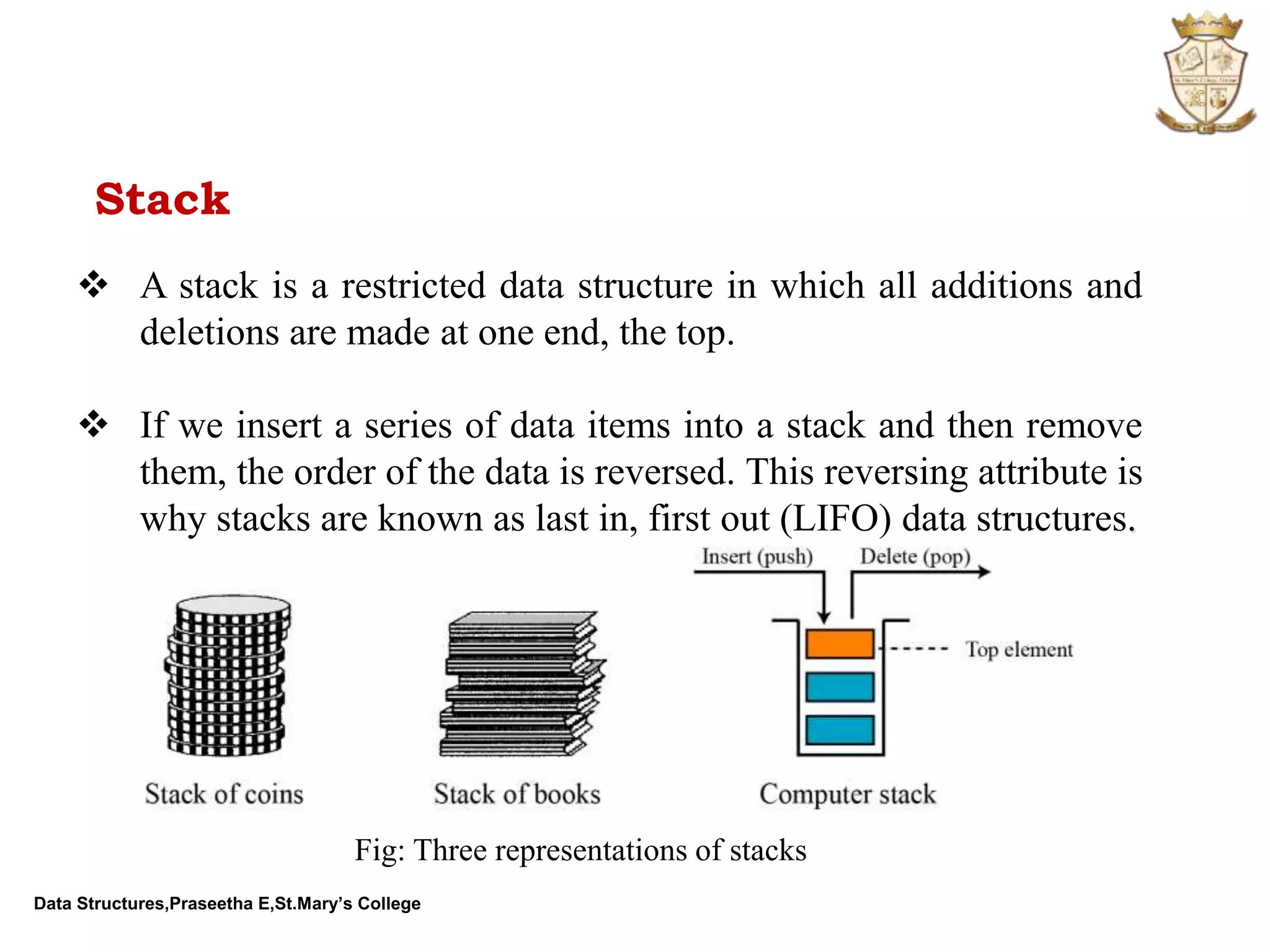
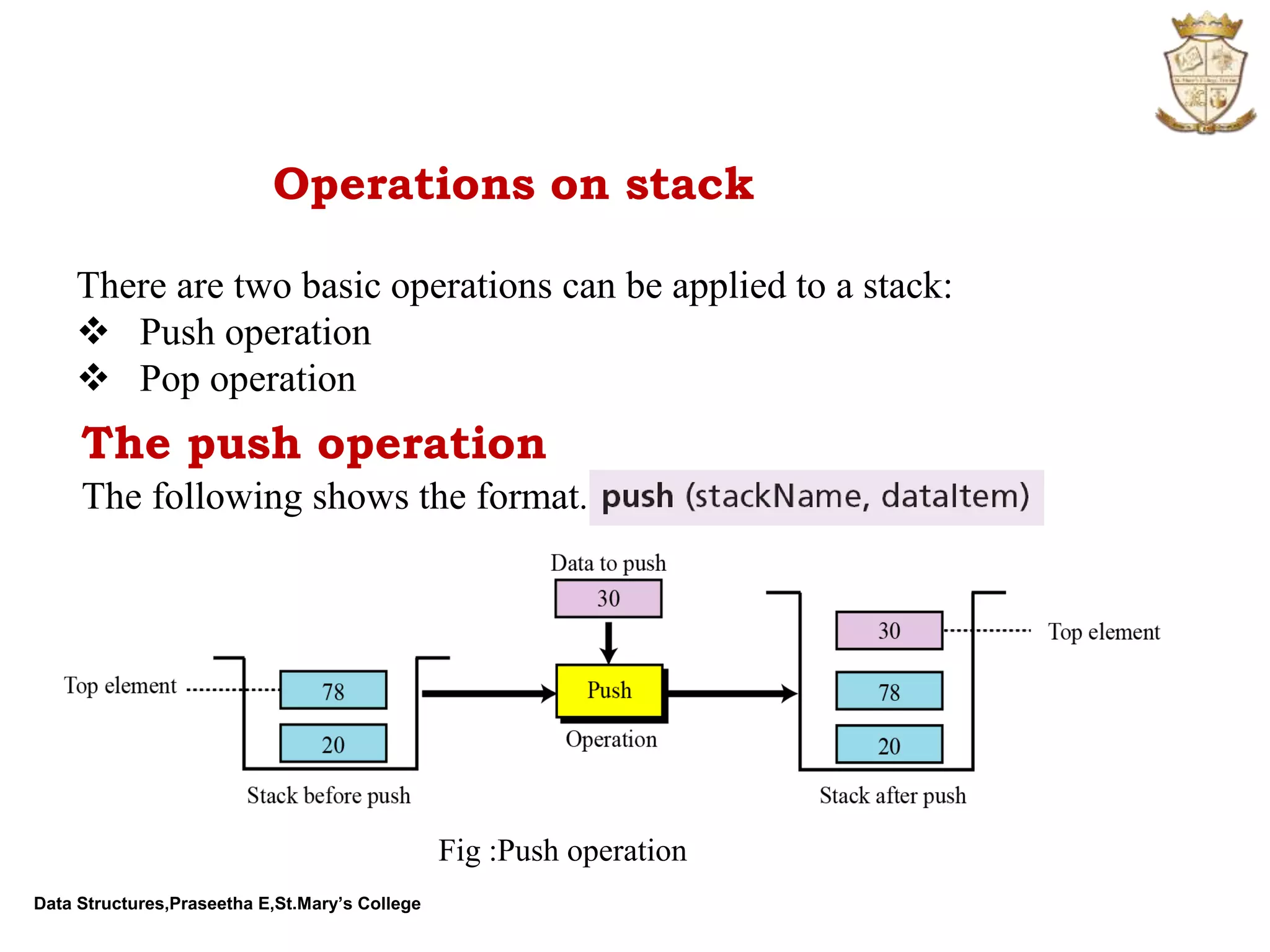
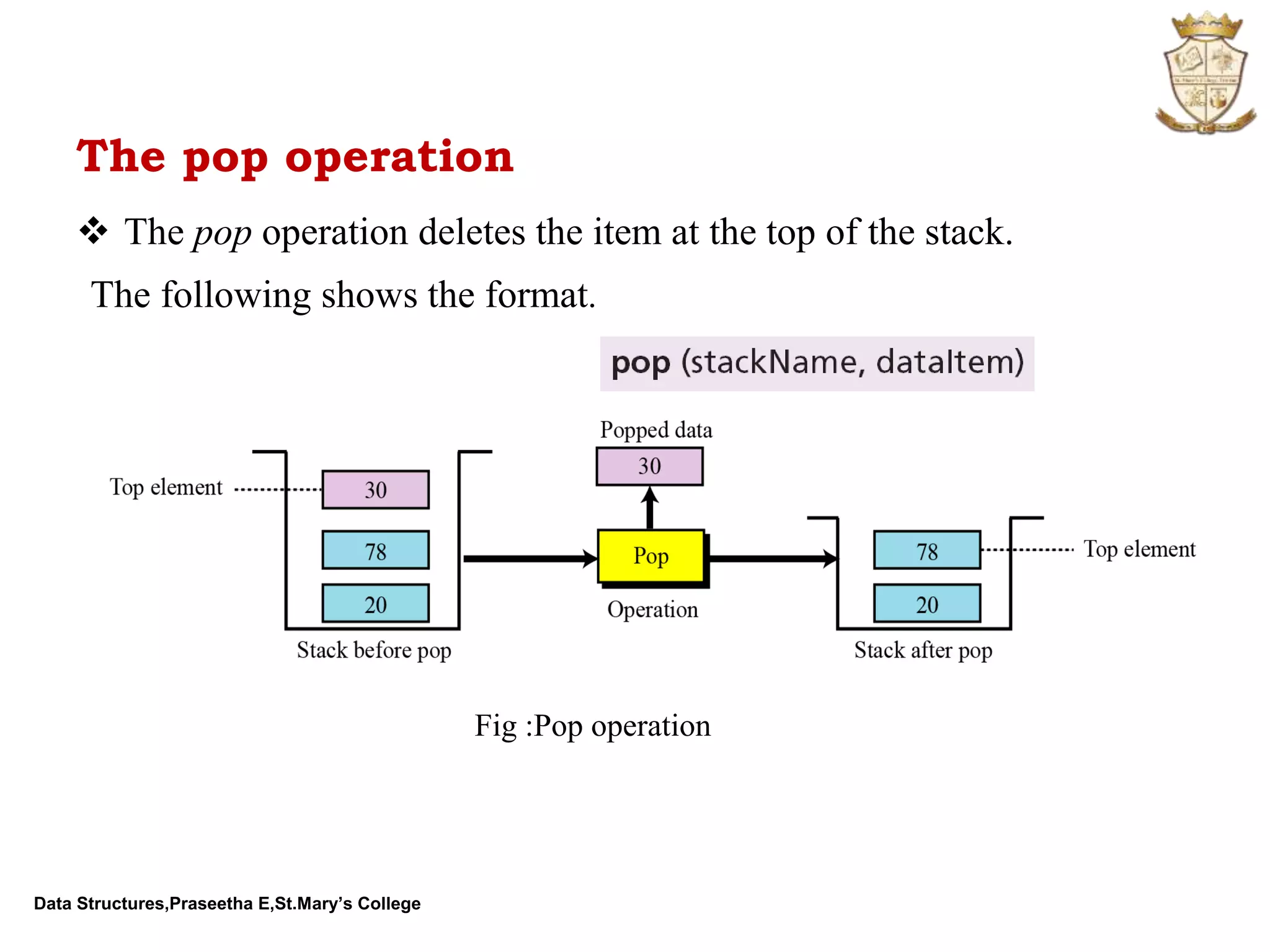
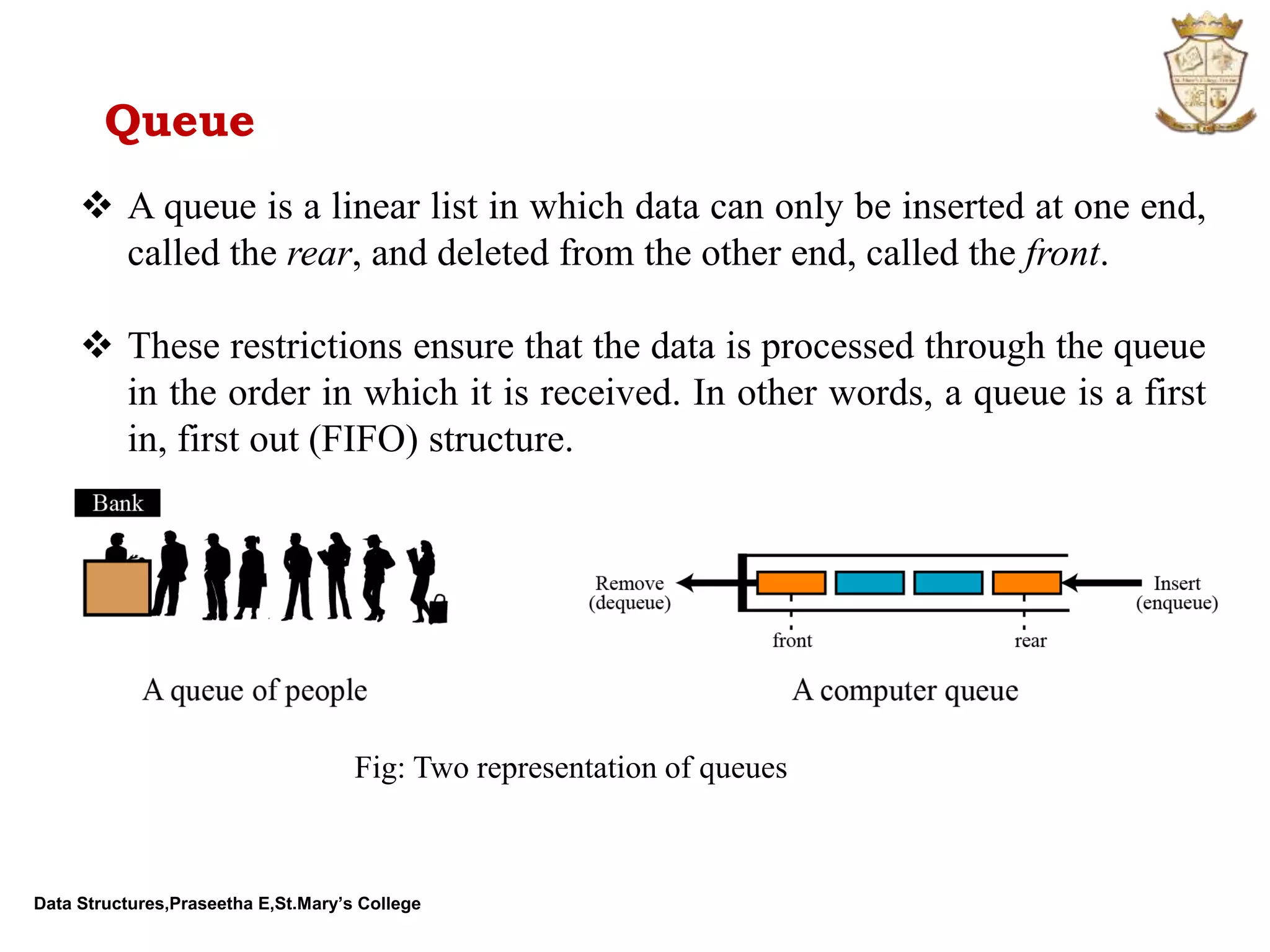
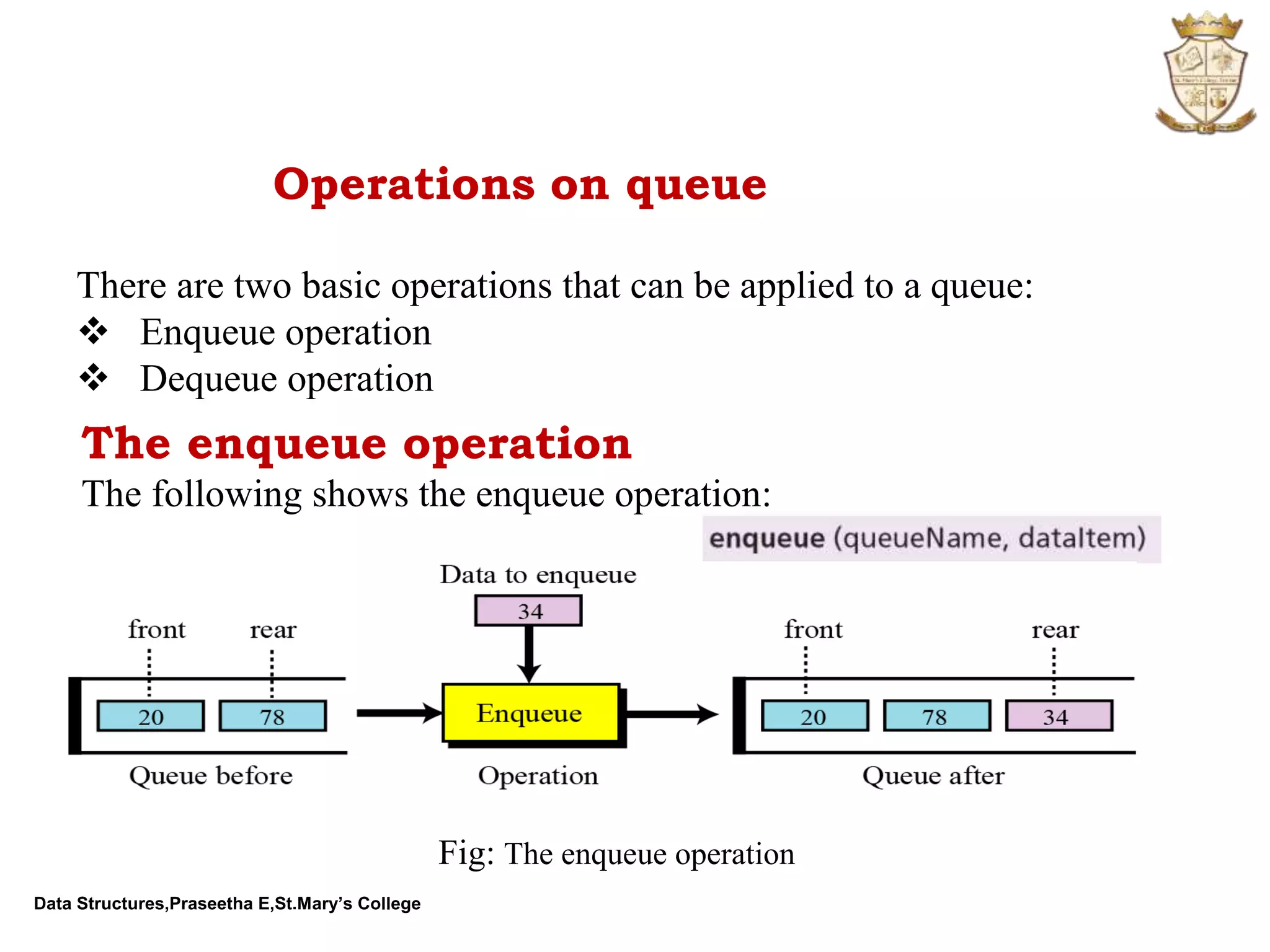
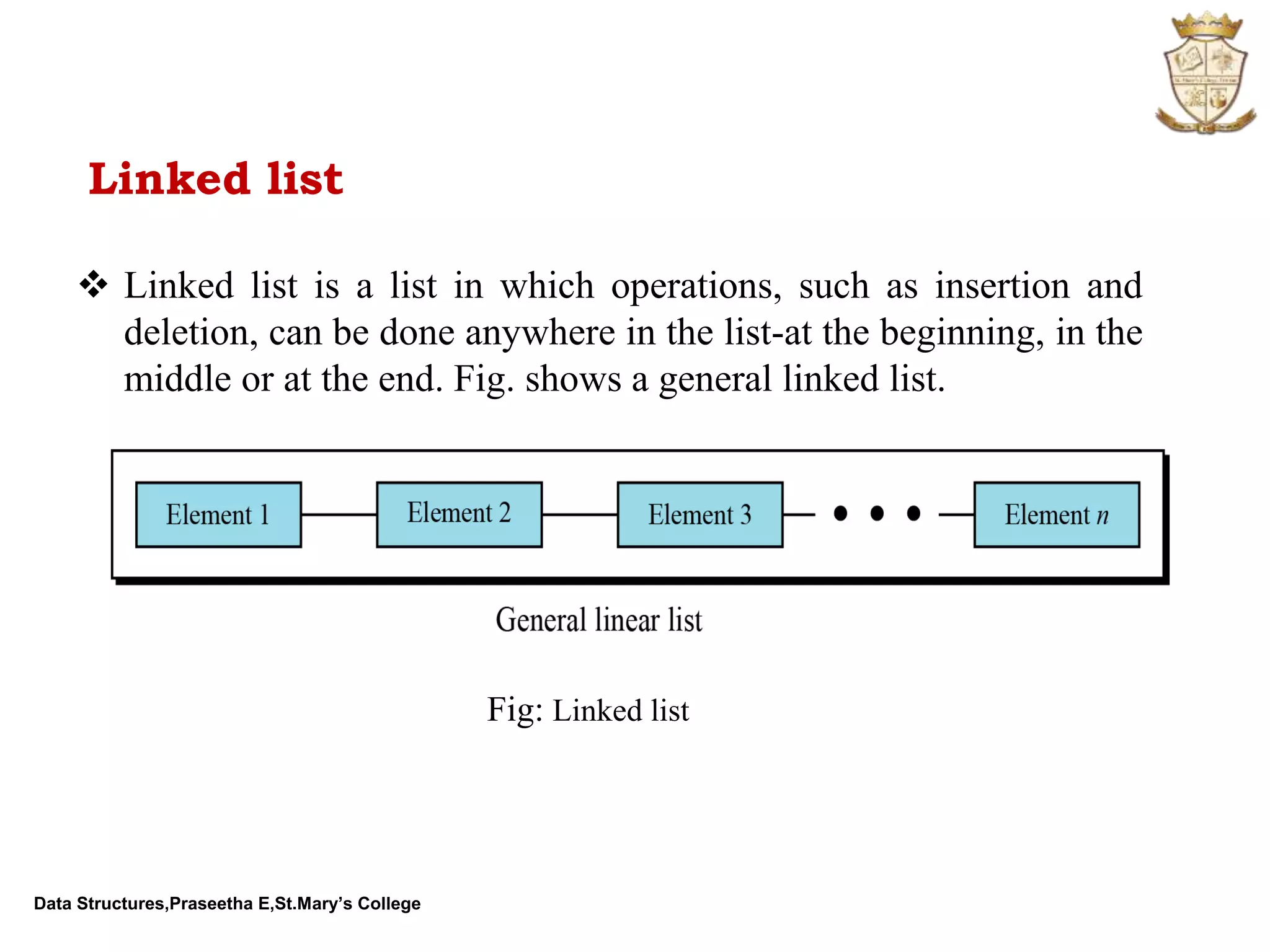
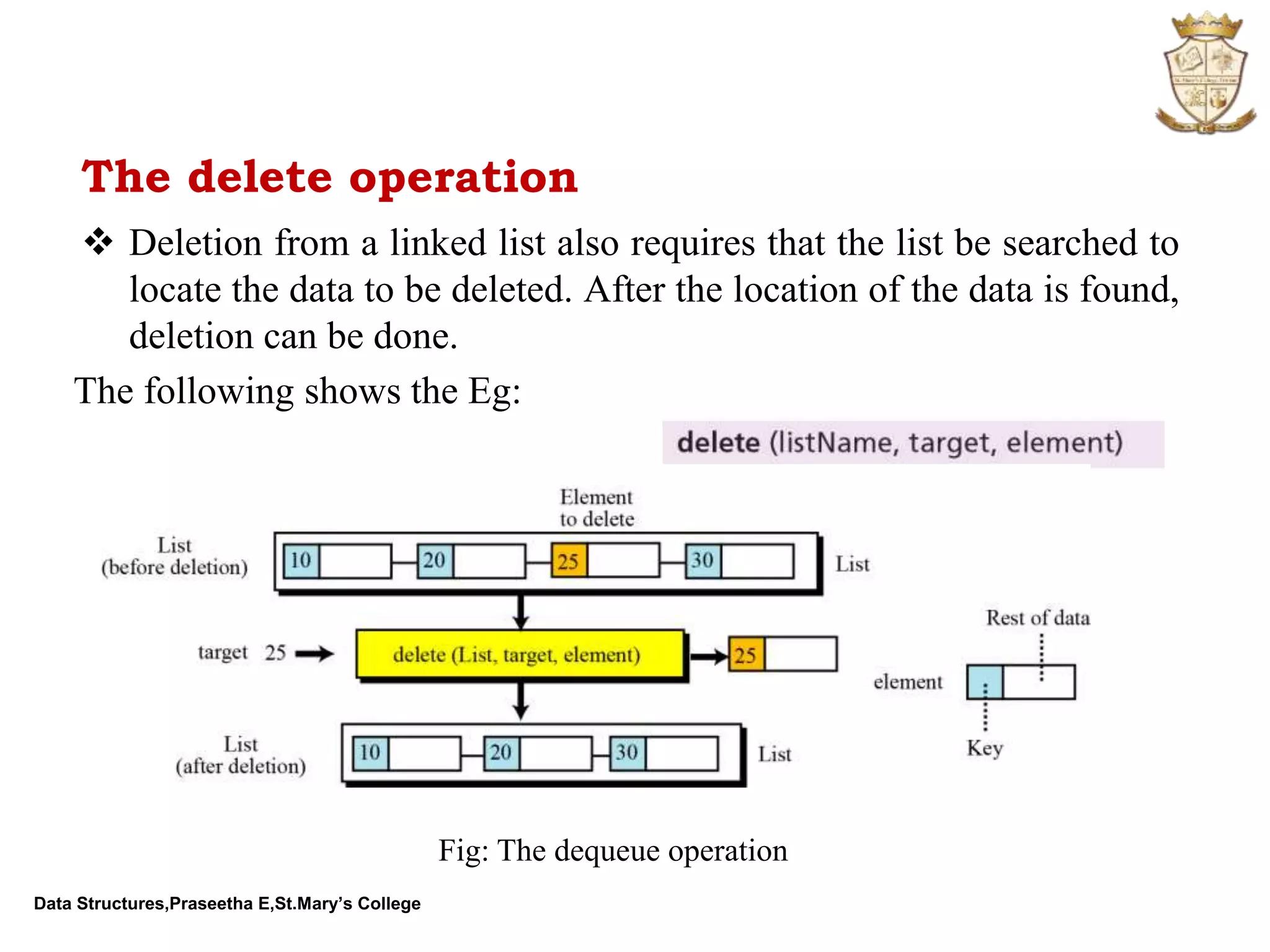
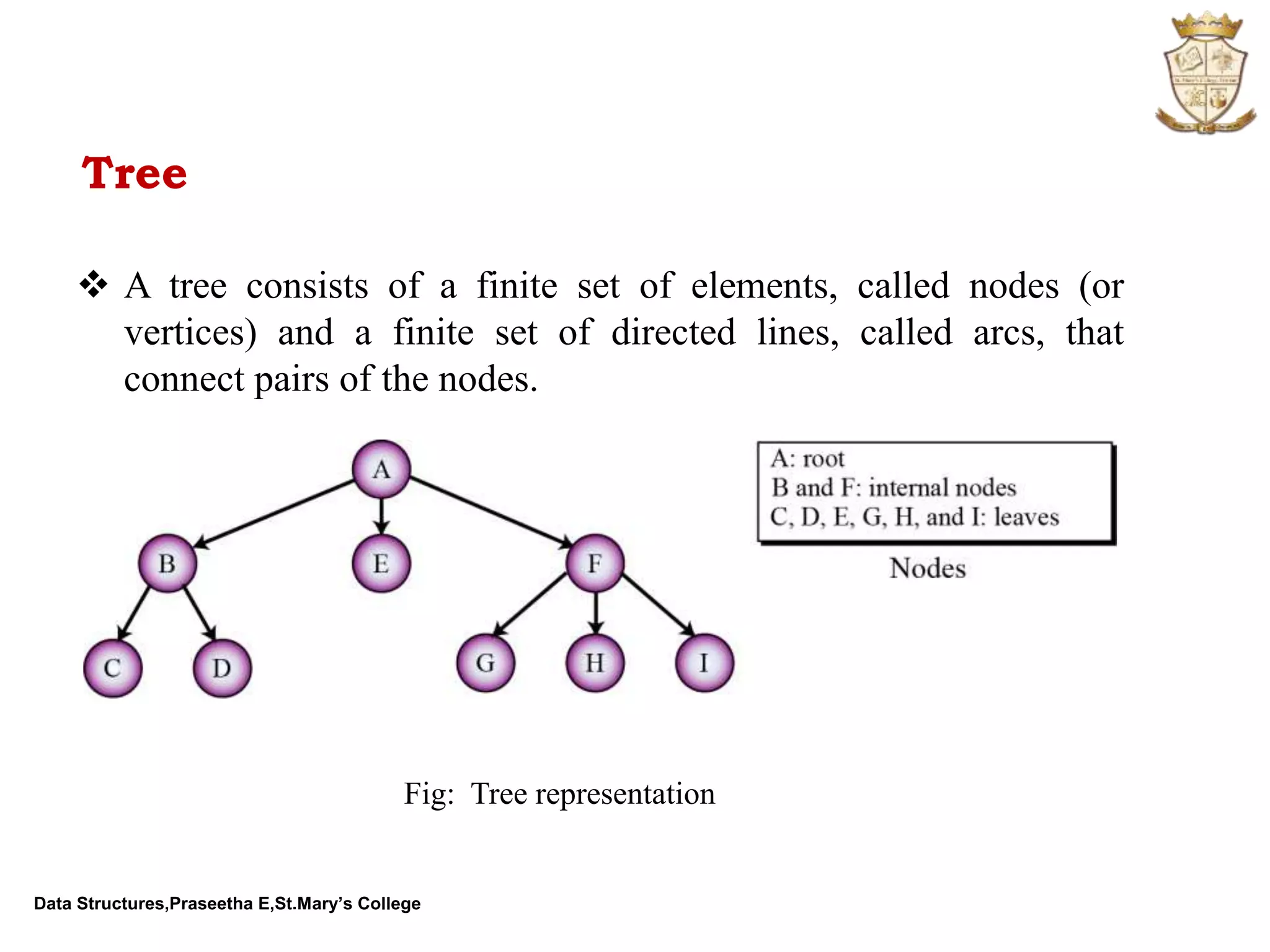
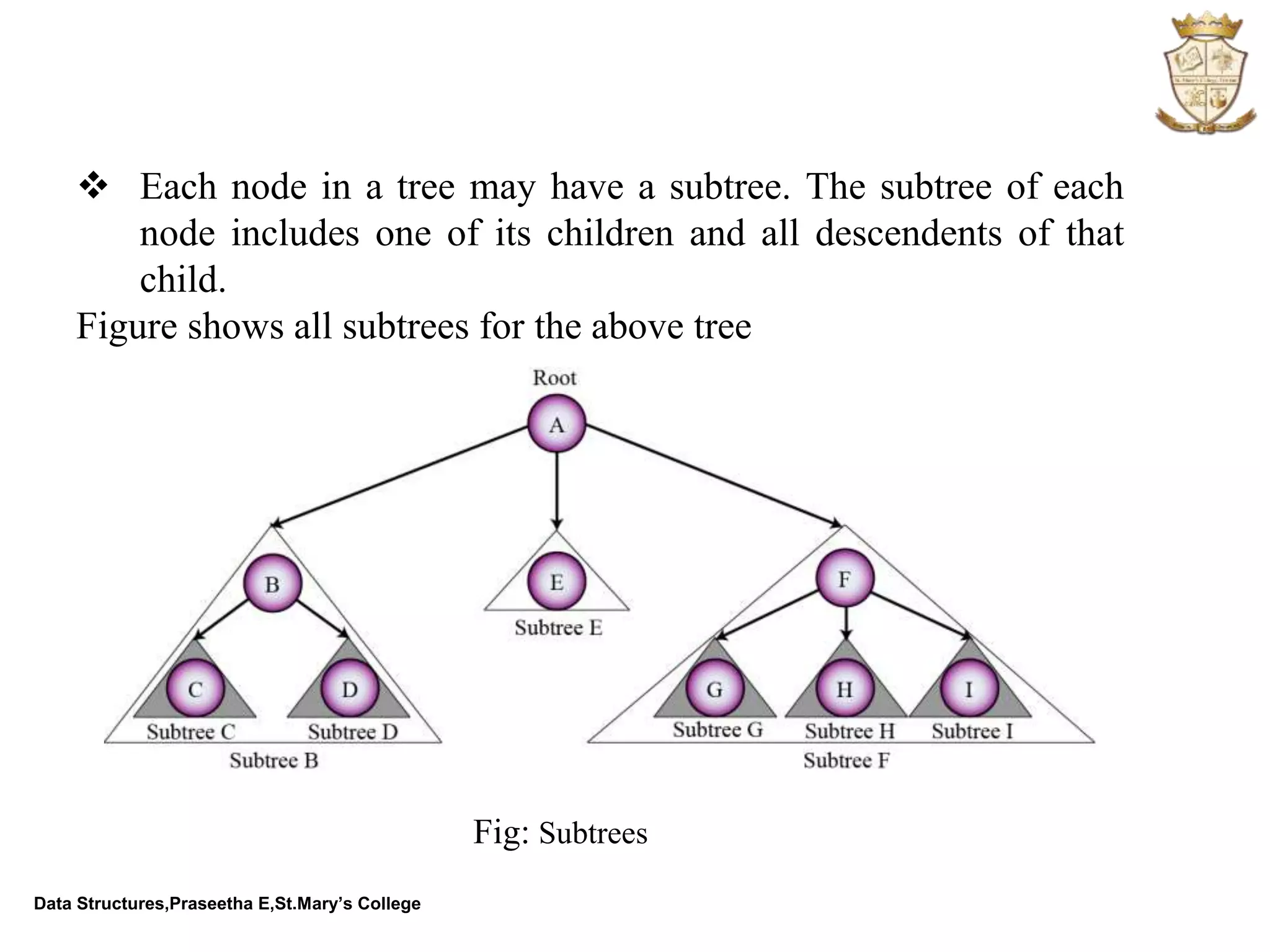
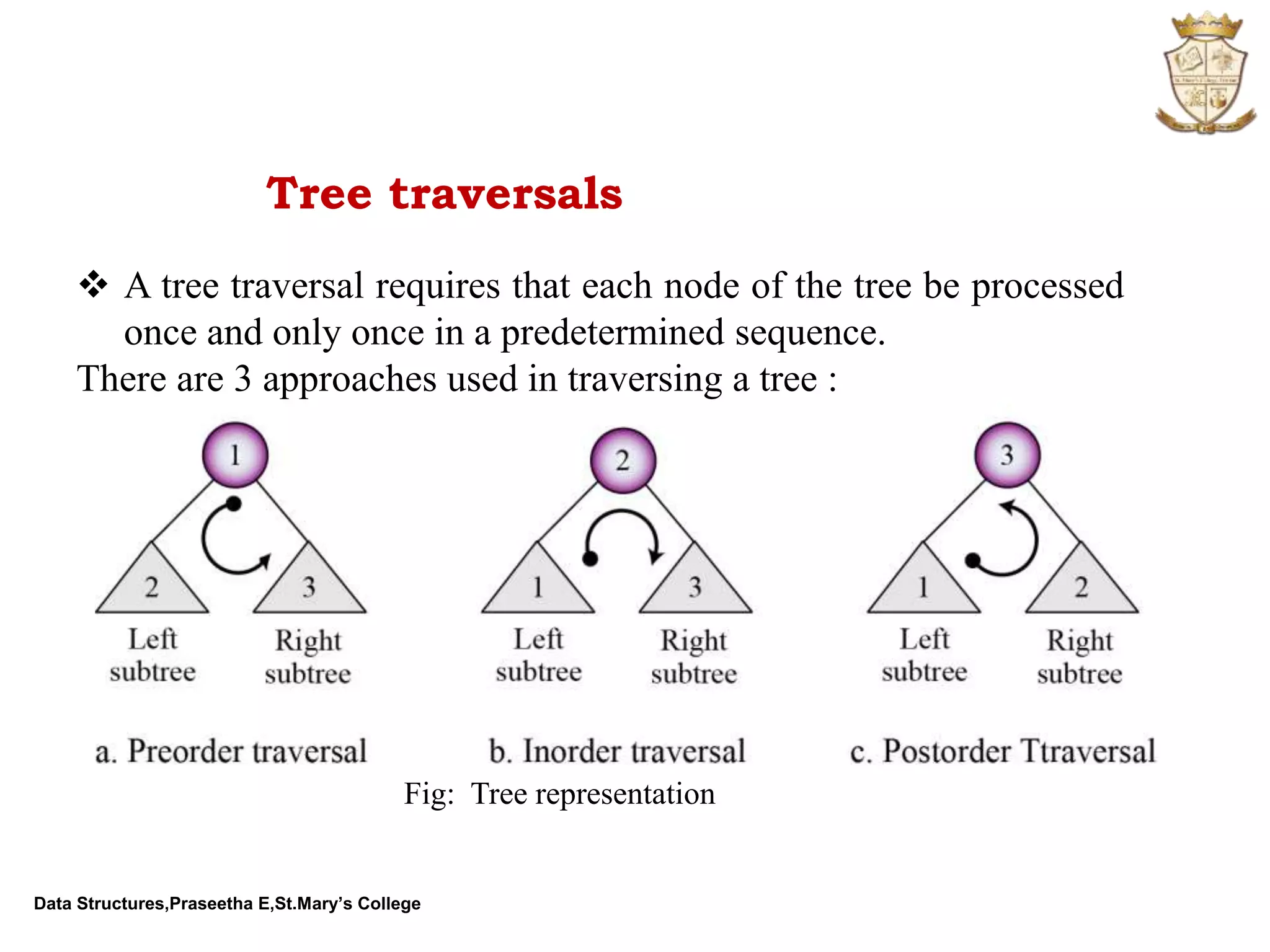
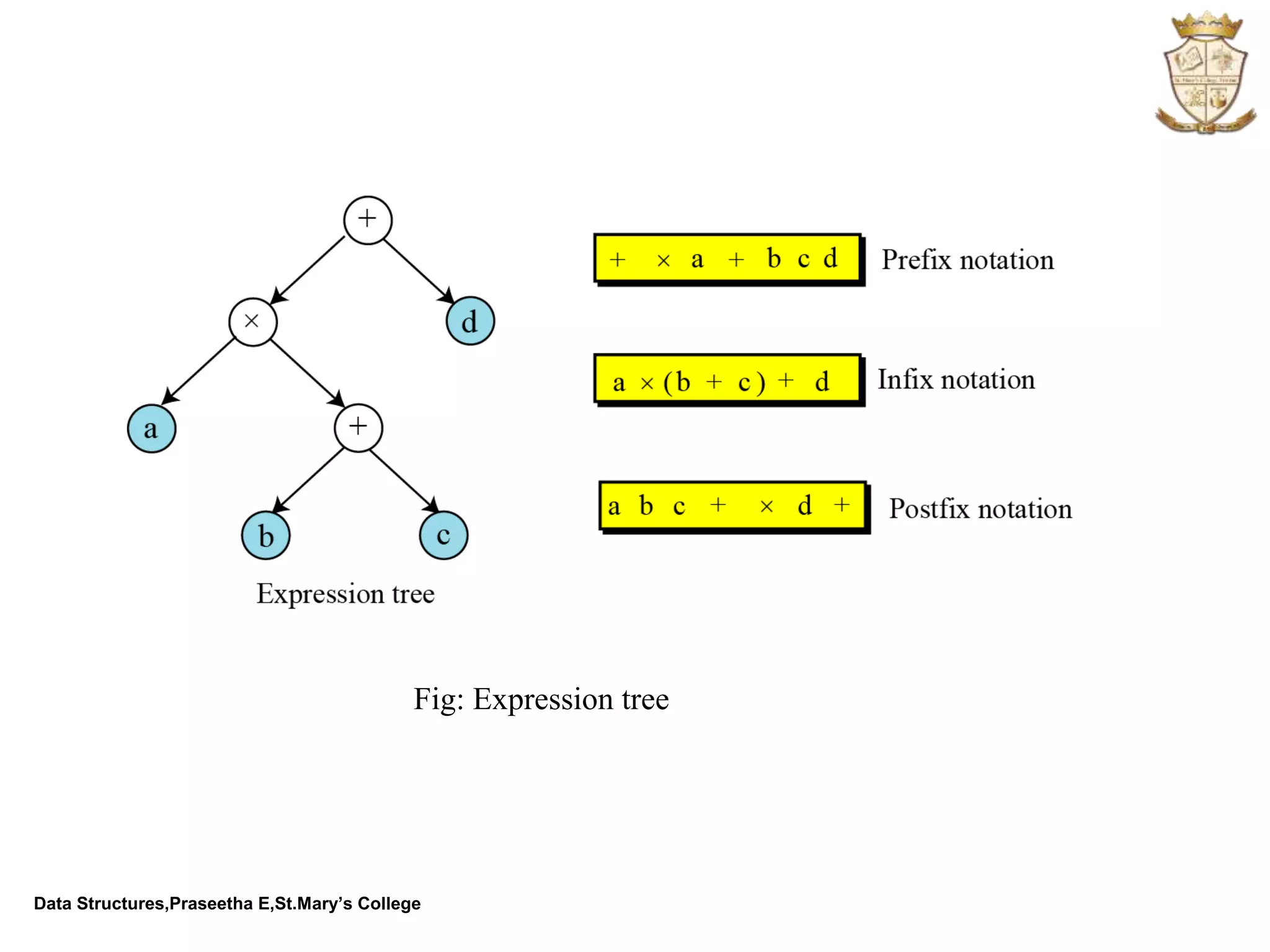
The document discusses abstract data types (ADTs) and several common data structures, including stacks, queues, linked lists, trees, and their applications. An ADT defines a data type and operations on that data type without specifying how those operations are implemented. Common programming languages define simple ADTs like integers, while more complex ADTs like lists, stacks and queues must be explicitly defined. The key operations and applications of each data structure are described.