Queue - Data Structure - Notes

Queue - Data Structure - Notes

• 1.
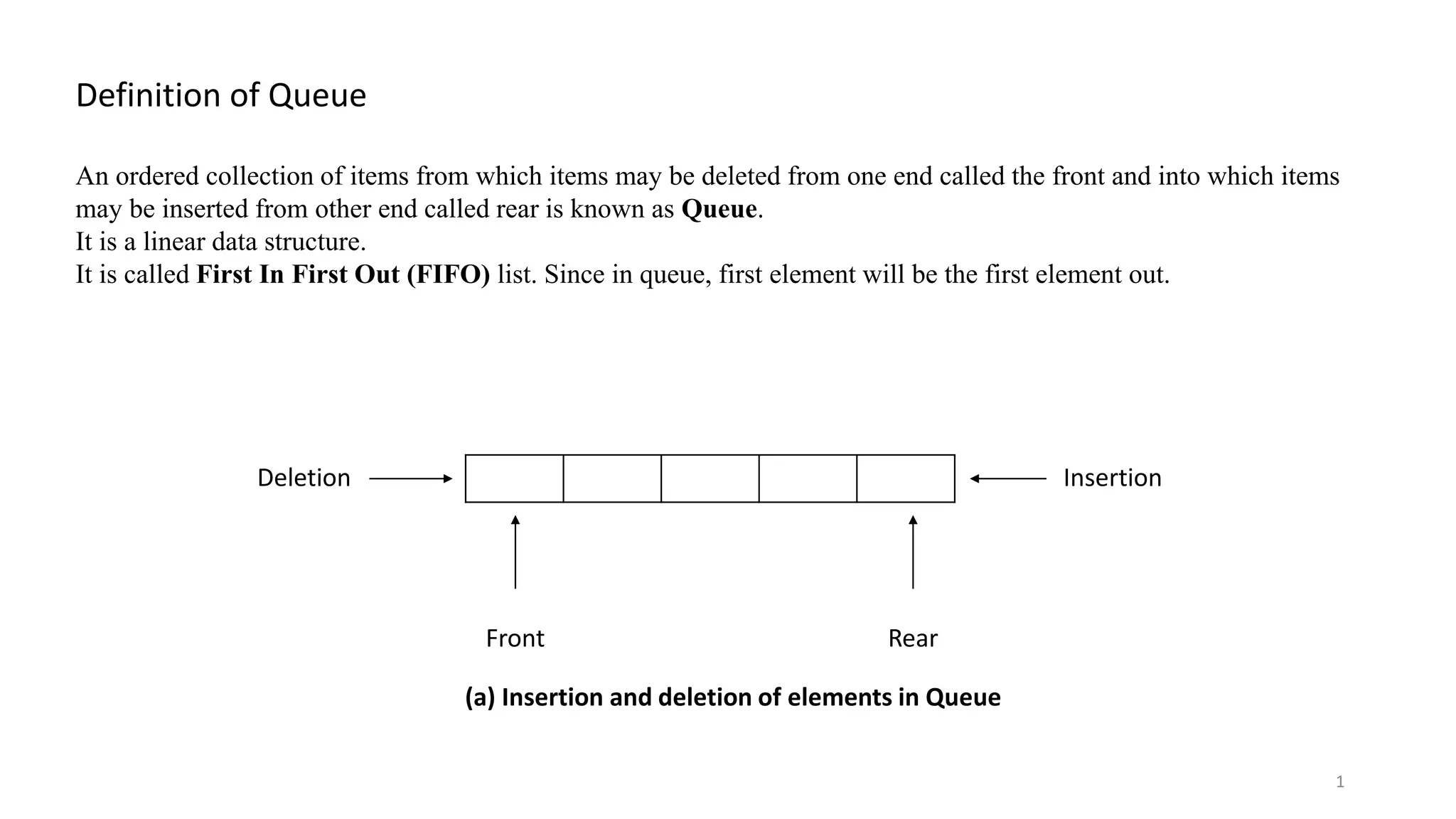
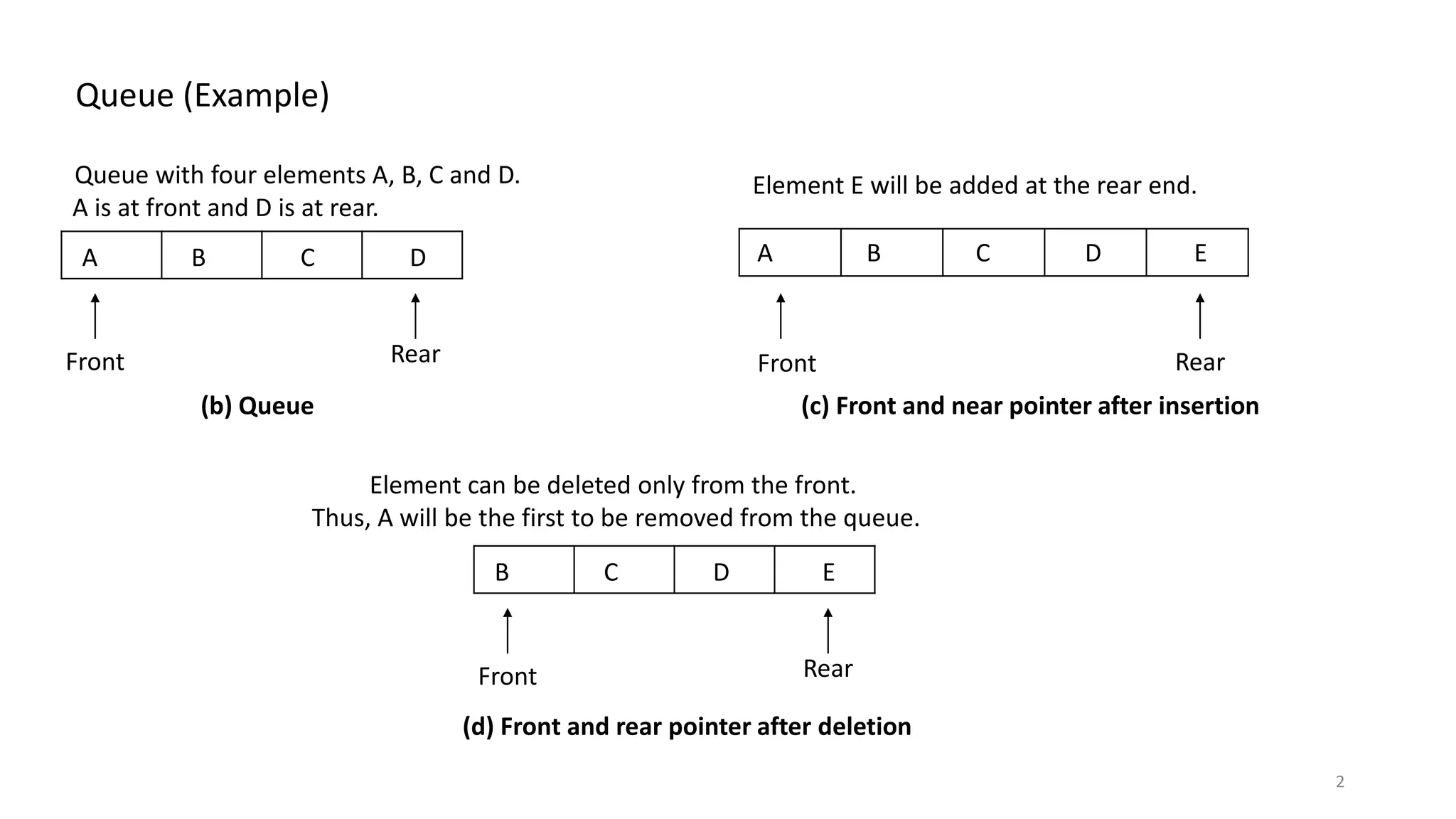
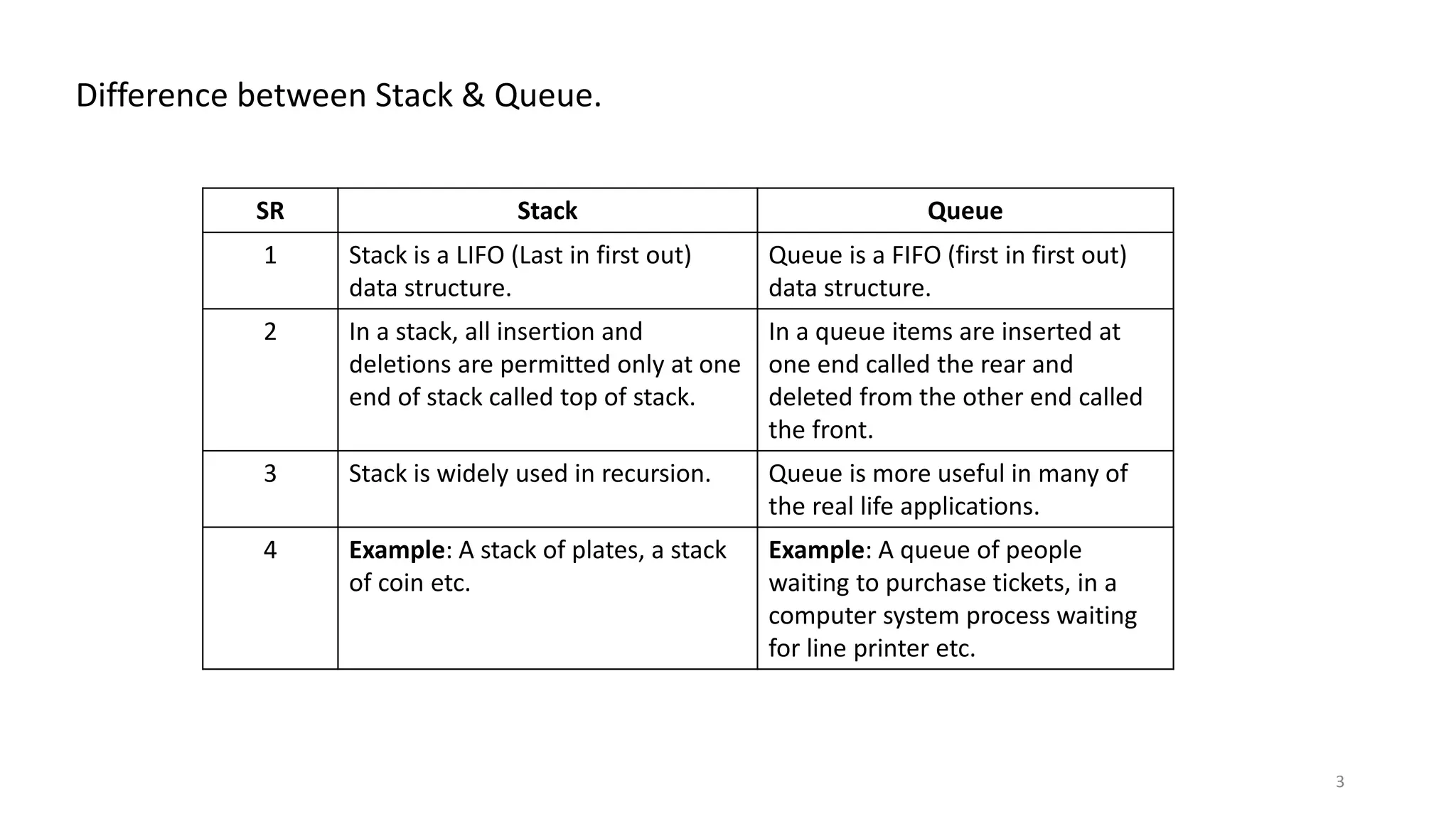
  Definition of Queue Anordered collection of items from which items may be deleted from one end called the front and into which items may be inserted from other end called rear is known as Queue. It is a linear data structure. It is called First In First Out (FIFO) list. Since in queue, first element will be the first element out. 1 Deletion Front Rear Insertion (a) Insertion and deletion of elements in Queue
• 2.
  Queue (Example) 2 Front Rear (b)Queue A B C D Front Rear A B C D E (c) Front and near pointer after insertion Front Rear (d) Front and rear pointer after deletion B C D E Element E will be added at the rear end.Queue with four elements A, B, C and D. A is at front and D is at rear. Element can be deleted only from the front. Thus, A will be the first to be removed from the queue.
• 3.
  Difference between Stack& Queue. 3 SR Stack Queue 1 Stack is a LIFO (Last in first out) data structure. Queue is a FIFO (first in first out) data structure. 2 In a stack, all insertion and deletions are permitted only at one end of stack called top of stack. In a queue items are inserted at one end called the rear and deleted from the other end called the front. 3 Stack is widely used in recursion. Queue is more useful in many of the real life applications. 4 Example: A stack of plates, a stack of coin etc. Example: A queue of people waiting to purchase tickets, in a computer system process waiting for line printer etc.
• 4.
  Operations on aQueue. 1. Create: Creates empty queue. 2. Insert: Add new element at rear. 3. Delete: Delete element at front. 4. Isempty: Checks queue is empty or not. 5. Isfull: Checks queue is full or not. 4
• 5.
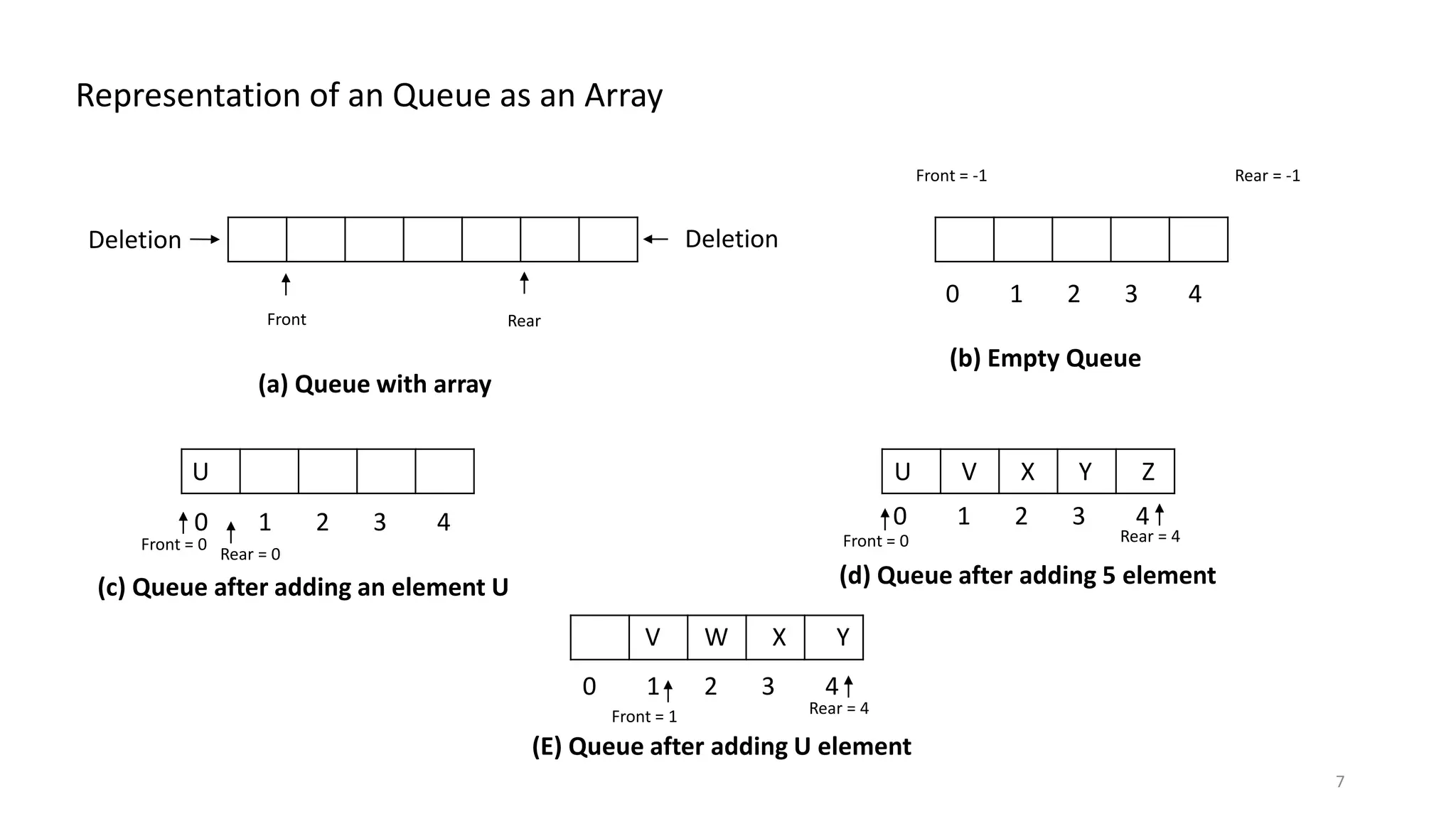
  Algorithm to insertand delete element in the Queue. 1. Create an empty queue by giving name and 2. Initially assign Rear = -1, front = -1. 3. If choice == Insert then if Rear == max-1 then print “queue is full” else Rear = Rear +1 q [Rear] = element 4. If choice == Delete then If front == -1 then print “queue is empty” else front = front +1 5. Stop 5
• 6.
  Queue as anabstract data type (1) Initialize the queue to be empty. (2) Check if the queue is empty or not. (3) Check if the queue is full or not. (4) Insert a new element in the queue if it is not full. (5) Retrieve the value of first element of the queue, if the queue is not empty. (6) Delete the first element from the queue if it is not empty. Queue abstract data type = Queue elements + Queue operations. 6
• 7.
  Representation of anQueue as an Array 7 Deletion Front Rear Deletion (a) Queue with array Front = -1 Rear = -1 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 (b) Empty Queue (c) Queue after adding an element U (d) Queue after adding 5 element Front = 0 Rear = 0 Front = 0 Rear = 4 Front = 1 U V X Y ZU V W X Y Rear = 4 (E) Queue after adding U element
• 8.
  Types of Queue 1.Linear Queue. 2. Circular Queue. 3. Double ended Queue. 4. Priority Queue. 8
• 9.
  Circular Queue full(overflow) 9 60 30 60 50 40 20 10 Q[5] Q[1] Q[4] Q[0] Q[3] Q[2] Circular queue full
• 10.
  10 Circular Queue Empty(underflow) 60 Q[5] Q[1] Q[4] Q[0] Q[3] Q[2] Circular queue empty
• 11.
  Circular Queue Diagram& Algorithm (to insert) 11 Algorithm to insert an element into circular Queue. Step 1: If front = 0 and rear = MAX -1 then write ‘circular queue is overflow’ else if front = -1 and rear =-1 then set front = rear = 0 else if rear = MAX -1 and front !=0 set rear = 0 else set rear = rear +1 Step 2: Set queue[rear] = val Step 3: Exit 60 60 Q[0] Q[1] Q[4] Q[2]Q[3] Q[4] Q[3] Q[2] Q[1] Q[0] Rear Rear Front Front 20 5 10 5 20 10 30 (a) (b) • If a new element is to be inserted in the queue, the position of the element to be inserted will be calculated by the relation as follows: Rear = (rear +1) % MAXSIZE • If we add an element 30 to the queue. The rear is calculated as follows: rear = (rear +1) % MAXSIZE =(2+1) % 5 =3
• 12.
  Circular Queue Diagram& Algorithm (to delete) 12 Algorithm to delete an element into circular Queue. Step 1: If front = -1 the write ‘queue underflow’ Step 2: Set val = queue[front] Step 3: if front = rear set front = rear = -1 else if front = MAX – 1 set front = 0 else set front = front = -1 Step 4: Exit 60 Q[0] Q[1] Q[2]Q[3] Q[4] Rear Front 20 5 10 (c) The front is calculated as follow: front = (0 + 1) % 5 = 1 4
• 13.
  Double ended Queue& Type 13 A deque is a list in which the elements can be inserted or deleted at either end. In a dequeue two pointers are maintained LEFT and RIGHT which point to either end of the dequeue. Front Rear Insertion Deletion Insertion Deletion Left = 3 Right = 7 0 1 2 3 4 5 6 7 8 9 29 37 45 54 63 (a) Double-ended queue (1) Input Restricted dequeue: In this dequeue, insertion can be done only at one of the dequeue while deletions can be done from both ends. Insertion Deletion Deletion (b) Input restricted dequeue
• 14.
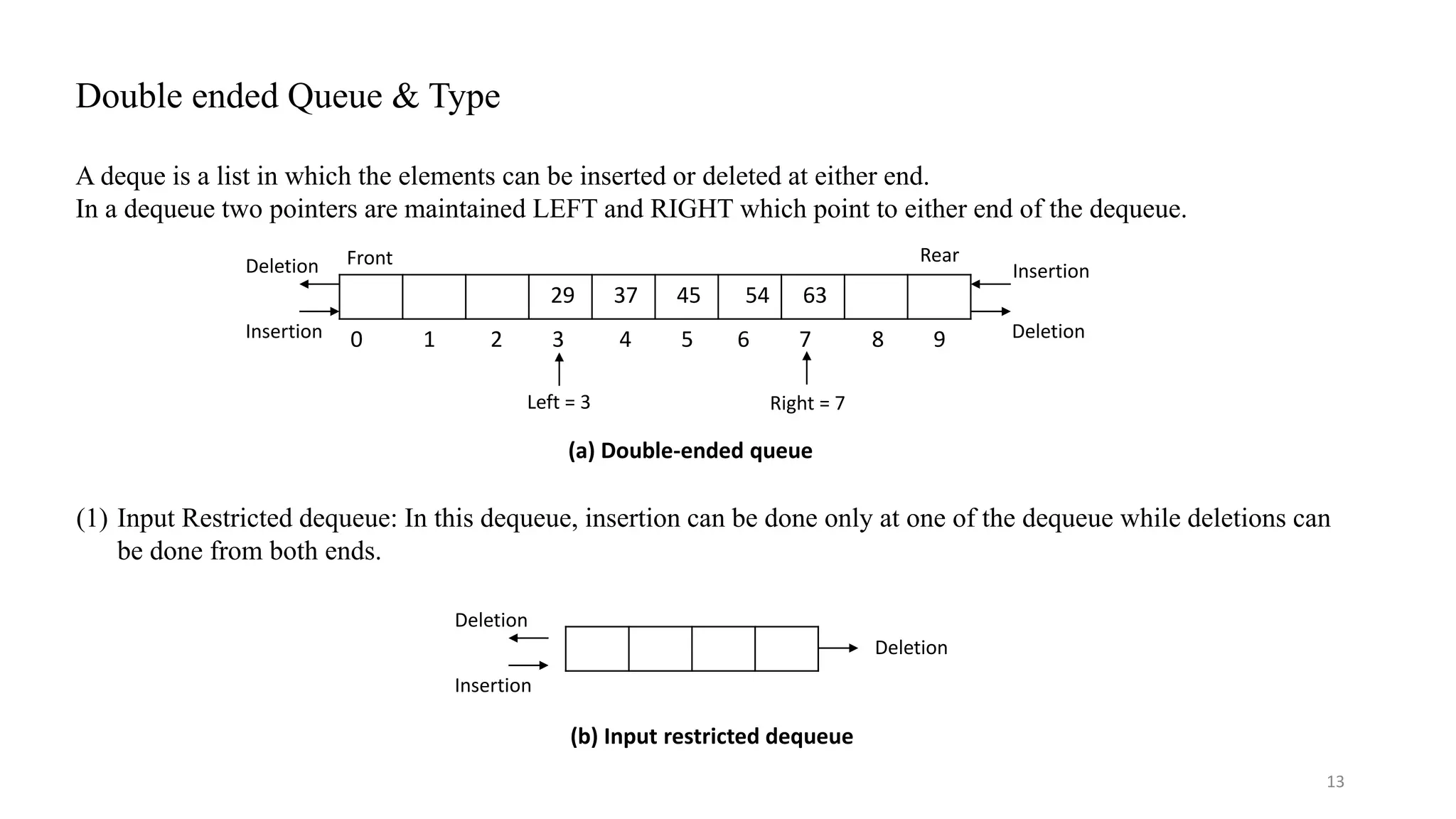
  Double Ended QueueAlgorithm to Insert at the Rear & Front End 14 Algorithm to insert at the Rear End. Step 1: if (Rear = (max -1)) then print “Queue is full” Step 2: set Rear = Rear +1 Step 3: Queue[Rear] = element Step 4: Exit Algorithm to insert at the Front End. Step 1: if front == 0 then print “Queue is full” rerun Step 2: front = front -1 Step 3: Queue[front] = element Step 4: Exit
• 15.
  Double Ended QueueAlgorithm to Delete from the Rear & Front End 15 Algorithm to delete at the Rear End. Step 1: if (front == rear) then print “Queue is empty” return Step 2: Rear = Rear -1 Step 3: element = Queue[Rear] Step 4: Exit Algorithm to insert at the Front End. Step 1: if (front == Rear) then print “Queue is empty” rerun Step 2: front = front +1 Step 3: element = Queue[front] Step 4: Exit
• 16.
  Priority Queue In apriority queue ( i ) each element is assign a priority ( ii ) The elements are processed according to • Highest priority element is processed before lower priority element. • Two elements of same priority are processed according to the order of insertion. A priority queue contains a collection of items that are waiting to be processed. In queue, items are removed for processing in the same order in which they are added to the queue. In a priority queue, however, each item, has a priority, and when its time to select an item, the item with the highest priority is the one that is order. 16 Types of Priority Queue 1. Ascending Priority Queue 2. Descending Priority Queue
• 17.
  Application of Queue •Queue are used in computer for scheduling of resources to application . These resources are CPU, Printer etc. • In batch Programming, multiple jobs are combined into a batch and the first program is executed first, the second is executed next and so on in a sequential manners. • A queue is used in break first search traversal of a graph & level wise traversal of tree. • Computer simulation, Airport simulation. 17