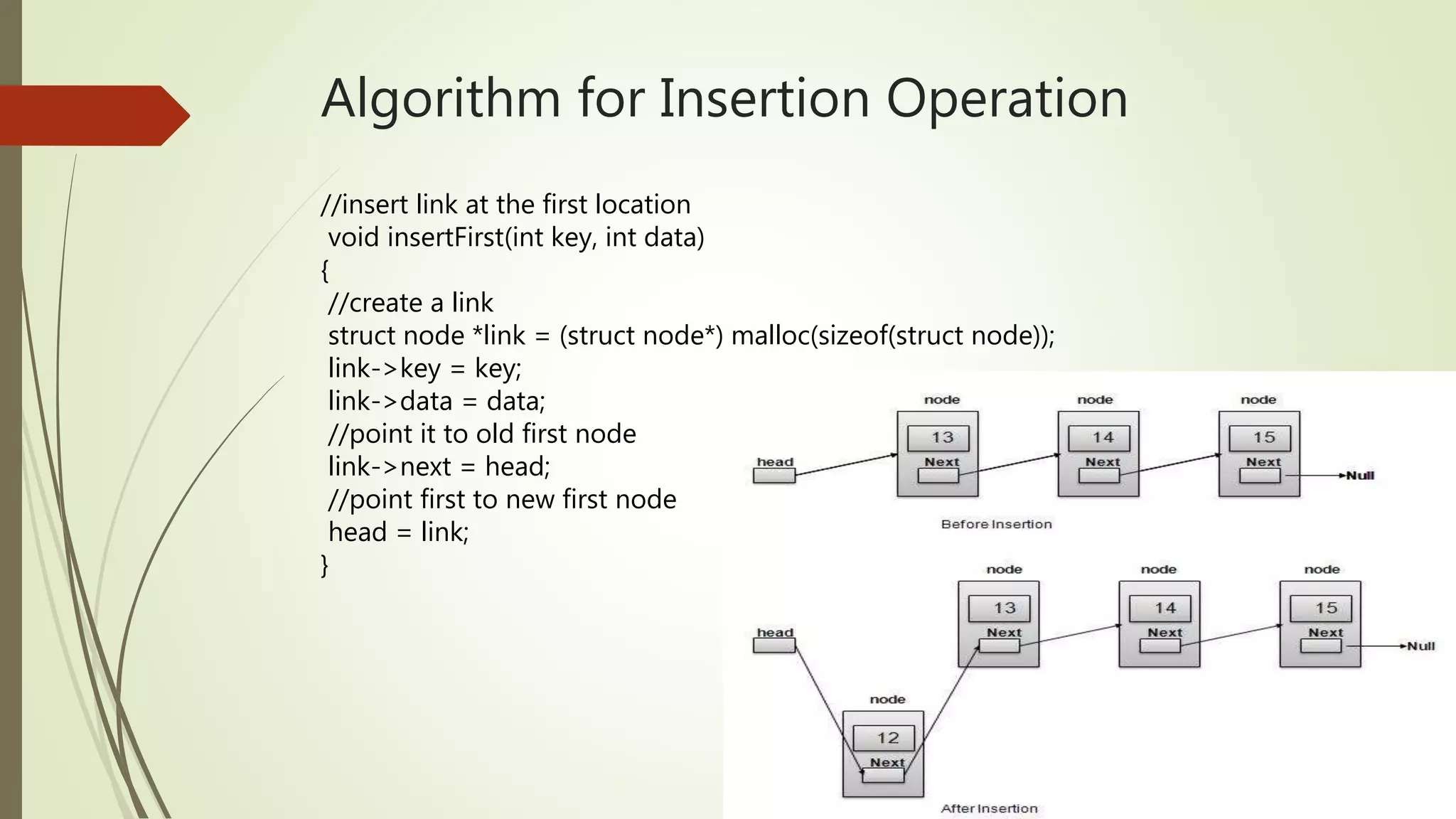
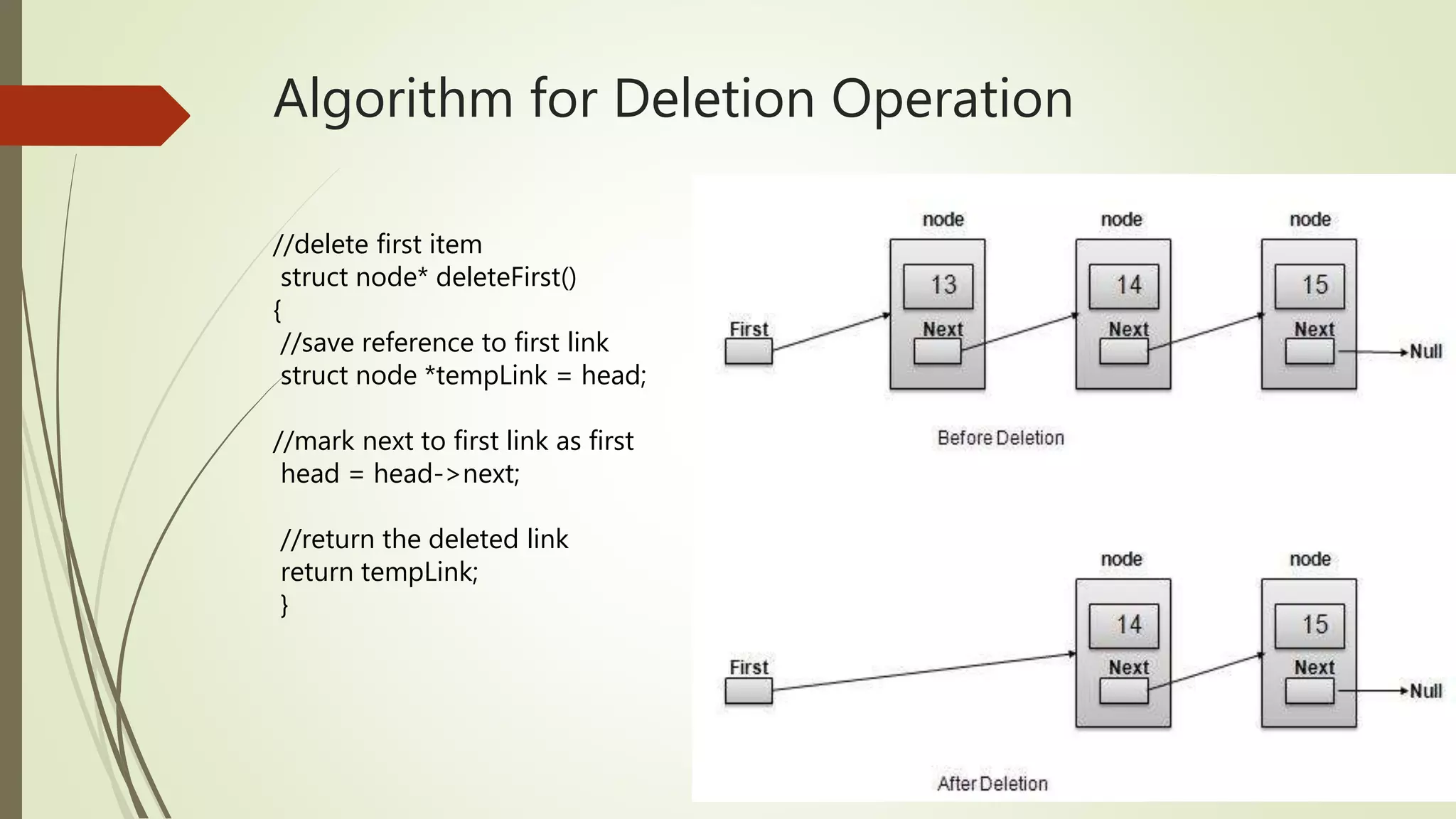
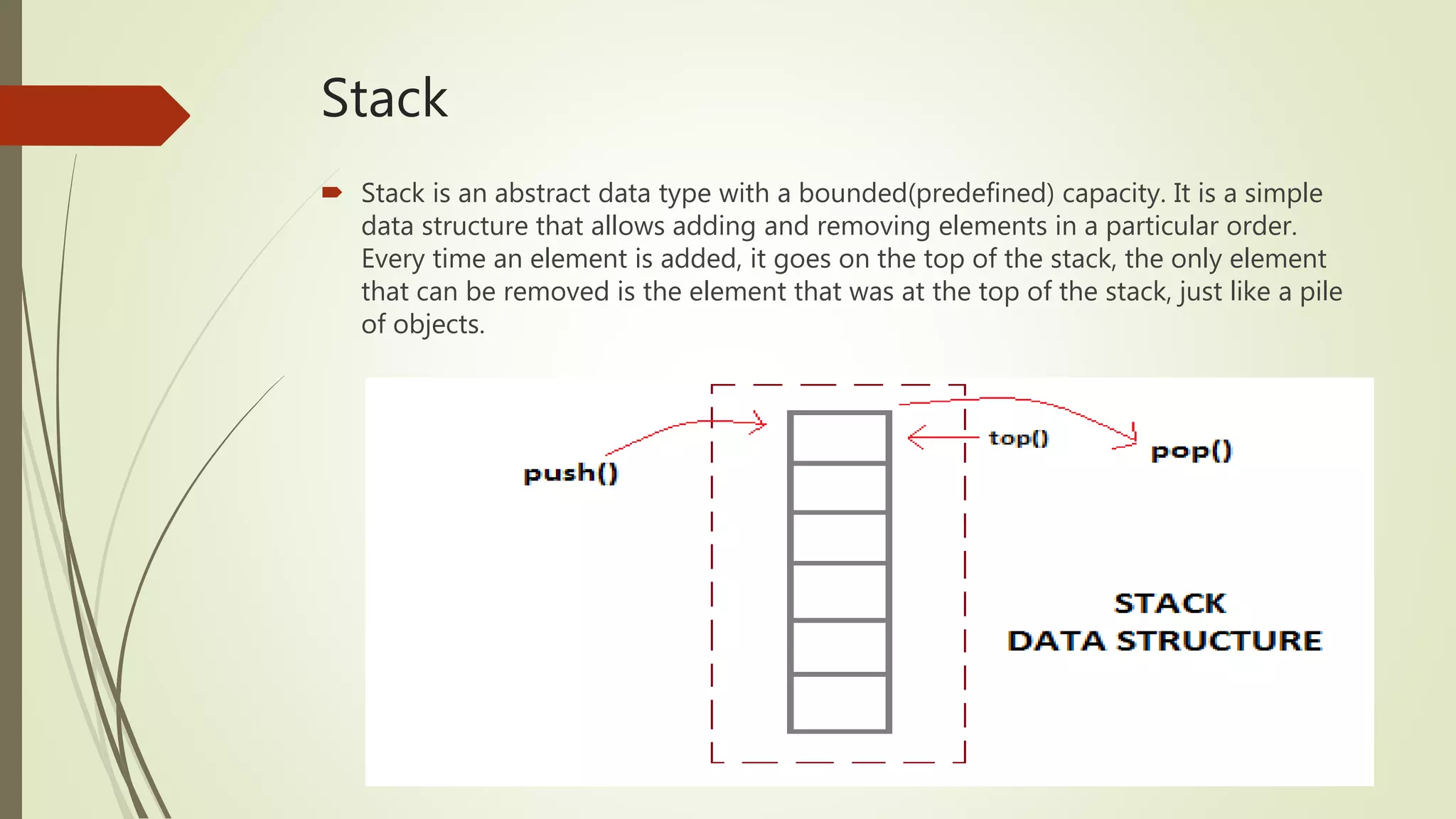
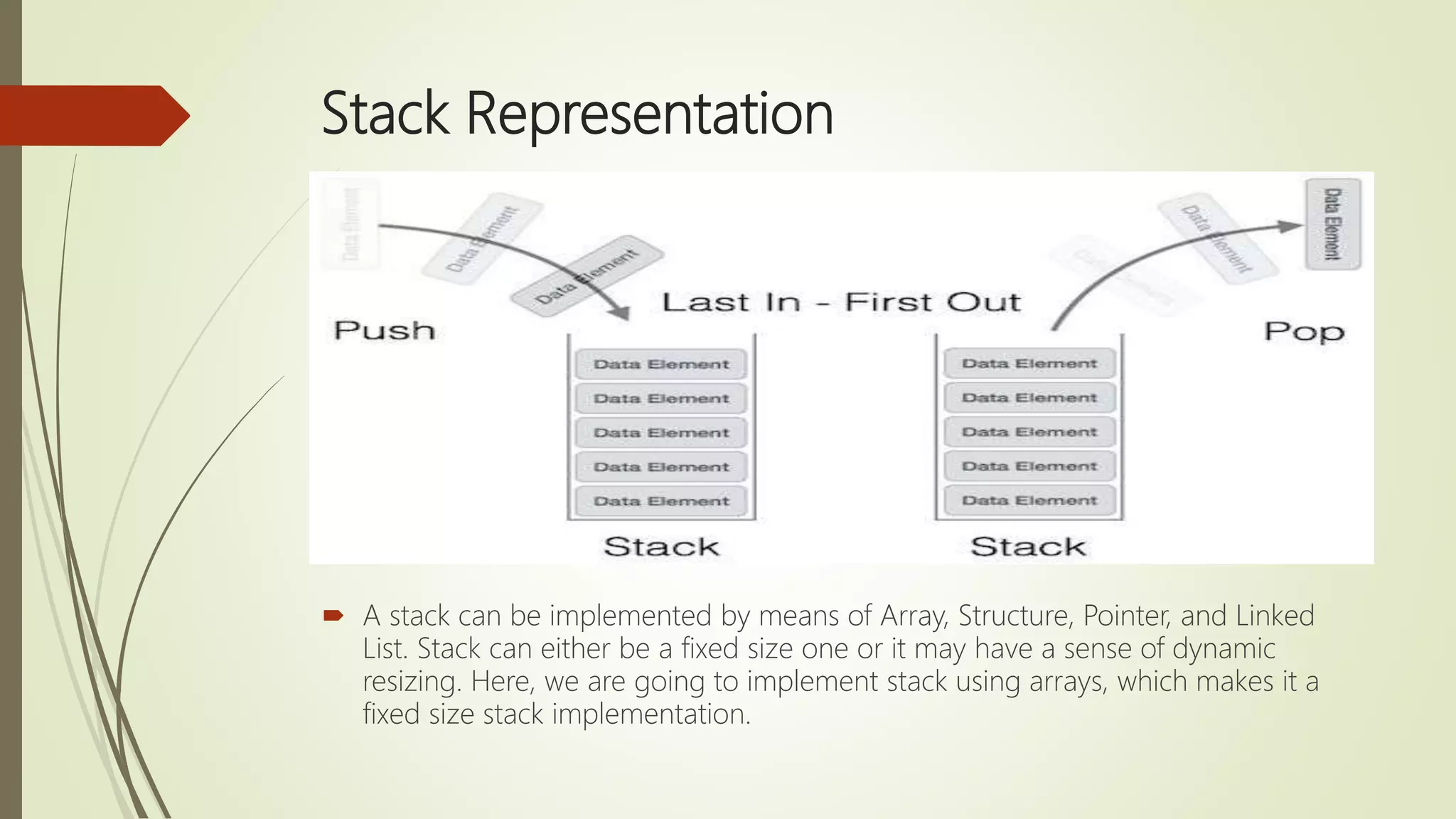
The document discusses data structures including stacks, queues, and linked lists, emphasizing their importance for efficient data management in complex applications. It defines basic operations for each structure, highlights their implementations in C++, and outlines the associated algorithms for operations like push, pop, enqueue, and dequeue. The document also explains different types of linked lists and their operations such as insertion, deletion, and traversal.





![Algorithm for PUSH Operation begin procedure push: stack, data if stack is full return null endif top ← top + 1 stack[top] ← data end procedure](https://image.slidesharecdn.com/datastructurestackqueue-171210081142/75/Data-structure-stack-queue-9-2048.jpg)
![Algorithm for Pop Operation begin procedure pop: stack if stack is empty return null endif data ← stack[top] top ← top – 1 return data end procedure](https://image.slidesharecdn.com/datastructurestackqueue-171210081142/75/Data-structure-stack-queue-10-2048.jpg)

![Program Implementation Using C++: #include<iostream.h> class stack { int a[5],i; public: void init(); void push(int n); void pop(); void display(); };](https://image.slidesharecdn.com/datastructurestackqueue-171210081142/75/Data-structure-stack-queue-12-2048.jpg)
![void stack::init() { i=0; for(int j=0;j<5;j++) { a[j]=0; } } void stack::push(int n) { if(i<5) { a[i]=n; i++; } else { cout<<"Stack is Full"; } }](https://image.slidesharecdn.com/datastructurestackqueue-171210081142/75/Data-structure-stack-queue-13-2048.jpg)
![void stack::pop() { if(i!=-1) { a[i]=0; i--; } else { cout<<"Stack is Empty"; } } void stack::display() { for(int j=0;j<i;j++) { cout<<a[j]<<endl; } }](https://image.slidesharecdn.com/datastructurestackqueue-171210081142/75/Data-structure-stack-queue-14-2048.jpg)




![Algorithm for enqueue Operation procedure enqueue(data) if queue is full return overflow endif rear ← rear + 1 queue[rear] ← data return true end procedure](https://image.slidesharecdn.com/datastructurestackqueue-171210081142/75/Data-structure-stack-queue-19-2048.jpg)
![Algorithm for dequeue Operation procedure dequeue if queue is empty return underflow end if data = queue[front] front ← front + 1 return true end procedure](https://image.slidesharecdn.com/datastructurestackqueue-171210081142/75/Data-structure-stack-queue-20-2048.jpg)

![Program for Queue #include<iostream> #include<conio.h> #include<stdlib.h> using namespace std; class queue { int queue1[5]; int rear,front;](https://image.slidesharecdn.com/datastructurestackqueue-171210081142/75/Data-structure-stack-queue-22-2048.jpg)
![public: queue() { rear=-1; front=-1; } void insert(int x) { if(rear > 4) { cout <<"queue over flow"; front=rear=-1; return; } queue1[++rear]=x; cout <<"inserted" <<x; }](https://image.slidesharecdn.com/datastructurestackqueue-171210081142/75/Data-structure-stack-queue-23-2048.jpg)
![void delet() { if(front==rear) { cout <<"queue under flow"; return; } cout <<"deleted" <<queue1[++front]; } void display() { if(rear==front) { cout <<" queue empty"; return; } for(int i=front+1;i<=rear;i++) cout <<queue1[i]<<" "; } };](https://image.slidesharecdn.com/datastructurestackqueue-171210081142/75/Data-structure-stack-queue-24-2048.jpg)