![¡ Log-linear models of the form: Pr( 𝑋= 𝑥) =exp{ 𝜃↑′ 𝑧( 𝑥)}/𝐾( 𝜃) ¡ The problem is the normalizing constant ¡ Solution: log-linear → logit. ¡ Consider conditional log-odds for a network x and a pair (i,j) of nodes: § 𝑋↓𝑖𝑗 ↓↑𝑐 : status of all pairs in x other than (i,j) § 𝑋↓𝑖𝑗 ↓↑+ : same network as x but 𝑥↓𝑖𝑗 =1 § 𝑋↓𝑖𝑗 ↓↑− : same network as x but 𝑥↓𝑖𝑗 = 0 𝑃( 𝑋↓𝑖𝑗 =1| 𝑋↓𝑖𝑗 ↓↑𝑐 )/𝑃( 𝑋↓𝑖𝑗 =0| 𝑋↓𝑖𝑗 ↓↑𝑐 ) =exp{ 𝜃↑+ 𝑠( 𝑋↓𝑖𝑗 ↓↑+ )}/exp{ 𝜃↑+ 𝑠( 𝑋↓𝑖𝑗 ↓↑− )} =exp( 𝜃↑+ [𝑠( 𝑋↓𝑖𝑗 ↓↑+ )− 𝑠( 𝑋↓𝑖𝑗 ↓↑− )]) log( 𝑃 𝑋↓𝑖𝑗 =1 𝑋↓𝑖𝑗 ↓↑𝑐 /𝑃 𝑋↓𝑖𝑗 =0 𝑋↓𝑖𝑗 ↓↑𝑐 ) = 𝜃↑+ [𝑠( 𝑋↓𝑖𝑗 ↓↑+ )− 𝑠( 𝑋↓𝑖𝑗 ↓↑− )] Exponential random graph modelling (p*)](https://image.slidesharecdn.com/burcupresentation-160316123322/75/Synthetic-Data-Generation-using-exponential-random-Graph-modeling-4-2048.jpg)
Uploaded byGraph-TA
Synthetic Data Generation using exponential random Graph modeling
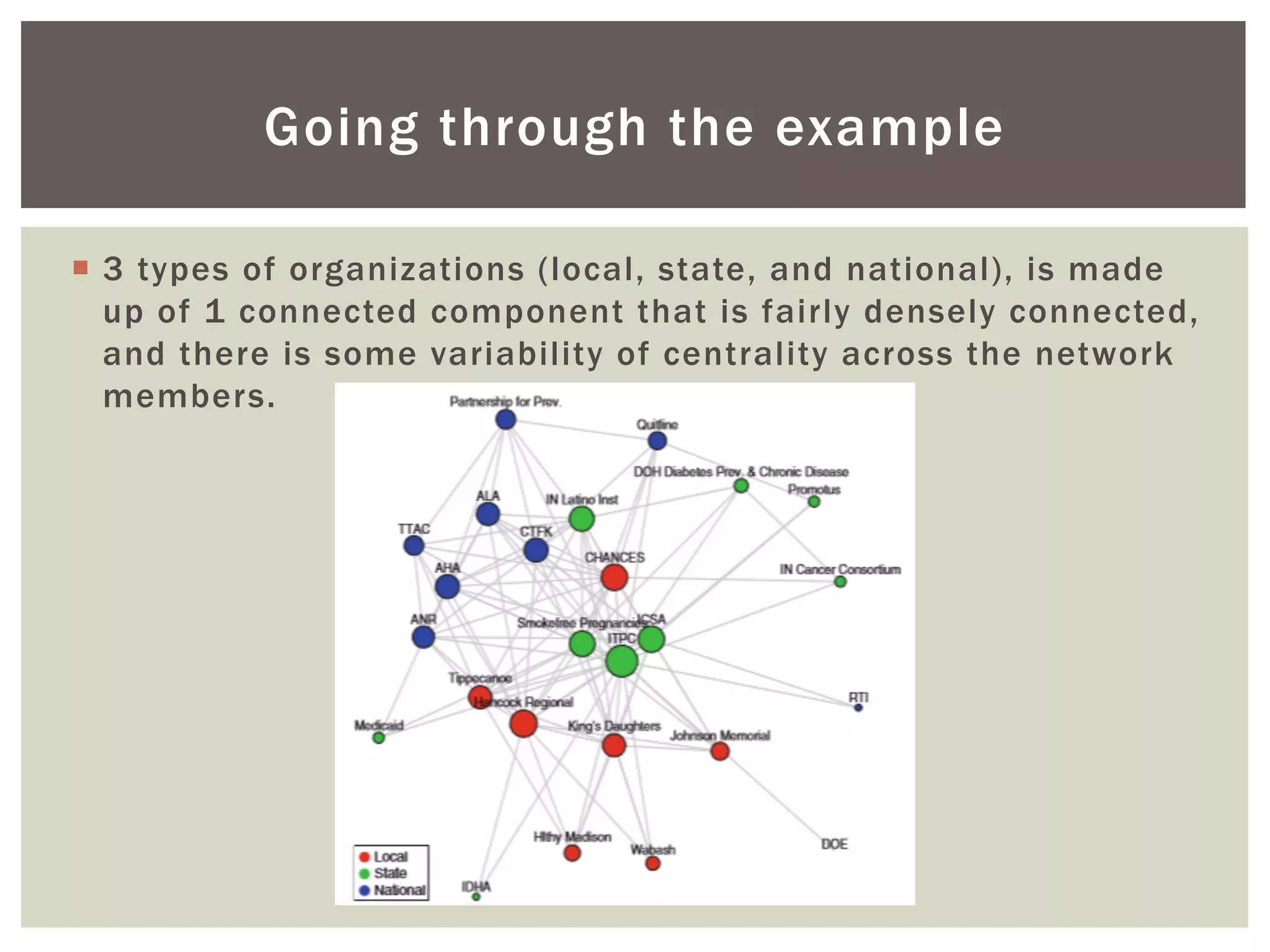
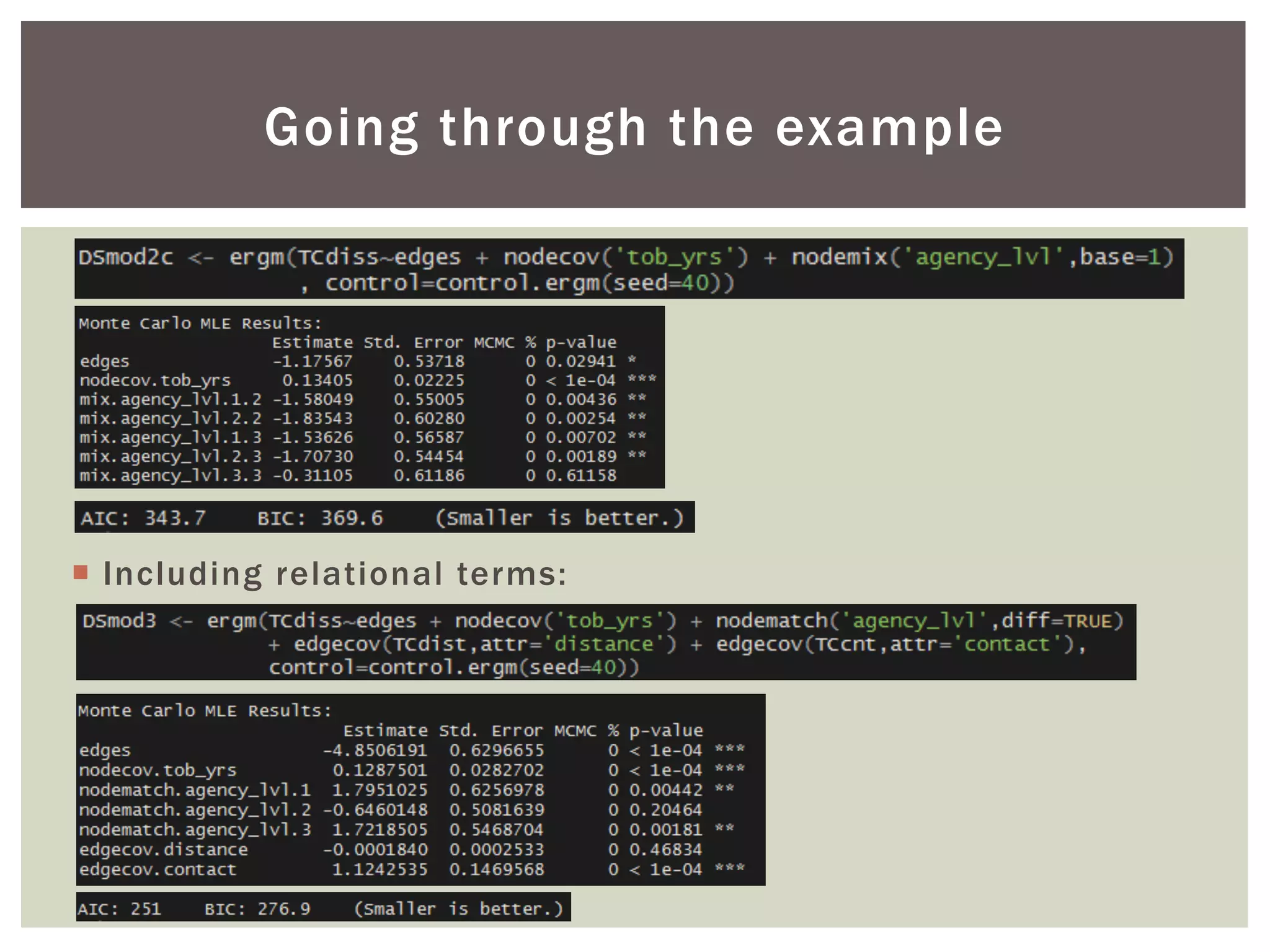
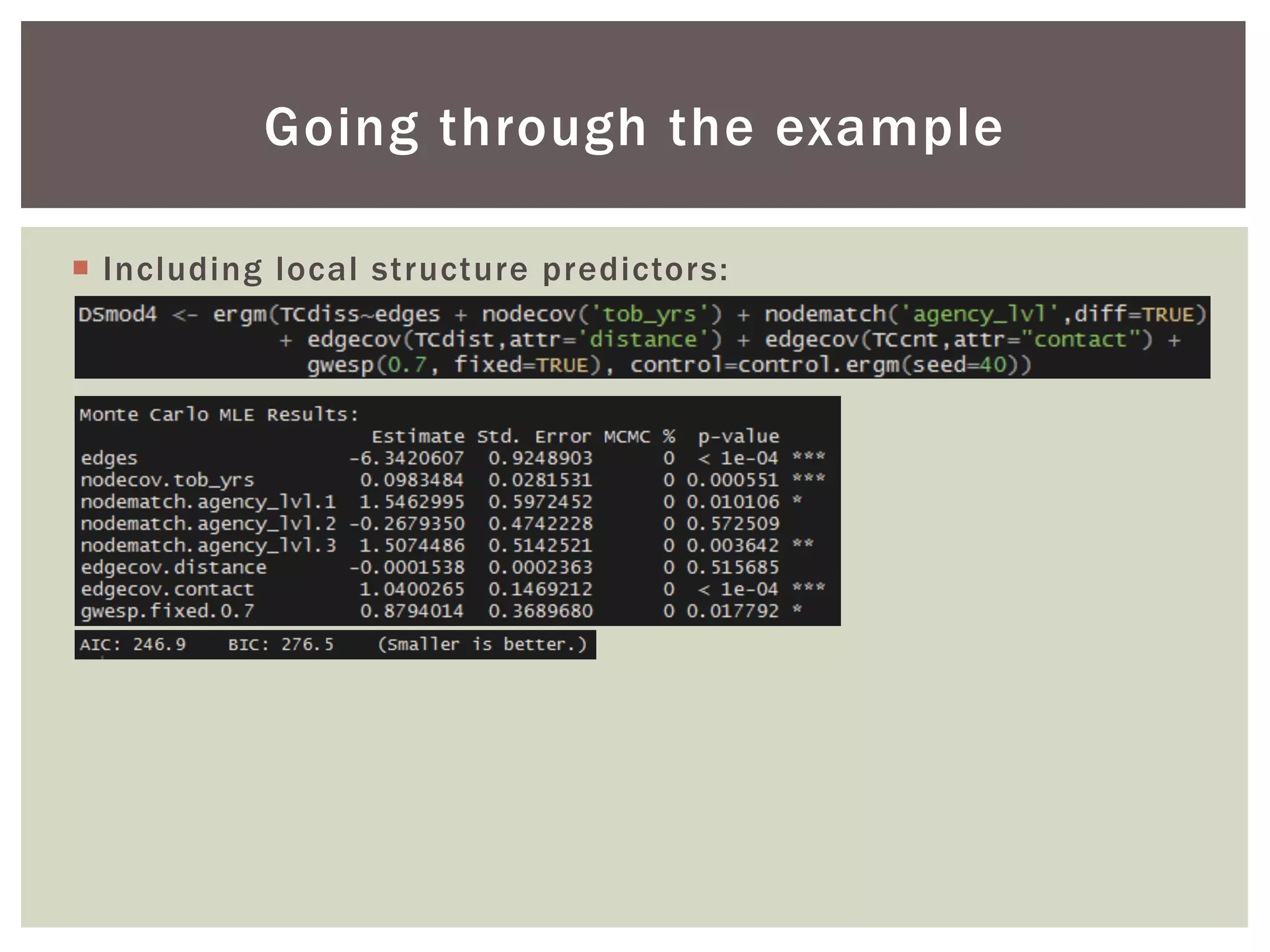
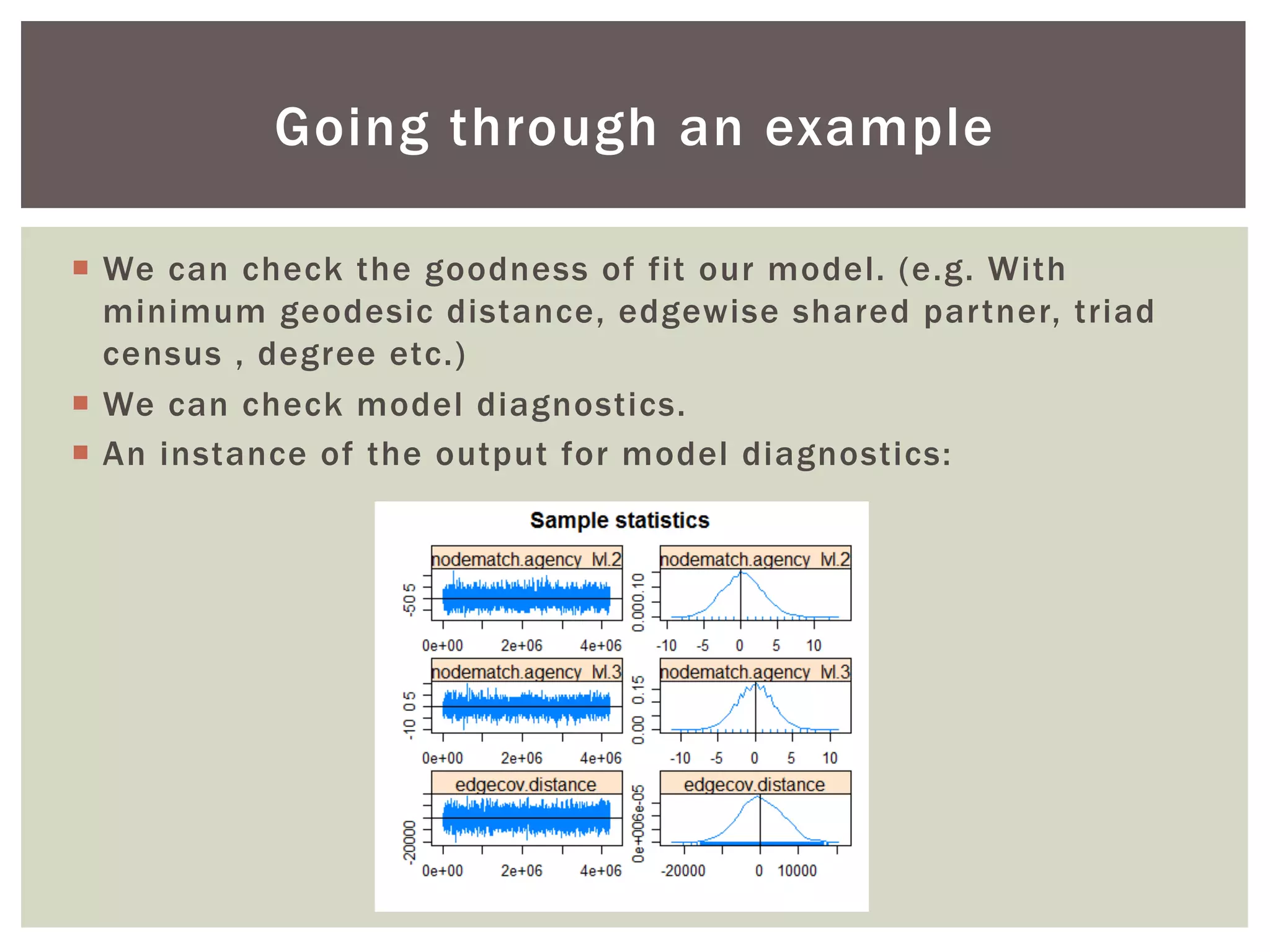
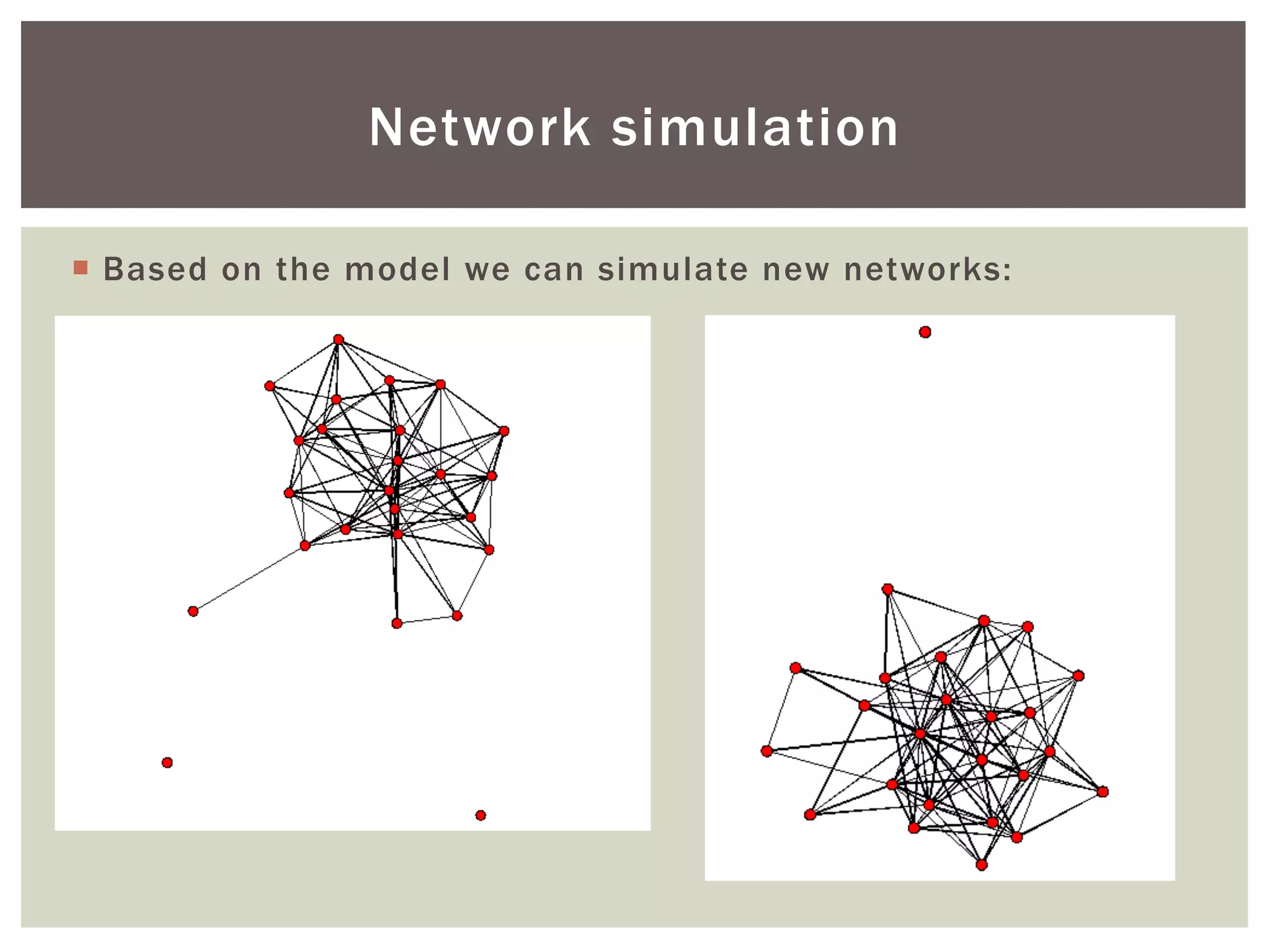
This document discusses using exponential random graph modeling to generate synthetic network data. It introduces exponential random graph models and how they use log-linear models and conditional log-odds to model network formation. An example network of tobacco control agencies is analyzed, including adding node attributes, edge attributes, and structural effects to the model. Model diagnostics and goodness of fit are evaluated. Finally, the trained model can be used to simulate new synthetic networks.
Synthetic Data Generation using exponential random Graph modeling
- 1. Burcu Kolbay Pedro Delicado ArnauPrat Pérez SYNTHETIC DATA GENERATION USING EXPONENTIAL RANDOM GRAPH MODELING
- 2. ¡ The needof the synthetic data ¡ Exponential Random Graph Modeling (In theory) ¡ Going through the example ¡ Network simulation Contents
- 3. ¡ Internet &Social Media ¡ Data Privacy Issues ¡ The need for testing process The need of the synthetic data
- 4. ¡ Log-linear modelsof the form: Pr( 𝑋= 𝑥) =exp{ 𝜃↑′ 𝑧( 𝑥)}/𝐾( 𝜃) ¡ The problem is the normalizing constant ¡ Solution: log-linear → logit. ¡ Consider conditional log-odds for a network x and a pair (i,j) of nodes: § 𝑋↓𝑖𝑗 ↓↑𝑐 : status of all pairs in x other than (i,j) § 𝑋↓𝑖𝑗 ↓↑+ : same network as x but 𝑥↓𝑖𝑗 =1 § 𝑋↓𝑖𝑗 ↓↑− : same network as x but 𝑥↓𝑖𝑗 = 0 𝑃( 𝑋↓𝑖𝑗 =1| 𝑋↓𝑖𝑗 ↓↑𝑐 )/𝑃( 𝑋↓𝑖𝑗 =0| 𝑋↓𝑖𝑗 ↓↑𝑐 ) =exp{ 𝜃↑+ 𝑠( 𝑋↓𝑖𝑗 ↓↑+ )}/exp{ 𝜃↑+ 𝑠( 𝑋↓𝑖𝑗 ↓↑− )} =exp( 𝜃↑+ [𝑠( 𝑋↓𝑖𝑗 ↓↑+ )− 𝑠( 𝑋↓𝑖𝑗 ↓↑− )]) log( 𝑃 𝑋↓𝑖𝑗 =1 𝑋↓𝑖𝑗 ↓↑𝑐 /𝑃 𝑋↓𝑖𝑗 =0 𝑋↓𝑖𝑗 ↓↑𝑐 ) = 𝜃↑+ [𝑠( 𝑋↓𝑖𝑗 ↓↑+ )− 𝑠( 𝑋↓𝑖𝑗 ↓↑− )] Exponential random graph modelling (p*)
- 5. ¡ «Tcnetworks» data: Inter-organizational relationship among 25 agencies within the the Indiana State Tobacco Control Program (2010). ¡ 3 types of inter-organizational ties: § Frequency of contact § Level of collaboration § Whether each pair of agencies communicated with one another. ¡ The network data include: § a number of node characteristics (e.g., tob yrs, which records how long an agency has been working in tobacco control), § edge characteristics, § a sociomatrix (TCdist) which contains the geographic distance between each pair of agencies. ¡ Vertex attributes: ¡ Our vertex attributes are: § Agency_cat § Agency_lvl § Lead_agency § Tob_yrs Going through the example
- 6. ¡ 3 typesof organizations (local, state, and national), is made up of 1 connected component that is fairly densely connected, and there is some variability of centrality across the network members. Going through the example
- 7. ¡ Start withbase model: ¡ Then we include node attributes: Going through the example
- 8. ¡ Including dyadicpredictors: Going through the example
- 9. Going through theexample ¡ Including relational terms:
- 10. ¡ Including localstructure predictors: Going through the example
- 11. ¡ We cancheck the goodness of fit our model. (e.g. With minimum geodesic distance, edgewise shared partner, triad census , degree etc.) ¡ We can check model diagnostics. ¡ An instance of the output for model diagnostics: Going through an example
- 12. ¡ Based onthe model we can simulate new networks: Network simulation
- 13. ¡ We willuse a social network data which includes several number of attributes. (Linkedin) ¡ From different type of attributes we can enrich the information we extract from the network. ¡ Based on these knowledge, we will be one step closer to generate synthetic data based on the dependency among the actors. Furthermore
- 14. ¡ A User'sGuide to Network Analysis in R 1st ed. 2015 Edition 165-187. ¡ Newman, Mark. Networks: an introduction. OUP Oxford, 2010. ¡ Goodreau, Steven M. "Advances in exponential random graph (p*) models applied to a large social network." Social Networks 29.2 (2007): 231-248. References
- 15.