Exploring Parallel Programming Models for Matrix Computation .pptx

Exploring Parallel Programming Models for Matrix Computation .pptx

• 1.
  Exploring Parallel ProgrammingModels for Matrix Computation Presented by Shovan Prita Paul Course Title: Cloud Computing Course Code: CSE 462 (Sessional) DEPARTMENT OF COMPUTER SCIENCE AND ENGINEERING HAJEE MOHAMMAD DANESH SCIENCE AND TECHNOLOGY UNIVERSITY, DINAJPUR-5200, BANGLADESH
• 2.
  Topics covered 1. Objectives 2.Problem Statement 3. Implementation Strategy 4. Deployment and Testing Environment 5. Results and Analysis 6. Challenges Encountered 7. Conclusion
• 3.
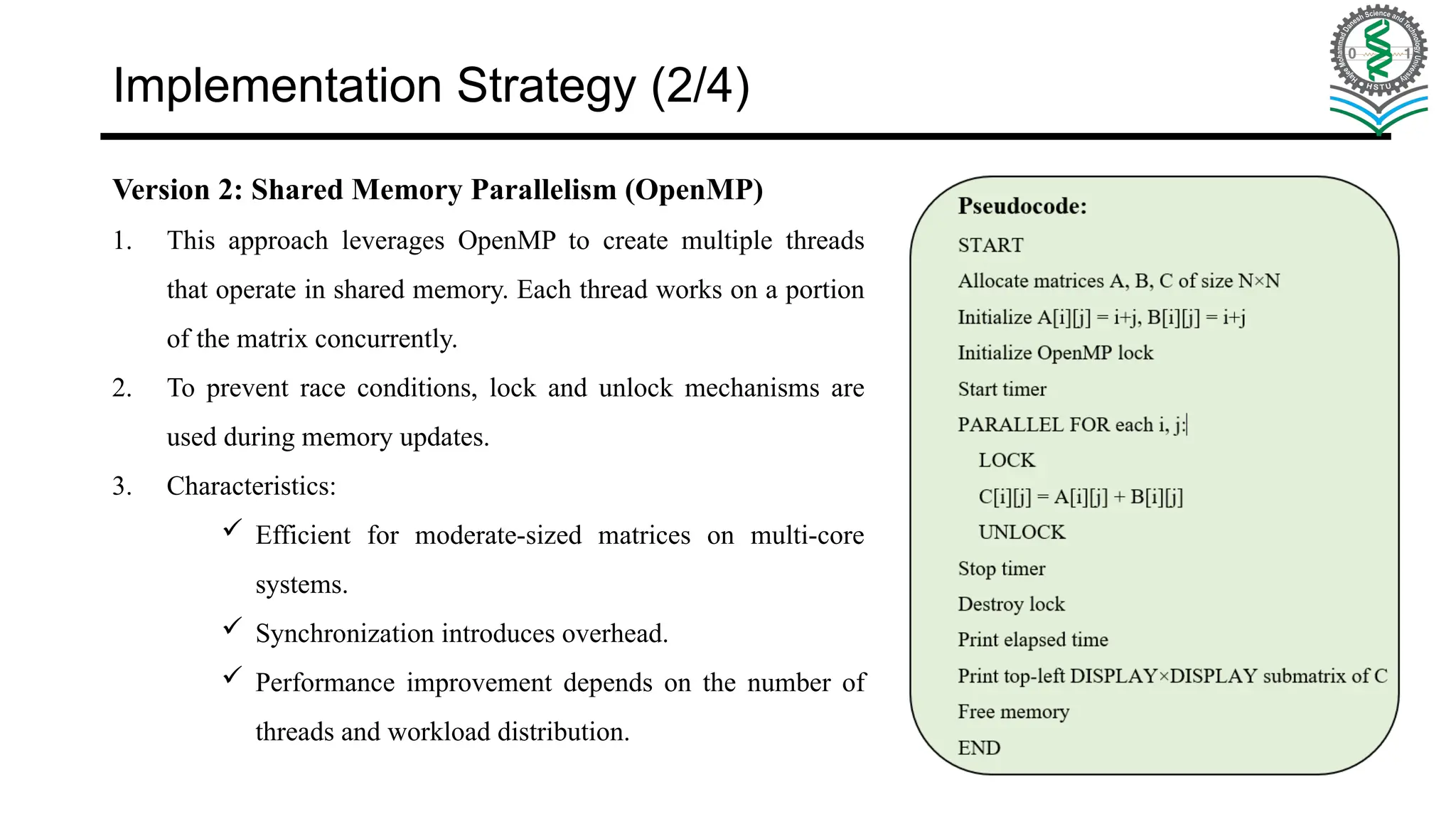
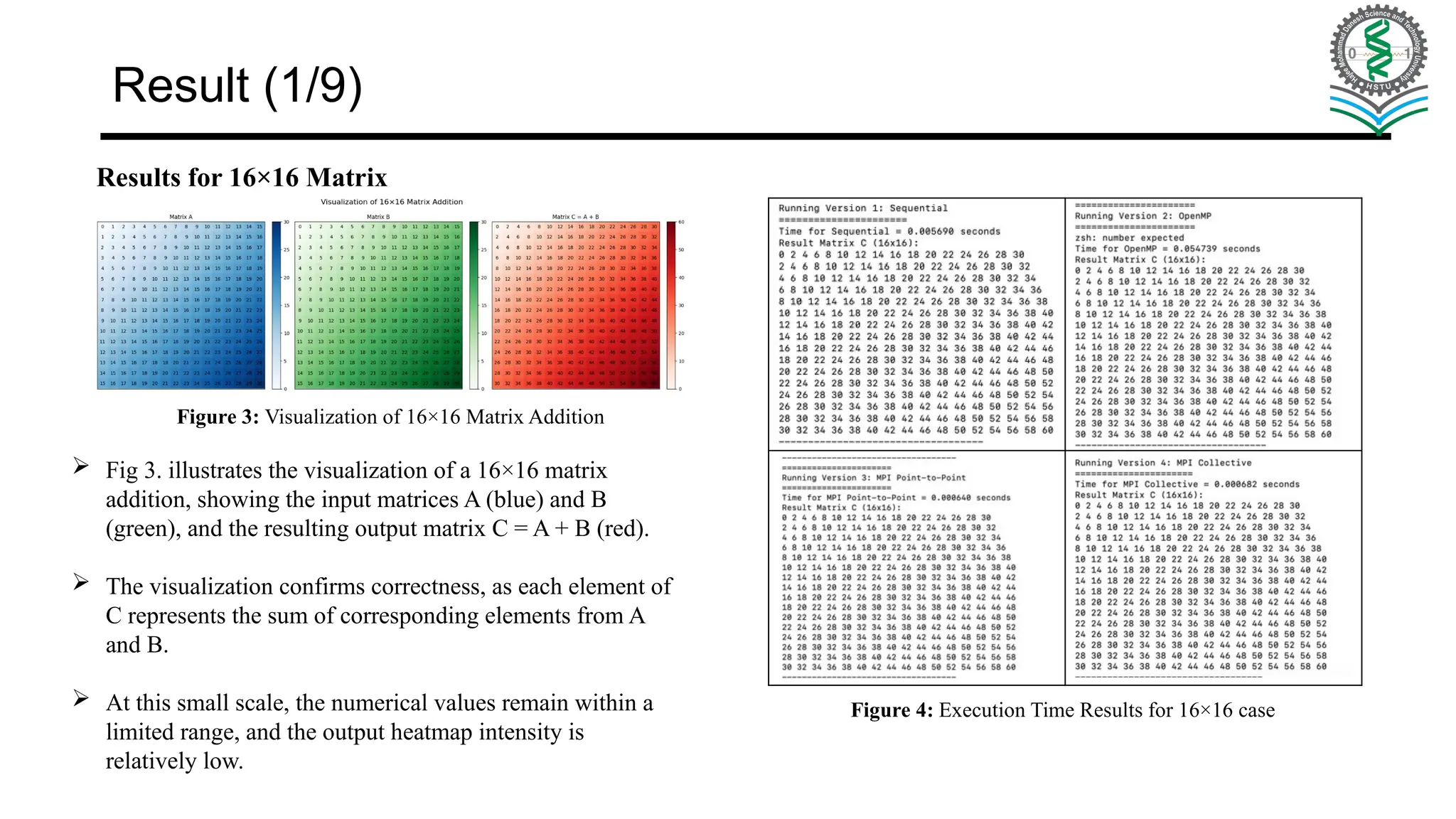
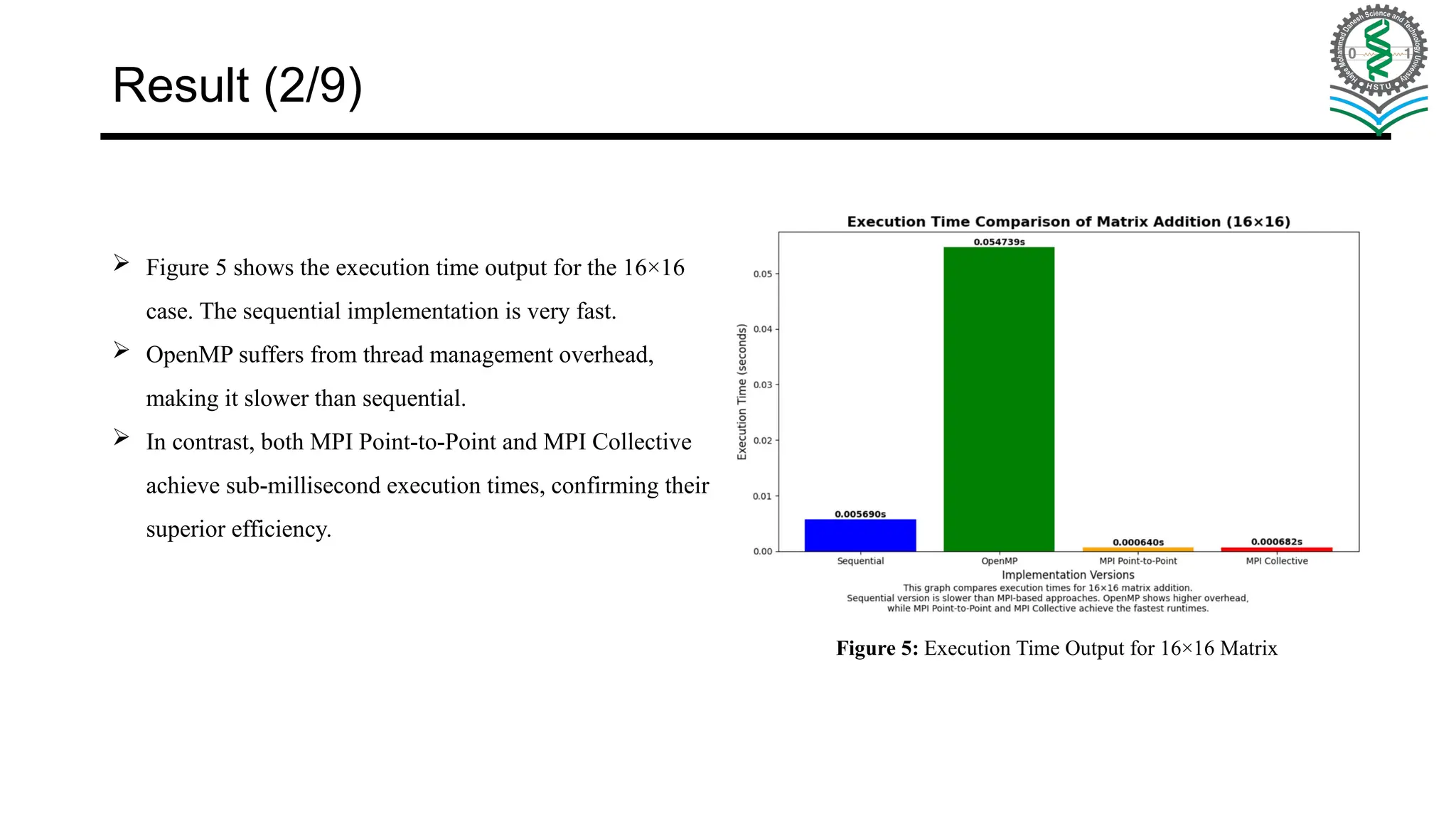
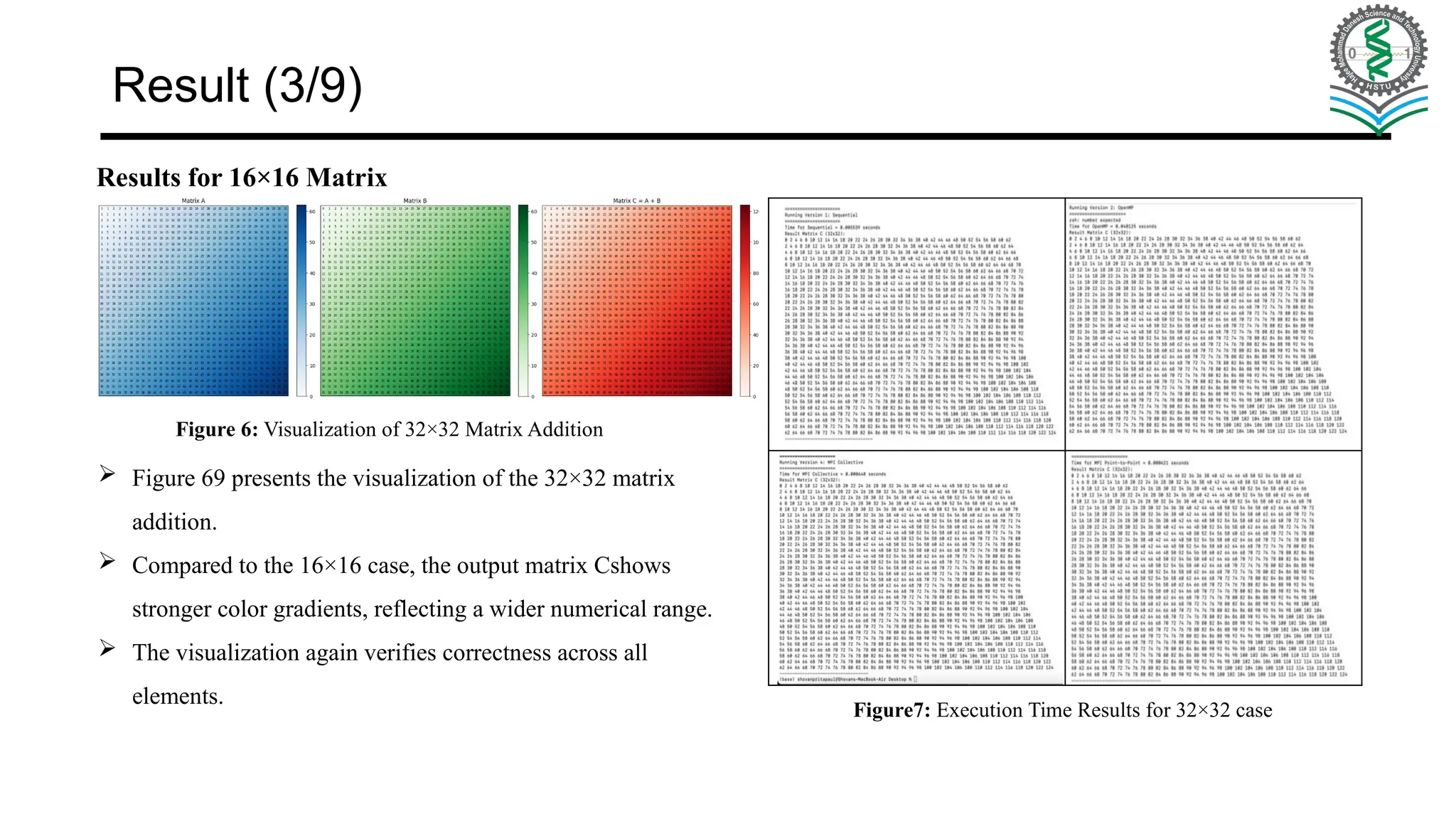
  Objectives Main Objective: 1. Implementmatrix addition using sequential, OpenMP, and MPI models on a 4-core system. 2. Compare performance, scalability, and efficiency across approaches. Learning Outcomes: 1. Sequential Execution – establish baseline time & complexity. 2. OpenMP (Shared Memory) – multi-threading, synchronization, and overhead analysis. 3. MPI Point-to-Point – message passing with Send/Recv, handle deadlocks & partitioning. 4. MPI Collective – use Scatter/Gather/Bcast/Reduce for simpler, scalable communication. Goal: Build hands-on understanding of trade-offs in parallel programming models.
• 4.
  Problem Statement Problem Statement: 1.Matrix operations are central in scientific computing, simulations, and ML. 2. Matrix addition (C = A + B) is chosen as the target task. Goal: Implement in sequential & parallel models, then compare execution time, scalability, and overhead. Approaches Considered: 1. Sequential – single-core baseline, element-by-element addition. 2. OpenMP (Shared Memory) – multi-threaded execution, synchronization with locks. 3. MPI Point-to-Point – partitioned computation with Send/Recv communication. 4. MPI Collective – optimized routines (Bcast, Scatter, Gather, Reduce) for scalable efficiency. Figure 1: Matrix Addition
• 5.
  Implementation Strategy (1/4) Version1: Sequential Programming 1. In this version, the computation is executed on a single processor core without any parallelism. 2. The program iterates through all elements of matrices A and B, computes their sum, and stores the result in matrix C. 3. Characteristics:  Simple to implement.  Provides a baseline for performance comparison.  Not scalable for large datasets.
• 6.
  Implementation Strategy (2/4) Version2: Shared Memory Parallelism (OpenMP) 1. This approach leverages OpenMP to create multiple threads that operate in shared memory. Each thread works on a portion of the matrix concurrently. 2. To prevent race conditions, lock and unlock mechanisms are used during memory updates. 3. Characteristics:  Efficient for moderate-sized matrices on multi-core systems.  Synchronization introduces overhead.  Performance improvement depends on the number of threads and workload distribution.
• 7.
  Implementation Strategy (3/4) Version3: MPI Point-to-Point Communication 1. Root process partitions matrices A and B into row blocks and distributes them using MPI_Send. 2. Worker processes compute local additions on their assigned sub-blocks. 3. Partial results are returned to the root via MPI_Recv and combined into the final matrix C. 4. Characteristics:  Suitable for distributed memory systems.  Requires explicit communication management using MPI_Send and MPI_Recv.  Offers flexibility but can be error-prone.  Risk of deadlocks if communication order and message tags are not carefully managed.
• 8.
  Implementation Strategy (4/4) Version4: MPI Collective Communication 1. This version improves efficiency by using MPI collective routines. 2. Instead of sending and receiving messages manually, built-in MPI functions handle data distribution and collection. 3. This reduces overhead and simplifies the implementation. 4. Characteristics:  Highly scalable and efficient.  Collective functions optimize communication patterns.  Best suited for large-scale matrix operations.
• 9.
  Deployment / TestingEnvironment To evaluate the performance of different parallel programming models, the implementations were tested in a controlled computing environment. 1. Processor: 4-core CPU for evaluating both shared and distributed memory approaches 2. Language: C/C++ for low-level memory control and efficient performance 3. Parallel Tools: OpenMP (shared memory) and MPI (distributed memory) 4. Testing Method: Matrix sizes of 16×16, 32×32, 64×64 and 1000x1000 with execution time measurements This environment allowed for a fair comparison between sequential and parallel models while highlighting the impact of synchronization and communication overheads. Figure 2: Matrix Addition by processor
• 10.
  Results for 16×16Matrix Figure 3: Visualization of 16×16 Matrix Addition  Fig 3. illustrates the visualization of a 16×16 matrix addition, showing the input matrices A (blue) and B (green), and the resulting output matrix C = A + B (red).  The visualization confirms correctness, as each element of C represents the sum of corresponding elements from A and B.  At this small scale, the numerical values remain within a limited range, and the output heatmap intensity is relatively low. Figure 4: Execution Time Results for 16×16 case Result (1/9)
• 11.
  Figure 5: ExecutionTime Output for 16×16 Matrix  Figure 5 shows the execution time output for the 16×16 case. The sequential implementation is very fast.  OpenMP suffers from thread management overhead, making it slower than sequential.  In contrast, both MPI Point-to-Point and MPI Collective achieve sub-millisecond execution times, confirming their superior efficiency. Result (2/9)
• 12.
  Results for 16×16Matrix Figure 6: Visualization of 32×32 Matrix Addition  Figure 69 presents the visualization of the 32×32 matrix addition.  Compared to the 16×16 case, the output matrix Cshows stronger color gradients, reflecting a wider numerical range.  The visualization again verifies correctness across all elements. Figure7: Execution Time Results for 32×32 case Result (3/9)
• 13.
  Figure 8: ExecutionTime Output for 32×32 Matrix  Figure 8 reports the execution time output for the 32×32 case. Sequential execution remains nearly constant.  OpenMP still incurs overhead but is relatively closer in performance to sequential compared to the 16×16 case.  MPI approaches continue to outperform both sequential and OpenMP, with MPI Collective maintaining the lowest execution time. Result (4/9)
• 14.
  Results for 16×16Matrix Figure 9: Visualization of 64×64 Matrix Addition  Figure 9 displays the visualization of the 64×64 matrix addition, where the output matrix C exhibits even more pronounced gradients.  The larger matrix size emphasizes the increase in the range of values, which further demonstrates correctness of the addition operation at scale. Figure 10: Execution Time Results for 64×64 case Result (5/9)
• 15.
  Figure 11: ExecutionTime Output for 64×64 Matrix  Figure 11 shows the execution time output for the 64×64 case.  Sequential execution remains stable, while OpenMP continues to show higher times due to synchronization overhead.  Both MPI implementations remain efficient, with MPI Collective slightly outperforming MPI Point-to-Point. Result (6/9)
• 16.
  Results for 1000×1000Matrix Figure 12: Visualization of 1000×1000 Matrix Addition  Figure 12 displays the visualization of the 1000×1000 matrix addition, where the output matrix C exhibits even more pronounced gradients.  The larger matrix size emphasizes the increase in the range of values, which further demonstrates correctness of the addition operation at scale. Figure 13: Execution Time Results for 1000×1000 case Result (7/9)
• 17.
  Figure 14: ExecutionTime Output for 1000×1000 Matrix  Figure 14 shows the execution time output for the 1000×1000 case.  Sequential execution remains stable, while OpenMP continues to show higher times due to synchronization overhead.  Both MPI implementations remain efficient, with MPI Collective slightly outperforming MPI Point-to-Point. Result (8/9)
• 18.
  From the data,it is clear that: Sequential: This is the baseline, offering consistent but slow performance without parallelization. OpenMP: This method is inefficient for small-scale problems due to parallelization overhead but can be highly effective on large workloads where the benefits of parallel processing outweigh the initial cost. MPI Point-to-Point: This method consistently performs well across all matrix sizes, showing the effectiveness of explicit message-based communication. MPI Collective: Similar to point-to-point, this approach is highly efficient for matrix operations, demonstrating that collective communication can be just as effective. Execution Time Measurements Summary Version 16×16 (s) 32×32 (s) 64×64 (s) 1000x1000(s) Sequential 0.005690 0.005539 0.005334 0.005340 OpenMP 0.054739 0.048125 0.056223 0.032742 MPI Point-to-Point 0.000640 0.000621 0.001001 0.001949 MPI Collective 0.000682 0.000648 0.000691 0.001922 Table 1. Execution time (s) for different approaches and matrix sizes Result (9/9)
• 19.
  Result (9/9) Overall ComparativeDiscussion  Correctness: The visualization outputs confirm accurate matrix addition across all tested sizes.  Sequential: Execution is stable but does not benefit from scalability, making it inefficient for larger inputs.  OpenMP: Performance for small matrices is poor due to significant parallelization overhead from thread management. However, based on the scaling trend, OpenMP performance should improve as the matrix size increases and the workload outweighs this initial cost.  MPI approaches: Both MPI Point-to-Point and MPI Collective achieve the fastest results, even for small matrices.  Best performer: MPI Collective consistently outperforms the other implementations, making it the most suitable method for large-scale matrix addition.
• 20.
  Challenges Encountered  OpenMPSynchronization Overhead:  Locks added significant delay despite independent thread work.  MPI Point-to-Point Communication:  Designing correct send/receive patterns was complex.  Risk of deadlocks resolved by strict communication order.  Load Balancing:  Uneven row distribution when N not divisible by process count.  Mitigated by assigning remainder rows to last process.  Small Matrix Sizes:  Overheads (threads, messages, sync) > computation for 16×16, 32×32  Parallelism not always beneficial at small scale.  System Constraints:  Limited to 4-core processor; larger-scale validation needs HPC cluster.
• 21.
  Conclusions This project exploredfour approaches to matrix addition: Sequential, OpenMP with synchronization, MPI Point-to- Point, and MPI Collective.  The Sequential version served as a reliable baseline with stable performance across all tested sizes.  The OpenMP version highlighted the performance cost of locks, showing that synchronization overhead can degrade performance when not necessary.  The MPI Point-to-Point version successfully demonstrated distributed communication but required careful design to avoid deadlocks and inefficiencies.  The MPI Collective version proved to be the most efficient and scalable approach, benefiting from optimized communication primitives that minimized latency and overhead. Overall, the experiments confirmed that while sequential execution is adequate for small matrices, MPI Collective offers the best scalability and performance for larger problems.
• 22.
  References [1] M. J.Quinn, Parallel Programming in C with MPI and OpenMP. New York, NY, USA: McGraw-Hill, 2004. [2] W. Gropp, E. Lusk, and A. Skjellum, Using MPI: Portable Parallel Programming with the Message Passing Interface, 3rd ed. Cambridge, MA, USA: MIT Press, 2014. [3] OpenMP Architecture Review Board, OpenMP Application Programming Interface, Version 5.2, Nov. 2023. [Online]. Available: https://www.openmp.org [4] Message Passing Interface Forum, MPI: A Message-Passing Interface Standard, Version 4.0, June 2021. [Online]. Available: https://www.mpi-forum.org [5] B. Wilkinson and M. Allen, Parallel Programming: Techniques and Applications Using Networked Workstations and Parallel Computers, 2nd ed. Upper Saddle River, NJ, USA: Pearson, 2005. [6] I. Foster, Designing and Building Parallel Programs: Concepts and Tools for Parallel Software Engineering. Reading, MA, USA: Addison-Wesley, 1995. [7] Lawrence Livermore National Laboratory (LLNL), MPI Tutorial. [Online]. Available: https://hpc-tutorials.llnl.gov/mpi/
• 23.
  THANK YOU Any Question ?