Downloaded 1,227 times
![ MERGE SORT (A,p,r) //divide if p < r then q= [ (p + r) / 2 ] MERGE SORT(A,p,q) MERGER SORT(A,q + 1,r) MERGE(A,p,q,r)](https://image.slidesharecdn.com/mergesortalgorithm-160901095302/75/Merge-sort-algorithm-5-2048.jpg)
![Merge(array A, int p, int q, int r) { array B[p..r] //temp array taken i = k = p // initialize pointers j = q+1 while (i <= q and j <= r) { if (A[i] <= A[j]) B[k++] = A[i++] else B[k++] = A[j++] } while (i <= q) B[k++] = A[i++] // copy any leftover to B while (j <= r) B[k++] = A[j++] for i = p to r A[i] = B[i] // copy B back to A }](https://image.slidesharecdn.com/mergesortalgorithm-160901095302/75/Merge-sort-algorithm-6-2048.jpg)
SD
Uploaded byShubham Dwivedi
PPTX, PDF31,821 views
Merge sort algorithm
Merge sort is a sorting algorithm based on the divide and conquer technique, with a worst-case time complexity of O(n log n). It works by recursively splitting the array into halves, sorting each half, and then merging them back together in a sorted order. Developed by John von Neumann for EDVAC in 1945, it efficiently handles sorting tasks through its systematic approach.
Related topics:
In this document
Powered by AI
Presenter's name is Shubham Dwivedi.
Merge sort is a divide and conquer sorting algorithm with a worst-case time complexity of Ο(n log n). It divides arrays into halves and combines them sorted.
Merge sort was invented by John von Neumann for EDVAC in 1945, following the divide and conquer paradigm.
The three steps of merge sort are: Divide the list, sort sublists recursively, and combine sorted lists.
Pseudocode of merge sort algorithm demonstrating the divide step and recursive calls.
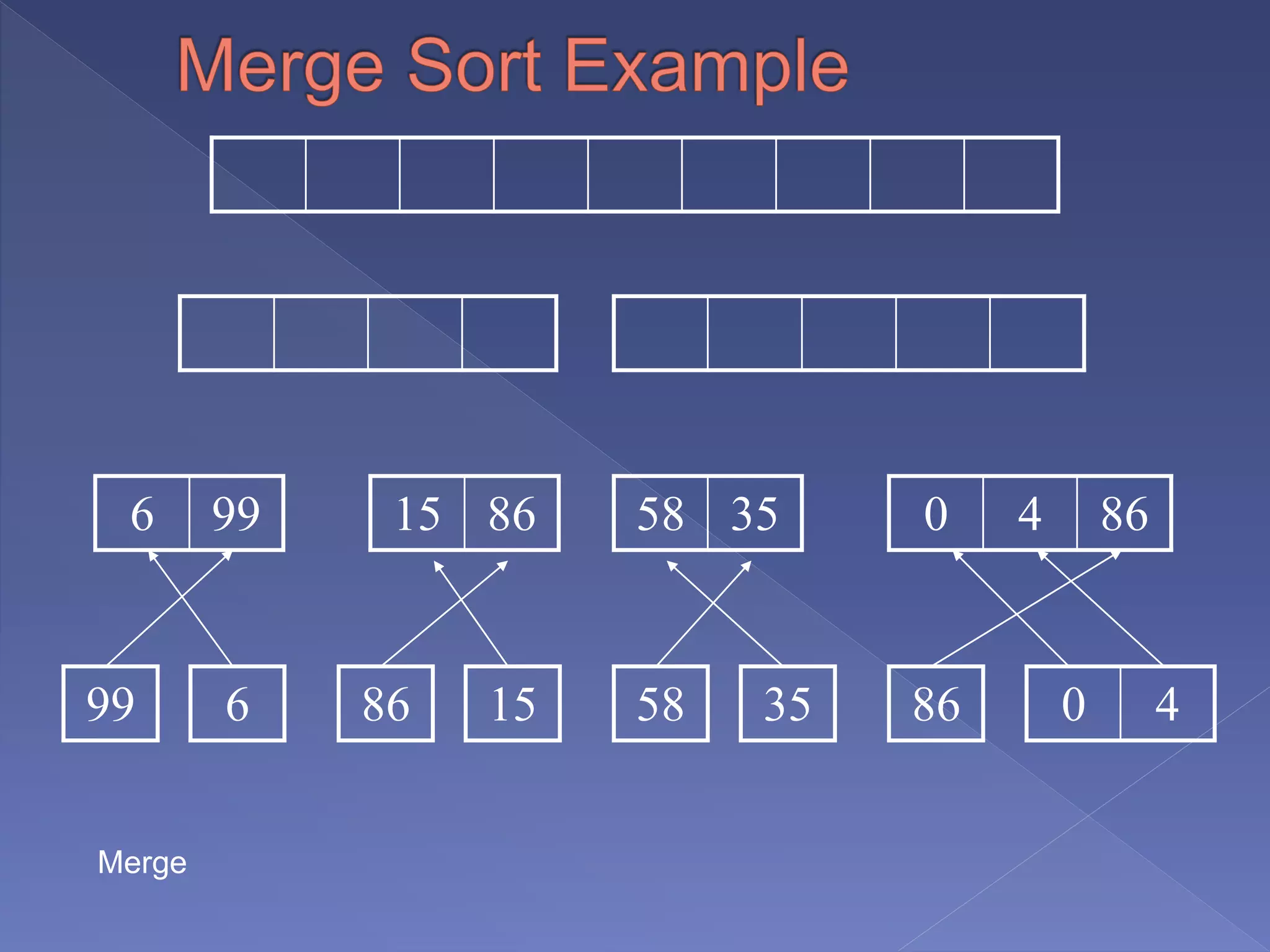
Detailed implementation of the merge function that combines two sorted sublists into one sorted list.
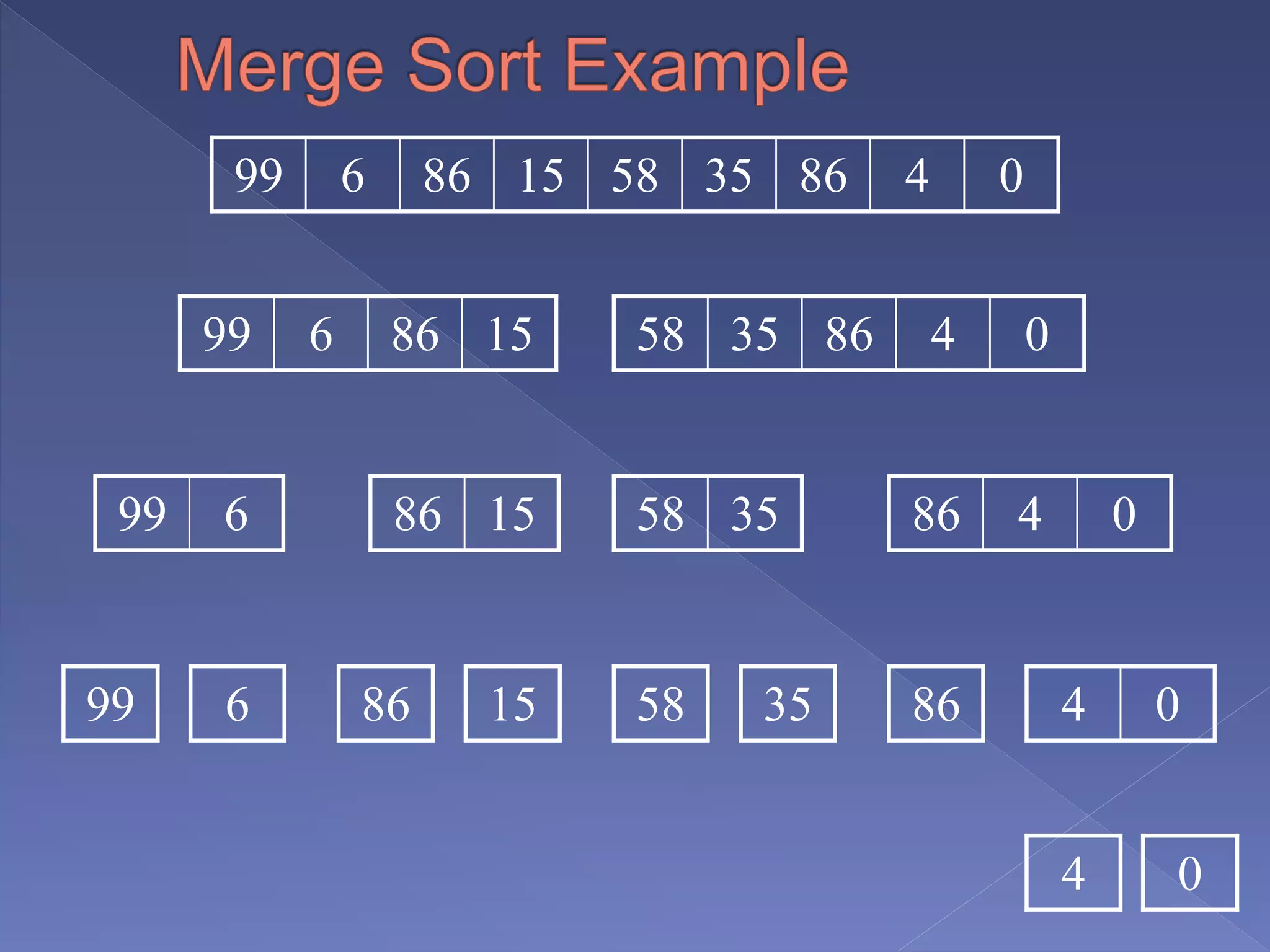
Showcasing an unsorted array: 99, 6, 86, 15, 58, 35, 86, 4, 0.
Repeated display of the unsorted array for clarity.
Visual representation of the sorting process as elements are rearranged during merging.
Continued illustration of sorting with the original array juxtaposed against intermediate stages.
Another step in the merging process, showing the array evolving towards a sorted format.
Visuals depicting the array as it merges towards a sorted order.
Showcasing the merging step with elements positioned to highlight the sorting process.
The final merging step presenting elements arranged in ascending order.
Final output of the merge sort process showcasing the sorted array: 0, 4, 6, 15, 35, 58, 86, 86, 99.
More Related Content
What's hot
Viewers also liked
Similar to Merge sort algorithm
More from Shubham Dwivedi
Recently uploaded
Merge sort algorithm
- 1.
- 2. Merge sortis a sorting technique based on divide and conquer technique. With worst- case time complexity being Ο(n log n), it is one of the most respected algorithms. Merge sort first divides the array into equal halves and then combines them in a sorted manner.
- 3. Invented by John vonNeumann (1903-1957) Follows divide and conquer paradigm. Developed merge sort for EDVAC in 1945
- 4. 1.Divide: Divide theunsorted list into two sub lists of about half the size. 2.Conquer: Sort each of the two sub lists recursively until we have list sizes of length 1,in which case the list itself is returned. 3.Combine: Merge the two-sorted sub lists back into one sorted list.
- 5. MERGE SORT(A,p,r) //divide if p < r then q= [ (p + r) / 2 ] MERGE SORT(A,p,q) MERGER SORT(A,q + 1,r) MERGE(A,p,q,r)
- 6. Merge(array A, intp, int q, int r) { array B[p..r] //temp array taken i = k = p // initialize pointers j = q+1 while (i <= q and j <= r) { if (A[i] <= A[j]) B[k++] = A[i++] else B[k++] = A[j++] } while (i <= q) B[k++] = A[i++] // copy any leftover to B while (j <= r) B[k++] = A[j++] for i = p to r A[i] = B[i] // copy B back to A }
- 7. 99 6 8615 58 35 86 4 0
- 8. 99 6 8615 58 35 86 4 0 99 6 86 15 58 35 86 4 0
- 9. 99 6 8615 58 35 86 4 0 99 6 86 15 58 35 86 4 0 86 1599 6 58 35 86 4 0
- 10. 99 6 8615 58 35 86 4 0 99 6 86 15 58 35 86 4 0 86 1599 6 58 35 86 4 0 99 6 86 15 58 35 86 4 0
- 11. 99 6 8615 58 35 86 4 0 99 6 86 15 58 35 86 4 0 86 1599 6 58 35 86 4 0 99 6 86 15 58 35 86 4 0 4 0
- 12. 99 6 8615 58 35 86 0 4 4 0Merge
- 13. 15 866 9958 35 0 4 86 99 6 86 15 58 35 86 0 4 Merge
- 14. 6 15 8699 0 4 35 58 86 15 866 99 58 35 0 4 86 Merge
- 15. 0 4 615 35 58 86 86 99 6 15 86 99 0 4 35 58 86 Merge