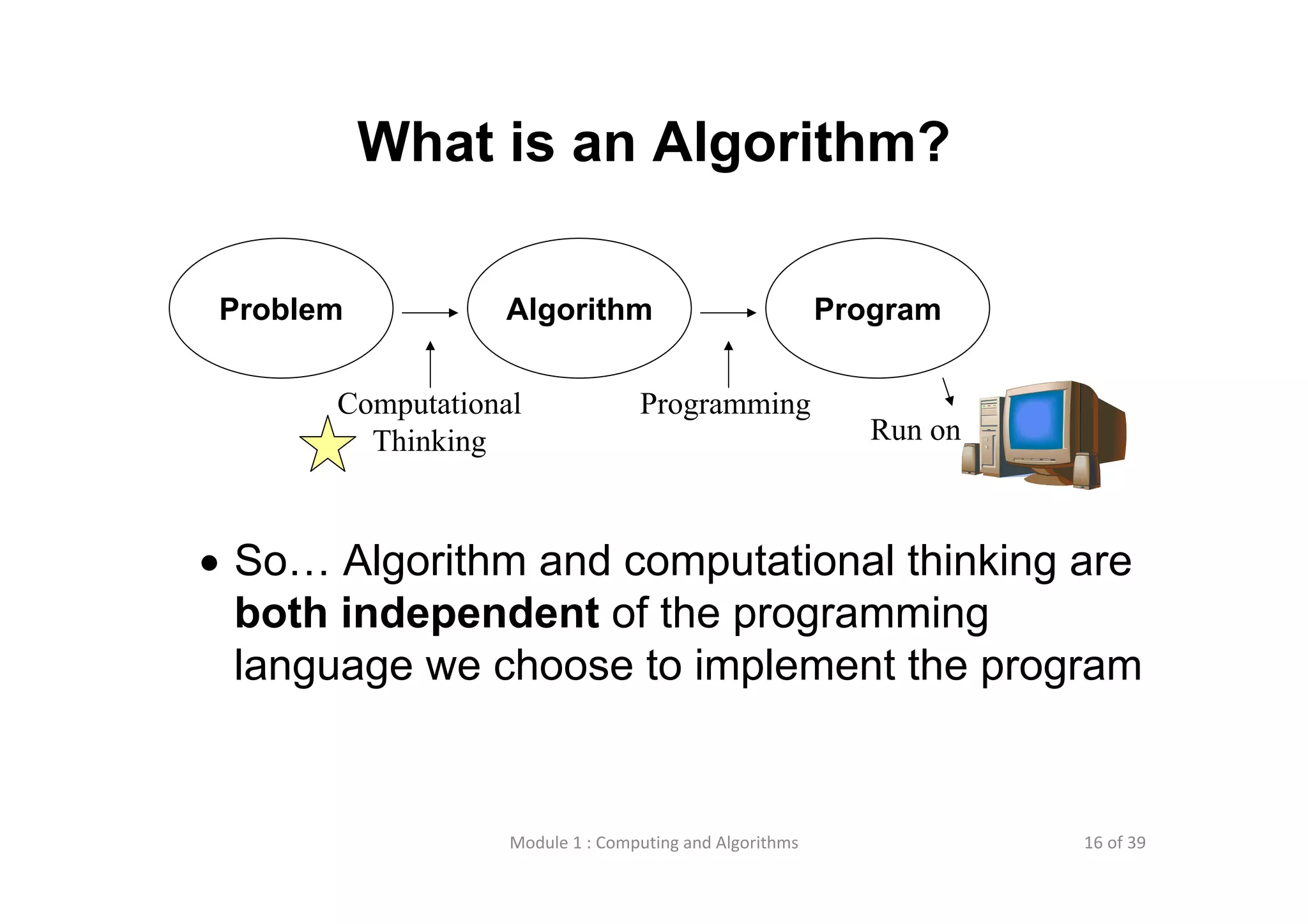
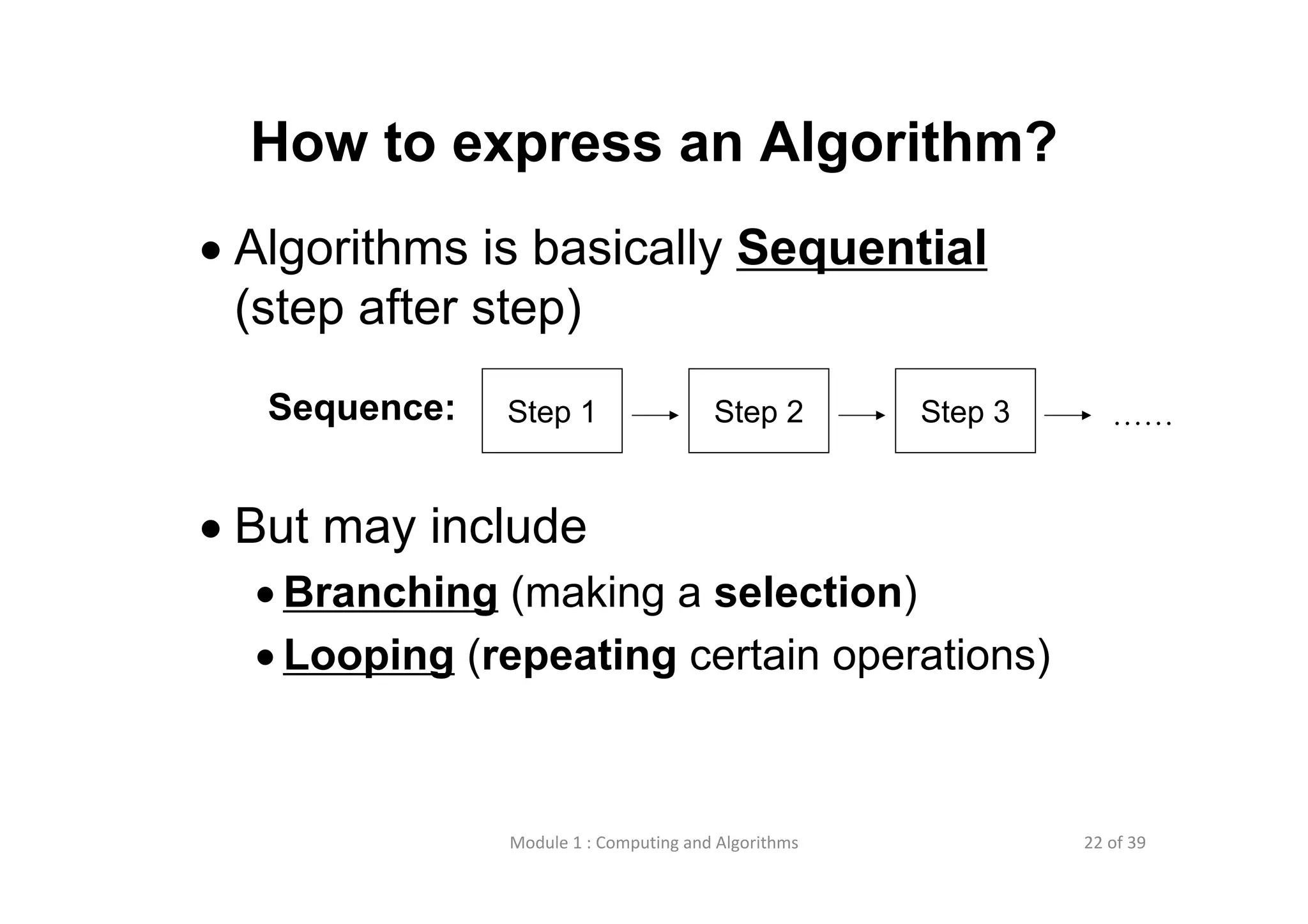
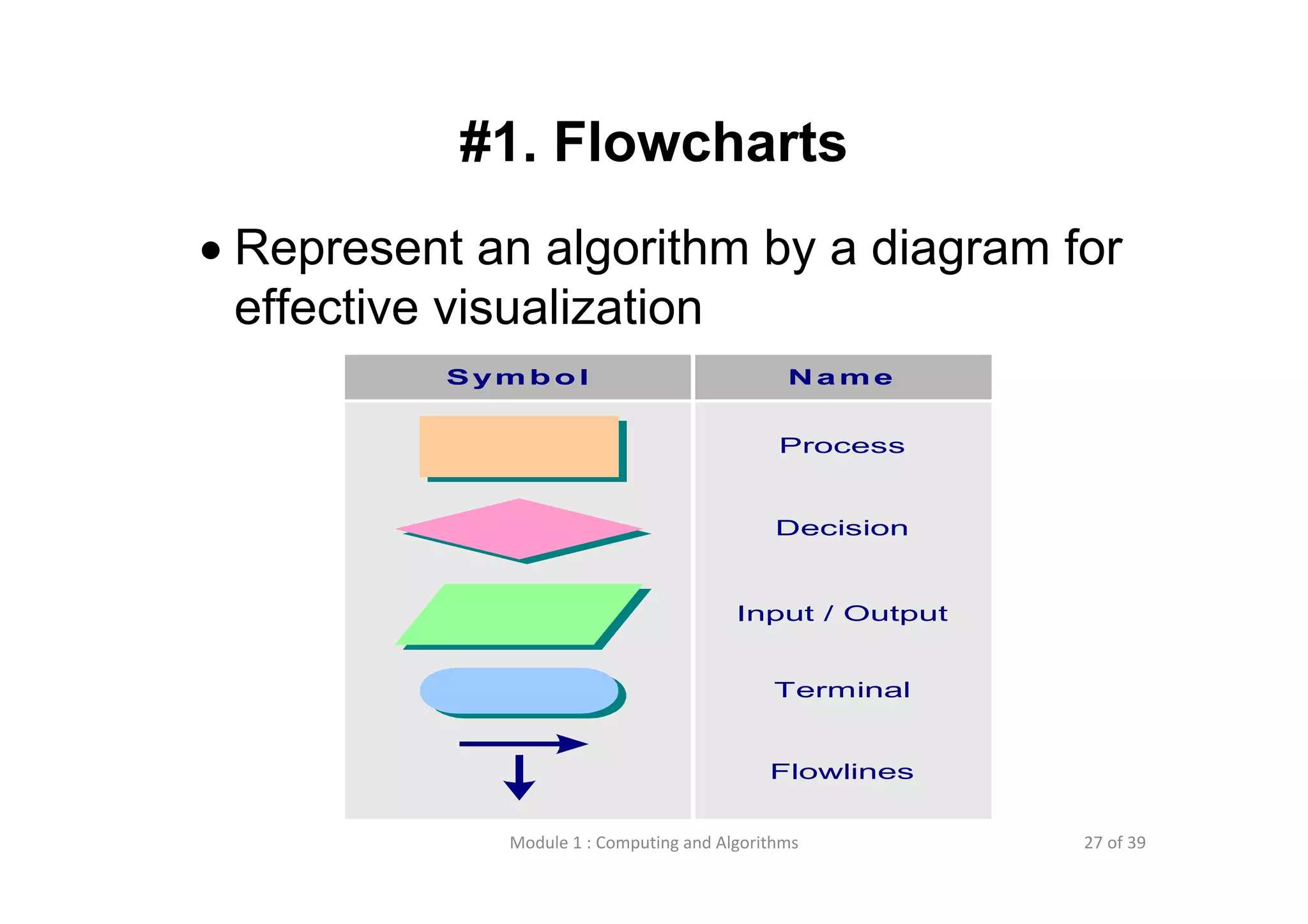
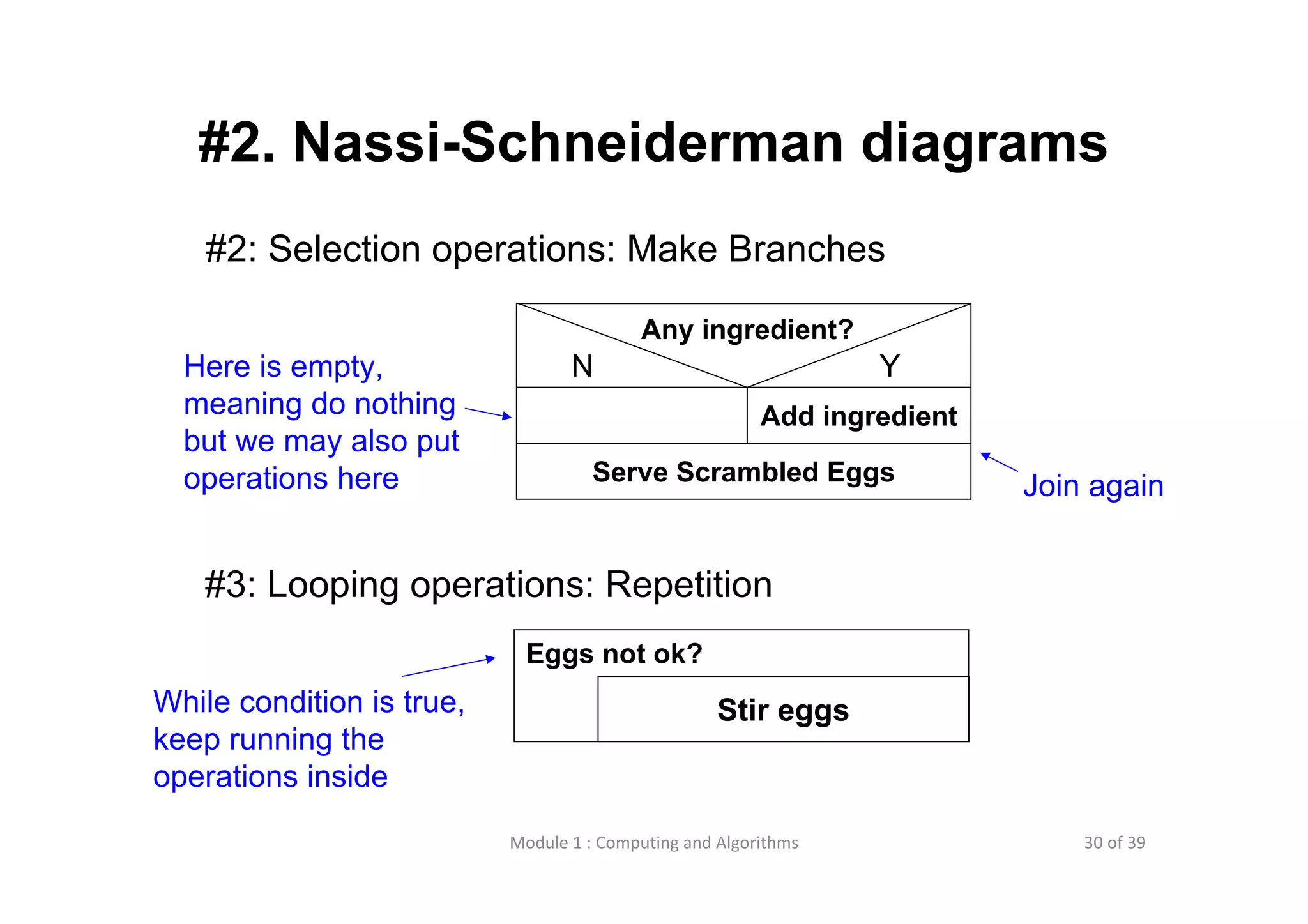
The document discusses computational thinking and algorithms. It defines computational thinking as a problem solving process involving analysis, modeling, understanding how computers work, logic, and procedure design. An algorithm is described as a detailed set of instructions to solve a problem, while a program is an implementation of an algorithm in a specific programming language. Common ways to express algorithms are through flowcharts, Nassi-Schneiderman diagrams, and pseudo-code. These allow visualizing an algorithm's sequential steps, branches, and loops.
![1 of 39Module 1 : Computing and Algorithms Introduction to Computational Thinking Module 1 : Computing and Algorithms Asst Prof Chi‐Wing FU, Philip Office: N4‐02c‐104 email: cwfu[at]ntu.edu.sg](https://image.slidesharecdn.com/lecture1computingandalgorithms-130525013914-phpapp01/75/Lecture-1-computing-and-algorithms-1-2048.jpg)































![37 of 39Module 1 : Computing and Algorithms More detail on these techniques later in this course Expressing an Algorithm • Important Note: • Must be unambiguous • Every step must be clear and precise • Specify the order of steps precisely [Sequence] • Consider all possible decision points [Branching and Looping] • Must terminate (No matter which representation you use)](https://image.slidesharecdn.com/lecture1computingandalgorithms-130525013914-phpapp01/75/Lecture-1-computing-and-algorithms-37-2048.jpg)

