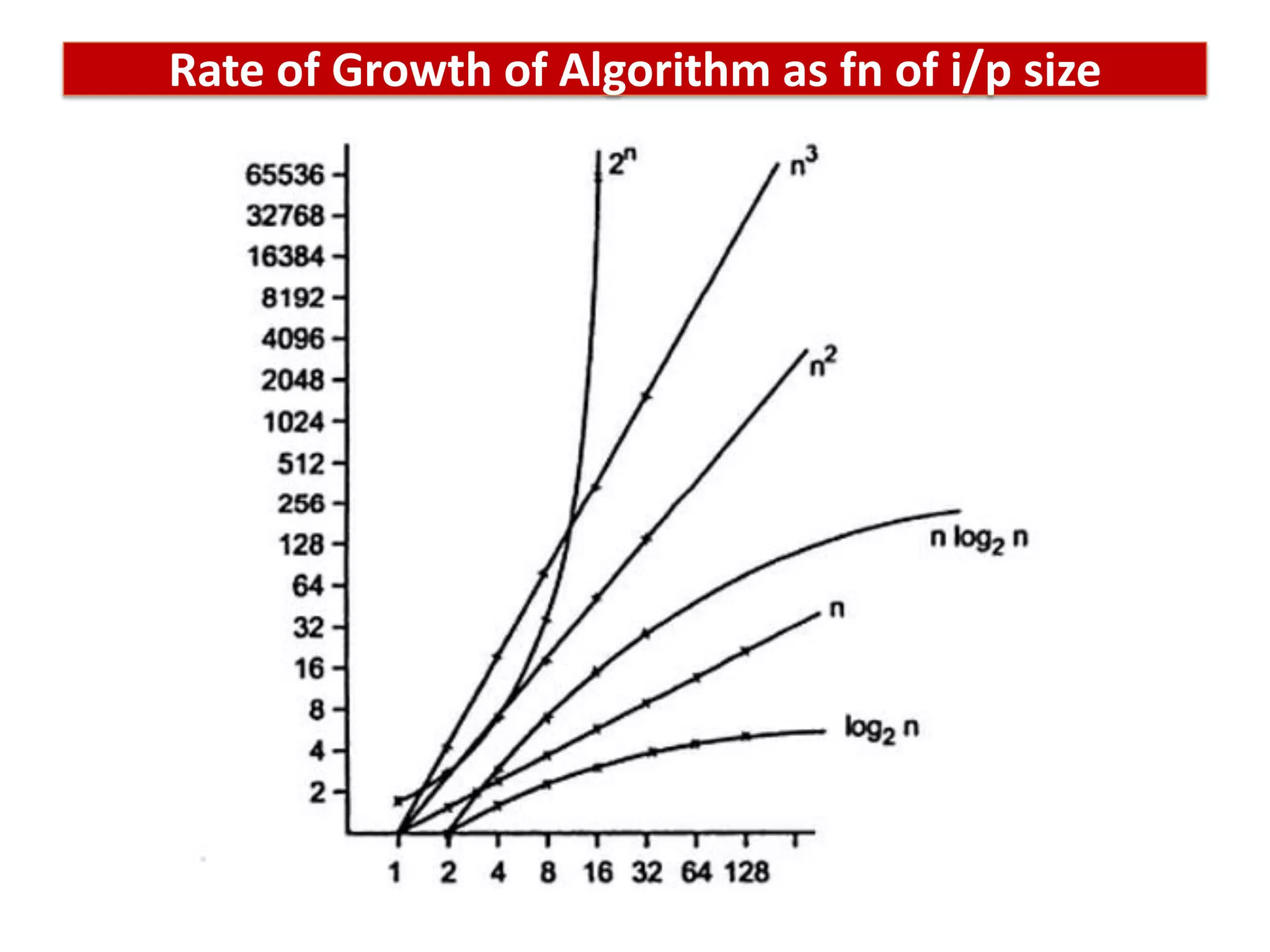
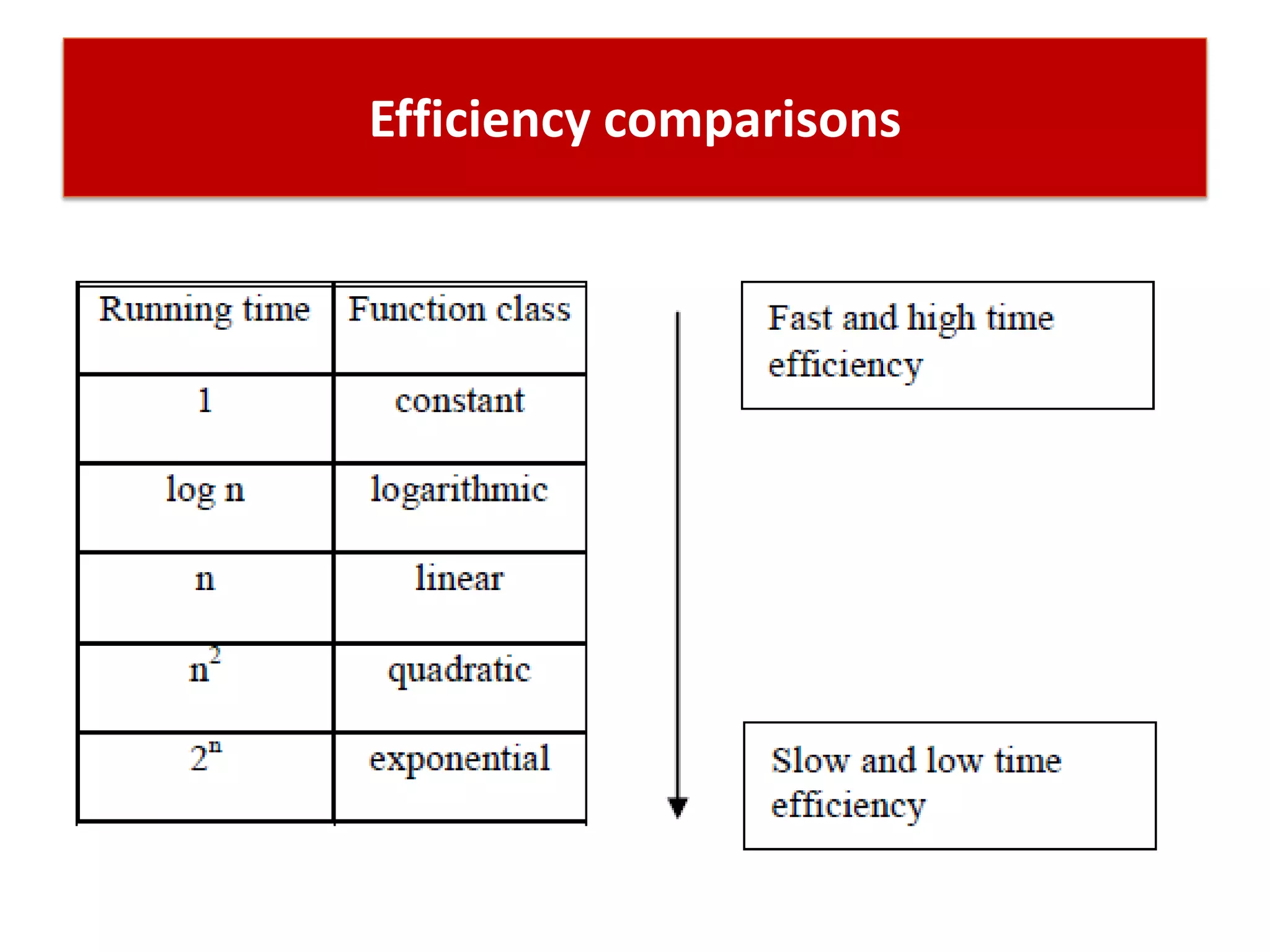
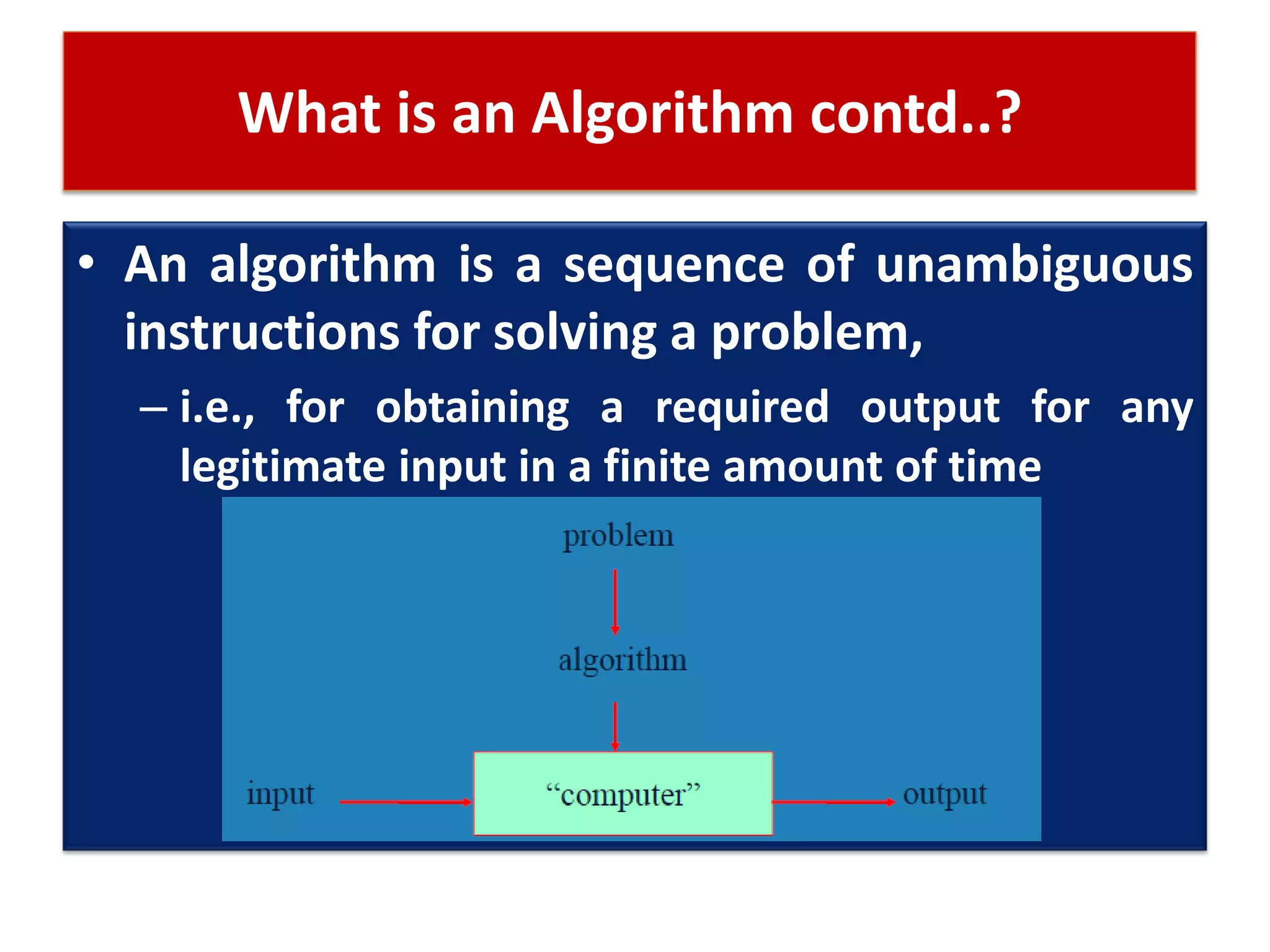
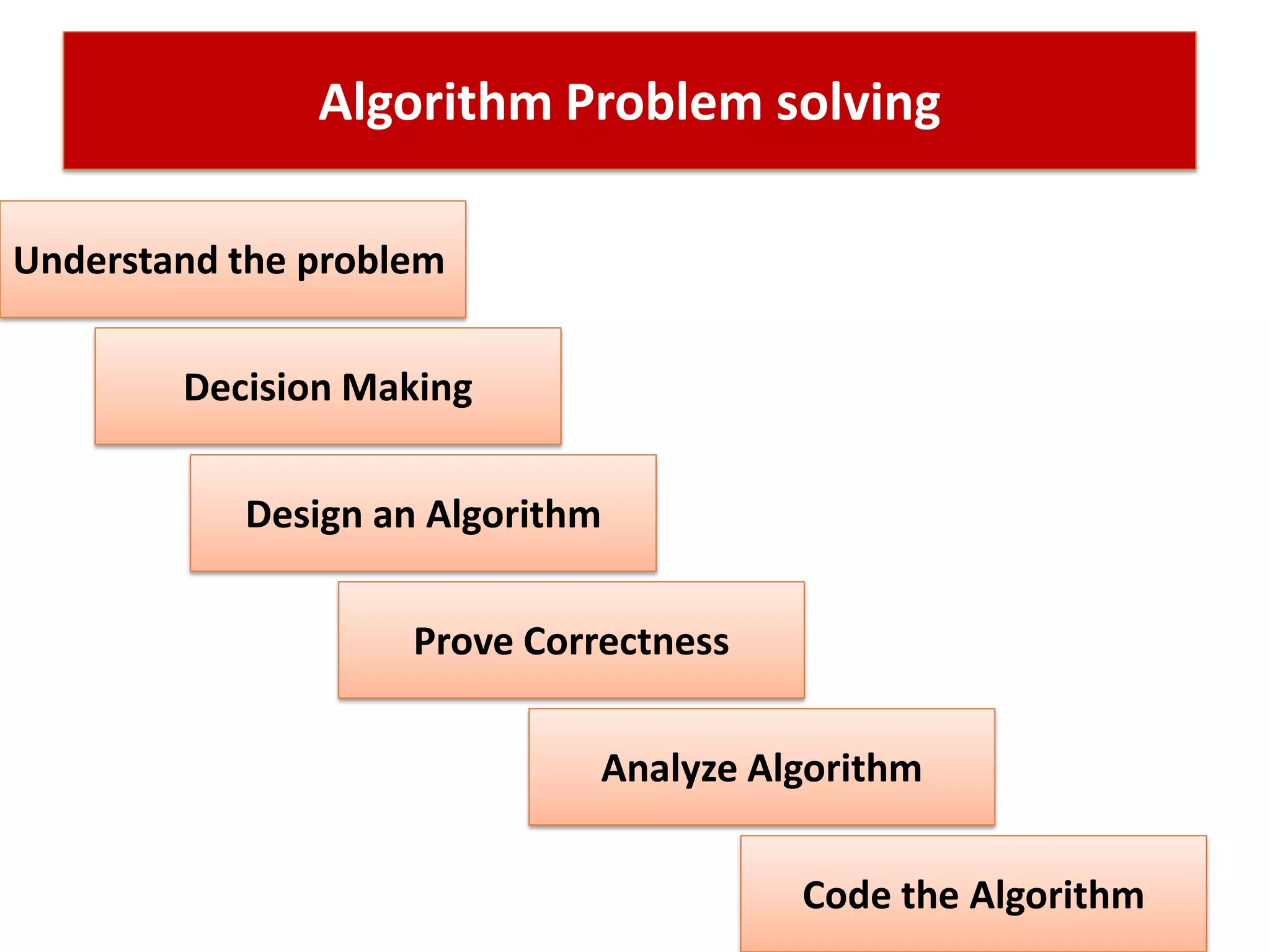
This document discusses algorithms and their role in computing. It defines an algorithm as a set of steps to solve a problem on a machine in a finite amount of time. Algorithms must be unambiguous, have defined inputs and outputs, and terminate. The document discusses designing algorithms, proving their correctness, and analyzing their performance and complexity. It provides examples of algorithm problems like sorting, searching, and graphs. The goal of analyzing algorithms is to evaluate and compare their performance as the problem size increases.


















![Linear Search Algorithm • Input: An array of n numbers and an element which is required to be searched in the given list • Output: Number exists in the list or not. Algorithm: 1. Input the size of list i.e. n 2. Read the n elements of array A 3. Input the item/element to be searched in the given list. 4. for each element in the array i=1 to n 5. if A[i]==item 6. Search successful, return 7. if i==n+1 8. Search unsuccessful. 9. Stop](https://image.slidesharecdn.com/lecture2-roleofalgorithmsincomputing-160326044620/75/Lecture-2-role-of-algorithms-in-computing-21-2048.jpg)




![How to calculate running time then? • Time complexity given in terms of FREQUENCY COUNT • Count denoting number of times of execution of statement. For (i=0; i <n;i++) { // St1 : 1, St 2 : n+1 , St 3 : n times sum = sum + a[i]; // n times } 3n + 2 ; O(n) neglecting constants and lower order terms](https://image.slidesharecdn.com/lecture2-roleofalgorithmsincomputing-160326044620/75/Lecture-2-role-of-algorithms-in-computing-26-2048.jpg)
![How to calculate running time then? for (i=0; i < n ; i ++) // 1 ; n+1 ; n times { for (j=0; j < n ; j ++) // n ; n(n+1) ; n(n) { c[i][j] = a[i][j] + b[i][j]; } } 3n2+4n+ 2 = O(n2)](https://image.slidesharecdn.com/lecture2-roleofalgorithmsincomputing-160326044620/75/Lecture-2-role-of-algorithms-in-computing-27-2048.jpg)