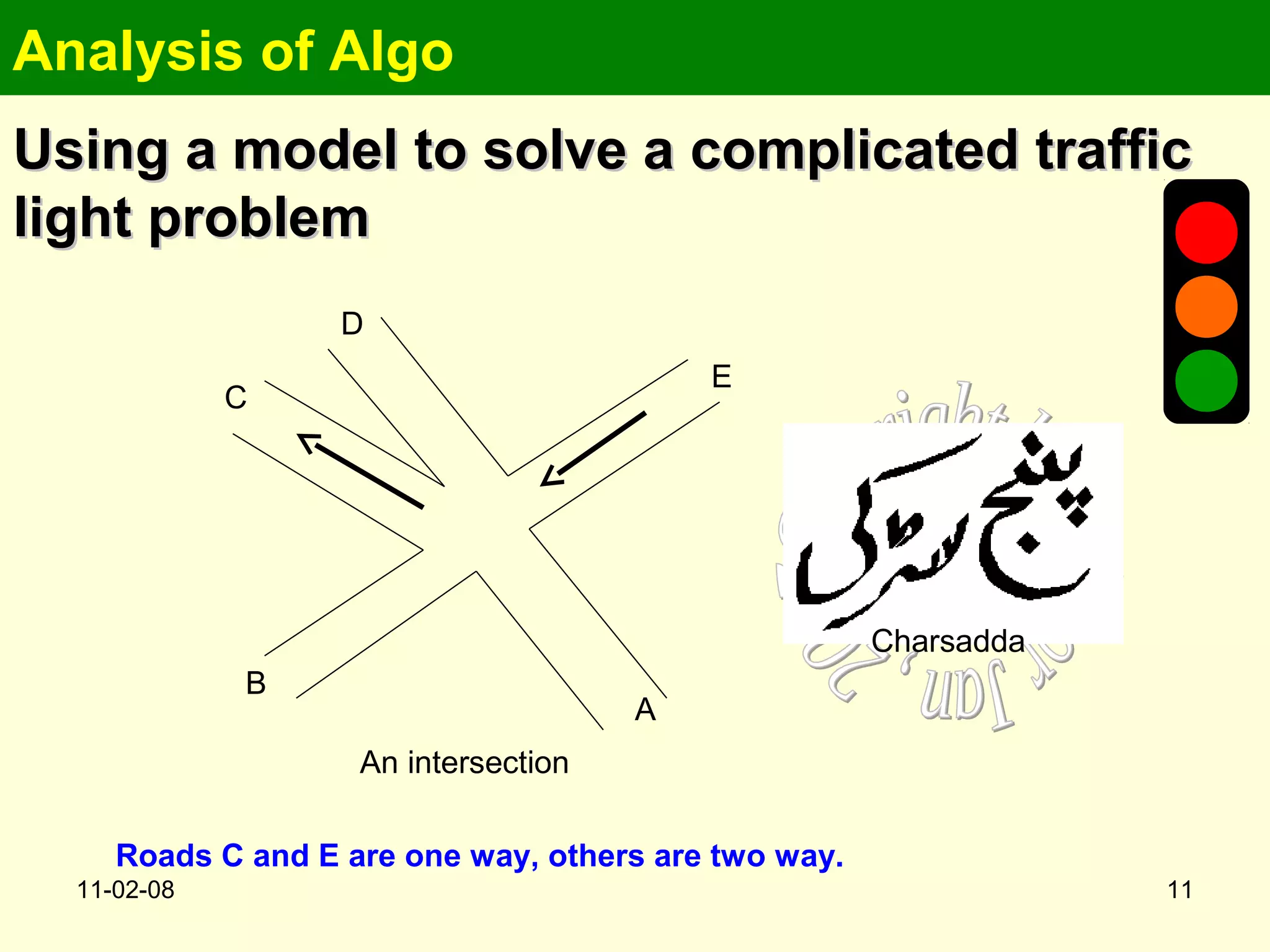
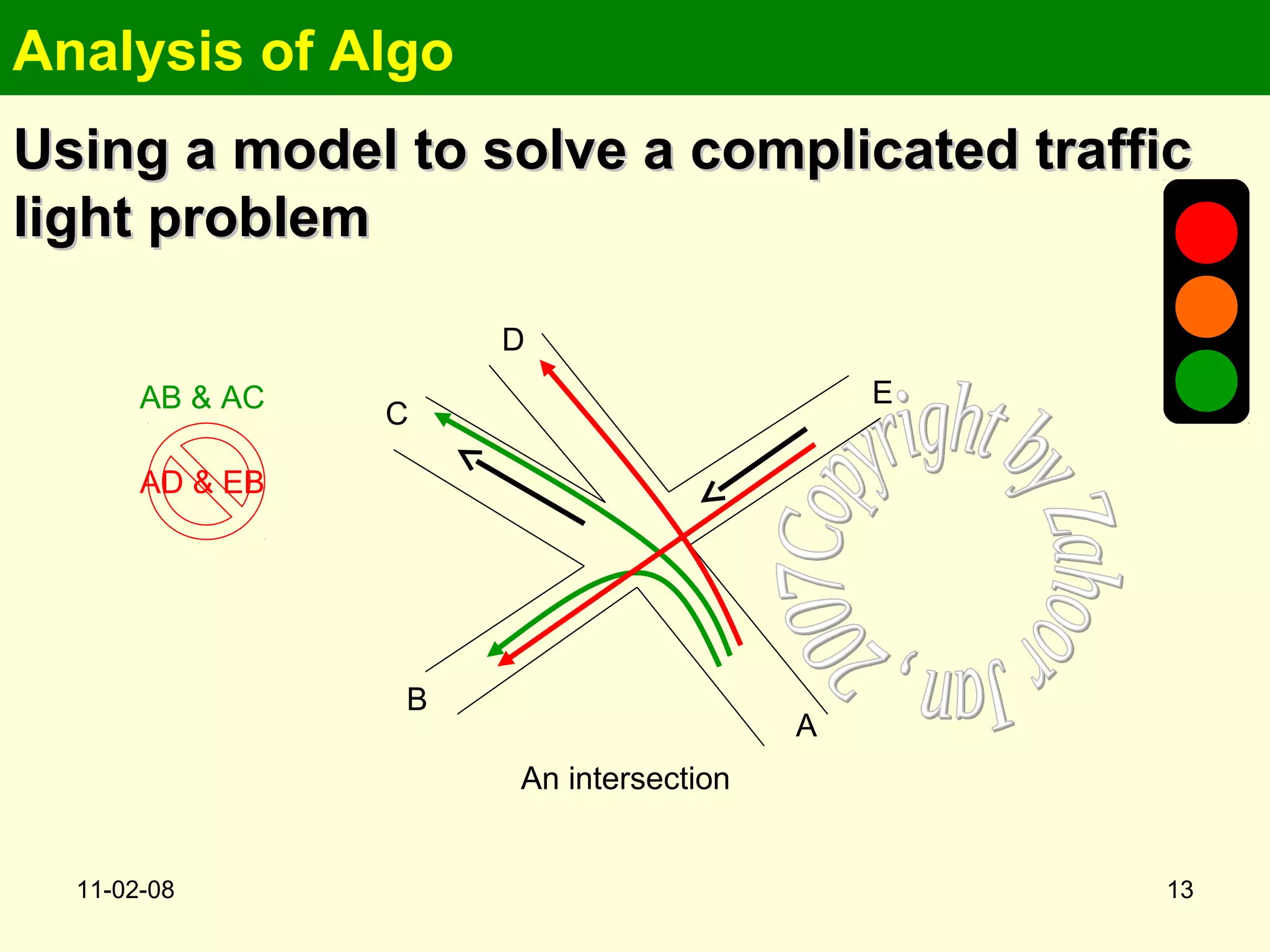
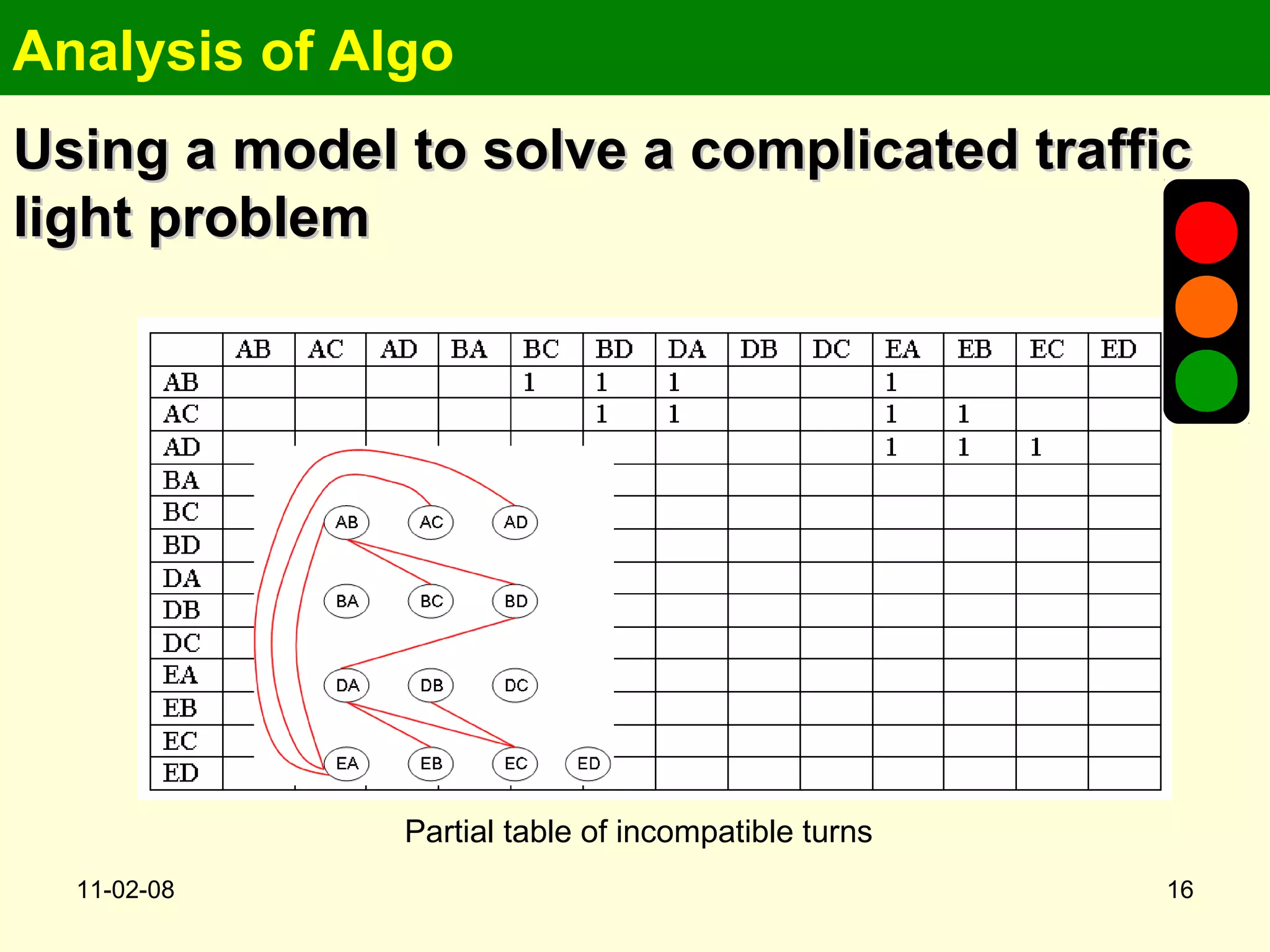
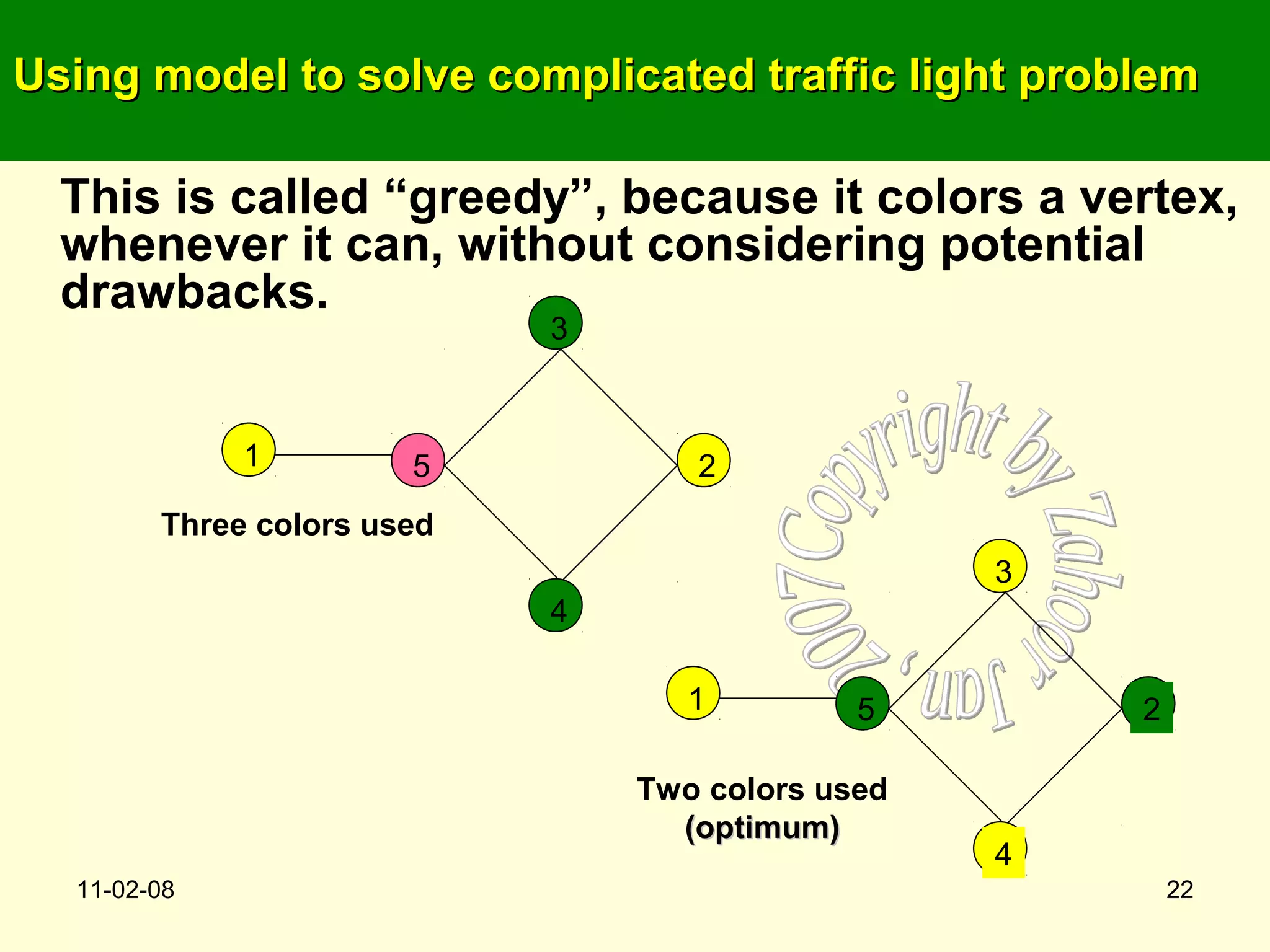
This document summarizes a lecture on analyzing algorithms. It discusses defining problems precisely, modeling problems mathematically, and designing algorithms to solve them. A specific example given is modeling a complex traffic intersection as a graph to determine the minimum number of traffic light phases. Colorings of the graph's vertices represent groups of permitted simultaneous turns. While finding optimal solutions is NP-complete, heuristics like greedy graph coloring can produce good approximations.