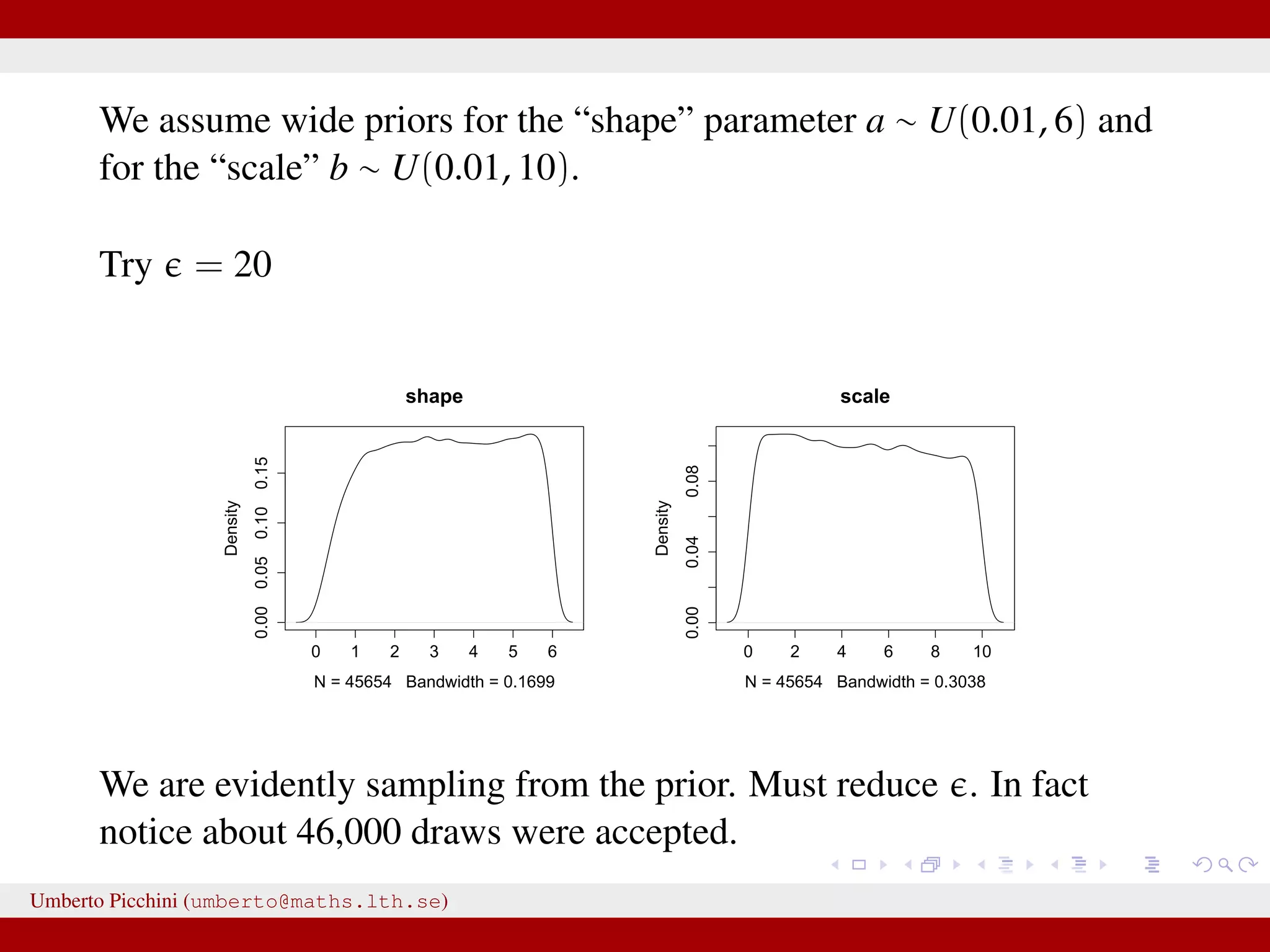
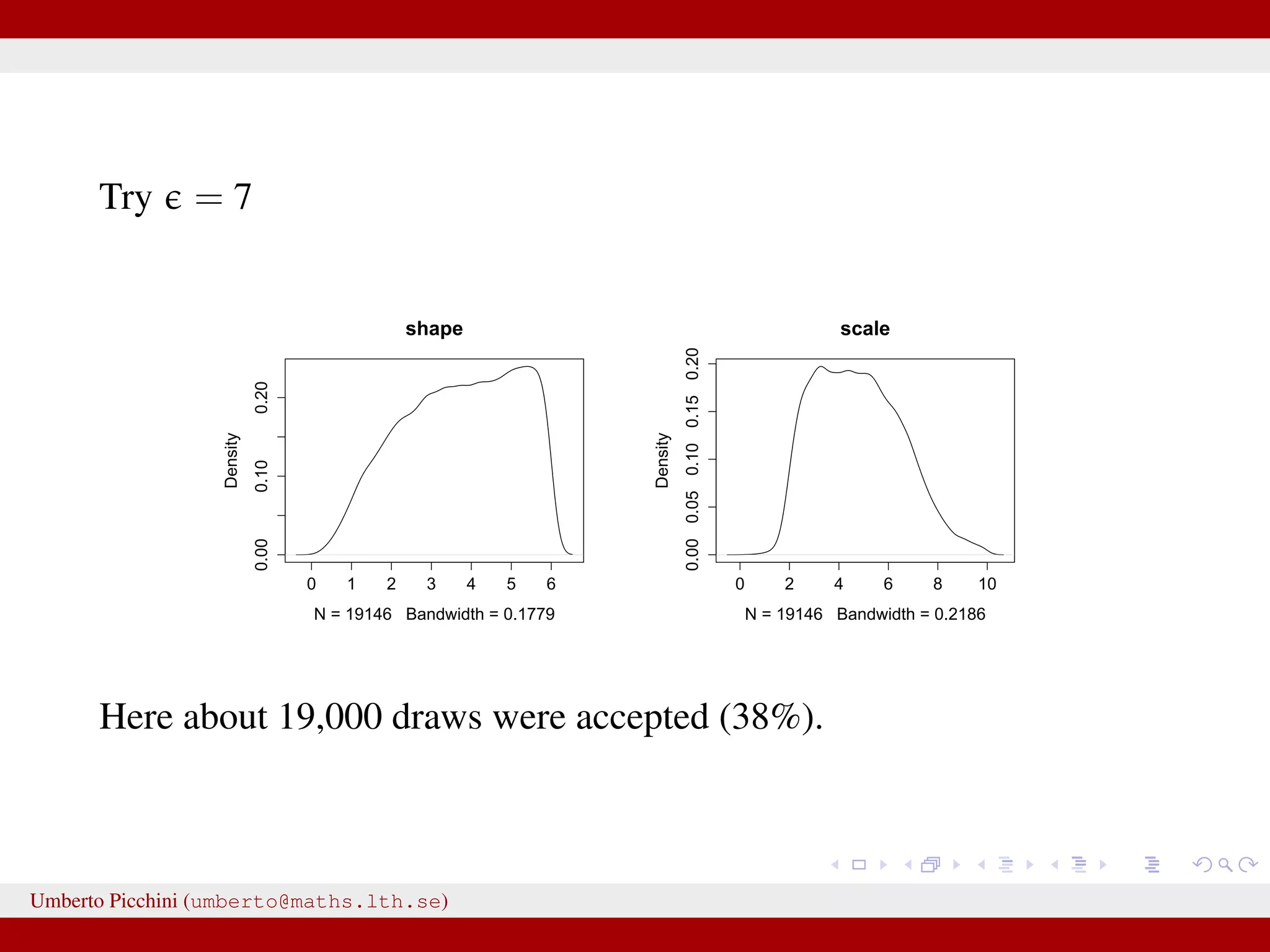
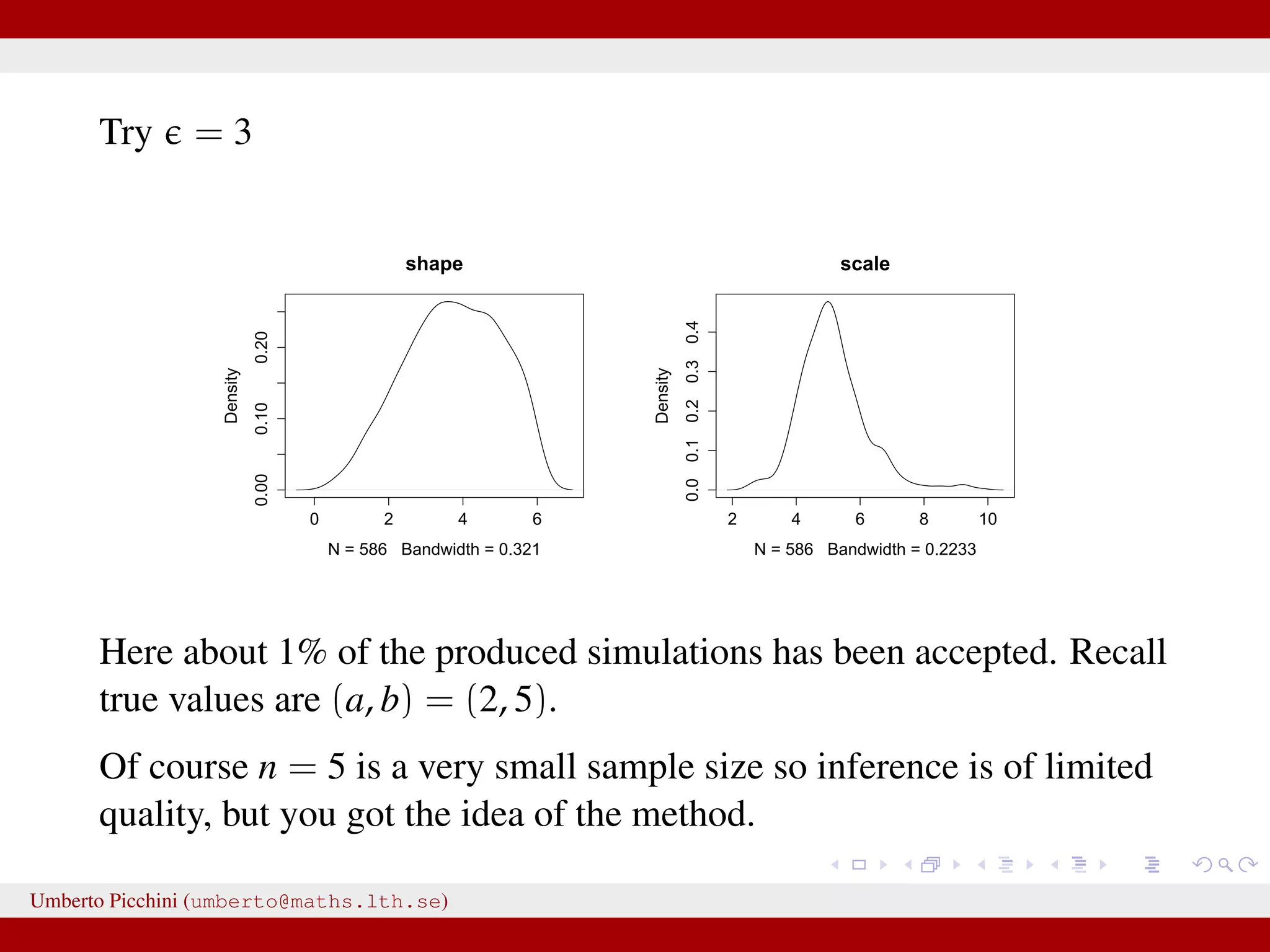
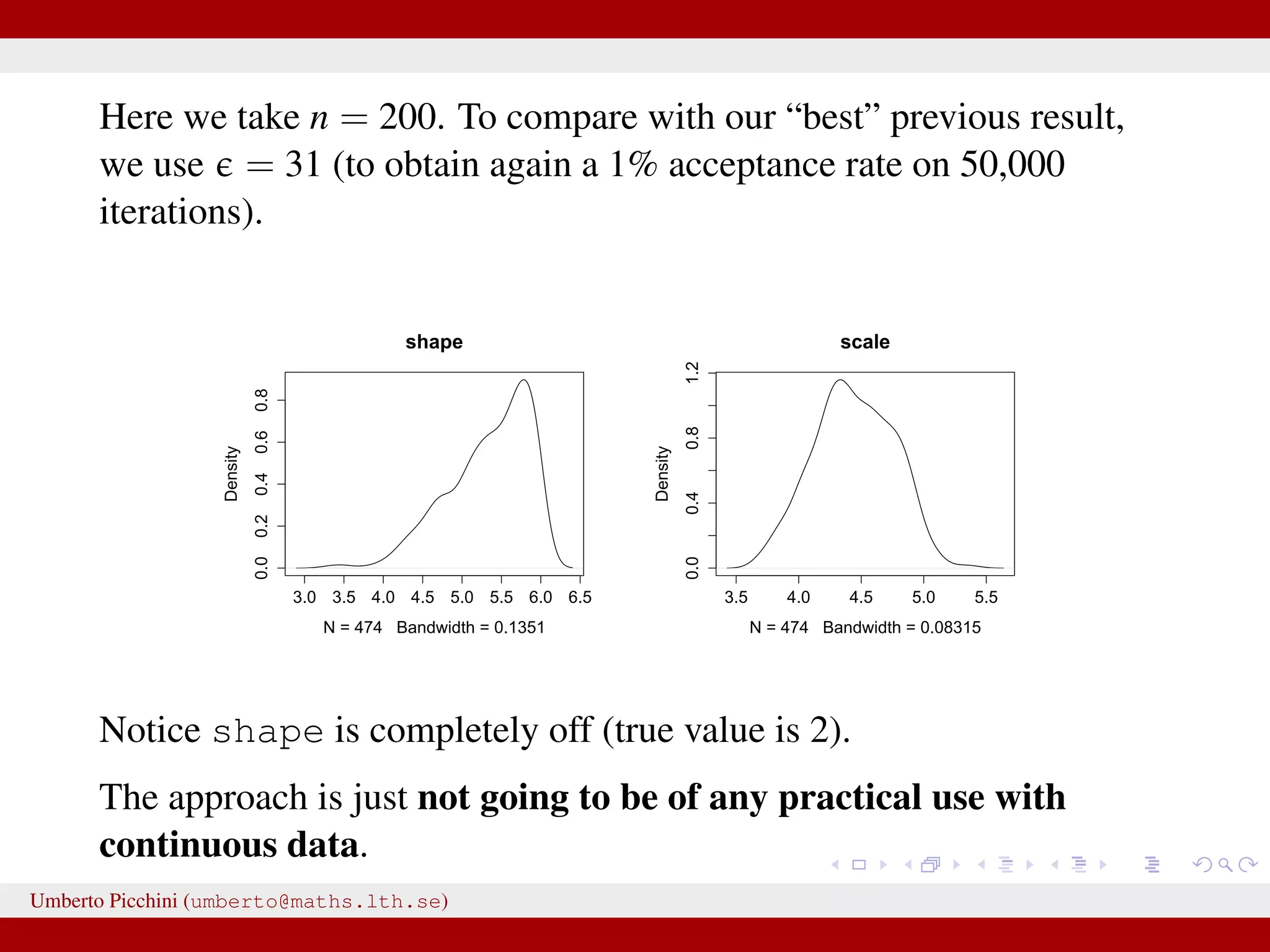
The document discusses the challenges and methodologies related to approximate Bayesian computation (ABC) for statistical inference, particularly when exact inference is impractical due to complex models or large datasets. It emphasizes the likelihood-free approach, where simulations from complex stochastic processes are used to estimate model parameters when traditional likelihood calculations are infeasible. Key concepts include the curse of dimensionality, the rejection sampling method, and the importance of formulating appropriate models to derive useful approximations.










![Gelman and Rubin, 1996 “[...] as emphasized in Rubin (1984), one of the great scientific advantages of simulation analysis of Bayesian methods is the freedom it gives the researcher to formulate appropriate models rather than be overly interested in analytically neat but scientifically inappropriate models.” Approximate Bayesian Computation and Synthetic Likelihoods are two approximate methods for inference, with ABC vastly more popular and with older origins. We will discuss ABC only. Umberto Picchini (umberto@maths.lth.se)](https://image.slidesharecdn.com/abcslides-160217212955/75/Intro-to-Approximate-Bayesian-Computation-ABC-11-2048.jpg)




![Likelihood free rejection sampling 1 simulate from the prior θ∗ ∼ π(θ) 2 plug θ∗ in your model and simulate a y∗ [this is the same as writing y∗ ∼ p(y|θ∗)] 3 if y∗ = y store θ∗. Go to step 1 and repeat. The above is a likelihood free algorithm: it does not require knowledge of the expression of p(y|θ). Each accepted θ∗ is such that θ∗ ∼ π(θ|y) exactly. We justify the result in next slide. Umberto Picchini (umberto@maths.lth.se)](https://image.slidesharecdn.com/abcslides-160217212955/75/Intro-to-Approximate-Bayesian-Computation-ABC-16-2048.jpg)



![Step 5: The posterior distribution is approximated with the accepted parameter points. The posterior distribution should have a nonnegligible probability for parameter values in a region This example application of ABC used simplifications for illustrative purposes. A number of review articles provide pointers to more realistic applications of ABC [9–11,14]. Figure 1. Parameter estimation by Approximate Bayesian Computation: a conceptual overview. doi:10.1371/journal.pcbi.1002803.g001 Umberto Picchini (umberto@maths.lth.se)](https://image.slidesharecdn.com/abcslides-160217212955/75/Intro-to-Approximate-Bayesian-Computation-ABC-20-2048.jpg)


















![Example from Sunnåker et al. 2013 [Large chunks from the cited article constitute the ABC entry in Wikipedia.] distribution for these models. Again, computational improvements for ABC in the space of models have been proposed, such as constructing a particle filter in the joint space of models and parameters [17]. Once the posterior probabilities of models have been estimated, one can make full use of the techniques of Bayesian model comparison. For instance, to compare the relative plausibilities of two models M1 and M2, one can compute their posterior ratio, which is related to the Bayes factor B1,2: p(M1DD) p(DDM1) p(M1) p(M1) additional bias due to the loss of information bias—for example, in the context of mod more subtle [12,18]. At the same time, some of the criticisms t at the ABC methods, in particular phylogeography [19–21], are not specific all Bayesian methods or even all statistic choice of prior distribution and param However, because of the ability of ABC-me more complex models, some of these g particular relevance in the context of ABC This section discusses these potential risk ways to address them (Table 2). Approximation of the Posterior A nonnegligible e comes with the price p(hDr(^DD,D)ƒe) instead of the true post sufficiently small tolerance, and a sensible resulting distribution p(hDr(^DD,D)ƒe) shou the actual target distribution p(hDD) reasona hand, a tolerance that is large enough th parameter space becomes accepted will yiel distribution. There are empirical studies of p(hDr(^DD,D)ƒe) and p(hDD) as a function of results for an upper e-dependent bound for estimates [24]. The accuracy of the pos expected quadratic loss) delivered by ABC also been investigated [25]. However, th distributions when e approaches zero, and distance measure used, is an important to Figure 2. A dynamic bistable hidden Markov model. doi:10.1371/journal.pcbi.1002803.g002 We have a hidden system state, moving between states {A,B} with probability θ, and stays in the current state with probability 1 − θ. Actual observations affected by measurement errors: probability to misread system states is 1 − γ for both A and B. Umberto Picchini (umberto@maths.lth.se)](https://image.slidesharecdn.com/abcslides-160217212955/75/Intro-to-Approximate-Bayesian-Computation-ABC-44-2048.jpg)



![Results at = 0 Dealing with a discrete state-space model allows the luxury to obtain results at = 0 (impossible with continuous states). Below: ABC posteriors (blue), true parameters (vertical red lines) and Beta prior (black). For θ we used a uniform prior in [0,1]. 0 0.2 0.4 0.6 0.8 1 0 1 2 3 4 5 θ 0 0.2 0.4 0.6 0.8 1 1.2 0 1 2 3 4 5 6 7 γ Remember: when using non-sufficient statistics results will be biased even with = 0. Umberto Picchini (umberto@maths.lth.se)](https://image.slidesharecdn.com/abcslides-160217212955/75/Intro-to-Approximate-Bayesian-Computation-ABC-49-2048.jpg)










![So Fearnhead & Prangle propose a regression-based approach to determine S(·) (prior to ABC-MCMC start): for the jth parameter in θ fit separately the linear regression models Sj(y) = ˆE(θj|y) = ˆβ (j) 0 + ˆβ(j) η(y), j = 1, 2, ..., dim(θ) [e.g. Sj(y) = ˆβ (j) 0 + ˆβ(j)η(y) = ˆβ (j) 0 + ˆβ (j) 1 y0 + · · · + ˆβ (j) n yn or you can let η(·) contain powers of y, say η(y, y2, y3, ...)] repeat the fitting separately for each θj. hopefully Sj(y) = ˆβ (j) 0 + ˆβ(j)η(y) will be “informative” for θj. Clearly, in the end we have as many summaries as the number of unknown parameters dim(θ). Umberto Picchini (umberto@maths.lth.se)](https://image.slidesharecdn.com/abcslides-160217212955/75/Intro-to-Approximate-Bayesian-Computation-ABC-61-2048.jpg)






