Workshop on Bayesian Inference for Latent Gaussian Models with Applications

ABC Methods for Bayesian Model Choice ABC Methods for Bayesian Model Choice Christian P. Robert Universit´ Paris-Dauphine, IuF, & CREST e http://www.ceremade.dauphine.fr/~xian February 5, 2011

ABC Methods for Bayesian Model Choice Approximate Bayesian computation Approximate Bayesian computation Approximate Bayesian computation ABC basics Alphabet soup Calibration of ABC ABC for model choice

ABC Methods for Bayesian Model Choice Approximate Bayesian computation ABC basics Untractable likelihoods Cases when the likelihood function f (y|θ) is unavailable and when the completion step f (y|θ) = f (y, z|θ) dz Z is impossible or too costly because of the dimension of z c MCMC cannot be implemented!

ABC Methods for Bayesian Model Choice Approximate Bayesian computation ABC basics Illustrations Example Stochastic volatility model: for Highest weight trajectories t = 1, . . . , T, 0.4 0.2 yt = exp(zt ) t , zt = a+bzt−1 +σηt , 0.0 −0.2 T very large makes it diﬃcult to −0.4 include z within the simulated 0 200 400 t 600 800 1000 parameters

ABC Methods for Bayesian Model Choice Approximate Bayesian computation ABC basics Illustrations Example Potts model: if y takes values on a grid Y of size k n and f (y|θ) ∝ exp θ Iyl =yi l∼i where l∼i denotes a neighbourhood relation, n moderately large prohibits the computation of the normalising constant

ABC Methods for Bayesian Model Choice Approximate Bayesian computation ABC basics Illustrations Example Inference on CMB: in cosmology, study of the Cosmic Microwave Background via likelihoods immensely slow to computate (e.g WMAP, Plank), because of numerically costly spectral transforms [Data is a Fortran program] [Kilbinger et al., 2010, MNRAS]

ABC Methods for Bayesian Model Choice Approximate Bayesian computation ABC basics Illustrations Example Coalescence tree: in population genetics, reconstitution of a common ancestor from a sample of genes via a phylogenetic tree that is close to impossible to integrate out [100 processor days with 4 parameters] [Cornuet et al., 2009, Bioinformatics]

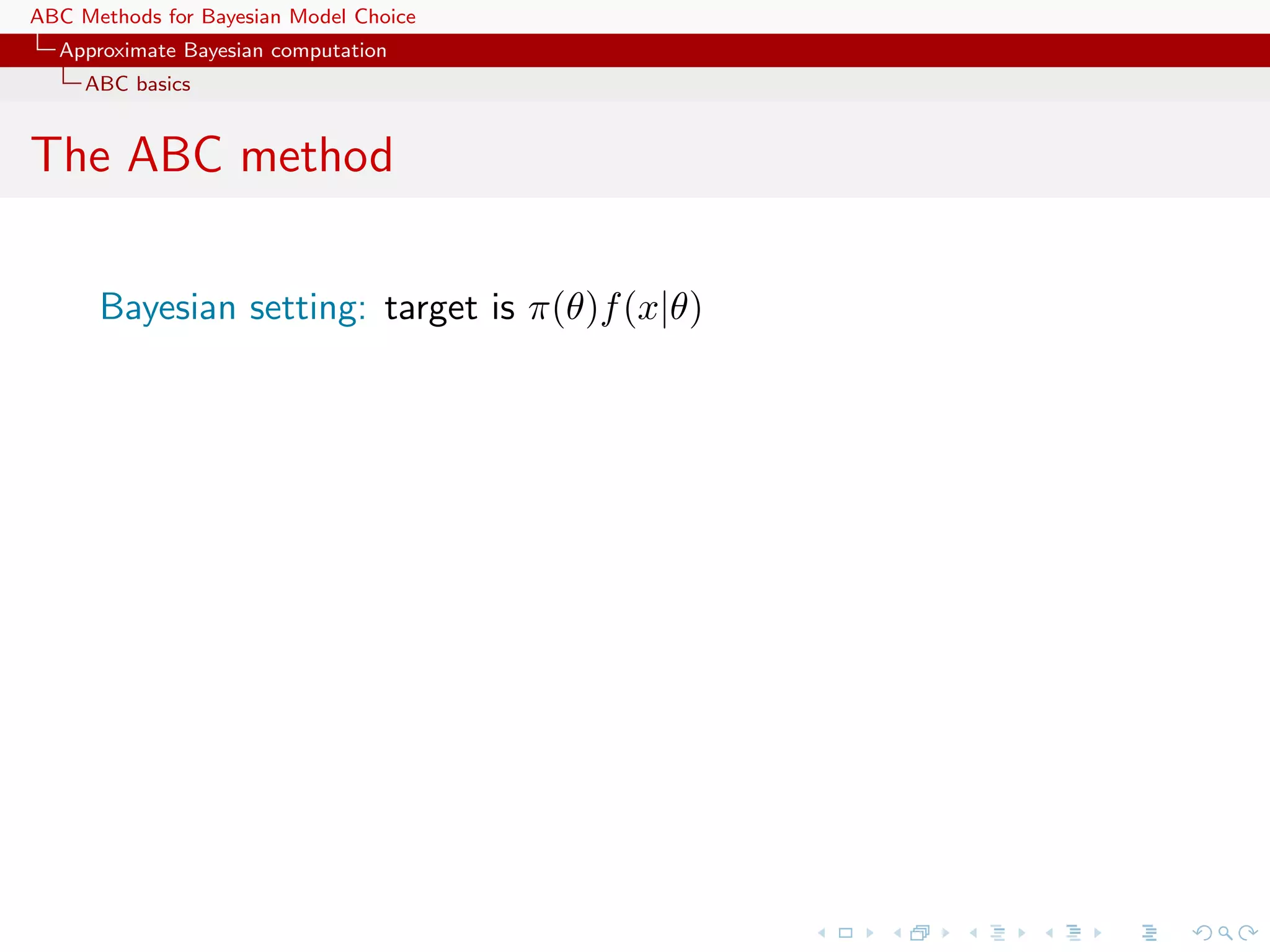
ABC Methods for Bayesian Model Choice Approximate Bayesian computation ABC basics The ABC method Bayesian setting: target is π(θ)f (x|θ)

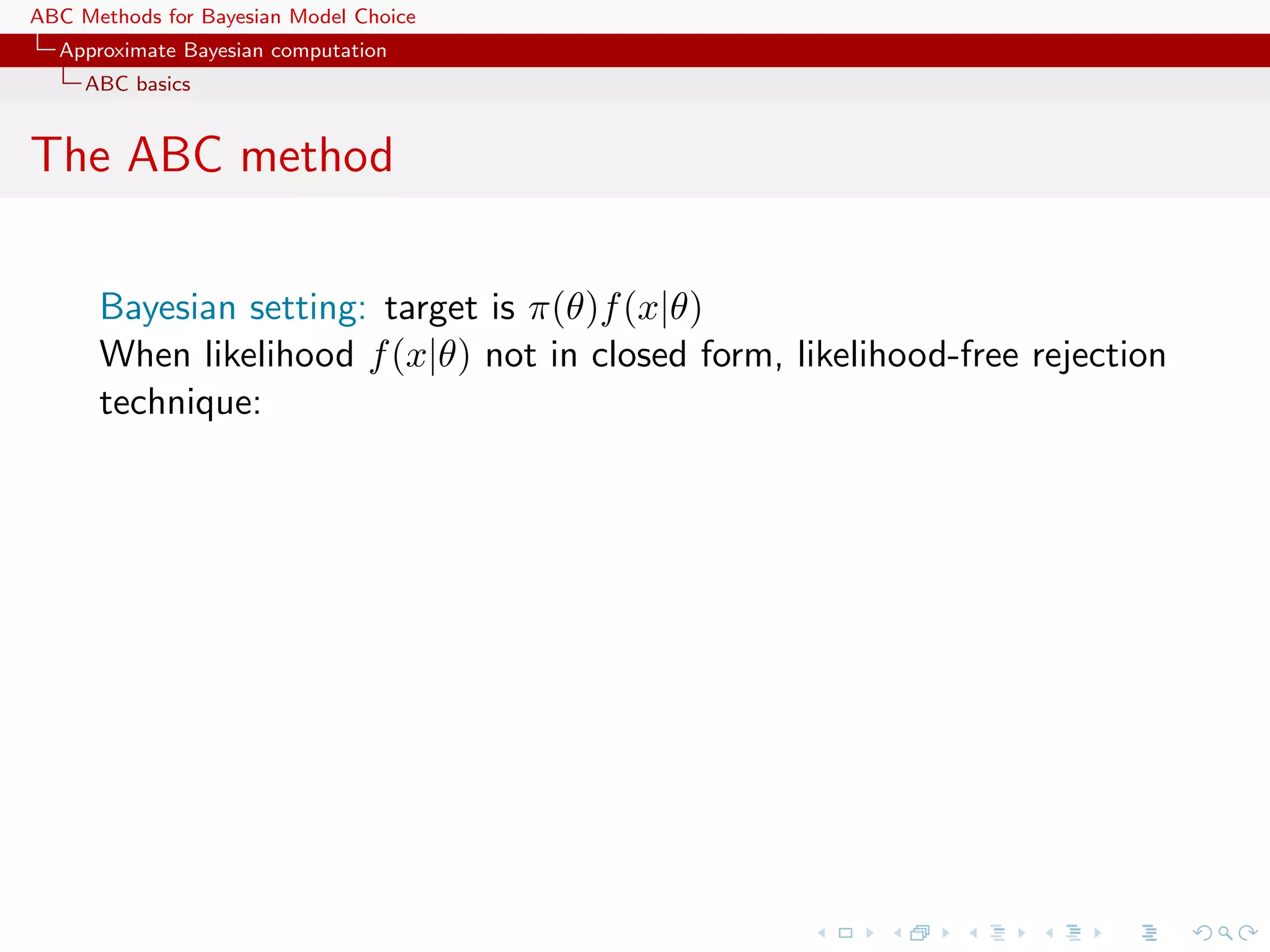
ABC Methods for Bayesian Model Choice Approximate Bayesian computation ABC basics The ABC method Bayesian setting: target is π(θ)f (x|θ) When likelihood f (x|θ) not in closed form, likelihood-free rejection technique:

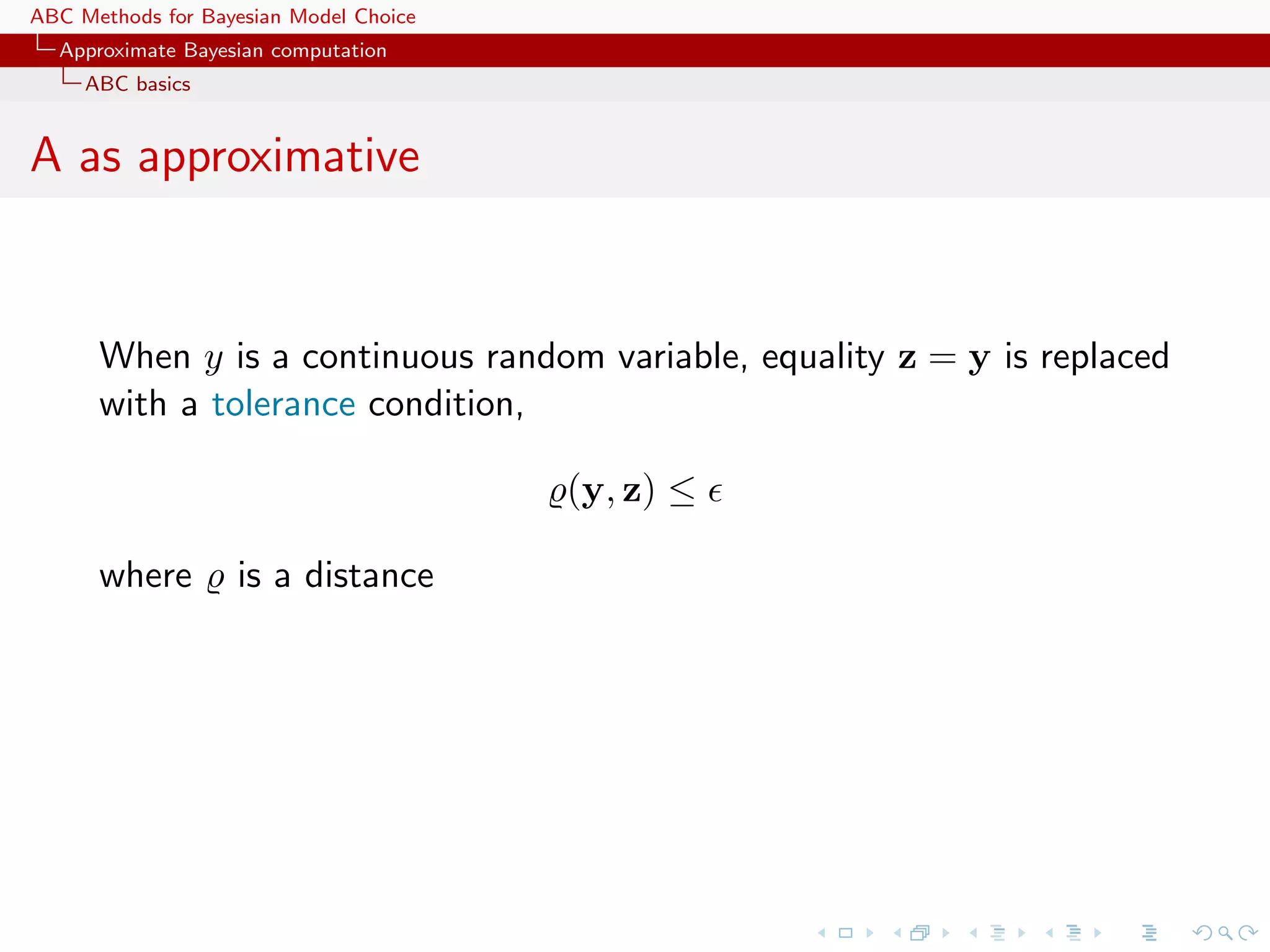
ABC Methods for Bayesian Model Choice Approximate Bayesian computation ABC basics The ABC method Bayesian setting: target is π(θ)f (x|θ) When likelihood f (x|θ) not in closed form, likelihood-free rejection technique: ABC algorithm For an observation y ∼ f (y|θ), under the prior π(θ), keep jointly simulating θ ∼ π(θ) , z ∼ f (z|θ ) , until the auxiliary variable z is equal to the observed value, z = y. [Tavar´ et al., 1997] e

ABC Methods for Bayesian Model Choice Approximate Bayesian computation ABC basics Why does it work?! The proof is trivial: f (θi ) ∝ π(θi )f (z|θi )Iy (z) z∈D ∝ π(θi )f (y|θi ) = π(θi |y) . [Accept–Reject 101]

ABC Methods for Bayesian Model Choice Approximate Bayesian computation ABC basics Earlier occurrence ‘Bayesian statistics and Monte Carlo methods are ideally suited to the task of passing many models over one dataset’ [Don Rubin, Annals of Statistics, 1984] Note Rubin (1984) does not promote this algorithm for likelihood-free simulation but frequentist intuition on posterior distributions: parameters from posteriors are more likely to be those that could have generated the data.

ABC Methods for Bayesian Model Choice Approximate Bayesian computation ABC basics A as approximative When y is a continuous random variable, equality z = y is replaced with a tolerance condition, (y, z) ≤ where is a distance

ABC Methods for Bayesian Model Choice Approximate Bayesian computation ABC basics A as approximative When y is a continuous random variable, equality z = y is replaced with a tolerance condition, (y, z) ≤ where is a distance Output distributed from π(θ) Pθ { (y, z) < } ∝ π(θ| (y, z) < )

ABC Methods for Bayesian Model Choice Approximate Bayesian computation ABC basics ABC algorithm Algorithm 1 Likelihood-free rejection sampler for i = 1 to N do repeat generate θ from the prior distribution π(·) generate z from the likelihood f (·|θ ) until ρ{η(z), η(y)} ≤ set θi = θ end for where η(y) deﬁnes a (maybe in-suﬃcient) statistic

ABC Methods for Bayesian Model Choice Approximate Bayesian computation ABC basics Output The likelihood-free algorithm samples from the marginal in z of: π(θ)f (z|θ)IA ,y (z) π (θ, z|y) = , A ,y ×Θ π(θ)f (z|θ)dzdθ where A ,y = {z ∈ D|ρ(η(z), η(y)) < }.

ABC Methods for Bayesian Model Choice Approximate Bayesian computation ABC basics Output The likelihood-free algorithm samples from the marginal in z of: π(θ)f (z|θ)IA ,y (z) π (θ, z|y) = , A ,y ×Θ π(θ)f (z|θ)dzdθ where A ,y = {z ∈ D|ρ(η(z), η(y)) < }. The idea behind ABC is that the summary statistics coupled with a small tolerance should provide a good approximation of the posterior distribution: π (θ|y) = π (θ, z|y)dz ≈ π(θ|y) .

ABC Methods for Bayesian Model Choice Approximate Bayesian computation ABC basics MA example Consider the MA(q) model q xt = t+ ϑi t−i i=1 Simple prior: uniform prior over the identiﬁability zone, e.g. triangle for MA(2)

ABC Methods for Bayesian Model Choice Approximate Bayesian computation ABC basics MA example (2) ABC algorithm thus made of 1. picking a new value (ϑ1 , ϑ2 ) in the triangle 2. generating an iid sequence ( t )−q<t≤T 3. producing a simulated series (xt )1≤t≤T

ABC Methods for Bayesian Model Choice Approximate Bayesian computation ABC basics MA example (2) ABC algorithm thus made of 1. picking a new value (ϑ1 , ϑ2 ) in the triangle 2. generating an iid sequence ( t )−q<t≤T 3. producing a simulated series (xt )1≤t≤T Distance: basic distance between the series T ρ((xt )1≤t≤T , (xt )1≤t≤T ) = (xt − xt )2 t=1 or between summary statistics like the ﬁrst q autocorrelations T τj = xt xt−j t=j+1

ABC Methods for Bayesian Model Choice Approximate Bayesian computation ABC basics Comparison of distance impact Evaluation of the tolerance on the ABC sample against both distances ( = 100%, 10%, 1%, 0.1%) for an MA(2) model

ABC Methods for Bayesian Model Choice Approximate Bayesian computation ABC basics Comparison of distance impact 4 1.5 3 1.0 2 0.5 1 0.0 0 0.0 0.2 0.4 0.6 0.8 −2.0 −1.0 0.0 0.5 1.0 1.5 θ1 θ2 Evaluation of the tolerance on the ABC sample against both distances ( = 100%, 10%, 1%, 0.1%) for an MA(2) model

ABC Methods for Bayesian Model Choice Approximate Bayesian computation ABC basics ABC advances Simulating from the prior is often poor in eﬃciency

ABC Methods for Bayesian Model Choice Approximate Bayesian computation ABC basics ABC advances Simulating from the prior is often poor in eﬃciency Either modify the proposal distribution on θ to increase the density of x’s within the vicinity of y... [Marjoram et al, 2003; Bortot et al., 2007, Sisson et al., 2007]

ABC Methods for Bayesian Model Choice Approximate Bayesian computation ABC basics ABC advances Simulating from the prior is often poor in eﬃciency Either modify the proposal distribution on θ to increase the density of x’s within the vicinity of y... [Marjoram et al, 2003; Bortot et al., 2007, Sisson et al., 2007] ...or by viewing the problem as a conditional density estimation and by developing techniques to allow for larger [Beaumont et al., 2002]

ABC Methods for Bayesian Model Choice Approximate Bayesian computation ABC basics ABC advances Simulating from the prior is often poor in eﬃciency Either modify the proposal distribution on θ to increase the density of x’s within the vicinity of y... [Marjoram et al, 2003; Bortot et al., 2007, Sisson et al., 2007] ...or by viewing the problem as a conditional density estimation and by developing techniques to allow for larger [Beaumont et al., 2002] .....or even by including in the inferential framework [ABCµ ] [Ratmann et al., 2009]

ABC Methods for Bayesian Model Choice Approximate Bayesian computation Alphabet soup ABC-NP Better usage of [prior] simulations by adjustement: instead of throwing away θ such that ρ(η(z), η(y)) > , replace θs with locally regressed θ∗ = θ − {η(z) − η(y)}T β ˆ [Csill´ry et al., TEE, 2010] e ˆ where β is obtained by [NP] weighted least square regression on (η(z) − η(y)) with weights Kδ {ρ(η(z), η(y))} [Beaumont et al., 2002, Genetics]

ABC Methods for Bayesian Model Choice Approximate Bayesian computation Alphabet soup ABC-MCMC Markov chain (θ(t) ) created via the transition function  θ ∼ Kω (θ |θ(t) ) if x ∼ f (x|θ ) is such that x = y   π(θ )Kω (t) |θ ) θ (t+1) = and u ∼ U(0, 1) ≤ π(θ(t) )K (θ |θ(t) ) ,  ω (θ  (t) θ otherwise,

ABC Methods for Bayesian Model Choice Approximate Bayesian computation Alphabet soup ABC-MCMC Markov chain (θ(t) ) created via the transition function  θ ∼ Kω (θ |θ(t) ) if x ∼ f (x|θ ) is such that x = y   π(θ )Kω (t) |θ ) θ (t+1) = and u ∼ U(0, 1) ≤ π(θ(t) )K (θ |θ(t) ) ,  ω (θ  (t) θ otherwise, has the posterior π(θ|y) as stationary distribution [Marjoram et al, 2003]

ABC Methods for Bayesian Model Choice Approximate Bayesian computation Alphabet soup ABC-MCMC (2) Algorithm 2 Likelihood-free MCMC sampler Use Algorithm 1 to get (θ(0) , z(0) ) for t = 1 to N do Generate θ from Kω ·|θ(t−1) , Generate z from the likelihood f (·|θ ), Generate u from U[0,1] , π(θ )Kω (θ(t−1) |θ ) if u ≤ I π(θ(t−1) Kω (θ |θ(t−1) ) A ,y (z ) then set (θ(t) , z(t) ) = (θ , z ) else (θ(t) , z(t) )) = (θ(t−1) , z(t−1) ), end if end for

ABC Methods for Bayesian Model Choice Approximate Bayesian computation Alphabet soup ABCµ [Ratmann, Andrieu, Wiuf and Richardson, 2009, PNAS] Use of a joint density f (θ, |y) ∝ ξ( |y, θ) × πθ (θ) × π ( ) where y is the data, and ξ( |y, θ) is the prior predictive density of ρ(η(z), η(y)) given θ and x when z ∼ f (z|θ)

ABC Methods for Bayesian Model Choice Approximate Bayesian computation Alphabet soup ABCµ [Ratmann, Andrieu, Wiuf and Richardson, 2009, PNAS] Use of a joint density f (θ, |y) ∝ ξ( |y, θ) × πθ (θ) × π ( ) where y is the data, and ξ( |y, θ) is the prior predictive density of ρ(η(z), η(y)) given θ and x when z ∼ f (z|θ) Warning! Replacement of ξ( |y, θ) with a non-parametric kernel approximation.

ABC Methods for Bayesian Model Choice Approximate Bayesian computation Alphabet soup ABCµ details Multidimensional distances ρk (k = 1, . . . , K) and errors k = ρk (ηk (z), ηk (y)), with ˆ 1 k ∼ ξk ( |y, θ) ≈ ξk ( |y, θ) = K[{ k −ρk (ηk (zb ), ηk (y))}/hk ] Bhk b ˆ then used in replacing ξ( |y, θ) with mink ξk ( |y, θ)

ABC Methods for Bayesian Model Choice Approximate Bayesian computation Alphabet soup ABCµ details Multidimensional distances ρk (k = 1, . . . , K) and errors k = ρk (ηk (z), ηk (y)), with ˆ 1 k ∼ ξk ( |y, θ) ≈ ξk ( |y, θ) = K[{ k −ρk (ηk (zb ), ηk (y))}/hk ] Bhk b ˆ then used in replacing ξ( |y, θ) with mink ξk ( |y, θ) ABCµ involves acceptance probability ˆ π(θ , ) q(θ , θ)q( , ) mink ξk ( |y, θ ) ˆ π(θ, ) q(θ, θ )q( , ) mink ξk ( |y, θ)

ABC Methods for Bayesian Model Choice Approximate Bayesian computation Alphabet soup ABCµ multiple errors [ c Ratmann et al., PNAS, 2009]

ABC Methods for Bayesian Model Choice Approximate Bayesian computation Alphabet soup ABCµ for model choice [ c Ratmann et al., PNAS, 2009]

ABC Methods for Bayesian Model Choice Approximate Bayesian computation Alphabet soup Questions about ABCµ For each model under comparison, marginal posterior on used to assess the ﬁt of the model (HPD includes 0 or not).

ABC Methods for Bayesian Model Choice Approximate Bayesian computation Alphabet soup Questions about ABCµ For each model under comparison, marginal posterior on used to assess the ﬁt of the model (HPD includes 0 or not). Is the data informative about ? [Identiﬁability] How is the prior π( ) impacting the comparison? How is using both ξ( |x0 , θ) and π ( ) compatible with a standard probability model? [remindful of Wilkinson] Where is the penalisation for complexity in the model comparison? [X, Mengersen & Chen, 2010, PNAS]

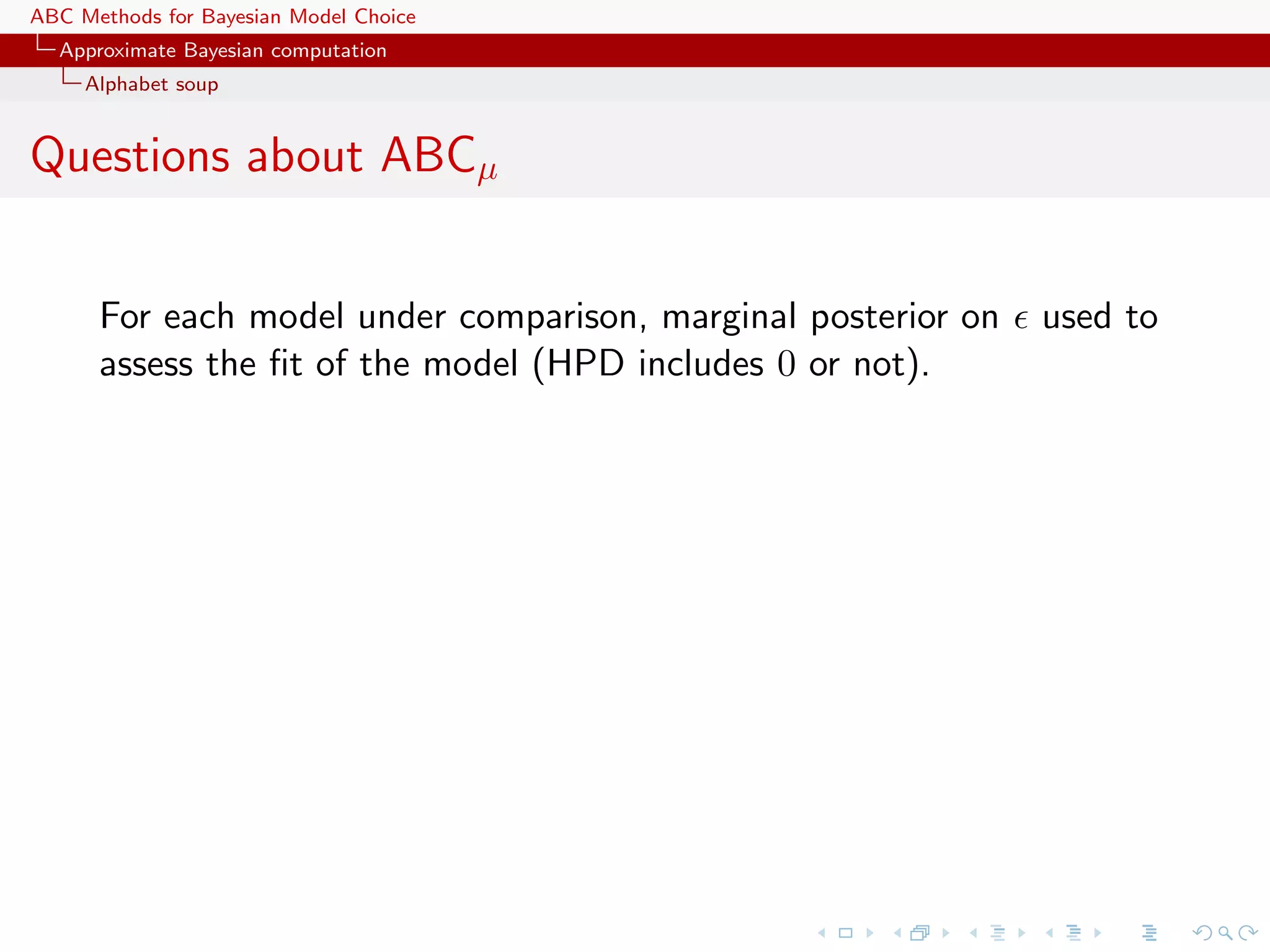
ABC Methods for Bayesian Model Choice Approximate Bayesian computation Alphabet soup A PMC version Use of the same kernel idea as ABC-PRC but with IS correction Generate a sample at iteration t by N (t) (t−1) (t−1) πt (θ ) ∝ ˆ ωj Kt (θ(t) |θj ) j=1 modulo acceptance of the associated xt , and use an importance (t) weight associated with an accepted simulation θi (t) (t) (t) ωi ∝ π(θi ) πt (θi ) . ˆ c Still likelihood free [Beaumont et al., Biometrika, 2009]

ABC Methods for Bayesian Model Choice Approximate Bayesian computation Alphabet soup Sequential Monte Carlo SMC is a simulation technique to approximate a sequence of related probability distributions πn with π0 “easy” and πT target. Iterated IS as PMC: particles moved from time n to time n via kernel Kn and use of a sequence of extended targets πn˜ n πn (z0:n ) = πn (zn ) ˜ Lj (zj+1 , zj ) j=0 where the Lj ’s are backward Markov kernels [check that πn (zn ) is a marginal] [Del Moral, Doucet & Jasra, Series B, 2006]

ABC Methods for Bayesian Model Choice Approximate Bayesian computation Alphabet soup ABC-SMC True derivation of an SMC-ABC algorithm Use of a kernel Kn associated with target π n and derivation of the backward kernel π n (z )Kn (z , z) Ln−1 (z, z ) = πn (z) Update of the weights M m=1 IA n (xm ) in win ∝ wi(n−1) M m=1 IA n−1 (xm i(n−1) ) when xm ∼ K(xi(n−1) , ·) in

ABC Methods for Bayesian Model Choice Approximate Bayesian computation Alphabet soup Properties of ABC-SMC The ABC-SMC method properly uses a backward kernel L(z, z ) to simplify the importance weight and to remove the dependence on the unknown likelihood from this weight. Update of importance weights is reduced to the ratio of the proportions of surviving particles Major assumption: the forward kernel K is supposed to be invariant against the true target [tempered version of the true posterior]

ABC Methods for Bayesian Model Choice Approximate Bayesian computation Alphabet soup Properties of ABC-SMC The ABC-SMC method properly uses a backward kernel L(z, z ) to simplify the importance weight and to remove the dependence on the unknown likelihood from this weight. Update of importance weights is reduced to the ratio of the proportions of surviving particles Major assumption: the forward kernel K is supposed to be invariant against the true target [tempered version of the true posterior] Adaptivity in ABC-SMC algorithm only found in on-line construction of the thresholds t , slowly enough to keep a large number of accepted transitions [Del Moral, Doucet & Jasra, 2009]

ABC Methods for Bayesian Model Choice Approximate Bayesian computation Calibration of ABC Which summary statistics? Fundamental difficulty of the choice of the summary statistic when there is no non-trivial sufficient statistic [except when done by the experimenters in the field]

ABC Methods for Bayesian Model Choice Approximate Bayesian computation Calibration of ABC Which summary statistics? Fundamental difficulty of the choice of the summary statistic when there is no non-trivial sufficient statistic [except when done by the experimenters in the field] Starting from a large collection of summary statistics is available, Joyce and Marjoram (2008) consider the sequential inclusion into the ABC target, with a stopping rule based on a likelihood ratio test.

ABC Methods for Bayesian Model Choice Approximate Bayesian computation Calibration of ABC Which summary statistics? Fundamental difficulty of the choice of the summary statistic when there is no non-trivial sufficient statistic [except when done by the experimenters in the field] Starting from a large collection of summary statistics is available, Joyce and Marjoram (2008) consider the sequential inclusion into the ABC target, with a stopping rule based on a likelihood ratio test. Does not taking into account the sequential nature of the tests Depends on parameterisation Order of inclusion matters.

ABC Methods for Bayesian Model Choice ABC for model choice ABC for model choice Approximate Bayesian computation ABC for model choice Model choice Gibbs random ﬁelds Generic ABC model choice

ABC Methods for Bayesian Model Choice ABC for model choice Model choice Bayesian model choice Several models M1 , M2 , . . . are considered simultaneously for a dataset y and the model index M is part of the inference. Use of a prior distribution. π(M = m), plus a prior distribution on the parameter conditional on the value m of the model index, πm (θ m ) Goal is to derive the posterior distribution of M , challenging computational target when models are complex.

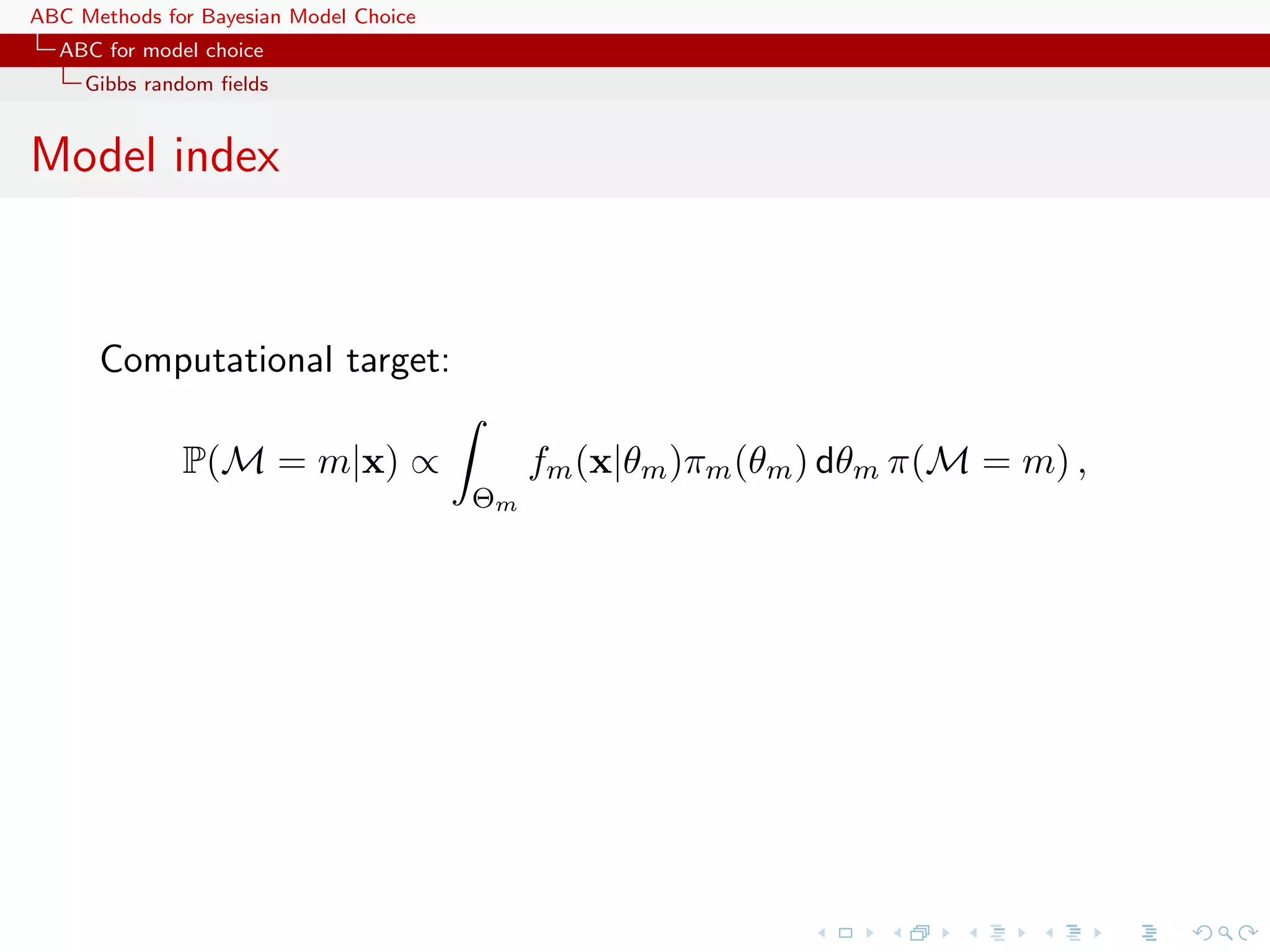
ABC Methods for Bayesian Model Choice ABC for model choice Model choice Generic ABC for model choice Algorithm 3 Likelihood-free model choice sampler (ABC-MC) for t = 1 to T do repeat Generate m from the prior π(M = m) Generate θ m from the prior πm (θ m ) Generate z from the model fm (z|θ m ) until ρ{η(z), η(y)} < Set m(t) = m and θ (t) = θ m end for [Toni, Welch, Strelkowa, Ipsen & Stumpf, 2009]

ABC Methods for Bayesian Model Choice ABC for model choice Model choice ABC estimates Posterior probability π(M = m|y) approximated by the frequency of acceptances from model m T 1 Im(t) =m . T t=1 Early issues with implementation: should tolerances be the same for all models? should summary statistics vary across models? should the distance measure ρ vary as well?

ABC Methods for Bayesian Model Choice ABC for model choice Model choice ABC estimates Posterior probability π(M = m|y) approximated by the frequency of acceptances from model m T 1 Im(t) =m . T t=1 Early issues with implementation: should tolerances be the same for all models? should summary statistics vary across models? should the distance measure ρ vary as well? Extension to a weighted polychotomous logistic regression estimate of π(M = m|y), with non-parametric kernel weights [Cornuet et al., DIYABC, 2009]

ABC Methods for Bayesian Model Choice ABC for model choice Model choice The Great ABC controversy [# 1?] On-going controvery in phylogeographic genetics about the validity of using ABC for testing Against: Templeton, 2008, 2009, 2010a, 2010b, 2010c argues that nested hypotheses cannot have higher probabilities than nesting hypotheses (!)

ABC Methods for Bayesian Model Choice ABC for model choice Model choice The Great ABC controversy [# 1?] On-going controvery in phylogeographic genetics about the validity of using ABC for testing Replies: Fagundes et al., 2008, Against: Templeton, 2008, Beaumont et al., 2010, Berger et 2009, 2010a, 2010b, 2010c al., 2010, Csill`ry et al., 2010 e argues that nested hypotheses point out that the criticisms are cannot have higher probabilities addressed at [Bayesian] than nesting hypotheses (!) model-based inference and have nothing to do with ABC...

ABC Methods for Bayesian Model Choice ABC for model choice Gibbs random fields Gibbs random fields Gibbs distribution The rv y = (y1 , . . . , yn ) is a Gibbs random field associated with the graph G if 1 f (y) = exp − Vc (yc ) , Z c∈C where Z is the normalising constant, C is the set of cliques of G and Vc is any function also called potential U (y) = c∈C Vc (yc ) is the energy function

ABC Methods for Bayesian Model Choice ABC for model choice Gibbs random fields Gibbs random fields Gibbs distribution The rv y = (y1 , . . . , yn ) is a Gibbs random field associated with the graph G if 1 f (y) = exp − Vc (yc ) , Z c∈C where Z is the normalising constant, C is the set of cliques of G and Vc is any function also called potential U (y) = c∈C Vc (yc ) is the energy function c Z is usually unavailable in closed form

ABC Methods for Bayesian Model Choice ABC for model choice Gibbs random ﬁelds Potts model Potts model Vc (y) is of the form Vc (y) = θS(y) = θ δyl =yi l∼i where l∼i denotes a neighbourhood structure

ABC Methods for Bayesian Model Choice ABC for model choice Gibbs random ﬁelds Potts model Potts model Vc (y) is of the form Vc (y) = θS(y) = θ δyl =yi l∼i where l∼i denotes a neighbourhood structure In most realistic settings, summation Zθ = exp{θ T S(x)} x∈X involves too many terms to be manageable and numerical approximations cannot always be trusted

ABC Methods for Bayesian Model Choice ABC for model choice Gibbs random ﬁelds Bayesian Model Choice Comparing a model with energy S0 taking values in Rp0 versus a model with energy S1 taking values in Rp1 can be done through the Bayes factor corresponding to the priors π0 and π1 on each parameter space exp{θ T S0 (x)}/Zθ 0 ,0 π0 (dθ 0 ) 0 Bm0 /m1 (x) = exp{θ T S1 (x)}/Zθ 1 ,1 π1 (dθ 1 ) 1

ABC Methods for Bayesian Model Choice ABC for model choice Gibbs random ﬁelds Neighbourhood relations Choice to be made between M neighbourhood relations m i∼i (0 ≤ m ≤ M − 1) with Sm (x) = I{xi =xi } m i∼i driven by the posterior probabilities of the models.

ABC Methods for Bayesian Model Choice ABC for model choice Gibbs random ﬁelds Model index Computational target: P(M = m|x) ∝ fm (x|θm )πm (θm ) dθm π(M = m) , Θm

ABC Methods for Bayesian Model Choice ABC for model choice Gibbs random ﬁelds Model index Computational target: P(M = m|x) ∝ fm (x|θm )πm (θm ) dθm π(M = m) , Θm If S(x) suﬃcient statistic for the joint parameters (M, θ0 , . . . , θM −1 ), P(M = m|x) = P(M = m|S(x)) .

ABC Methods for Bayesian Model Choice ABC for model choice Gibbs random fields Sufficient statistics in Gibbs random fields

ABC Methods for Bayesian Model Choice ABC for model choice Gibbs random fields Sufficient statistics in Gibbs random fields Each model m has its own sufficient statistic Sm (·) and S(·) = (S0 (·), . . . , SM −1 (·)) is also (model-)sufficient.

ABC Methods for Bayesian Model Choice ABC for model choice Gibbs random fields Sufficient statistics in Gibbs random fields Each model m has its own sufficient statistic Sm (·) and S(·) = (S0 (·), . . . , SM −1 (·)) is also (model-)sufficient. For Gibbs random fields, 1 2 x|M = m ∼ fm (x|θm ) = fm (x|S(x))fm (S(x)|θm ) 1 = f 2 (S(x)|θm ) n(S(x)) m where n(S(x)) = {˜ ∈ X : S(˜ ) = S(x)} x x c S(x) is therefore also sufficient for the joint parameters

ABC Methods for Bayesian Model Choice ABC for model choice Gibbs random ﬁelds ABC model choice Algorithm ABC-MC Generate m∗ from the prior π(M = m). ∗ Generate θm∗ from the prior πm∗ (·). Generate x∗ from the model fm∗ (·|θm∗ ). ∗ Compute the distance ρ(S(x0 ), S(x∗ )). Accept (θm∗ , m∗ ) if ρ(S(x0 ), S(x∗ )) < . ∗ Note When = 0 the algorithm is exact

ABC Methods for Bayesian Model Choice ABC for model choice Gibbs random ﬁelds Toy example iid Bernoulli model versus two-state ﬁrst-order Markov chain, i.e. n f0 (x|θ0 ) = exp θ0 I{xi =1} {1 + exp(θ0 )}n , i=1 versus n 1 f1 (x|θ1 ) = exp θ1 I{xi =xi−1 } {1 + exp(θ1 )}n−1 , 2 i=2 with priors θ0 ∼ U(−5, 5) and θ1 ∼ U(0, 6) (inspired by “phase transition” boundaries).

ABC Methods for Bayesian Model Choice ABC for model choice Gibbs random ﬁelds Toy example (2) 10 5 5 BF01 BF01 0 ^ ^ 0 −5 −5 −40 −20 0 10 −10 −40 −20 0 10 BF01 BF01 (left) Comparison of the true BF m0 /m1 (x0 ) with BF m0 /m1 (x0 ) (in logs) over 2, 000 simulations and 4.106 proposals from the prior. (right) Same when using tolerance corresponding to the 1% quantile on the distances.

ABC Methods for Bayesian Model Choice ABC for model choice Generic ABC model choice Back to suﬃciency ‘Suﬃcient statistics for individual models are unlikely to be very informative for the model probability. This is already well known and understood by the ABC-user community.’ [Scott Sisson, Jan. 31, 2011, ’Og]

ABC Methods for Bayesian Model Choice ABC for model choice Generic ABC model choice Back to sufficiency ‘Sufficient statistics for individual models are unlikely to be very informative for the model probability. This is already well known and understood by the ABC-user community.’ [Scott Sisson, Jan. 31, 2011, ’Og] If η1 (x) sufficient statistic for model m = 1 and parameter θ1 and η2 (x) sufficient statistic for model m = 2 and parameter θ2 , (η1 (x), η2 (x)) is not always sufficient for (m, θm )

ABC Methods for Bayesian Model Choice ABC for model choice Generic ABC model choice Back to sufficiency ‘Sufficient statistics for individual models are unlikely to be very informative for the model probability. This is already well known and understood by the ABC-user community.’ [Scott Sisson, Jan. 31, 2011, ’Og] If η1 (x) sufficient statistic for model m = 1 and parameter θ1 and η2 (x) sufficient statistic for model m = 2 and parameter θ2 , (η1 (x), η2 (x)) is not always sufficient for (m, θm ) c Potential loss of information at the testing level

ABC Methods for Bayesian Model Choice ABC for model choice Generic ABC model choice Limiting behaviour of B12 (T → ∞) ABC approximation T t=1 Imt =1 Iρ{η(zt ),η(y)}≤ B12 (y) = T , t=1 Imt =2 Iρ{η(zt ),η(y)}≤ where the (mt , z t )’s are simulated from the (joint) prior

ABC Methods for Bayesian Model Choice ABC for model choice Generic ABC model choice Limiting behaviour of B12 (T → ∞) ABC approximation T t=1 Imt =1 Iρ{η(zt ),η(y)}≤ B12 (y) = T , t=1 Imt =2 Iρ{η(zt ),η(y)}≤ where the (mt , z t )’s are simulated from the (joint) prior As T go to inﬁnity, limit Iρ{η(z),η(y)}≤ π1 (θ 1 )f1 (z|θ 1 ) dz dθ 1 B12 (y) = Iρ{η(z),η(y)}≤ π2 (θ 2 )f2 (z|θ 2 ) dz dθ 2 η Iρ{η,η(y)}≤ π1 (θ 1 )f1 (η|θ 1 ) dη dθ 1 = η , Iρ{η,η(y)}≤ π2 (θ 2 )f2 (η|θ 2 ) dη dθ 2 η η where f1 (η|θ 1 ) and f2 (η|θ 2 ) distributions of η(z)

ABC Methods for Bayesian Model Choice ABC for model choice Generic ABC model choice Limiting behaviour of B12 ( → 0) When goes to zero, η η π1 (θ 1 )f1 (η(y)|θ 1 ) dθ 1 B12 (y) = η , π2 (θ 2 )f2 (η(y)|θ 2 ) dθ 2

ABC Methods for Bayesian Model Choice ABC for model choice Generic ABC model choice Limiting behaviour of B12 ( → 0) When goes to zero, η η π1 (θ 1 )f1 (η(y)|θ 1 ) dθ 1 B12 (y) = η , π2 (θ 2 )f2 (η(y)|θ 2 ) dθ 2 Bayes factor based on the sole observation of η(y)

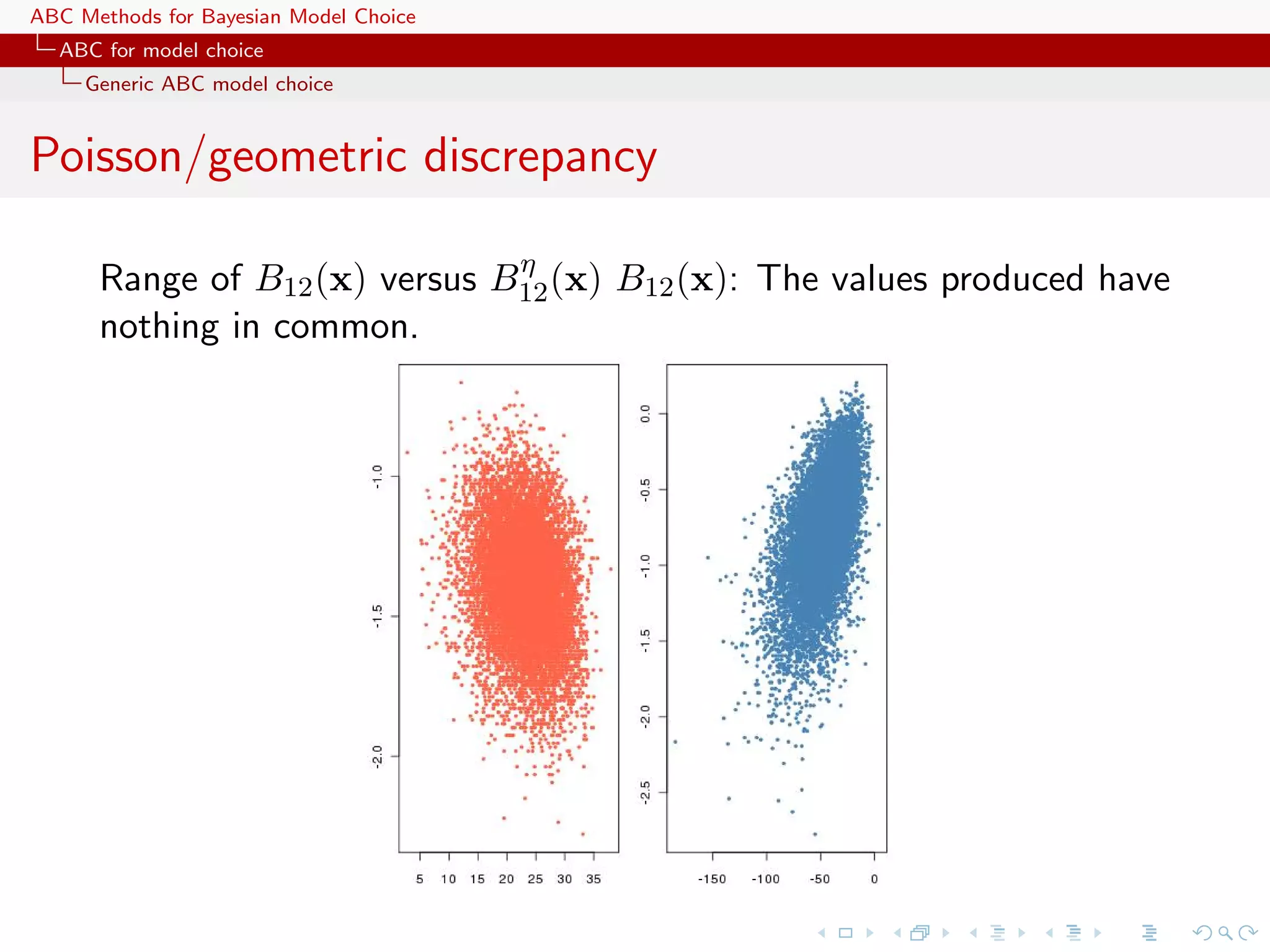
ABC Methods for Bayesian Model Choice ABC for model choice Generic ABC model choice Limiting behaviour of B12 (under suﬃciency) If η(y) suﬃcient statistic for both models, fi (y|θ i ) = gi (y)fiη (η(y)|θ i ) Thus η Θ1 π(θ 1 )g1 (y)f1 (η(y)|θ 1 ) dθ 1 B12 (y) = η Θ2 π(θ 2 )g2 (y)f2 (η(y)|θ 2 ) dθ 2 η g1 (y) π1 (θ 1 )f1 (η(y)|θ 1 ) dθ 1 = η g2 (y) π2 (θ 2 )f2 (η(y)|θ 2 ) dθ 2 g1 (y) η = B (y) . g2 (y) 12 [Didelot, Everitt, Johansen & Lawson, 2011]

ABC Methods for Bayesian Model Choice ABC for model choice Generic ABC model choice Limiting behaviour of B12 (under sufficiency) If η(y) sufficient statistic for both models, fi (y|θ i ) = gi (y)fiη (η(y)|θ i ) Thus η Θ1 π(θ 1 )g1 (y)f1 (η(y)|θ 1 ) dθ 1 B12 (y) = η Θ2 π(θ 2 )g2 (y)f2 (η(y)|θ 2 ) dθ 2 η g1 (y) π1 (θ 1 )f1 (η(y)|θ 1 ) dθ 1 = η g2 (y) π2 (θ 2 )f2 (η(y)|θ 2 ) dθ 2 g1 (y) η = B (y) . g2 (y) 12 [Didelot, Everitt, Johansen & Lawson, 2011] No discrepancy only when cross-model sufficiency

ABC Methods for Bayesian Model Choice ABC for model choice Generic ABC model choice Poisson/geometric example Sample x = (x1 , . . . , xn ) from either a Poisson P(λ) or from a geometric G(p) Sum n S= yi = η(x) i=1 suﬃcient statistic for either model but not simultaneously Discrepancy ratio g1 (x) S!n−S / i yi ! = g2 (x) 1 n+S−1 S

ABC Methods for Bayesian Model Choice ABC for model choice Generic ABC model choice Poisson/geometric discrepancy η Range of B12 (x) versus B12 (x) B12 (x): The values produced have nothing in common.

ABC Methods for Bayesian Model Choice ABC for model choice Generic ABC model choice Formal recovery Creating an encompassing exponential family T T f (x|θ1 , θ2 , α1 , α2 ) ∝ exp{θ1 η1 (x) + θ1 η1 (x) + α1 t1 (x) + α2 t2 (x)} leads to a suﬃcient statistic (η1 (x), η2 (x), t1 (x), t2 (x)) [Didelot, Everitt, Johansen & Lawson, 2011]

ABC Methods for Bayesian Model Choice ABC for model choice Generic ABC model choice Formal recovery Creating an encompassing exponential family T T f (x|θ1 , θ2 , α1 , α2 ) ∝ exp{θ1 η1 (x) + θ1 η1 (x) + α1 t1 (x) + α2 t2 (x)} leads to a suﬃcient statistic (η1 (x), η2 (x), t1 (x), t2 (x)) [Didelot, Everitt, Johansen & Lawson, 2011] In the Poisson/geometric case, if i xi ! is added to S, no discrepancy

ABC Methods for Bayesian Model Choice ABC for model choice Generic ABC model choice Formal recovery Creating an encompassing exponential family T T f (x|θ1 , θ2 , α1 , α2 ) ∝ exp{θ1 η1 (x) + θ1 η1 (x) + α1 t1 (x) + α2 t2 (x)} leads to a suﬃcient statistic (η1 (x), η2 (x), t1 (x), t2 (x)) [Didelot, Everitt, Johansen & Lawson, 2011] Only applies in genuine suﬃciency settings... c Inability to evaluate loss brought by summary statistics

ABC Methods for Bayesian Model Choice ABC for model choice Generic ABC model choice Meaning of the ABC-Bayes factor ‘This is also why focus on model discrimination typically (...) proceeds by (...) accepting that the Bayes Factor that one obtains is only derived from the summary statistics and may in no way correspond to that of the full model.’ [Scott Sisson, Jan. 31, 2011, ’Og]

ABC Methods for Bayesian Model Choice ABC for model choice Generic ABC model choice Meaning of the ABC-Bayes factor ‘This is also why focus on model discrimination typically (...) proceeds by (...) accepting that the Bayes Factor that one obtains is only derived from the summary statistics and may in no way correspond to that of the full model.’ [Scott Sisson, Jan. 31, 2011, ’Og] In the Poisson/geometric case, if E[yi ] = θ0 > 0, η (θ0 + 1)2 −θ0 lim B12 (y) = e n→∞ θ0

ABC Methods for Bayesian Model Choice ABC for model choice Generic ABC model choice MA(q) divergence 1.0 1.0 1.0 1.0 0.8 0.8 0.8 0.8 0.6 0.6 0.6 0.6 0.4 0.4 0.4 0.4 0.2 0.2 0.2 0.2 0.0 0.0 0.0 0.0 1 2 1 2 1 2 1 2 Evolution [against ] of ABC Bayes factor, in terms of frequencies of visits to models MA(1) (left) and MA(2) (right) when equal to 10, 1, .1, .01% quantiles on insuﬃcient autocovariance distances. Sample of 50 points from a MA(2) with θ1 = 0.6, θ2 = 0.2. True Bayes factor equal to 17.71.

ABC Methods for Bayesian Model Choice ABC for model choice Generic ABC model choice MA(q) divergence 1.0 1.0 1.0 1.0 0.8 0.8 0.8 0.8 0.6 0.6 0.6 0.6 0.4 0.4 0.4 0.4 0.2 0.2 0.2 0.2 0.0 0.0 0.0 0.0 1 2 1 2 1 2 1 2 Evolution [against ] of ABC Bayes factor, in terms of frequencies of visits to models MA(1) (left) and MA(2) (right) when equal to 10, 1, .1, .01% quantiles on insuﬃcient autocovariance distances. Sample of 50 points from a MA(1) model with θ1 = 0.6. True Bayes factor B21 equal to .004.

ABC Methods for Bayesian Model Choice ABC for model choice Generic ABC model choice Further comments ‘There should be the possibility that for the same model, but different (non-minimal) [summary] statistics (so ∗ different η’s: η1 and η1 ) the ratio of evidences may no longer be equal to one.’ [Michael Stumpf, Jan. 28, 2011, ’Og] Using different summary statistics [on different models] may indicate the loss of information brought by each set but agreement does not lead to trustworthy approximations.

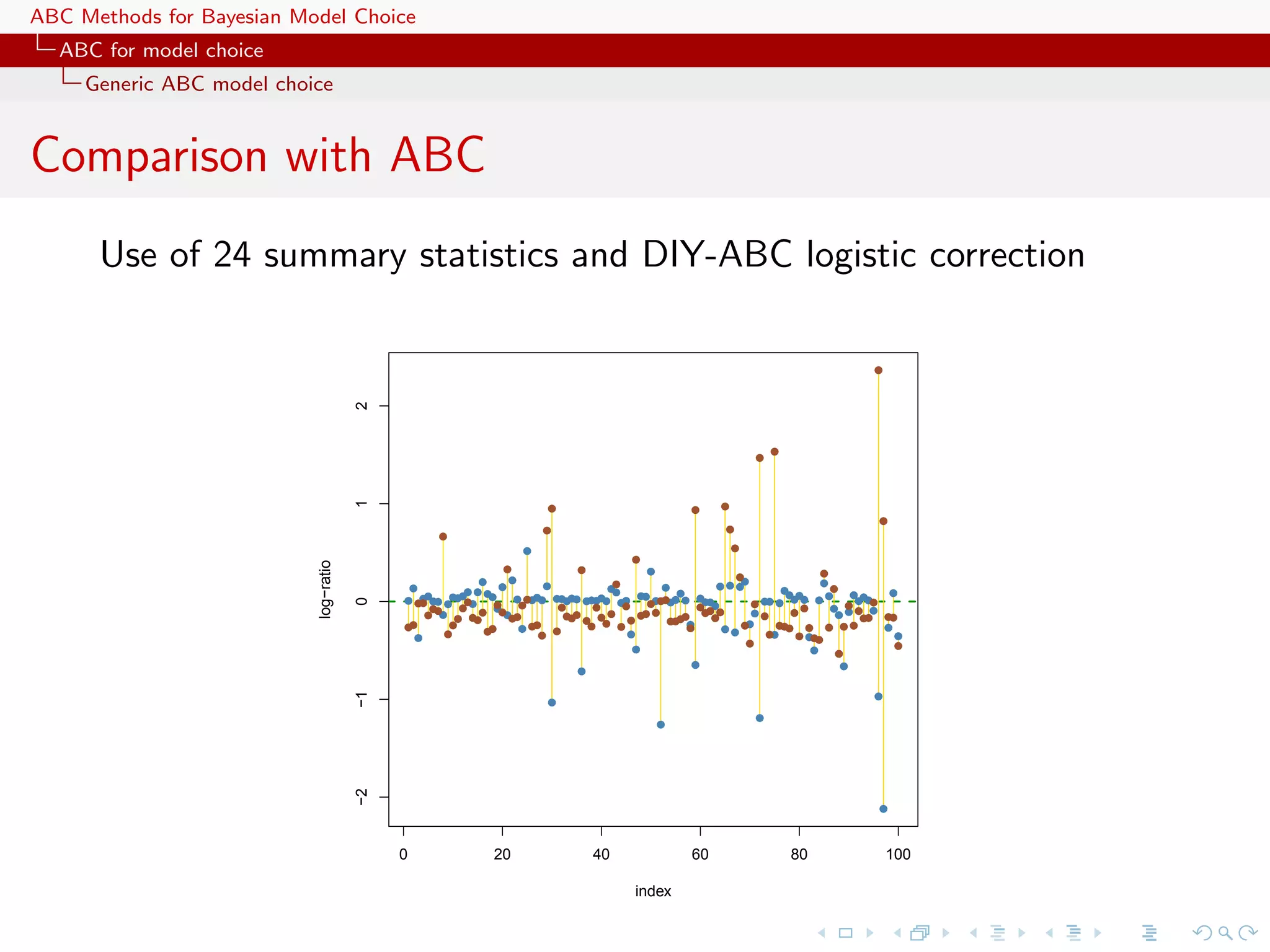
ABC Methods for Bayesian Model Choice ABC for model choice Generic ABC model choice A population genetics evaluation Population genetics example with 3 populations 2 scenari 15 individuals 5 loci single mutation parameter

ABC Methods for Bayesian Model Choice ABC for model choice Generic ABC model choice A population genetics evaluation Population genetics example with 3 populations 2 scenari 15 individuals 5 loci single mutation parameter 24 summary statistics 2 million ABC proposal importance [tree] sampling alternative

ABC Methods for Bayesian Model Choice ABC for model choice Generic ABC model choice Stability of importance sampling 1.0 1.0 1.0 1.0 1.0 q q 0.8 0.8 0.8 0.8 0.8 0.6 0.6 0.6 0.6 0.6 q 0.4 0.4 0.4 0.4 0.4 0.2 0.2 0.2 0.2 0.2 0.0 0.0 0.0 0.0 0.0

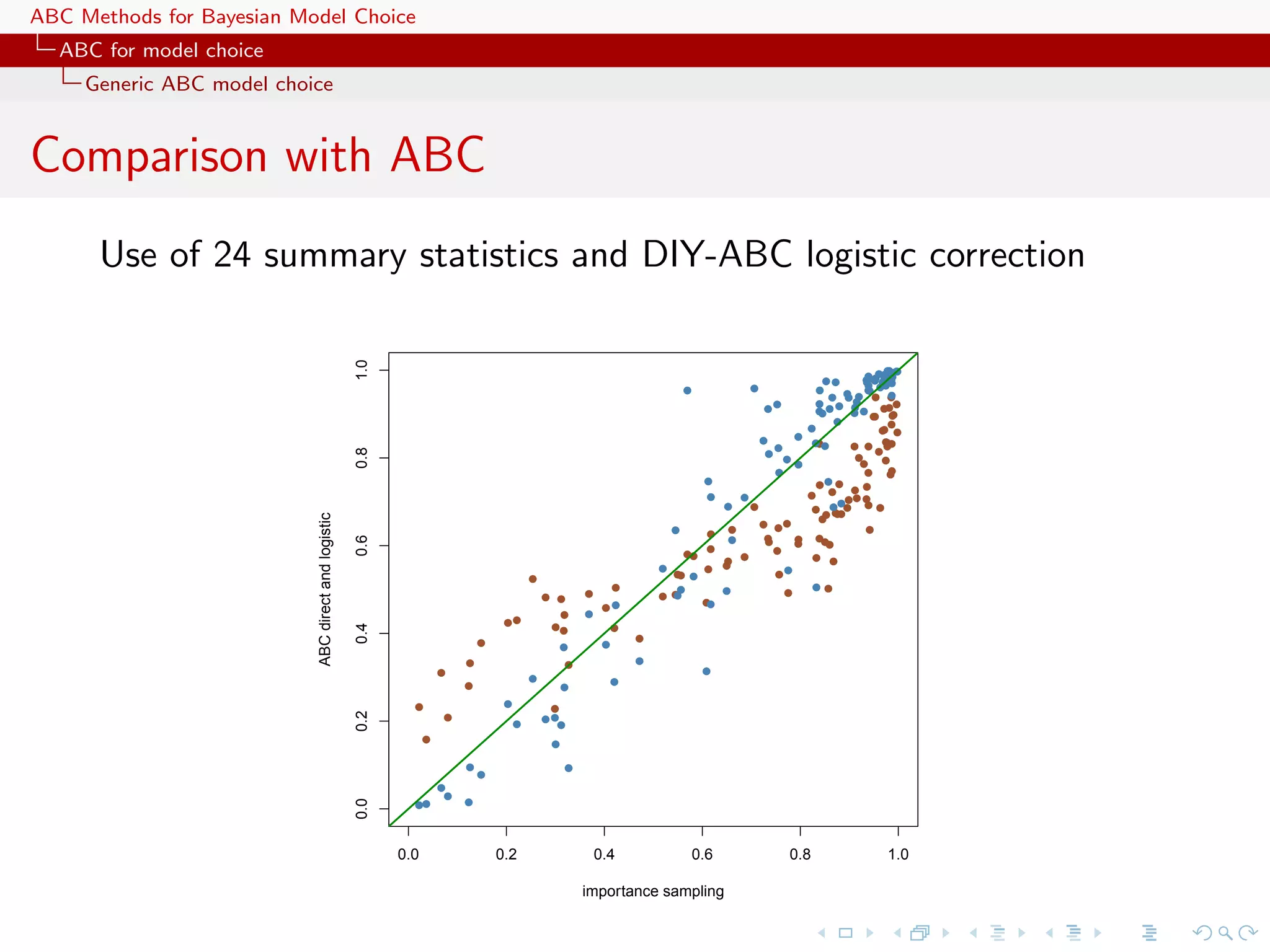
ABC Methods for Bayesian Model Choice ABC for model choice Generic ABC model choice Comparison with ABC Use of 24 summary statistics and DIY-ABC logistic correction 1.0 qq qq qq qq qqq qq q q qq q q qq q q q q q q q q q q qq q q qq q q q qq qq qq q q q q qq q q q q q q q q q q q qq q q q qq q q 0.8 q q q q q q q q q q q q qq q q q q q q q qq q q q q q qqq q q qq q ABC direct and logistic q q qq q q q q q q q 0.6 q q q qq q q qq q q q q q q q q q q q q q q q q q q q q q q q q q qq qq q q qq 0.4 qq q q q q q q q q q q q q q q q q q 0.2 q qq q q q q q q q q q q 0.0 qq 0.0 0.2 0.4 0.6 0.8 1.0 importance sampling

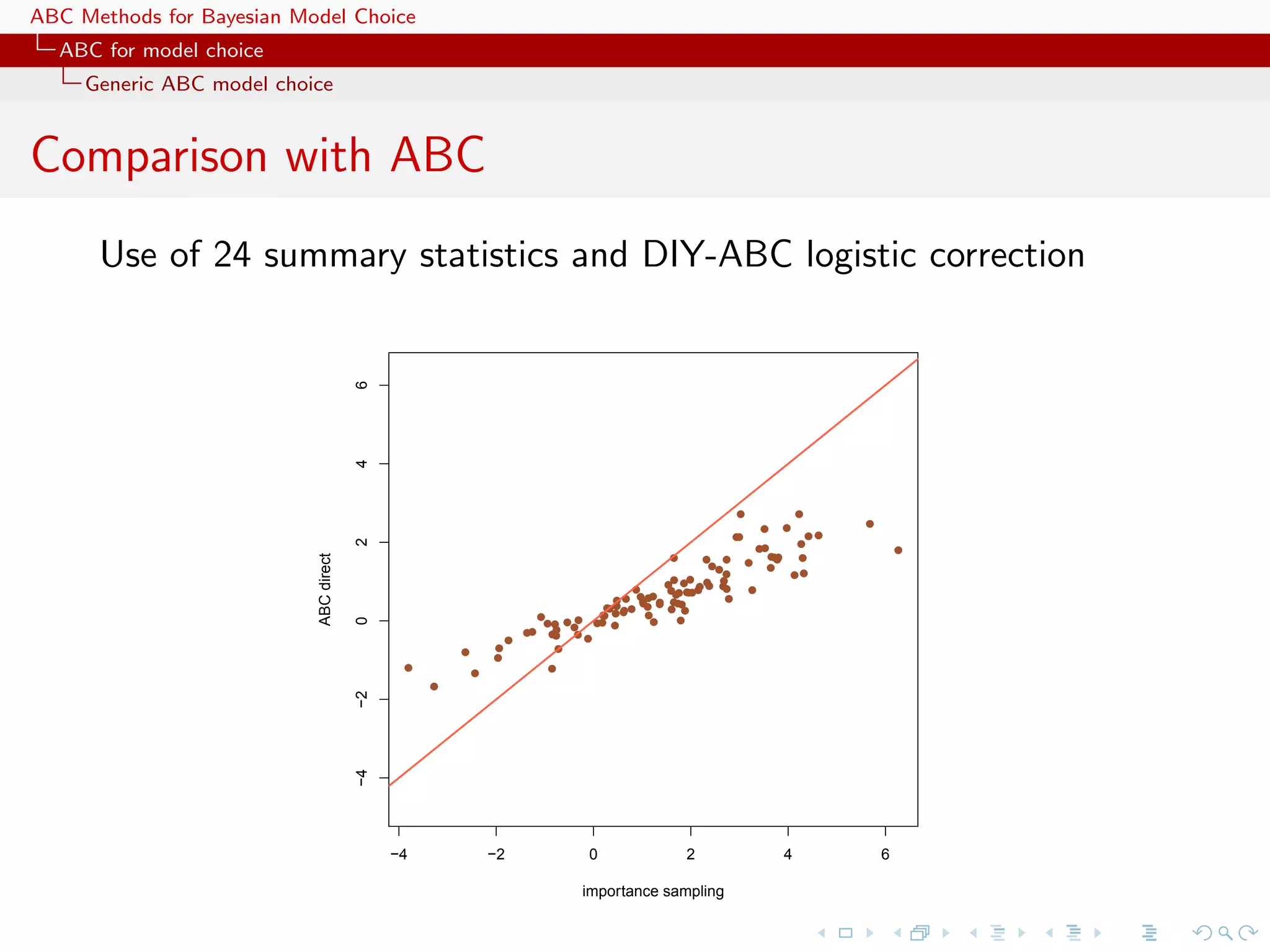
ABC Methods for Bayesian Model Choice ABC for model choice Generic ABC model choice Comparison with ABC Use of 24 summary statistics and DIY-ABC logistic correction 6 4 q q q q q q q qq 2 q q q q qq ABC direct q q q qq q qq q q q q qq qq q qq q q q q q qq q q q q q qq q q qq q qq q q qq q q q qqq q q q q q q q q 0 qq qq q q q q qq qq q q qq q q q q q q q q −2 −4 −4 −2 0 2 4 6 importance sampling

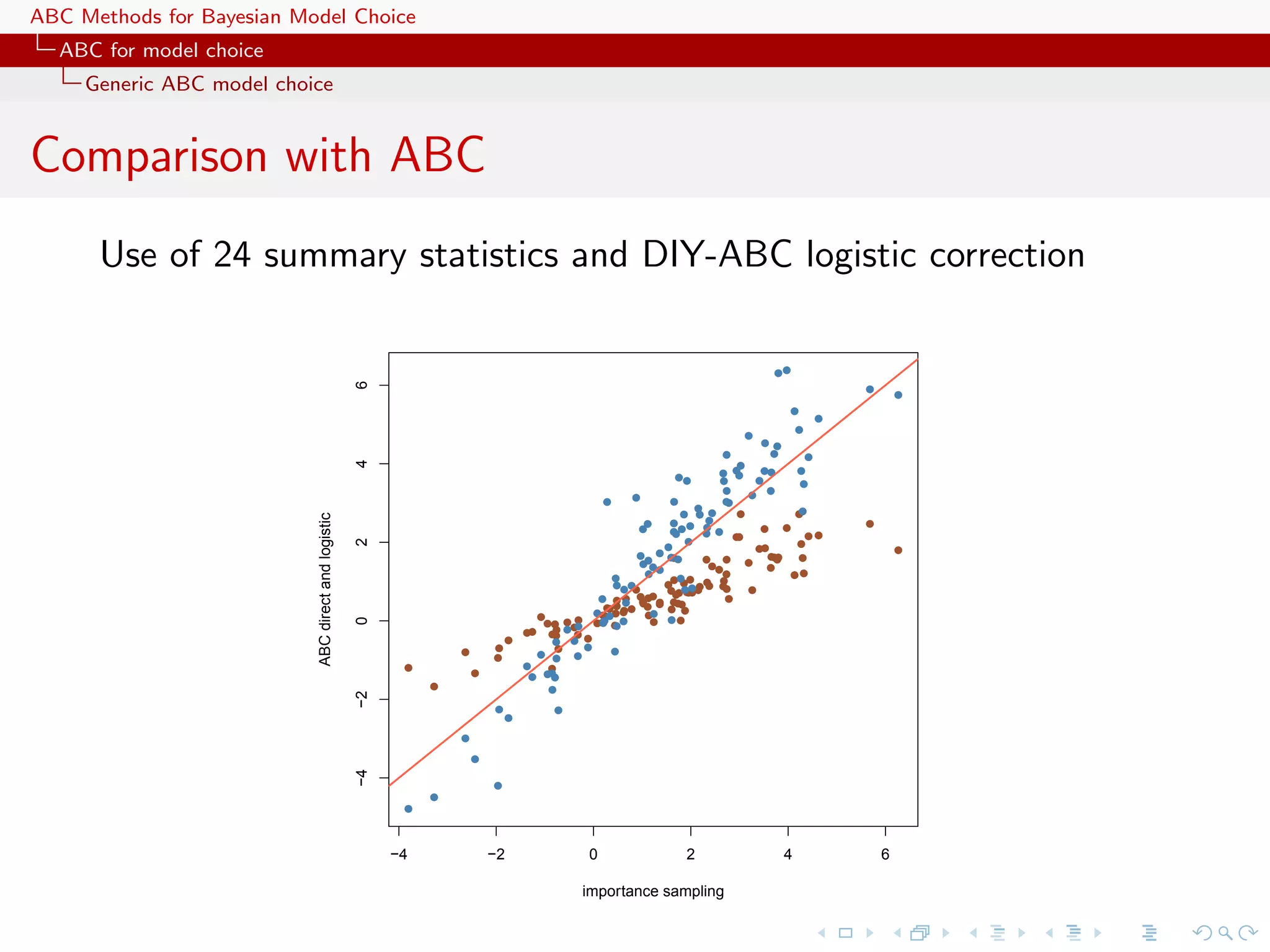
ABC Methods for Bayesian Model Choice ABC for model choice Generic ABC model choice Comparison with ABC Use of 24 summary statistics and DIY-ABC logistic correction qq 6 q q q q q q q q q q q 4 q qq q qq qq q q q q q q q q q q qq q q q q q q q ABC direct and logistic q q q q q q q qq q q q q q q q qq q 2 q q q q q qq q qq q q q qq qq q qq qq q q q qq q q qq qq qq q q qqqq qq q q q qqqqq qq q q q qq q q q q qq q qq q q qqq q q qqqqq q q qq q q qq q q q qq 0 qq qqq q q qq q qqq q q q q q q q q q q q q q q q q q q q q qq q q −2 q q q q q −4 q q q −4 −2 0 2 4 6 importance sampling

ABC Methods for Bayesian Model Choice ABC for model choice Generic ABC model choice Comparison with ABC Use of 24 summary statistics and DIY-ABC logistic correction q 2 q q 1 q q q q q q q q q q log−ratio q q q q q qq q q q qqq q q q q q q q qq q q q q q qq qq q qq q q qqqqqq q q qqqq qq qq q qq qq q qq q qq qq q q q qq q qq q q qqq q 0 q q q q qq q q q qq q q q q q q qq q qq q qq qq q qq qqq qq qq q q q q qq q qqqq q q q q q q q q qq qqq q qq qq q q qq q q q q qq q q qq q q q q q q q q qq qqqq q q q q q q q q q −1 q q q q −2 q 0 20 40 60 80 100 index

ABC Methods for Bayesian Model Choice ABC for model choice Generic ABC model choice The only safe cases Besides speciﬁc models like Gibbs random ﬁelds, using distances over the data itself escapes the discrepancy... [Toni & Stumpf, 2010;Sousa et al., 2009]

ABC Methods for Bayesian Model Choice ABC for model choice Generic ABC model choice The only safe cases Besides specific models like Gibbs random fields, using distances over the data itself escapes the discrepancy... [Toni & Stumpf, 2010;Sousa et al., 2009] ...and so does the use of more informal model fitting measures [Ratmann, Andrieu, Richardson and Wiujf, 2009]

Workshop on Bayesian Inference for Latent Gaussian Models with Applications

More Related Content

What's hot

Similar to Workshop on Bayesian Inference for Latent Gaussian Models with Applications

More from Christian Robert

Recently uploaded

Workshop on Bayesian Inference for Latent Gaussian Models with Applications