Functional Programming in Scala: Notes

Scala and Functional Programming Roberto Casadei October 2, 2015 R. Casadei Scala and FP October 2, 2015 1 / 56

About these notes I am a learner, not an expert These notes are essentially a work of synthesis and integration from many sources, such as “Functional Programming in Scala” [Chiusano and Bjarnason, 2014] University notes Web sources: Wikipedia, Blogs, etc. (references in slides) R. Casadei Scala and FP October 2, 2015 2 / 56

Outline 1 FP in Scala Basics Functional data structures Handling errors without exceptions Strict/non-strict functions, laziness Purely functional state Functional library design Common structures in FP Monoids Monads R. Casadei Scala and FP October 2, 2015 3 / 56

FP in Scala Basics Outline 1 FP in Scala Basics Functional data structures Handling errors without exceptions Strict/non-strict functions, laziness Purely functional state Functional library design Common structures in FP Monoids Monads R. Casadei Scala and FP October 2, 2015 4 / 56

FP in Scala Basics Functional programming FP is a paradigm where programs are built using only pure functions (i.e., functions without side-effect). A function has a side effect if it does something other than simply return a result Performing any of the following actions directly would involve a side-effect Reassigning a variable, modifying a data structure in place, or setting a field on an object, ... Throwing an exception or halting with an error, ... Printing to the console or reading user input, writing or reading to a file, ... Drawing on the screen, ... One may ask: how is it even possible to write useful programs without side effects? FP is a restriction on how we write programs, but not on what programs can be written In many cases, programs that seem to necessitate side effects have some purely functional analogues In other cases, we can structure code so that effects occur but are not observable FP approach: we will restrict ourself to constructing programs using only pure functions By accepting this restriction, we foster modularity. Because of their modularity, pure functions are easier to test, to reuse, to parallelize, to generalize, and to reason about One general idea is to represent effects as values and then define functions to work with these values R. Casadei Scala and FP October 2, 2015 5 / 56

FP in Scala Basics Purity and referential transparency An expression e is referentially transparent if for all programs p, all occurrences of e in p can be replaced by the result of evaluating e, without affecting the observable behavior of p. A function f is pure if the expression f(x) is referentially transparent for all referentially transparent x RT enables a mode of reasoning about program evaluation called the substitution model We fully expand every part of an expression, replacing all variables with their referents, and then reduce it to its simplest form. At each step we replace a term with an equivalent one; we say that computation proceeds by substituting equals by equals. In other words, RT enables equational reasoning for programs. Side effects make reasoning about program behavior more difﬁcult: you need to keep track of all the state changes that may occur in order to understand impure functions. By contrast, the substitution model is simple to reason about since effects of evaluation are purely local and we need not mentally simulate sequences of state updates to understand a block of code: understanding requires only local reasoning. Modular programs consist of components that can be understood and reused independently of the whole, such that the meaning of the whole depends only on the meaning of the components and the rules governing their composition. A pure function is modular and composable because it separates the logic of the computation itself from “how to obtain the input” and “what to do with the result”. It is a black box. Input is obtained in exactly one way: via the args of the function. And the output is simply computed and returned. Keeping each of these concerns separate, the logic of computation is more reusable. A way of removing a side effect X is to return it as function result. When doing so, typically you end up separating the concern of creating it from the concern of interpretating/executing/applying it. This usually involves creating a new type or a ﬁrst-class value (object) for X. R. Casadei Scala and FP October 2, 2015 6 / 56

FP in Scala Basics Exercises from Chapter 2: Getting started with FP in Scala I Ex. 2.1: Write a recursive function to get the nth Fibonacci number . The ﬁrst two Fibonacci numbers are 0 and 1. The nth number is always the sum of the previous two—the sequence begins 0, 1, 1, 2, 3, 5. Your deﬁnition should use a local tail-recursive function. 1 def fibs(n: Int) = { 2 @annotation.tailrec def ifibs(a:Int, b:Int, n:Int): Int = { 3 if(n <= 0) b 4 else ifibs(b,a+b,n-1) 5 } 6 ifibs(0,1,n-1) 7 } 8 (1 to 15) map fibs // Vector(1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610) Ex 2.3:: Let’s consider currying, which converts a function f of two args into a function of one arg that partially applies f. Here again there’s only one impl that compiles. Write this impl. 1 def partial1[A,B,C](a: A, f: (A,B) => C): B => C = (b: B) => f(a, b) 2 3 def curry[A,B,C](f: (A, B) => C): A => (B => C) = { 4 // partial1(_,f) 5 a => b => f(a,b) 6 } 7 8 def sum(x:Int, y:Int) = x+y 9 val incByOne = partial1(1, sum) // incByOne: Int => Int = <function1> 10 incByOne(7) // res: Int = 8 11 val csum = curry(sum) // csum: Int => (Int => Int) = <function1> 12 csum(3)(7) // res: Int = 10 Ex 2.4:: Implement uncurry , which reverses the transformation of curry . Note that since => associates to the right, A => (B => C) can be written as A => B => C. R. Casadei Scala and FP October 2, 2015 7 / 56

FP in Scala Basics Exercises from Chapter 2: Getting started with FP in Scala II 1 def uncurry[A,B,C](f: A => B => C): (A, B) => C = { 2 // (a: A, b: B) => f(a)(b) // Verbose 3 // (a, b) => f(a)(b) // Use type inference 4 f(_)(_) // Use syntax sugar 5 } 6 7 val ucsum = uncurry(csum); sum(1,2) // 3 Ex 2.5:: Implement the higher-order function that composes two functions. 1 def compose[A,B,C](f: B => C, g: A => B): A => C = a => f(g(a)) 2 3 val incByTwo = compose(incByOne, incByOne) 4 incByTwo(2) // 4 Ex. 2.2: Impl isSorted, which checks if an Array[A] is sorted according to a given comparison function. 1 def isSortedNaive[A](as: Array[A], ordered: (A,A) => Boolean): Boolean = { 2 as sliding(2,1) map(e => ordered(e(0),e(1))) reduceLeft (_&&_) 3 } 4 // Note: building the pairs is not inefficient because ’sliding’ returns a (lazy) iterator 5 // And applying map to a lazy iterator also returns a lazy iterator 6 // But we could do better: we could stop at the first false! 7 8 def isSortedNaive2[A](as: Array[A], ordered: (A,A) => Boolean): Boolean = { 9 def sortAcc( acc: (Boolean, A), next: A): (Boolean,A) = (acc._1 && ordered(acc._2,next), next) 10 as.tail.foldLeft[(Boolean,A)]((true, as.head))(sortAcc)._1 11 } 12 // Note: leverage on short-circuit && (i.e., doesn’t check ’ordered’ after a first ’false’) 13 // But we could do better: we could stop at the first false! 14 15 def isSorted[A](as: Array[A], ordered: (A,A) => Boolean): Boolean = { 16 @annotation.tailrec def isSorted2[A](as: Array[A], ordered: (A,A) => Boolean, prev: Boolean, start: Int): Boolean = { 17 if(prev == false || (as.length-start)<2) prev 18 else isSorted2(as, ordered, ordered(as(start+0),as(start+1)), start+2) 19 } 20 isSorted2(as, ordered, true, 0) 21 } R. Casadei Scala and FP October 2, 2015 8 / 56

FP in Scala Basics Exercises from Chapter 2: Getting started with FP in Scala III 22 // Arrays have access to item (apply) in constant time, length is also immediate 23 // Thus we couldn’t use drop(2) or tail because tail takes O(logN) 24 25 def isSortedSolution[A](as: Array[A], gt: (A,A) => Boolean): Boolean = { 26 @annotation.tailrec def go(n: Int): Boolean = 27 if (n >= as.length-1) true else if (gt(as(n), as(n+1))) false else go(n+1) 28 } 29 go(0) 30 } 31 32 // BEST-CASE 33 val array = (2 +: (1 to 10000000).toArray) 34 time { isSortedNaive[Int](array, (_<_)) } // Elapsed time: 6348ms ; res = false 35 time { isSortedNaive2[Int](array, (_<_)) } // Elapsed time: 2279ms ; res = false 36 time { isSorted[Int](array, (_<_)) } // Elapsed time: 0.82ms ; res = false 37 // WORST-CASE 38 val array2 = (1 to 10000000).toArray 39 time { isSortedNaive[Int](array2, (_<_)) } // Elapsed time: 7436ms; res = true 40 time { isSortedNaive2[Int](array2, (_<_)) } // Elapsed time: 2073ms; res = true 41 time { isSorted[Int](array2, (_<_)) } // Elapsed time: 187ms ; res = true R. Casadei Scala and FP October 2, 2015 9 / 56

FP in Scala Basics Functional data structures A functional data structure is operated on using only pure functions. Therefore, it is immutable by deﬁnition Since they are immutable, there’s no need to copy them: they can be shared (data sharing) and new objects only need to reference them and their differences Moreover, data sharing of immutable data often lets us implement functions more efﬁciently; we can always return immutable data structures without having to worry about subsequent code modifying our data R. Casadei Scala and FP October 2, 2015 10 / 56

FP in Scala Basics Exercises from Chapter 3: Functional data structures I Ex 3.2: Implement the function tail for removing the first element of a List. Note that the function takes constant time. What are different choices you could make in your implementation if the List is Nil? 1 def tail[A](lst: List[A]): List[A] = lst match { 2 case Nil => sys.error("tail on empty list") 3 case hd :: tail => tail 4 } 5 tail(List(1,2,3)) // List(2,3) Ex 3.3: Using the same idea, impl replaceHead for replacing the 1st elem of a List with a different value. 1 def replaceHead[A](lst: List[A], newHead: A): List[A] = lst match { 2 case Nil => sys.error("replaceHead on empty list") 3 case hd :: tail => newHead :: tail 4 } 5 replaceHead(List(1,2,3), 7) // List(7,2,3) Ex 3.4: Generalize tail to drop, which removes the first n elems from a list. Note that this function takes time proportional only to the number of elements being dropped—we don’t need to make a copy of the entire List. 1 def drop[A](lst: List[A], n: Int): List[A] = lst match { 2 case hd :: tail if n>0 => drop(tail, n-1) 3 case _ => lst 4 } 5 drop(List(1,2,3,4,5), 3) // List(4, 5) Ex 3.5: Impl dropWhile, which removes elems from the List prefix as long as they match a predicate. 1 def dropWhile[A](l: List[A], f: A => Boolean): List[A] = l match { 2 case hd :: tl if f(hd) => dropWhile(tl, f) 3 case _ => l 4 } 5 dropWhile[Int](List(2,4,6,7,8), n => n%2==0) // List(7, 8) R. Casadei Scala and FP October 2, 2015 11 / 56

FP in Scala Basics Exercises from Chapter 3: Functional data structures II Ex 3.6: Implement a function, init, that returns a List consisting of all but the last element of a List . So, given List(1,2,3,4), init will return List(1,2,3). Why can’t this function be implemented in constant time like tail? 1 // Because you must traverse the entire list 2 def init[A](l: List[A]): List[A] = l match { 3 case hd :: Nil => Nil 4 case hd :: tl => hd :: init(tl) // Risk for stack overflow for large lists!!! 5 } 6 7 def initSolution[A](l: List[A]): List[A] = { 8 val buf = new collection.mutable.ListBuffer[A] 9 @annotation.tailrec def go(cur: List[A]): List[A] = cur match { 10 case Nil => sys.error("init of empty list") 11 case Cons(_,Nil) => List(buf.toList: _*) 12 case Cons(h,t) => buf += h; go(t) 13 } 14 go(l) 15 } // NOTE: the buffer is internal, so the mutation is not observable and RT is preserved!!! 16 17 init((1 to 5).toList) // List(1, 2, 3, 4) Ex 3.9: Compute the length of a list using foldRight. 1 def length[A](as: List[A]): Int = as.foldRight(0)((_,acc)=>acc+1) 2 3 length((5 to 10).toList) // res57: Int = 6 Ex 3.10: Write foldLeft 1 @annotation.tailrec 2 def foldLeft[A,B](as: List[A], z: B)(f: (B, A) => B): B = as match { 3 case Nil => z 4 case hd :: tl => foldLeft(tl, f(z, hd))(f) 5 } 6 foldLeft(List(5,6,7),0)(_+_) // res: Int = 18 R. Casadei Scala and FP October 2, 2015 12 / 56

FP in Scala Basics Exercises from Chapter 3: Functional data structures III Ex 3.12: Write a function that returns the reverse of a list (given List(1,2,3) it returns List(3,2,1)). See if you can write it using a fold. 1 def reverse[A](lst: List[A]): List[A] = lst.foldLeft(List[A]())( (acc,e) => e :: acc) 2 3 reverse( 1 to 5 toList ) // List(5, 4, 3, 2, 1) Ex 3.13 (HARD): Can you write foldLeft in terms of foldRight? How about the other way around? Implementing foldRight via foldLeft is useful because it lets us implement foldRight tail-recursively, which means it works even for large lists without overﬂowing the stack. 1 def foldLeft[A,B](as: List[A], z: B)(f: (B, A) => B): B = { 2 as.reverse.foldRight(z)( (a,b) => f(b,a) ) 3 } 4 5 def foldRight[A,B](as: List[A], z: B)(f: (A, B) => B): B = { 6 as.reverse.foldLeft(z)( (a,b) => f(b,a) ) 7 } 8 9 // The following impls are interesting but not stack-safe 10 def foldRightViaFoldLeft2[A,B](l: List[A], z: B)(f: (A,B) => B): B = 11 foldLeft(l, (b:B) => b)((g,a) => b => g(f(a,b)))(z) 12 13 def foldLeftViaFoldRight2[A,B](l: List[A], z: B)(f: (B,A) => B): B = 14 foldRight(l, (b:B) => b)((a,g) => b => g(f(b,a)))(z) Ex 3.14: Implement append in terms of either foldLeft or foldRight. 1 def append[A](l: List[A], r: List[A]): List[A] = l.foldRight(r)(_::_) 2 3 append(1 to 3 toList, 5 to 9 toList) // List(1, 2, 3, 5, 6, 7, 8, 9) Ex 3.15 (HARD): Write a function that concatenates a list of lists into a single list. Its runtime should be linear in the total length of all lists. R. Casadei Scala and FP October 2, 2015 13 / 56

FP in Scala Basics Exercises from Chapter 3: Functional data structures IV 1 def concat[A](l: List[List[A]]): List[A] = foldRight(l, Nil:List[A])(append) 2 // Since append takes time proportional to its first argument, and this first argument never grows 3 // because of the right-associativity of foldRight, this function is linear in the total length of all lists. 4 5 concat(List(List(1,2),List(3,4))) // List(1,2,3,4) Ex 3.20: Write a function flatMap that works like map except that the function given will return a list instead of a single result, and that list should be inserted into the final resultinglist. 1 def flatMap[A,B](as: List[A])(f: A => List[B]): List[B] = concat( as.map(f) ) 2 3 flatMap(List(1,2,3))(i => List(i,i)) // List(1,1,2,2,3,3) Ex 3.21: Use flatMap to implement filter 1 def filter[A](as: List[A])(f: A => Boolean): List[A] = as.flatMap( e => if(f(e)) List(e) else Nil ) 2 3 filter(1 to 10 toList)(_%2==0) // List(2, 4, 6, 8, 10) R. Casadei Scala and FP October 2, 2015 14 / 56

FP in Scala Basics Handling errors without exceptions We said that throwing an exception breaks referential transparency The technique is based on a simple idea: instead of throwing an exception, we return a value indicating an exceptional condition has occurred. The big idea is that we can represent failures and exceptions with ordinary values, and write functions that abstract out common patterns of error handling. Possible alternatives to exceptions Return a bogus value – not so good: for some output types we might not have a sentinel value; may also allow errors to silently propagate; moreover, it demands a special policy or calling convention of callers Return null – not so good: it is only valid for non-primitive types; may also allow errors to silently propagate Force the caller to supply an argument which tells us what to do in case we don’t know how to handle the input – not so good: it requires the immediate callers have direct knowledge of how to handle the undeﬁned case Option[T] – QUITE GOOD! We explicitly represent the return type that may not always have a deﬁned value. We can think of this as deferring to the caller for the error handling strategy. Either[T] lets us track a reason for a failure 1 def safeDiv(x: Double, y: Double): Either[Exception, Double] = 2 try { Right(x / y) } catch { case e: Exception => Left(e) } R. Casadei Scala and FP October 2, 2015 15 / 56

FP in Scala Basics Option usage I 1 def lookupByName(name: String): Option[Employee] = ... 2 val joeDepartment: Option[String] = lookupByName("Joe").map(_.department) 3 // Note that we don’t need to explicitly check the result of lookupByName("Joe"); 4 // we simply continue the computation as if no error occurred}, inside the argument to map Note that we don’t have to check None at each stage of the computation. We can apply several transformations and then check for None when ready. A common pattern is to transform an Option via calls to map, flatMap, and/or filter, and then use getOrElse to do error handling at the end. 1 val dept = lookupByName("Joe").map(_.dept).filter(_ != "Accounting").getOrElse("Default Dept") Another common idiom is to do to convert None back to an exception 1 o.getOrElse(throw new Exception("FAIL")) Option lifting It may be easy to jump to the conclusion that once we start using Option , it infects our entire code base. One can imagine how any callers of methods that take or return Option will have to be modified to handle either Some or None. But this simply doesn’t happen, and the reason why is that we can lift ordinary functions to become functions that operate on Option. For example, the map function lets us operate on values of type Option[A] using a function of type A => B, returning Option[B]. Another way of looking at this is that map turns a function f: A => B into a function of type Option[A] => Option[B] R. Casadei Scala and FP October 2, 2015 16 / 56

FP in Scala Basics Option usage II 1 def inc(x: Int) = x+1 2 Some(5) map inc // res: Option[Int] = Some(6) 3 None map inc // res: Option[Int] = None It’s also possible to lift a function by using a for-comprehension, which in Scala is a convenient syntax for writing a sequence of nested calls to map and ﬂatMap You can lift a PartialFunction[A,B] to a PartialFunction[A,Option[B]] by calling its lift method Converting exception-based APIs to Option-based APIs We may introduce a Try function for the purpose 1 // The function is non-strict or lazy argument (Note the use of call-by-name param) 2 def Try[A](a: => A): Option[A] = try Some(a) catch { case e: Exception => None } Suppose now we need to call a function insuranceRateQuote(age: Int, numOfTickets: Int): Double if the parsing of both age and numOfTickets is successful (they may arrive from a web request...). If we use Try(age.toInt) and get an option, how can we call that method? We can use pattern matching but that’s going to be tedious. We could leverage on a function map2 that combines two Option values and, if either Option value is None, then the return value is too. R. Casadei Scala and FP October 2, 2015 17 / 56

FP in Scala Basics Option usage III 1 def map2[A,B,C](a: Option[A], b: Option[B])(f: (A, B) => C): Option[C] = (a,b) match { 2 case (Some(a),Some(b)) => Some(f(a,b)) 3 case _ => None 4 } 5 // Another solution 6 def map2[A,B,C](a: Option[A], b: Option[B])(f: (A, B) => C): Option[C] = 7 a flatMap (aa => b map (bb => f(aa, bb))) 8 9 map2[Int,Int,Int](Some(1),None )(_+_) // None 10 map2[Int,Int,Int](None, Some(1))(_+_) // None 11 map2[Int,Int,Int](Some(3),Some(1))(_+_) // Some(4) Then we could implement our Option-based API 1 def parseInsuranceRateQuote(age: String, numOfTickets: String): Option[Double] = { 2 val optAge: Option[Int] = Try { age.toInt } 3 val optTickets: Option[Int] = Try { numberOfSpeedingTickets.toInt } 4 map2(optAge, optTickes)(insuranceRateQuote) 5 } map2 allows to lift any 2-arg function. We could also deﬁne map3, map4, .... But we could generalize it in a function sequence that combines a list of Options into one Option containing a list of all the Some values in the original list. If the original list contains None even once, the result of the function should be None; otherwise the result should be Some with a list of all the values R. Casadei Scala and FP October 2, 2015 18 / 56

FP in Scala Basics Option usage IV 1 def sequence[A](a: List[Option[A]]): Option[List[A]] = Try { 2 a map (o => o match { case Some(x) => x }) 3 } 4 5 // Another solution 6 def sequence[A](a: List[Option[A]]): Option[List[A]] = a match { 7 case Nil => Some(Nil) 8 case h :: t => h flatMap (hh => sequence(t) map (hh :: _)) 9 } 10 11 // Another solution 12 def sequence_1[A](a: List[Option[A]]): Option[List[A]] = 13 a.foldRight[Option[List[A]]](Some(Nil))((x,y) => map2(x,y)(_ :: _)) 14 15 sequence(List(Some(1),Some(2),Some(3))) // Some(List(1, 2, 3)) 16 sequence(List(Some(1),None,Some(3))) // None Sometimes we’ll want to map over a list using a function that might fail, returning None if applying it to any element of the list returns None. For example 1 def parseInts(a: List[String]): Option[List[Int]] = sequence(a map (i => Try(i.toInt))) But it’s inefﬁcient since it traverses the list twice. Try to impl a generic traverse that looks at the list once. 1 /* Note: it assumes that f has no side effects */ 2 def traverse[A, B](a: List[A])(f: A => Option[B]): Option[List[B]] = Try { 3 a.map(x => f(x) match { case Some(y) => y }) 4 } 5 6 def parseInts(a: List[String]): Option[List[Int]] = traverse(a)(i => Try(i.toInt)) 7 8 parseInts( List("1","2","3") ) // Some(List(1, 2, 3)) 9 parseInts( List("1","2","a", "3") ) // None R. Casadei Scala and FP October 2, 2015 19 / 56

FP in Scala Basics Either usage I Option[T] doesn’t tell us anything about what went wrong in the case of an exceptional condition. All it can do is to give us None, indicating that there’s no value to be had. Sometimes we want to no more, e.g., a string with some info or the exception that happened We could deﬁne a type Either which is a disjoint union of two types. We use the Left data constructor for errors, and Right for success case. Note: as for Option, there’s a Either type in the Scala library which is slighly different from the one used here for pedagogical purpose 1 sealed abstract class Either[+E, +A] { 2 def map[B](f: A => B): Either[E, B] 3 def flatMap[EE >: E, B](f: A => Either[EE, B]): Either[EE, B] 4 def orElse[EE >: E,B >: A](b: => Either[EE, B]): Either[EE, B] 5 def map2[EE >: E, B, C](b: Either[EE, B])(f: (A, B) => C): Either[EE, C] 6 } 7 case class Left[+E](value: E) extends Either[E, Nothing] 8 case class Right[+A](value: A) extends Either[Nothing, A] 9 10 // Example: mean 11 def mean(xs: IndexedSeq[Double]): Either[String, Double] = 12 if (xs.isEmpty) Left("mean of empty list!") else Right(xs.sum / xs.length) 13 14 // Example: Try 15 def Try[A](a: => A): Either[Exception, A] = try Right(a) catch { case e: Exception => Left(e) } 16 17 // Example: Either can be used in for-comprehension 18 def parseInsuranceRateQuote(age: String, numOfTickets: String): Either[Exception,Double] = 19 for { a <- Try { age.toInt }; tickets <- Try { numOfTickets.toInt } } 20 yield insuranceRateQuote(a, tickets) R. Casadei Scala and FP October 2, 2015 20 / 56

FP in Scala Basics Exercises from Chapter 4: Handling errors without exceptions I Ex 5.1: implement the funtions of the Option trait. As you impl each function, try to think about what it means and in what situations you’d use it. 1 sealed trait Option[+A] 2 case class Some[+A](get: A) extends Option[A] 3 case object None extends Option[Nothing] 4 5 // Impl of methods 6 sealed trait Option[+A] { 7 // Apply f, which may fail, to the Option if not None. 8 // Map is similar to flatMap but f() doesn’t need to wrap its result in an Option 9 def map[B](f: A => B): Option[B] = this match { 10 case None => None 11 case Some(a) => Some(f(a)) // Note, wrt to ’flatMap’, here we wrap the result 12 } 13 14 // Apply f, which may fail, to the Option if not None. 15 // Similar to map, but f is expected to return an option 16 def flatMap[B](f: A => Option[B]): Option[B] = map(f) getOrElse None 17 18 // Another impl of flatMap 19 def flatMap[B](f: A => Option[B]): Option[B] = this match { 20 case None => None 21 case Some(a) => f(a) // Note, wrt to ’map’, here we don’t wrap the result 22 } 23 24 def getOrElse[B >: A](default: => B): B = this match { 25 case None => default 26 case Some(a) => a 27 } 28 29 // Provide an alternative option value (note: doesn’t eval ob unless needed) 30 def orElse[B >: A](ob: => Option[B]): Option[B] = this map (Some(_)) getOrElse ob 31 32 def orElse[B >: A](ob: => Option[B]): Option[B] = this match { 33 case None => ob 34 case _ => this 35 } 36 37 // Convert Some to None if the value doesn’t satisfy f 38 def filter(f: A => Boolean): Option[A] = this match { R. Casadei Scala and FP October 2, 2015 21 / 56

FP in Scala Basics Exercises from Chapter 4: Handling errors without exceptions II 39 case Some(a) if f(a) => this 40 case _ => None 41 } 42 } Note that in map/flatMap the function is not run if this option is None! Ex 4.2: Implement the variance function in terms of flatMap. If the mean of a sequence is m, the variance is the mean of math.pow(x-m, 2) for each element x in the sequence. 1 def mean(xs: Seq[Double]): Option[Double] = 2 if (xs.isEmpty) None else Some(xs.sum / xs.length) 3 def variance(s: Seq[Double]): Option[Double] = 4 mean(s) flatMap (m => mean(s.map(x => math.pow(x-m, 2)))) 5 variance(List(5,7,8)) // Some(1.5554) 6 variance(List()) // None 7 8 // WITH MAP 9 def mean2(xs: Seq[Double]): Double = xs.sum / xs.length 10 // If xs.isEmpty (i.e., xs.length = 0), mean2 will return Double.NaN 11 def varianceWithMap(s: Seq[Double]): Option[Double] = 12 mean(s) map (m => mean2(s.map(x => math.pow(x-m, 2)))) 13 // But here you’ll never get NaN because the first map gives you None for empty lists As the implementation of variance demonstrates, with flatMap we can construct a computation with multiple stages, any of which may fail, and the computation will abort as soon as the first failure is encountered, since None.flatMap(f) will immediately return None, without running f. Ex 4.6: implement versions of map, flatMap, orElse, map2 on Either that operate on the Right value R. Casadei Scala and FP October 2, 2015 22 / 56

FP in Scala Basics Exercises from Chapter 4: Handling errors without exceptions III 1 sealed trait Either[+E, +A] { 2 def map[B](f: A => B): Either[E, B] = this match { 3 case Right(a) => Right(f(a)) 4 case Left(e) => Left(e) 5 } 6 7 def flatMap[EE >: E, B](f: A => Either[EE, B]): Either[EE, B] = this match { 8 case Right(a) => f(a) 9 case Left(e) => Left(e) 10 } 11 12 def orElse[EE >: E,B >: A](b: => Either[EE, B]): Either[EE, B] = this match { 13 case Right(a) => Right(a) 14 case Left(_) => b 15 } 16 17 def map2[EE >: E, B, C](b: Either[EE, B])(f: (A, B) => C): Either[EE, C] = 18 flatMap(aa => b.flatMap(bb => Right(f(aa,bb)))) 19 } Ex 4.7: impl sequence and traverse for Either. These should return the ﬁrst error encountered (if any) 1 def sequence[E, A](es: List[Either[E, A]]): Either[E, List[A]] = { 2 def seqhelp[E, A](es: List[Either[E, A]], res: List[A]): Either[E, List[A]] = es match { 3 case Nil => Right(res) 4 case Left(e) :: _ => Left(e) 5 case Right(a) :: tl => seqhelp(tl, res :+ a) 6 } 7 seqhelp(es, List[A]()) 8 } 9 sequence(List(Right(1),Right(2),Right(3))) // Right(List(1, 2, 3)) 10 sequence(List(Right(1),Left("err"),Right(3),Left("err2"))) // Left(err1) 11 12 def traverse[E,A,B](es: List[A])(f: A => Either[E, B]): Either[E, List[B]] = 13 es.foldRight[Either[E,List[B]]](Right(Nil))((a, b) => f(a).map2(b)(_ :: _)) 14 15 // sequence can be impl in terms of traverse 16 def sequence[E, A](es: List[Either[E, A]]): Either[E, List[A]] = 17 traverse(es)(a => a) R. Casadei Scala and FP October 2, 2015 23 / 56

FP in Scala Basics Exercises from Chapter 4: Handling errors without exceptions IV Ex 4.8: In our impl, map2 is only able to report one error. What would you need to change in order to report both errors? If we want to accumulate multiple errors, a simple approach is a new data type that lets us keep a list of errors in the data constructor that represents failures: 1 trait Partial[+A,+B] 2 case class Errors[+A](get: Seq[A]) extends Partial[A,Nothing] 3 case class Success[+B](get: B) extends Partial[Nothing,B] There is a type very similar to this called Validation in the Scalaz library R. Casadei Scala and FP October 2, 2015 24 / 56

FP in Scala Basics Strict/non-strict functions, laziness If the evaluation of an expression runs forever or throws an error instead of returning a deﬁnite value, we say that the expression does not terminate, or that it evaluates to bottom. Formally, a function f is strict if the expression f(x) evaluates to bottom for all x that evaluate to bottom. A strict function always evaluates its arguments. Instead, a non-strict function may choose not to evaluate one or more of its arguments. 1 // For example, || and && boolean functions are non-strict 2 false && sys.error("failure") // res: Boolean = false You can write non-strict functions by using call-by-name params (which are passed unevaluated to the function) or lazy evaluation (aka by-need evaluation) In general, the unevaluated form of an expression is called a thunk, and we can force the thunk to evaluate the expression and get a result Laziness improves modularity by separating the description of an expression from the evaluation of that expression. R. Casadei Scala and FP October 2, 2015 25 / 56

FP in Scala Basics Lazy lists (streams) I Consider the following code 1 List(1,2,3,4).map(_ + 10).filter(_ % 2 == 0).map(_ * 3) How it it evaluated? Each transformation will produce a temporary list that only ever gets used as input for the next transformation and is then immediately discarded Wouldn’t it be nice if we could somehow fuse sequences of transformations like this into a single pass and avoid creating temporary data structures? We could rewrite the code into a while loop by hand, but ideally we’d like to have this done automatically while retaining the same high-level compositional style Separating program description from evaluation. With Stream, we’re able to build up a computation that produces a sequence of elements without running the steps of that computation until we actually need those elements. We’ll see how chains of transformations on streams can be fused into a single pass through the use of laziness R. Casadei Scala and FP October 2, 2015 26 / 56

FP in Scala Basics Lazy lists (streams) II Simple implementation of Stream 1 sealed trait Stream[+A]{ 2 def headOption(): Option[A] = this match { 3 case Empty => None 4 case Cons(h, t) => Some(h()) // Explicit force of h 5 } 6 } 7 case object Empty extends Stream[Nothing] 8 case class Cons[+A](h: () => A, t: () => Stream[A]) extends Stream[A] 9 10 object Stream { 11 def cons[A](hd: => A, tl: => Stream[A]): Stream[A] = { 12 lazy val head = hd 13 lazy val tail = tl 14 Cons(() => head, () => tail) 15 } 16 def empty[A]: Stream[A] = Empty 17 def apply[A](as: A*): Stream[A] = if (as.isEmpty) empty else cons(as.head, apply(as.tail: _*)) 18 } Note cons takes explicit thunks instead of regular strict values In headOption, we explicitly force the head thunk Memoizing streams and avoiding recomputations We typically want to cache the values of a Cons node, once they are forced This is achieved using lazy vals in cons The empty smart constructor returns Empty but annotates it as a Stream[A] which is better for type inference in some cases. R. Casadei Scala and FP October 2, 2015 27 / 56

FP in Scala Basics Lazy lists (streams) III Helper functions for inspecting stream: write toList, take, drop, takeWhile (exercises 5.1, 5.2, 5.3) 1 sealed trait Stream[+A] { 2 def toListRecursive: List[A] = this match { 3 case Empty => Nil 4 case Cons(hd,tl) => hd() :: tl().toList() // Will stack overflow for large stream 5 } 6 def toList: List[A] = { 7 @annotation.tailrec def go(s: Stream[A], acc: List[A]): List[A] = s match { 8 case Cons(hd,tl) => go(tl(), hd()::acc) 9 case _ => acc 10 }; go(this, List()).reverse // the reverse is not optimal (second pass) 11 } 12 def toListFast: List[A] = { // Using a mutable list buffer 13 val buf = new collection.mutable.ListBuffer[A] 14 @annotation.tailrec def go(s: Stream[A]): List[A] = s match { 15 case Cons(h,t) => { buf += h(); go(t()) } 16 case _ => buf.toList 17 }; go(this) 18 } 19 def take(n: Int): Stream[A] = this match { // Note: take generates its answer lazily 20 case Cons(h, t) if n>=1 => Cons(h(), tl().take(n-1)) 21 case Cons(h, t) if n==0 => Cons(h(), empty) 22 case _ => empty 23 } 24 @annotation.tailrec def drop(n: Int): Stream[A] = this match { // Not lazy 25 case Cons(_, t) if n>0 => t().drop(n-1) 26 case _ => this 27 } 28 def takeWhile(p: A => Boolean): Stream[A] = this match { 29 case Cons(h, t) if p(h()) => Cons(h(), t().takeWhile(p)) 30 case _ => empty 31 } 32 @annotation.tailrec def dropWhile(p: A => Boolean): Stream[A] = this match { 33 case Cons(h, t) if p(h()) => t().dropWhile(p) 34 case _ => this 35 } R. Casadei Scala and FP October 2, 2015 28 / 56

FP in Scala Basics Lazy lists (streams) IV Separating program description from program evaluation 1 sealed trait Stream[+A] { 2 3 def foldRight[B](z: => B)(f: (A, => B) => B): B = this match { 4 case Cons(h,t) => f(h(), t().foldRight(z)(f)) // NOTE THE CALL TO f() 5 case _ => z 6 } If f, which is non-strict in its 2nd arg, choses to not evaluate it, this terminates the traversal early. And since foldRight can terminate the traversal early, we can reuse it to implement exists and other useful methods 1 def exists(p: A => Boolean): Boolean = foldRight(false)((a,b) => p(a)||b) Ex 5.4: impl forAll which checks if all elems of the stream match a given predicate. It should terminate the traversal as soon as a nonmatching value is encountered. 1 def forAll(p: A => Boolean): Boolean = foldRight(true)((a,b) => p(a)&&b) Use foldRight to impl takeWhile (ex. 5.5) 1 def takeWhile(p: A => Boolean): Stream[A] = 2 foldRight(empty[A])((a,b) => if(p(a)) Cons(a,b) else empty) Use foldRight to impl headOption (ex. 5.6 HARD) 1 def headOption: Option[A] = 2 foldRight(None)((a,_) => ) R. Casadei Scala and FP October 2, 2015 29 / 56

FP in Scala Basics Lazy lists (streams) V Ex. 5.7: Implement map, ﬁlter, append, ﬂatMap using foldRight. The append method should be non-strict in its argument. 1 def map[B](f: A => B): Stream[B] = 2 foldRight(empty[B])((a,t) => Cons(f(a), t)) 3 4 def filter(p: A => Boolean): Stream[A] = 5 foldRight(empty[A])((a,t) => if(p(a)) Cons(a,t) else t) 6 7 def append[B>:A](s: => Stream[B]): Stream[B] = foldRight(s)((a,t) => Cons(a,t)) 8 9 def flatMap(f: A => Stream[B]): Stream[B] = 10 foldRight(empty[B])((a,t) => f(a) append t) Note that these implementations are incremental: they don’t fully generate their answers. It’s not until some other computation looks at the elements of the resulting Stream that the computation to generate that Stream actually takes place. Because of this incremental nature, we can call these functions one after another without fully instantiating the intermediate results Program trace for Stream 1 Stream(1,2,3,4).map(_ + 10).filter(_ % 2 == 0).toList 2 cons(11, Stream(2,3,4).map(_ + 10)).filter(_ % 2 == 0).toList // apply ’map’ to 1st elem 3 Stream(2,3,4).map(_ + 10).filter(_ % 2 == 0).toList // apply ’filter’ to 1st elem 4 cons(12, Stream(3,4).map(_ + 10)).filter(_ % 2 == 0).toList // apply ’map’ to 2nd elem 5 12 :: Stream(3,4).map(_ + 10).filter(_ % 2 == 0).toList // apply ’filter’ and produce elem 6 12 :: cons(13, Stream(4).map(_ + 10)).filter(_ % 2 == 0).toList 7 12 :: Stream(4).map(_ + 10).filter(_ % 2 == 0).toList 8 12 :: cons(14, Stream().map(_ + 10)).filter(_ % 2 == 0).toList 9 12 :: 14 :: Stream().map(_ + 10).filter(_ % 2 == 0).toList // apply ’filter’ to 4th elem 10 12 :: 14 :: List() // map and filter have no more work to do, and empty stream becomes empty list R. Casadei Scala and FP October 2, 2015 30 / 56

FP in Scala Basics Lazy lists (streams) VI Since intermediate streams aren’t instantiated, it’s easy to reuse existing combinators in novel ways without having to worry that we’re doing more processing of the stream than necessary. For example, we can reuse filter to define find, a method to return just the first element that matches if it exists. Even though filter transforms the whole stream, that transformation is done lazily, so find terminates as soon as a match is found. 1 def find(p: A => Boolean): Option[A] = filter(p).headOption R. Casadei Scala and FP October 2, 2015 31 / 56

FP in Scala Basics Inﬁnite streams and corecursion I Because they’re incremental, the functions we’ve written also work for inﬁnite streams. 1 val ones: Stream[Int] = Stream.cons(1, ones) 2 ones.take(5).toList // List(1,1,1,1,1) 3 ones.exists(_ % 2 != 0) // true 4 ones.forAll(_ == 1) // OPSSSS! It’ll never terminate R. Casadei Scala and FP October 2, 2015 32 / 56

FP in Scala Basics Infinite streams and corecursion II Ex 5.8: impl constant(k) which returns an infinite stream of a constant value k 1 object Stream { 2 def constant[A](a: A): Stream[A] = Cons(a, constant(a)) 3 4 // We can make it more efficient with just one object referencing itself 5 def constant[A](a: A): Stream[A] = { 6 lazy val tail: Stream[A] = Cons(() => a, () => tail) 7 tail 8 } Ex 5.9: impl from(n) which returns the infinite stream n, n + 1, n + 2, .. 1 def from(n: Int): Stream[Int] = Cons(n, from(n+1)) Ex 5.10: impl fibs which returns an infinite stream of Fibonacci numbers 1 def fibs(): Stream[Int] = { 2 def fib(x1: Int, x2: Int): Stream[Int] = Cons(x1, fib(x2, x1+x2)) 3 Cons(0, 1) 4 } Ex 5.11: write a more general stream-building function called unfold. It takes an initial state, and a function for producing both the next state and the next value in the generated stream. Option is used to indicate when the Stream should be terminated, if at all 1 def unfold[A, S](z: S)(f: S => Option[(A, S)]): Stream[A] = f(z) match { 2 case None => Empty 3 case Some((res, nextState)) => Cons(res, unfold(nextState)(f)) 4 } R. Casadei Scala and FP October 2, 2015 33 / 56

FP in Scala Basics Inﬁnite streams and corecursion III The unfold function is an example of corecursive function. Whereas a recursive function consumes data, a corecursive function produces data. And whereas recursive functions terminate by recursing on smaller inputs, corecursive functions need not terminate so long as they remain productive, which just means that we can always evaluate more of the result in a ﬁnite amount of time. The unfold function is productive as long as f terminates, since we just need to run the function f one more time to generate the next element of the Stream. Corecursion is also sometimes called guarded recursion, and productivity is also sometimes called cotermination. R. Casadei Scala and FP October 2, 2015 34 / 56

FP in Scala Basics Purely functional state I Think of java.util.Random. We can assume that this class has some internal state that gets updated after each invocation, since we would otherwise get the same "random" value each time. Because these state updates are performed as a side effect, these methods are not referentially transparent. The key to recovering referential transparency is to make these state updates explicit. That is, do not update the state as a side effect, but simply return the new state along with the value we are generating. In effect, we separate the computing of the next state from the concern of propagating that state throughout the program There is no global mutable memory being used – we simply return the next state back to the caller. Whenever we use this pattern, we make users of the API responsible for threading the computed next state through their programs Common pattern: functions of type S => (A, S) describe state actions that transform S states R. Casadei Scala and FP October 2, 2015 35 / 56

FP in Scala Basics Purely functional state II 1 trait RNG { 2 def nextInt: (Int, RNG) 3 } 4 5 case class SimpleRNG(seed: Long) extends RNG { 6 def nextInt: (Int, RNG) = { 7 val newSeed = (seed * 0x5DEECE66DL + 0xBL) & 0xFFFFFFFFFFFFL 8 val nextRNG = SimpleRNG(newSeed) 9 val n = (newSeed >>> 16).toInt 10 (n, nextRNG) 11 } 12 } 13 14 val rng1 = new SimpleRNG(77) // rng1: SimpleRNG = SimpleRNG(77) 15 val (n1, rng2) = rng1.nextInt // n1: Int = 29625665, rng2: RNG = SimpleRNG(1941547601620) 16 val (n2, rng3) = rng2.nextInt // n2: Int = 1226233105, rng3: RNG = SimpleRNG(80362412771407) 17 18 val int: Rand[Int] = _.nextInt 19 val (n3, rng4) = int(rng) 20 21 def ints(count: Int)(rng: RNG): (List[Int], RNG) = count match { 22 case n if n<=0 => (Nil, rng) 23 case n => { 24 val (r, rng2) = rng.nextInt 25 val (tail, rngLast) = ints(n-1)(rng2) 26 (r :: tail, rngLast) 27 } 28 } 29 30 val (rints, rng5) = ints(3)(rng4) // rints: List[Int] = List(-615319858, -1013832981, 88185503) 31 // rng2: RNG = SimpleRNG(5779325172636) R. Casadei Scala and FP October 2, 2015 36 / 56

FP in Scala Basics Purely functional state III Ex 6.1: impl a RNG to gen a nonNegativeInt (between 0 and Int.MaxValue). Handle the corner case of Int.MinValue which hasn’t a non-negative counterpart. 1 def nonNegativeInt(rng: RNG): (Int, RNG) = { 2 val (i, r) = rng.nextInt 3 (if(i<0) -(i+1) else i, r) 4 } Ex 6.2: impl a RNG of double values between 0 and 1 (NOT inclusive) 1 def double(rng: RNG): (Double, RNG) = { 2 val (n, r) = nonNegativeInt(rng) 3 (n / (Int.MaxValue.toDouble + 1), r) 4 } Ex 6.3: impl a RNG to gen a (Int, Double) pair 1 def intDouble(rng: RNG): ((Int,Double), RNG) = { 2 val (i, r1) = rng.nextInt 3 val (d, r2) = double(r1) 4 ((i, d), r2) 5 } Ex 6.4: impl a function to generate a list of random ints 1 def ints(count: Int)(rng: RNG): (List[Int], RNG) = { 2 @annotation.tailrec def go(n: Int, r: RNG, acc: List[Int]): (List[Int], RNG) = n match { 3 case n if n<=0 => (acc, r) 4 case n => { val (i,r2) = r.nextInt; go(n-1, r2, i::acc) } 5 } 6 go(count, rng, List()) 7 } R. Casadei Scala and FP October 2, 2015 37 / 56

FP in Scala Basics Purely functional state IV A better API for state actions Since it’s pretty tedious and repetitive to pass the state along ourselves, we want our combinators to pass the state from one action to the next automatically 1 // Type alias for the RNG state action data type 2 // Rand[A] is a function that expects a RNG to produce A values (and the next state) 3 type Rand[+A] = RNG => (A, RNG) 4 5 // The "unit" action passes the RNG state through without using it, 6 // always returning a constant value rather than a random value. 7 def unit[A](a: A): Rand[A] = rng => (a, rng) 8 9 // The "map" action transforms the output of a state action without modifying the state itself 10 def map[A,B](s: Rand[A])(f: A => B): Rand[B] = rng => { 11 val (a, rng2) = s(rng) 12 (f(a), rng2) 13 } 14 15 // EX 6.6 The "map2" action combines 2 RNG actions into one using a binary rather than unary fn. 16 def map2[A,B,C](ra: Rand[A], rb: Rand[B])(f: (A, B) => C): Rand[C] = rng => { 17 val (a, r1) = ra(rng) 18 val (b, r2) = rb(r1) 19 (f(a,b), r2) 20 } 21 22 def both[A,B](ra: Rand[A], rb: Rand[B]): Rand[(A,B)] = map2(ra, rb)((_, _)) 23 24 // EX 6.7. The "sequence" action combines a List of transitions into a single transition 25 def sequence[A](fs: List[Rand[A]]): Rand[List[A]] = rng => { 26 @annotation.tailrec 27 def go(lst: List[Rand[A]], acc: List[A], rng: RNG): Rand[List[A]] = lst match { 28 case Nil => unit(acc)(_) 29 case gen :: tl => { val (x,r) = gen(rng); go(tl, x::acc, r) } 30 } 31 go(fs, List(), rng)(rng) 32 } 33 // Another solution 34 def sequence[A](fs: List[Rand[A]]): Rand[List[A]] = 35 fs.foldRight(unit(List[A]()))((f, acc) => map2(f, acc)(_ :: _)) R. Casadei Scala and FP October 2, 2015 38 / 56

FP in Scala Basics Purely functional state V 36 37 // "flatMap" allows us to generate a random A with a function Rand[A], 38 // and then take that A and choose a Rand[B] based on its value 39 def flatMap[A,B](f: Rand[A])(g: A => Rand[B]): Rand[B] = rng => { 40 val (a, rnga) = f(rng) 41 g(a)(rnga) 42 } Now we can implement previous functions more easily 1 // EXERCISE 6.5: use ’map’ to reimplement ’double’ in a more elengant way 2 val randDouble: Rand[Double] = map(nonNegativeInt)(_ / (Int.MaxValue.toDouble+1)) 3 4 val randIntDouble: Rand[(Int,Double)] = both((_:RNG).nextInt, randDouble) 5 6 // EXERCISE 6.7: use ’sequence’ to reimplement ’ints’ 7 def ints(n: Int): Rand[List[Int]] = sequence((1 to n).map(_ => (_:RNG).nextInt).toList) 8 9 // EXERCISE 6.8: use ’flatMap’ to implement ’nonNegativeLessThan’ 10 def nonNegativeLessThan(ub: Int): Rand[Int] = 11 flatMap(nonNegativeInt)(n => if(n>=ub) nonNegativeLessThan(ub) else unit(n)) 12 13 // EXERCISE 6.9: reimpl map and map2 in terms of flatMap 14 def map[A,B](s: Rand[A])(f: A => B): Rand[B] = 15 flatMap(s)(a => unit(f(a))) 16 17 def map2[A,B,C](ra: Rand[A], rb: Rand[B])(f: (A, B) => C): Rand[C] = 18 flatMap(ra)(a => flatMap(rb)(b => unit(f(a,b)))) 19 // for(a <- ra; b <- rb) yield(unit(f(a,b))) 20 // To use for-comprehension we need to add flatMap to Rand[T] R. Casadei Scala and FP October 2, 2015 39 / 56

FP in Scala Basics Purely functional state VI We can generalize it 1 case class State[S,+A](run: S => (A,S)) { 2 def apply(s: S) = run(s) 3 4 def unit[A](a: A): State[S, A] = new State(s => (a, s)) 5 6 def map[B](f: A => B): State[S, B] = new State(s => { 7 val (a, s2) = run(s) 8 (f(a), s2) 9 }) 10 11 def map2[B,C](rb: State[S,B])(f: (A, B) => C): State[S,C] = new State(s => { 12 val (a, s2a) = run(s) 13 val (b, s2b) = rb.run(s) 14 (f(a,b), s2a) 15 }) 16 17 def flatMap[B](g: A => State[S,B]): State[S, B] = new State[S,B]( s => { 18 val (a, s2) = run(s) 19 g(a, s2) 20 }) 21 } 22 23 type Rand[A] = State[RNG, A] 24 25 val int: Rand[Int] = new State(rng => rng.nextInt) 26 def ints(count: Int): Rand[List[Int]] = count match { 27 case n if n<=0 => new State(s => (Nil, s)) 28 case n => new State (rng => { 29 val (r, rng2) = rng.nextInt 30 val (tail, rngLast) = ints(n-1).run(rng2) 31 (r :: tail, rngLast) 32 }) 33 } 34 35 val randomNums = ints(3).map(lst => lst map (_.toDouble)).run(new SimpleRNG(0)) 36 // randomNums: (List[Double], RNG) = (List(0.0, 4232237.0, 1.7880379E8),SimpleRNG(11718085204285)) Purely functional imperative programming R. Casadei Scala and FP October 2, 2015 40 / 56

FP in Scala Basics Purely functional state VII In the imperative programming paradigm, a program is a sequence of statements where each statement may modify the program state. That’s exactly what we’ve been doing, except that our “statements” are really State actions, which are really functions FP and imperative programming are not necessarily the opposite: it is reasonable to maintain state without side effects We implemented some combinators like map, map2, and ultimately ﬂatMap to handle the propagation of the state from one statement to the next. But in doing so, we seem to have lost a bit of the imperative mood... That’s not actually the case! 1 val ns: Rand[List[Int]] = int.flatMap(x => int.flatMap(y => ints(x).map(xs => xs.map(_ % y)))) 2 3 val ns: Rand[List[Int]] = for { 4 x <- int; 5 y <- int; 6 xs <- ints(x) 7 } yield xs.map(_ % y) // Oh yeah! Now it really seems imperative! ;) To facilitate this kind of imperative programming with for-comprehensions (or ﬂatMaps), we really only need two primitive State combinators: one for reading the state and one for writing the state 1 def get[S]: State[S, S] = State(s => (s, s)) // pass state along and returns it as value 2 def set[S](s: S): State[S, Unit] = State(_ => ((), s)) // ignores current state 3 def modify[S](f: S => S): State[S, Unit] = for { 4 s <- get // get current state 5 _ <- set(f(s)) // set new state 6 } yield () get, set, map, map2, flatMap are all the tools we need to implement any kind of state machine or stateful program in a purely functional way R. Casadei Scala and FP October 2, 2015 41 / 56

FP in Scala Functional library design Outline 1 FP in Scala Basics Functional data structures Handling errors without exceptions Strict/non-strict functions, laziness Purely functional state Functional library design Common structures in FP Monoids Monads R. Casadei Scala and FP October 2, 2015 42 / 56

FP in Scala Functional library design Functional library design Our main concern is to make our library highly composable and modular. Algebraic reasoning may come handy: an API can be described by an algebra that obeys specific laws Our fundamental assumption is that our library admits absolutely no side effects The difficulty of the design process is in refining the first general ideas of what we want to achieve and finding data types and functions that enable such functionality It may be useful to start off with simple examples R. Casadei Scala and FP October 2, 2015 43 / 56

FP in Scala Functional library design Purely function parallelism I We’ll strive to separate the concern of describing a computation from actually running it. We’d like to be able to “create parallel computations”, but what does that mean exactly? We may initially consider a simple, parallelizable computation – the sum of a list of integers. 1 def sum(ints: Seq[Int]): Int = ints.foldLeft(0)((a,b) => a + b) Ehy, we can break the sequence into parts that can be processed in parallel! 1 def sum(ints: IndexedSeq[Int]): Int = 2 if(ints.size <= 1){ 3 ints.headOption getOrElse 0 4 } else { 5 val (l,r) = ints.splitAt(ints.length/2) 6 sum(l) + sum(r) 7 } Any data type we might choose to represent our parallel computations needs to be able to contain a result, which should be of some meaningful type. Of course, we also require some way of extracting that result. We invent Par[A], our container type for our result def unit[A](a: => A): Par[A] takes an unevaluated A and returns a computation that may evaluate it in a separate thread; it creates a unit of parallelism that just wraps a single value def get[A](a: Par[A]): A for extracting the resulting value from the parallel computation 1 def sum(ints: IndexedSeq[Int]): Int = 2 if(ints.size <= 1){ 3 ints.headOption getOrElse 0 4 } else { 5 val (l,r) = ints.splitAt(ints.length/2) 6 val sumL: Par[Int] = Par.unit(sum(l)) 7 val sumR: Par[Int] = Par.unit(sum(r)) 8 Par.get(sumL) + Par.get(sumR) 9 } R. Casadei Scala and FP October 2, 2015 44 / 56

FP in Scala Functional library design Purely function parallelism II We require unit to begin evaluating its arg concurrently and return immediately. But then, calling get arguably breaks refential transparency: if we replace sumL and sumR with their deﬁnitions, the program is no longer parallel! As soon as we pass the Par to get, we explicitly wait for it, exposing the side effect. So it seems we want to avoid calling get, or at least delay calling it until the very end. R. Casadei Scala and FP October 2, 2015 45 / 56

FP in Scala Common structures in FP Outline 1 FP in Scala Basics Functional data structures Handling errors without exceptions Strict/non-strict functions, laziness Purely functional state Functional library design Common structures in FP Monoids Monads R. Casadei Scala and FP October 2, 2015 46 / 56

FP in Scala Common structures in FP Common structures in functional design We were getting comfortable with considering data types in terms of their algebras, i.e., the operations they support and the laws that govern these operations The algebras of different data types often share certain patterns in common R. Casadei Scala and FP October 2, 2015 47 / 56

FP in Scala Common structures in FP Monoids In abstract algebra, a monoid is an algebraic structure with a single associative binary operation and an identity element. In category theory, a monoid is a category with a single object Thus, monoids capture the idea of function composition within a set A monoid is a purely algebraic structure (i.e., it is deﬁned only by its algebra) Examples The algebra of string concatenation – We can concatenate “a”+“b” to get “ab”; that operation is associative, i.e., (a+b)+c=a+(b+c) and the empty string is an identity element for that operation. Integer addition (0 is identity elem); multiplication (1 is identity) The boolean operators && and || (identity is true and false, respectively) So, a monoid is an algebra that consists of: Some type A An associative binary operation op An identity value zero for that operation 1 trait Monoid[A] { 2 def op(a1: A, a2: A): A 3 def zero: A 4 } 5 6 val stringMonoid = new Monoid[String] { 7 def op(a1: String, a2: String) = a1 + a2 8 val zero = "" 9 } The laws of associativity and identity are known as the monoid laws R. Casadei Scala and FP October 2, 2015 48 / 56

FP in Scala Common structures in FP More on monoids I Exercise 10.2: give a monoid for combining Option values 1 def optionMonoid[A]: Monoid[Option[A]] = new Monoid[Option[A]] { 2 def op(op1: Option[A], op2: Option[A]): Option[A] = op1 orElse op2 3 def zero: Option[A] = None 4 } Exercise 10.3: give a monoid for endofunctions (i.e., functions with same argument and return type) 1 def endoMonoid[A]: Monoid[A => A] = new Monoid[A => A] { 2 def op(f1: A=>A, f2: A=>A): A => A = f1 compose f2 3 def zero: A=>A = a => a 4 } Use ScalaCheck properties to test your monoids 1 import org.scalacheck.Prop.forAll 2 val o = optionMonoid[Int] 3 val opAssociativity = forAll { 4 (a:Option[Int], b:Option[Int], c:Option[Int]) => o.op(o.op(a,b),c) == o.op(a,o.op(b,c)) 5 } 6 val identity = forAll { (a: Option[Int]) => o.op(o.zero, a) == a && o.op(a, o.zero) == a } 7 (opAssociativity && identity).check // OK: passed 100 tests (On terminology) Having vs. being a monoid: sometimes people talk about a type being a monoid versus having a monoid instance. Actually the monoid is both the type and the instance satisfying the laws. More precisely, the type A forms a monoid under the operations deﬁned by the Monoid[A] instance. In summary, a monoid is simply a type A and an implementation of Monoid[A] that satisﬁes the laws. Stated tersely, a monoid is a type together with a binary operation (op) over that type, satisfying associativity and having an identity element (zero). R. Casadei Scala and FP October 2, 2015 49 / 56

FP in Scala Common structures in FP More on monoids II So what’s the matter? Just like any abstraction, a monoid is useful to the extent that we can write useful generic code assuming only the capabilities provided by the abstraction. Can we write any interesting programs, knowing nothing about a type other than that it forms a monoid? We’ll see that the associative property enables folding any Foldable data type and gives the ﬂexibility of doing so in parallel. Monoids are also compositional, and you can use them to assemble folds in a declarative and reusable way. R. Casadei Scala and FP October 2, 2015 50 / 56

FP in Scala Common structures in FP Working with monoids I Folding lists with monoids Look at the type signature of foldLeft/Right – what happens when A=B? 1 def foldRight[B](z: B)(f: (A, B) => B): B 2 def foldLeft[B](z: B)(f: (B, A) => B): B The components of a monoid ﬁt these argument types like a glove. 1 val words = List("a","b","c") 2 val s = words.foldRight(stringMonoid.zero)(stringMonoid.op) // "abc" 3 val t = words.foldLeft(stringMonoid.zero)(stringMonoid.op) // "abc" Note that it doesn’t matter if we choose foldLeft or foldRight when folding with a monoid; we should get the same result. This is precisely because the laws of associativity and identity hold. We can write a general function concatenate that folds a list with a monoid: 1 def concatenate[A](as: List[A], m: Monoid[A]): A = as.foldLeft(m.zero)(m.op) But what if our list has an element type that doesn’t have a Monoid instance? Well, we can always map over the list to turn it into a type that does 1 // EXERCISE 10.5 2 def foldMap[A,B](as: List[A], m: Monoid[B])(f: A => B): B = 3 (as map f).foldLeft(m.zero)(m.op) 4 5 // EXERCISE 10.6 (HARD) You can also write foldLeft and foldRight using foldMap 6 def foldRight[A, B](as: List[A])(z: B)(f: (A, B) => B): B = 7 foldMap(as, endoMonoid[B])(f.curried)(z) 8 9 def foldLeft[A, B](as: List[A])(z: B)(f: (B, A) => B): B = 10 foldMap(as, dual(endoMonoid[B]))(a => b => f(b, a))(z) R. Casadei Scala and FP October 2, 2015 51 / 56

FP in Scala Common structures in FP Working with monoids II Associativity and parallelism The fact that a monoid’s operation is associative means we can choose how we fold a data structure like a list. But if we have a monoid, we can reduce a list using a balanced fold, which can be more efﬁcient for some operations (where the cost of each op is proportional to the size of its args) and also allows for parallelism 1 op(a, op(b, op(c, d))) // folding to the right (right associative) 2 op(op(op(a, b), c), d) // folding to the left (left associative) 3 op(op(a,b), op(c,d)) // balanced fold (note that you can parallelize inner ops) R. Casadei Scala and FP October 2, 2015 52 / 56

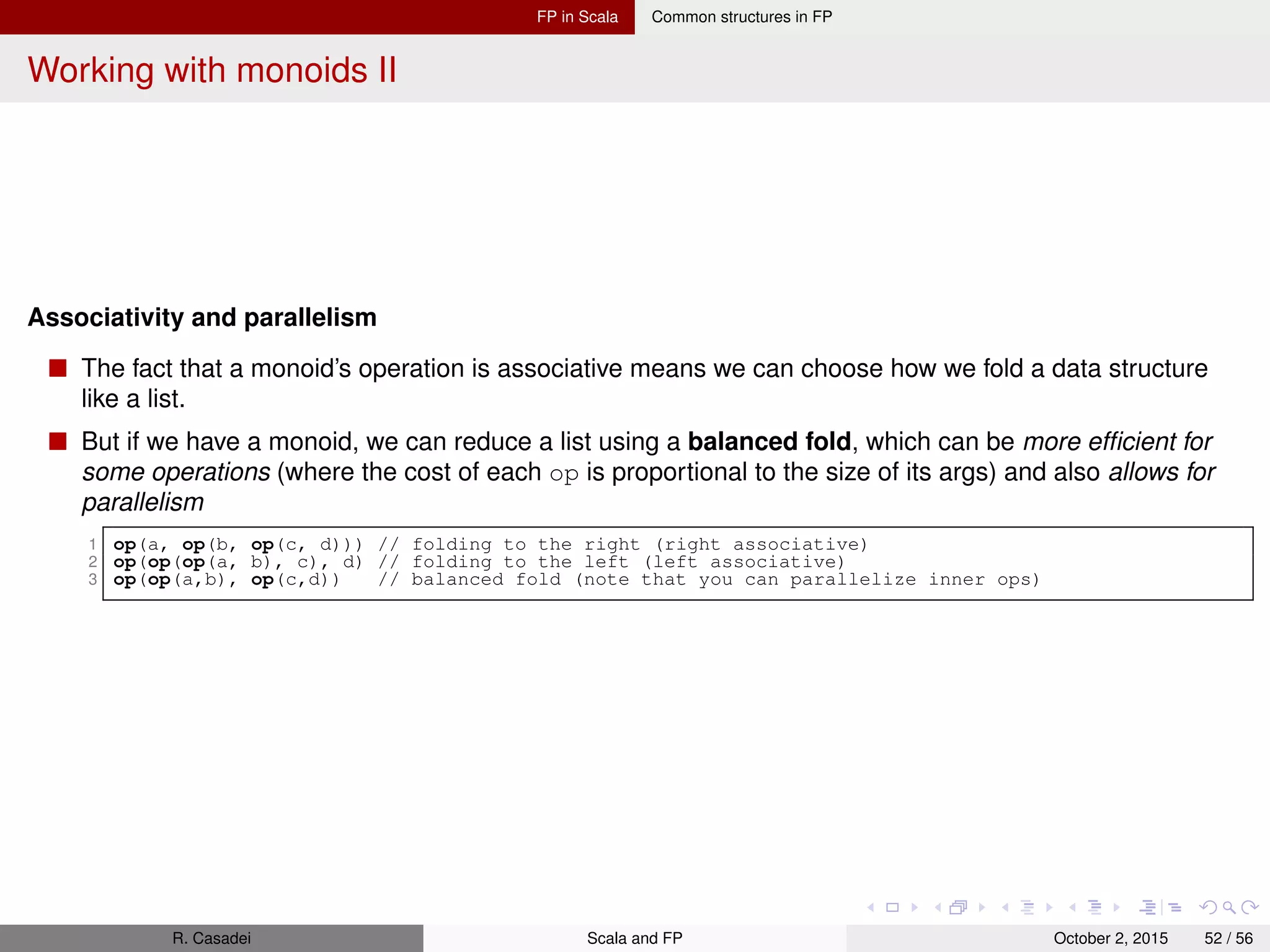
FP in Scala Common structures in FP Foldable data structures Many data structures can be folded (lists, trees, streams, ...) When we’re writing code that needs to process data contained in one of these structures, we often don’t care about the speciﬁc shape of the structure (whether it is a list or tree, lazy or not, ...) 1 trait Foldable[F[_]] { 2 def foldRight[A,B](as: F[A])(z: B)(f: (A,B) => B): B 3 def foldLeft[A,B](as: F[A])(z: B)(f: (B,A) => B): B 4 def foldMap[A,B](as: F[A])(f: A => B)(mb: Monoid[B]): B 5 def concatenate[A](as: F[A])(m: Monoid[A]): A = foldLeft(as)(m.zero)(m.op) 6 } The syntax F[_] indicates that F is not a type but a type constructor that takes one type argument. Thus, Foldable is a higher-order type constructor (or higher-kinded type) Just like values and functions have types, types and type constructors have kinds. Scala uses kinds to track how many type arguments a type constructor takes, whether it’s co- or contravariant in those arguments, and what the kinds of those arguments are. R. Casadei Scala and FP October 2, 2015 53 / 56

FP in Scala Common structures in FP Composing monoids You can compose monoids If types A and B are monoids, then the tuple (A,B) is also a monoid (called their product) 1 def productMonoid[A,B](A: Monoid[A], B: Monoid[B]): Monoid[(A,B)] = new Monoid[(A,B)]{ 2 // ... 3 } Some data structures form interesting monoids as long as the types of the elements they contain also form monoids. For instance, there’s a monoid for merging key-value Maps, as long as the value type is a monoid. 1 def mapMergeMonoid[K,V](V: Monoid[V]): Monoid[Map[K, V]] = new Monoid[Map[K, V]] { 2 def zero = Map[K,V]() 3 def op(a: Map[K, V], b: Map[K, V]) = (a.keySet ++ b.keySet).foldLeft(zero) { (acc,k) => 4 acc.updated(k, V.op(a.getOrElse(k, V.zero),b.getOrElse(k, V.zero))) 5 } 6 } 7 8 val M: Monoid[Map[String, Map[String, Int]]] = mapMergeMonoid(mapMergeMonoid(intAddition)) 9 val m1 = Map("o1" -> Map("i1" -> 1, "i2" -> 2)); val m2 = Map("o1" -> Map("i2" -> 3)) 10 val m3 = M.op(m1, m2) // Map(o1 -> Map(i1 -> 1, i2 -> 5)) Use monoids to fuse traversals: the fact that multiple monoids can be composed into one means that we can perform multiple calculations simultaneously when folding a data structure. For example, we can take the length and sum of a list at the same time in order to calculate the mean 1 val m = productMonoid(intAddition, intAddition) 2 val p = listFoldable.foldMap(List(1,2,3,4))(a => (1, a))(m) // p: (Int, Int) = (4, 10) 3 val mean = p._1 / p._2.toDouble // mean: Double = 2.5 R. Casadei Scala and FP October 2, 2015 54 / 56

FP in Scala Common structures in FP Functors: generalizing the map function Before we implemented several different combinator libraries. In each case, we proceeded by writing a small set of primitives and then a number of combinators deﬁned purely in terms of those primitives. We noted some similarities between derived combinators across the libraries we wrote; e.g., we we implemented a map function for each data type, to lift a function taking one argument “into the context of” some data type 1 def map[A,B](ga: Gen[A])(f: A => B): Gen[B] 2 3 def map[A,B](oa: Option[A])(f: A => B): Option[A] We can capture the idea of “a data type that implements map” as a Scala trait 1 trait Functor[F[_]] { 2 def map[A,B](fa: F[A])(f: A => B): F[B] 3 } In category theory, functors can be thought of as homomorphisms (i.e., structure-preserving maps between two algebraic structures) between categories R. Casadei Scala and FP October 2, 2015 55 / 56

Appendix References References I Chiusano, P. and Bjarnason, R. (2014). Functional Programming in Scala. Manning Publications Co., Greenwich, CT, USA, 1st edition. R. Casadei Scala and FP October 2, 2015 56 / 56

Functional Programming in Scala: Notes

More Related Content

What's hot

Viewers also liked

Similar to Functional Programming in Scala: Notes

More from Roberto Casadei

Recently uploaded

Functional Programming in Scala: Notes