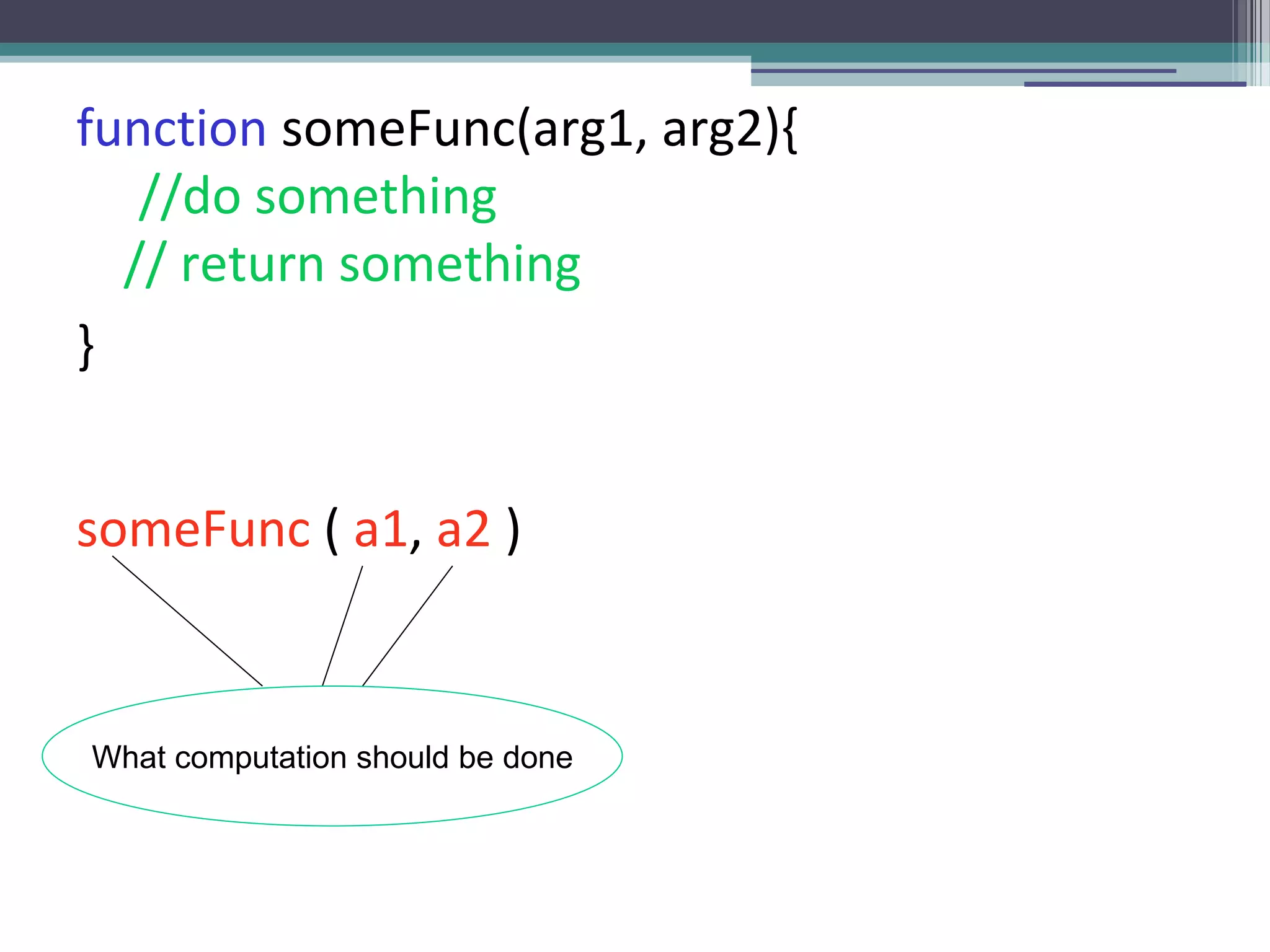
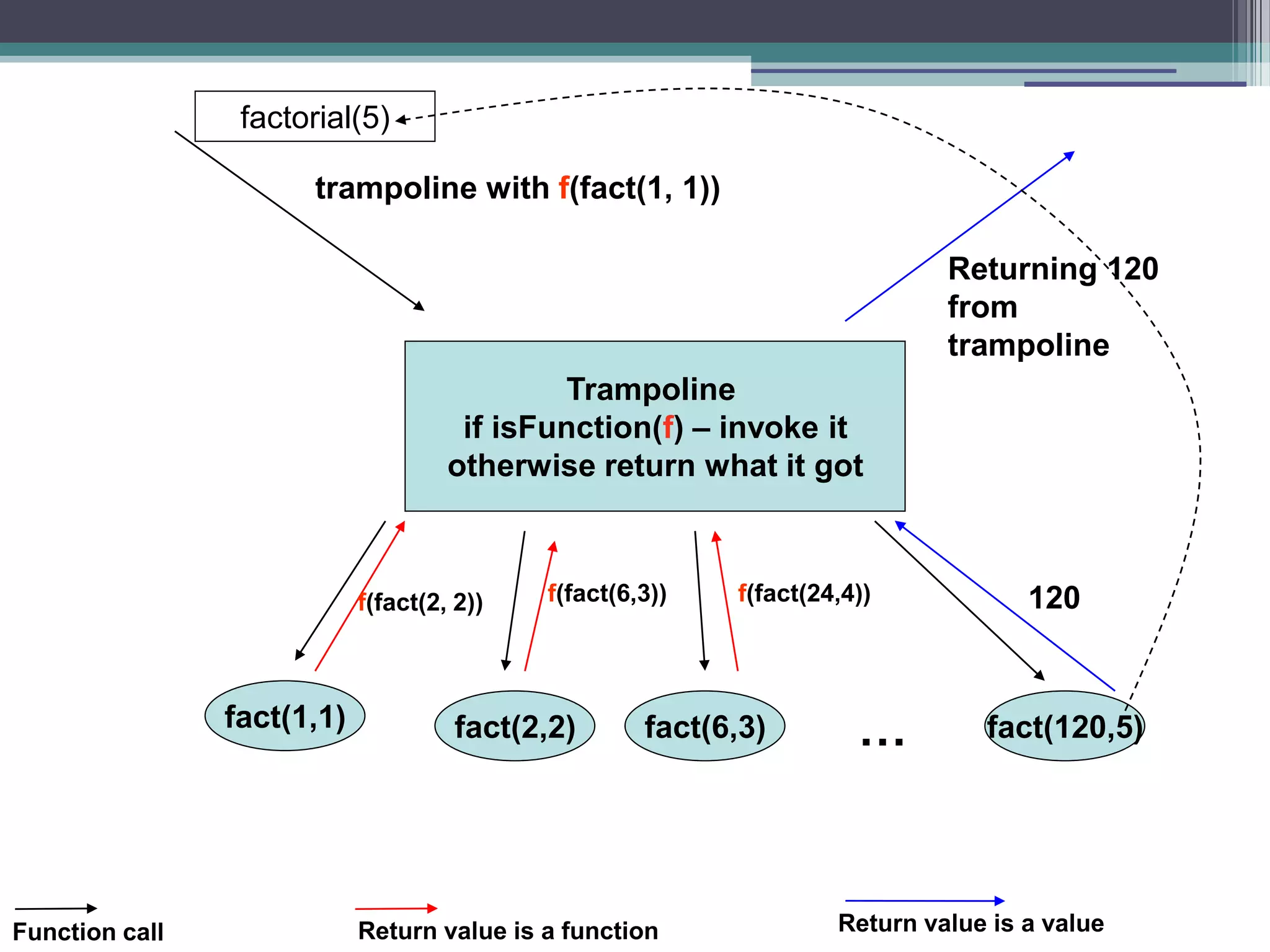
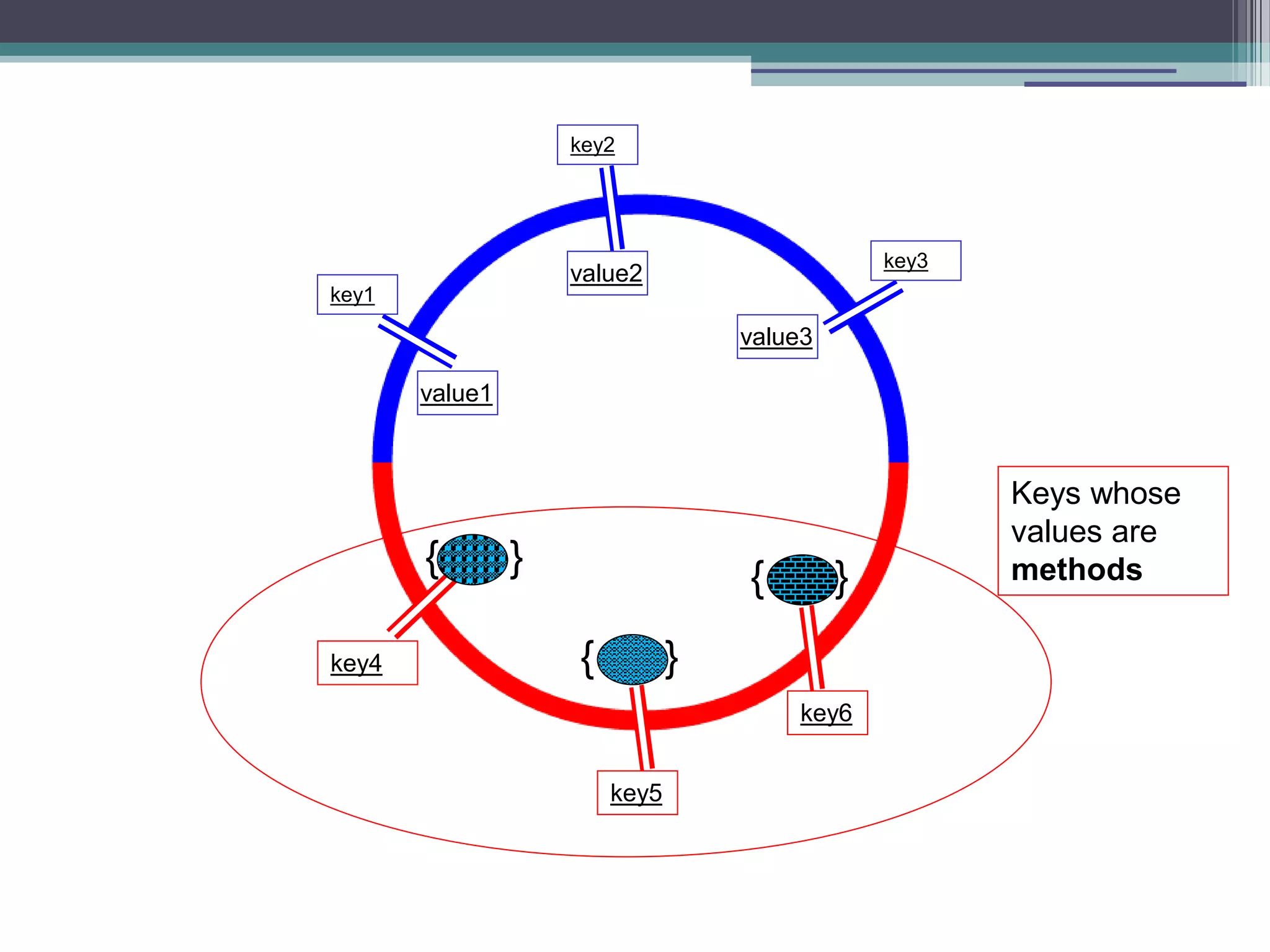
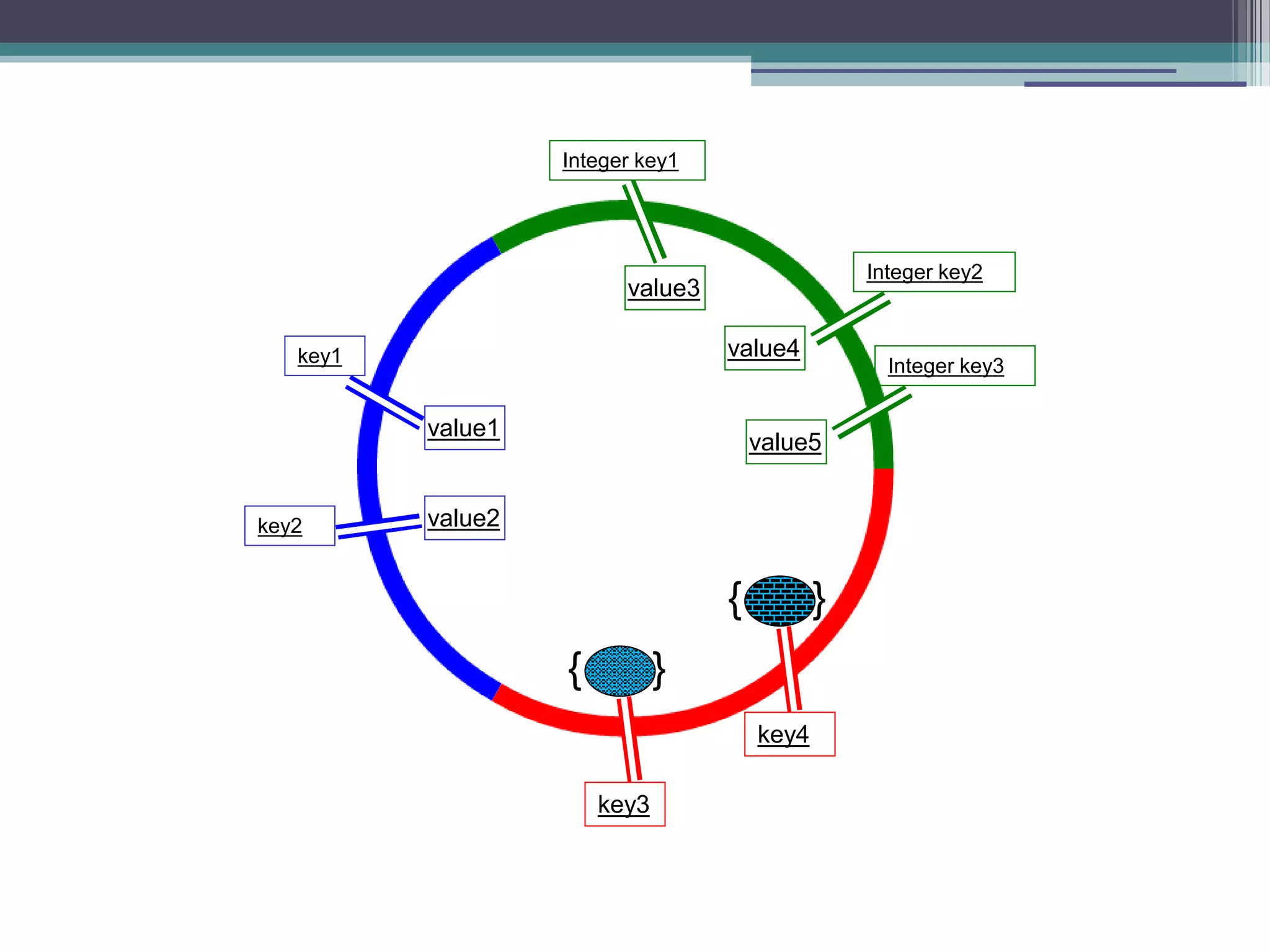
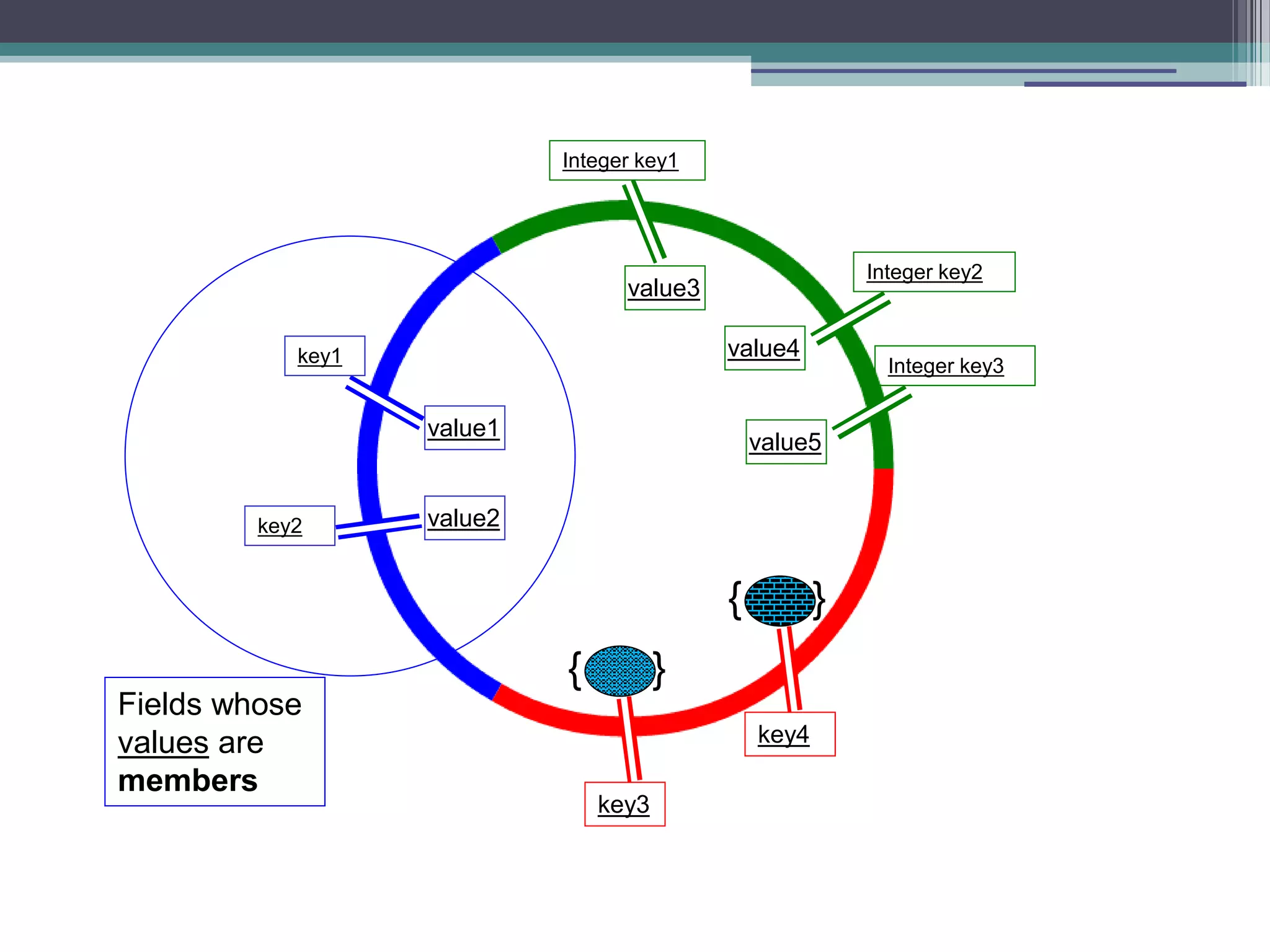
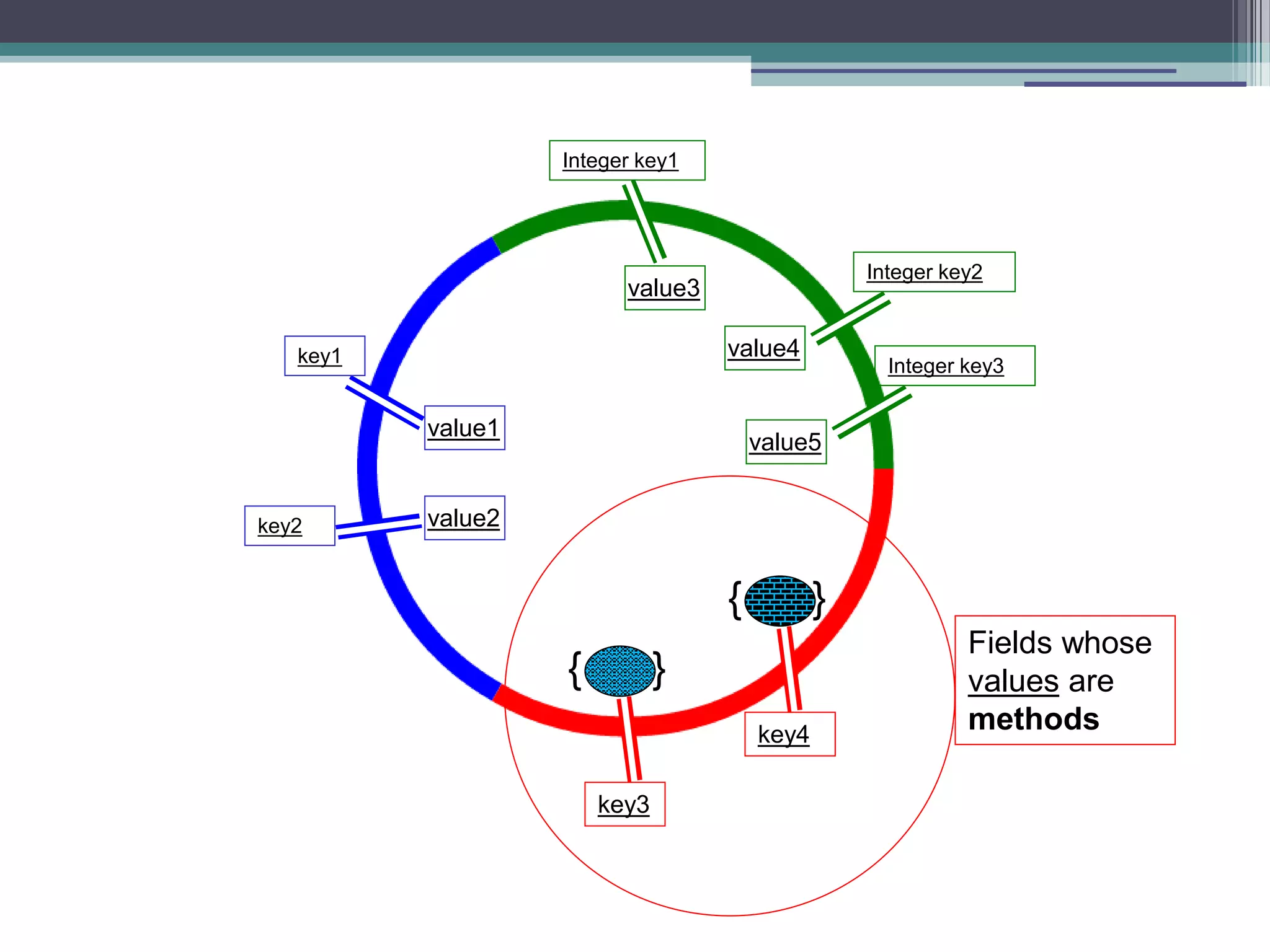
The document discusses a presentation about functional programming in JavaScript. It will cover inner functions and closures, higher order functions, and decomplecting calls patterns. It will discuss how these functional programming concepts can improve performance, provide different perspectives on objects, avoid array mistakes, and allow for recursion. The presentation will provide an overview of functional programming and JavaScript, and then do a deep dive into combining the two paradigms.










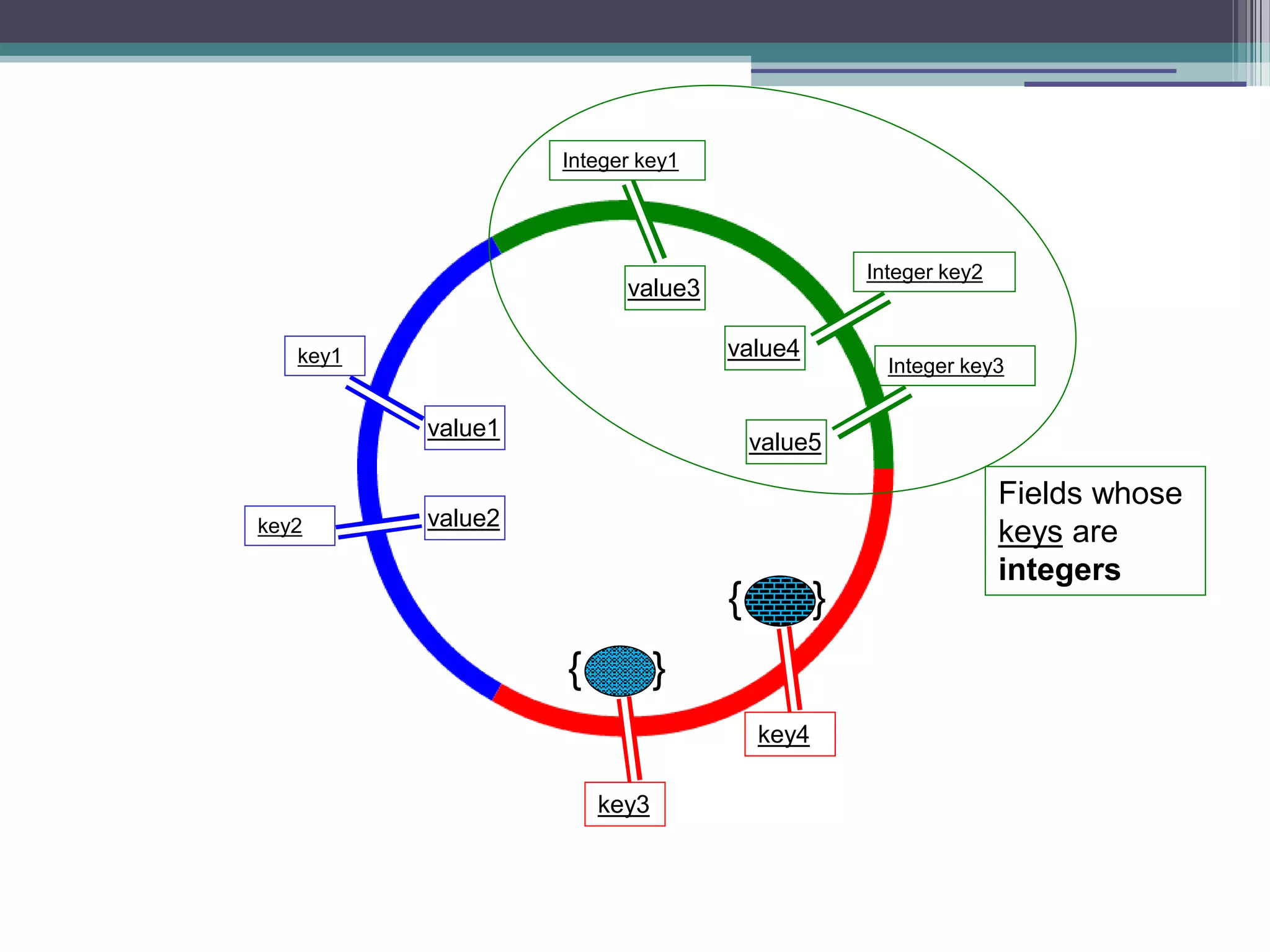

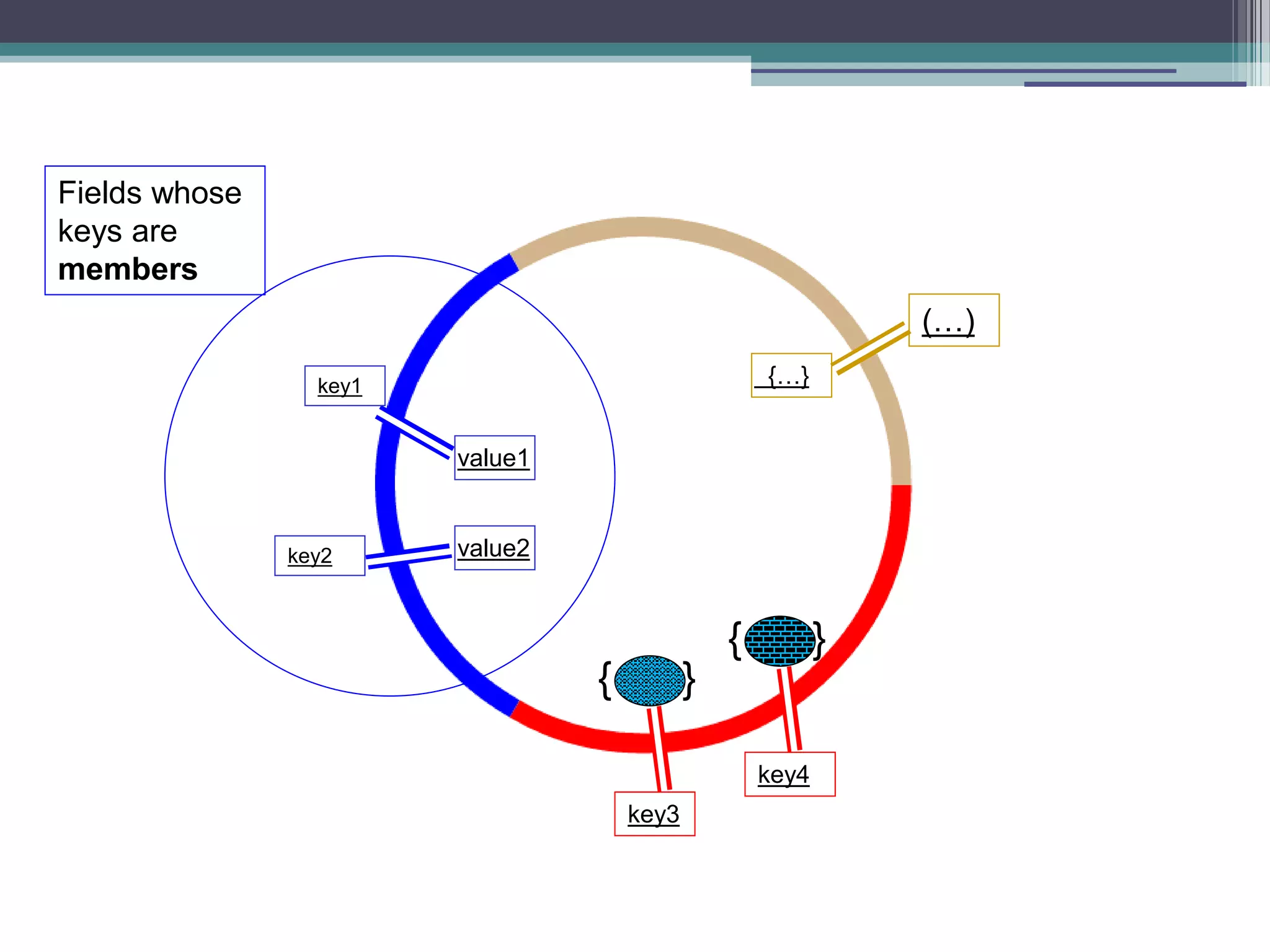
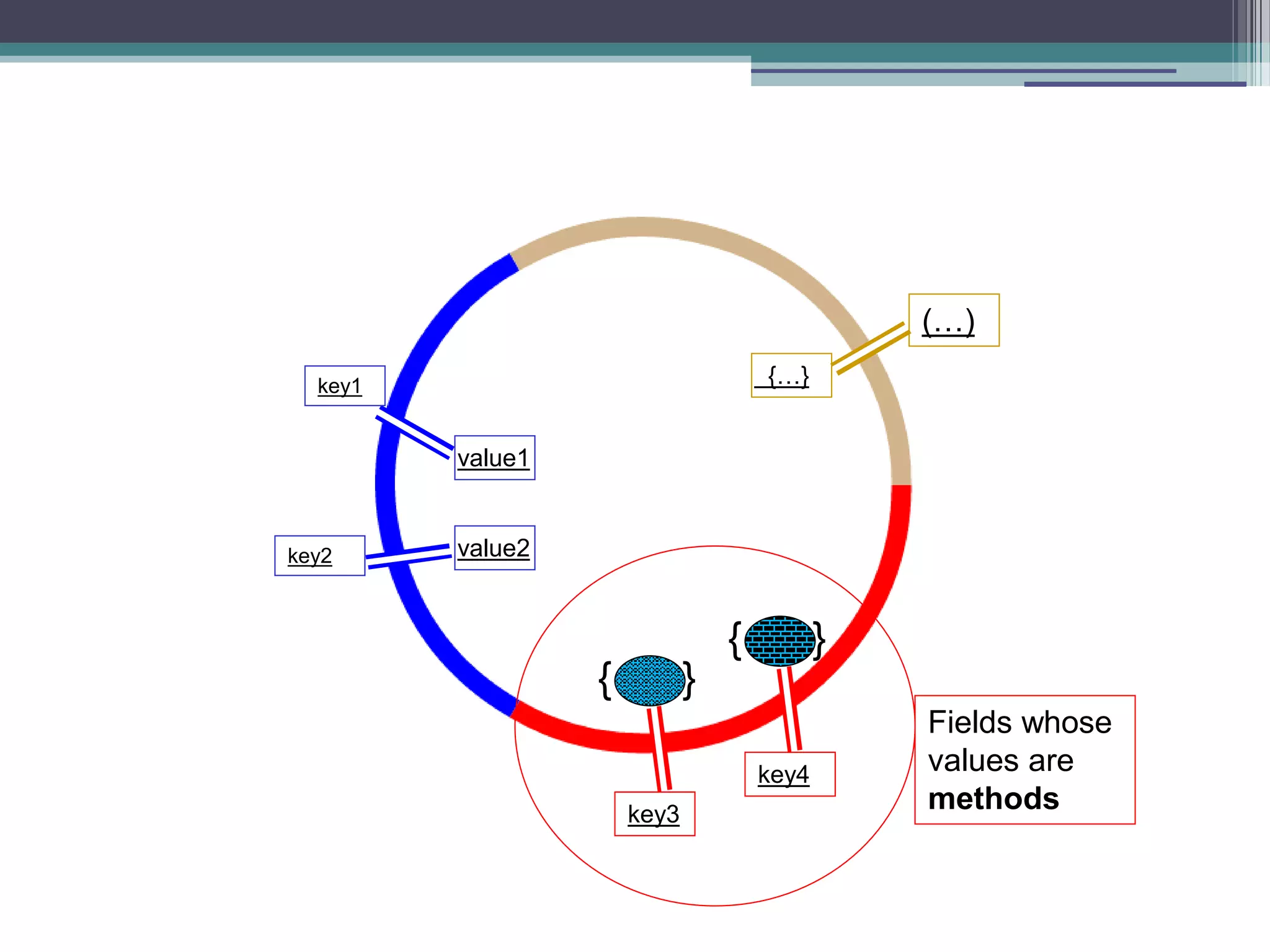
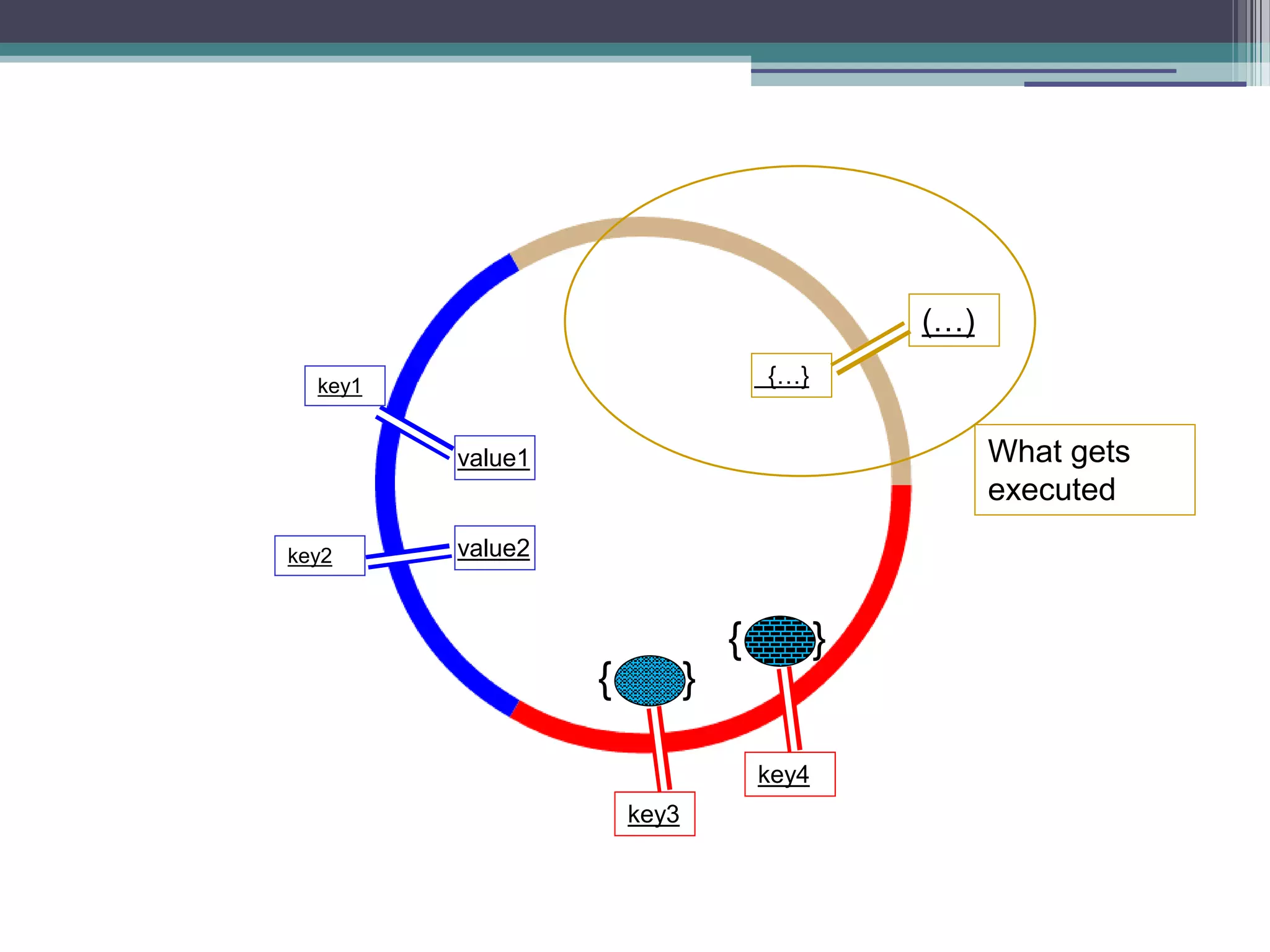



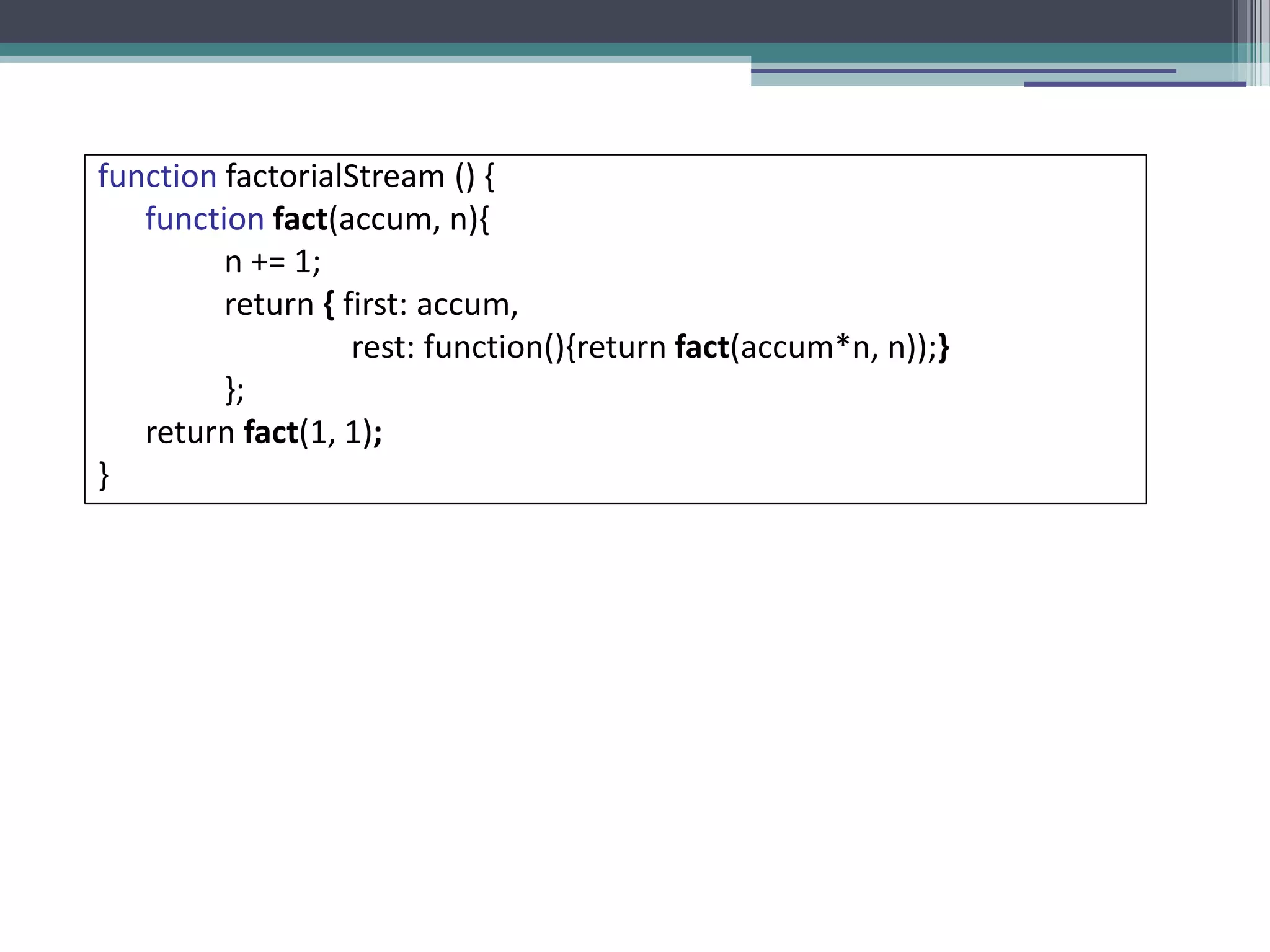
![Fibonacci using inner function function fastFib(n){ var memo = [0,1]; var fib = function(n){ var result = memo[n]; if(result !== undefined) return result; result = fib(n-1) + fib(n-2); memo[n] = result; return result; } return fib(n); } fastFib(10) results in 19 calls to the fib function (time complexity - O(n)) An inner function](https://image.slidesharecdn.com/fpjs-iltechtalks-140909045639-phpapp02/75/Functional-Programming-in-Javascript-IL-Tech-Talks-week-27-2048.jpg)



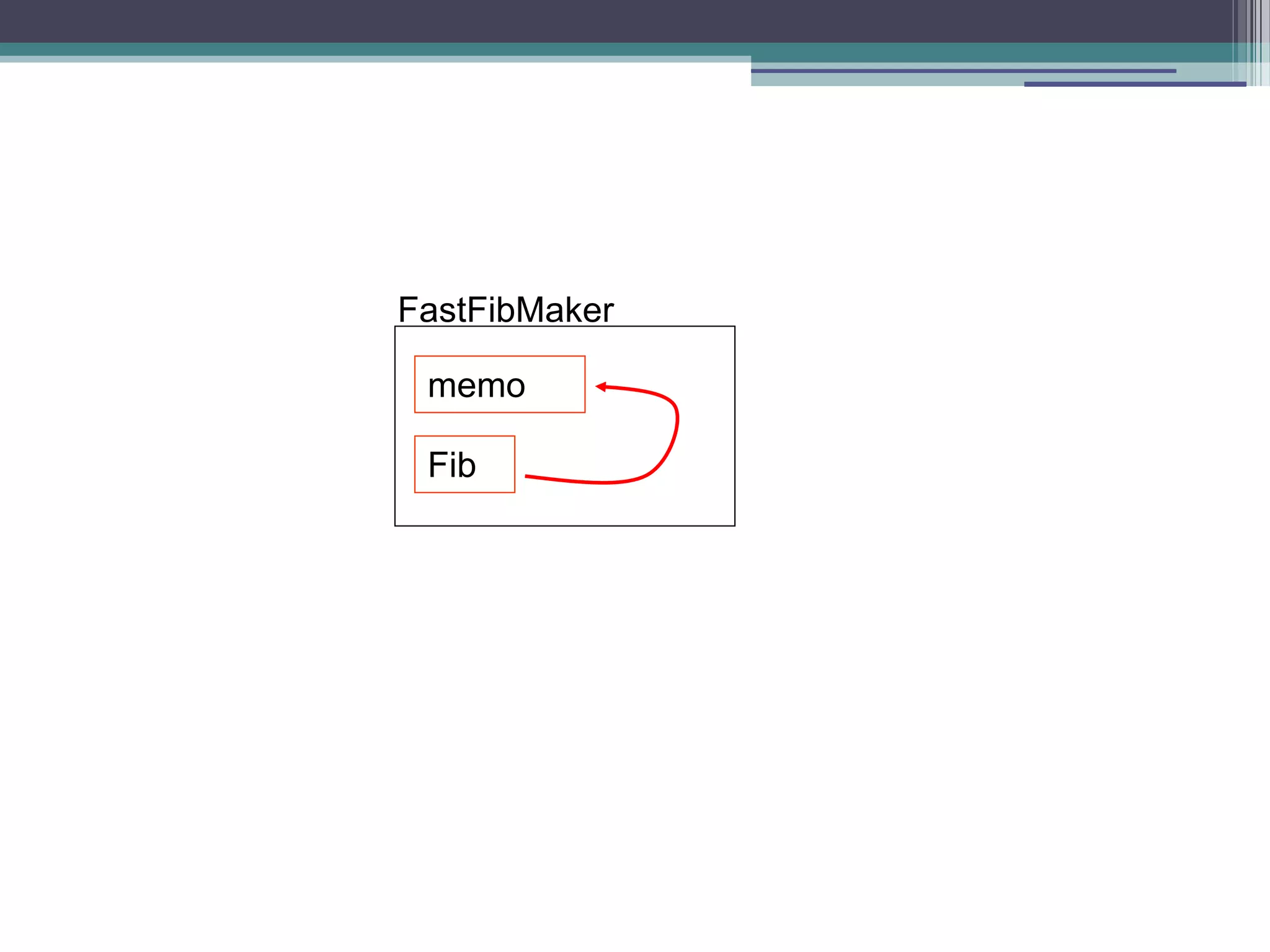
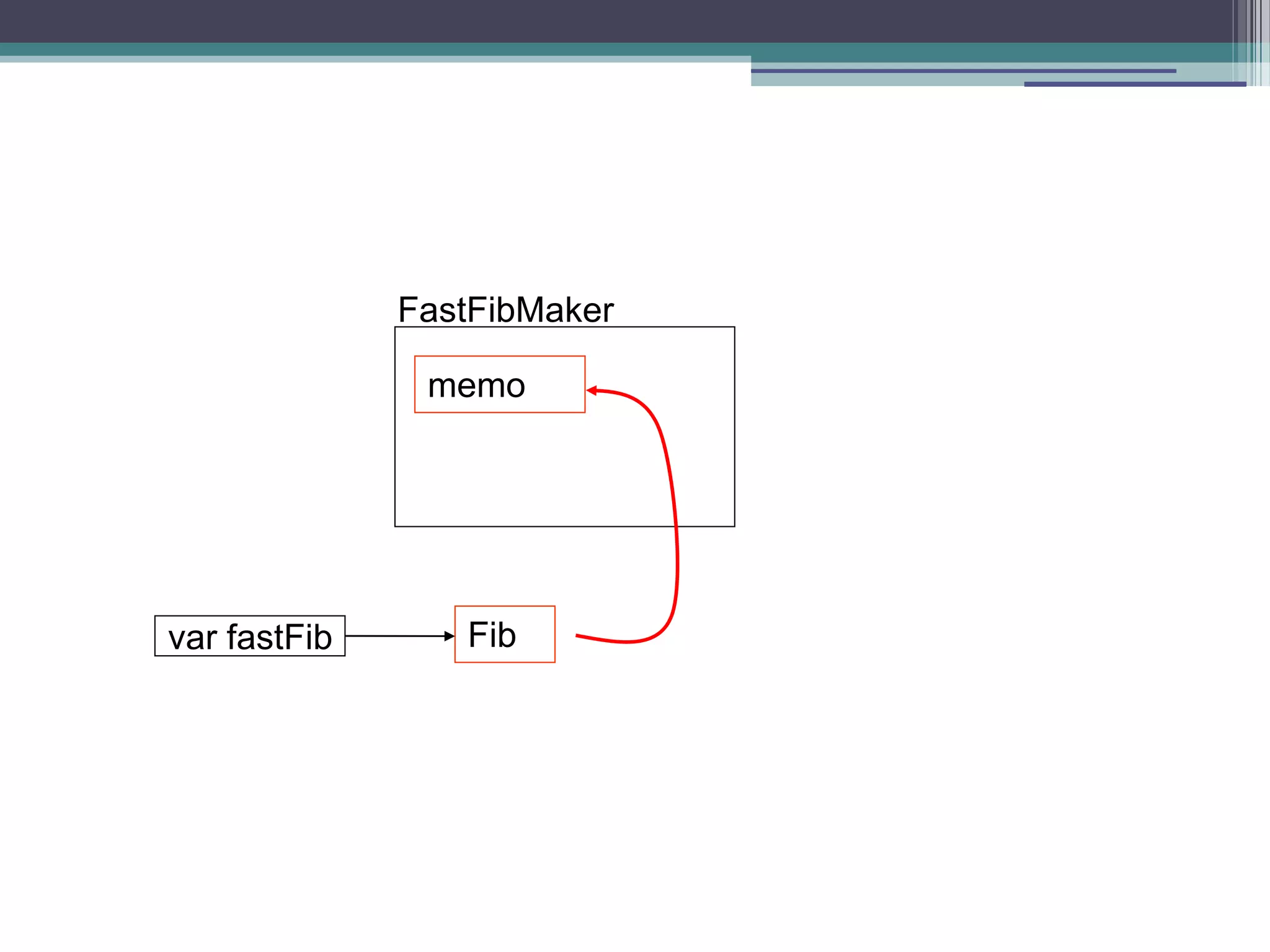
![Fibonacci using closure function fastFibMaker(){ var memo = [0,1]; var fib = function(n){ var result = memo[n]; if (result !== undefined) return result; result = fib(n-1) + fib(n-2); memo[n] = result; return result; } return fib; } var theFib = fastFibMaker(); // returns a function theFib (10); // 19 calls to fib theFib (10); // 1 call to fib](https://image.slidesharecdn.com/fpjs-iltechtalks-140909045639-phpapp02/75/Functional-Programming-in-Javascript-IL-Tech-Talks-week-31-2048.jpg)
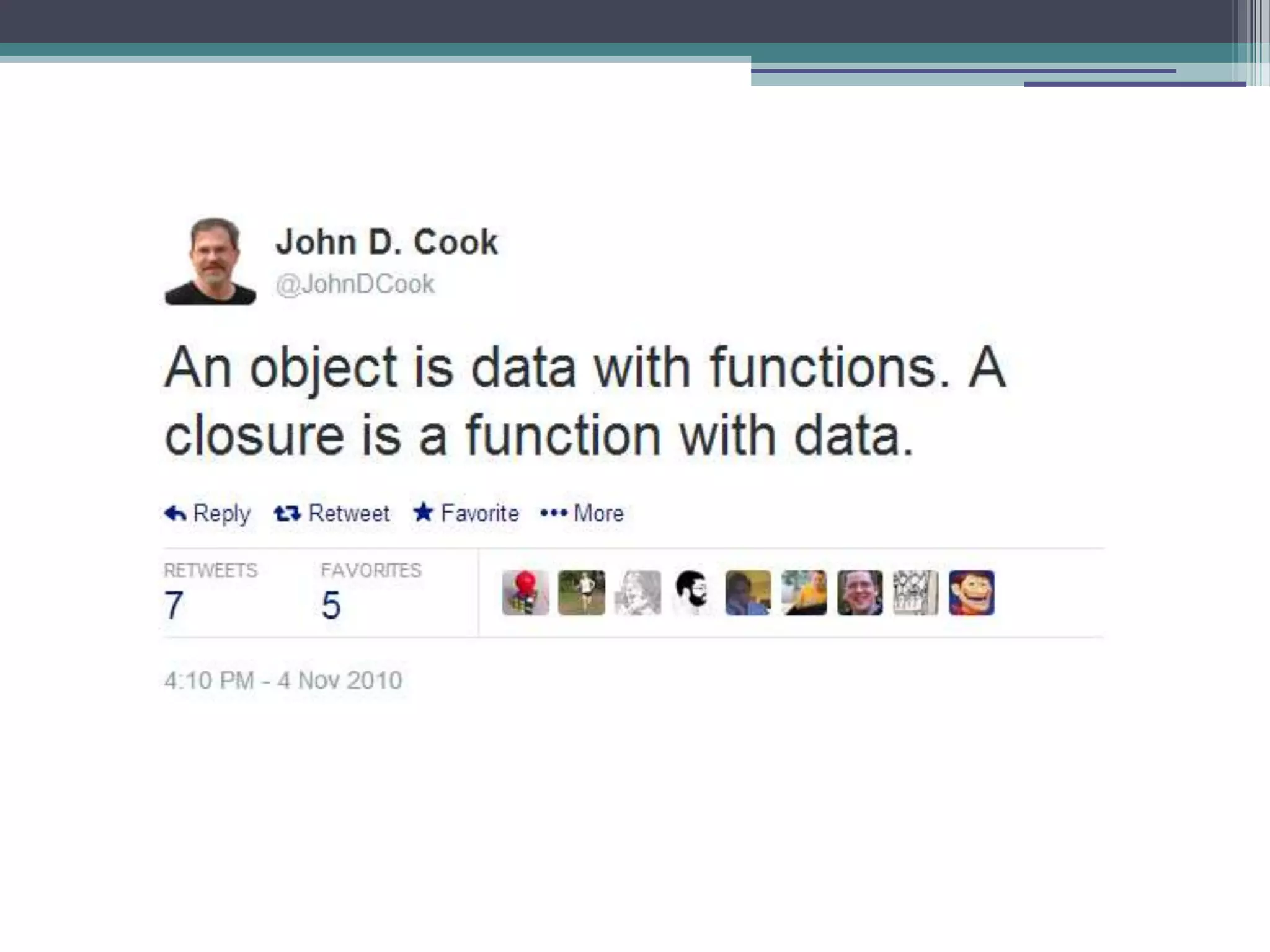


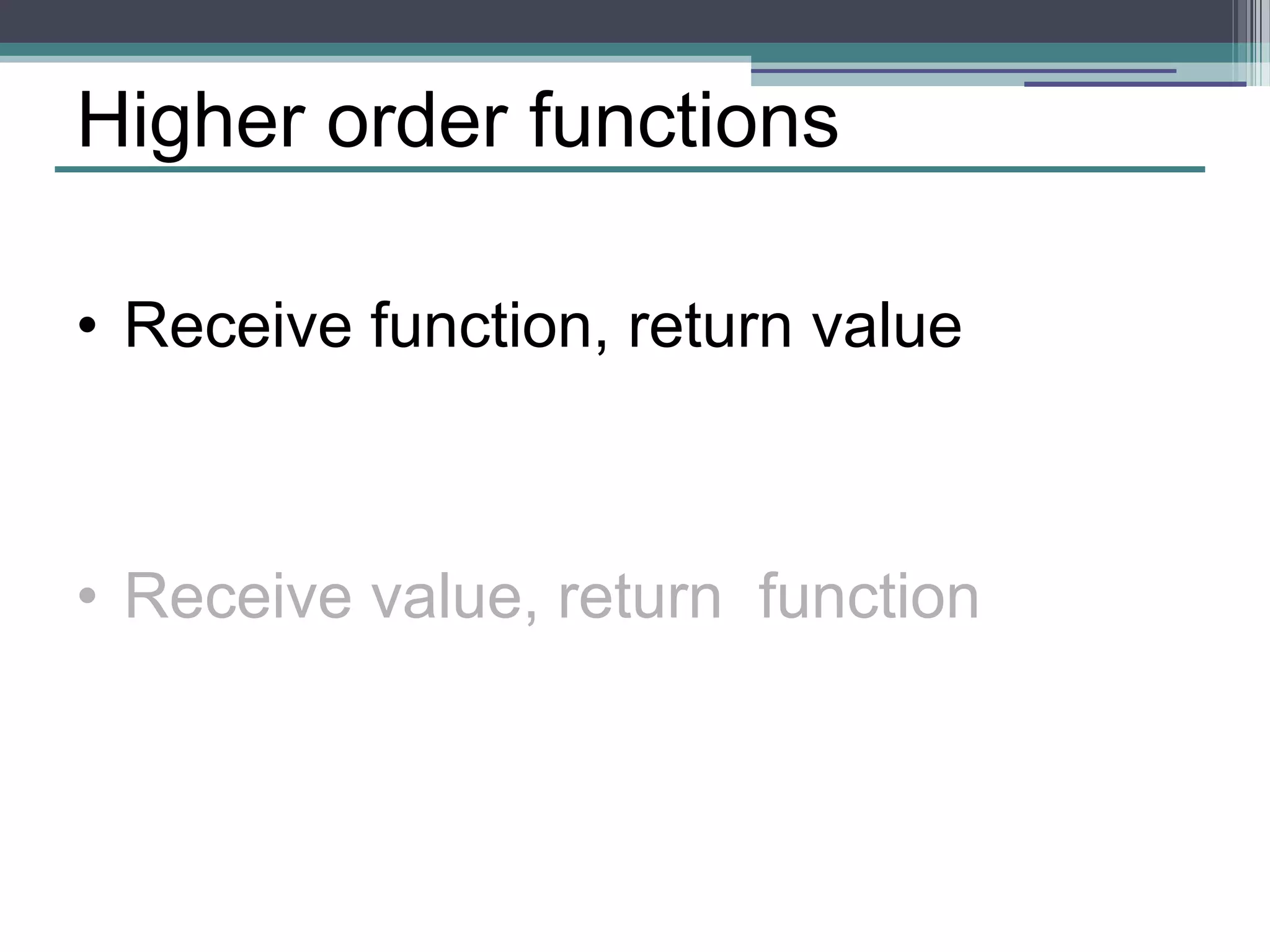



![Building a value out of an array var i, res = seed; for (i=0 ; i<arr.length ;i ++) res = someFunc(res, arr[i]);](https://image.slidesharecdn.com/fpjs-iltechtalks-140909045639-phpapp02/75/Functional-Programming-in-Javascript-IL-Tech-Talks-week-42-2048.jpg)
![Building a value out of an array var i, res = seed; for (i=0 ; i<arr.length ;i ++) res = someFunc(res, arr[i]); This is just the same as res = arr.reduce(someFunc, seed);](https://image.slidesharecdn.com/fpjs-iltechtalks-140909045639-phpapp02/75/Functional-Programming-in-Javascript-IL-Tech-Talks-week-43-2048.jpg)
![Creating an array out of an array var i, res = []; for (i=0 ; i<arr.length ;i ++) res.push(someFunc(arr[i]));](https://image.slidesharecdn.com/fpjs-iltechtalks-140909045639-phpapp02/75/Functional-Programming-in-Javascript-IL-Tech-Talks-week-44-2048.jpg)
![Creating an array out of an array var i, res = []; for (i=0 ; i<arr.length ;i ++) res.push(someFunc(arr[i])); This is just the same as res = arr.map(someFunc);](https://image.slidesharecdn.com/fpjs-iltechtalks-140909045639-phpapp02/75/Functional-Programming-in-Javascript-IL-Tech-Talks-week-45-2048.jpg)
![Selecting items from an array var i, res = []; for (i=0 ; i<arr.length ;i ++){ if (pred(arr[i])) res.push(arr[i]); } This is just the same as res = arr.filter(someFunc);](https://image.slidesharecdn.com/fpjs-iltechtalks-140909045639-phpapp02/75/Functional-Programming-in-Javascript-IL-Tech-Talks-week-46-2048.jpg)
![Selecting items from an array var i, res = []; for (i=0 ; i<arr.length ;i ++){ if (pred(arr[i])) res.push(arr[i]); } This is just the same as res = arr.filter(pred);](https://image.slidesharecdn.com/fpjs-iltechtalks-140909045639-phpapp02/75/Functional-Programming-in-Javascript-IL-Tech-Talks-week-47-2048.jpg)

![And combination of these var i, tmp, res = seed; for(i=0;i<arr.length;i++){ if(pred(arr[i])){ tmp = mapFn(arr[i]); res = redFn(res, tmp); } } var res = arr.filter(pred).map(mapFn).reduce(redFunc);](https://image.slidesharecdn.com/fpjs-iltechtalks-140909045639-phpapp02/75/Functional-Programming-in-Javascript-IL-Tech-Talks-week-49-2048.jpg)
![And combination of these var i, tmp, res = seed; for(i=0;i<arr.length;i++){ if(pred(arr[i])){ tmp = mapFn(arr[i]); res = redFn(res, tmp); } } var res = arr.filter(pred).map(mapFn).reduce(redFn, seed);](https://image.slidesharecdn.com/fpjs-iltechtalks-140909045639-phpapp02/75/Functional-Programming-in-Javascript-IL-Tech-Talks-week-50-2048.jpg)
![Boilerplatting var i, tmp, res = seed; for(i=0;i<arr.length;i++){ if(pred(arr[i])){ tmp = mapFn(arr[i]); res = redFn(res, tmp); } } var res = arr.filter(pred).map(mapFn).reduce(redFn, seed); That’s just boilerplate code !!!](https://image.slidesharecdn.com/fpjs-iltechtalks-140909045639-phpapp02/75/Functional-Programming-in-Javascript-IL-Tech-Talks-week-51-2048.jpg)
![What can bite you here? var i, tmp, res = seed; for(i=0;i<arr.length;i++){ if(pred(arr[i])){ tmp = mapFn(arr[i]); res = redFn(res, tmp); } } What will happen if you copy & paste the loop’s code without copying the declaration of i ? var res = arr.filter(pred).map(mapFn).reduce(redFn, seed);](https://image.slidesharecdn.com/fpjs-iltechtalks-140909045639-phpapp02/75/Functional-Programming-in-Javascript-IL-Tech-Talks-week-52-2048.jpg)
![What can bite you here? var i, tmp, res = seed; for(i=0;i<arr.length;i++){ if(pred(arr[i])){ tmp = mapFn(arr[i]); res = redFn(res, tmp); } } Once in a while you’ll have an off by one error var res = arr.filter(pred).map(mapFn).reduce(redFn, seed);](https://image.slidesharecdn.com/fpjs-iltechtalks-140909045639-phpapp02/75/Functional-Programming-in-Javascript-IL-Tech-Talks-week-53-2048.jpg)
![What can bite you here? var i, tmp, res = seed; for(i=0;i<arr.length;i++){ if(pred(arr[i])){ tmp = mapFn(arr[i]); res = redFn(res, tmp); } } What if there’s a hole ? var res = arr.filter(pred).map(mapFn).reduce(redFn, seed);](https://image.slidesharecdn.com/fpjs-iltechtalks-140909045639-phpapp02/75/Functional-Programming-in-Javascript-IL-Tech-Talks-week-55-2048.jpg)

![Same same but different arr = [1,2,3] arr[4] = 4 var res = 0; for(var i=0;i<arr.length;i++){ res += arr[i]; } arr.reduce(add, 0) NaN 10](https://image.slidesharecdn.com/fpjs-iltechtalks-140909045639-phpapp02/75/Functional-Programming-in-Javascript-IL-Tech-Talks-week-57-2048.jpg)


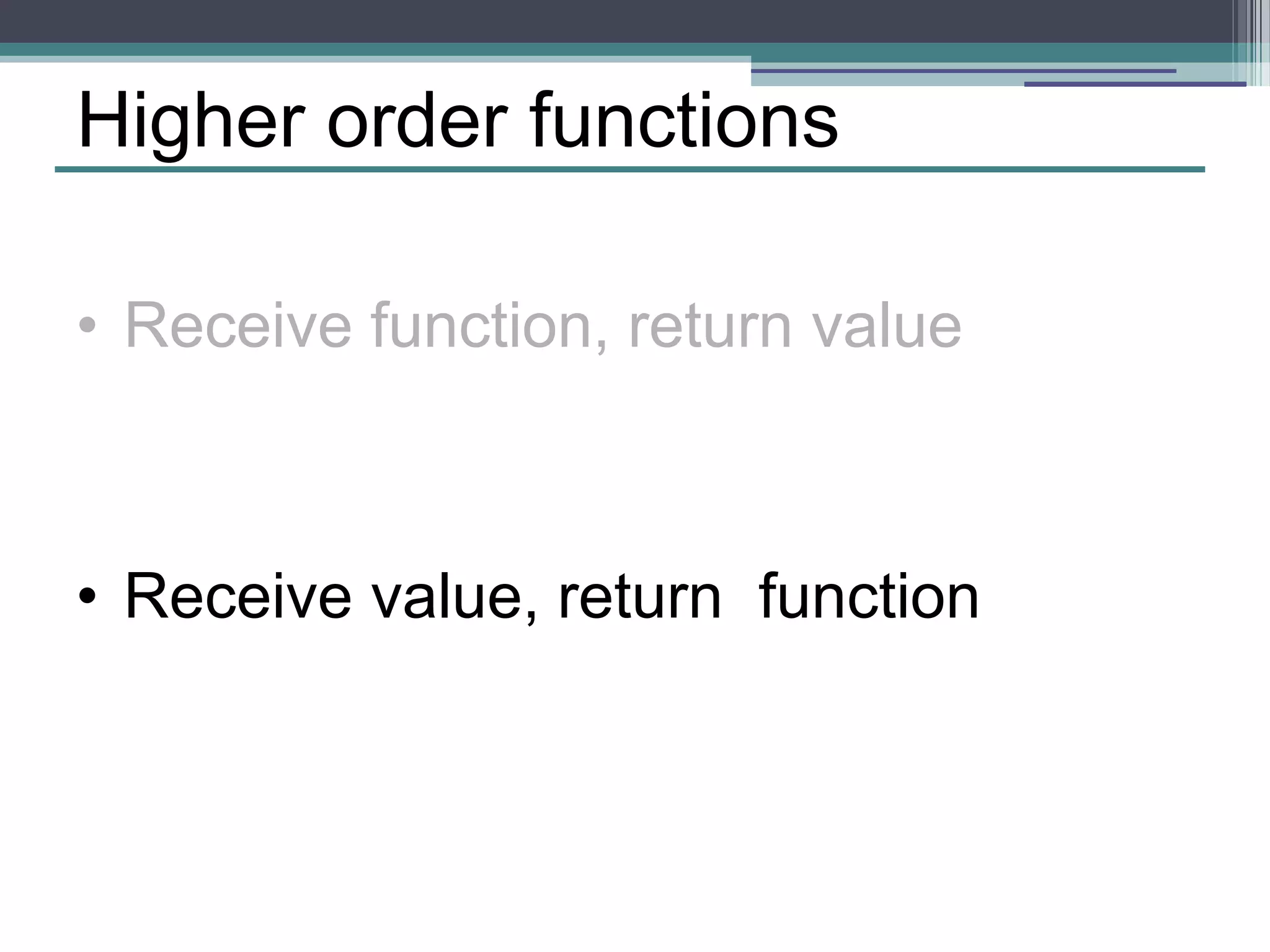



![Fan out function fanOutMaker(/* fns*/){ var fns = arguments; return function(/* arguments */){ var res = []; for (var i=0,l=fns.length;i<l;i++){ res.push(fns[i].apply(null, arguments)); } return res; } }](https://image.slidesharecdn.com/fpjs-iltechtalks-140909045639-phpapp02/75/Functional-Programming-in-Javascript-IL-Tech-Talks-week-65-2048.jpg)
![Fan out function fanOutMaker(/* fns*/){ var fns = arguments; return function(/* arguments */){ var res = []; for (var i=0,l=fns.length;i<l;i++){ res.push(fns[i].apply(null, arguments)); } return res; } } Not the same](https://image.slidesharecdn.com/fpjs-iltechtalks-140909045639-phpapp02/75/Functional-Programming-in-Javascript-IL-Tech-Talks-week-66-2048.jpg)
![Fan out function fanOutMaker(/* fns*/){ var fns = arguments; return function(/* arguments */){ var res = []; for (var i=0,l=fns.length;i<l;i++){ res.push(fns[i].apply(null, arguments)); } return res; } } Call each of the closured fns with current argument](https://image.slidesharecdn.com/fpjs-iltechtalks-140909045639-phpapp02/75/Functional-Programming-in-Javascript-IL-Tech-Talks-week-67-2048.jpg)