Functional Design Patterns (DevTernity 2018)

Functional Design Patterns @ScottWlaschin fsharpforfunandprofit.com DevTernity 2018 Edition

This talk A whirlwind tour of many sights Don't worry if you don't understand everything

Me I've been programming a long time

I used to be a normal programmer...

And then I was introduced to some functional programmers…

https://www.flickr.com/photos/37511372@N08/5488671752/ Haskell programmers F#/OCaml programmers Visual Basic programmers Lisp programmers

Now I can say this with a straight face: “A monad is just a monoid in the category of endofunctors, what’s the problem?”

• Single Responsibility Principle • Open/Closed principle • Dependency Inversion Principle • Interface Segregation Principle • Factory pattern • Strategy pattern • Decorator pattern • Visitor pattern OO pattern/principle

• Single Responsibility Principle • Open/Closed principle • Dependency Inversion Principle • Interface Segregation Principle • Factory pattern • Strategy pattern • Decorator pattern • Visitor pattern OO pattern/principle Borg response

• Single Responsibility Principle • Open/Closed principle • Dependency Inversion Principle • Interface Segregation Principle • Factory pattern • Strategy pattern • Decorator pattern • Visitor pattern • Functions • Functions • Functions, also • Functions • You will be assimilated! • Functions again • Functions • Resistance is futile! OO pattern/principle FP equivalent Seriously, FP patterns are different

Overview • 3 Core Principles of FP design • Pattern 1: Functions as parameters • Pattern 2: Composing multi-parameter functions • Pattern 3: "bind" • Pattern 4: "map" • Pattern 5: Monoids

THREE CORE PRINCIPLES OF FUNCTIONAL PROGRAMMING There are more...

Core principles of FP Function Types are not classes Functions are things Composition everywhere

Core principle: Functions are things Function

The Tunnel of Transformation Function apple -> banana A function is a standalone thing, not attached to a class

let z = 1 1 let addOne x = x + 1 int-> int

int->(int->int)int int->int Function as output

intInt ->int Function as input (int->int)->int

int int Function as parameterint->int int->int

Core principle: Composition everywhere

Function 1 apple -> banana Function 2 banana -> cherry

>> Function 1 apple -> banana Function 2 banana -> cherry

New Function apple -> cherry Can't tell it was built from smaller functions! Where did the banana go?

Composition works at all scales

Low-level operation ToUpper stringstring

Low-level operation Service AddressValidator For those under 30... Validation Result Address Low-level operation Low-level operation a "service" is just like a microservice but without the "micro" in front

Service Use-case UpdateProfileData ChangeProfile Result ChangeProfile Request Service Service

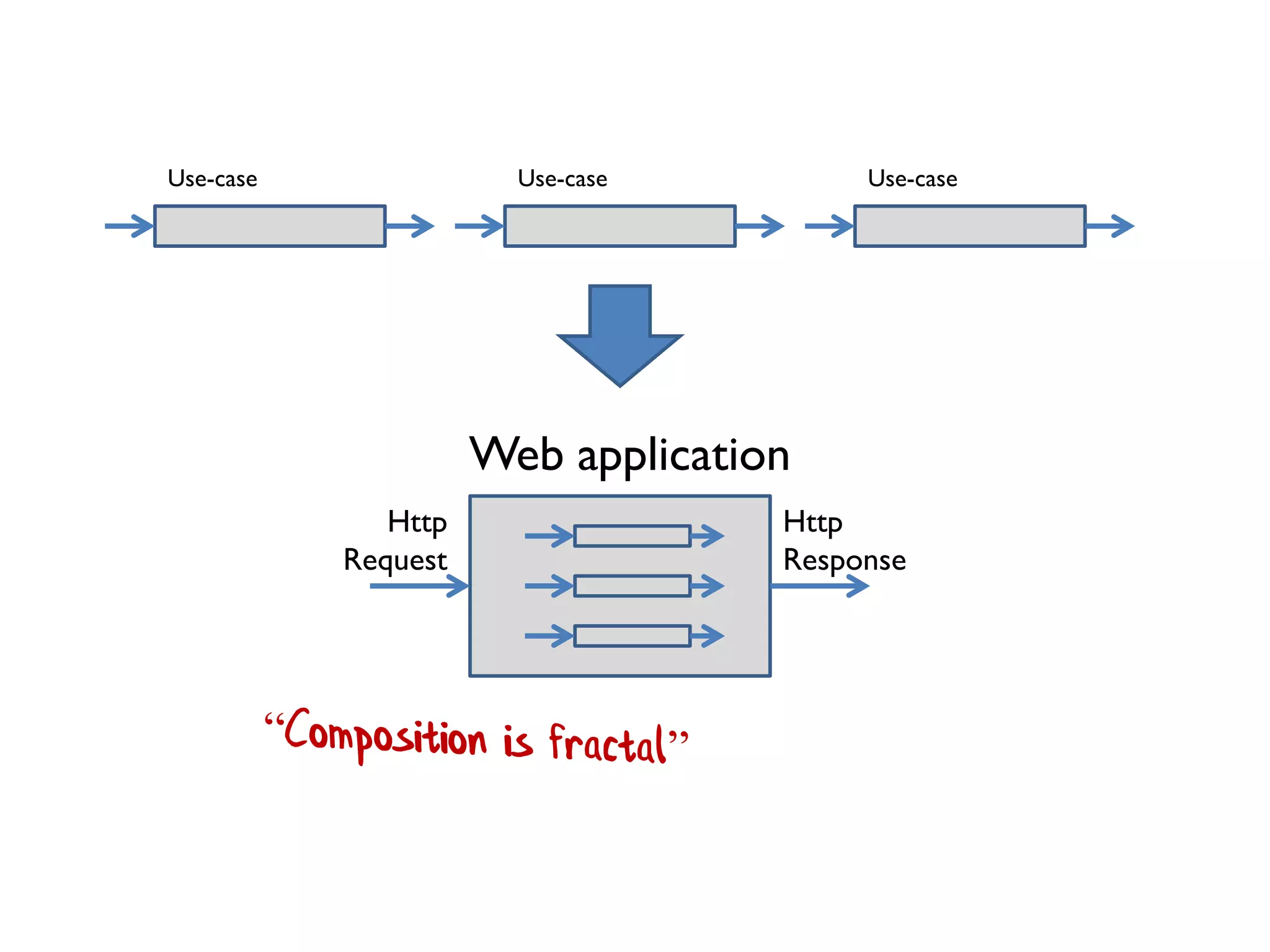
Use-case Web application Http Response Http Request Use-case Use-case

Core principle: Types are not classes So, what is a type then?

Set of valid inputs Set of valid outputs Function A type is a just a name for a set of things

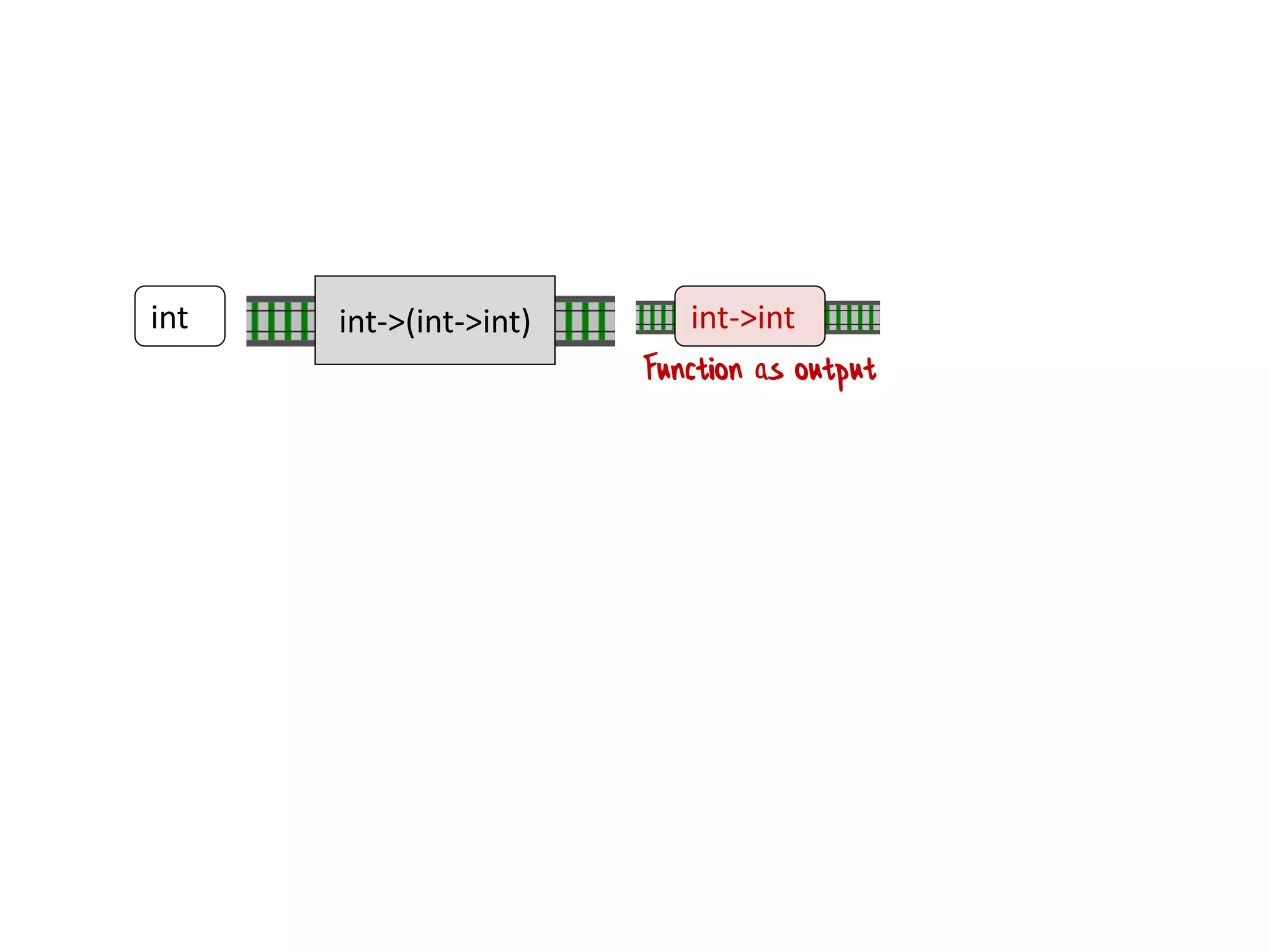
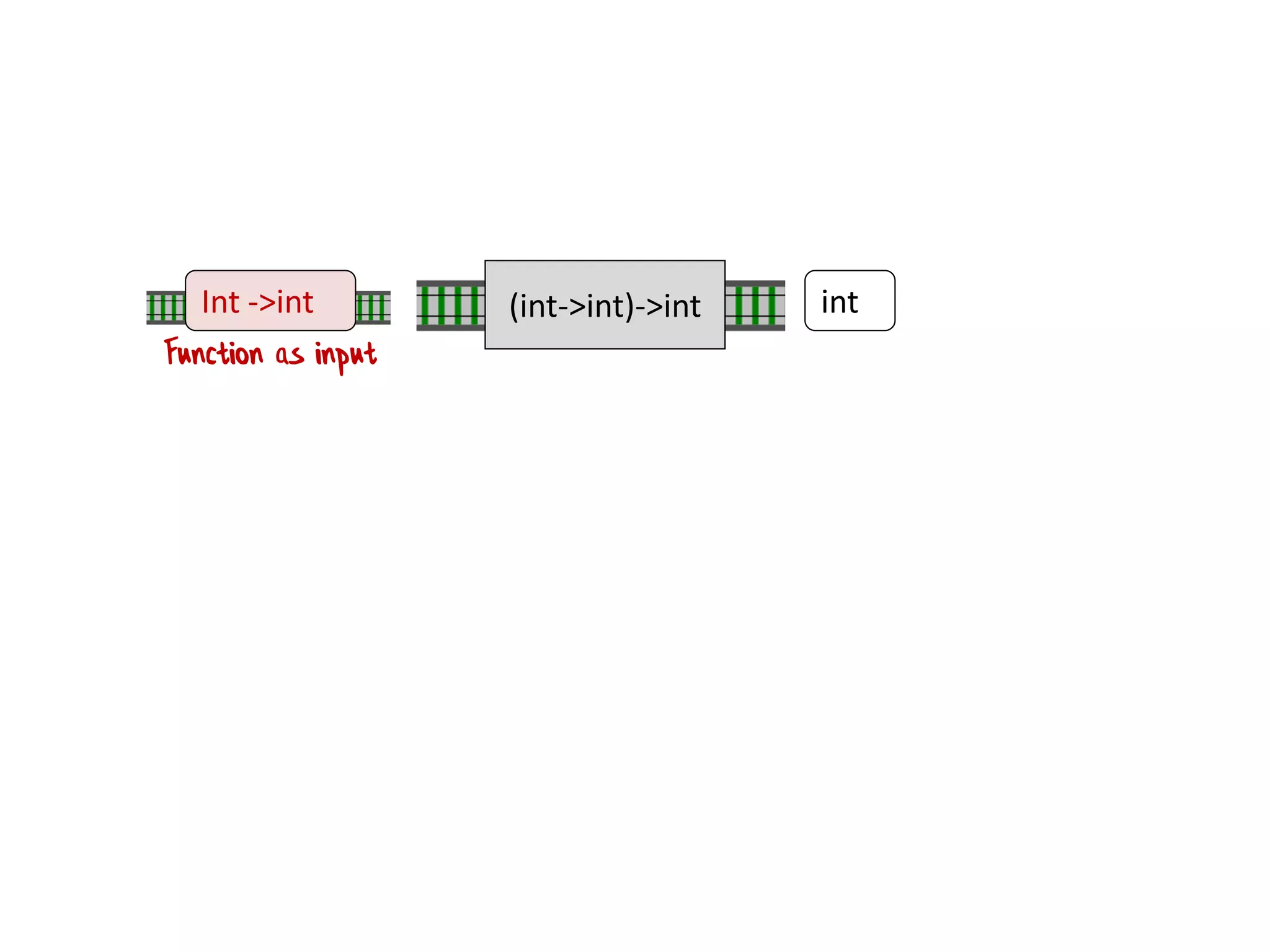
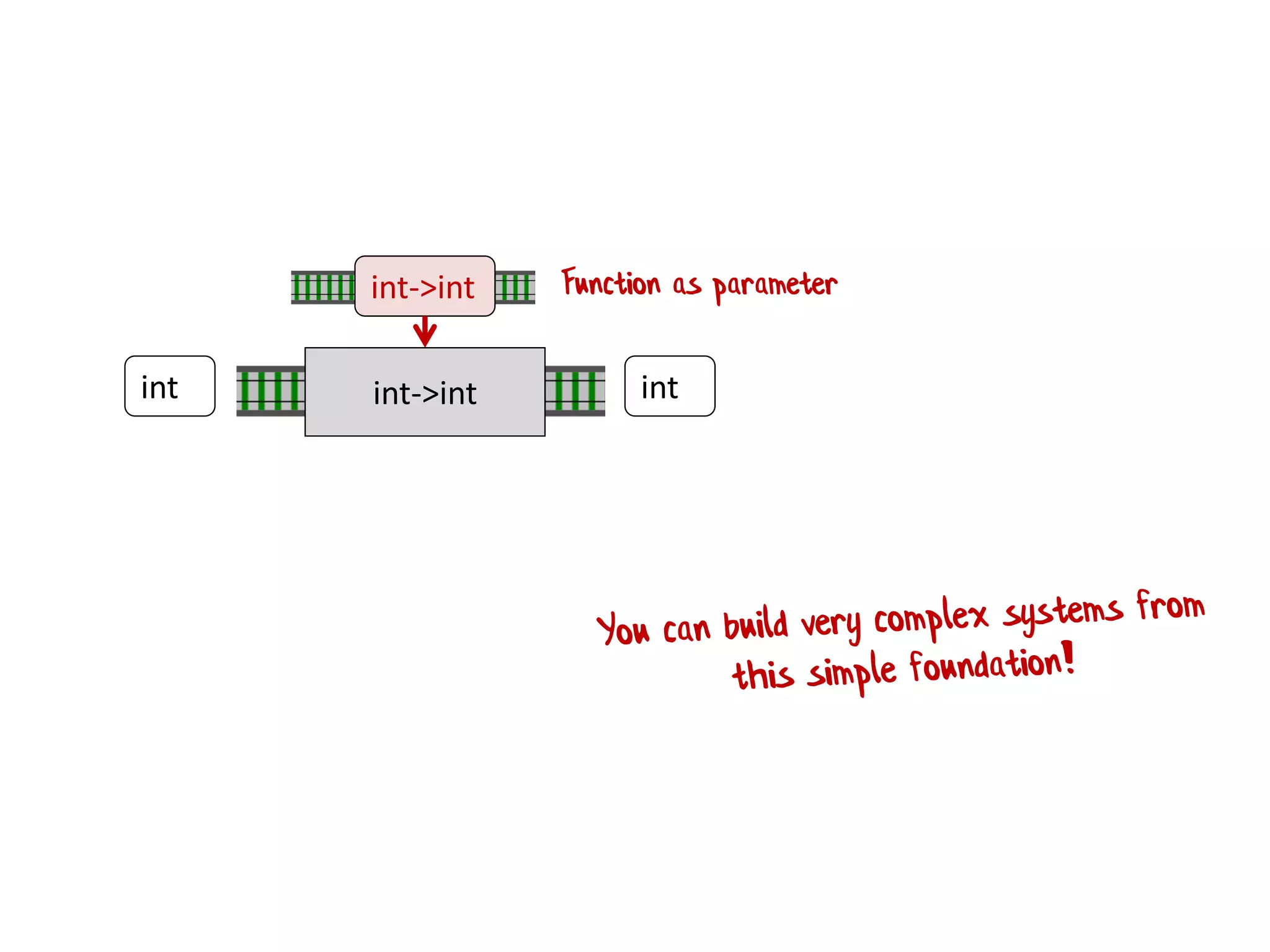
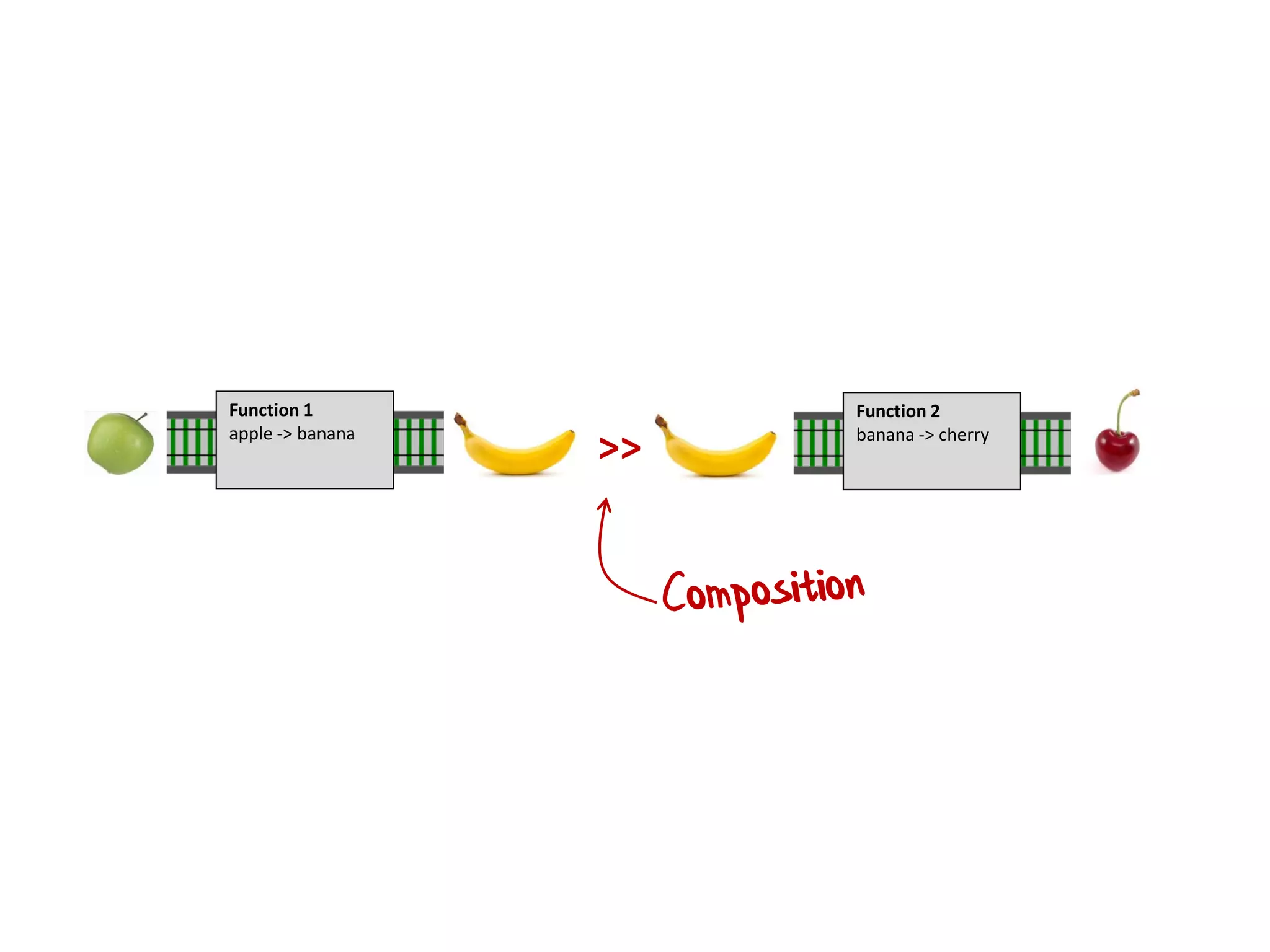
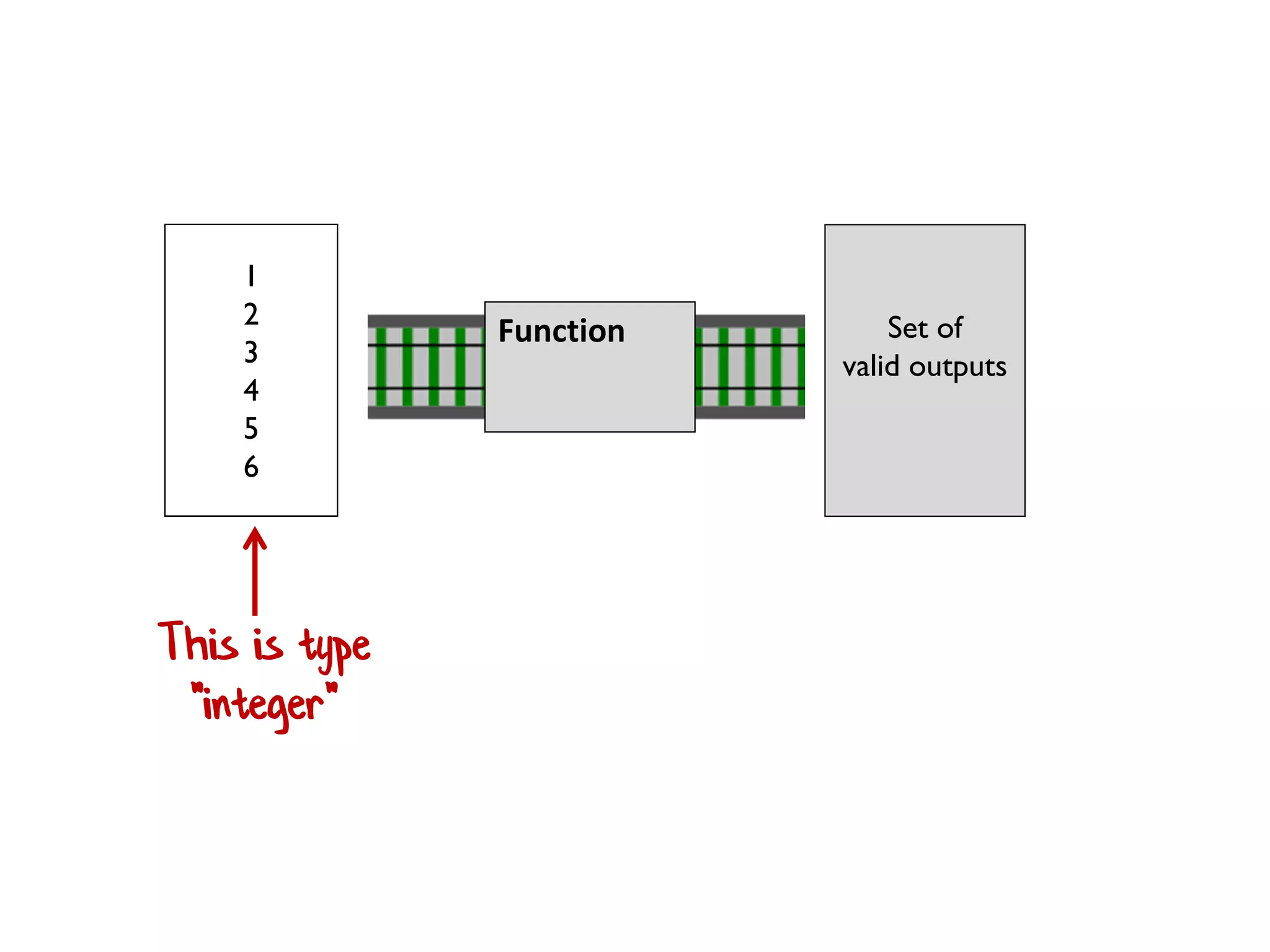
Set of valid inputs Set of valid outputs Function 1 2 3 4 5 6 This is type "integer"

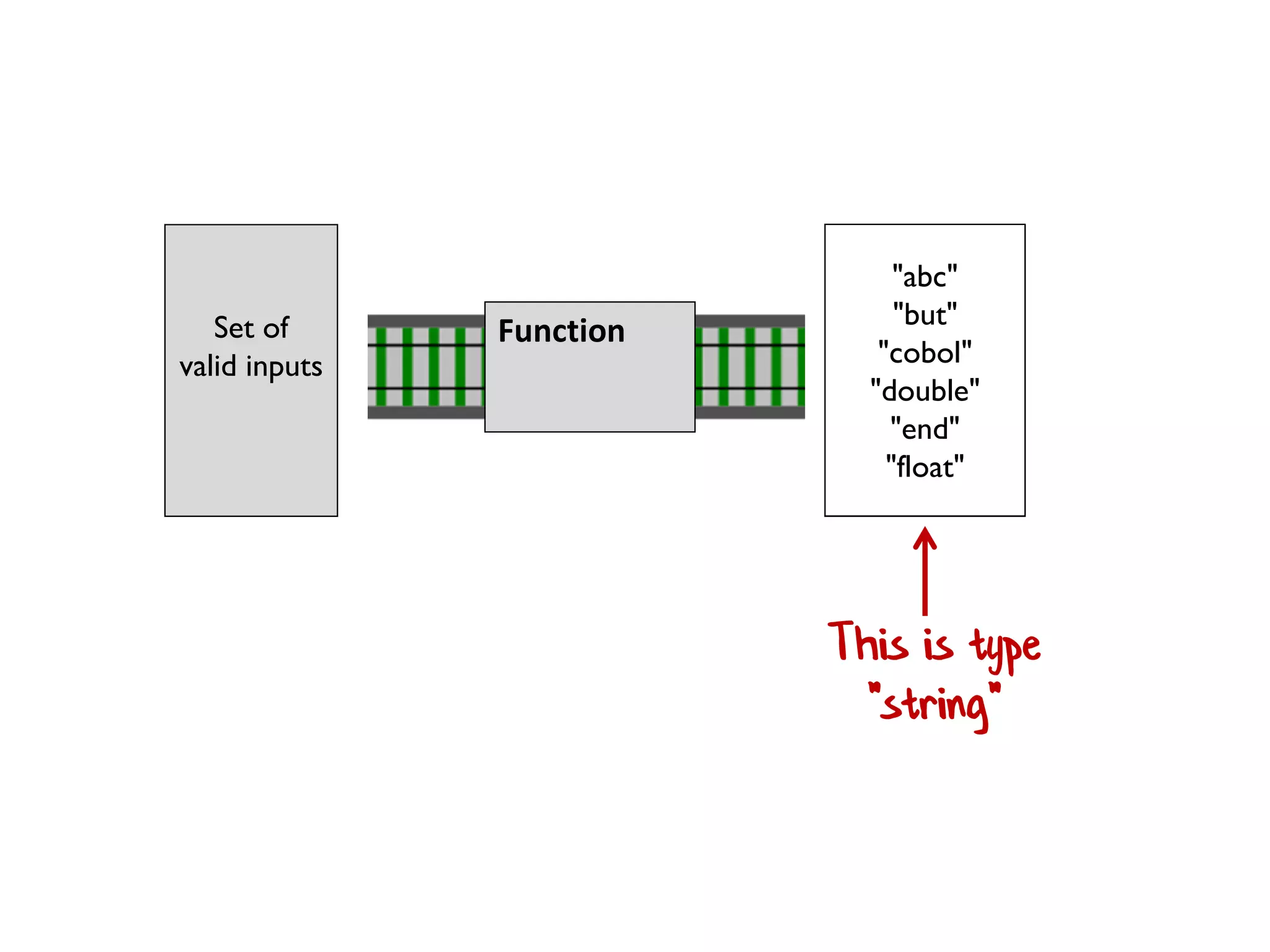
Set of valid inputs Set of valid outputs Function This is type "string" "abc" "but" "cobol" "double" "end" "float"

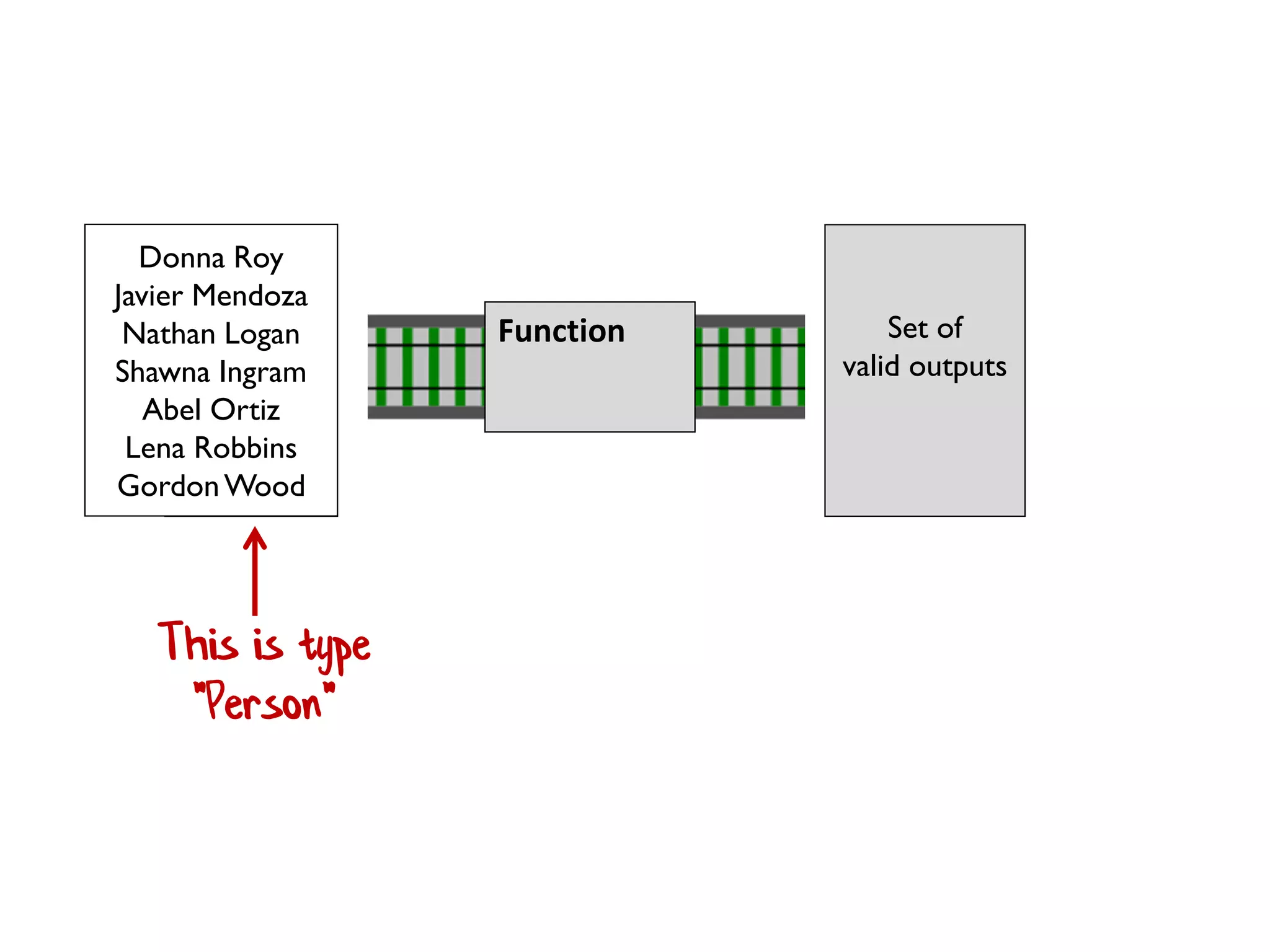
Set of valid inputs Set of valid outputs Function This is type "Person" Donna Roy Javier Mendoza Nathan Logan Shawna Ingram Abel Ortiz Lena Robbins GordonWood

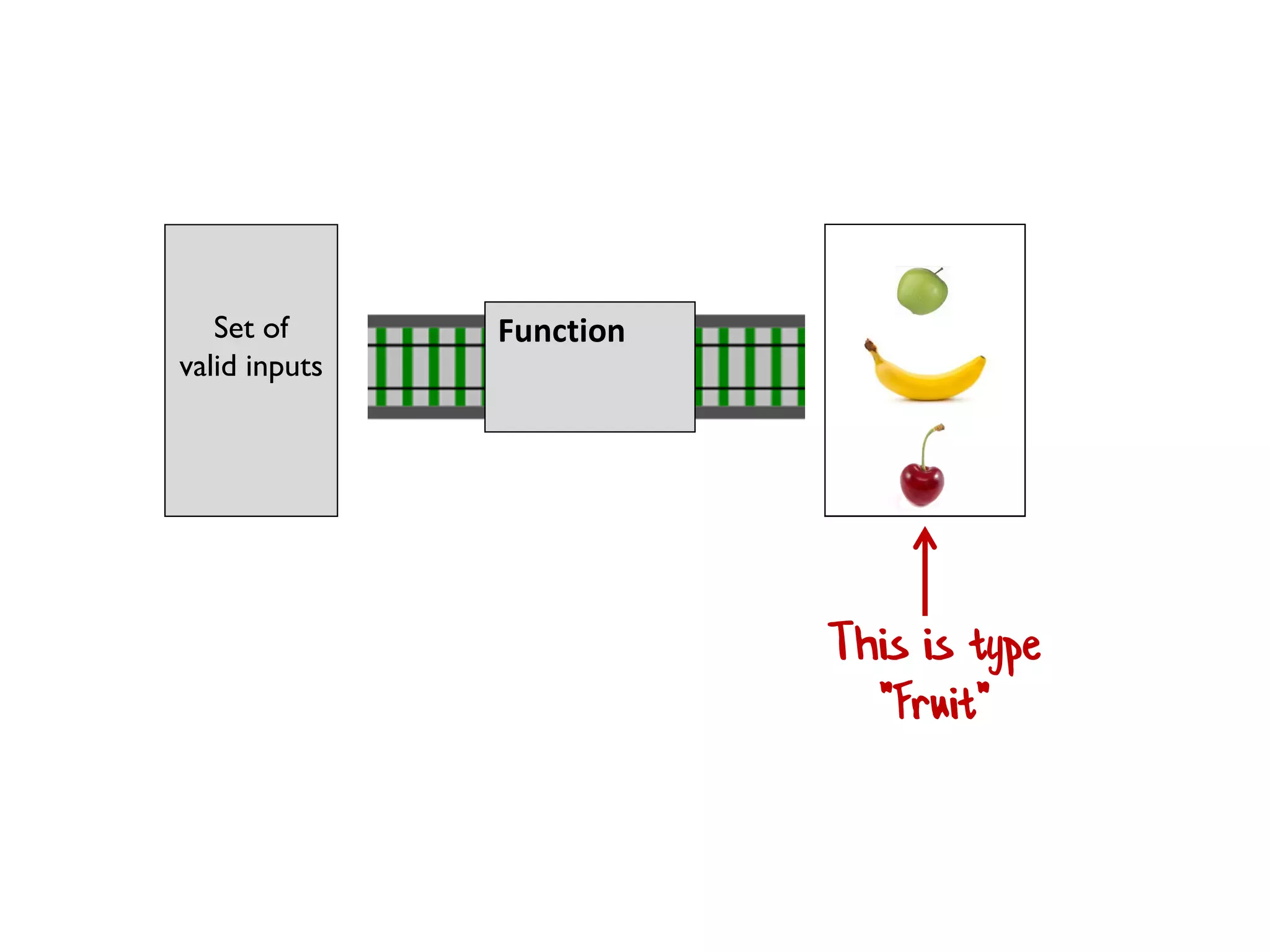
Set of valid inputs Set of valid outputs Function This is type "Fruit"

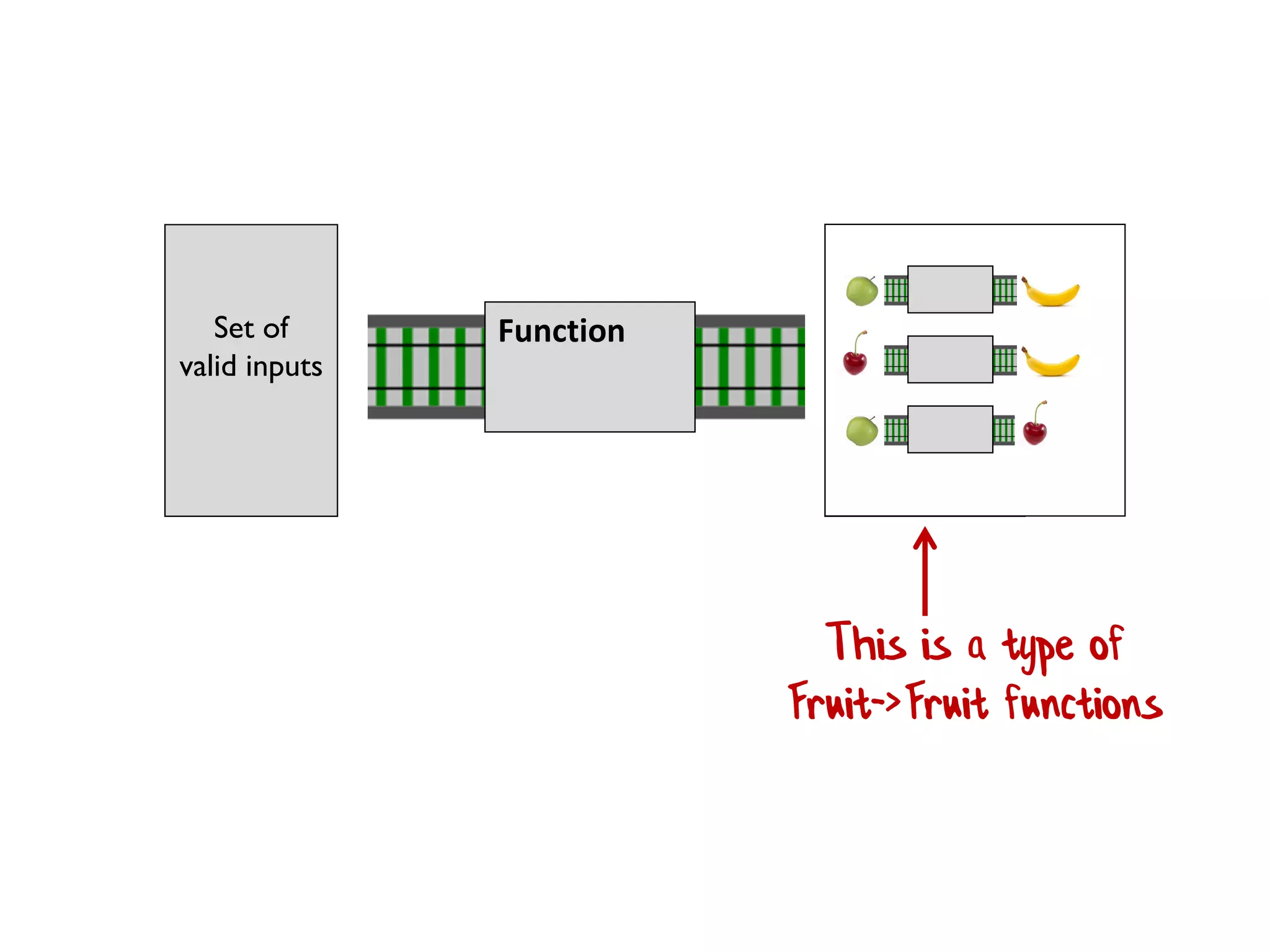
Set of valid inputs Set of valid outputs Function This is a type of Fruit->Fruit functions

Composition everywhere: Types can be composed too "Algebraic type system" "Composable type system"

New types are built from smaller types by: Composing with “AND” Composing with “OR”

Example: tuples, structs, records FruitSalad = One each of and and “AND” types (Record types) type FruitSalad = { Apple: AppleVariety Banana: BananaVariety Cherry: CherryVariety }

Snack = or or “OR” types (Choice types) type Snack = | Apple of AppleVariety | Banana of BananaVariety | Cherry of CherryVariety

Real world example of type composition

Example of some requirements: We accept three forms of payment: Cash, Check, or Card. For Cash we don't need any extra information For Checks we need a check number For Cards we need a card type and card number

interface IPaymentMethod {..} class Cash() : IPaymentMethod {..} class Check(int checkNo): IPaymentMethod {..} class Card(string cardType, string cardNo) : IPaymentMethod {..} In OOP you would probably implement it as an interface and a set of subclasses, like this:

type CheckNumber = int type CardNumber = string In FP you would probably implement by composing types, like this:

type CheckNumber = ... type CardNumber = … type CardType = Visa | Mastercard type CreditCardInfo = { CardType : CardType CardNumber : CardNumber }

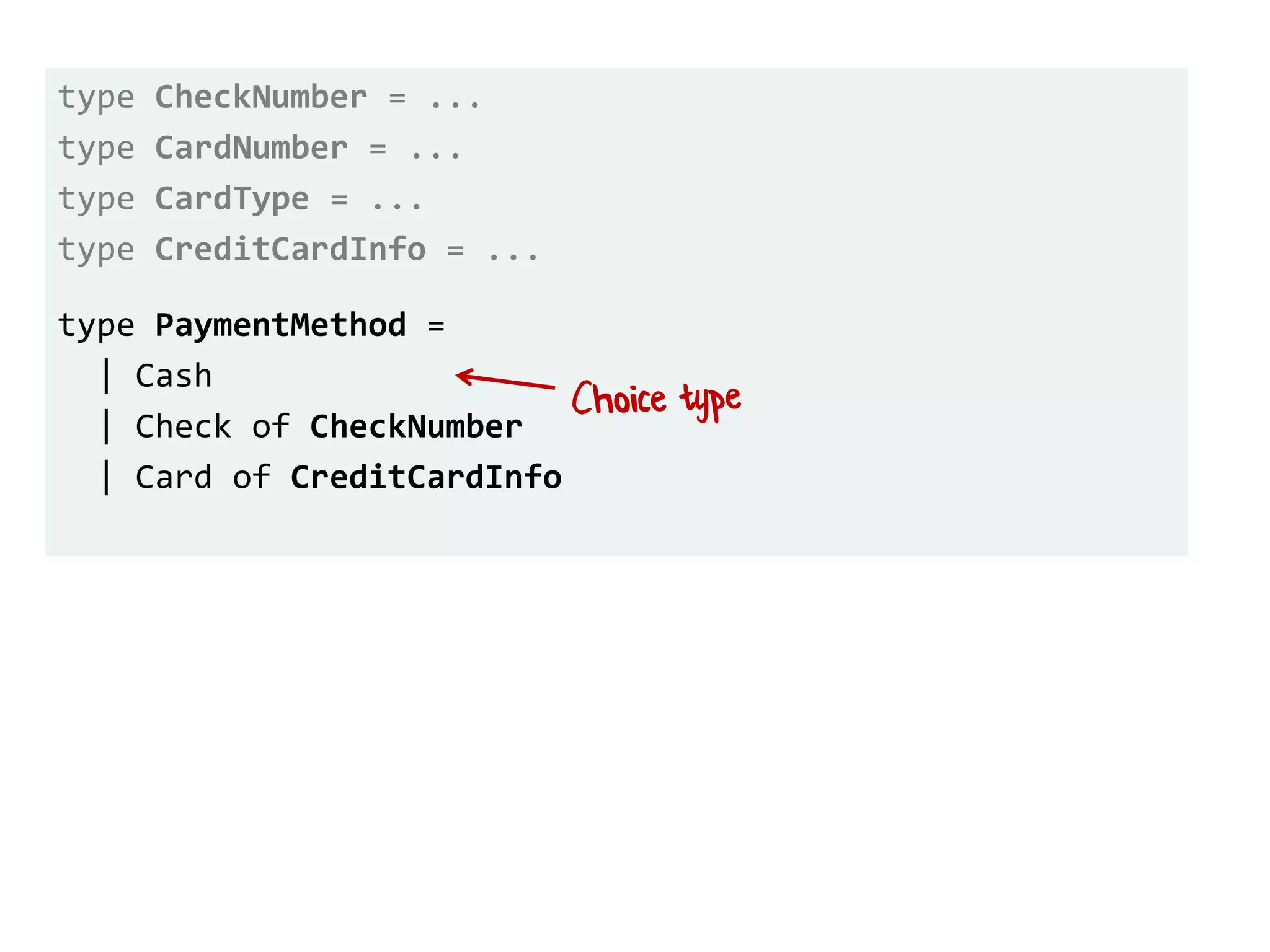
type CheckNumber = ... type CardNumber = ... type CardType = ... type CreditCardInfo = ... type PaymentMethod = | Cash | Check of CheckNumber | Card of CreditCardInfo

type CheckNumber = ... type CardNumber = ... type CardType = ... type CreditCardInfo = ... type PaymentMethod = | Cash | Check of CheckNumber | Card of CreditCardInfo type PaymentAmount = decimal type Currency = EUR | USD

type CheckNumber = ... type CardNumber = ... type CardType = ... type CreditCardInfo = ... type PaymentMethod = | Cash | Check of CheckNumber | Card of CreditCardInfo type PaymentAmount = decimal type Currency = EUR | USD type Payment = { Amount : PaymentAmount Currency: Currency Method: PaymentMethod }

type CheckNumber = int type CardNumber = string type CardType = Visa | Mastercard type CreditCardInfo = CardType * CardNumber type PaymentMethod = | Cash | Check of CheckNumber | Card of CreditCardInfo type PaymentAmount = decimal type Currency = EUR | USD type Payment = { Amount : PaymentAmount Currency: Currency Method: PaymentMethod }

Design principle: Use static types for domain modelling and documentation Static types only! Sorry Clojure and JS developers 

A big topic and not enough time   More on DDD and designing with types at fsharpforfunandprofit.com/ddd

PATTERN 1: FUNCTIONS AS PARAMETERS

Guideline: Parameterize all the things

let printList() = for i in [1..10] do printfn "the number is %i" i

So parameterize the data let printList aList = for i in aList do printfn "the number is %i" i

let printList aList = for i in aList do printfn "the number is %i" i

let printList anAction aList = for i in aList do anAction i So parameterize the action as well: We've decoupled the behavior from the data. Any list, any action!

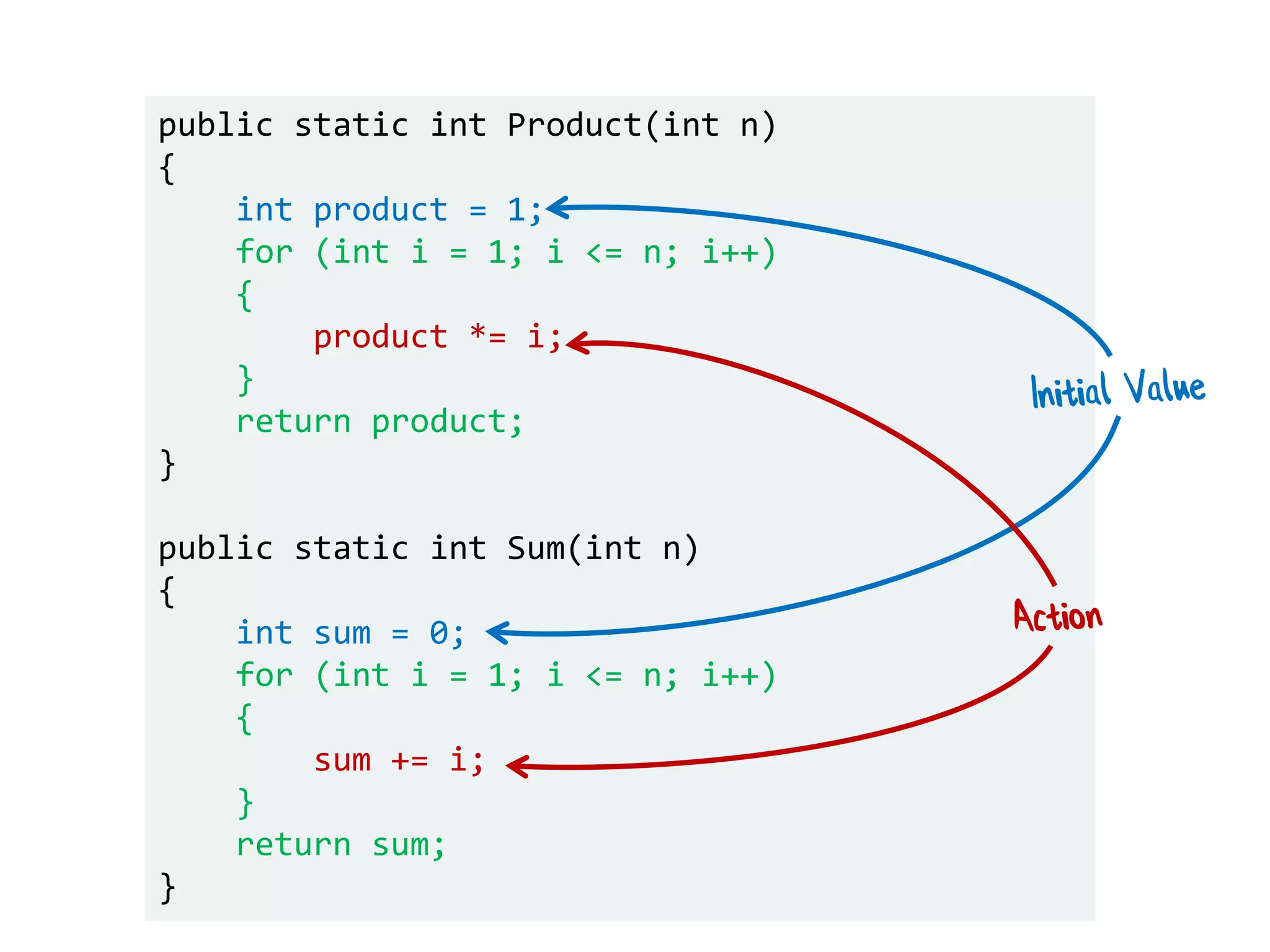
public static int Product(int n) { int product = 1; for (int i = 1; i <= n; i++) { product *= i; } return product; } public static int Sum(int n) { int sum = 0; for (int i = 1; i <= n; i++) { sum += i; } return sum; }

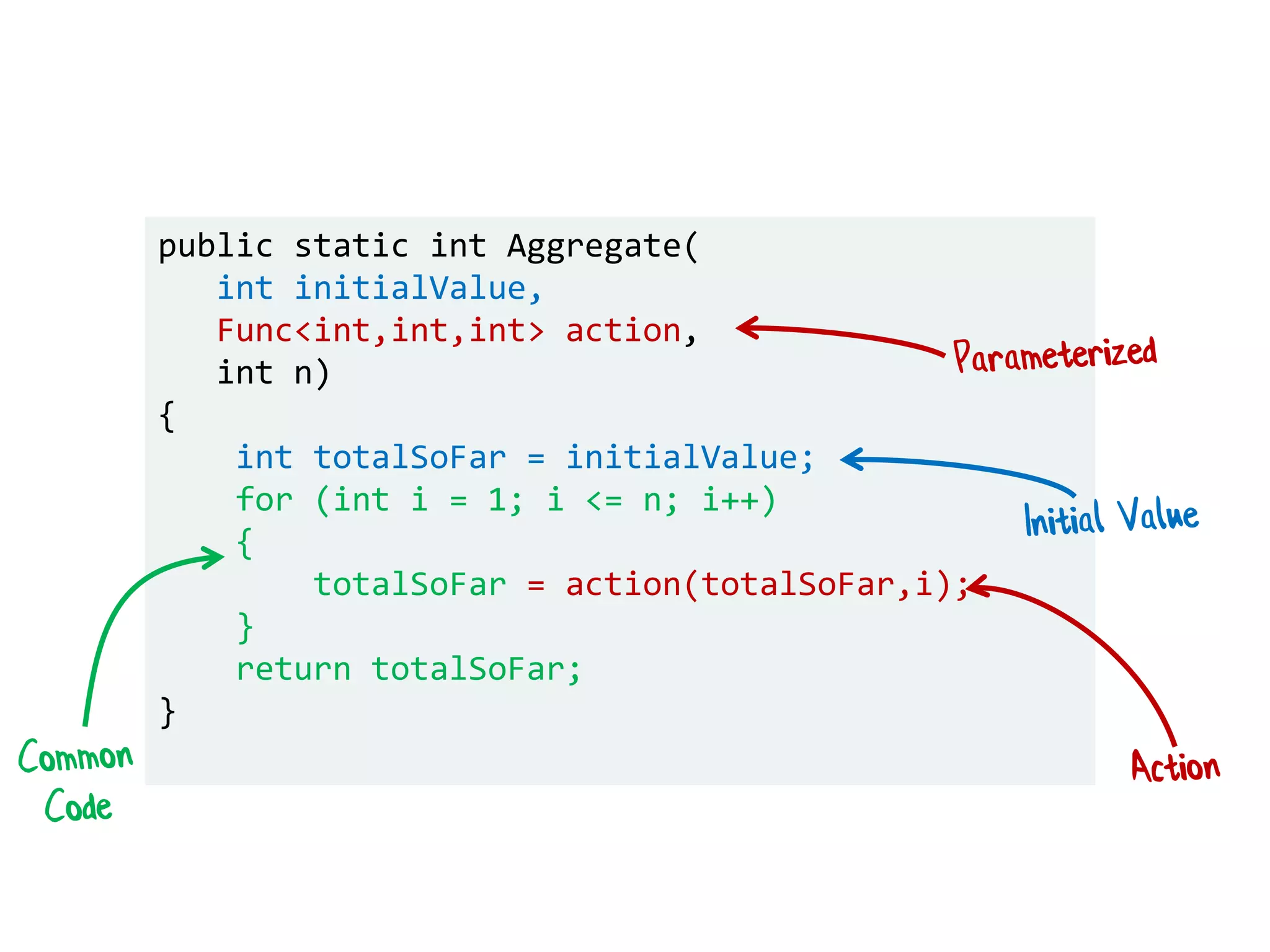
public static int Aggregate( int initialValue, Func<int,int,int> action, int n) { int totalSoFar = initialValue; for (int i = 1; i <= n; i++) { totalSoFar = action(totalSoFar,i); } return totalSoFar; }

Tip: Function types are "interfaces"

interface IBunchOfMethods { int DoSomething(int x); string DoSomethingElse(int x); void DoAThirdThing(string x); } Let's take the Single Responsibility Principle and the Interface Segregation Principle to the extreme... Every interface should have only one method!

interface IBunchOfMethods { int DoSomething(int x); } An interface with one method is a just a function type type DoSomething: int -> int

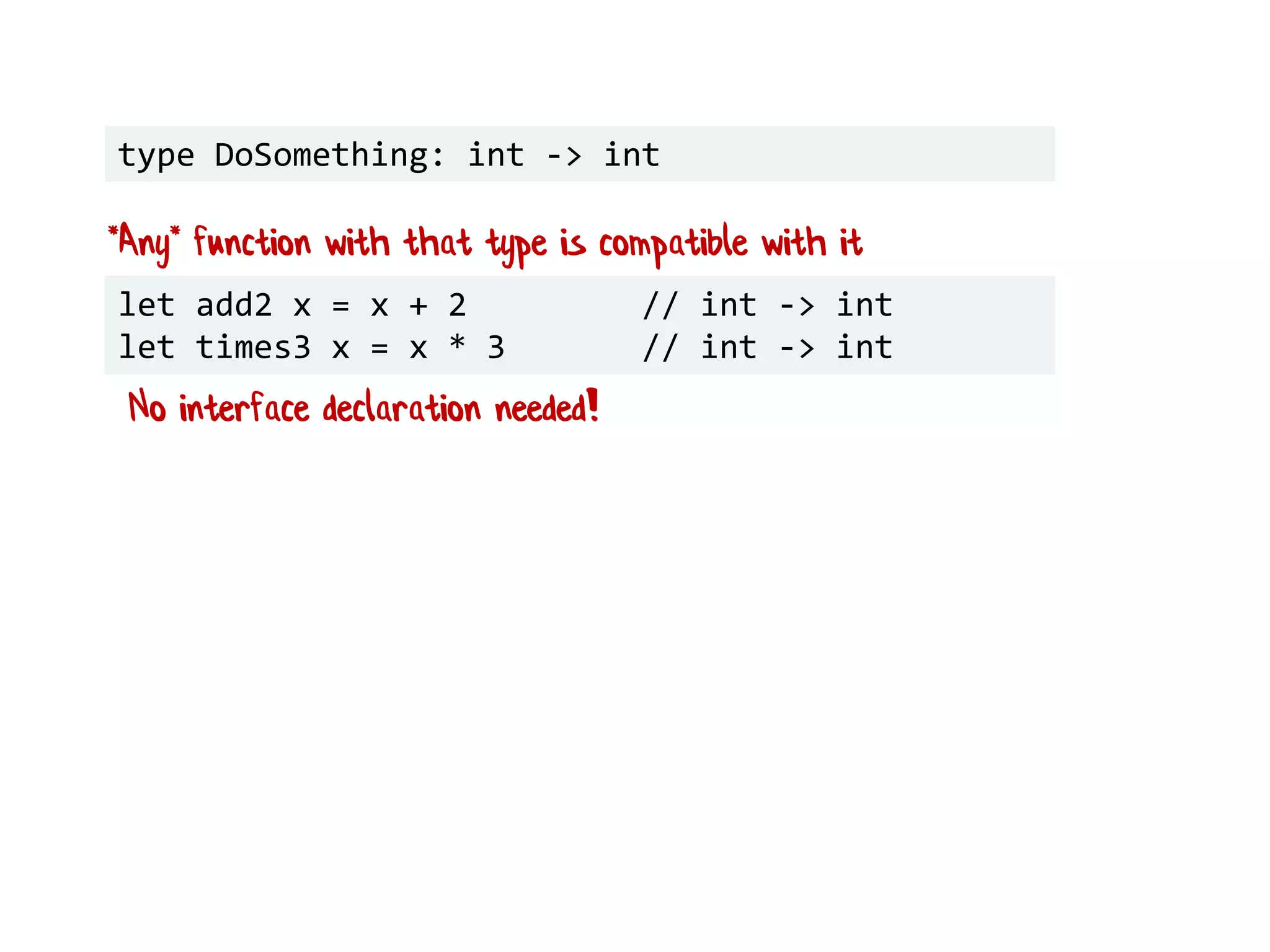
type DoSomething: int -> int *Any* function with that type is compatible with it let add2 x = x + 2 // int -> int let times3 x = x * 3 // int -> int No interface declaration needed!

let isEven x = ... // int -> bool isEvenint bool Log the input Log the output

let isEven x = ... // int -> bool isEvenint bool isEvenint boollogint int logbool bool Compose!

let isEven x = ... // int -> bool isEvenint bool logint log boolisEven

let isEven x = ... // int -> bool isEvenint bool int log bool let isEvenWithLogging = // int -> bool Substitutable for original isEven isEvenWithLogging

Tip: "Use interfaces for loose coupling" Use function parameters for loose coupling

PATTERN 2: COMPOSING MULTI-PARAMETER FUNCTIONS

Bad news: Composition patterns only work for functions that have one parameter! 

Good news! Every function can be turned into a one parameter function 

let add x y = x + y let add = (fun x y -> x + y) let add x = (fun y -> x + y) int-> int->int int-> int->int int-> (int->int) Normal function (Two parameters)

let add x y = x + y let add = (fun x y -> x + y) let add x = (fun y -> x + y) int-> int->int int-> int->int int-> (int->int)

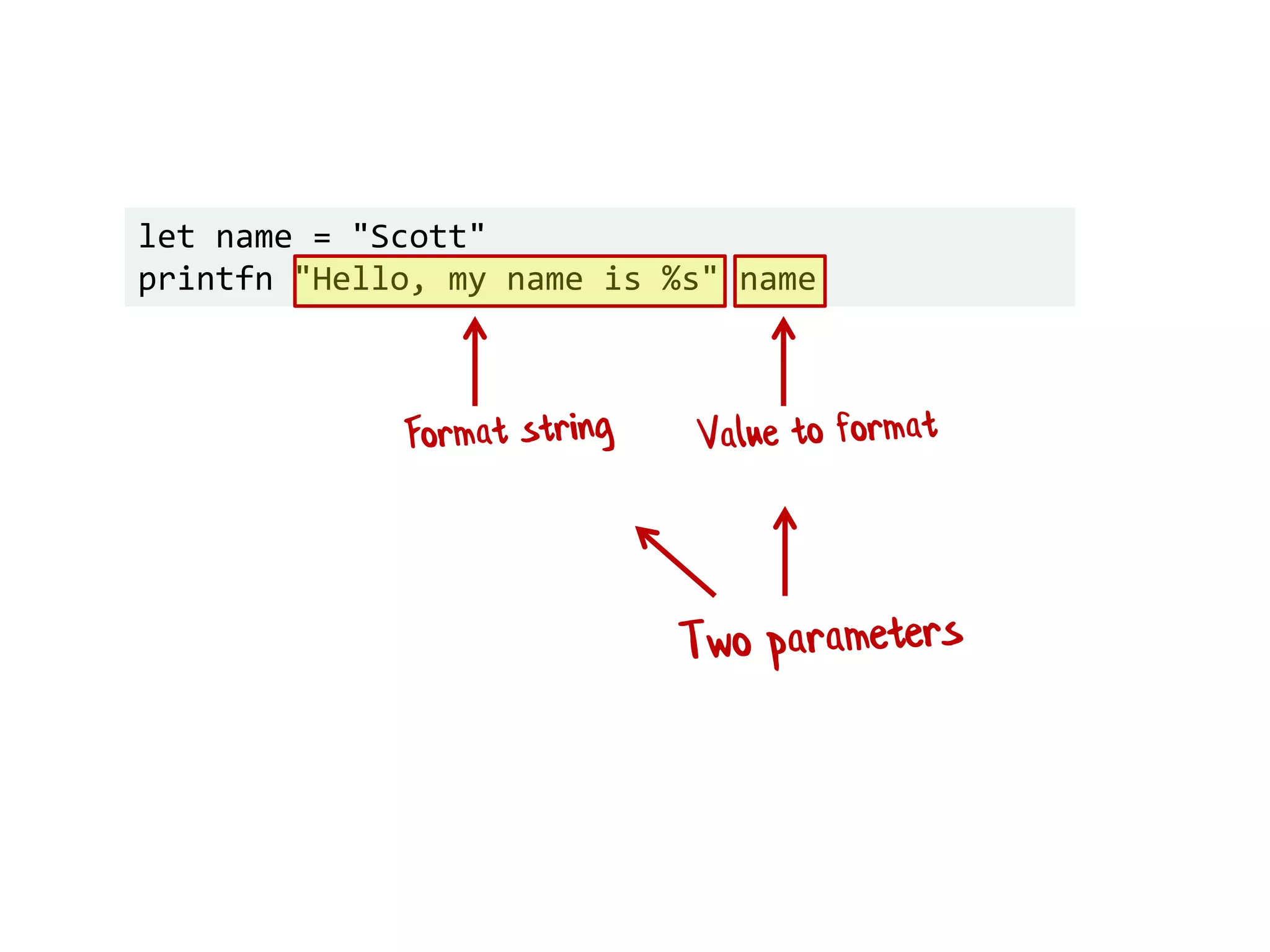
let name = "Scott" printfn "Hello, my name is %s" name

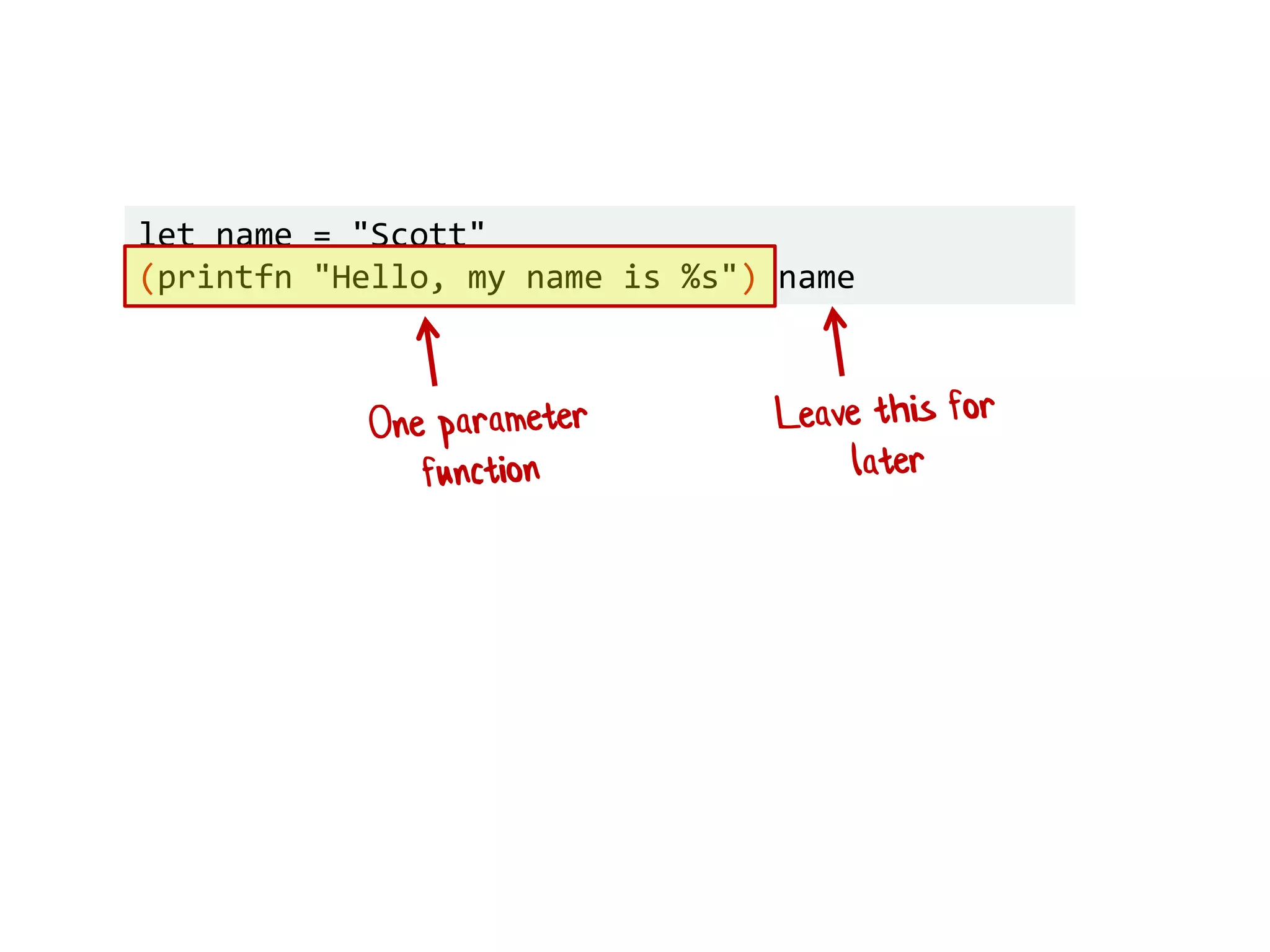
let name = "Scott" (printfn "Hello, my name is %s") name

let hello = (printfn "Hello, my name is %s") Can reuse "hello" in many places now! let name = "Scott" hello name let name = "Alice" hello name

Example: Partial application with lists

let names = ["Alice"; "Bob"; "Scott"] List.iter hello names //foreach name in names let hello = printfn "Hello, my name is %s"

let add1 = (+) 1 let equals2 = (=) 2 [1..100] |> List.map add1 |> List.filter equals2

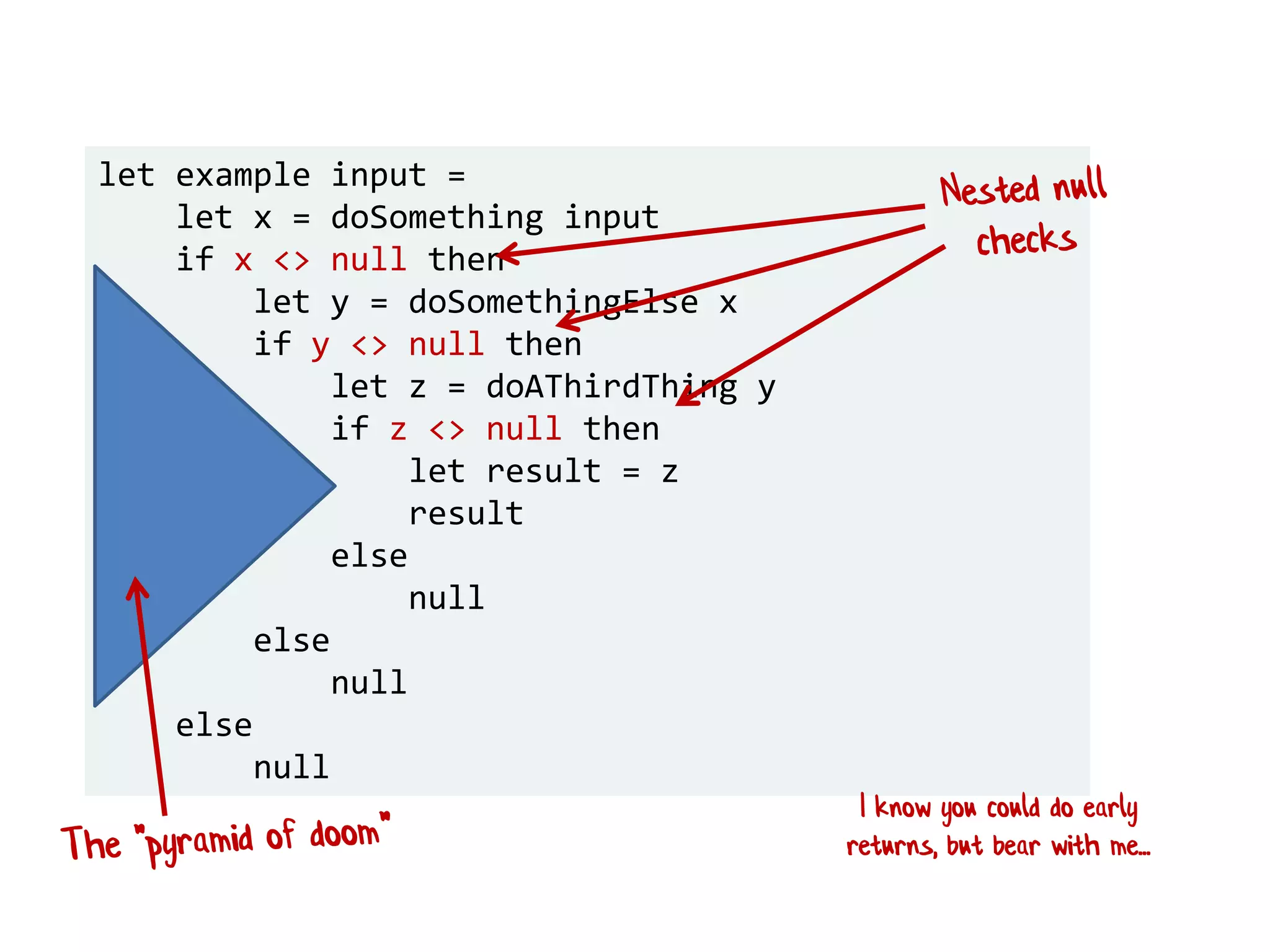
let example input = let x = doSomething input if x <> null then let y = doSomethingElse x if y <> null then let z = doAThirdThing y if z <> null then let result = z result else null else null else null I know you could do early returns, but bear with me...

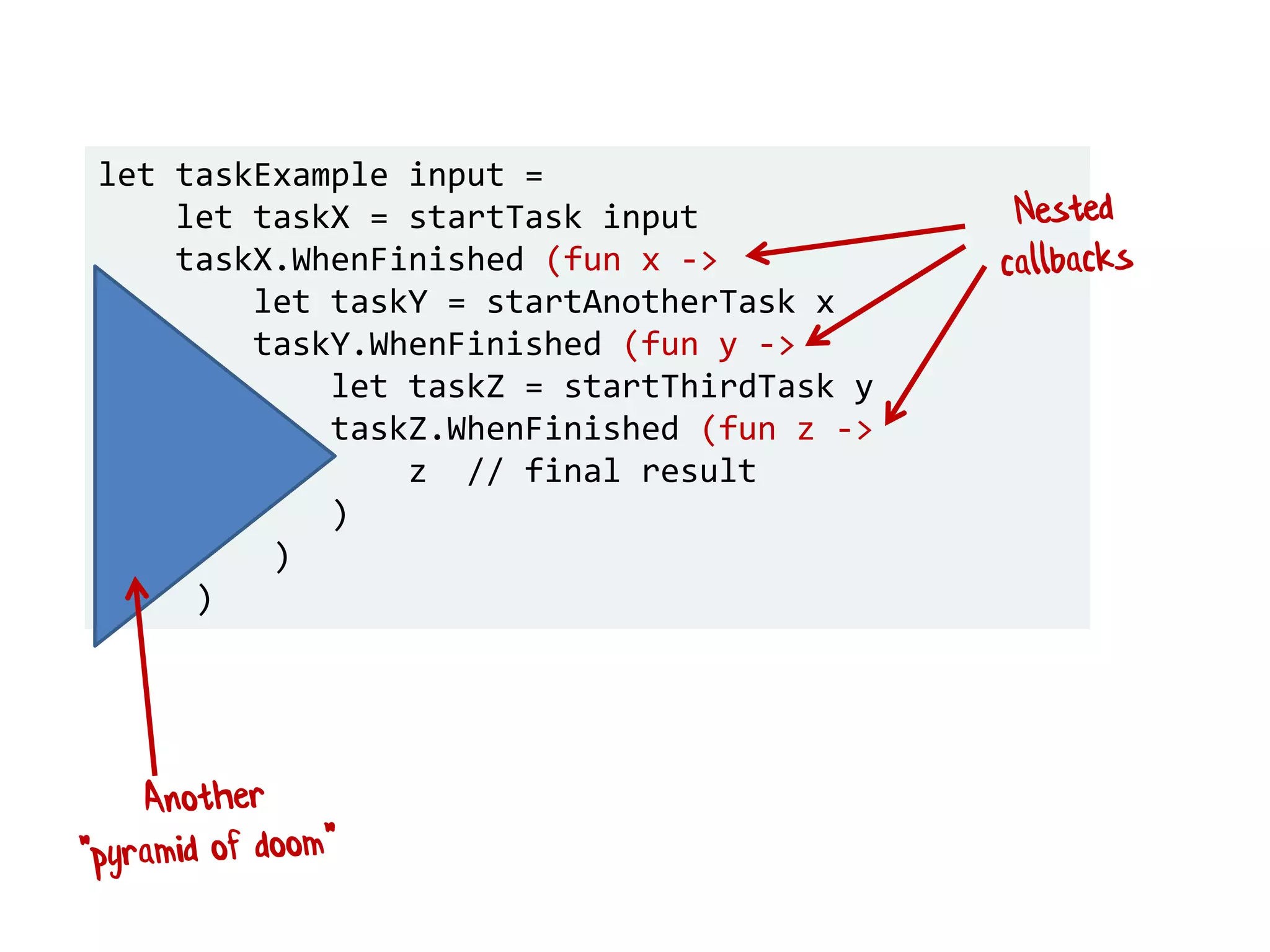
let taskExample input = let taskX = startTask input taskX.WhenFinished (fun x -> let taskY = startAnotherTask x taskY.WhenFinished (fun y -> let taskZ = startThirdTask y taskZ.WhenFinished (fun z -> z // final result ) ) )

let example input = let x = doSomething input if x <> null then let y = doSomethingElse x if y <> null then let z = doAThirdThing y if z <> null then let result = z result else null else null else null Nulls are a code smell: replace with Option! Let's fix this!

let example input = let x = doSomething input if x.IsSome then let y = doSomethingElse (x.Value) if y.IsSome then let z = doAThirdThing (y.Value) if z.IsSome then let result = z.Value Some result else None else None else None Much more elegant, yes? No! This is fugly! But there is a pattern we can exploit...

let example input = let x = doSomething input if x.IsSome then let y = doSomethingElse (x.Value) if y.IsSome then let z = doAThirdThing (y.Value) if z.IsSome then // do something with z.Value // in this block else None else None else None

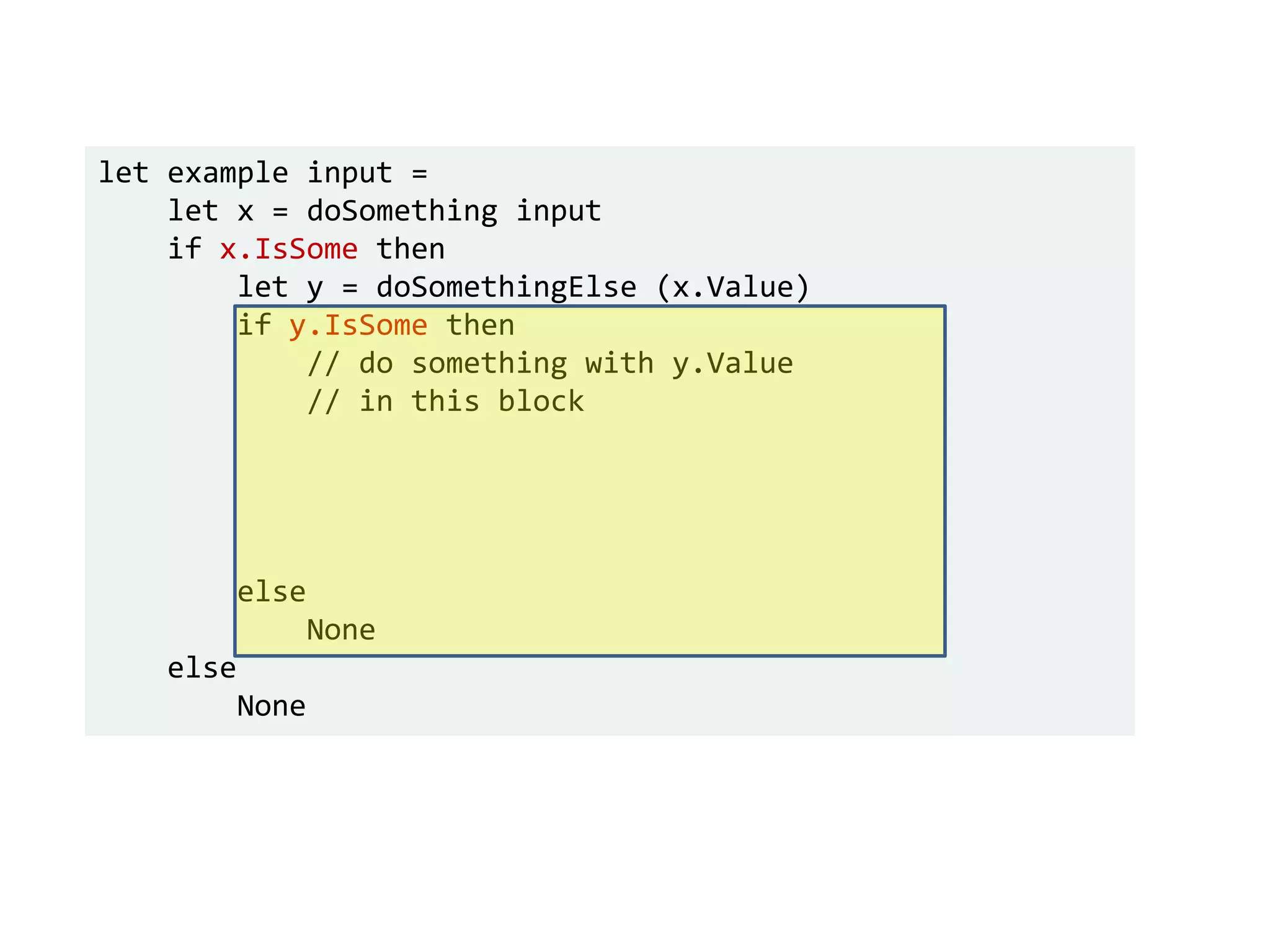
let example input = let x = doSomething input if x.IsSome then let y = doSomethingElse (x.Value) if y.IsSome then // do something with y.Value // in this block else None else None

let example input = let x = doSomething input if x.IsSome then // do something with x.Value // in this block else None Can you see the pattern?

if opt.IsSome then //do something with opt.Value else None

let ifSomeDo f opt = if opt.IsSome then f opt.Value else None

let example input = doSomething input |> ifSomeDo doSomethingElse |> ifSomeDo doAThirdThing |> ifSomeDo ... let ifSomeDo f opt = if opt.IsSome then f opt.Value else None

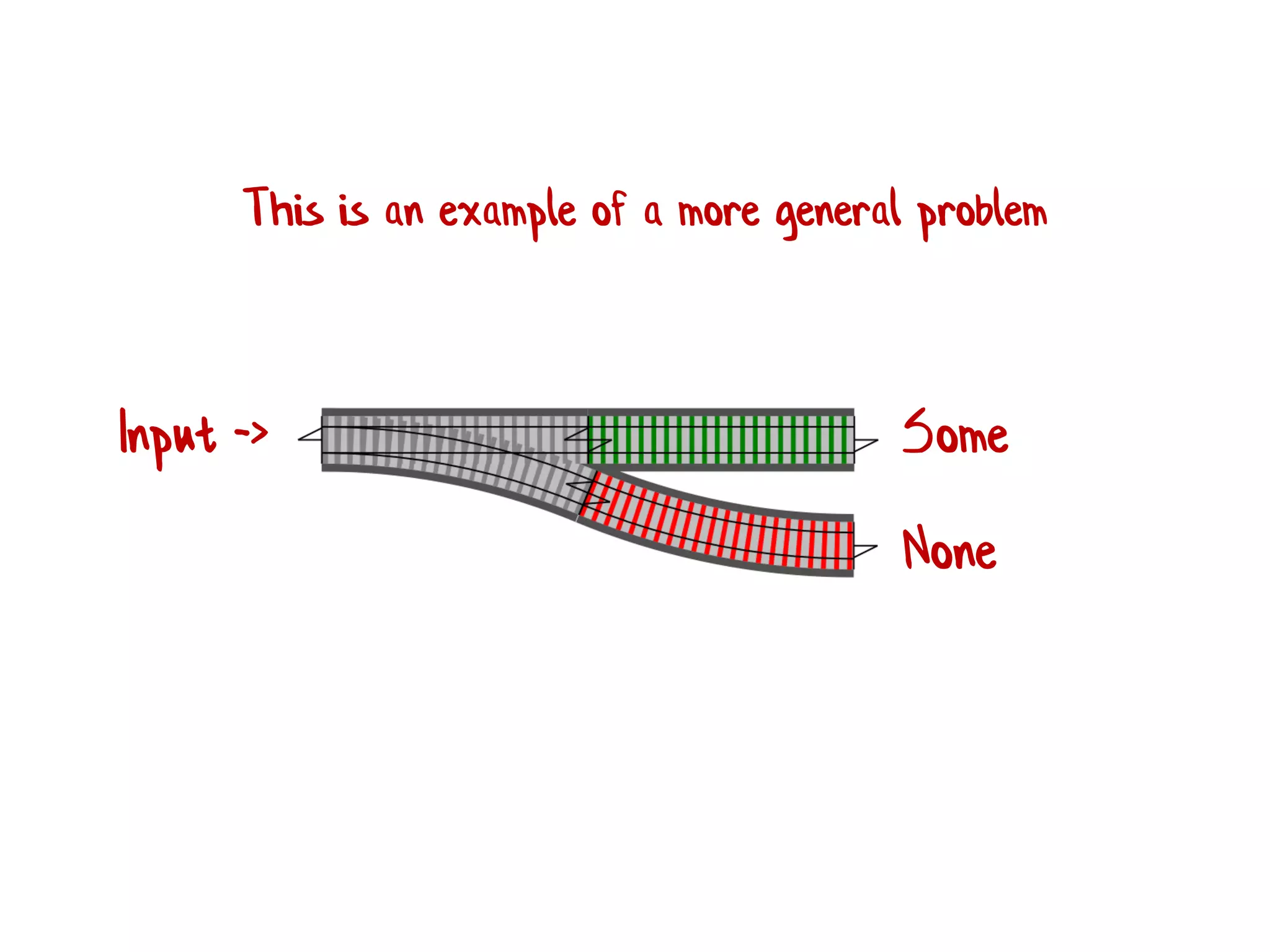
Some None Input -> This is an example of a more general problem

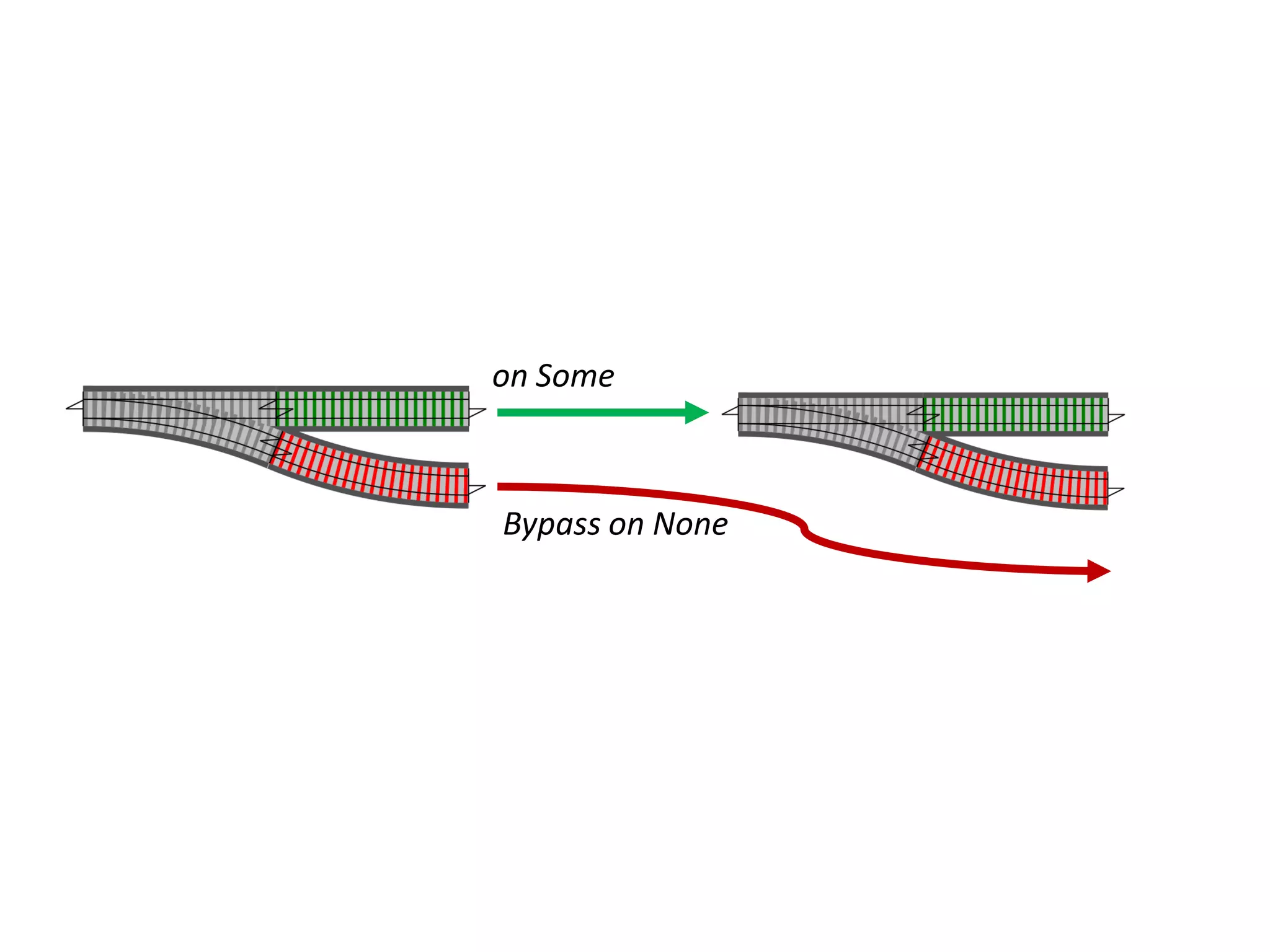
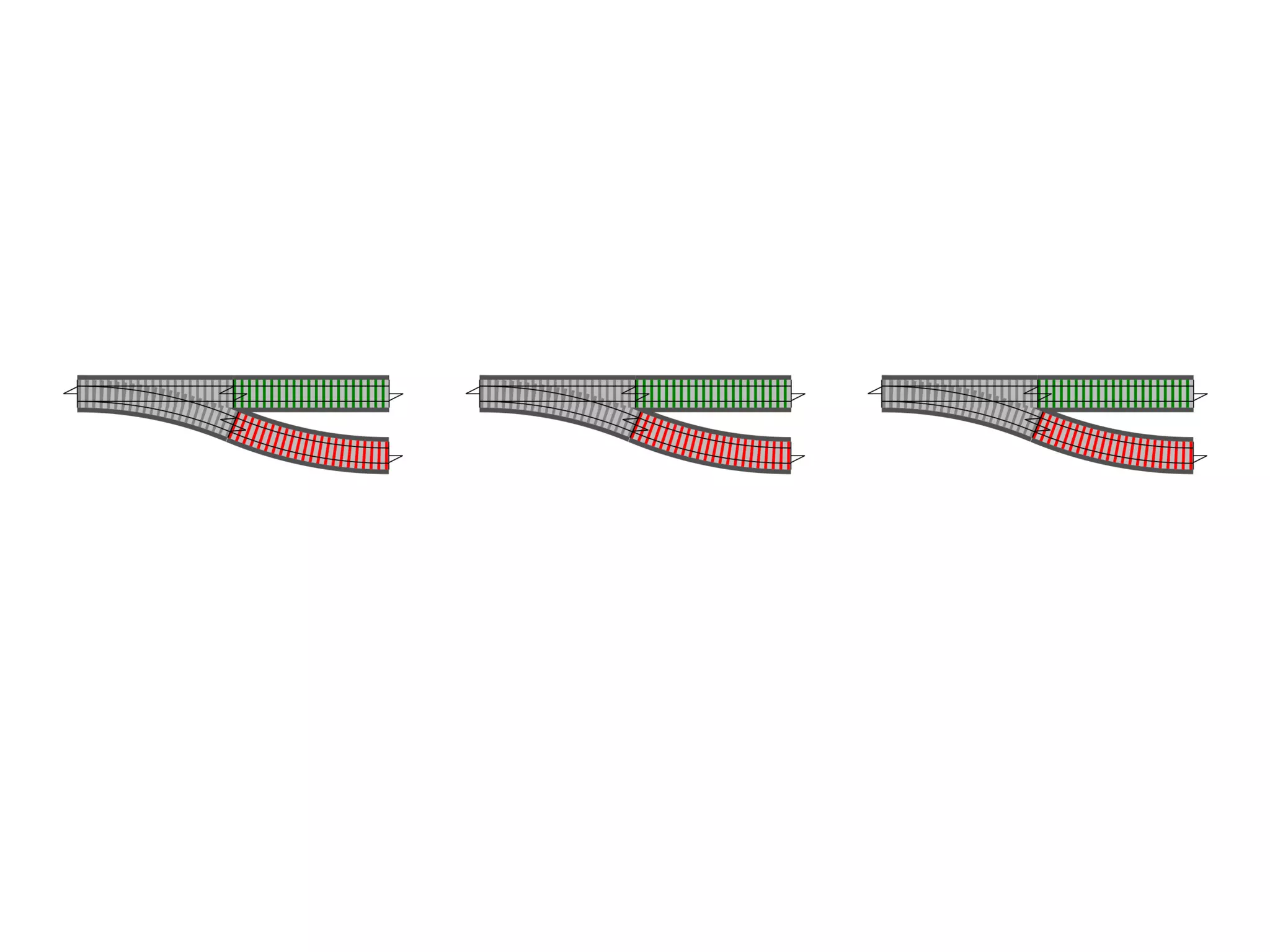
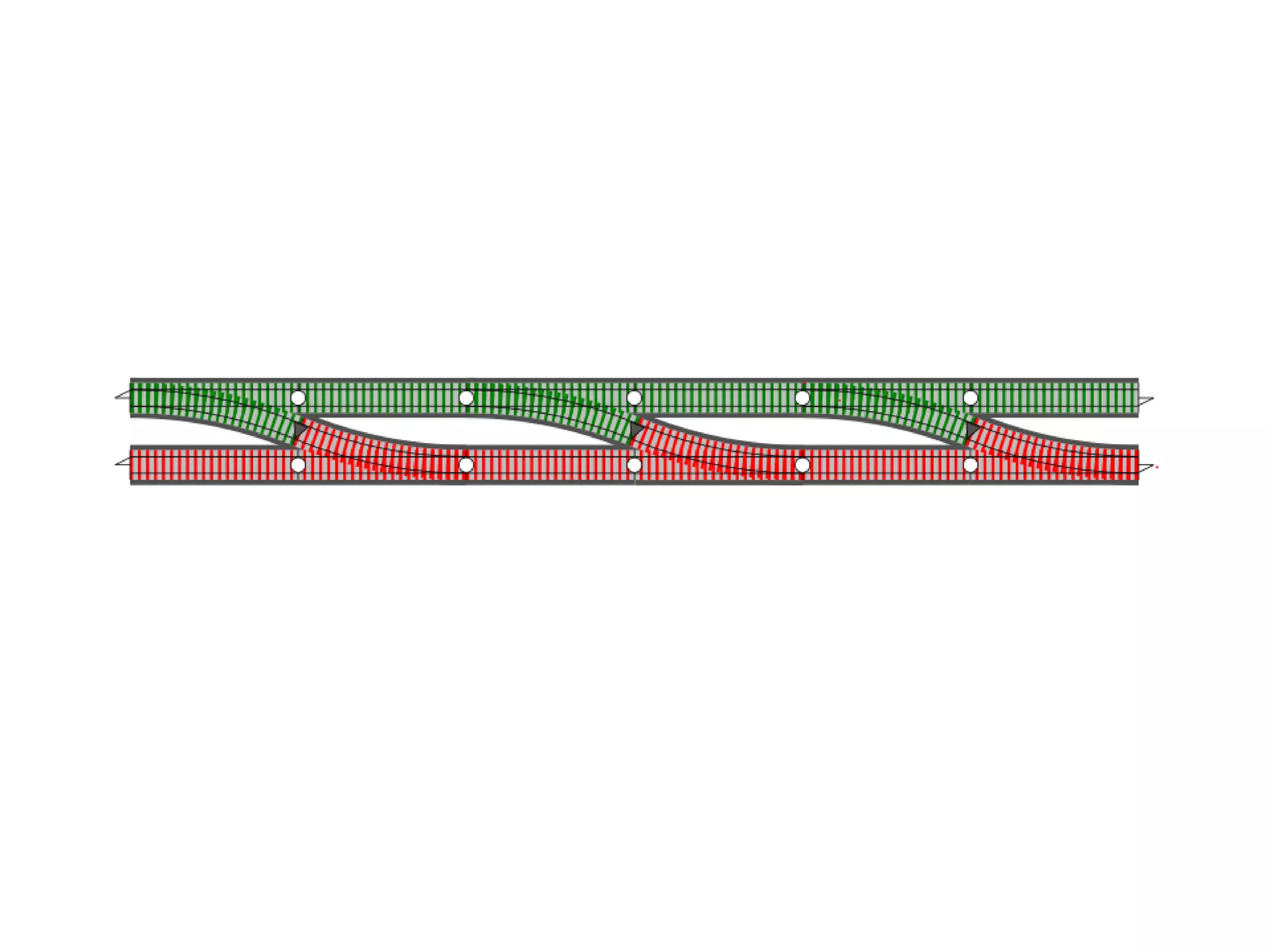
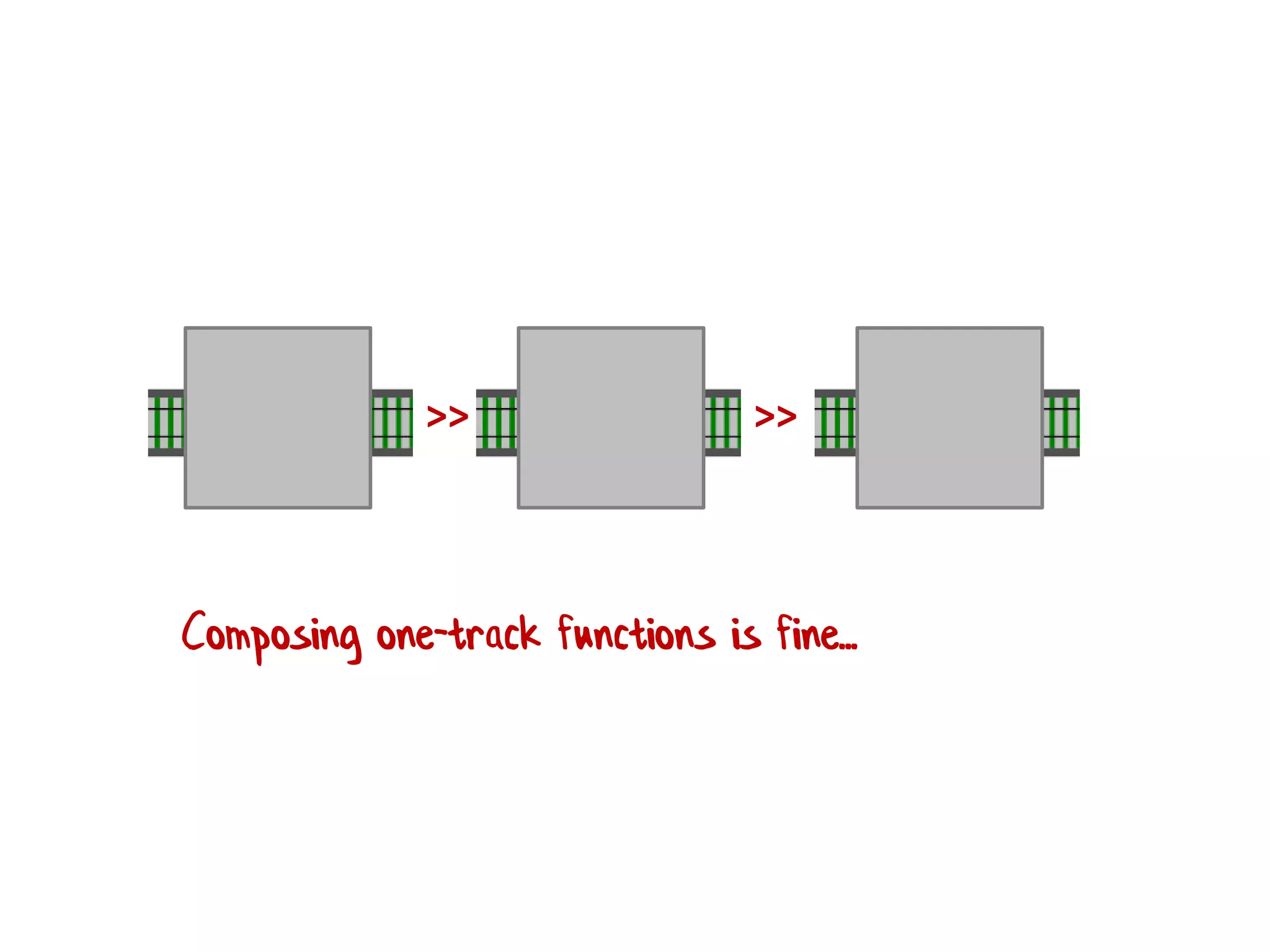
>> >> Composing one-track functions is fine...

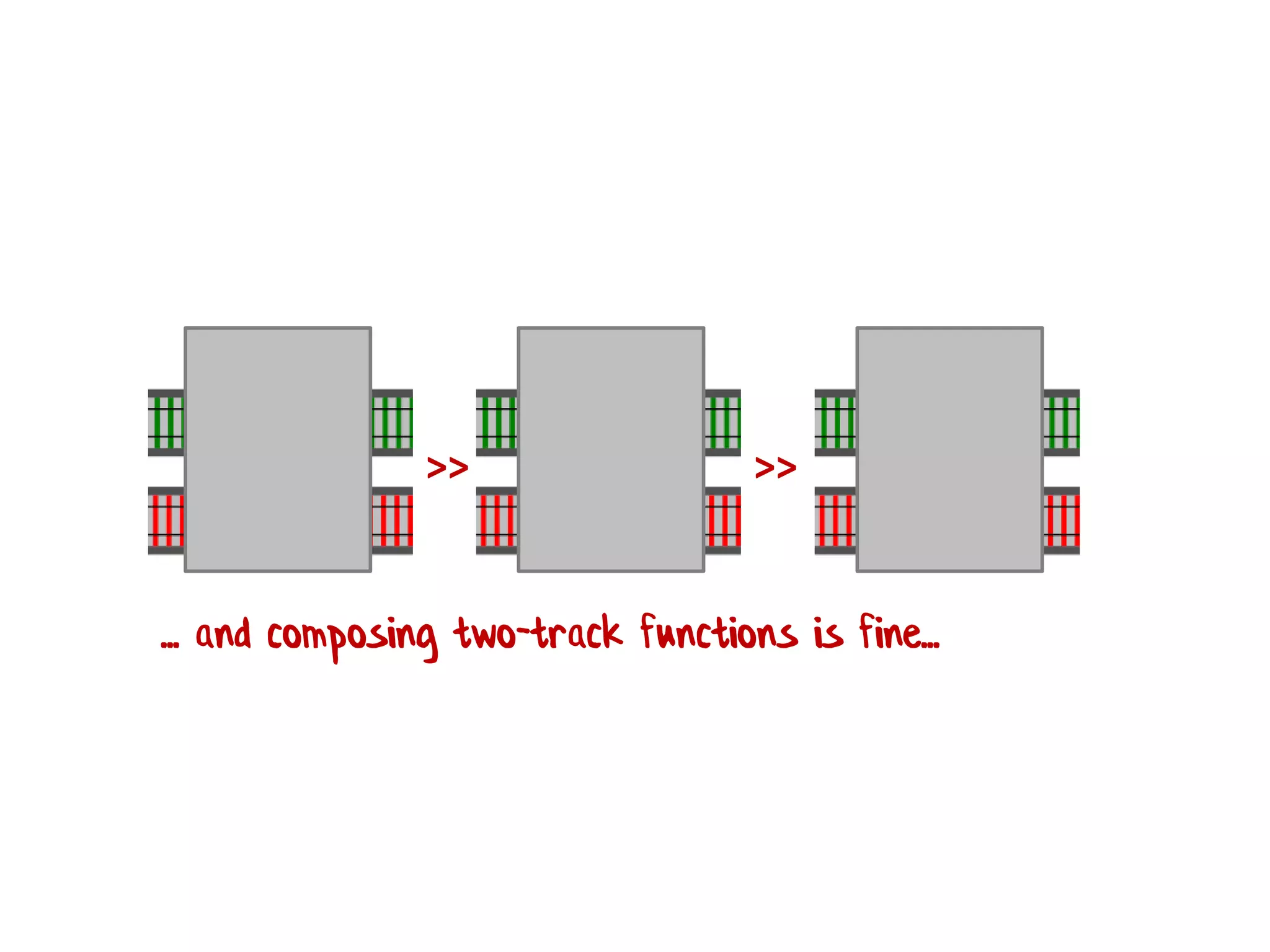
>> >> ... and composing two-track functions is fine...

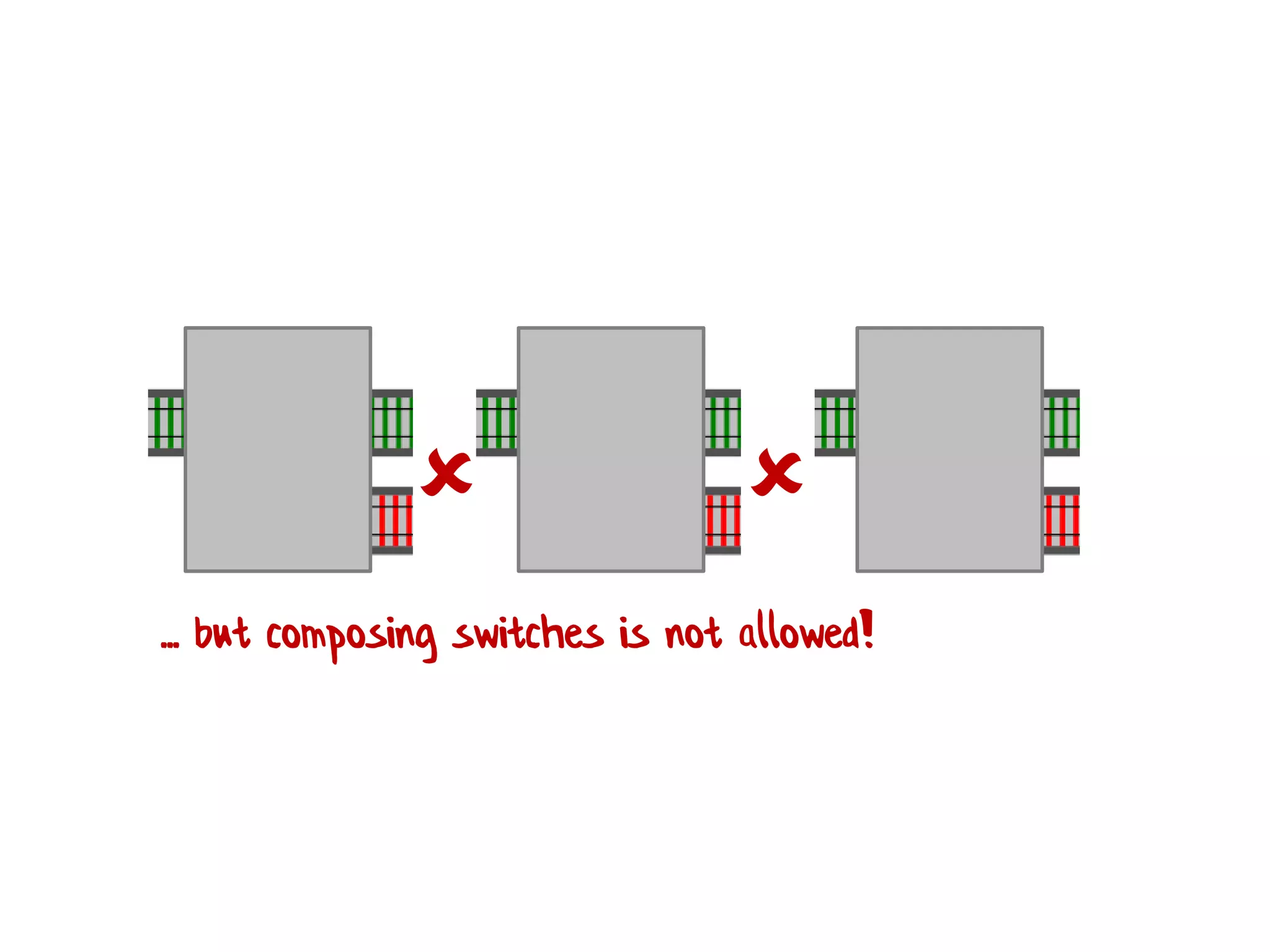
  ... but composing switches is not allowed!

How to combine the mismatched functions?

“Bind” is the answer! Bind all the things!

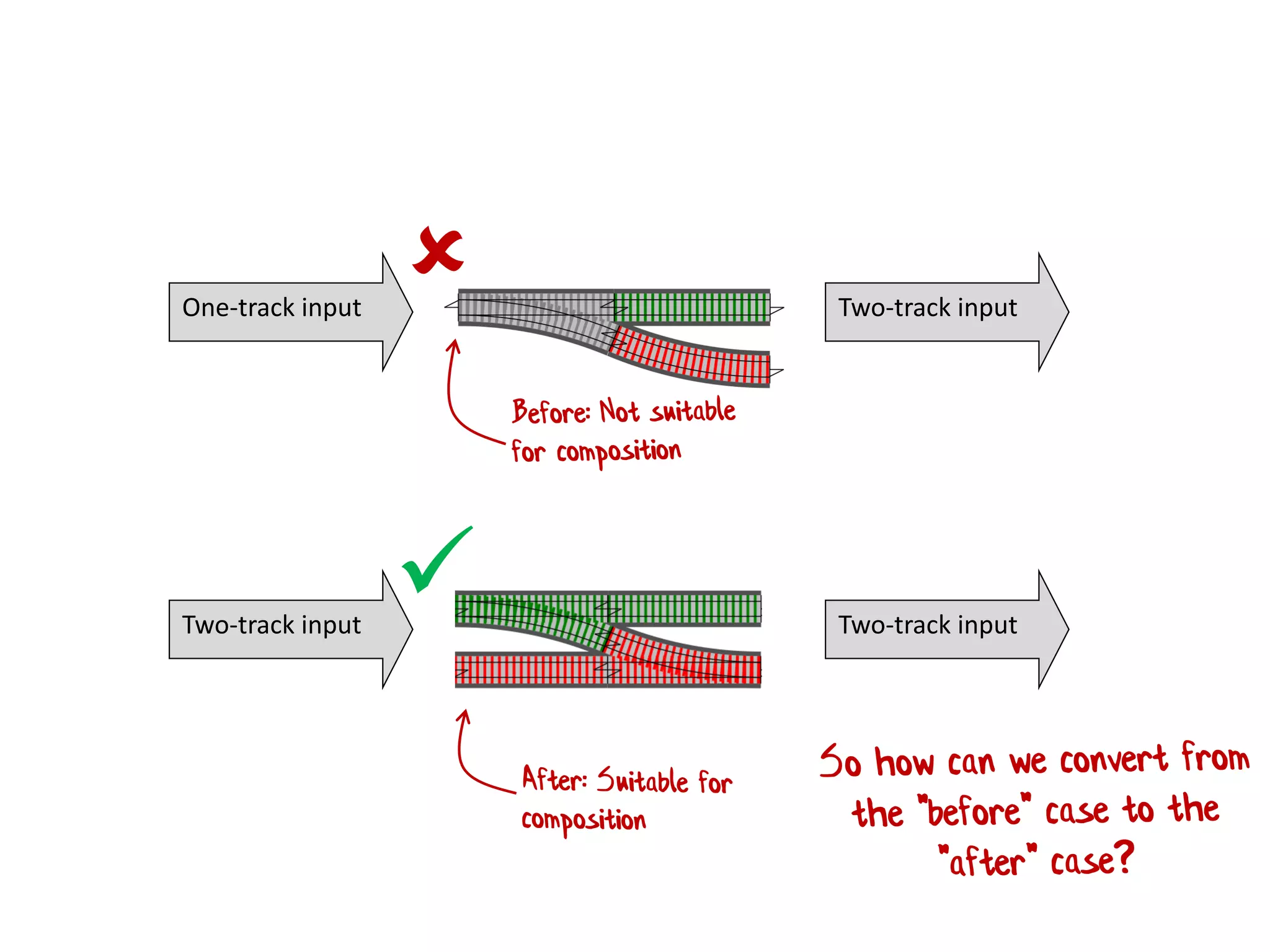
Two-track input Two-track input One-track input Two-track input  

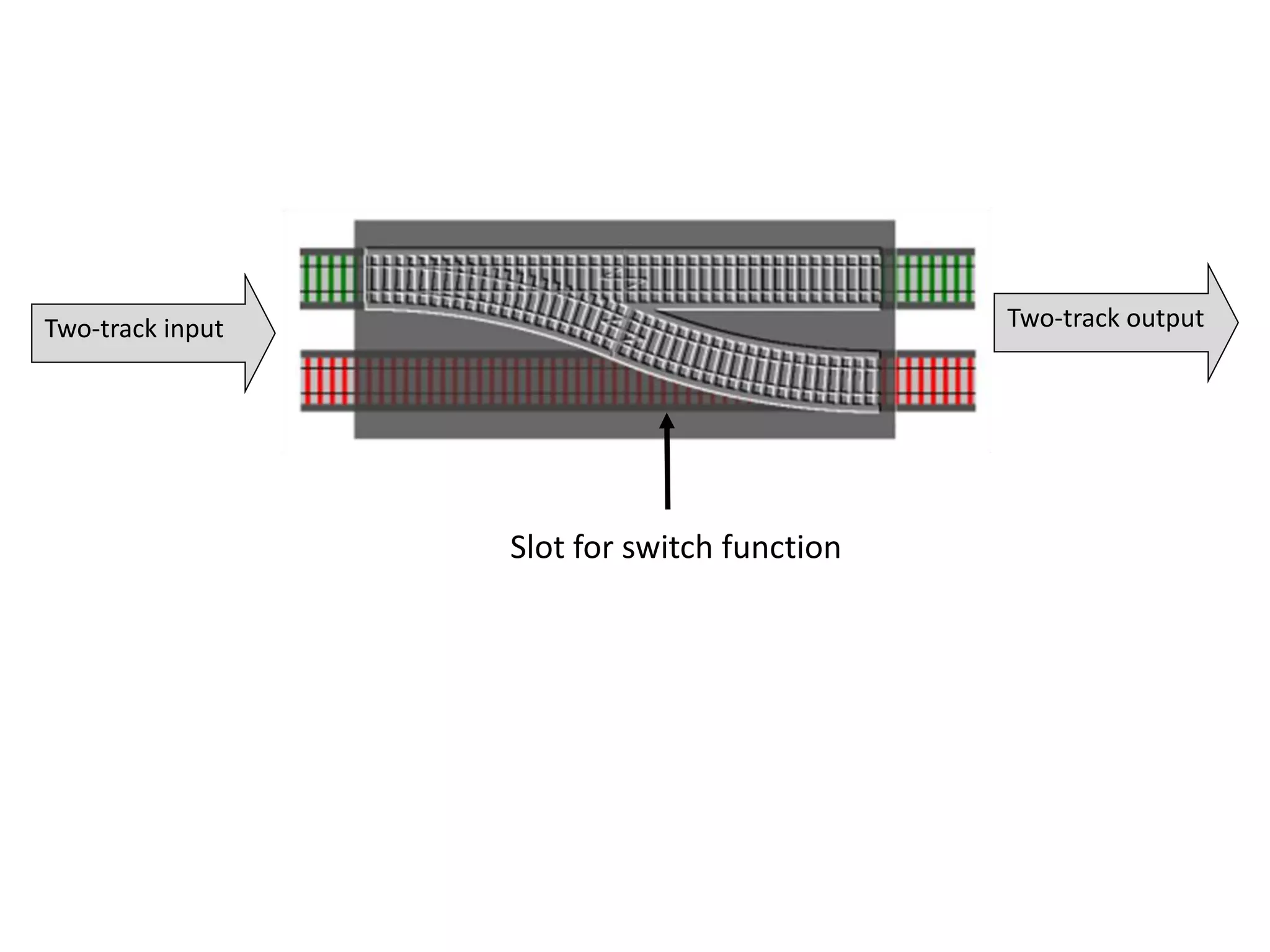
Two-track input Slot for switch function Two-track output

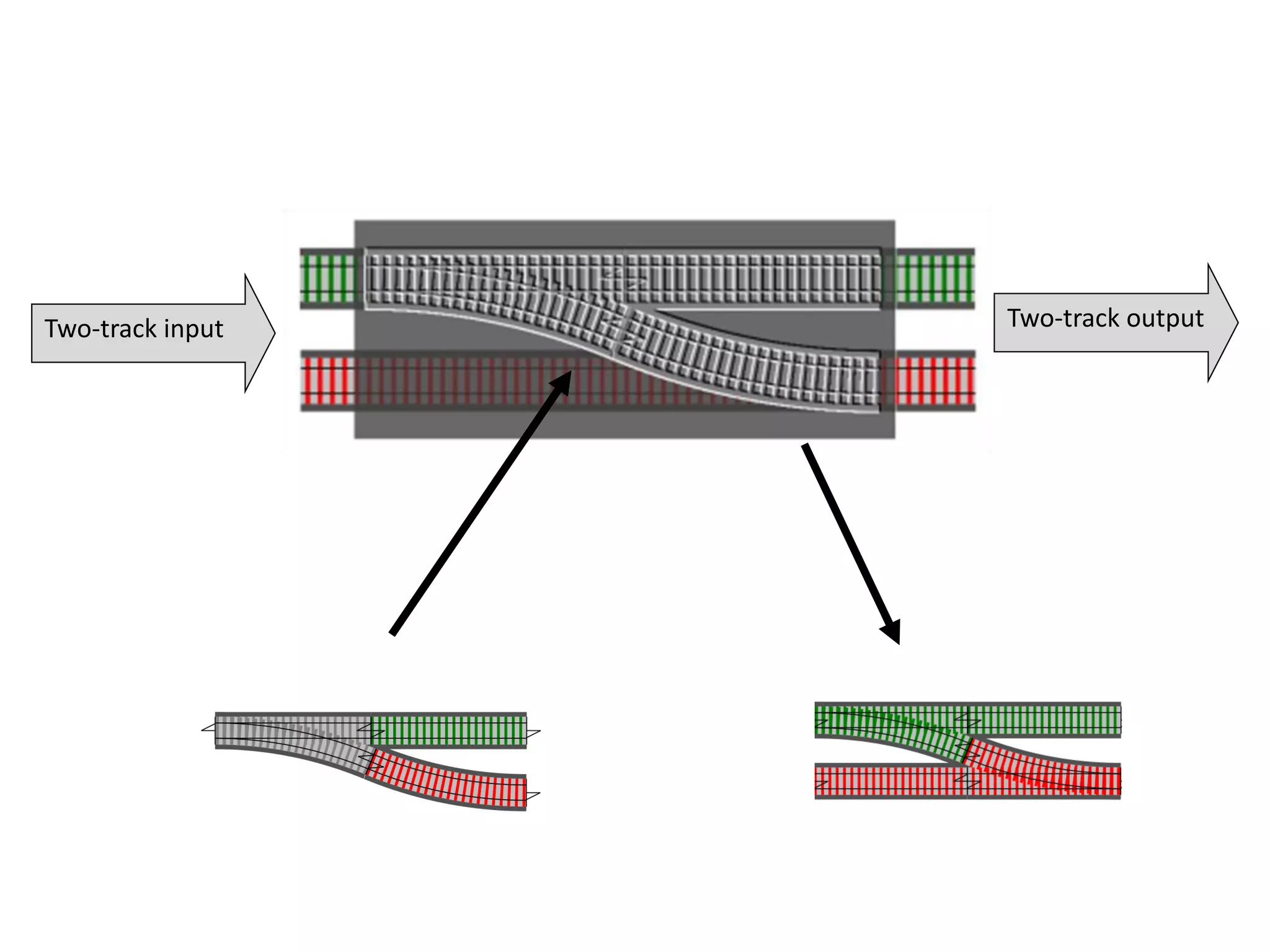
Two-track input Two-track output

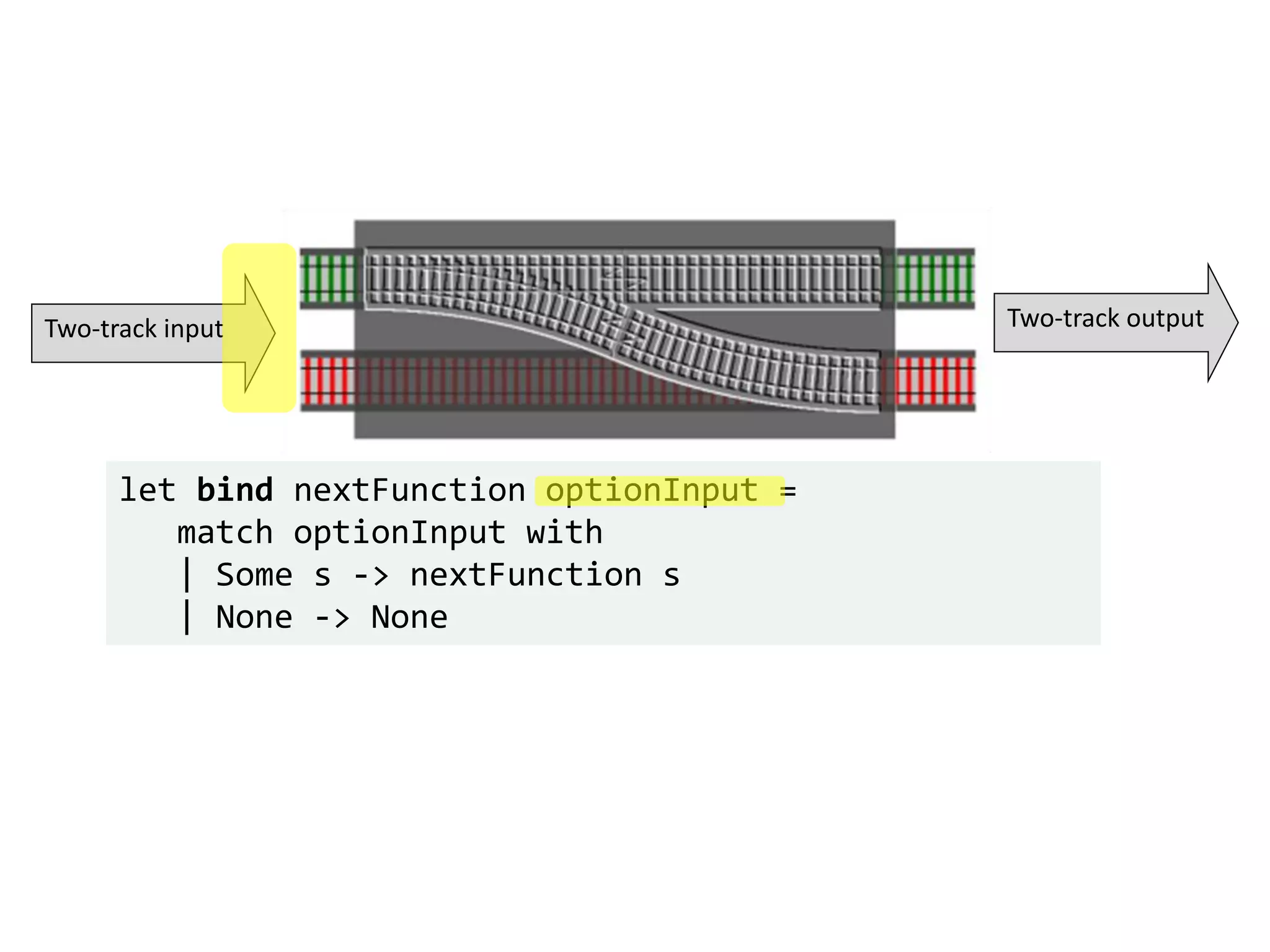
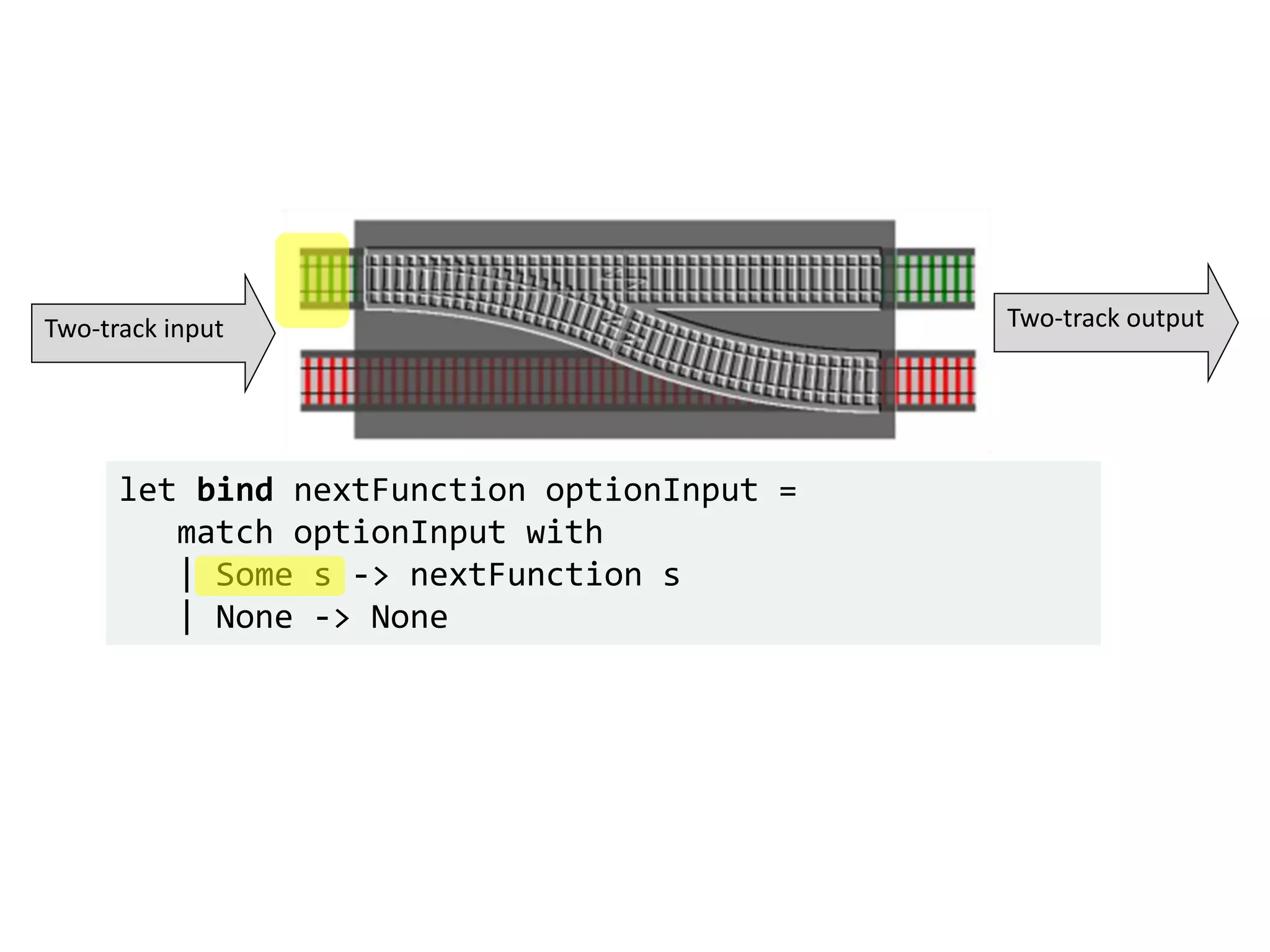
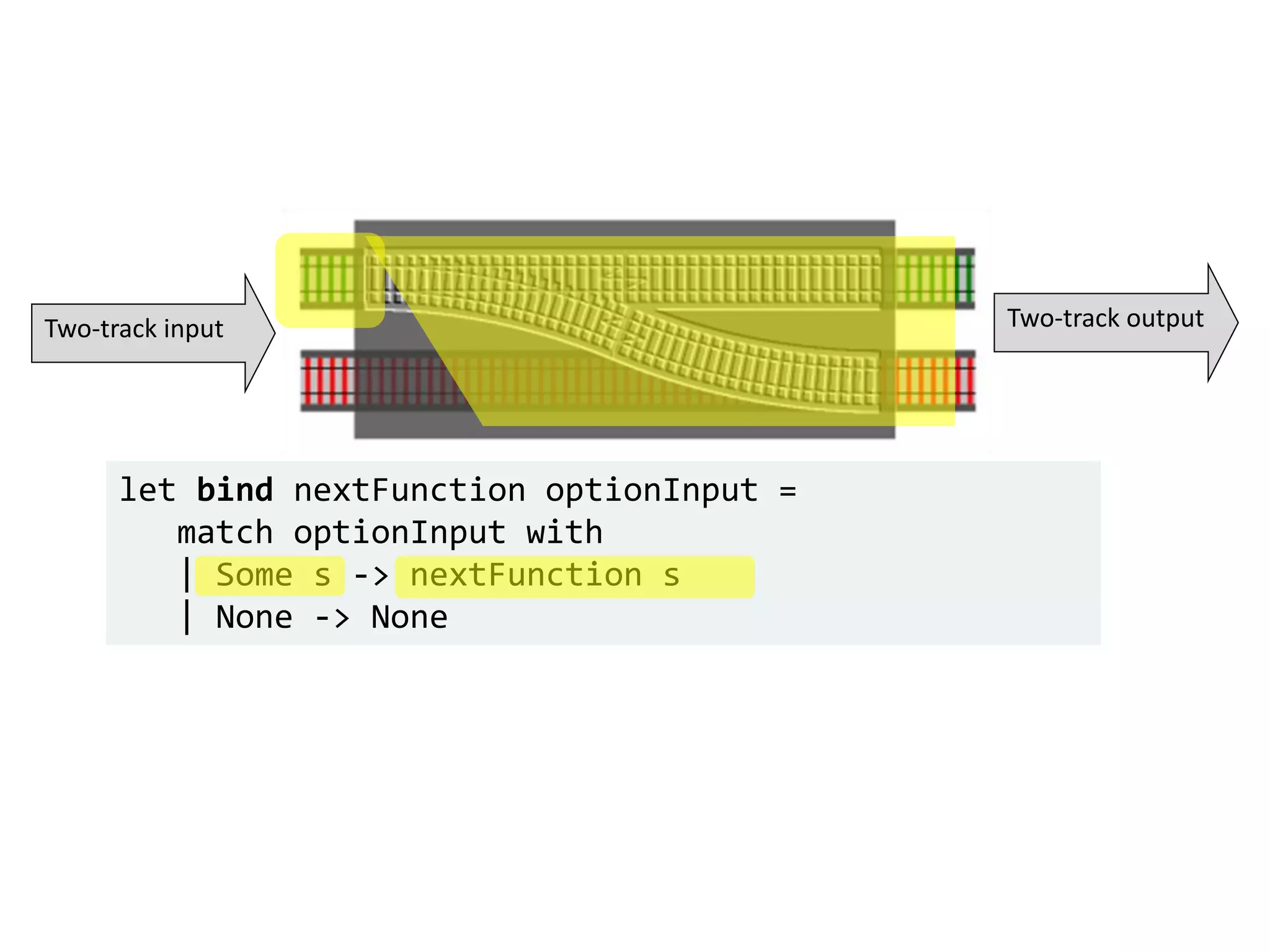
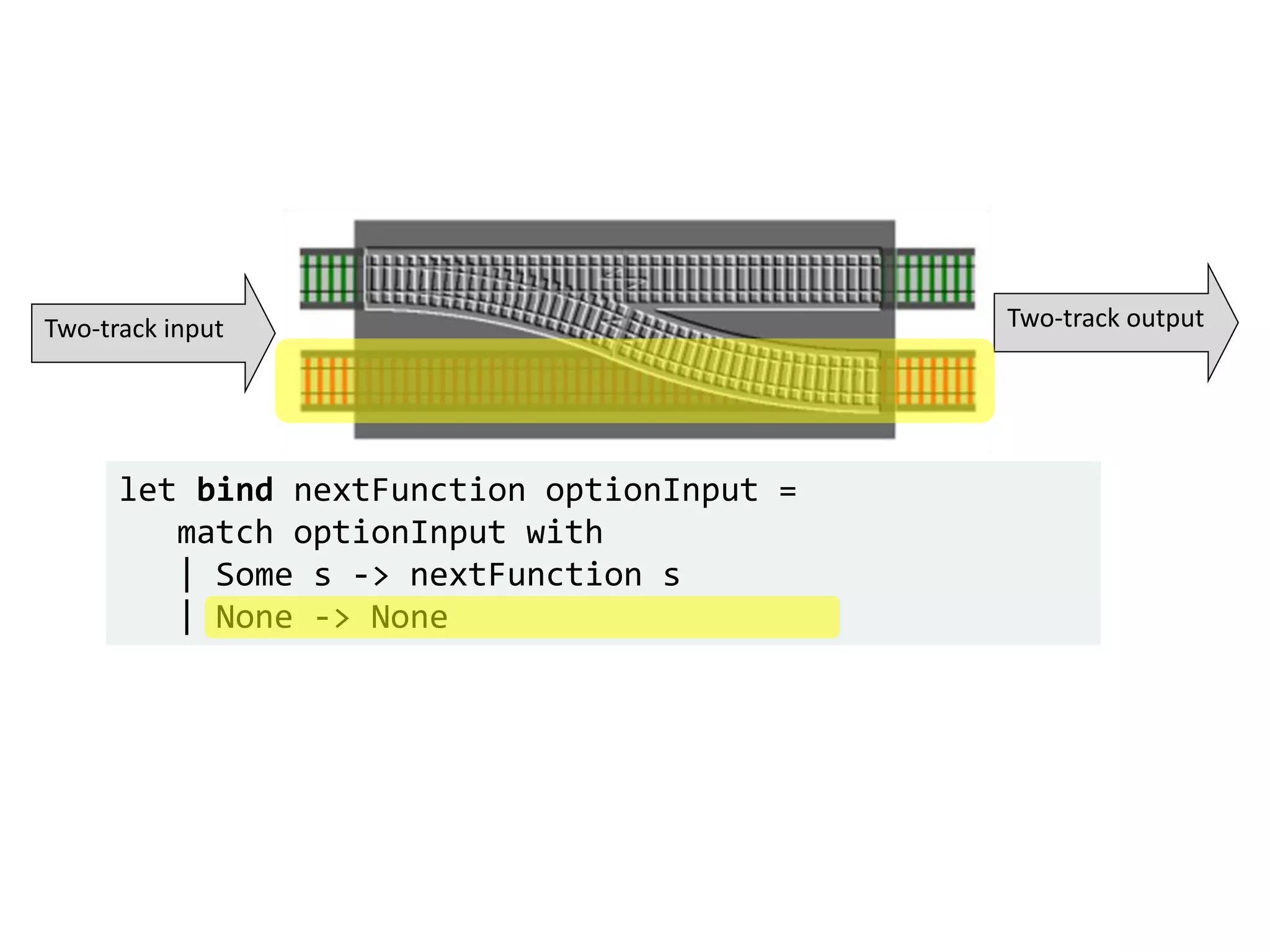
let bind nextFunction optionInput = match optionInput with | Some s -> nextFunction s | None -> None Two-track input Two-track output

Pattern: Use bind to chain options

let example input = let x = doSomething input if x.IsSome then let y = doSomethingElse (x.Value) if y.IsSome then let z = doAThirdThing (y.Value) if z.IsSome then let result = z.Value Some result else None else None else None Before

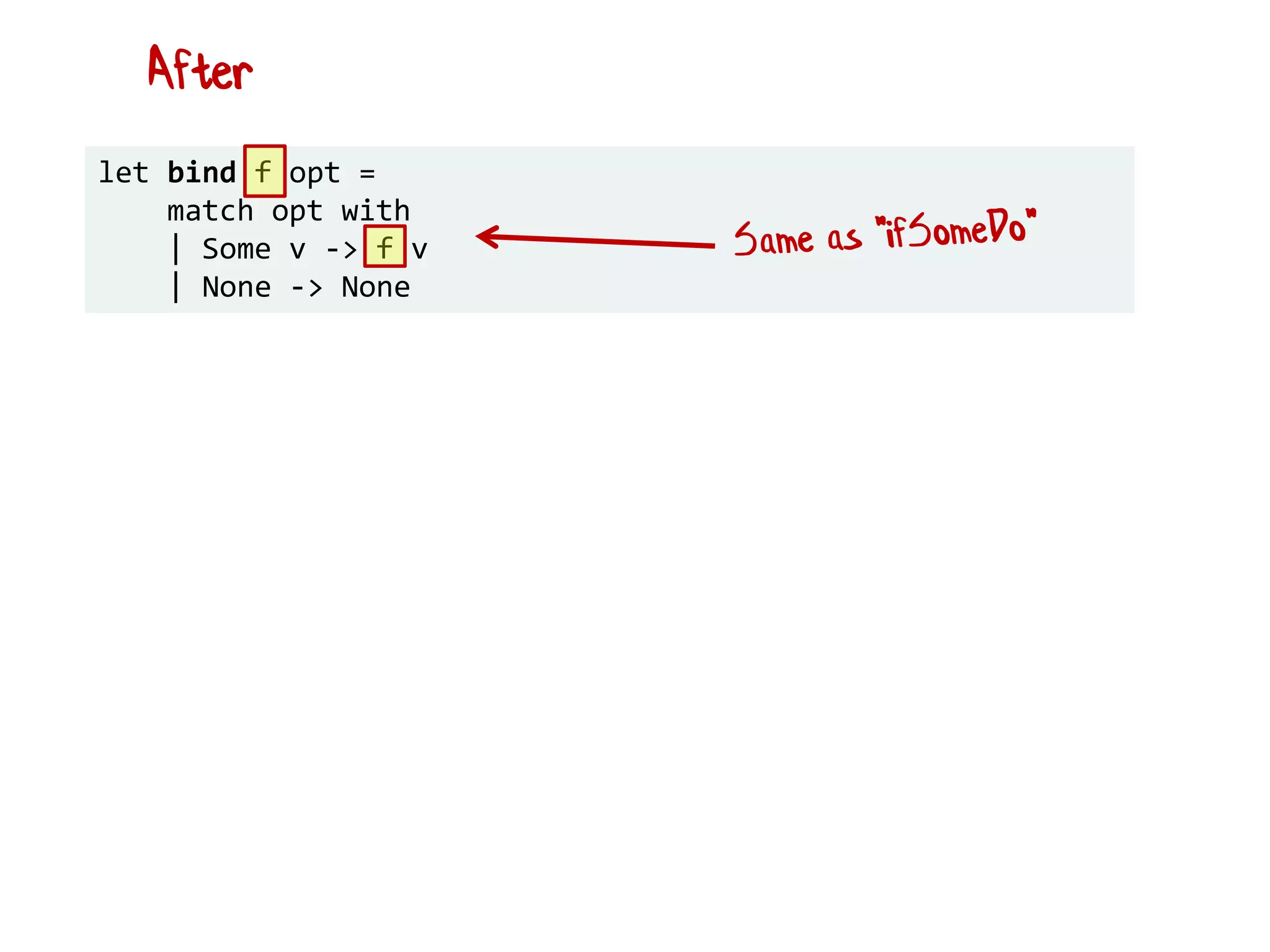
let bind f opt = match opt with | Some v -> f v | None -> None After

Pattern: Use bind to chain tasks a.k.a "promise" "future"

let taskExample input = let taskX = startTask input taskX.WhenFinished (fun x -> let taskY = startAnotherTask x taskY.WhenFinished (fun y -> let taskZ = startThirdTask y taskZ.WhenFinished (fun z -> z // final result ) ) ) Before

let taskBind f task = task.WhenFinished (fun taskResult -> f taskResult) let taskExample input = startTask input |> taskBind startAnotherTask |> taskBind startThirdTask |> taskBind ... This pattern is also a “monadic bind” After

Pattern: Use bind to chain error handlers

string UpdateCustomerWithErrorHandling() { var request = receiveRequest(); validateRequest(request); canonicalizeEmail(request); db.updateDbFromRequest(request); smtpServer.sendEmail(request.Email) return "OK"; }

string UpdateCustomerWithErrorHandling() { var request = receiveRequest(); var isValidated = validateRequest(request); if (!isValidated) { return "Request is not valid" } canonicalizeEmail(request); db.updateDbFromRequest(request); smtpServer.sendEmail(request.Email) return "OK"; }

string UpdateCustomerWithErrorHandling() { var request = receiveRequest(); var isValidated = validateRequest(request); if (!isValidated) { return "Request is not valid" } canonicalizeEmail(request); var result = db.updateDbFromRequest(request); if (!result) { return "Customer record not found" } smtpServer.sendEmail(request.Email) return "OK"; }

string UpdateCustomerWithErrorHandling() { var request = receiveRequest(); var isValidated = validateRequest(request); if (!isValidated) { return "Request is not valid" } canonicalizeEmail(request); try { var result = db.updateDbFromRequest(request); if (!result) { return "Customer record not found" } } catch { return "DB error: Customer record not updated" } smtpServer.sendEmail(request.Email) return "OK"; }

string UpdateCustomerWithErrorHandling() { var request = receiveRequest(); var isValidated = validateRequest(request); if (!isValidated) { return "Request is not valid" } canonicalizeEmail(request); try { var result = db.updateDbFromRequest(request); if (!result) { return "Customer record not found" } } catch { return "DB error: Customer record not updated" } if (!smtpServer.sendEmail(request.Email)) { log.Error "Customer email not sent" } return "OK"; }

Tip: Use a Result type for error handling

Request SuccessValidate Failure type Result = | Ok of SuccessValue | Error of ErrorValue Define a choice type

Request SuccessValidate Failure let validateInput input = if input.name = "" then Error "Name must not be blank" else if input.email = "" then Error "Email must not be blank" else Ok input // happy path

FP terminology • A monad is – A data type – With an associated bind/flatMap function (and some other stuff) – With a sensible implementation (monad laws). • A monadic function is – A switch/points function – bind/flatMap is used to compose them

Tip: Monads are a general purpose way of composing functions with complex outputs

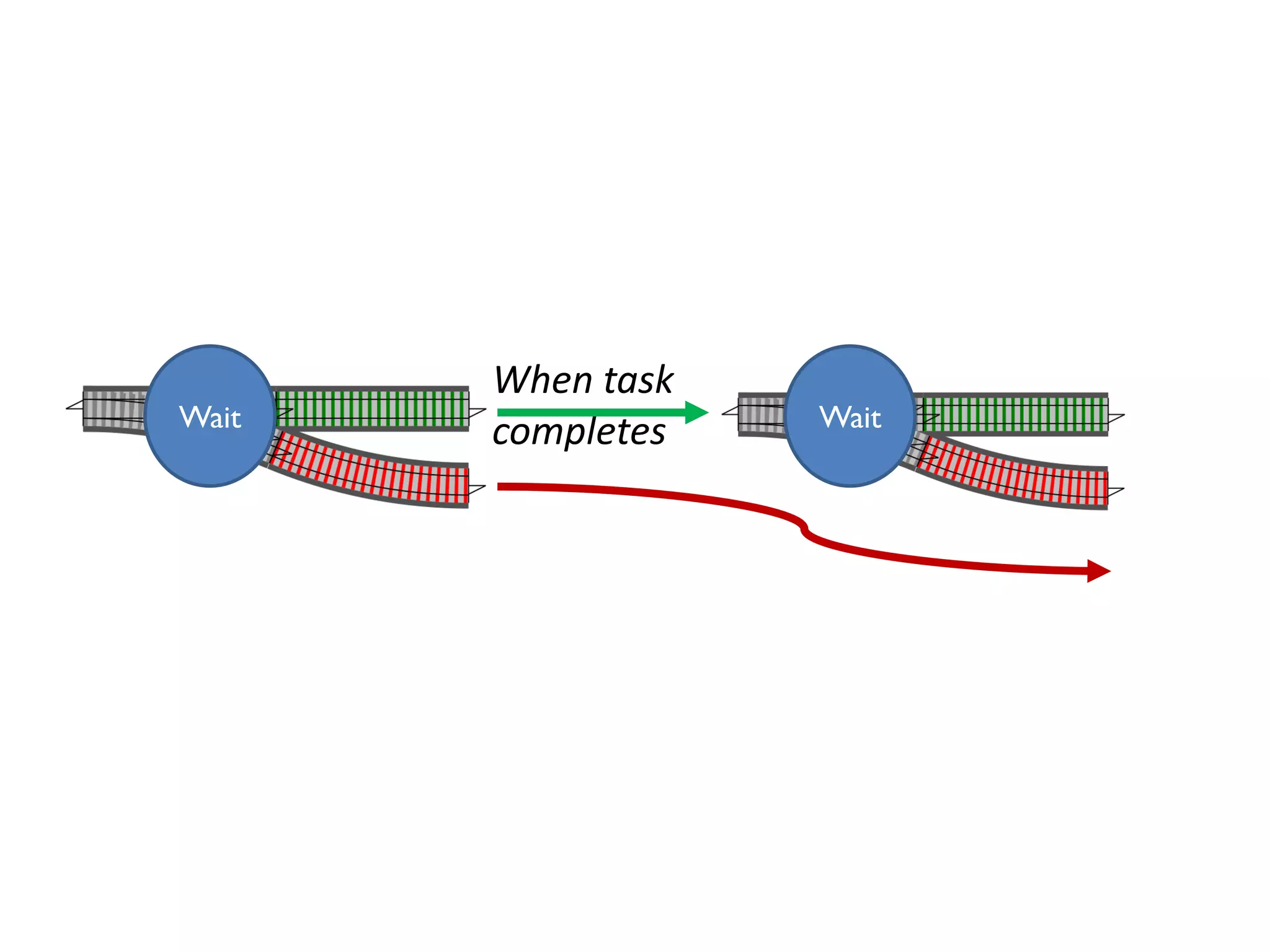
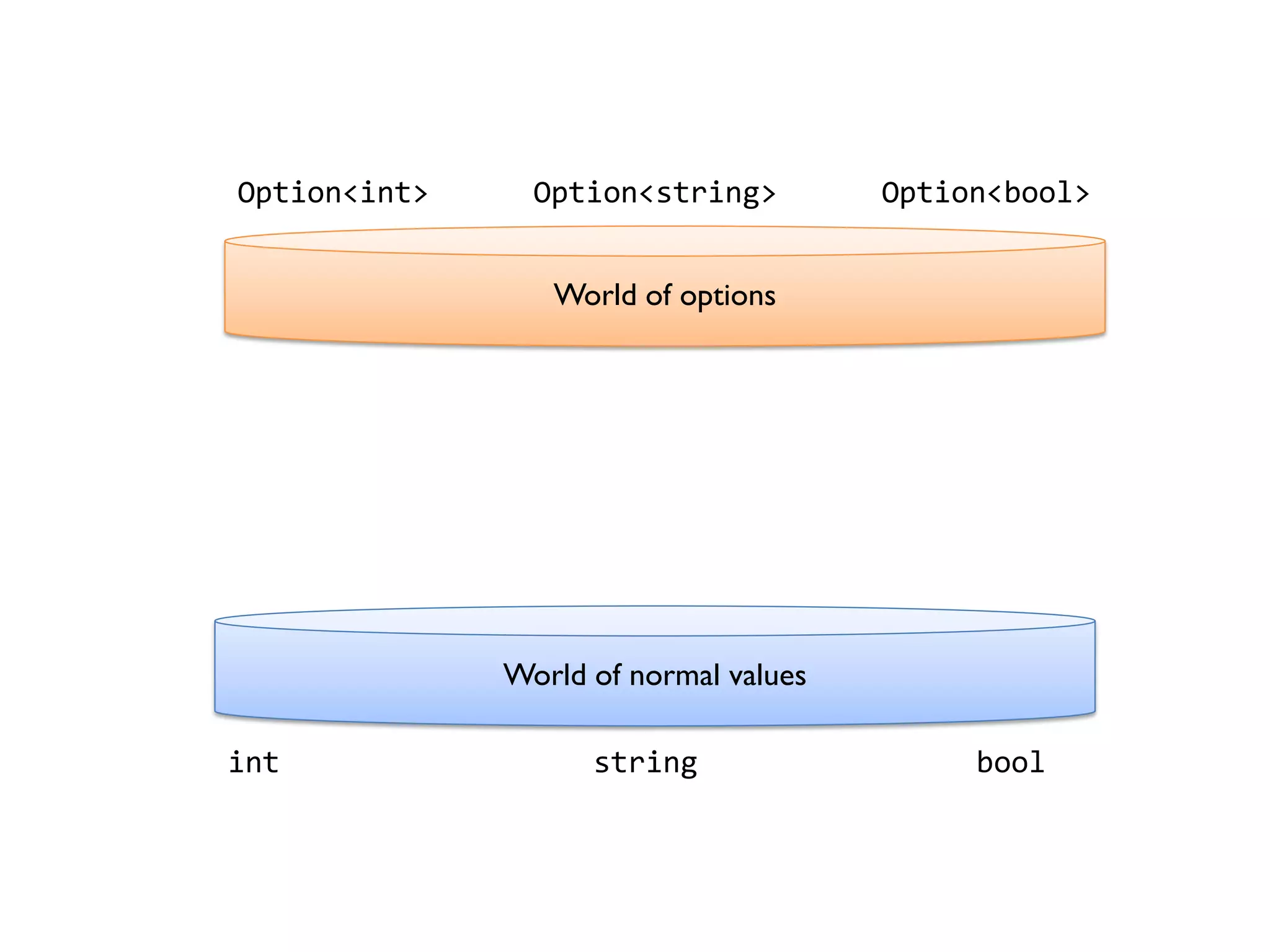
World of normal values int string bool World of options Option<int> Option<string> Option<bool>

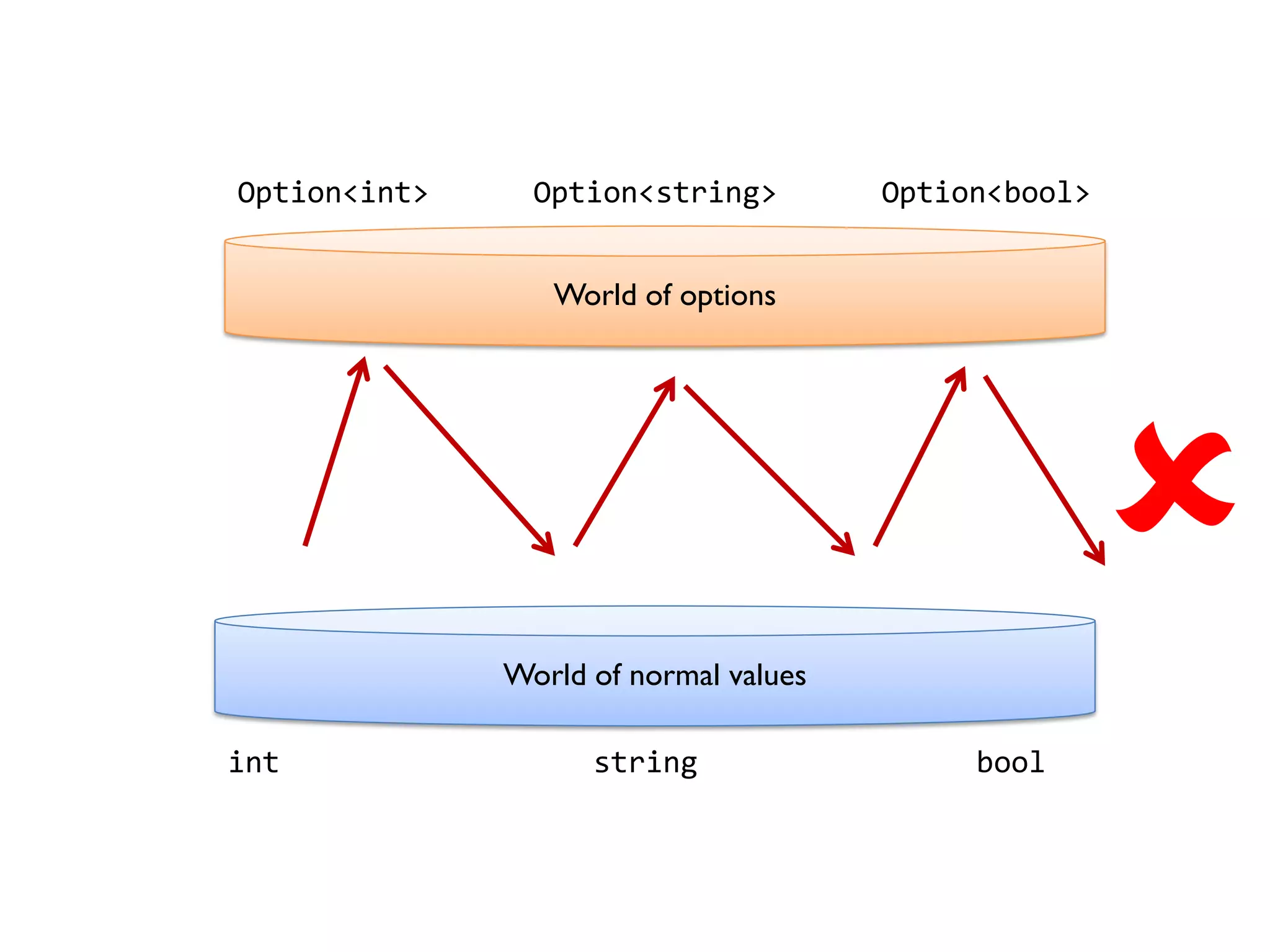
World of options World of normal values int string bool Option<int> Option<string> Option<bool> 

World of options World of normal values Option<int> Option<string> Option<bool>  int string bool

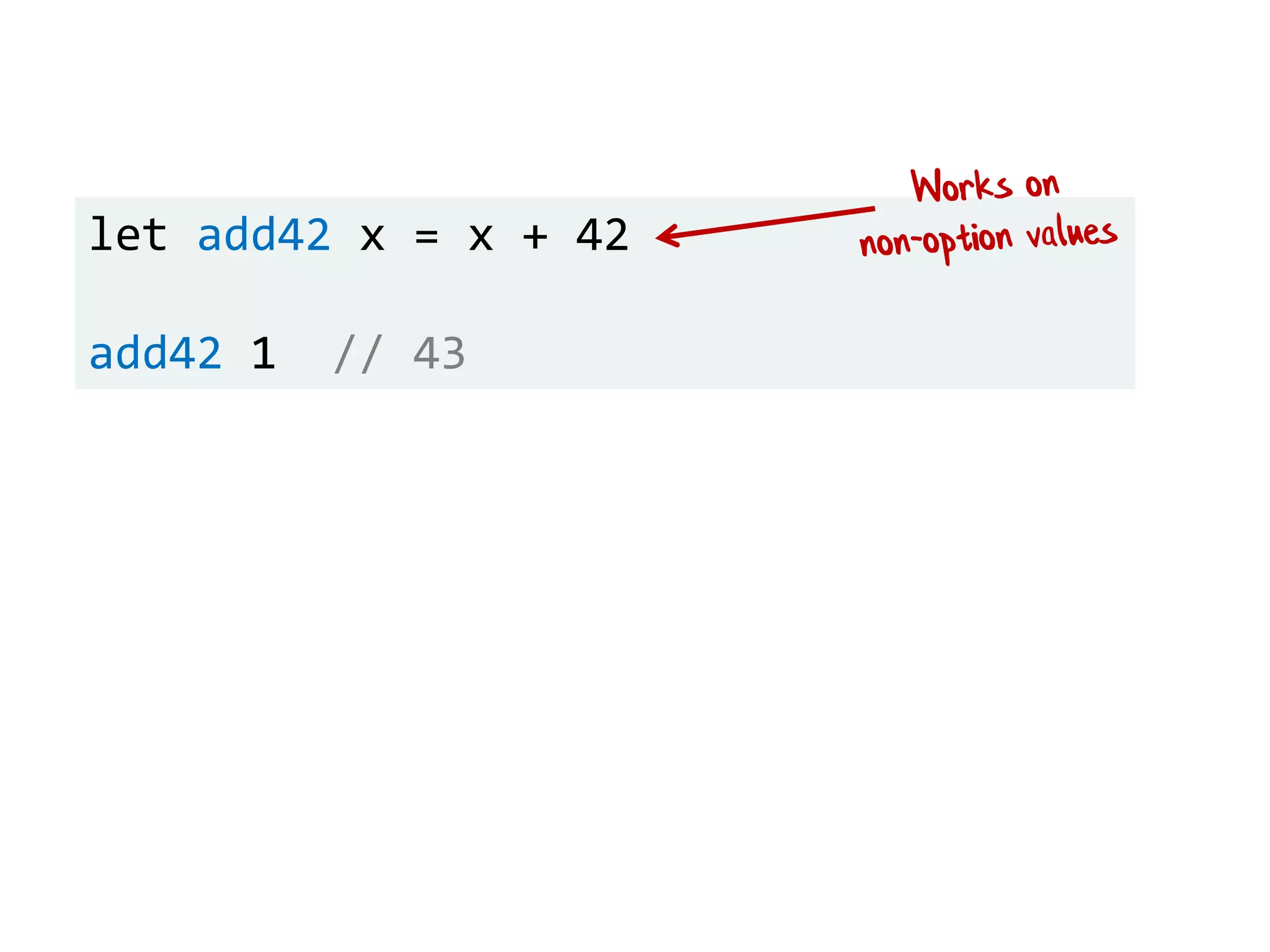
let add42 x = x + 42 add42 1 // 43

let add42ToOption opt = if opt.IsSome then let newVal = add42 opt.Value Some newVal else None 

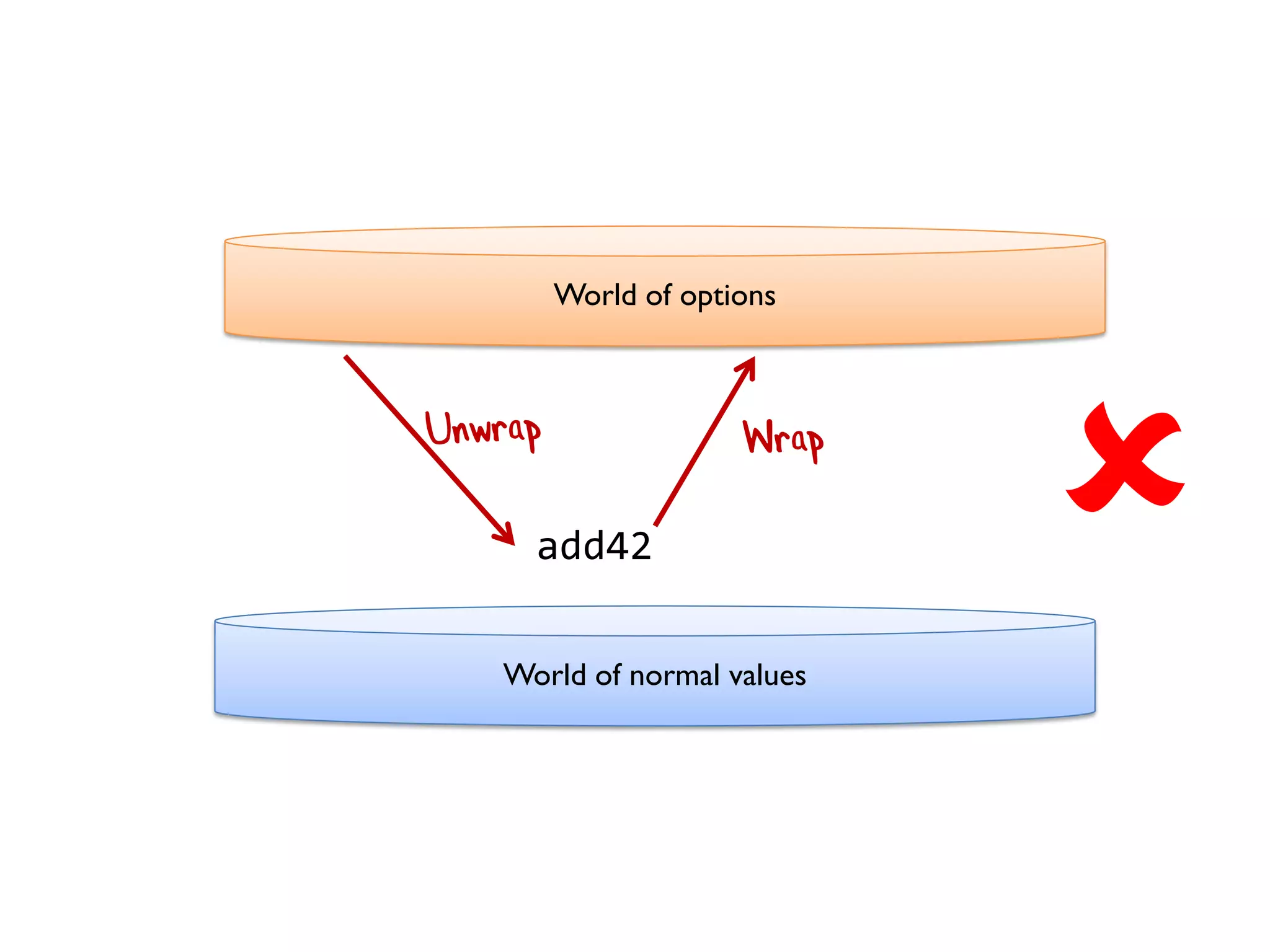
World of options World of normal values add42 

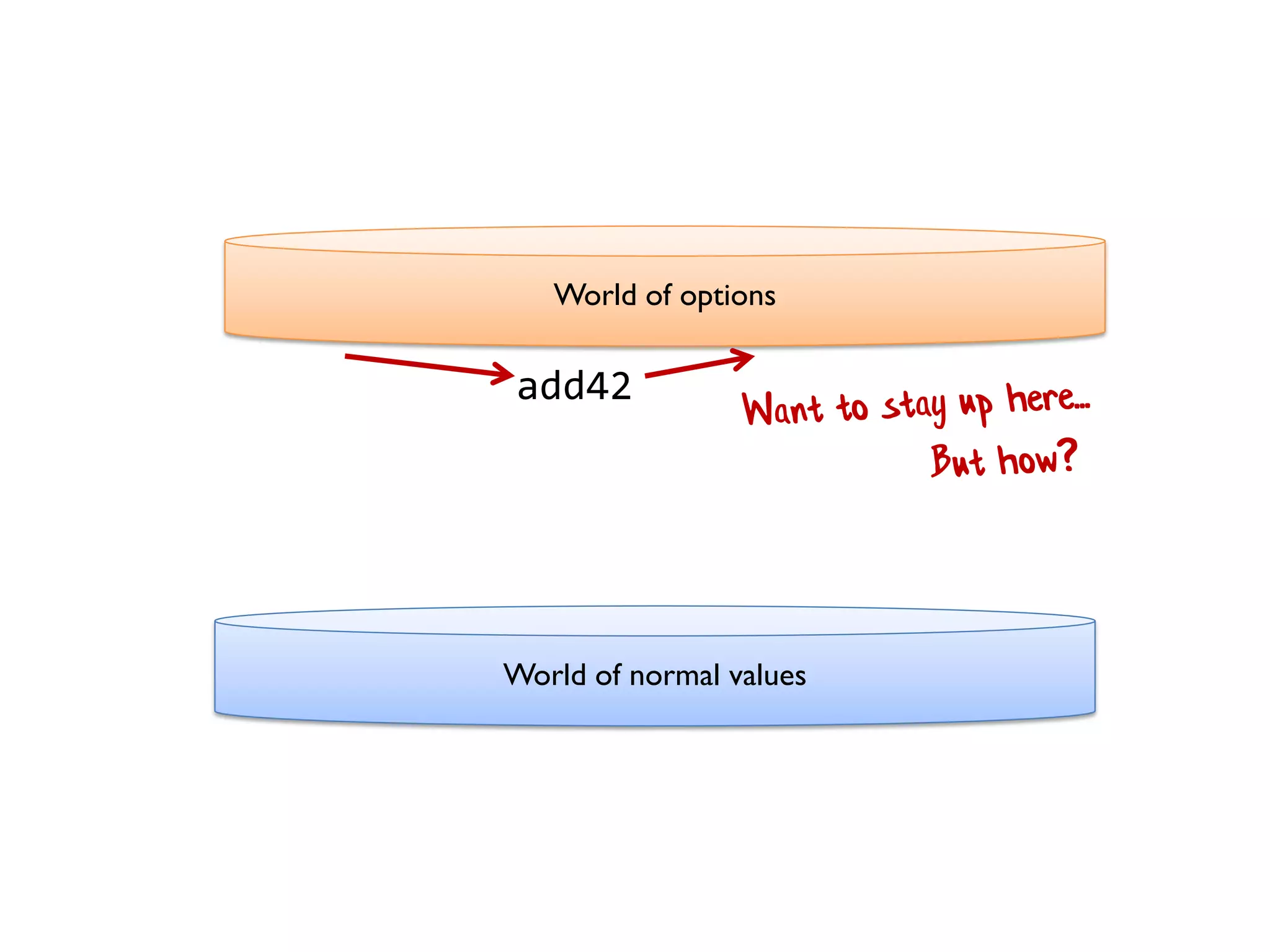
World of options World of normal values add42

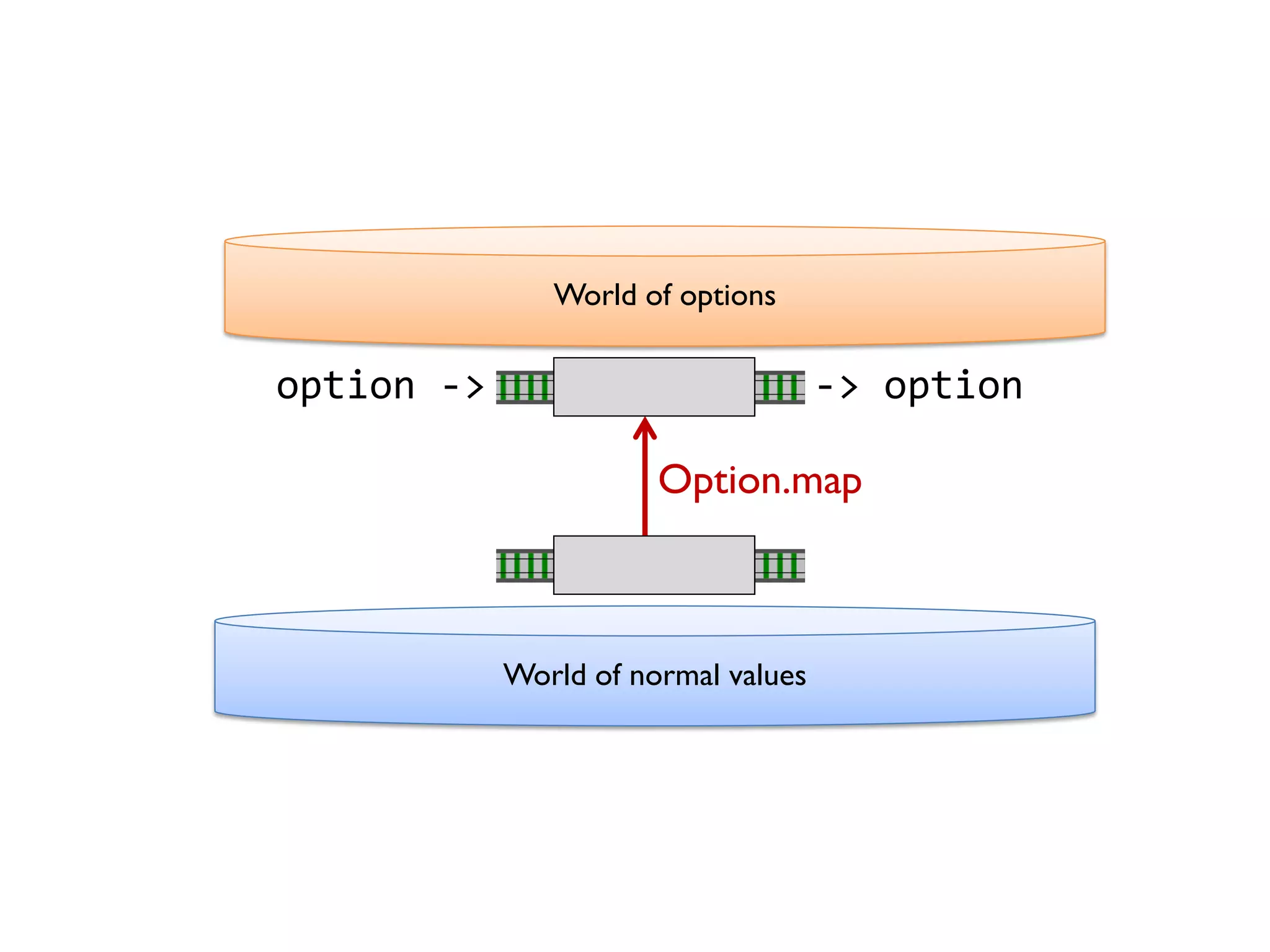
World of options World of normal values option -> -> option Option.map

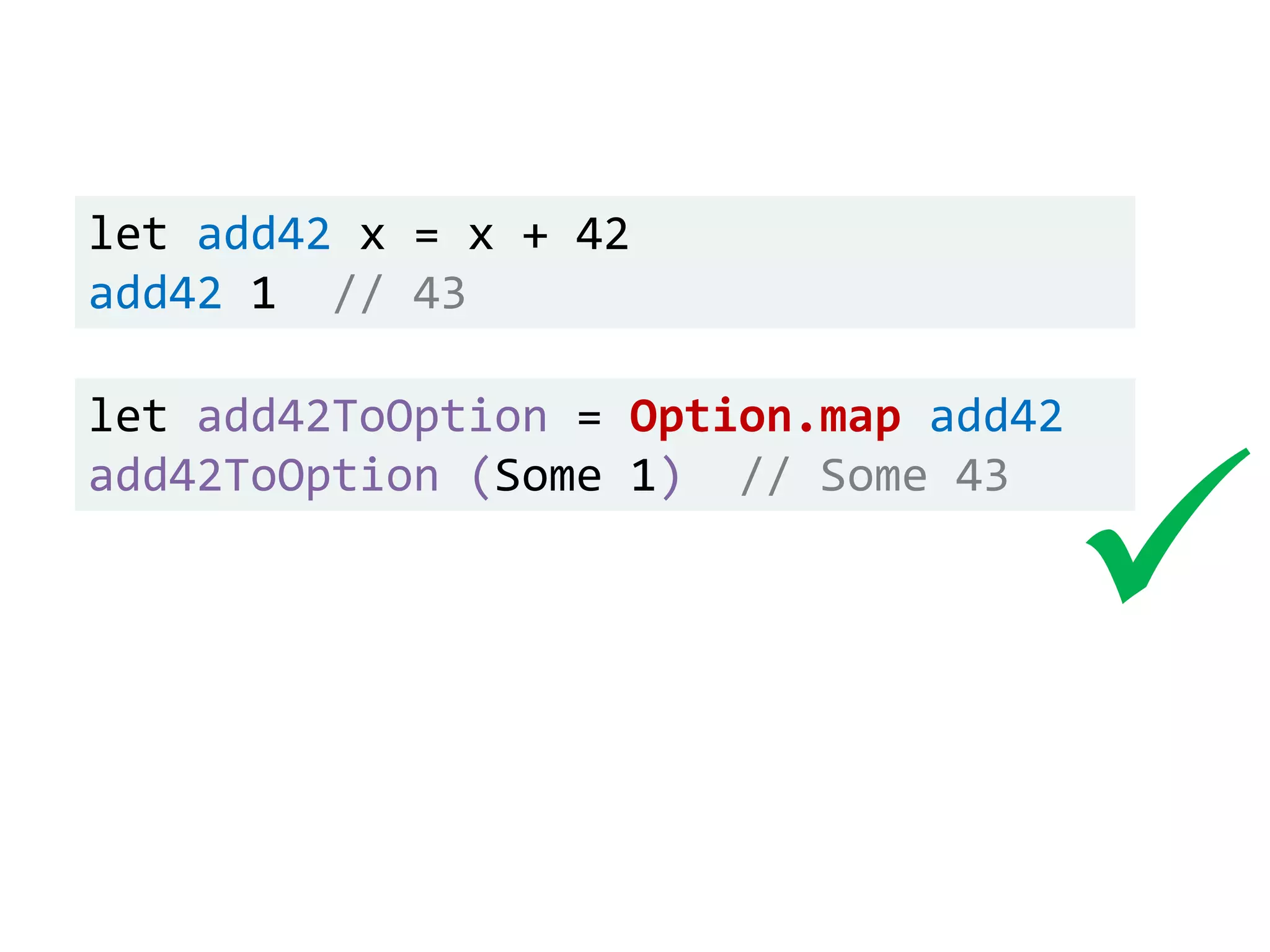
let add42 x = x + 42 add42 1 // 43 let add42ToOption = Option.map add42 add42ToOption (Some 1) // Some 43 

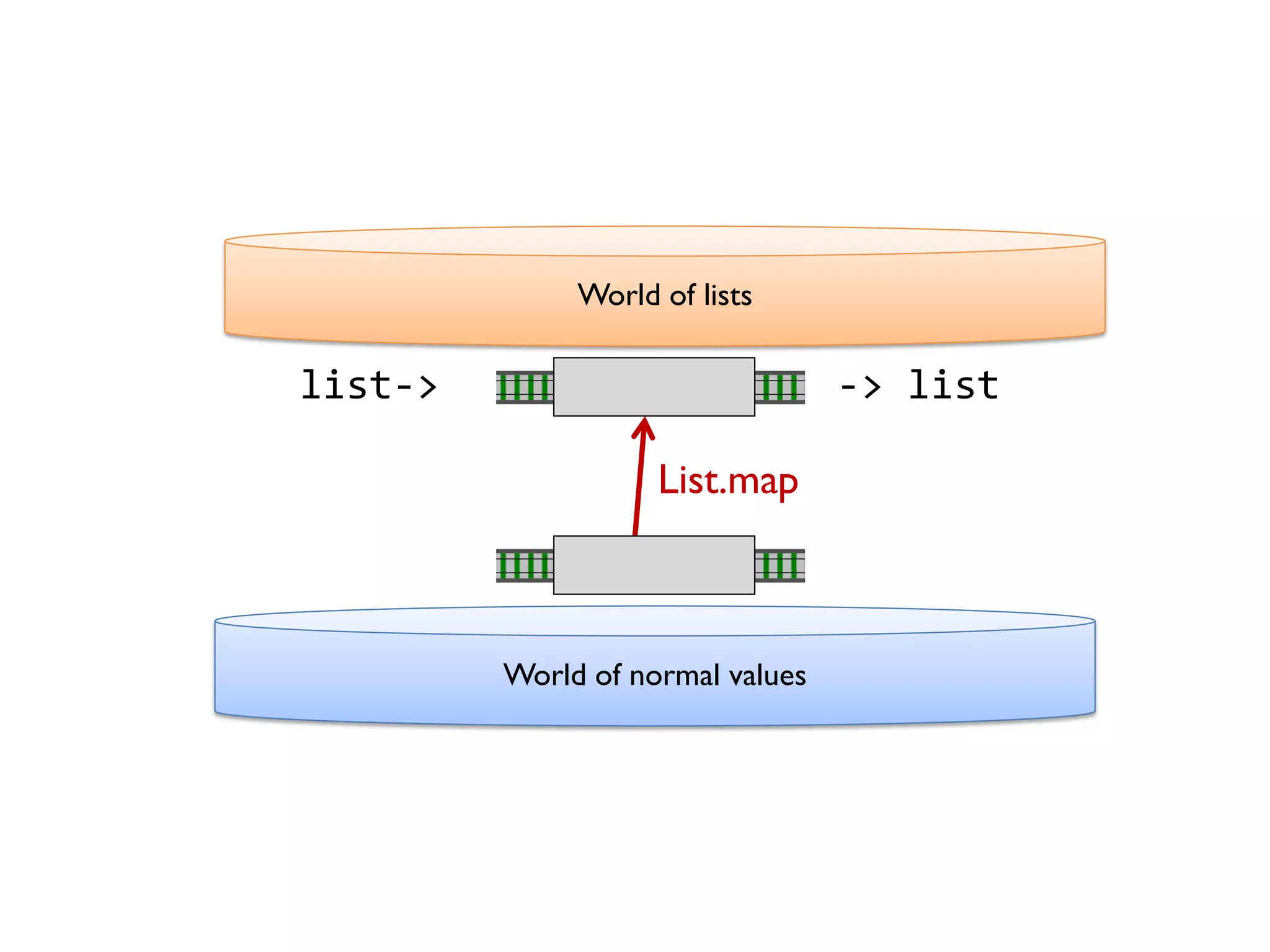
World of lists World of normal values List.map list-> -> list

let add42ToEach = List.map add42 add42ToEach [1;2;3] // [43;44;45]

World of async World of normal values async<T> -> -> async<U> Async.map

Guideline: Most wrapped generic types have a “map”. Use it!

Guideline: If you create your own generic type, create a “map” for it.

FP terminology • A functor is – A data type – With an associated "map" function (with a sensible implementation)

1 + 2 = 3 1 + (2 + 3) = (1 + 2) + 3 1 + 0 = 1 0 + 1 = 1

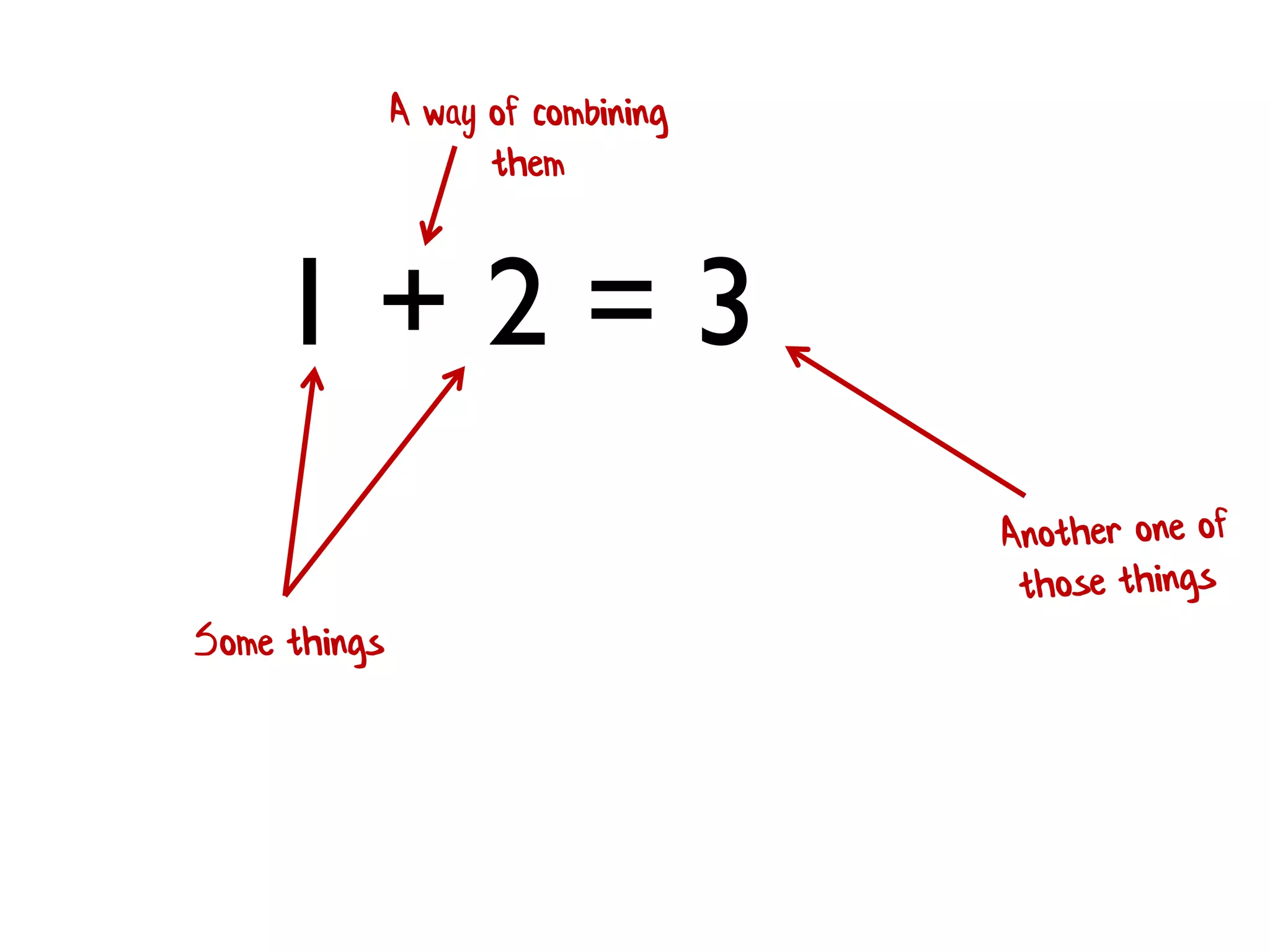
1 + 2 = 3 Some things A way of combining them

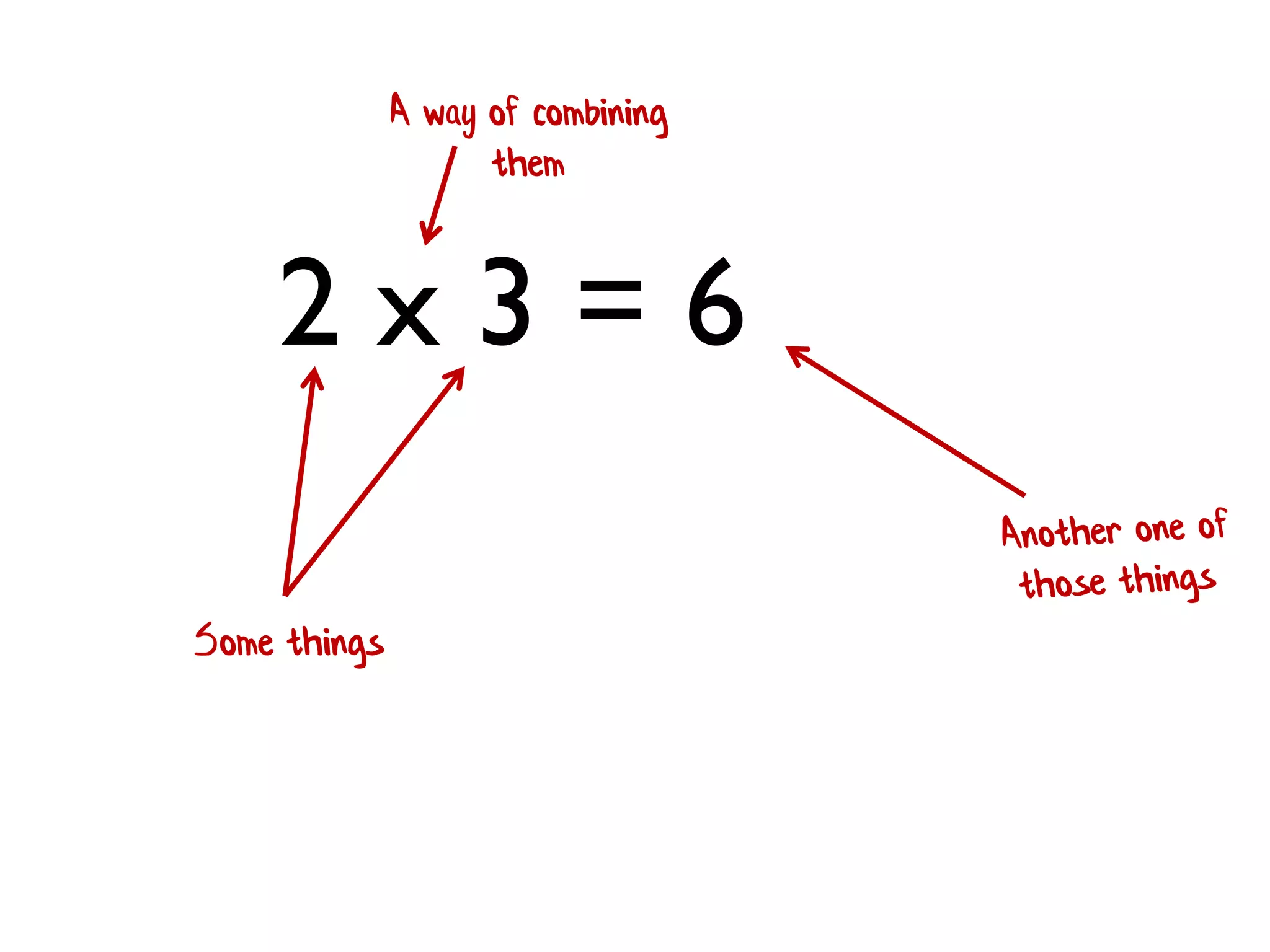
2 x 3 = 6 Some things A way of combining them

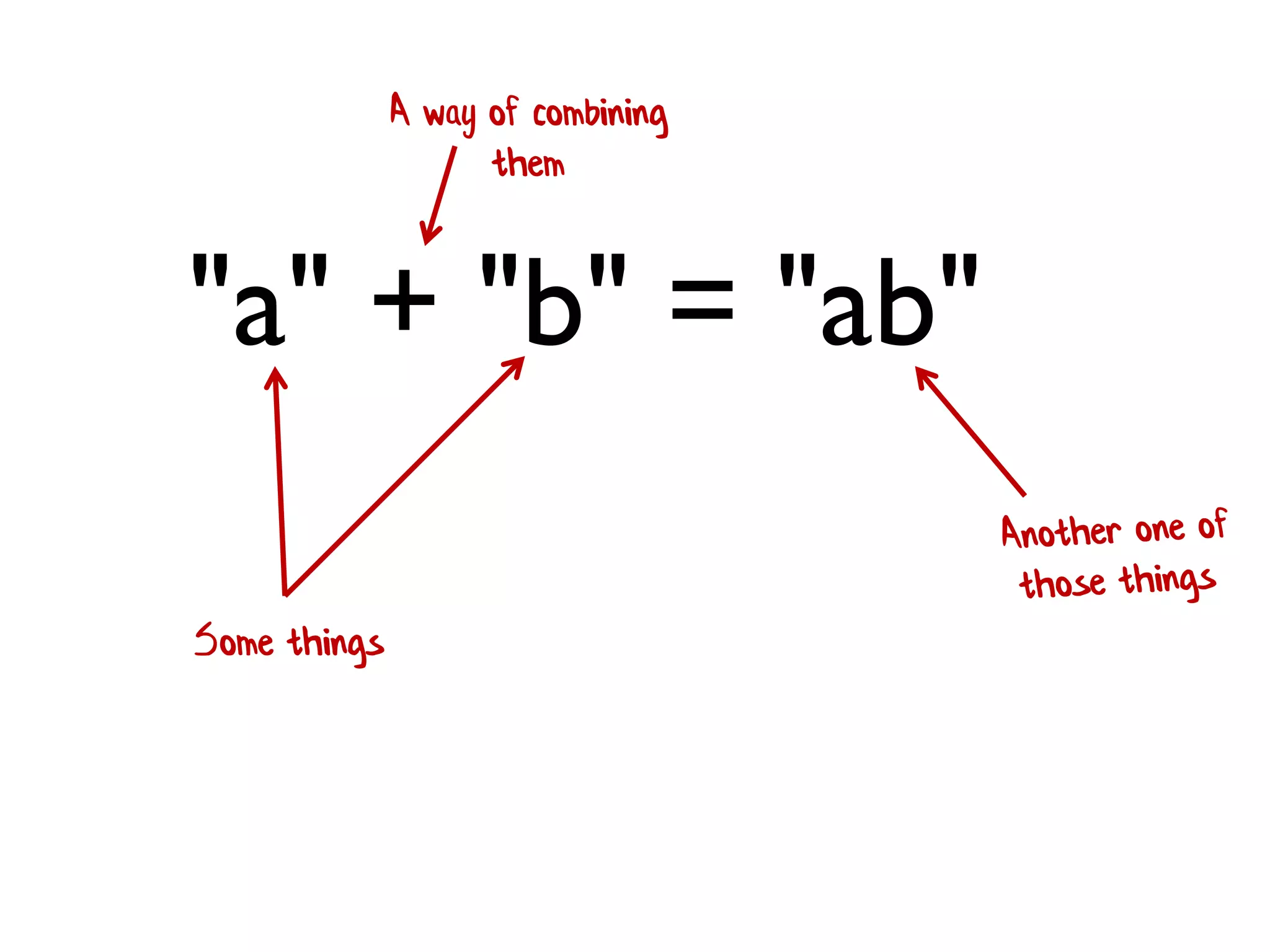
"a" + "b" = "ab" Some things A way of combining them

concat([a],[b]) = [a; b] Some things A way of combining them

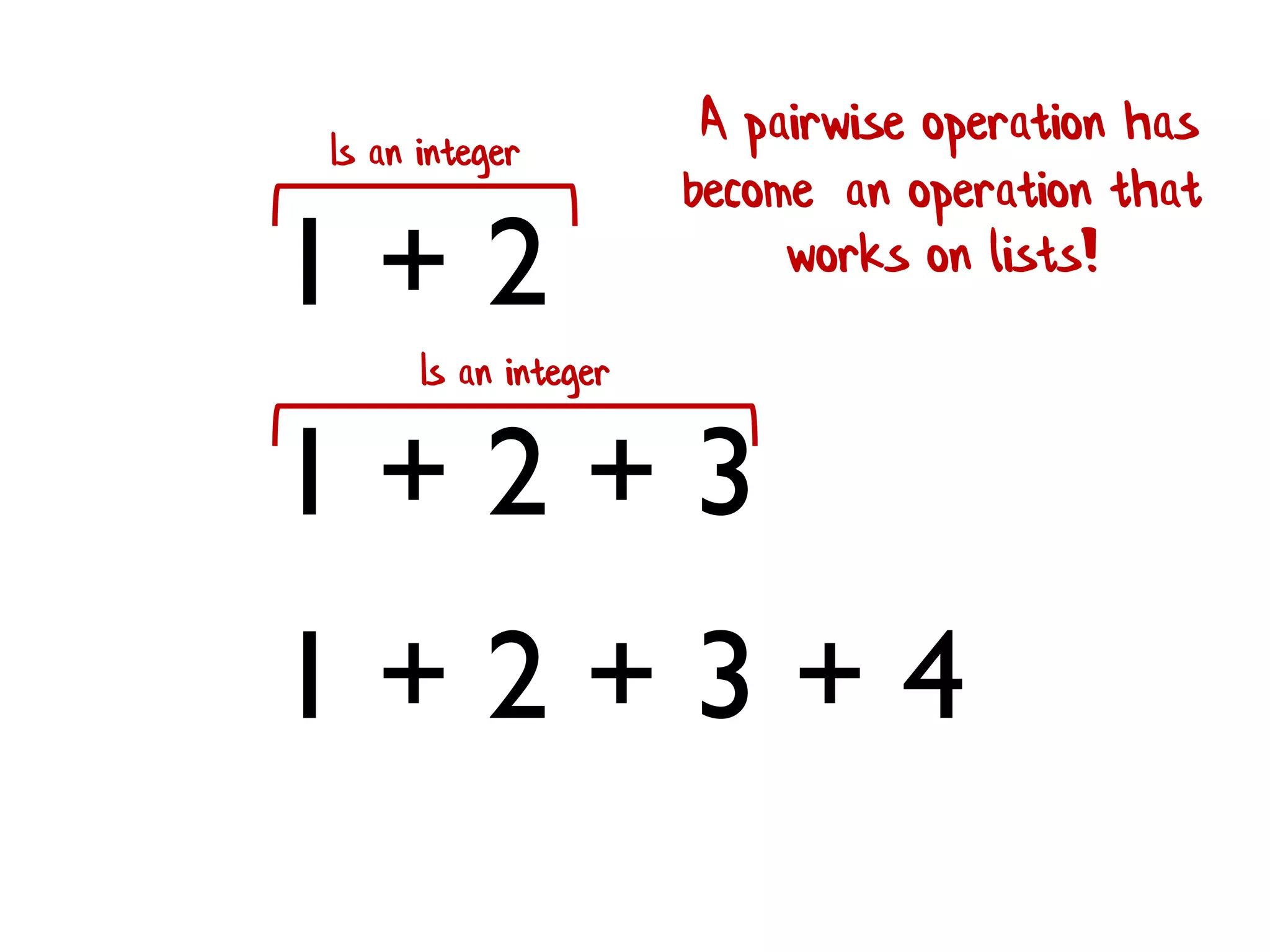
1 + 2 1 + 2 + 3 1 + 2 + 3 + 4 Is an integer Is an integer A pairwise operation has become an operation that works on lists!

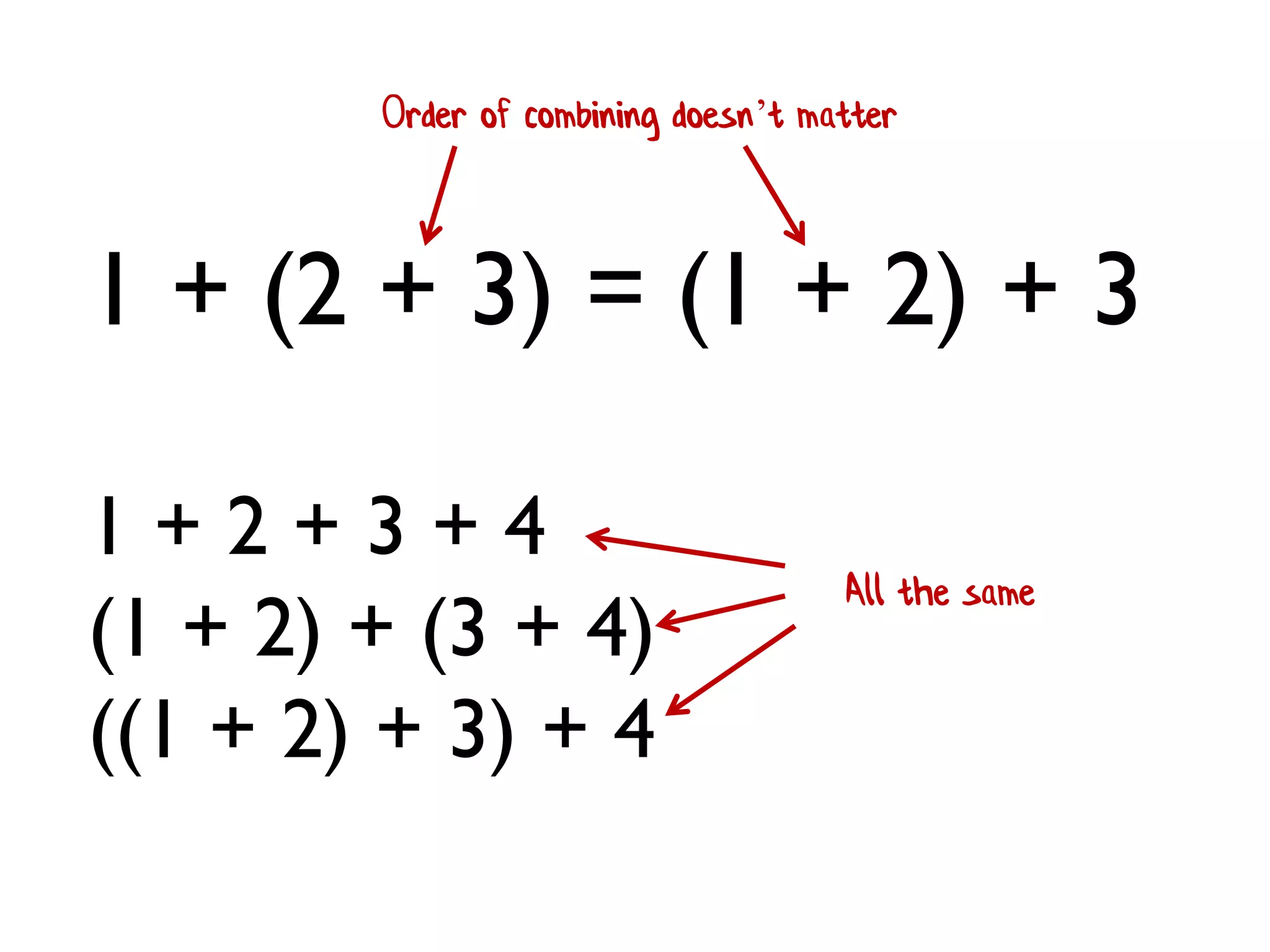
1 + (2 + 3) = (1 + 2) + 3 Order of combining doesn’t matter 1 + 2 + 3 + 4 (1 + 2) + (3 + 4) ((1 + 2) + 3) + 4 All the same

1 - (2 - 3) = (1 - 2) - 3 Order of combining does matter

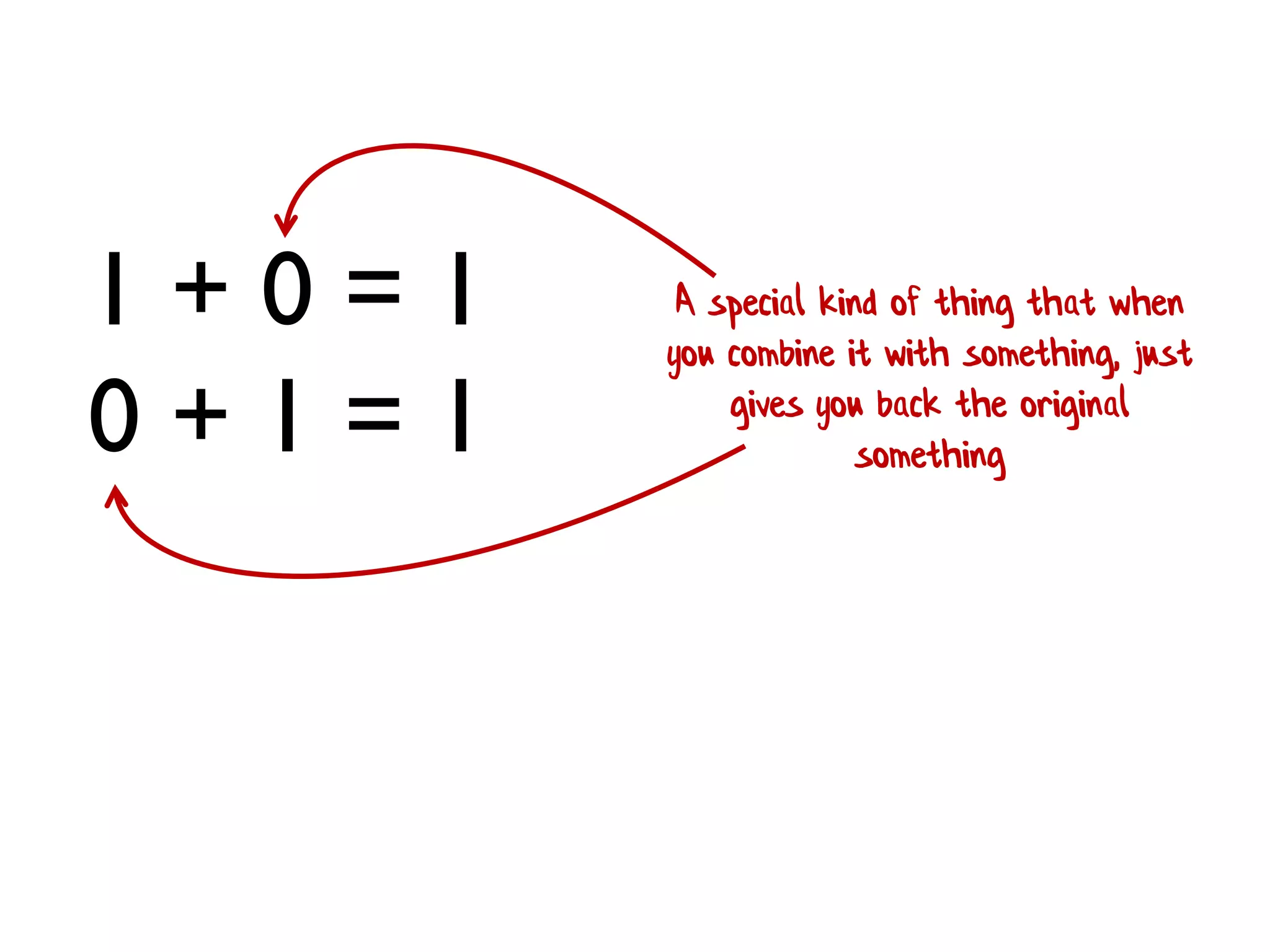
1 + 0 = 1 0 + 1 = 1 A special kind of thing that when you combine it with something, just gives you back the original something

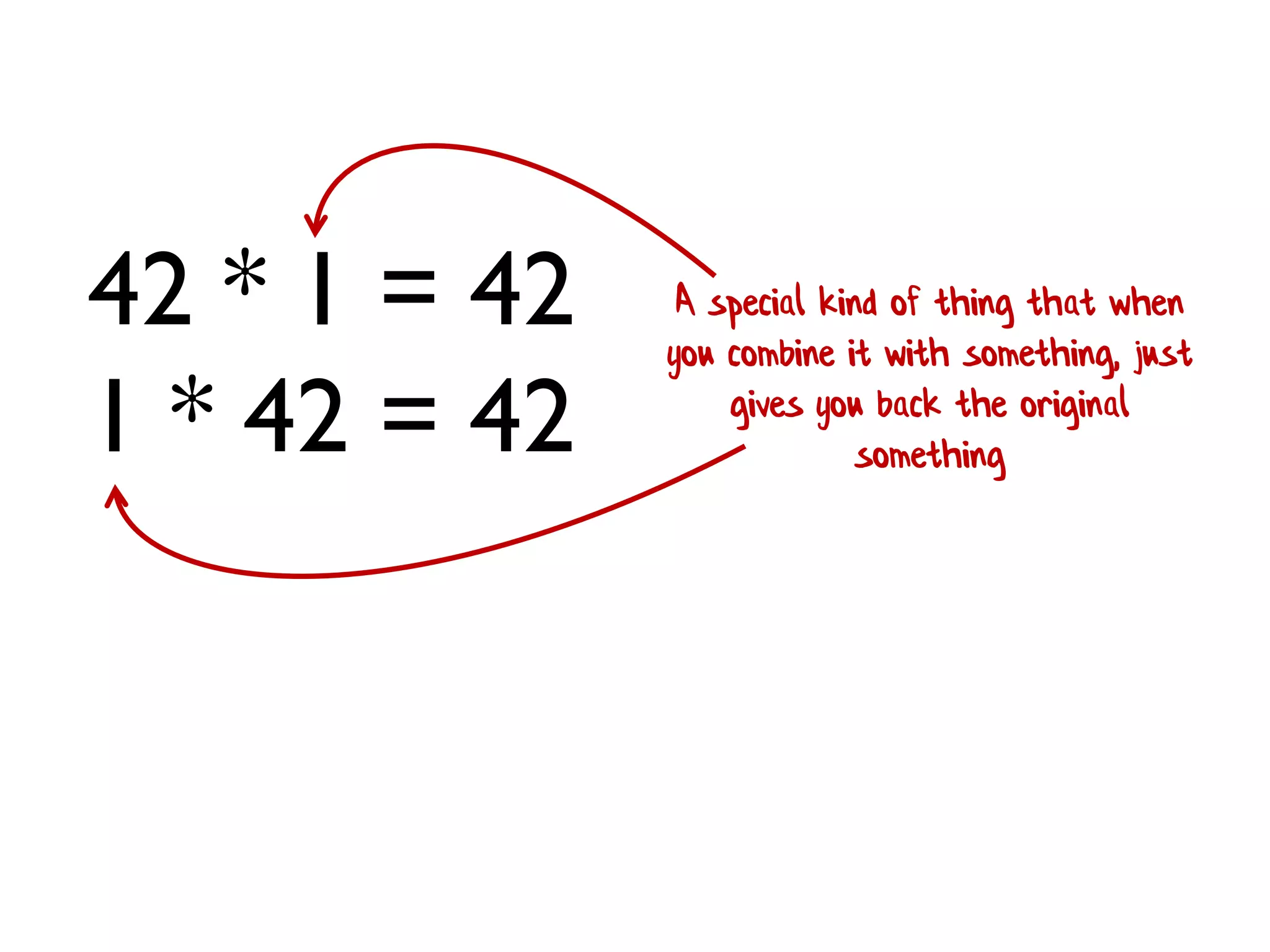
42 * 1 = 42 1 * 42 = 42 A special kind of thing that when you combine it with something, just gives you back the original something

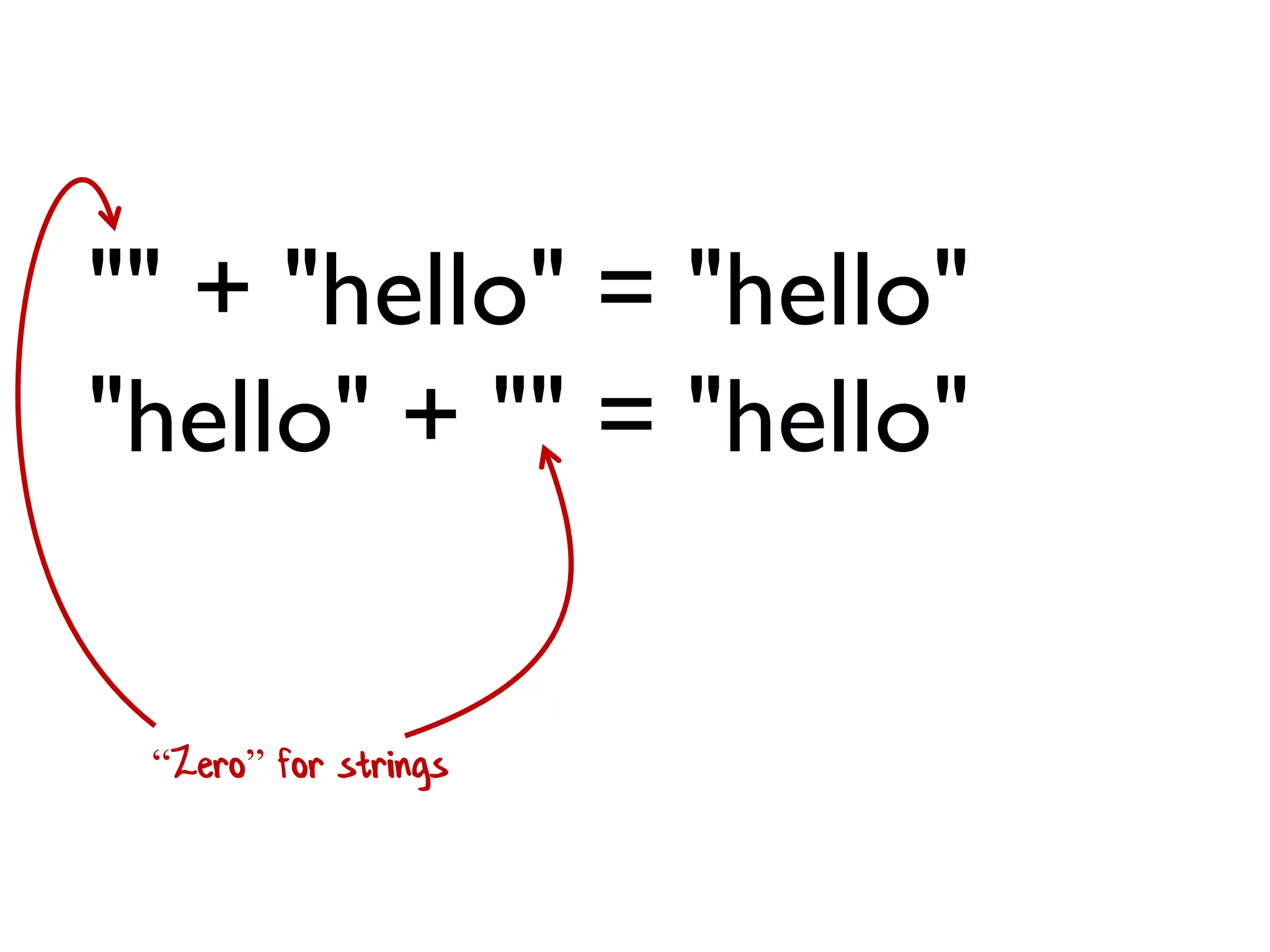
"" + "hello" = "hello" "hello" + "" = "hello" “Zero” for strings

• You start with a bunch of things, and some way of combining them two at a time. • Rule 1 (Closure):The result of combining two things is always another one of the things. • Rule 2 (Associativity):When combining more than two things, which pairwise combination you do first doesn't matter. • Rule 3 (Identity element):There is a special thing called "zero" such that when you combine any thing with "zero" you get the original thing back. A monoid!

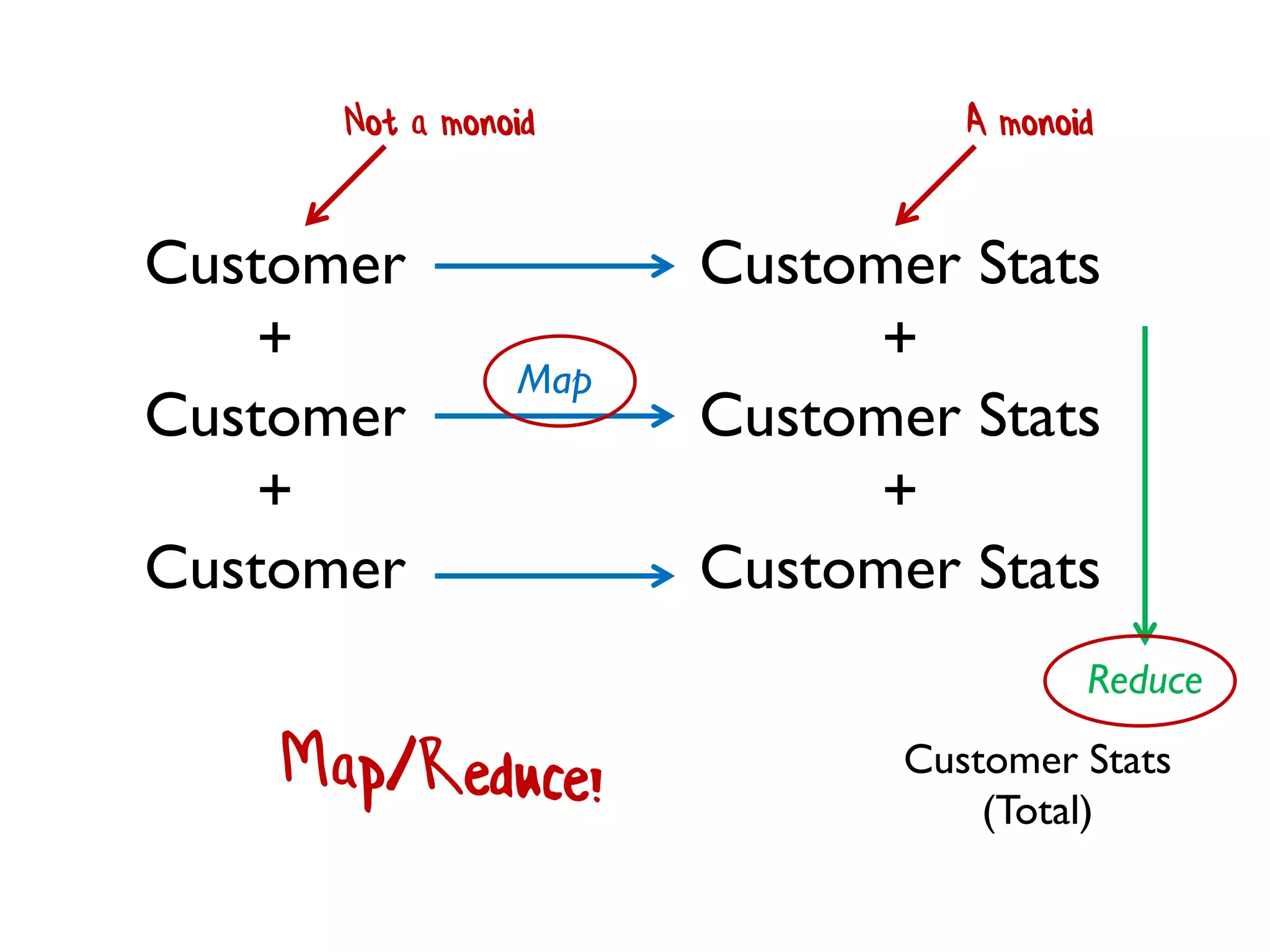
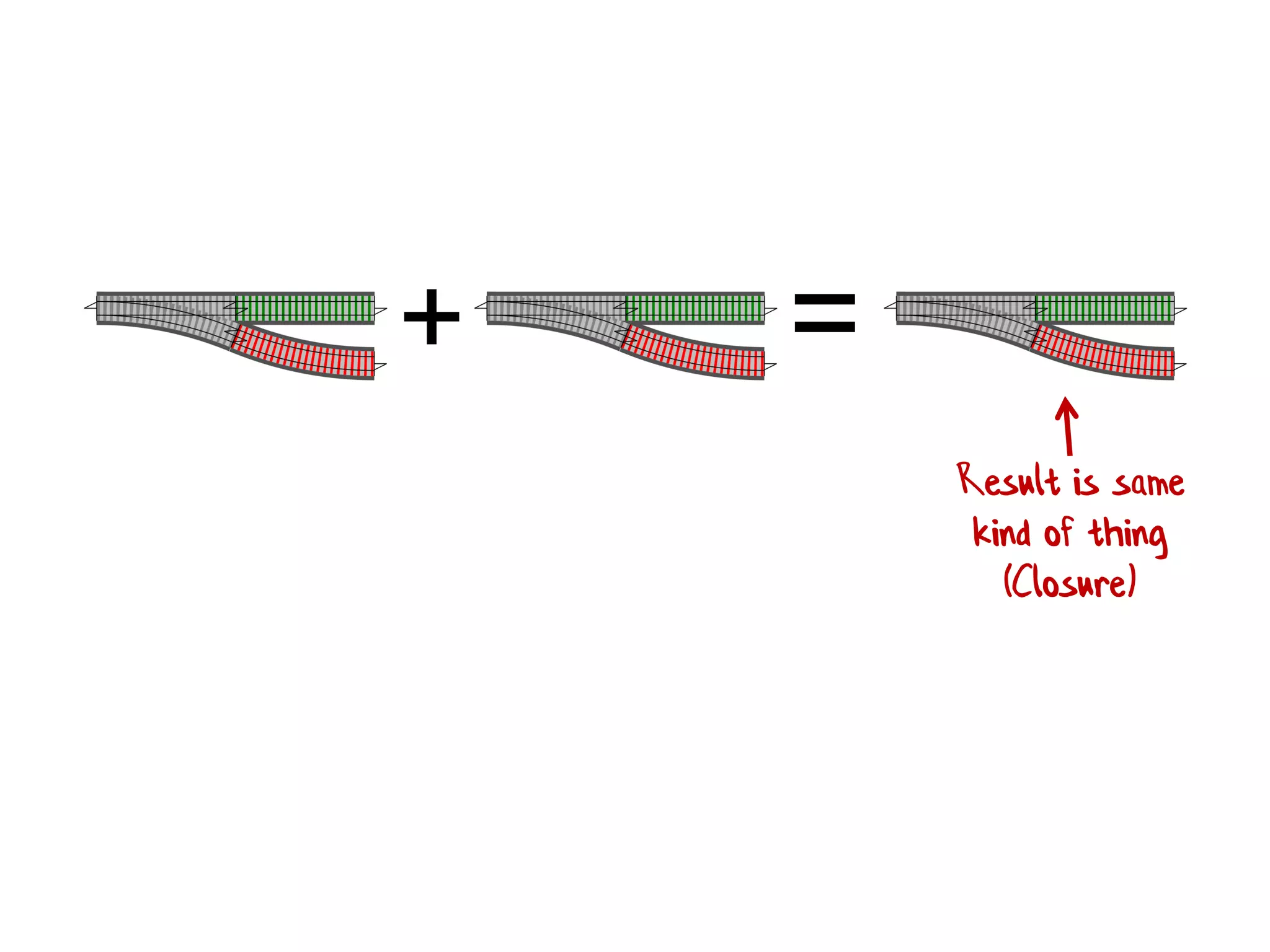
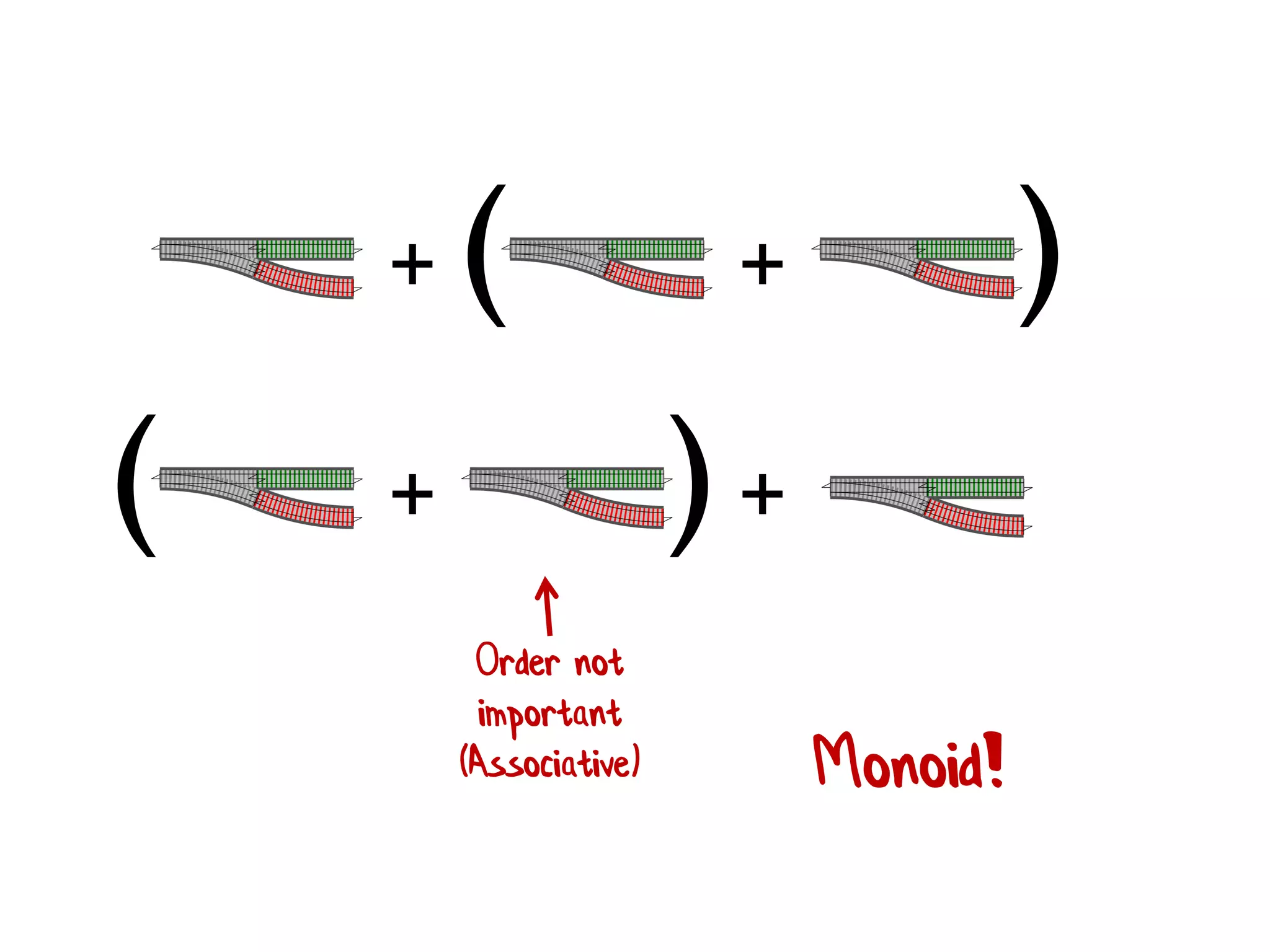
• Rule 1 (Closure):The result of combining two things is always another one of the things. • Benefit: converts pairwise operations into operations that work on lists. 1 + 2 + 3 + 4 [ 1; 2; 3; 4 ] |> List.reduce (+) We'll see this a lot!

1 * 2 * 3 * 4 [ 1; 2; 3; 4 ] |> List.reduce (*) • Rule 1 (Closure):The result of combining two things is always another one of the things. • Benefit: converts pairwise operations into operations that work on lists.

"a" + "b" + "c" + "d" [ "a"; "b"; "c"; "d" ] |> List.reduce (+) • Rule 1 (Closure):The result of combining two things is always another one of the things. • Benefit: converts pairwise operations into operations that work on lists.

• Rule 2 (Associativity):When combining more than two things, which pairwise combination you do first doesn't matter. • Benefit: Divide and conquer, parallelization, and incremental accumulation.

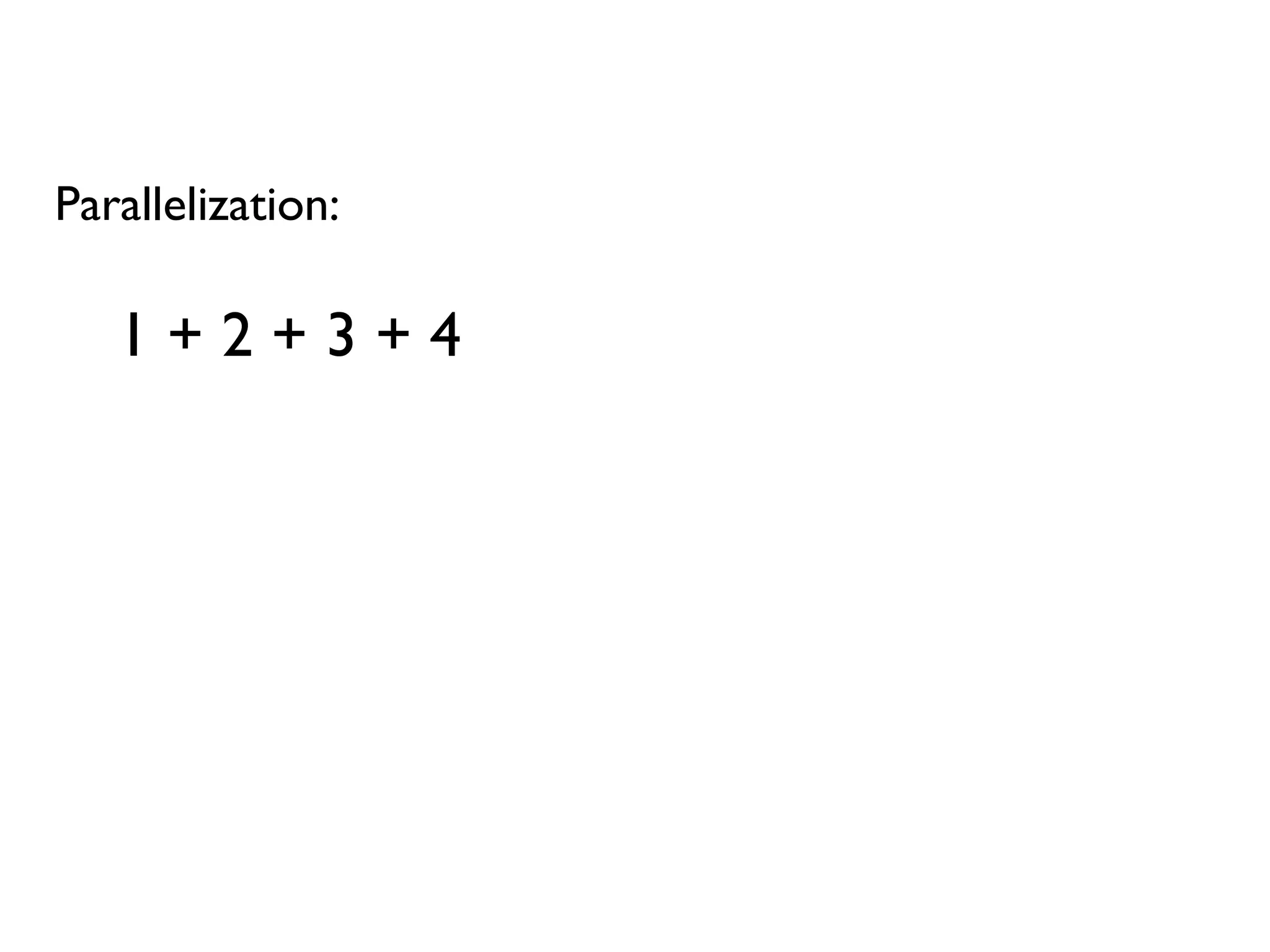
Parallelization: 1 + 2 + 3 + 4

Parallelization: (1 + 2) (3 + 4) 3 + 7

Incremental accumulation (1 + 2 + 3)

Incremental accumulation (1 + 2 + 3) + 4

Incremental accumulation (6) + 4

• How can I use reduce on an empty list? • In a divide and conquer algorithm, what should I do if one of the "divide" steps has nothing in it? • When using an incremental algorithm, what value should I start with when I have no data?

• Rule 3 (Identity element):There is a special thing called "zero" such that when you combine any thing with "zero" you get the original thing back. • Benefit: Initial value for empty or missing data

Tip: Simplify aggregation code with monoids

type OrderLine = {Qty:int; Total:float} let orderLines = [ {Qty=2; Total=19.98} {Qty=1; Total= 1.99} {Qty=3; Total= 3.99} ] How to add them up?

type OrderLine = {Qty:int; Total:float} let addPair line1 line2 = let newQty = line1.Qty + line2.Qty let newTotal = line1.Total + line2.Total {Qty=newQty; Total=newTotal} orderLines |> List.reduce addPair // {Qty=6; Total= 25.96} Any combination of monoids is also a monoid Write a pairwise combiner Profit!

Pattern: Convert non-monoids to monoids

Customer + Customer + Customer Customer Stats + Customer Stats + Customer Stats Reduce Map Not a monoid A monoid Customer Stats (Total)

Hadoop make me a sandwich https://twitter.com/daviottenheimer /status/532661754820829185

Pattern: Seeing monoids everywhere

Monoids in the real world Metrics guideline: Use counters rather than rates Alternative metrics guideline: Make sure your metrics are monoids • incremental updates • can handle missing data

Is function composition a monoid? >> Function 1 apple -> banana Function 2 banana -> cherry New Function apple -> cherry Not the same thing. Not a monoid 

Is function composition a monoid? >> Function 1 apple -> apple Same thing Function 2 apple -> apple Function 3 apple -> apple A monoid! 

=+ Result is same kind of thing (Closure)

+ Order not important (Associative) Monoid! +( ) ++( )

Monad laws • Closure, Associativity, Identity – The monad laws are just the monoid definitions in diguise • What happens if you break the monad laws? – You go to jail – You lose monoid benefits such as aggregation

"A monad is just a monoid in the category of endofunctors"

Review • Partial Application – For composing functions with multiple parameters • Bind/Monads – For composing functions with effects • Map/Functors – For composing functions without leaving the other world • Monoids – A general pattern for composing things

Review • Partial Application – For composing functions with multiple parameters • Bind/Monads – For composing functions with effects • Map/Functor – For composing functions without leaving the other world • Monoids – A pattern for composing things

Slides and video here fsharpforfunandprofit.com/fppatterns Functional Design Patterns Thank you!

Functional Design Patterns (DevTernity 2018)

More Related Content

What's hot

Similar to Functional Design Patterns (DevTernity 2018)

More from Scott Wlaschin

Recently uploaded

In this document

Functional Design Patterns (DevTernity 2018)