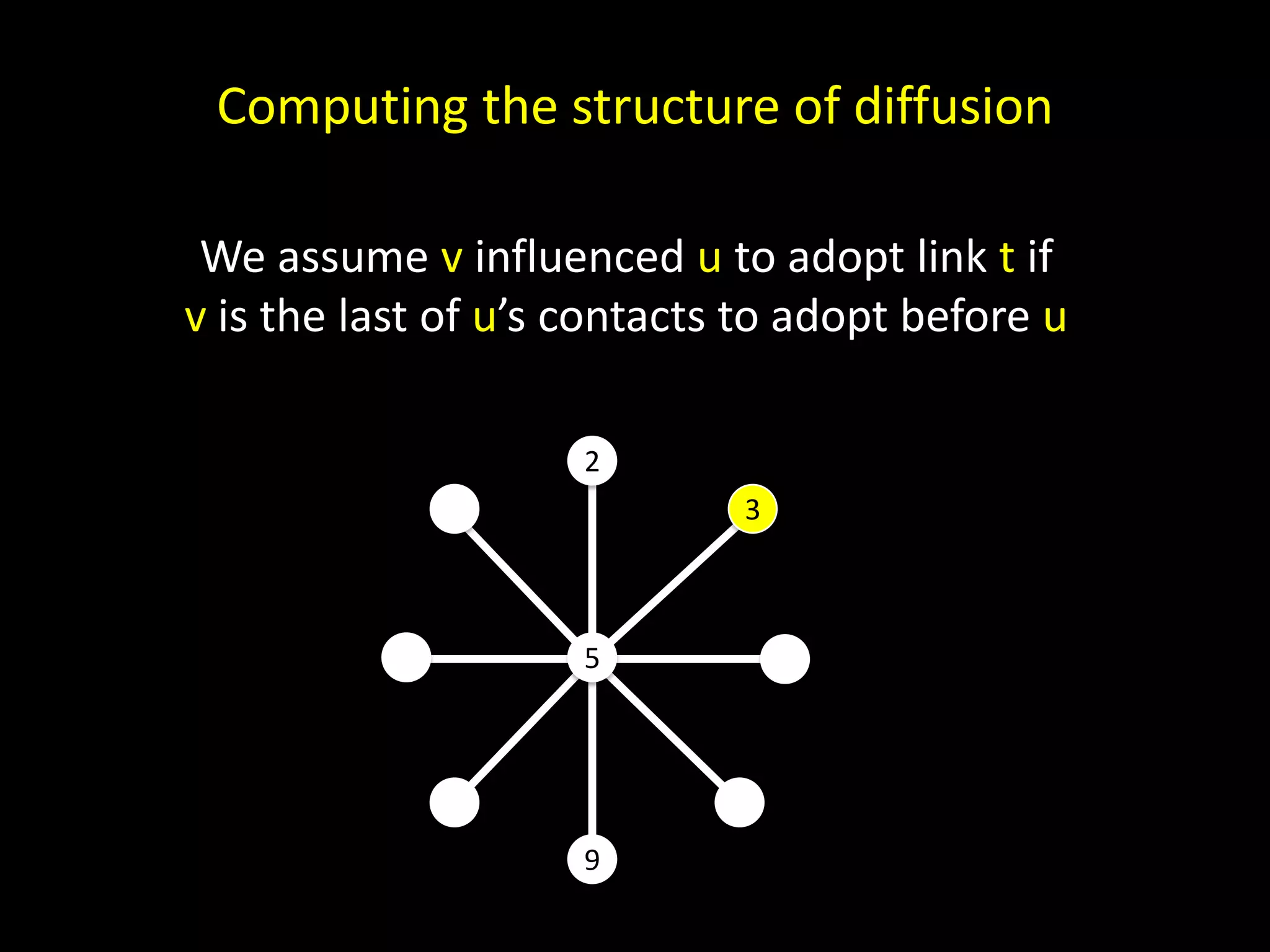
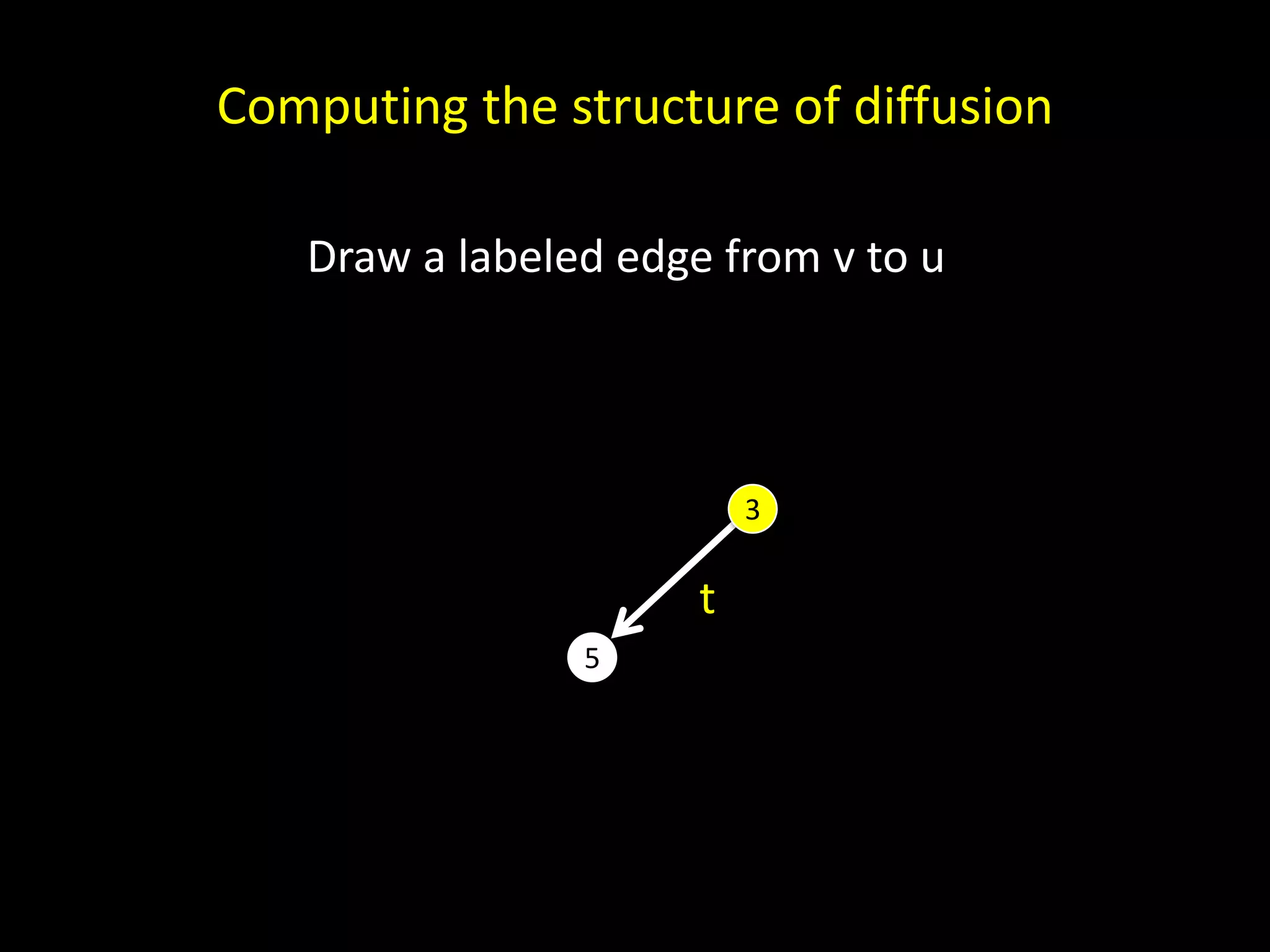
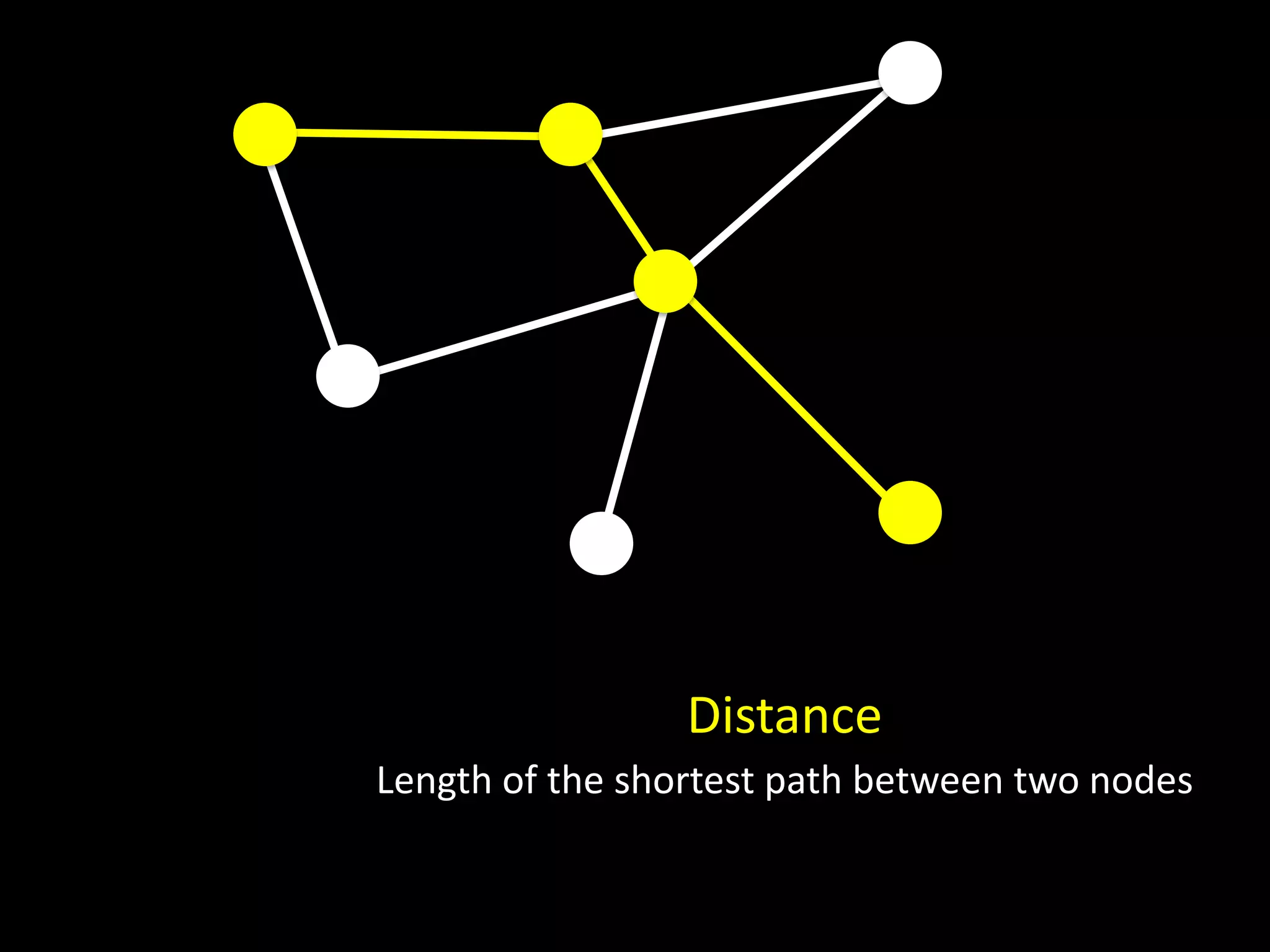
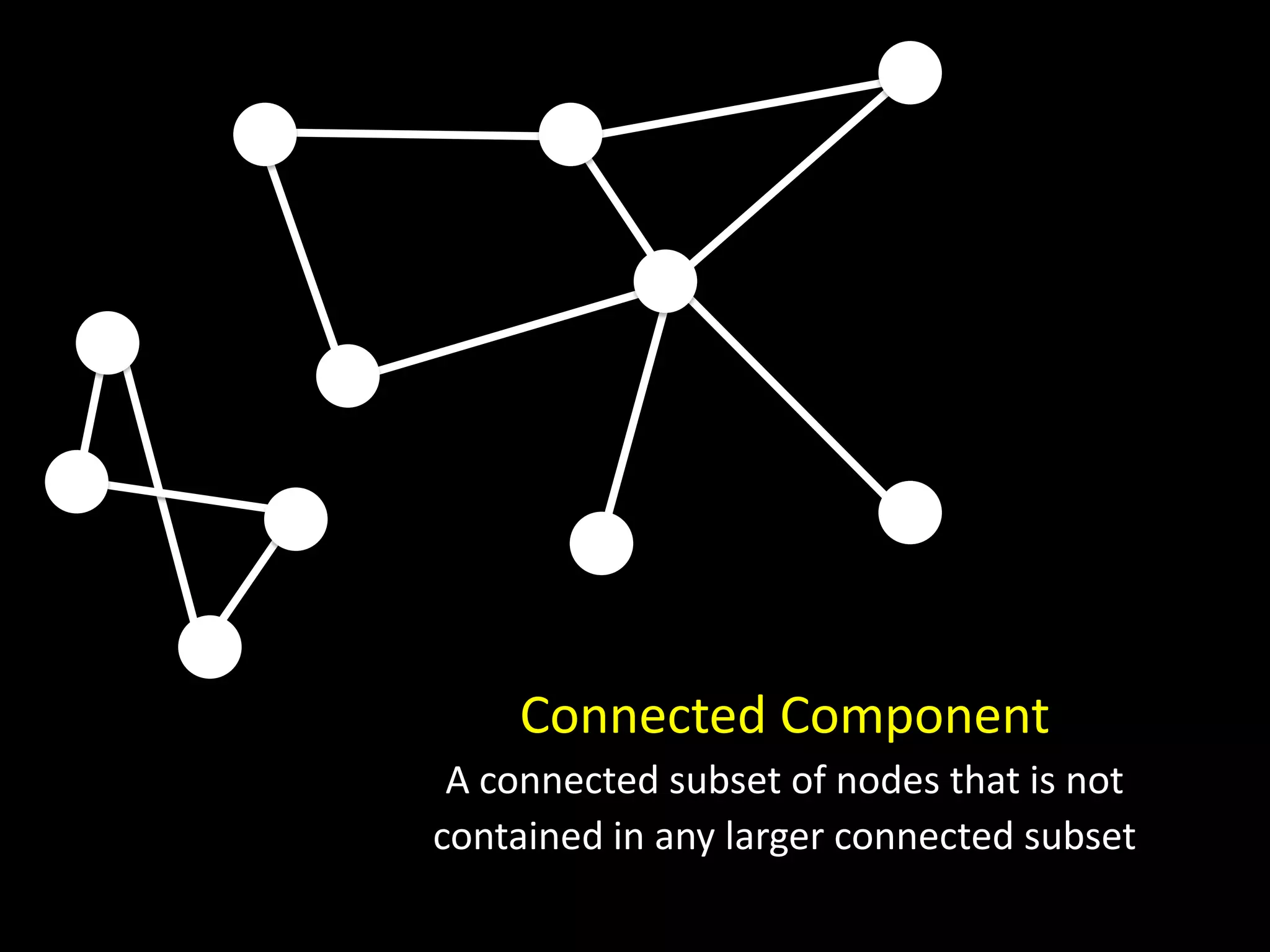
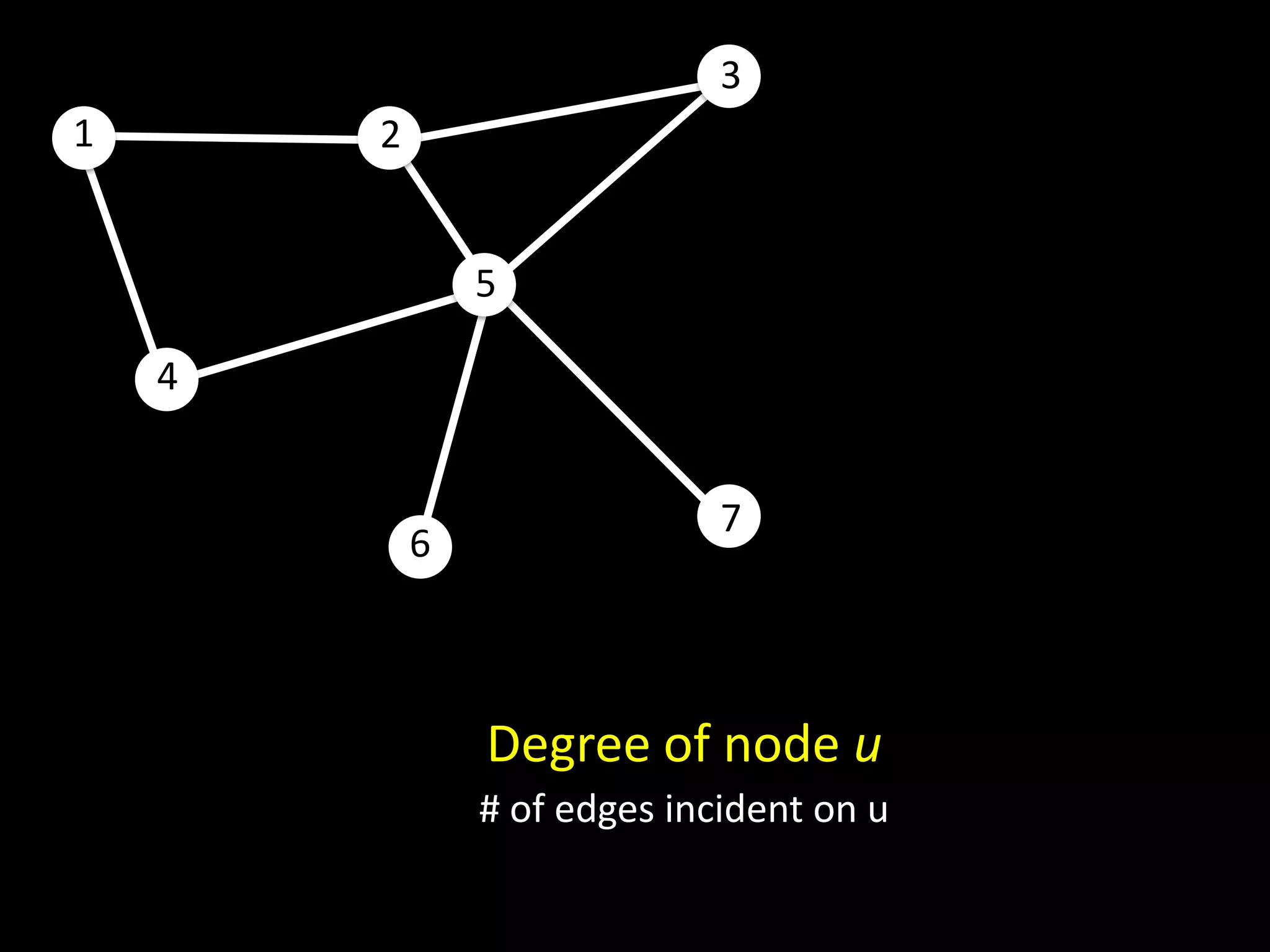
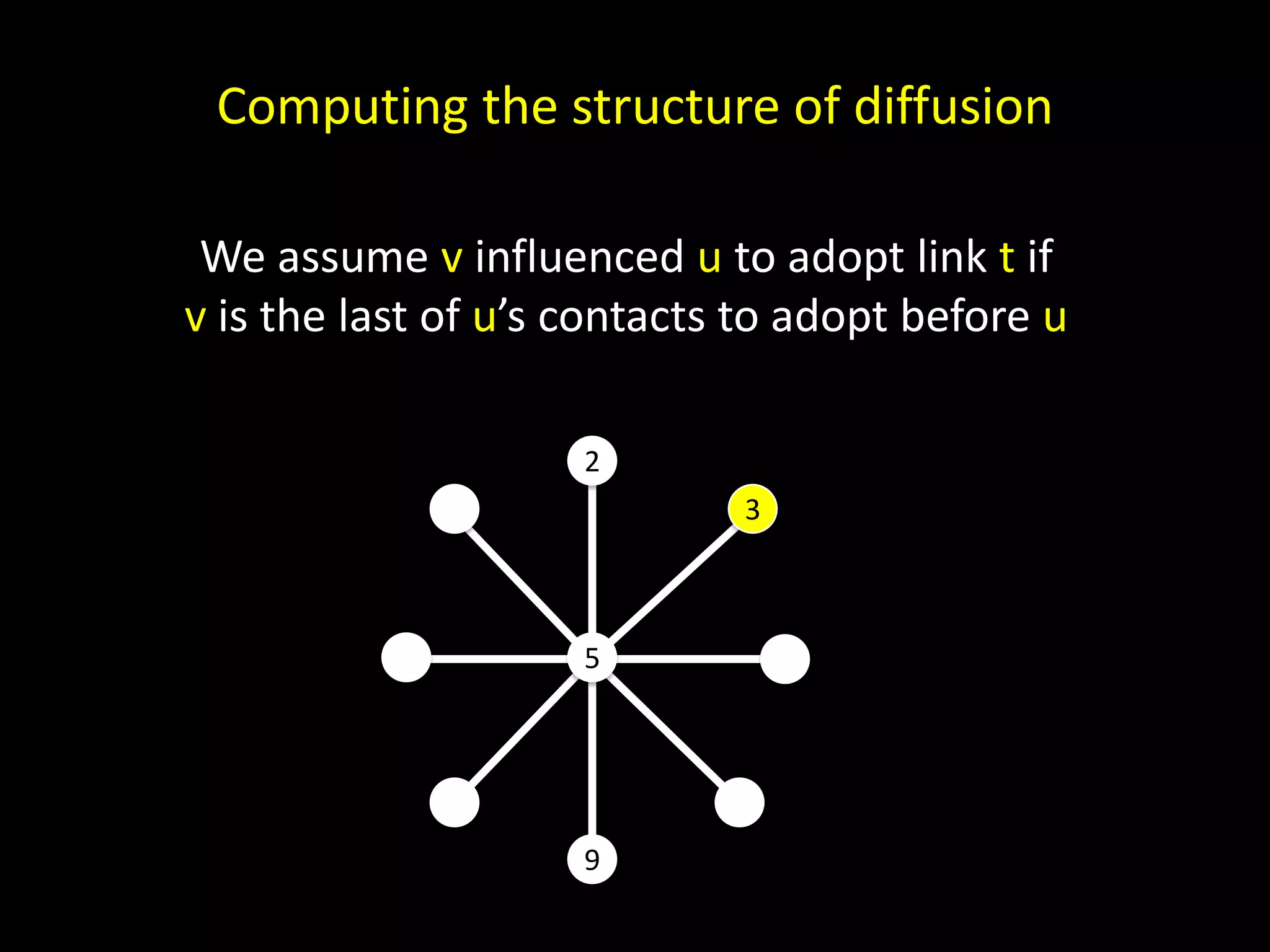
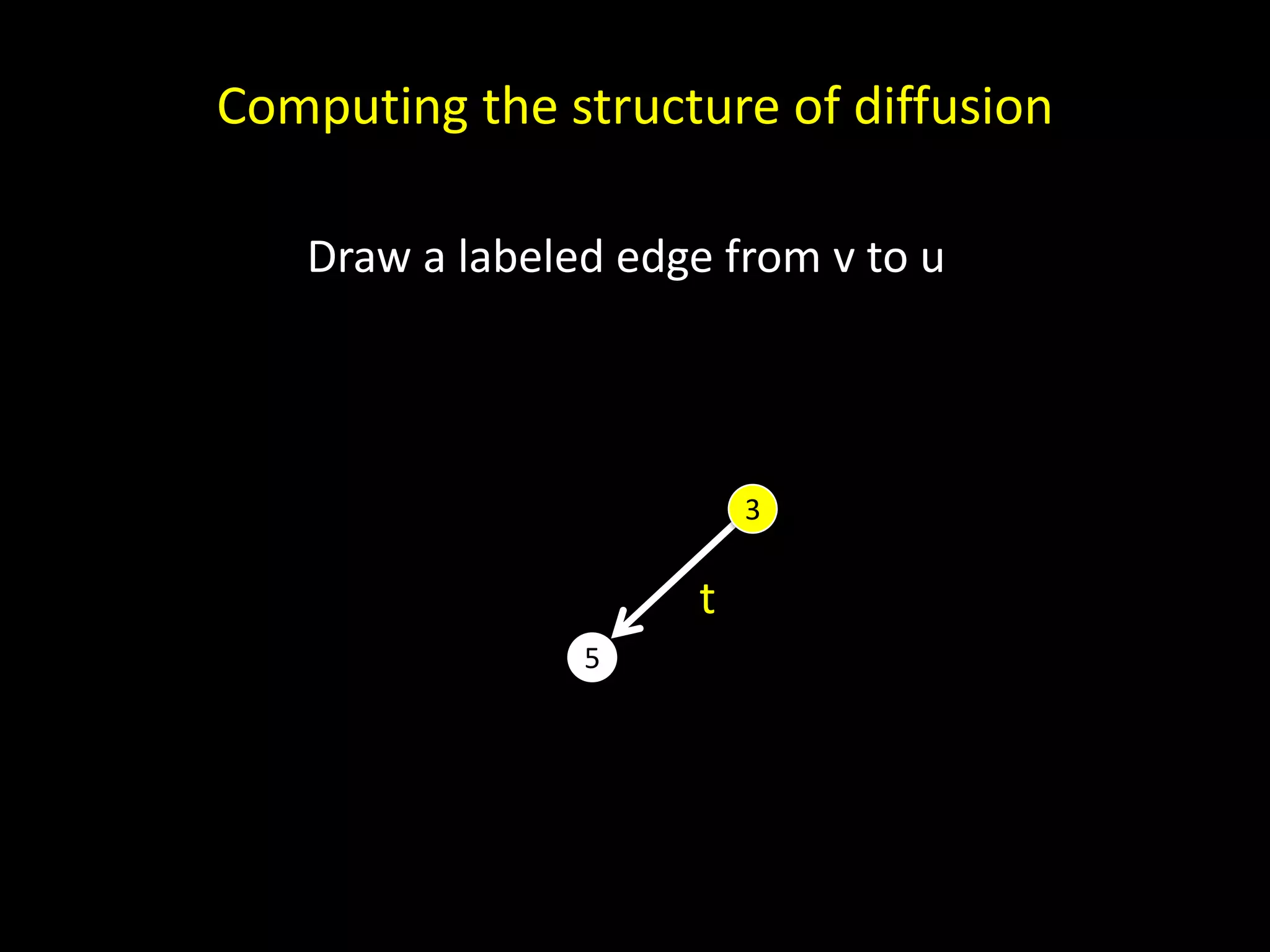
The document discusses techniques for analyzing networks and diffusion processes on networks. It describes breadth-first search to find distances between nodes, connected components to identify distinct subgraphs, triangle counting to measure clustering, and methods to model diffusion by identifying influencer relationships between nodes based on time-stamped adoption data.

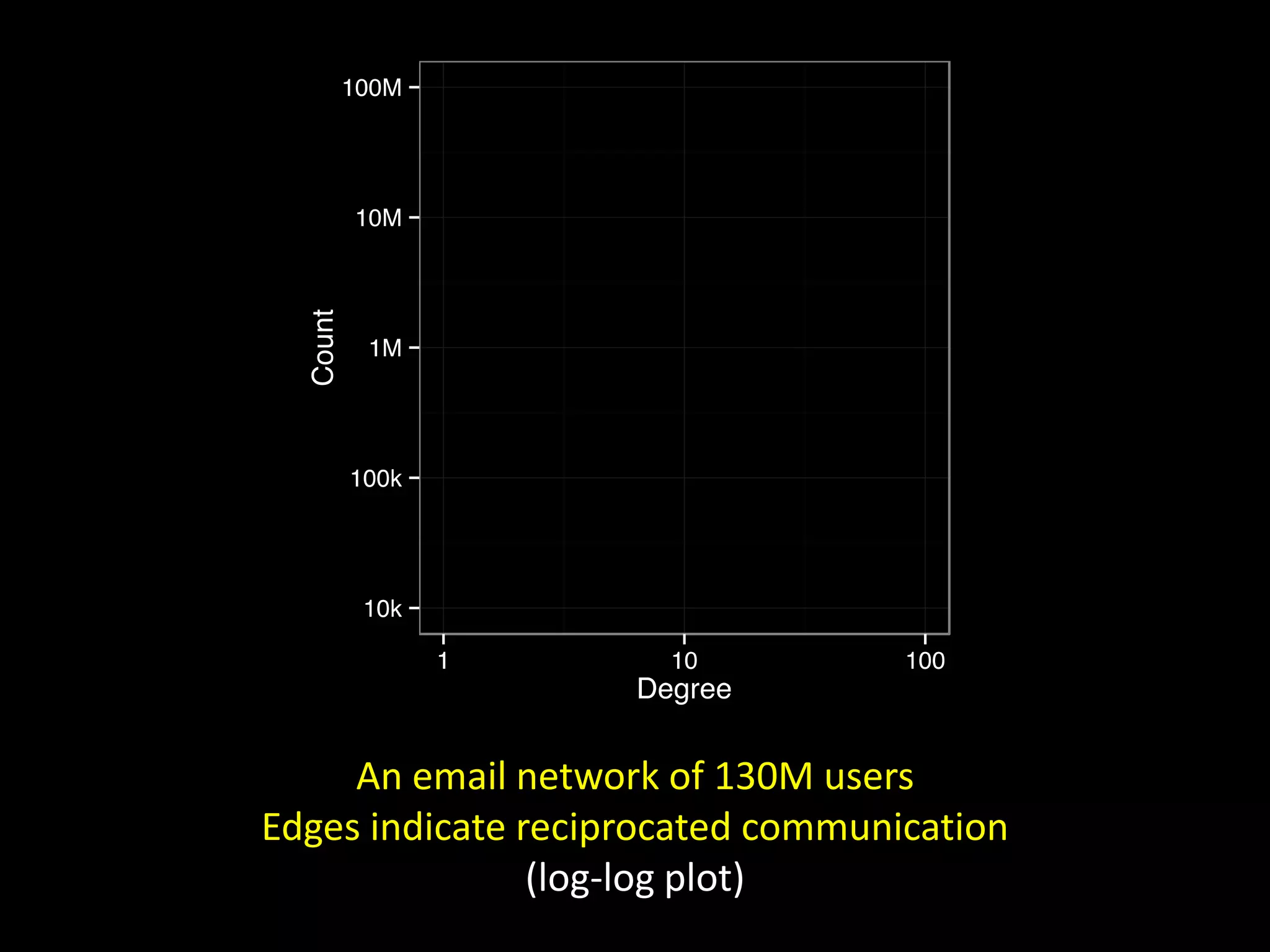
![Corporate E-mail Communication [ Adamic & Adar, 2004 ] via Easley & Kleinberg](https://image.slidesharecdn.com/networks2-130312124643-phpapp02/75/Computational-Social-Science-Lecture-06-Networks-Part-II-2-2048.jpg)

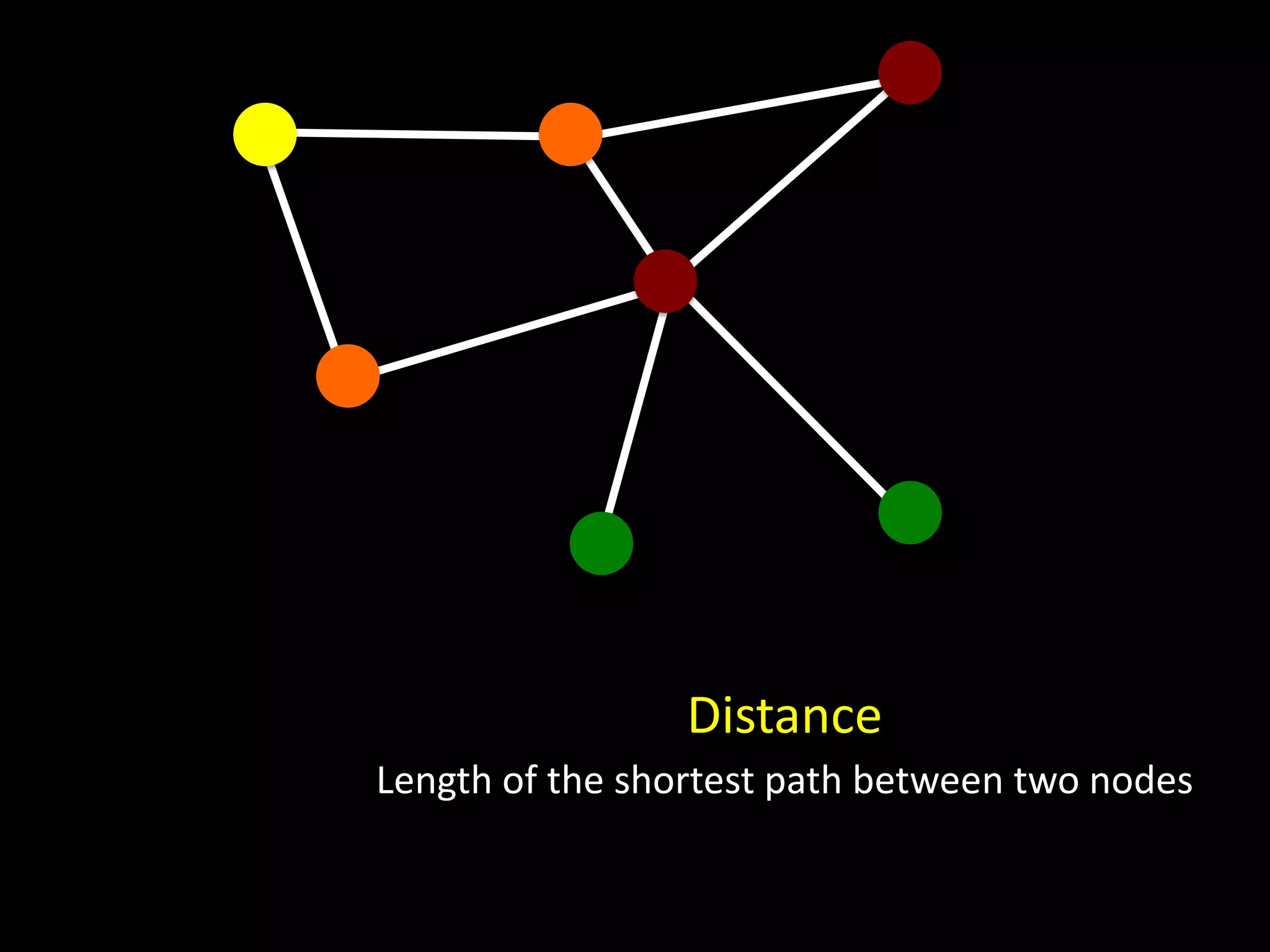
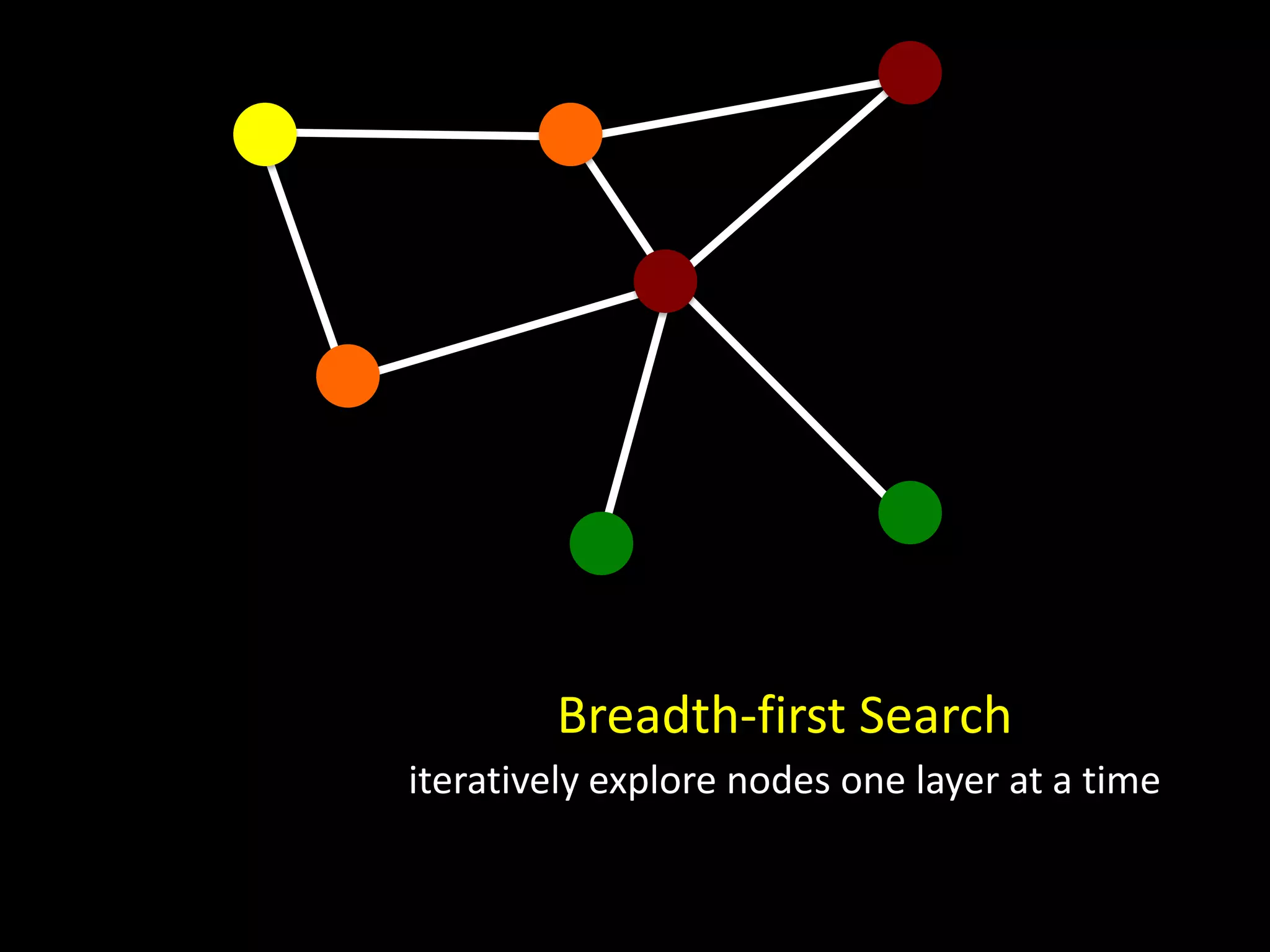
![# initialize distances dist = {} for u in G: dist[u] = NA dist [u0] = 0 d=0 periphery = { u0 } while len(periphery) > 0: # find nodes one step away from the periphery next_level = {} for u in periphery: next_level += { w for w in neighbors[u] if dist[w] == NA } # update distances d += 1 for u in next_level: dist[u] = d # update periphery periphery = next_level](https://image.slidesharecdn.com/networks2-130312124643-phpapp02/75/Computational-Social-Science-Lecture-06-Networks-Part-II-8-2048.jpg)

![BFS @ scale undirected network Input: edge list, distances (u, d) 1. join distances with edge list 2. foreach (u, d, w) output (w, d+1) [ also output (u0, 0) ] 3. group by w, and output min d](https://image.slidesharecdn.com/networks2-130312124643-phpapp02/75/Computational-Social-Science-Lecture-06-Networks-Part-II-10-2048.jpg)



















![Counting Triangles In memory for u in nodes: triangles[u] = 0 for w in neighbors[u]: triangles[u] += len(neighbors[w] & neighbors[u]) triangles[u] = triangles[u] / 2](https://image.slidesharecdn.com/networks2-130312124643-phpapp02/75/Computational-Social-Science-Lecture-06-Networks-Part-II-38-2048.jpg)







![Computing Homophily 1. Join edges (u, v) by u, demographics (w, race) by w 2. Join edges (u, v, urace) by v, demographics (w, race) by w 3. Group edges (u, v, urace, vrace) by sorted([urace, vrace])](https://image.slidesharecdn.com/networks2-130312124643-phpapp02/75/Computational-Social-Science-Lecture-06-Networks-Part-II-47-2048.jpg)
![Computing Homophily 1. Join edges (u, v) by u, demographics (w, race) by w 2. Join edges (u, v, urace) by v, demographics (w, race) by w 3. Group edges (u, v, urace, vrace) by sorted([urace, vrace]) 4. Count edges in each group 5. Normalize the table](https://image.slidesharecdn.com/networks2-130312124643-phpapp02/75/Computational-Social-Science-Lecture-06-Networks-Part-II-48-2048.jpg)




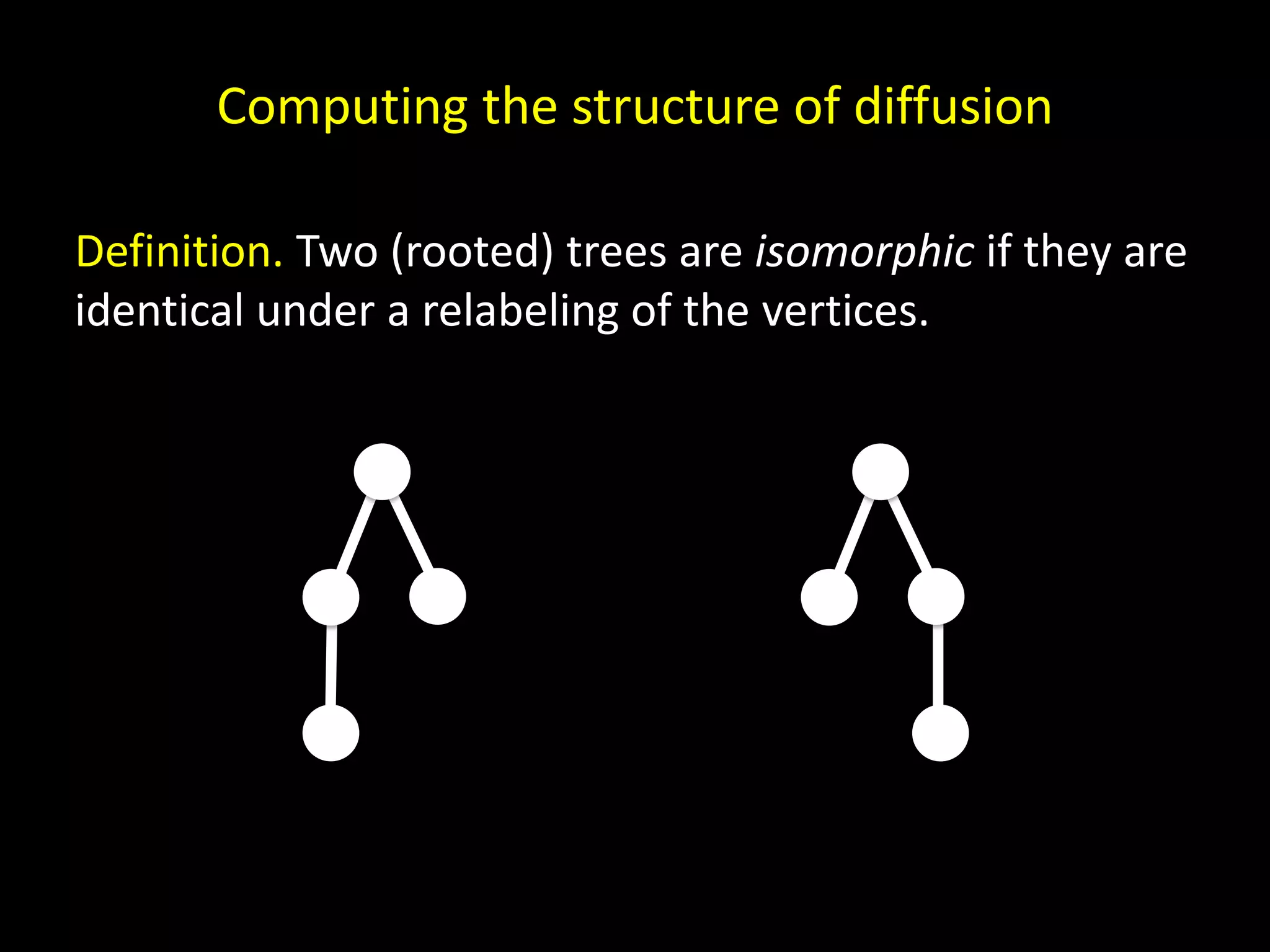
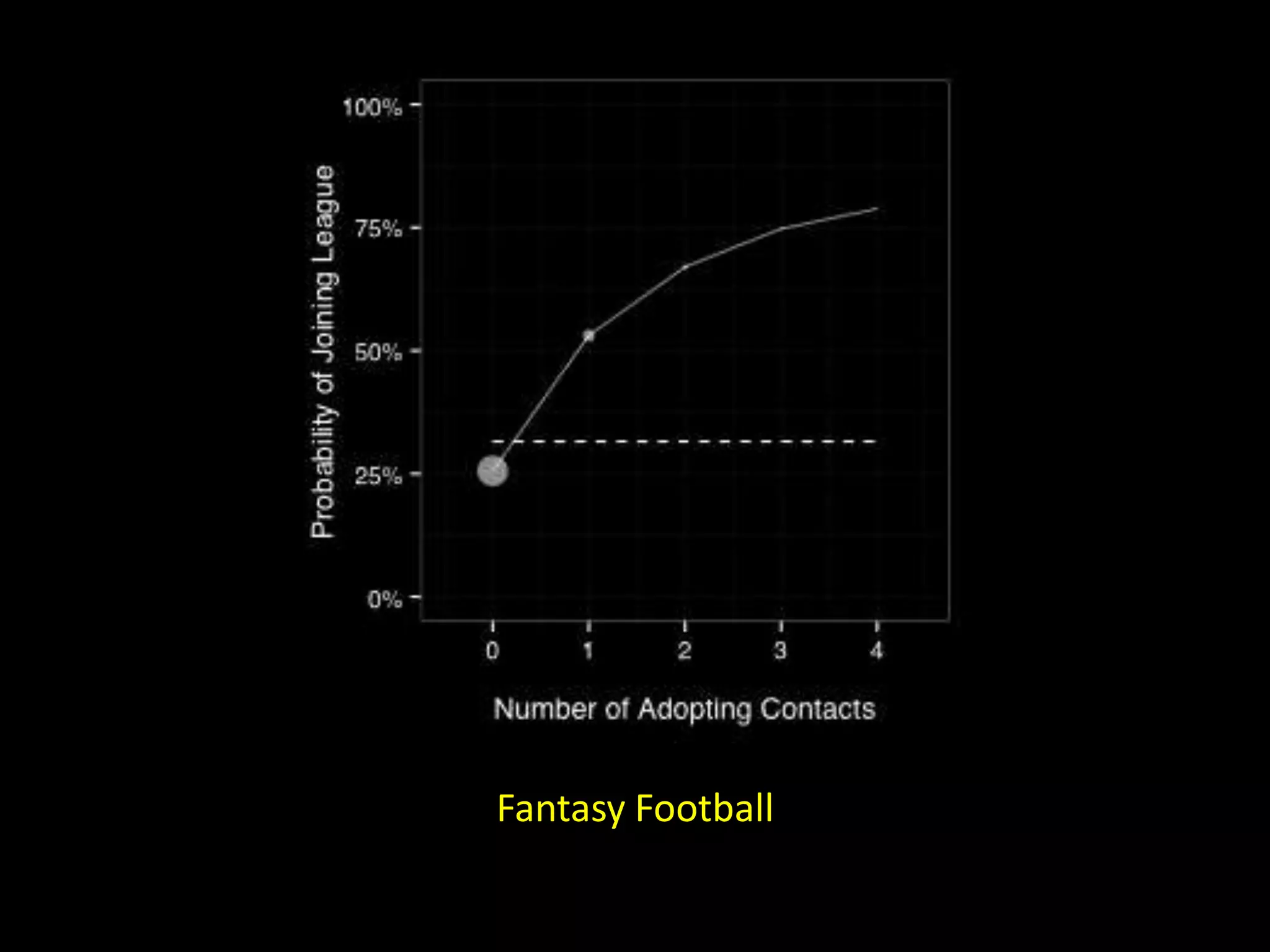
![x (x) (x, x) ((x)) (x, (x)) Basis. The canonical name c(T) for the one-node tree T is x. Induction. If T has more than one node, let T1, . . . ,Tk denote the subtrees of the root indexed such that c(T1) ≤ c(T2) ≤ · · · ≤ c(Tk) under the lexicographic order. Then the canonical name for T is (c(T1), . . . ,c(Tk)). Aho et al. [1974]](https://image.slidesharecdn.com/networks2-130312124643-phpapp02/75/Computational-Social-Science-Lecture-06-Networks-Part-II-57-2048.jpg)