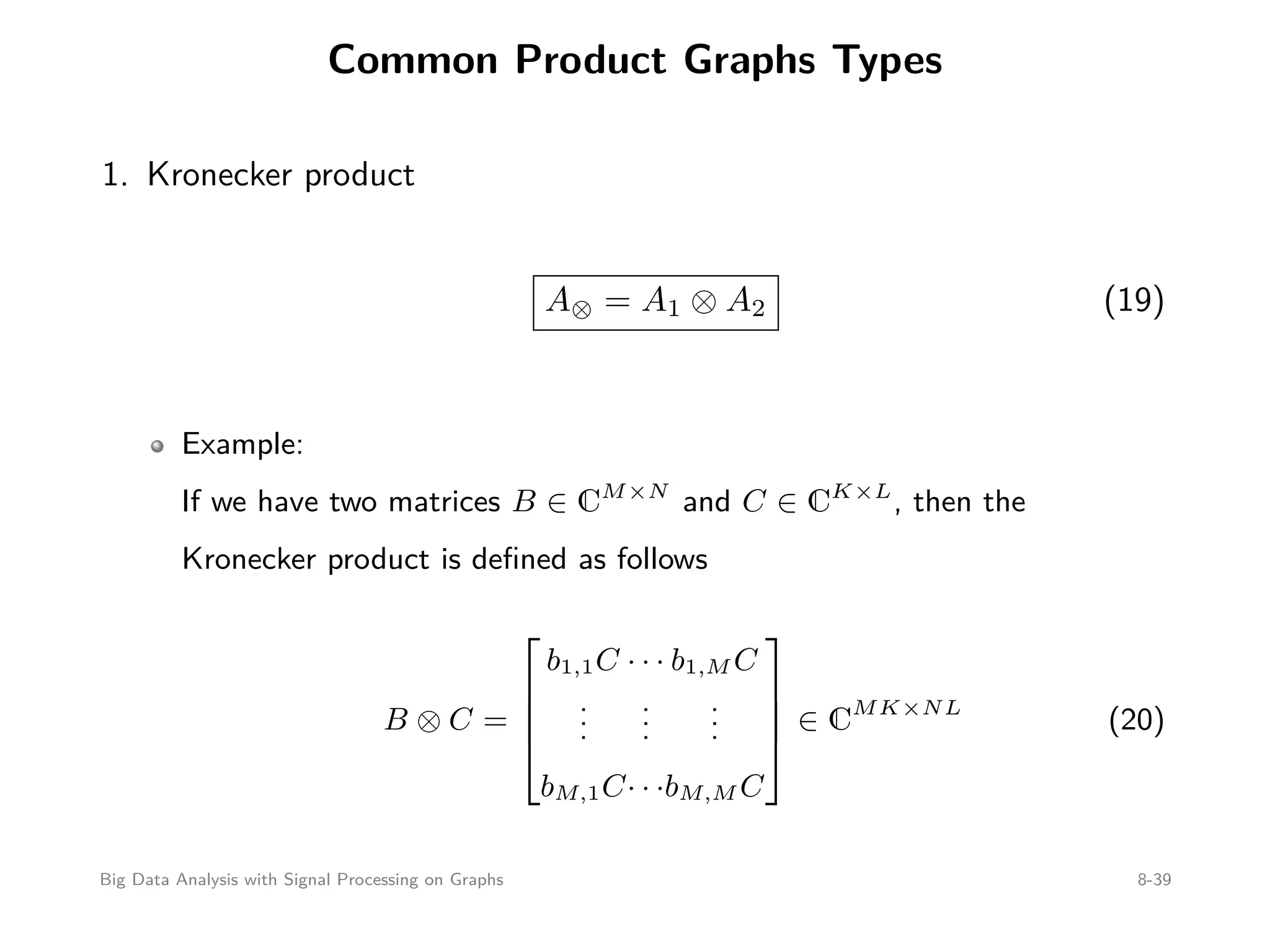
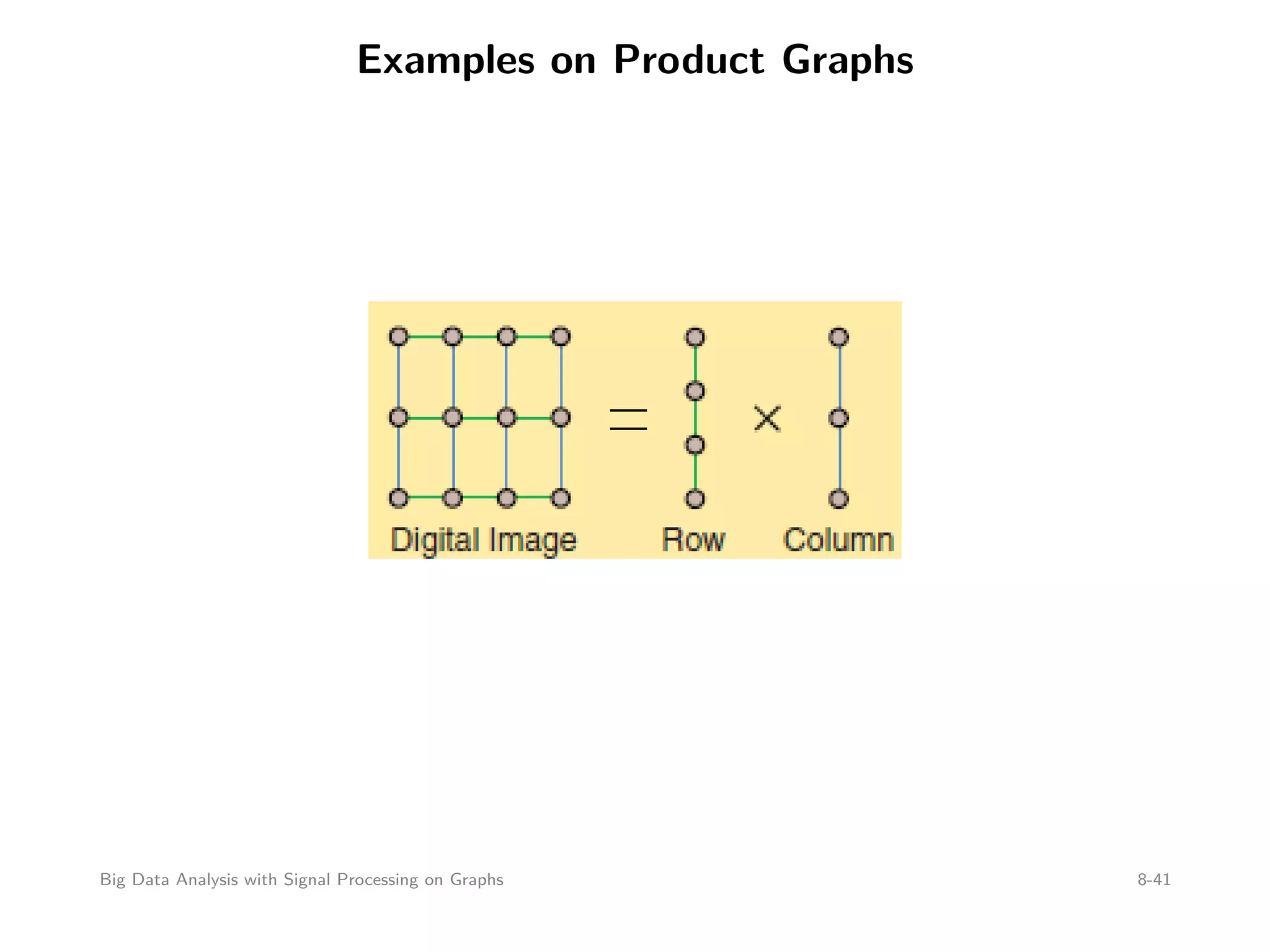
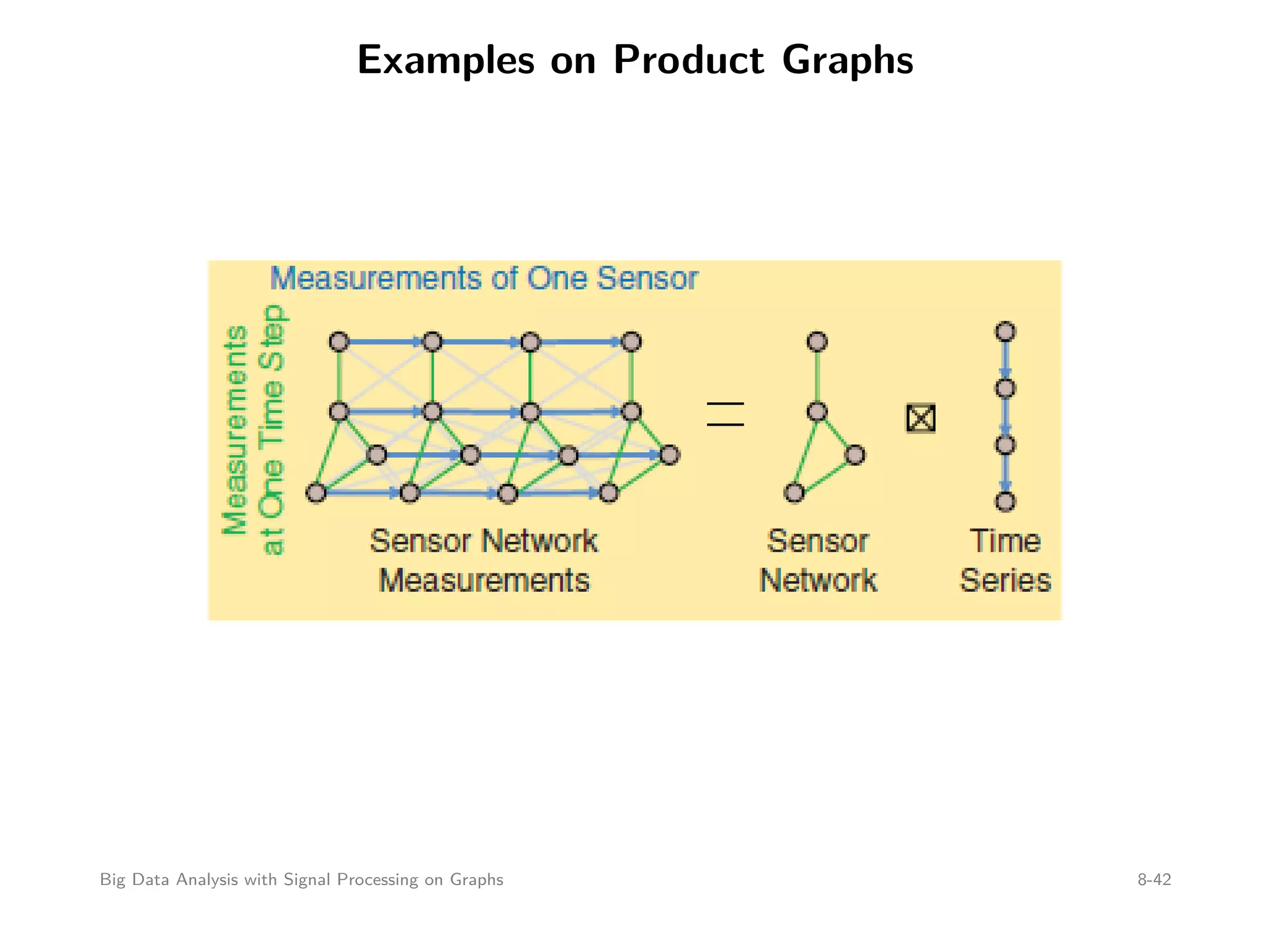
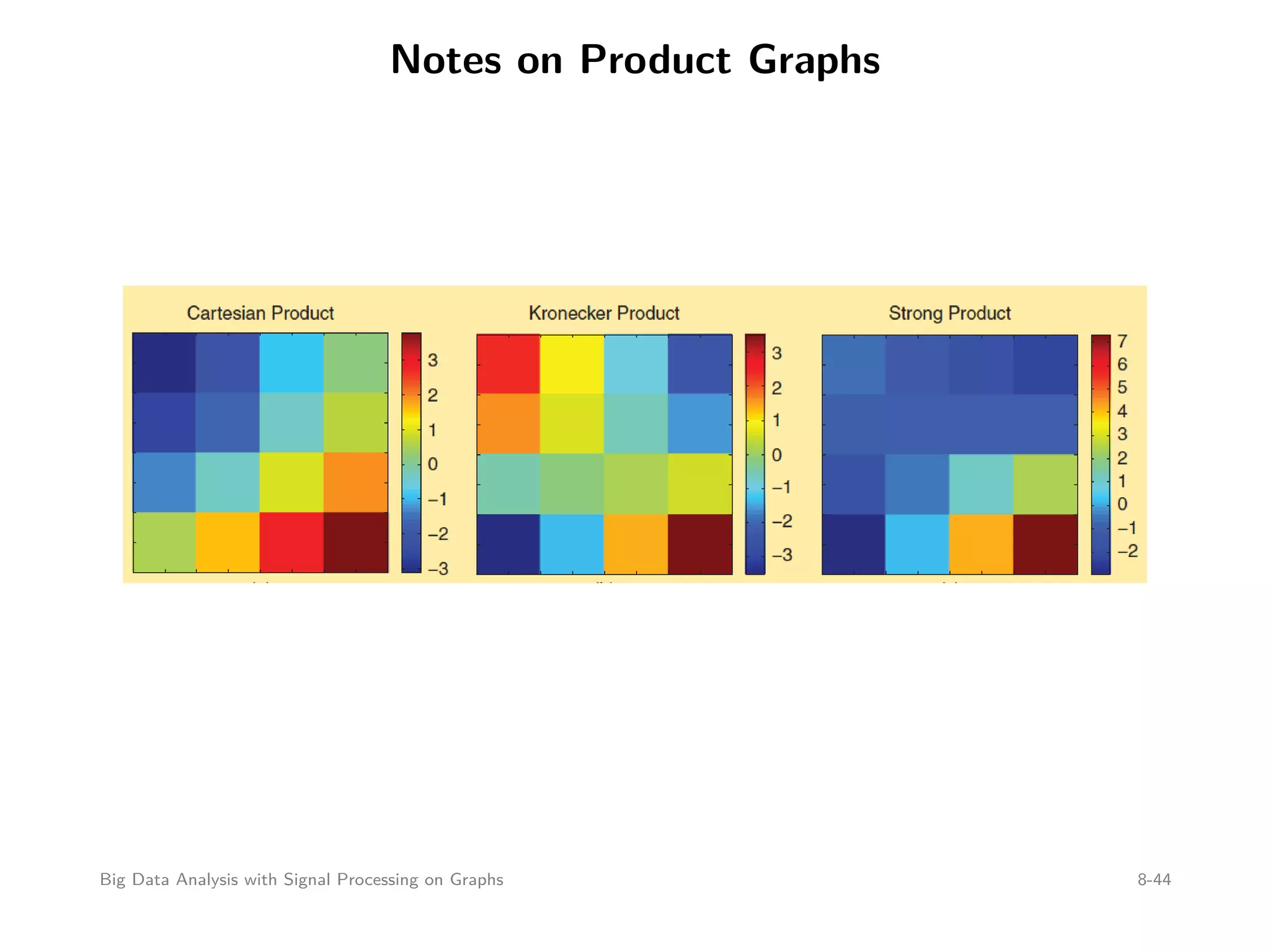
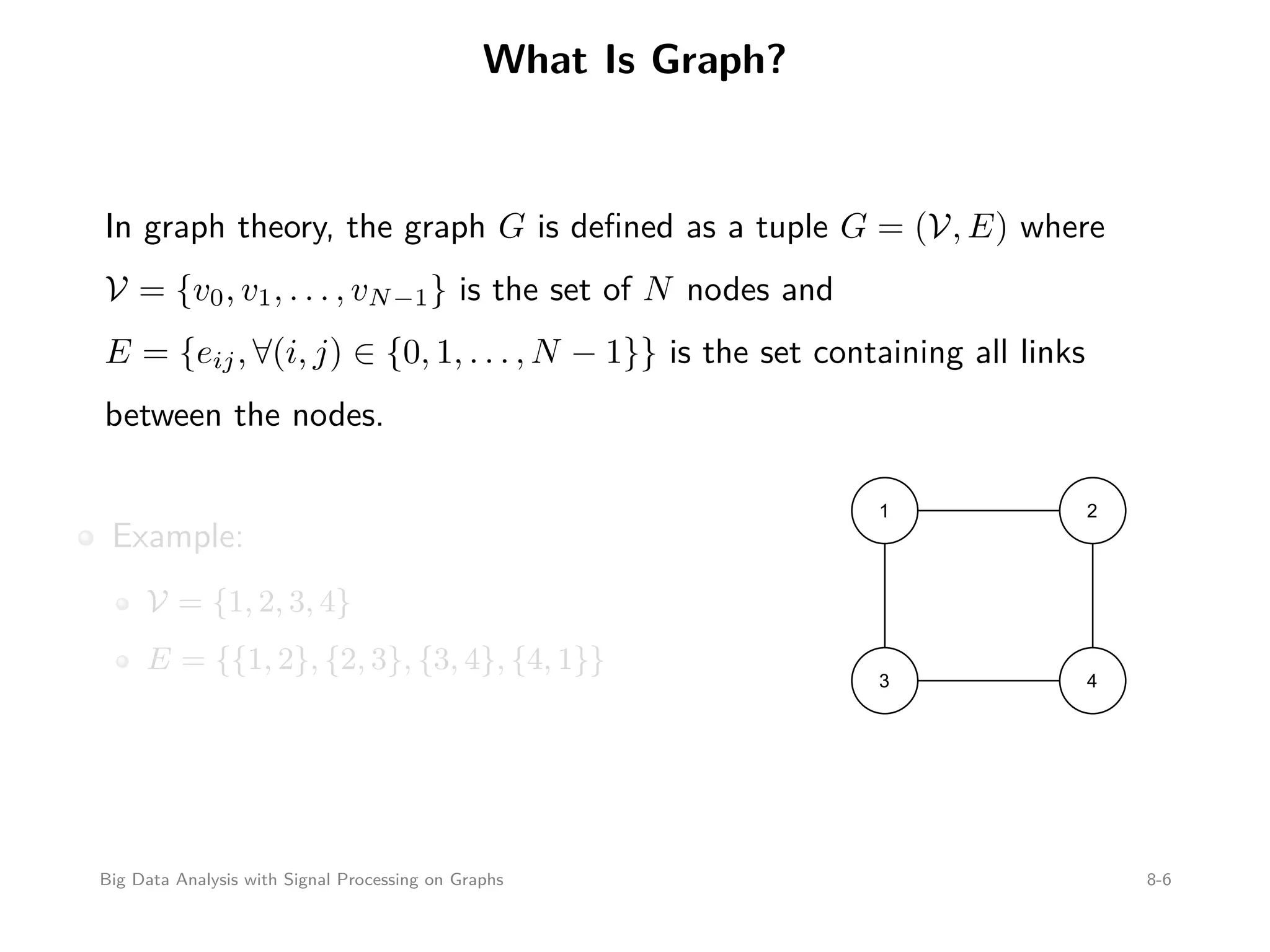
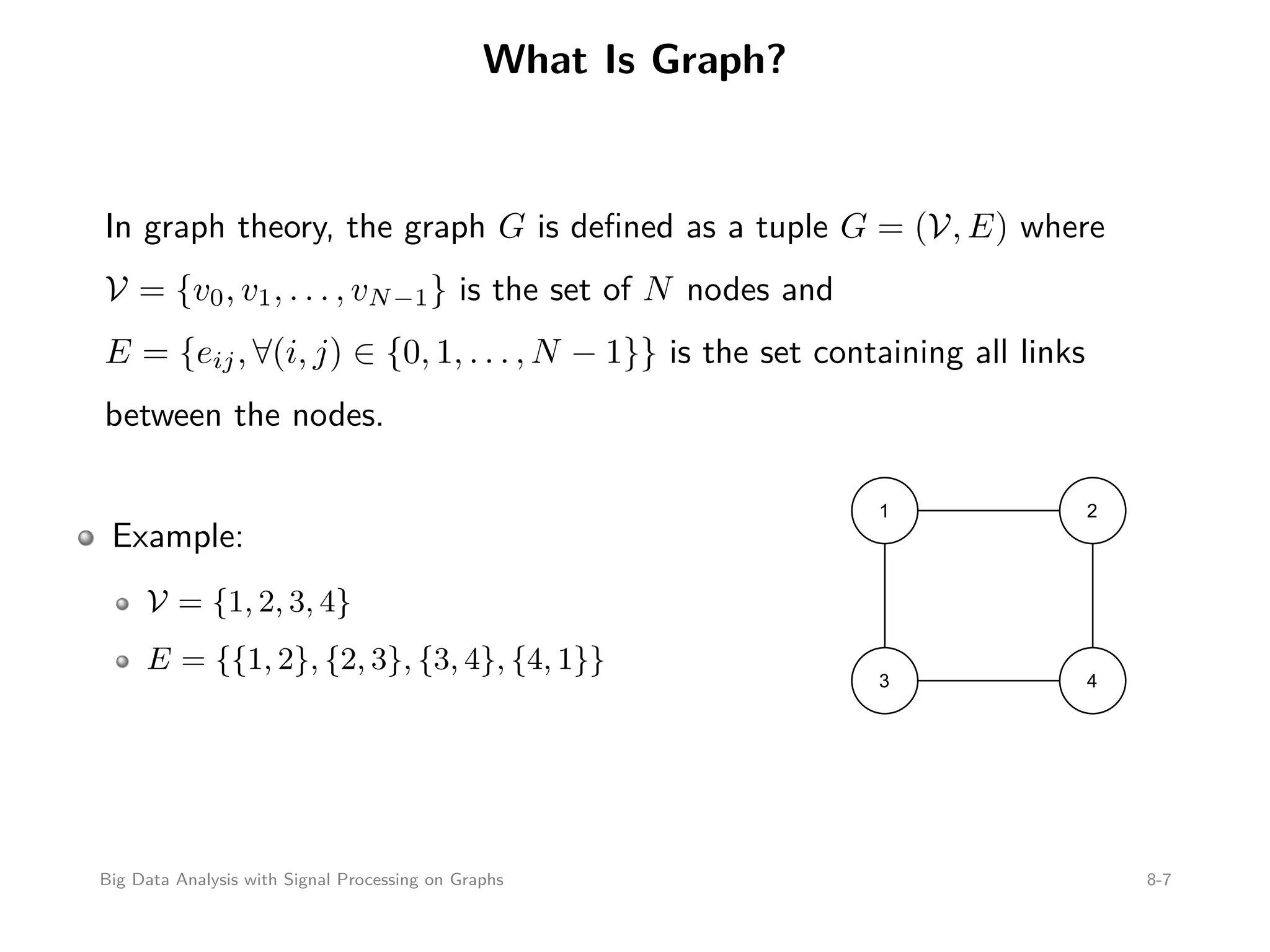
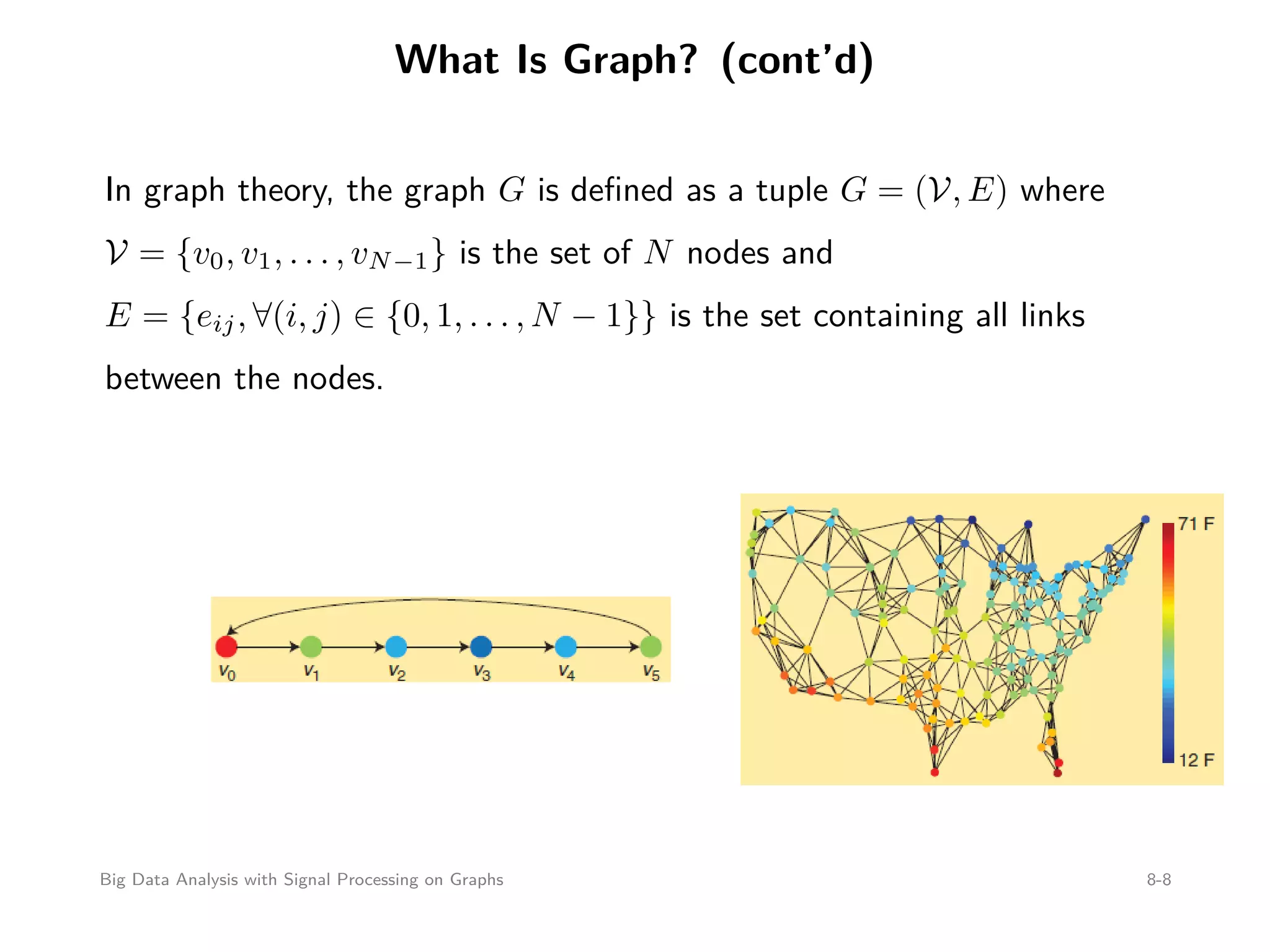
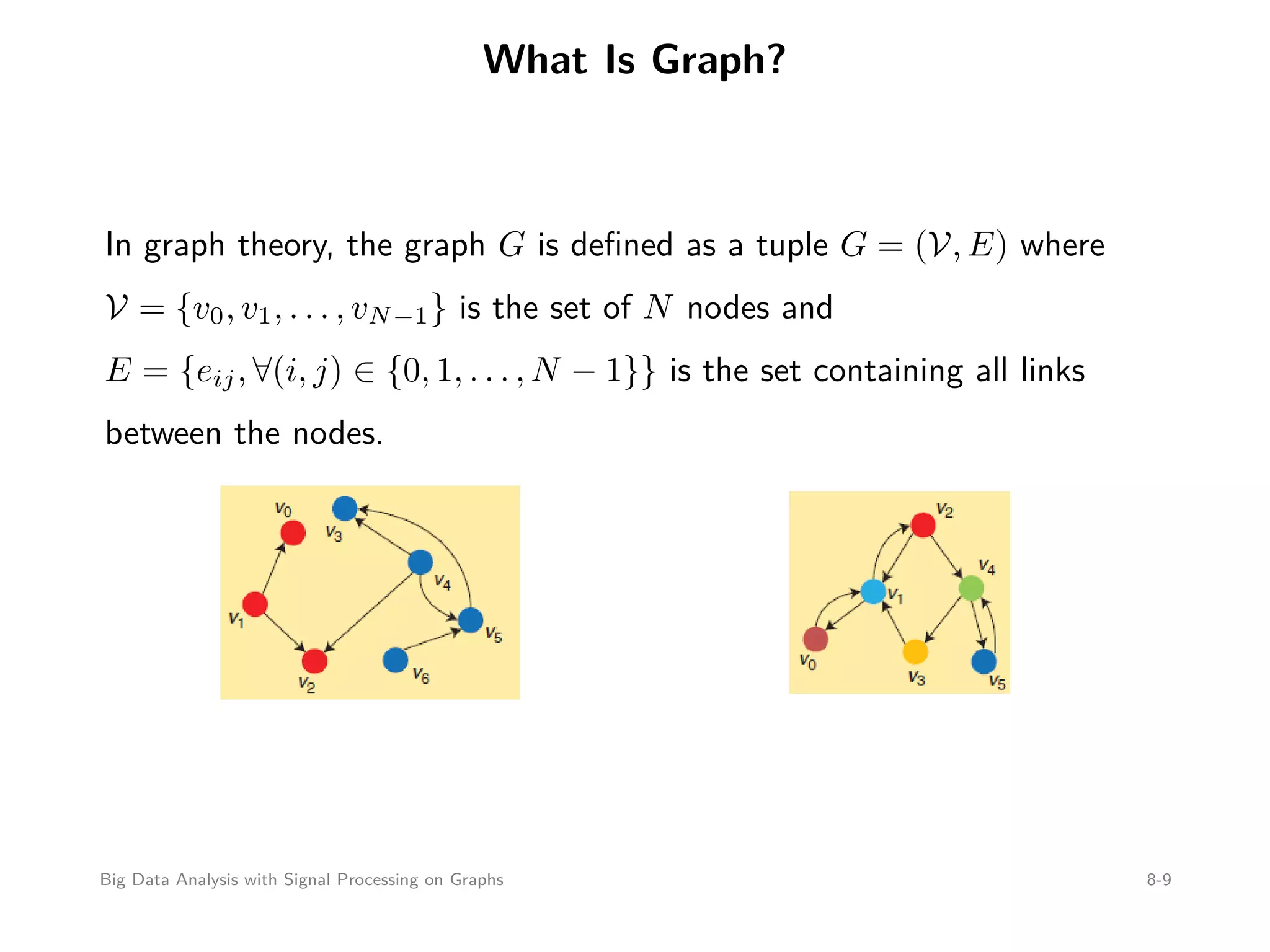
This document discusses signal processing on graphs and big data analysis using graph theory concepts. It begins with introducing fundamental graph theory terms like nodes, edges, and adjacency matrices. It then explains how to define graph signals and how signal processing concepts like shifting, filtering, and Fourier transforms can be generalized to graphs. In particular, it describes how the graph shift replaces time shifts, graph filters are polynomials of the graph shift matrix, and the graph Fourier transform uses the eigenvectors of the graph shift matrix as the basis. The document concludes by discussing how eigenvalues represent frequencies on graphs and how filters affect the frequency content of graph signals.







![Graph Signals Given the graph, the data set forms a graph signal, defined as a map s : V → C, vn → sn (1) It is convenient to write graph signals as vectors s = [s0, s1, . . . , sN−1] T ∈ CN×1 (2) Big Data Analysis with Signal Processing on Graphs 8-12](https://image.slidesharecdn.com/bigdataseif-151007135408-lva1-app6891/75/Big-Data-Analysis-with-Signal-Processing-on-Graphs-12-2048.jpg)
![Graph Shift In DSP, a signal shift, implemented as a time delay ˜s = [ ˜s0, ˜s1, . . . , ˜sN−1] T = Cs (3) where C is the N × N cyclic shift matrix. DSP on Graphs extends the concept of shift to general graphs by defining the graph shift as a local operation that replaces a signal value sn at node vn by a linear combination of the values at neighbors of vn weighted by their edge weights: ˜sn = m∈Nn An,msm (4) Big Data Analysis with Signal Processing on Graphs 8-13](https://image.slidesharecdn.com/bigdataseif-151007135408-lva1-app6891/75/Big-Data-Analysis-with-Signal-Processing-on-Graphs-13-2048.jpg)
![Graph Shift (cont’d) It can be interpreted as a first-order interpolation, weighted averaging, or regression on graphs, which is a widely used operation in graph regression, distributed consensus, telecommunications. Then, the graph shift is written as ˜s = [ ˜s0, ˜s1, . . . , ˜sN−1] T = As (5) Big Data Analysis with Signal Processing on Graphs 8-14](https://image.slidesharecdn.com/bigdataseif-151007135408-lva1-app6891/75/Big-Data-Analysis-with-Signal-Processing-on-Graphs-14-2048.jpg)
![Graph Filters and Z-Transform In signal processing, a filter is a system H(.) that takes an input signal s and outputs a signal: ˜s = [ ˜s0, ˜s1, . . . , ˜sN−1] T = H(s) (6) Among the most widely used filters are linear shift-ivariant (LSI) ones. The z-transform provides a convenient representation for signals and filters in DSP. (In short) An alternative representation for the output signal is given by ˜s = h(C)s (7) where h(c) = N−1 n=0 hnCn (Resultant is a circulant matrix) Big Data Analysis with Signal Processing on Graphs 8-15](https://image.slidesharecdn.com/bigdataseif-151007135408-lva1-app6891/75/Big-Data-Analysis-with-Signal-Processing-on-Graphs-15-2048.jpg)
![Graph Filters and Z-Transform In signal processing, a filter is a system H(.) that takes an input signal s and outputs a signal: ˜s = [ ˜s0, ˜s1, . . . , ˜sN−1] T = H(s) (6) Among the most widely used filters are linear shift-ivariant (LSI) ones. The z-transform provides a convenient representation for signals and filters in DSP. (In short) An alternative representation for the output signal is given by ˜s = h(C)s (7) where h(c) = N−1 n=0 hnCn (Resultant is a circulant matrix) Big Data Analysis with Signal Processing on Graphs 8-16](https://image.slidesharecdn.com/bigdataseif-151007135408-lva1-app6891/75/Big-Data-Analysis-with-Signal-Processing-on-Graphs-16-2048.jpg)
![Graph Filters and Z-Transform In signal processing, a filter is a system H(.) that takes an input signal s and outputs a signal: ˜s = [ ˜s0, ˜s1, . . . , ˜sN−1] T = H(s) (6) Among the most widely used filters are linear shift-ivariant (LSI) ones. The z-transform provides a convenient representation for signals and filters in DSP. (In short) An alternative representation for the output signal is given by ˜s = h(C)s (7) where h(c) = N−1 n=0 hnCn (Resultant is a circulant matrix) Big Data Analysis with Signal Processing on Graphs 8-17](https://image.slidesharecdn.com/bigdataseif-151007135408-lva1-app6891/75/Big-Data-Analysis-with-Signal-Processing-on-Graphs-17-2048.jpg)
![Graph Filters and Z-Transform In signal processing, a filter is a system H(.) that takes an input signal s and outputs a signal: ˜s = [ ˜s0, ˜s1, . . . , ˜sN−1] T = H(s) (6) Among the most widely used filters are linear shift-ivariant (LSI) ones. The z-transform provides a convenient representation for signals and filters in DSP. (In short) An alternative representation for the output signal is given by ˜s = h(C)s (7) where h(c) = N−1 n=0 hnCn (Resultant is a circulant matrix) Big Data Analysis with Signal Processing on Graphs 8-18](https://image.slidesharecdn.com/bigdataseif-151007135408-lva1-app6891/75/Big-Data-Analysis-with-Signal-Processing-on-Graphs-18-2048.jpg)

![Graph Fourier Transform Mathematically, a Fourier transform with respect to a set of operators is the expansion of a signal into a basis of the operators eigen functions. Since in signal processing the operators of interest are filters, DSPG defines the Fourier transform with respect to the graph filters. ˜s = [ ˜s0, ˜s1, . . . , ˜sN−1] T = GFT{s} (10) Big Data Analysis with Signal Processing on Graphs 8-20](https://image.slidesharecdn.com/bigdataseif-151007135408-lva1-app6891/75/Big-Data-Analysis-with-Signal-Processing-on-Graphs-20-2048.jpg)
![Graph Fourier Transform Mathematically, a Fourier transform with respect to a set of operators is the expansion of a signal into a basis of the operators eigen functions. Since in signal processing the operators of interest are filters, DSPG defines the Fourier transform with respect to the graph filters. ˜s = [ ˜s0, ˜s1, . . . , ˜sN−1] T = GFT{s} (10) Big Data Analysis with Signal Processing on Graphs 8-21](https://image.slidesharecdn.com/bigdataseif-151007135408-lva1-app6891/75/Big-Data-Analysis-with-Signal-Processing-on-Graphs-21-2048.jpg)
![Graph Fourier Transform (cont’d) For simplicity, assume that A is diagonalizable and its decomposition is A = V ΛV −1 (11) where the columns vn of the matrix V = [v0 · · · vN−1] ∈ CN×N are the eigenvectors of A and Λ = diag(λ0, . . . , λN−1) are eigenvalues of A In general A can be diagonalized using Jordan decomposition. Big Data Analysis with Signal Processing on Graphs 8-22](https://image.slidesharecdn.com/bigdataseif-151007135408-lva1-app6891/75/Big-Data-Analysis-with-Signal-Processing-on-Graphs-22-2048.jpg)
![Graph Fourier Transform (cont’d) For simplicity, assume that A is diagonalizable and its decomposition is A = V ΛV −1 (11) where the columns vn of the matrix V = [v0 · · · vN−1] ∈ CN×N are the eigenvectors of A and Λ = diag(λ0, . . . , λN−1) are eigenvalues of A In general A can be diagonalized using Jordan decomposition. Big Data Analysis with Signal Processing on Graphs 8-23](https://image.slidesharecdn.com/bigdataseif-151007135408-lva1-app6891/75/Big-Data-Analysis-with-Signal-Processing-on-Graphs-23-2048.jpg)
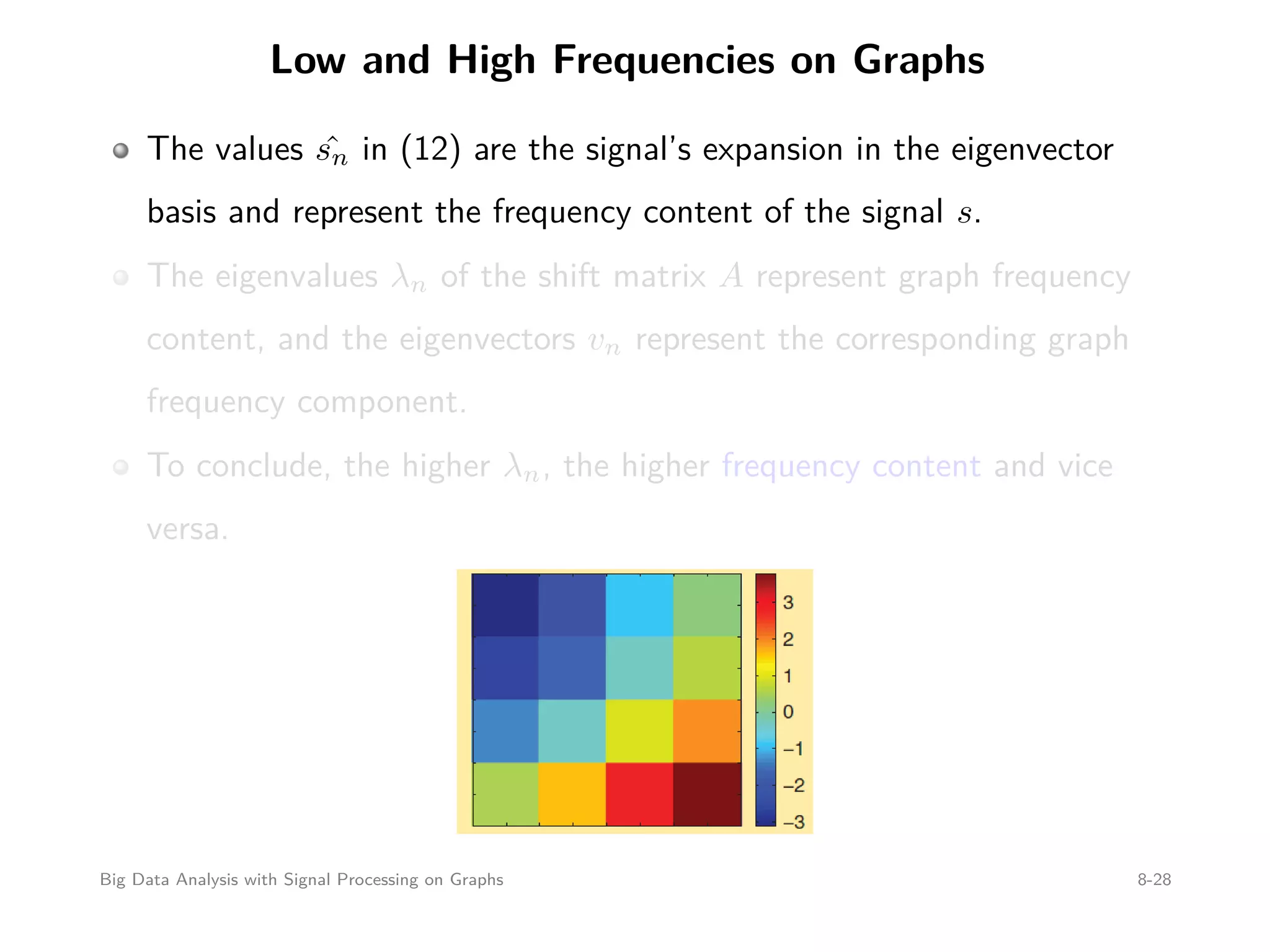
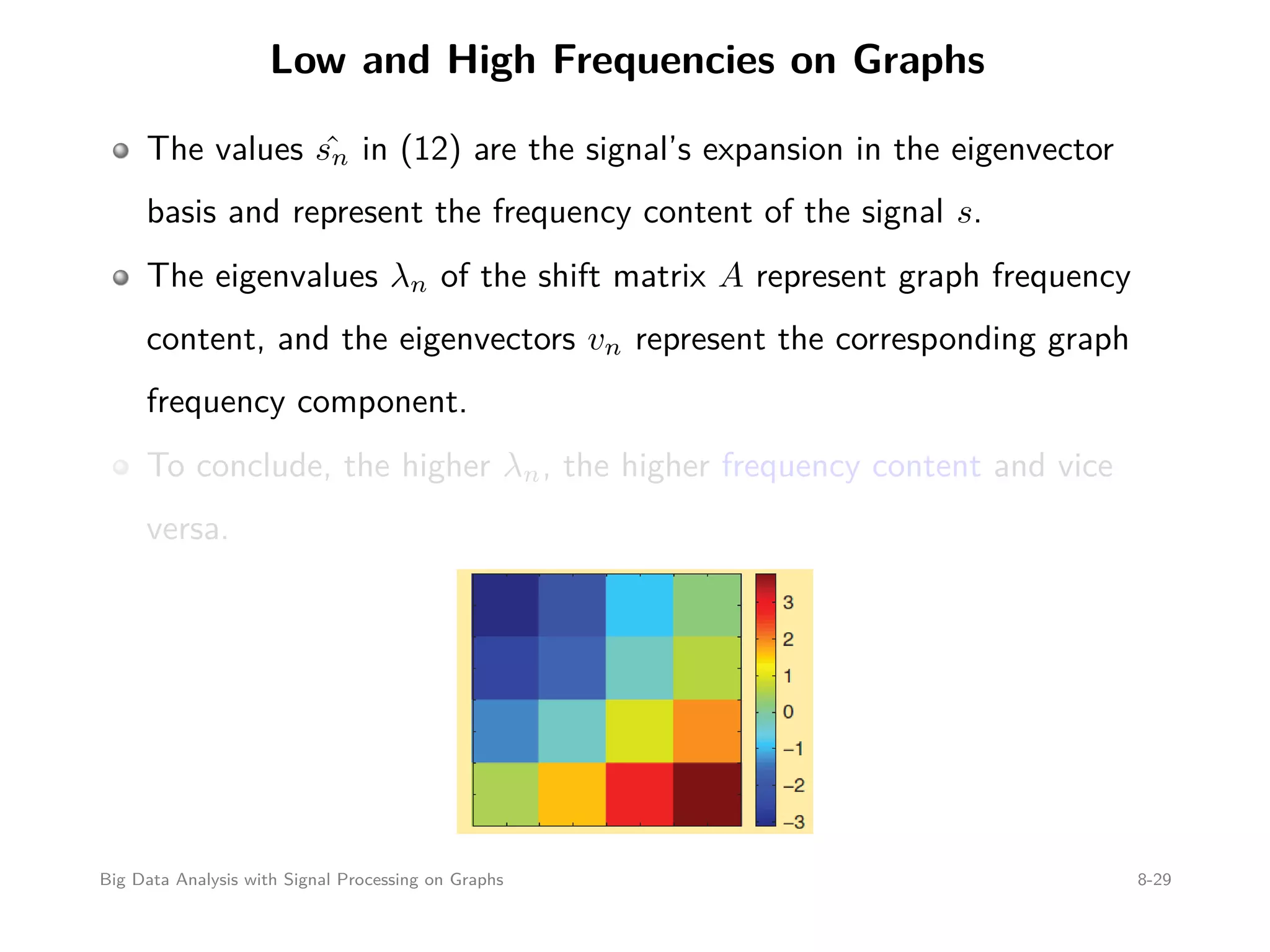
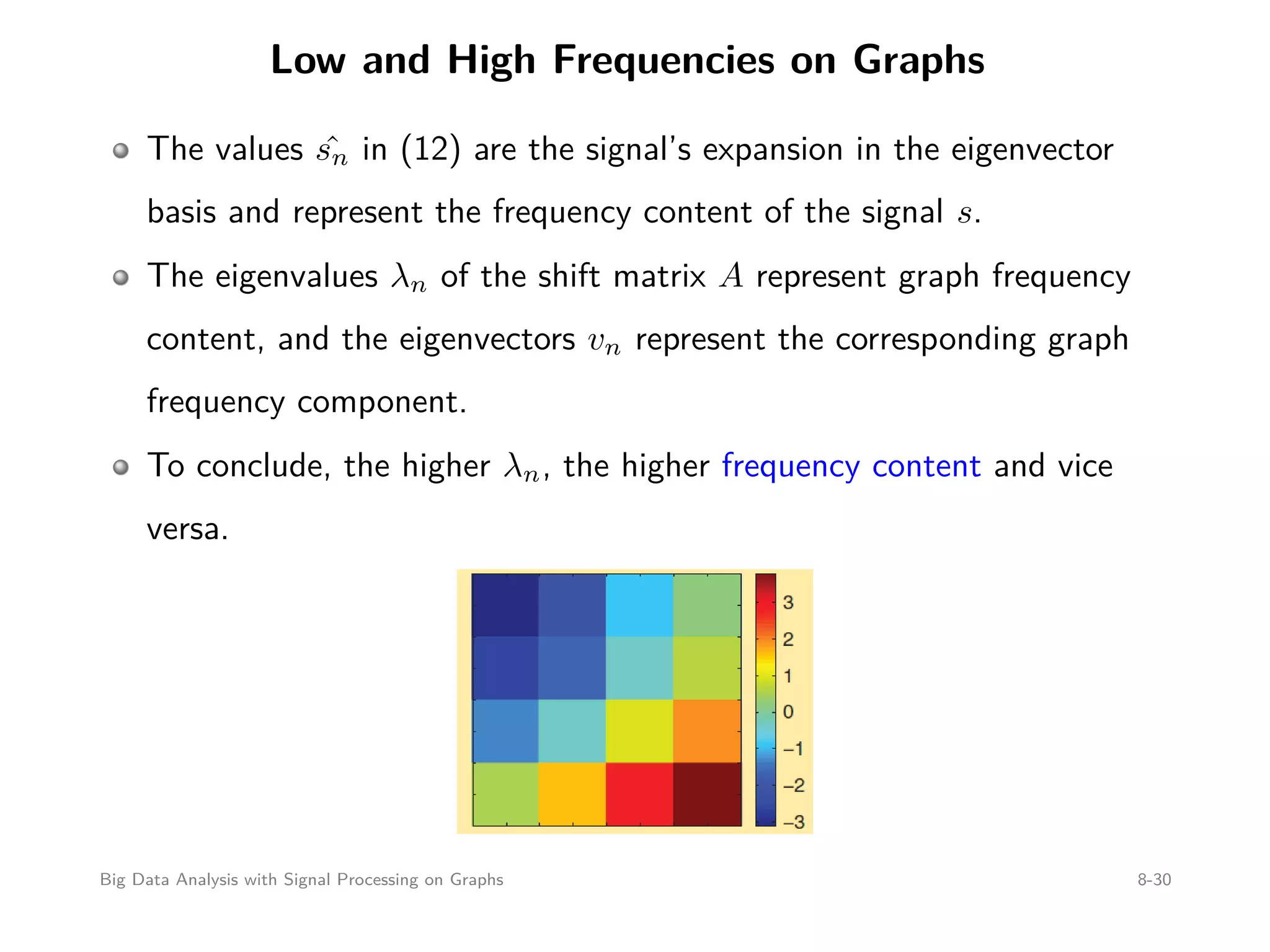
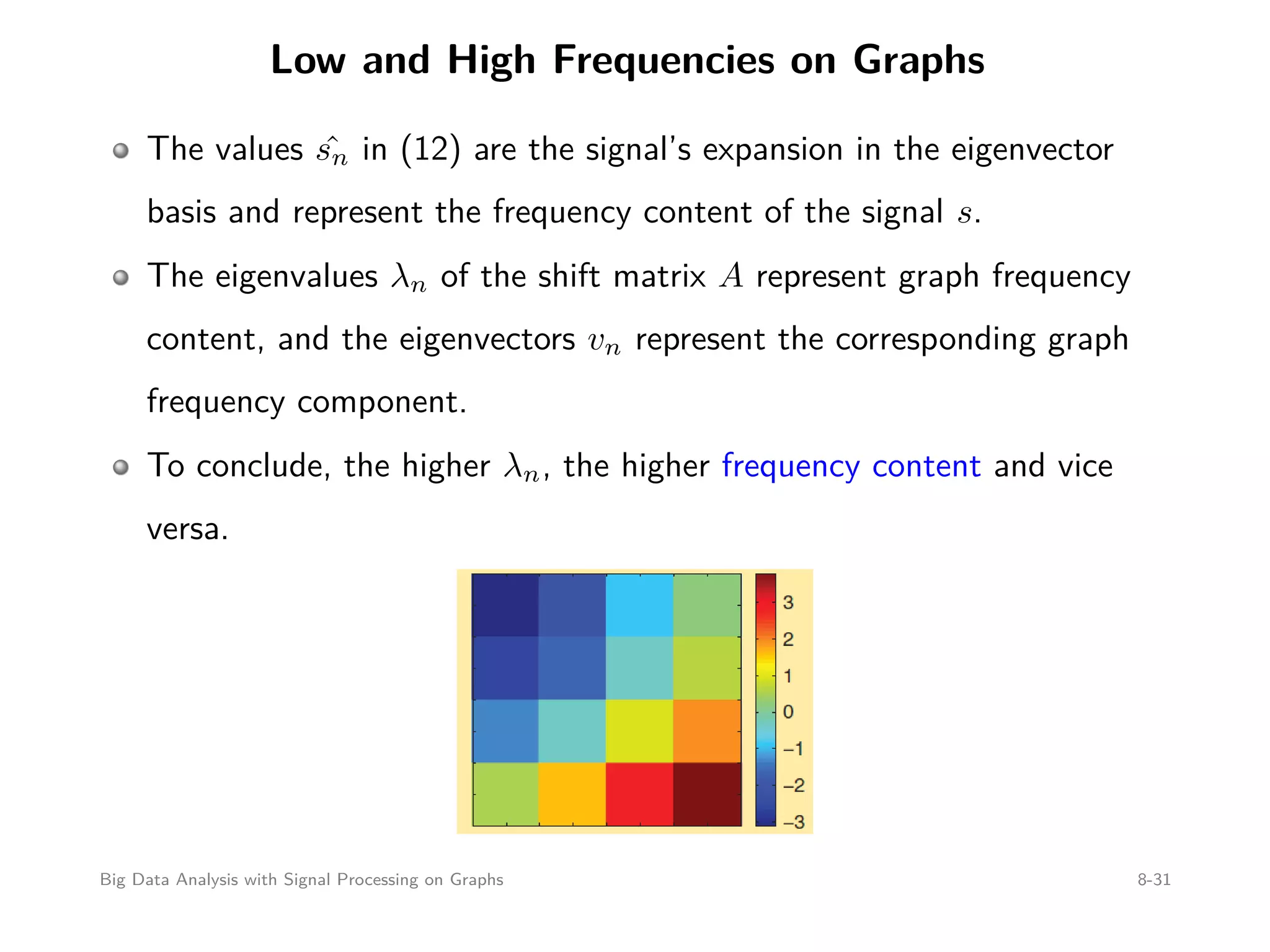
![Graph Fourier Transform (cont’d) The eigenfunctions of graph filters h(A) are given by the eigenvectors of the graph shift matrix A Since the expansion into the eigenbasis is given by the multiplication with the inverse eigenvector matrix, which always exists, the graph Fourier transform is well defined and computed as ˆs = [ ˆs0, ˆs1, . . . , ˆsN−1] T = V −1 s (12) = Fs (13) where F = V −1 is the graph Fourier transform matrix. Big Data Analysis with Signal Processing on Graphs 8-24](https://image.slidesharecdn.com/bigdataseif-151007135408-lva1-app6891/75/Big-Data-Analysis-with-Signal-Processing-on-Graphs-24-2048.jpg)
![Graph Fourier Transform (cont’d) The eigenfunctions of graph filters h(A) are given by the eigenvectors of the graph shift matrix A Since the expansion into the eigenbasis is given by the multiplication with the inverse eigenvector matrix, which always exists, the graph Fourier transform is well defined and computed as ˆs = [ ˆs0, ˆs1, . . . , ˆsN−1] T = V −1 s (12) = Fs (13) where F = V −1 is the graph Fourier transform matrix. Big Data Analysis with Signal Processing on Graphs 8-25](https://image.slidesharecdn.com/bigdataseif-151007135408-lva1-app6891/75/Big-Data-Analysis-with-Signal-Processing-on-Graphs-25-2048.jpg)
![Graph Fourier Transform (cont’d) The eigenfunctions of graph filters h(A) are given by the eigenvectors of the graph shift matrix A Since the expansion into the eigenbasis is given by the multiplication with the inverse eigenvector matrix, which always exists, the graph Fourier transform is well defined and computed as ˆs = [ ˆs0, ˆs1, . . . , ˆsN−1] T = V −1 s (12) = Fs (13) where F = V −1 is the graph Fourier transform matrix. Big Data Analysis with Signal Processing on Graphs 8-26](https://image.slidesharecdn.com/bigdataseif-151007135408-lva1-app6891/75/Big-Data-Analysis-with-Signal-Processing-on-Graphs-26-2048.jpg)