QMC Program: Trends and Advances in Monte Carlo Sampling Algorithms Workshop, Approximate Bayesian Computation for Inference in Generative Models for Large-scale Network Data - Antonietta Mira, Dec 13, 2017

Approximate Bayesian Computation for inference in generative models for large-scale network data Antonietta Mira Data Science, Group, ICS Università della Svizzera italiana, USI, Lugano, Switzerland and Department of Science and High Technology, DISAT Università dell’Insubria, Como, Italy joint with JP Onnela, Sixing Chen Harvard School of Public Health, US Ritabrata Dutta ICS, USI 13.12.17, SAMSI, USA 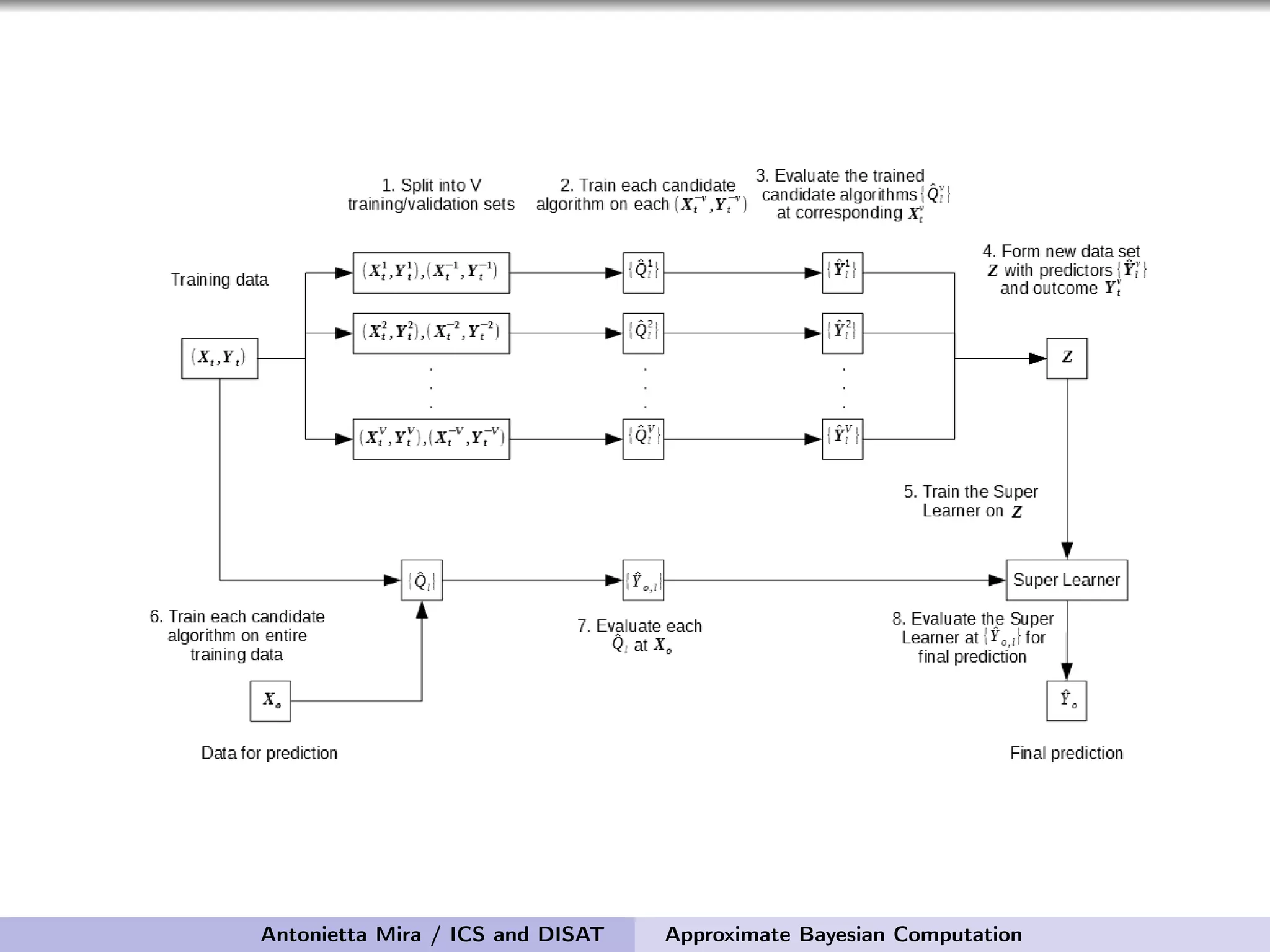Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

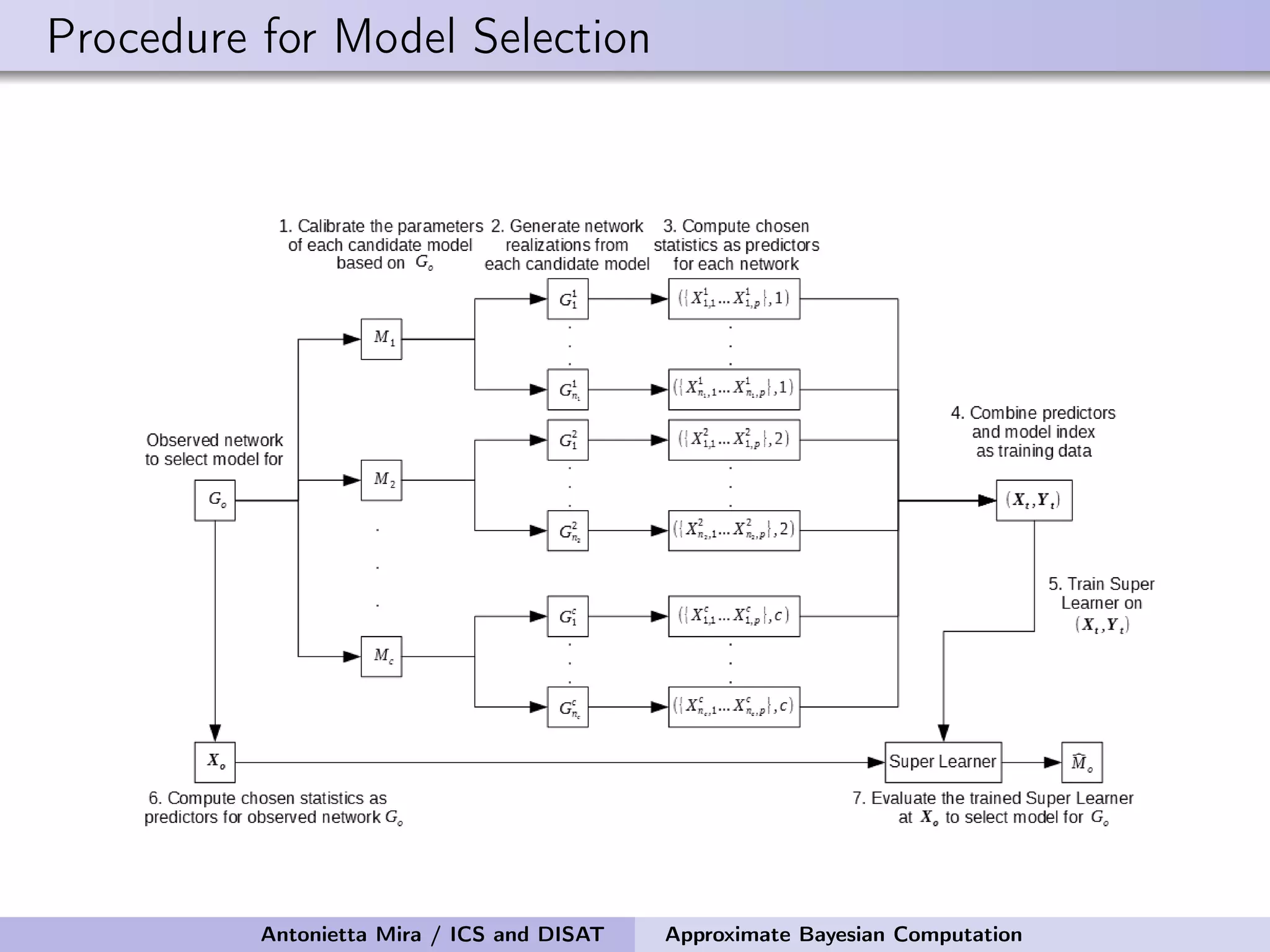
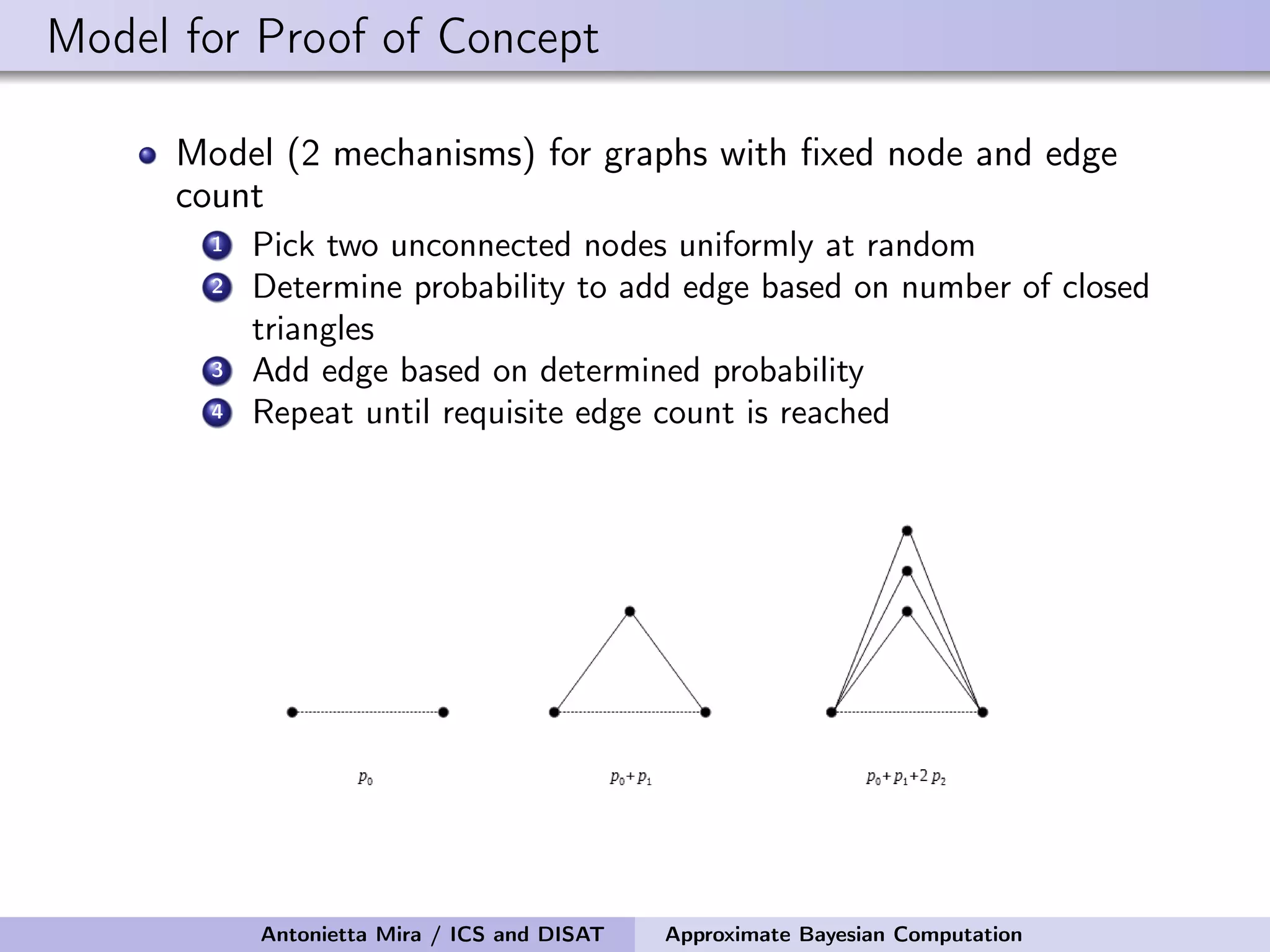
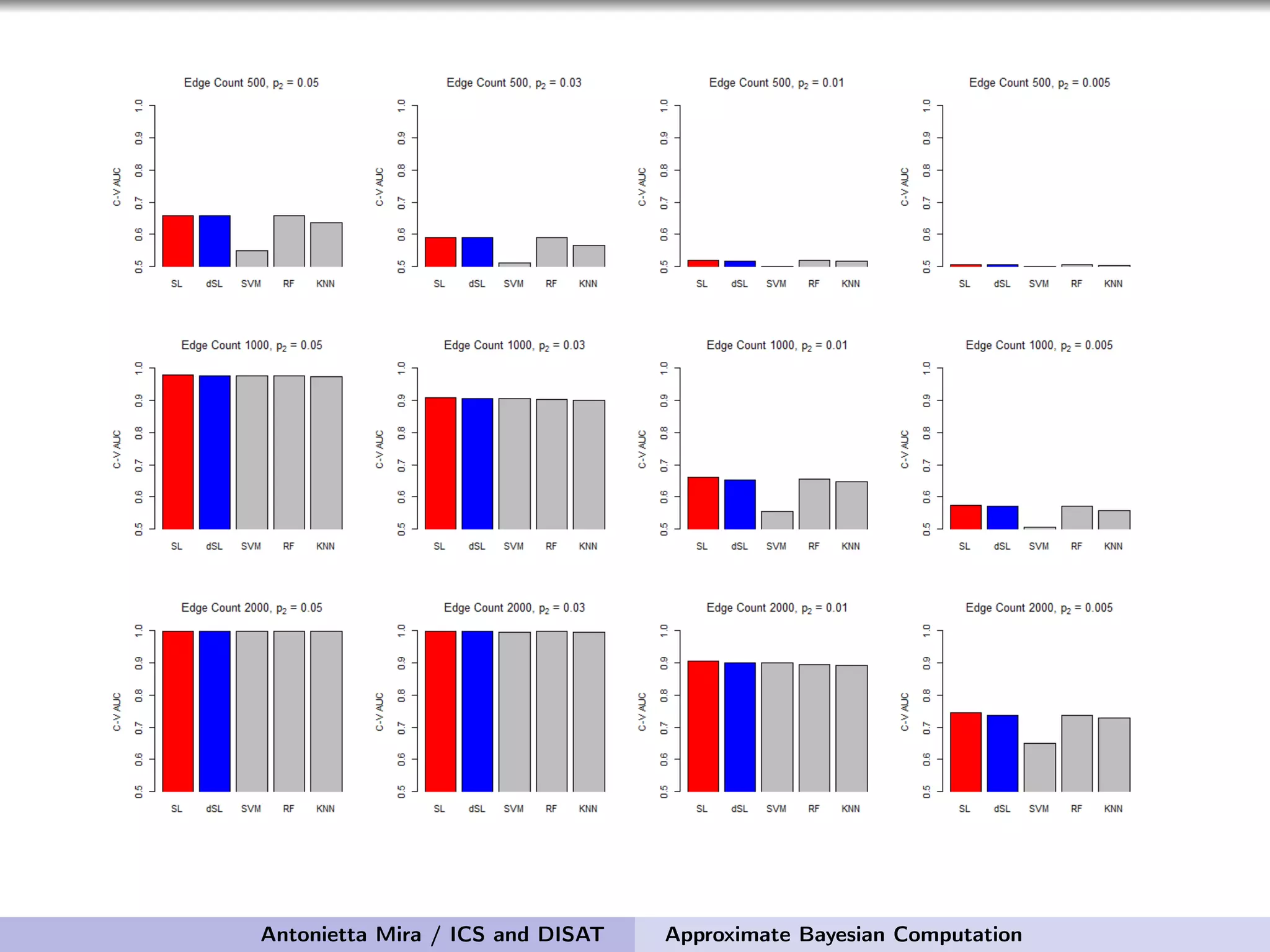
Agenda Large-scale network data and Network models Approximate Bayesian Computation ABC for large-scale network data Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Large-scale network data: Digitized Relationship Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

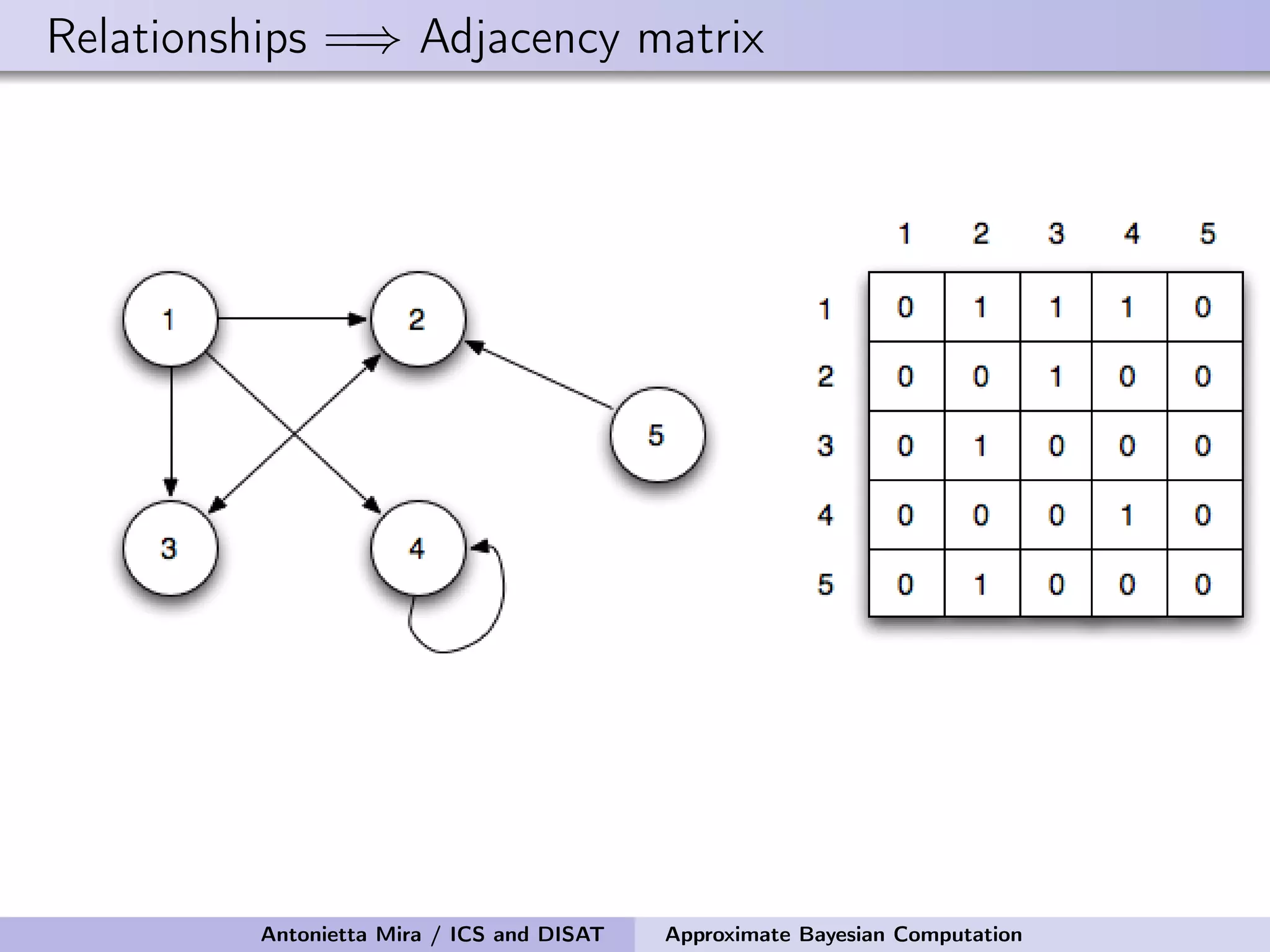
Relationships =⇒ Adjacency matrix Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

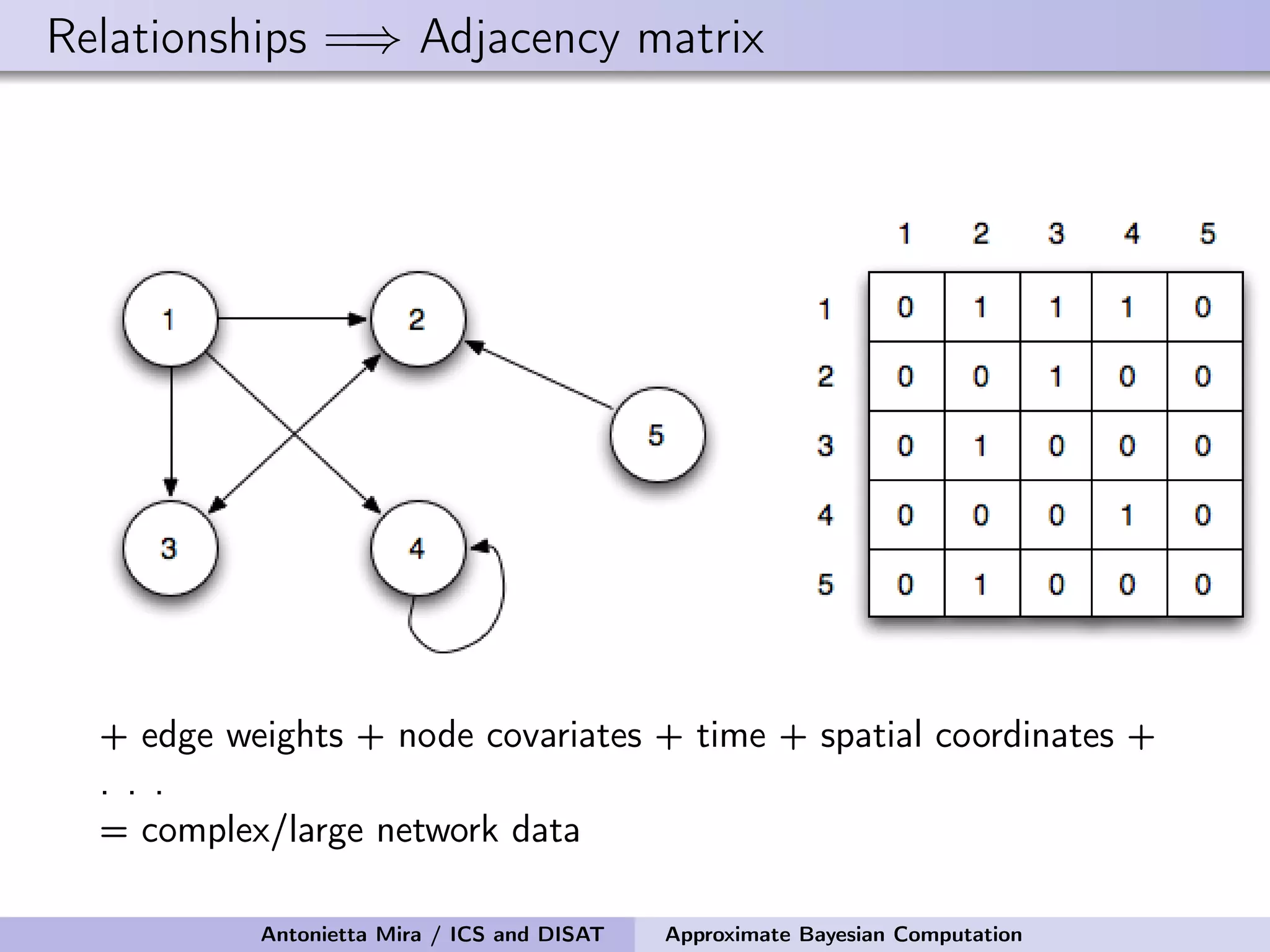
Relationships =⇒ Adjacency matrix + edge weights + node covariates + time + spatial coordinates + . . . = complex/large network data Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Network data social network: friendships ﬁnancial network: EU overnight interbank money transfer economy: EU countries import-export biology/ genetics networks: protein-protein interaction communication network: CDR information / knowledge network: patents citation / collaboration network: wikipedia / co-authorship Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Motivation Systems of scientiﬁc and societal interest have large numbers of interacting components Representation as networks: node = component, edge = interaction Diﬀerent models of network data: Models of network structure (e.g. Erdös-Rényi) Models of dynamical processes on networks (e.g. SI model) Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Communication network of 7 million nodes + 23 million ties JP Onnela et al. PNAS, 2007 Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Big picture of statistical inference GIVEN: Data = y = (y1, . . . , yn) Model which describes data, py|θ(y|θ) indexed by Parameters = θ = (θ1, . . . , θd ) Prior probability density function for θ, pθ WANTED: Some probabilistic statement about θ and model point estimation conﬁdence/credible intervals hypothesis testing prediction model selection Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Two types of models Statistical model py|θ(yi |θ) = 1 √ 2πσ2 exp − 1 2σ2 (yi − µ)2 , θ = (µ, σ) Generative model → given θ = (µ, σ) →zi ∼ N(0, 1) →yi = µ + σzi →yi ∼ py|θ(yi |θ) In some setting easier to give the model in the generative form Sometimes there is no 1:1 correspondence bwn statistical and generative model Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Likelihood-based statistical inference Likelihood function: L(θ) ∝ py|θ(y|θ) Plays a central role in statistical inference Maximum likelihood estimation: ˆθMLE = argmaxθ L(θ) Bayesian inference: pθ|y (θ|y) ∝ L(θ)pθ(θ) Not available for generative models Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Why generative models? Allow to use knowledge domain on how the data were generated without having to make excessive compromises in the modeling Scale well with big data No limits on the number of unobserved/latent variables Easier to study the eﬀect of interventions on generative models rather than statistical models LFI: Procedure to obtain probabilistic statements about θ even if likelihood is not available, as for generative models ABC: is a LFI methodology Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Examples of generative models Astrophysics: Simulating the formation of galaxies, stars, or planets Evolutionary biology: Simulating species evolution Ecology: Simulating species migration over time Neuroscience: Simulating neural circuits Epidemiology: Simulating the spread of an infectious disease Meteorology: Simulating weather prediction Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Approximate Bayesian Computation (ABC) Starting point is Bayes’ theorem: p(θ|y) = p(y|θ)p(θ) p(y) p(θ|y) = posterior p(y|θ) = likelihood p(θ) = prior p(y) = evidence Evaluation of the LHD may be computationally expensive or infeasible, ruling out both likelihood-based and posterior-based inference Approximate Bayesian Computation (ABC) avoids direct evaluation of the LHD and approximates it by generating synthetic data (synthetic observations) by simulation from the model Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Approximate Bayesian Computation (ABC) ABC rejection sampler is the simplest form of ABC ABC rejection sampler Sample parameter θ∗ from the prior p(θ) Simulate dataset y∗ under the given model speciﬁed by θ∗: y∗ ∼ p(·|θ∗) Accept θ∗ if d(y∗, y) ≤ Distance measure d(y∗, y) determines the level of discrepancy between the simulated data y∗ and the observed data y The accepted θ∗ are approximately distributed according to the desired posterior and, crucially, obtained without the need of explicitly evaluating the LHD Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

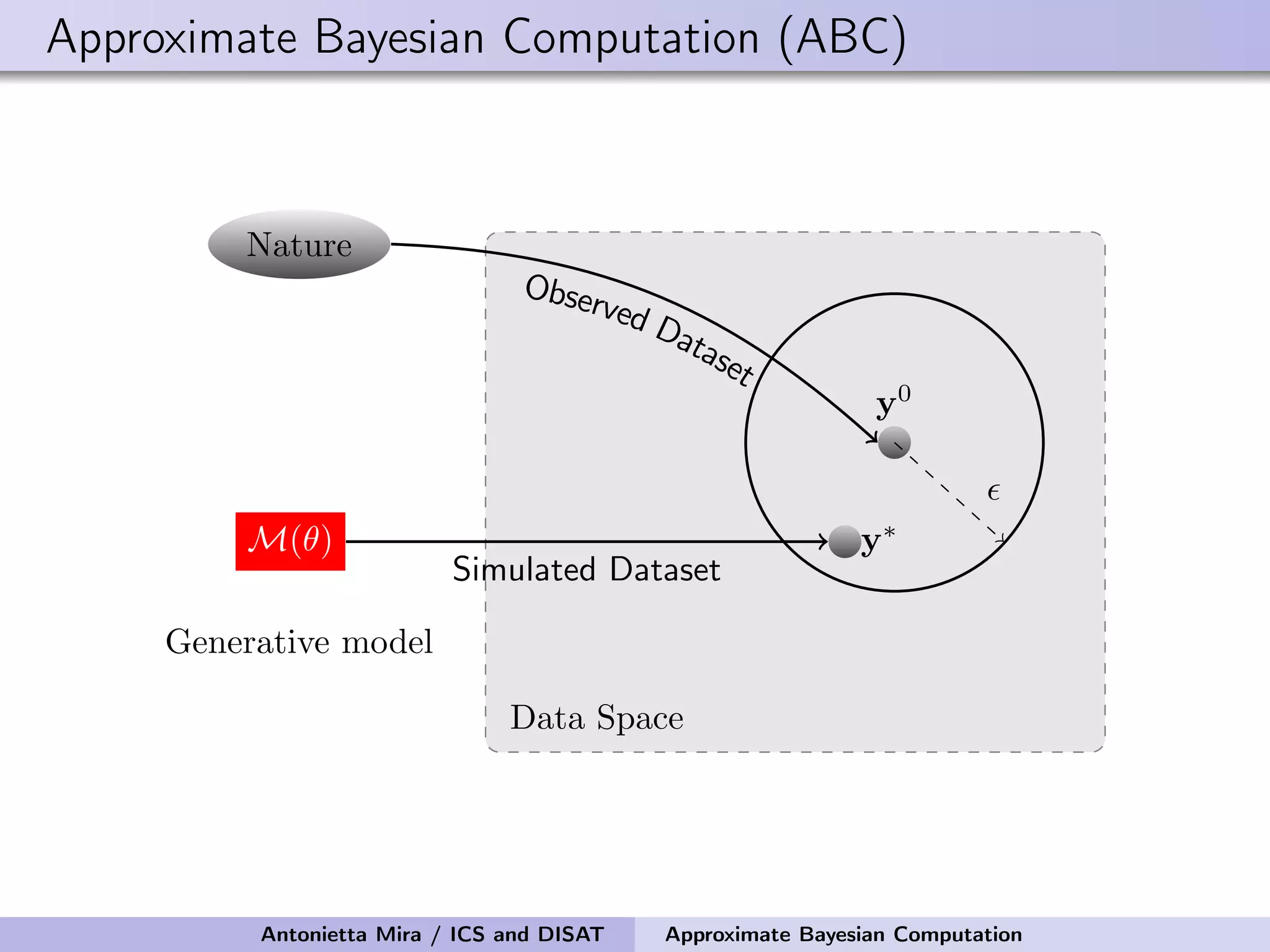
Approximate Bayesian Computation (ABC) M(θ) Generative model Nature y0 y∗ Observed Dataset Simulated Dataset Data Space Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Approximate Bayesian Computation (ABC) It may be unfeasible to compute the distance d(y∗, y) for high-dimensional data Lower dimensional summary statistic S(y) to capture the relevant information in y Comparison is done between S(y∗) and S(y): accept θ∗ if d(S(y∗), S(y)) ≤ Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Principle behind likelihood-free inference Replace LHD, py (y|θ), by SUMMARY LHD pS (S(y)|θ) where S(y) = summary statistics But pS (S(y)|θ) is also unknown Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Principle behind likelihood-free inference Replace LHD, py (y|θ), by SUMMARY LHD pS (S(y)|θ) where S(y) = summary statistics But pS (S(y)|θ) is also unknown Use an APPROXIMATE SUMMARY LHD: ˜pS (S(y)|θ), based on pseudo data y∗ generated from the model The POSTERIOR is also approximate and summarized: ˜pS (θ|S(y)) ∝ p(θ)˜pS (S(y)|θ) Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

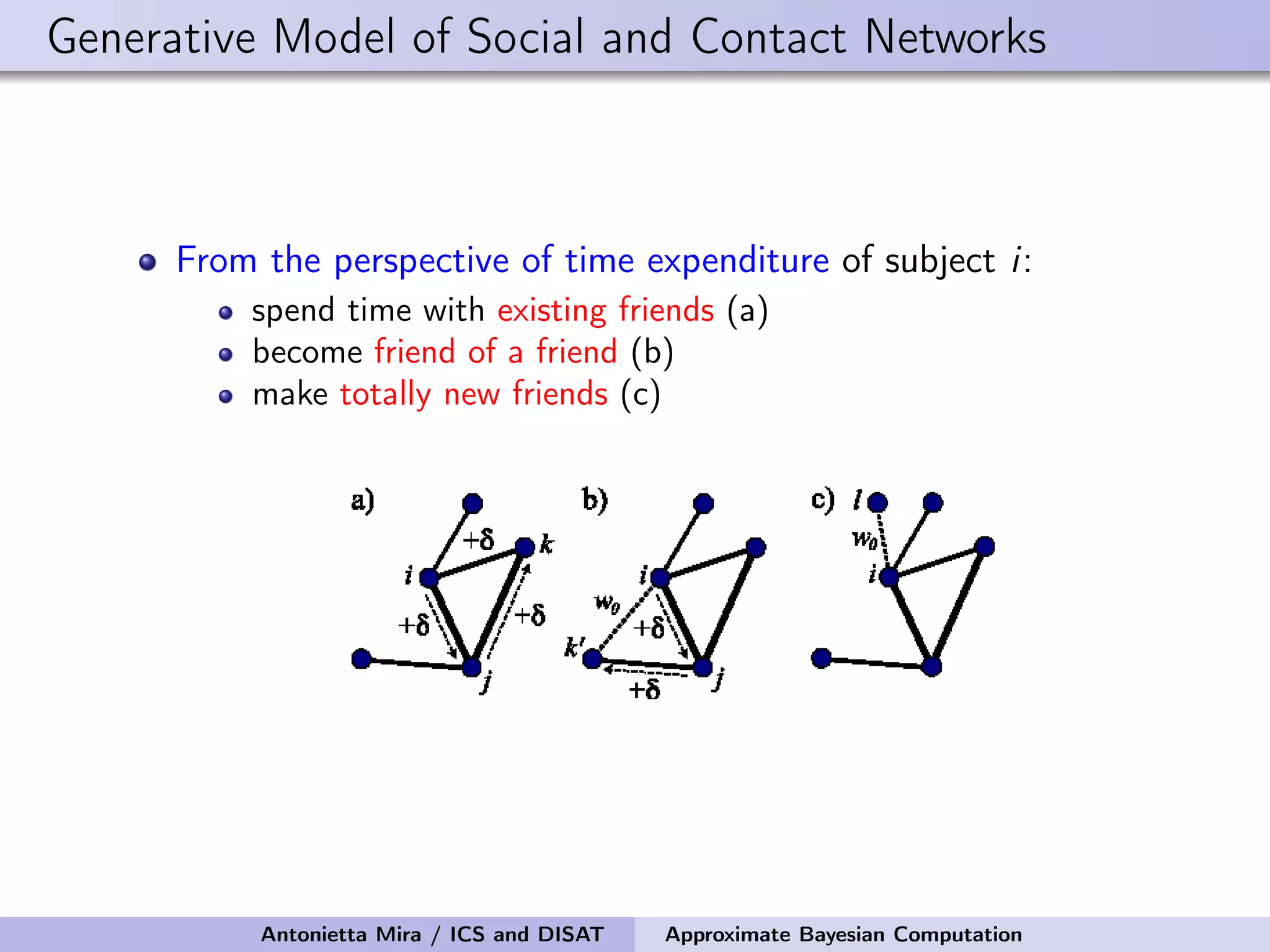
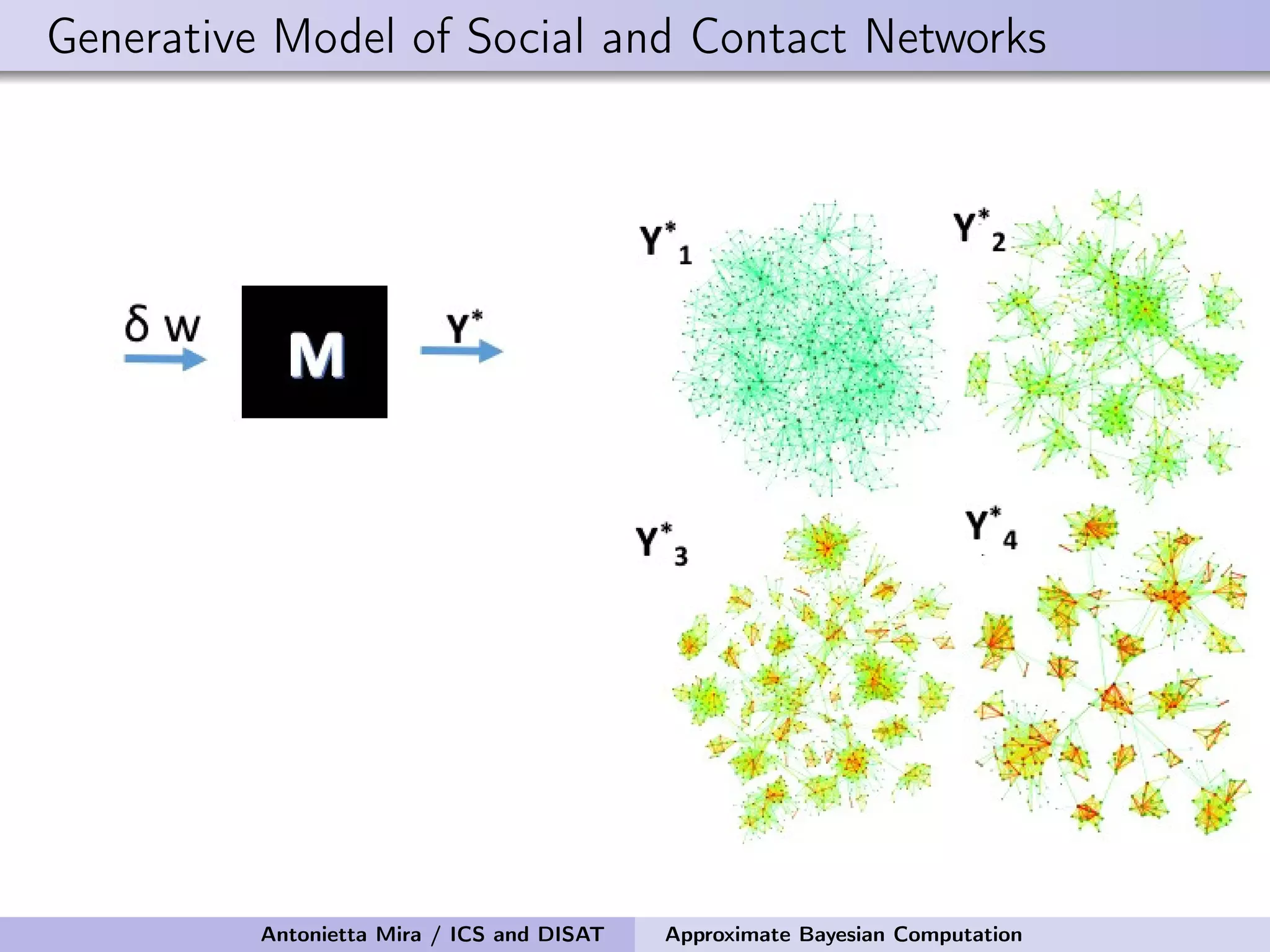
Approximate Bayesian Computation (ABC) If S is sufficient wrt θ, then it contains all information in y about θ (by definition), and using S(y) in place of the full dataset does not introduce any error For most models it may be impossible to find sufficient statistics S, in which case application relevant summary statistics are used Use of non-sufficient summary statistics introduces a further level of approximation Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Network Models Distinction between two types of models of network structure: Statistical models (e.g. ERGM, Goyal-Blitzstein-DeGruttola) DATA DRIVEN Pros: inference on model parameters; hypothesis testing; model selection Cons: scalability; hard to incorporate domain knowledge Generative models (e.g. Price model) KNOWLEDGE DRIVEN assume that microscopic mechanisms that govern network formation and evolution are known, ask what happens if we apply these mechanisms repeatedly Pros: scalability, easy to incorporate knowledge, intervention Cons: no inferential tools; no model comparison Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Generative Model of Social and Contact Networks From the perspective of time expenditure of subject i: spend time with existing friends (a) become friend of a friend (b) make totally new friends (c) Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Generative Model of Social and Contact Networks Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

ABC for Generative Network Models ABC + generative network model = generic + sound inferential framework ABC rejection sampler for generative network models Observe an empirical graph G Set up generative network model M Sample parameter θ∗ from the prior p(θ) Simulate graph G∗ from model M using parameter θ∗ Accept θ∗ if d(S(G∗), S(G)) ≤ Some simple network summaries: degree sequence, k-stars, subgraph counts, centrality measures (betweenness, eigenvector, random walk, etc.), etc. Can use KNN to identify points in the space of summary statistics close to S(G) From Rejection-ABC to SMC-ABC by Drovandi+Pettitt, 2015 Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Exact inference for Erdös-Rényi (ER) For the Erdös-Rényi model the LHD is available: Aij = dyad (pair of nodes): value 1 (connected) or 0 (not connected) Yij = RV coding the state of the dyad p = P(Yij = 1) N = number of nodes n = number of dyads: N(N − 1)/2 (undirected) and N(N − 1) (directed) L = number of connected dyads (suﬃcient statistics) LHD = p(G|p) = i=j P(yij = Aij ) = i=j pAij (1−p)1−Aij = pL (1−p)n−L MLE = ˆp = L/n = proportion of connected dyads to all dyads Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Exact Bayesian inference for ER Beta prior p(θ) = Beta(α = 5, β = 50) Beta posterior p(θ|D) = Beta(α + L, β + [N(N − 1)/2) − L]) Bayesian Estimator = posterior mean Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Approximate Bayesian inference for Erdös-Rényi Simulate observed ER graph G from a model with N = 100 and p = 0.05 Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Approximate Bayesian inference for Erdös-Rényi Simulate observed ER graph G from a model with N = 100 and p = 0.05 Number of edges = summary statistic = S(G) = L Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Approximate Bayesian inference for Erdös-Rényi Simulate observed ER graph G from a model with N = 100 and p = 0.05 Number of edges = summary statistic = S(G) = L We perform 100,000 draws from the prior pi For each pi , we generate a sequence of graphs G1 i , . . . , GK i , compute corresponding summary statistics S(G1 i ), . . . , S(GK i ), retain pi if S(Gi ) = Li = L = S(G) We retained only 162 values of pi Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

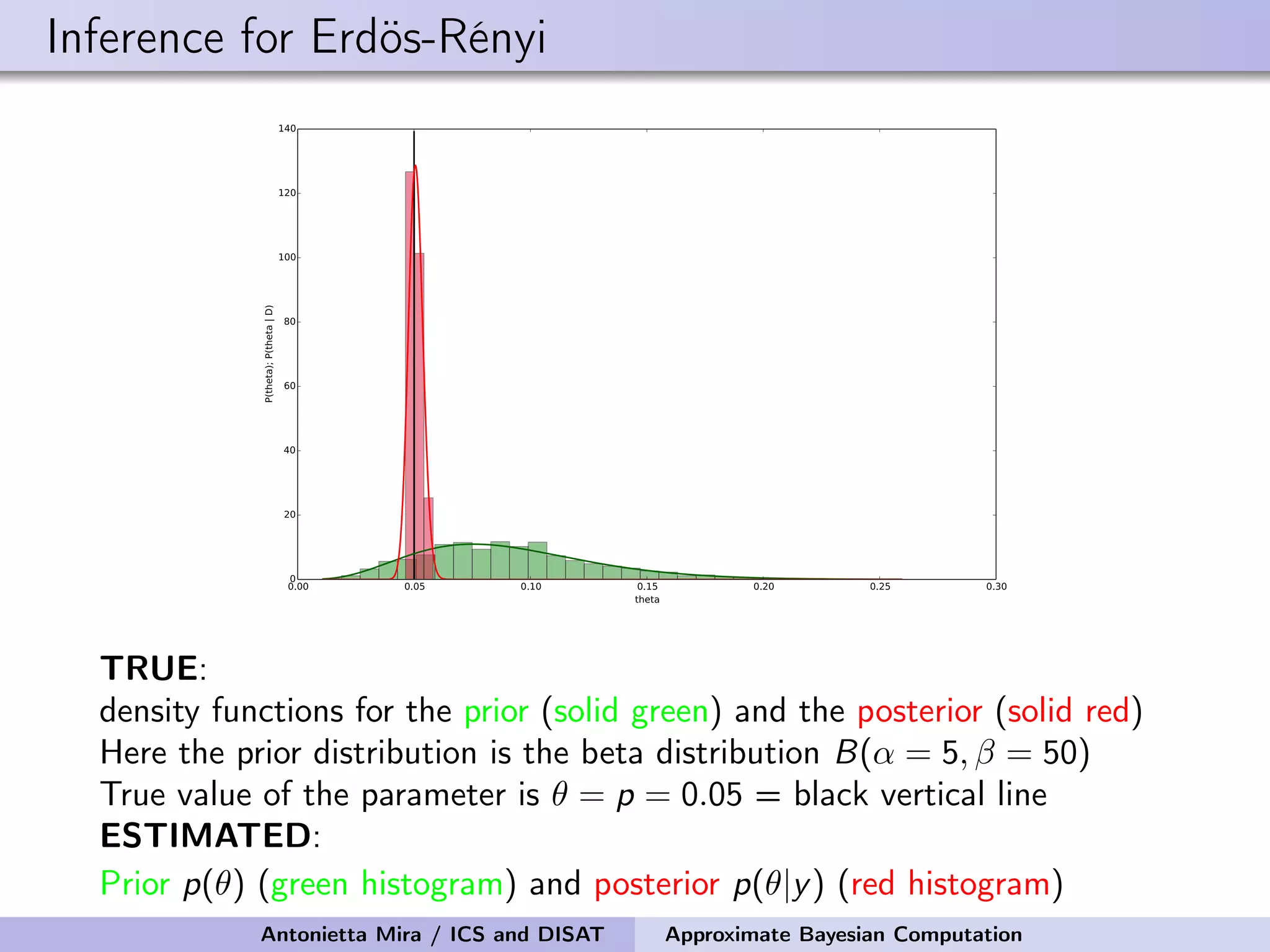
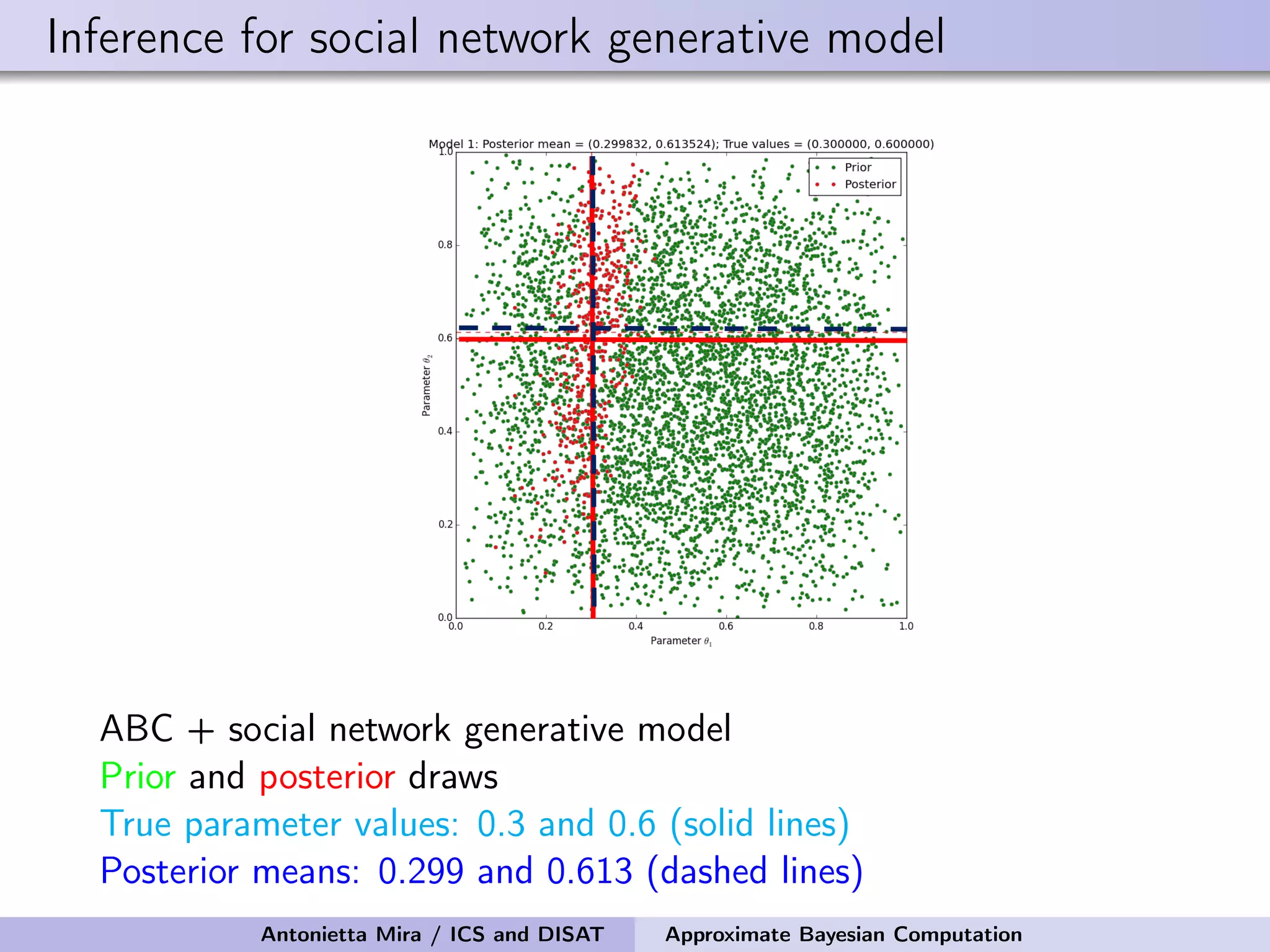
Approximate Bayesian inference for Erdös-Rényi Simulate observed ER graph G from a model with N = 100 and p = 0.05 Number of edges = summary statistic = S(G) = L We perform 100,000 draws from the prior pi For each pi , we generate a sequence of graphs G1 i , . . . , GK i , compute corresponding summary statistics S(G1 i ), . . . , S(GK i ), retain pi if S(Gi ) = Li = L = S(G) We retained only 162 values of pi The mean and median of the prior are 0.091 and 0.086 the 95% prior credible interval is [0.031, 0.178] The mean and median of the posterior are 0.050 and 0.050 the 95% posterior credible interval is [0.043, 0.055] Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Approximate Bayesian inference for Erdös-Rényi Degree distribution = summary statistic = S(G) KS = distance measure We performed 100,000 draws from the prior For each pi , we generate a sequence of graphs G1 i , . . . , GK i , compute corresponding summaries S(G1 i ), . . . , S(GK i ), obtain a sequence of distances y1 i = d(S(G1 i ), S(G)), . . . , yK i = d(S(GK i ), S(G)) Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Approximate Bayesian inference for Erdös-Rényi Pool the distances yk i for all values of i and s: 100, 000 · K total Choose a cutoﬀ value d∗ = 10th percentile Higher acceptance rate: 761 Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Approximate Bayesian inference for Erdös-Rényi Pool the distances yk i for all values of i and s: 100, 000 · K total Choose a cutoﬀ value d∗ = 10th percentile Higher acceptance rate: 761 The mean and median of the prior are 0.09 and 0.09 the 95% prior CI is [0.03, 0.18] The mean and median of the posterior are 0.05, 0.05 the 95% posterior CI is [0.04, 0.06] Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Inference for Erdös-Rényi TRUE: density functions for the prior (solid green) and the posterior (solid red) Here the prior distribution is the beta distribution B(α = 5, β = 50) True value of the parameter is θ = p = 0.05 = black vertical line ESTIMATED: Prior p(θ) (green histogram) and posterior p(θ|y) (red histogram) Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Approximate Bayesian inference for Easley-Kleinberg (EK) The EK model is a simple model of directed networks Unlike ER, the EK model is a growing network model new vertices attach themselves to existing ones using a preferential attachment rule: each new node is not equally likely to attach itself to any of the existing nodes but, instead, has a preference for some nodes over others based on their degree More speciﬁcally, linear preferential attachment speciﬁes that an incoming node will attach to an existing vertex vi with probability proportional to its degree ki More complicated functions of ki are possible, and in general one can incorporate nodal attributes, or covariates, in the expression for the attachment function RESULTS: Similar performance to the Erdös-Rényi model Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Inference for social network generative model ABC + social network generative model Prior and posterior draws True parameter values: 0.3 and 0.6 (solid lines) Posterior means: 0.299 and 0.613 (dashed lines) Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Summary Simulator-based models: Generative model for networks Challenge: Inference of parameters of generative model is challenging due to intractability of likelihood function Solution: Approximate Bayesian Computation Application: ABC works for diﬀerent mechanistic models Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Spreading Process on Network We study the spread of an epidemic / fake news on a network: Can be considered as a spreading process on a network Data = a ﬁxed and known human contact interaction network = a ﬁxed and know social network (N) Data = at some time points over a period of observation we know which nodes in the network are infected = we know which websites report the fake news Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Simple spreading process: Susceptible-Infected (SI) Rate of diﬀusion (θ): How fast a disease or a fake news spreads on a network? Seed-node (nsn): Can we infer the source of the infection or of the fake news? Algorithm 1 SI spreading process, over the network N starting at n0 SN, for each time-point t = 0, . . . , T 1: for t = 0 to T do 2: It = Infected nodes at time t 3: for each i ∈ It do 4: Select j from the neighbors of i with equal probability 5: If neighbor j is already infected, do nothing If not, infect it with probability θ 6: end for 7: end for Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Inference of SI process on networks? M : SI y (θ, nsn)? Inference of the parameters (θ, nsn) deﬁning the SI process Challenging problem: due to the intractability of the likelihood New types of inferencial schemes are required Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

ABC for spreading process on networks ABC for spreading process Observe temporal data on network y Set up a model M described by SI process Sample parameter θ∗, n∗ SN from the prior p(θ, nSN) Simulate temporal data y∗ from model M using θ∗, n∗ SN Accept θ∗, n∗ SN if d(S(y∗), S(y)) ≤ using application relevant summaries S For inference, we use simulated annealing ABC SABC, Statistics and Computing, 2015 Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Simulated network topologies Network structure and its connectivity aﬀect the disease spread Two diﬀerent network topologies 1 Barabasi-Albert network (BA): scale-free degree distribution 2 Erdös-Rènyi network (ER): edges are independent and equally likely 3 BA(m=4) and ER(p=0.05) network with 100 nodes 4 First observed time slice: t0 5 Length of the simulated SI process: T Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Details of ABC Need to deﬁne: 1 Model M: SI process as a generative model 2 Summary statistics S : y → S(y) 3 discrepancy measure d(S(y), S(y∗)) Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Details of ABC Statistics: Two summary statistics s = (s1, s2, . . . , sT ), si = proportion of infected nodes at ti If whole network is infected at time τ, then st = 1 for t > τ G = (G1, G2, . . . , GT ), Gi = sub-graph of infected nodes at ti Distance: Two distances combined 1 d1(s1 , s2 ) = 1 T T t=1(s1 t − s2 t )2 2 d2(G1 , G2 ) = 1 T T t=1 i∈G1 t j∈G2 t ρ(i,j) ρmax , where ρ(i, j) = the shortest path between nodes i and j and ρmax = maximum shortest path length on the network 3 Final distance: d((s1 , G1 ), (s2 , G2 )) = 1 2 d1(s1 , s2 ) + d2(G1 , G2 ) Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

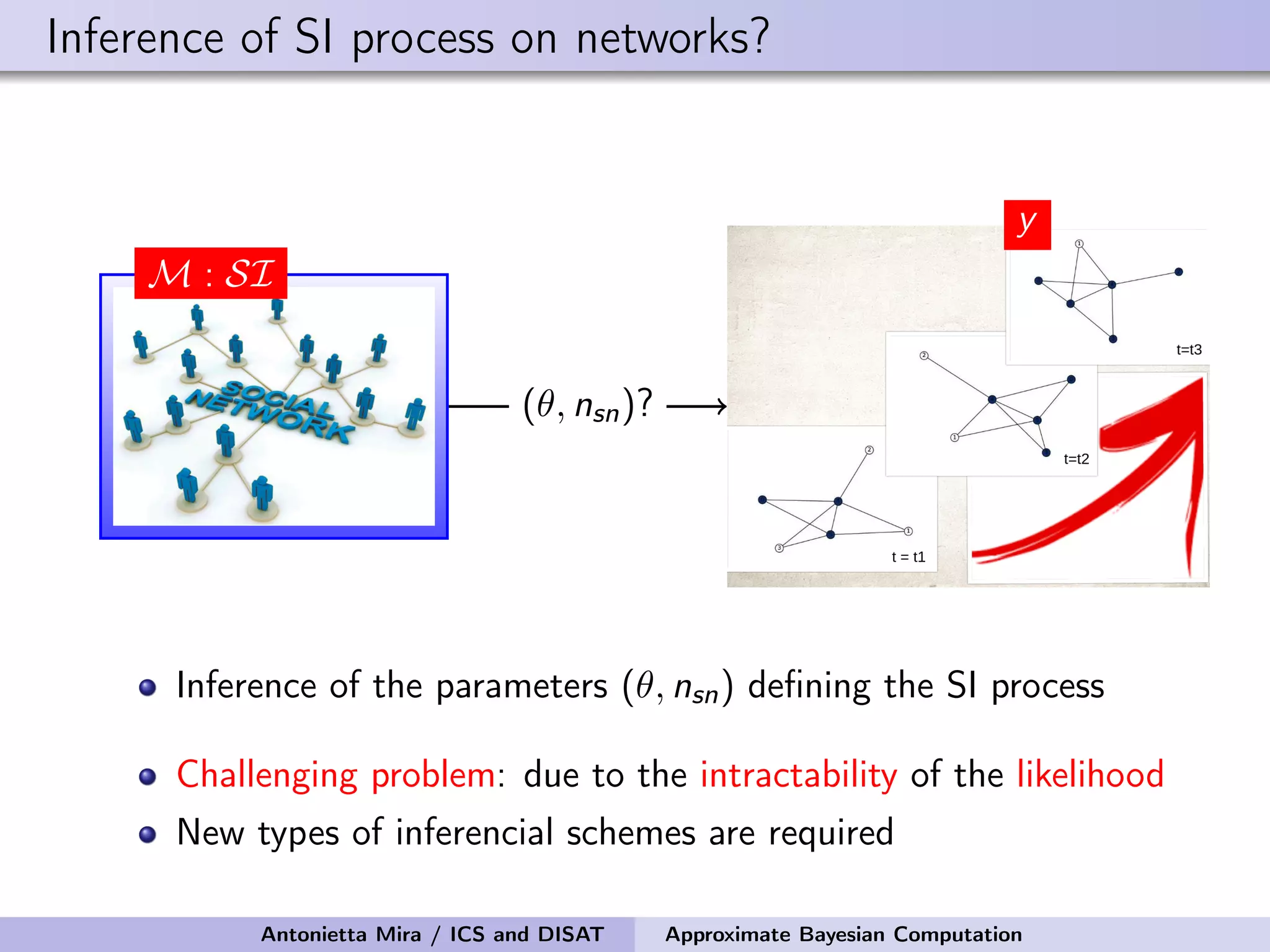
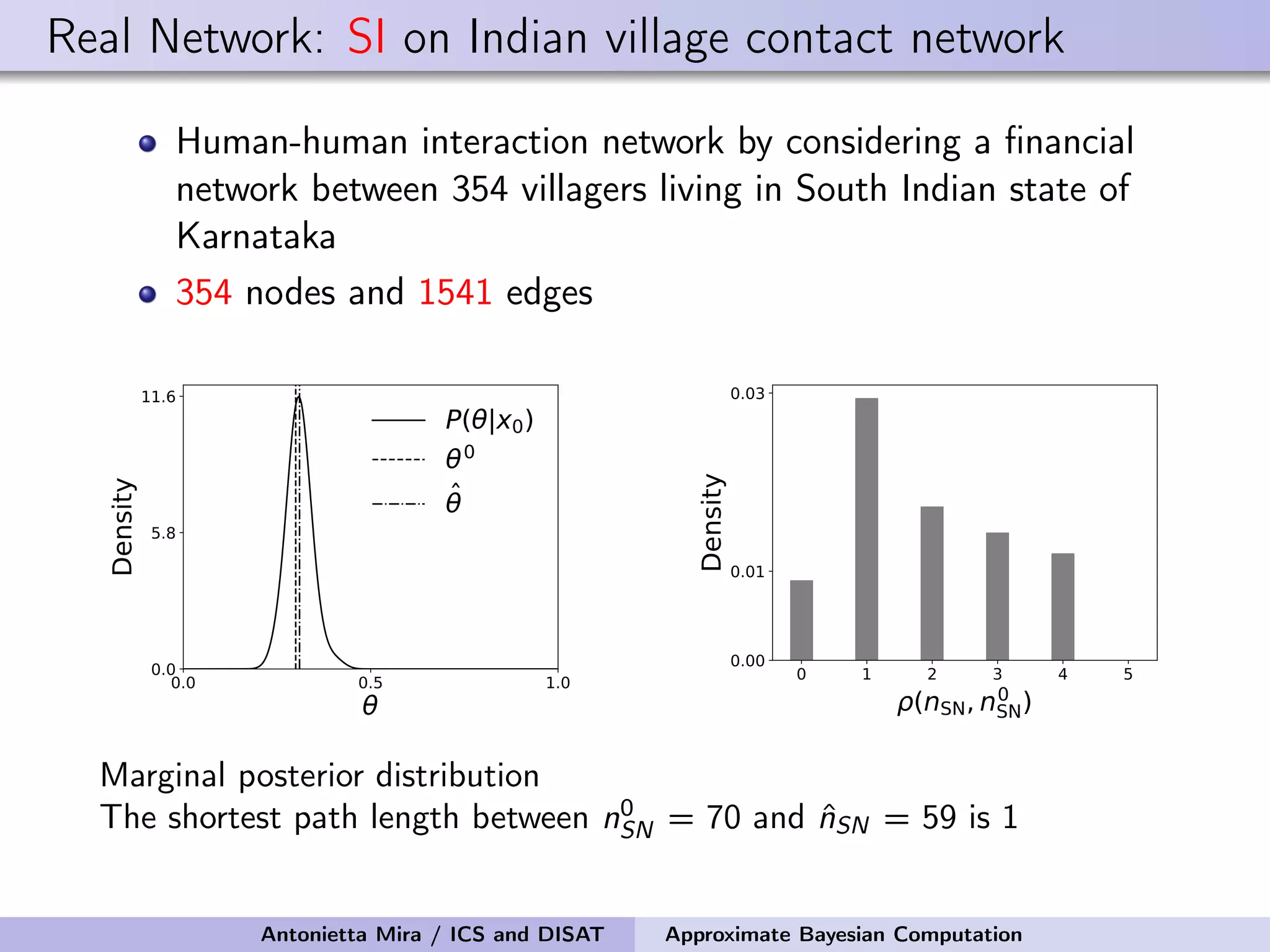
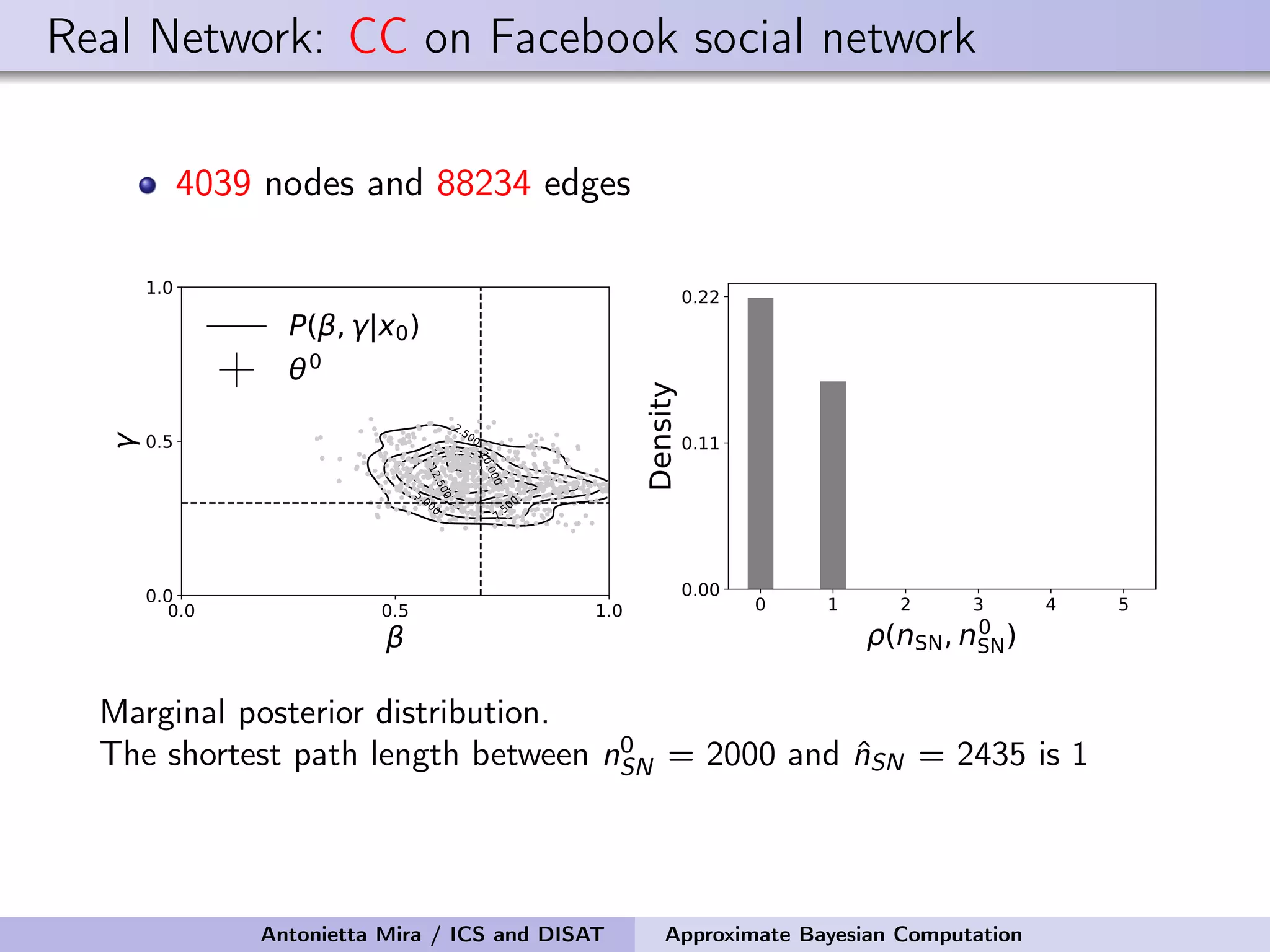
Details of ABC Prior on the seed node: Uniform on the infected nodes at t1 Prior on the infectivity parameter: Uniform on [0, 1] Perturbation Kernel: A perturbation kernel used to explore the parameter space is deﬁned as a distribution on (θ, nSN) given the present parameter values (θ∗, n∗ SN), K((θ, nSN)|(θ∗, n∗ SN)) = K1(θ|θ∗, ˆσ)K2(nSN|n∗ SN) where K1 = Gaussian with ˆσ being the variance of the θ sampled in the previous step of SABC optimally rescaled K2 = discrete distribution on the neighboring nodes of n∗ SN with each node having a probability inversely proportional to its degree Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

BA (top) & ER (bottom): marginal posterior (SI) First observed time slice: t0 = 20 Length of the simulated SI process: T = 70 0.0 0.5 1.0 θ 0.0 4.7 9.4 Density P(θ|x0) θ0 0 1 2 3 4 5 ρ(nSN,n0 SN) 0.00 0.07 0.14 Density 0.0 0.5 1.0 θ 0.0 3.4 6.9 Density P(θ|x0) θ0 0 1 2 3 4 5 ρ(nSN,n0 SN) 0.00 0.03 0.06 Density Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

BA (top) & ER (bottom): Bayes Estimate (SI) Average over 100 simulated dataset for same true parameter value 0.0 0.5 1.0 ̂θ 0.0 ̂.6 9.1 Density θ0 0 1 2 3 4 5 ρ( ̂nSN,n0 SN̂ 0.00 0.34 0.69 Density 0.0 0.5 1.0 ̂θ 0.0 4.̂ 8.5 Density θ0 0 1 2 3 4 5 ρ( ̂nSN,n0 SN̂ 0.00 0.20 0.39 Density Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Complex contagion process (CC): Modeling fake news on social network Rate of exposure (β): Can we infer the rate of exposure of a node to infected nodes? Threshold (γ): Can we infer the percentage of infected neighboring nodes needed to infect a new node or to make it believe the fake news? Seed-node (nsn): Can we infer the source of the infection or of the fake news? For algorithmic details please consult Dutta et. al. 2017 Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

BA (top) & ER (bottom): marginal posterior (CC) First observed time slice: t0 = 20 Length of the simulated SI process: T = 120 0.0 0.5 1.0 β 0.0 0.5 1.0 γ 1.0 00 1.000 2 .0 0 0 3 .0 0 0 4.0 00 5.000 6.000 P(β, γ|x0) θ0 0 1 2 3 4 5 ρ(nSN,n0 SN) 0.00 0.32 0.64 Density 0.0 0.5 1.0 β 0.0 0.5 1.0 γ 2 .0 0 0 4.000 6.000 8.0 00 10.0 00 P(β, γ|x0) θ0 0 1 2 3 4 5 ρ(nSN,n0 SN) 0.00 0.25 0.50 Density Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

BA (top) & ER (bottom): Bayes Estimate (CC) Over 100 simulated dataset for same true parameter value 0.0 0.5 1.0 ̂ β 0.0 0.5 1.0 ̂γ 15.0 00 ̂0.000 45.0 00 θ0 0 1 2 3 4 5 ρ( ̂nSN,n0 SN̂ 0.00 0.48 0.97 Density 0.0 0.5 1.0 ̂ β 0.0 0.5 1.0 ̂γ 10.0 00 ̂0.0 003 0 .0 0 0 40.000 θ0 0 1 2 3 4 5 ρ( ̂nSN,n0 SN̂ 0.00 0.38 0.77 Density Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

BA (left) & ER (right): Dependence of inference on ∆t = T − t0 0.0 0.5 1.0 θ 0.0 5.1 10.2 Density ΔT =10 ΔT =Δ0 ΔT =50 θ0 0.0 0.5 1.0 θ 0.0 4.1 8.2 Density ΔT =10 ΔT =Δ0 ΔT =50 θ0 0.0 0.5 1.0 β 0.0 0.5 1.0 γ 0 .8 0 0 1 .6 0 0 2.40 0 3.200 4.0 00 0 .8 0 0 0.800 0.8 00 1 .6 0 0 2 .4 0 0 3.20 0 4.0 00 0 .8 0 0 0 .8 0 0 1.60 0 2.400 3 .2 0 0 4 .0 0 0 4.80 0 ΔT Δ 28 ΔT Δ 46 ΔT Δ 100 θ0 0.0 0.5 1.0 β 0.0 0.5 1.0 γ 0 .6 0 0 1.200 1 .8 0 0 2.4 00 3 .0 0 0 3.600 1.5 00 3.0 00 4 .5 0 0 6.000 7.500 1 .5 0 0 3.0 00 4.5 00 6.0 00 7.5 00 ΔT Δ 28 ΔT Δ 46 ΔT Δ 100 θ0 Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Real Network: SI on Indian village contact network Human-human interaction network by considering a ﬁnancial network between 354 villagers living in South Indian state of Karnataka 354 nodes and 1541 edges 0.0 0.5 1.0 θ 0.0 5.8 11.6 Density P(θ|x0) θ0 ̂θ 0 1 2 3 4 5 ρ(nSN,n0 SN) 0.00 0.01 0.03 Density Marginal posterior distribution The shortest path length between n0 SN = 70 and ˆnSN = 59 is 1 Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Real Network: CC on Facebook social network 4039 nodes and 88234 edges 0.0 0.5 1.0 β 0.0 0.5 1.0 γ 2.500 5 .0 0 0 7 .5 0 0 10.0 00 12.5 00 P(β, γ|x0) θ0 0 1 2 3 4 5 ρ(nSN,n0 SN) 0.00 0.11 0.22 Density Marginal posterior distribution. The shortest path length between n0 SN = 2000 and ˆnSN = 2435 is 1 Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Summary Simulator-based models: A diffusion process on a fixed network Challenge: Inference of parameters of spreading process and seed-node is challenging due to intractability of likelihood Solution: Approximate Bayesian Computation Application: ABC works for different simulated and real network topologies Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Computational facility ABCPy: A python suite of ABC: user friendly and modular Paralleized: The most popular ABC algorithms are parallelized Super-computers: Work done in collaboration with Centro Svizzero di Calcolo Scientiﬁco - CSCS Usability: In collaboration with CSCS, we oﬀer to infer model/parameter of your problem using the most powerful super computer in Europe (CRAY) Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

ABC for Model Comparison Standard Bayesian approach to model comparison involves Bayes factors and posterior probabilities of model index Posterior probabilities are poorly estimated by ABC (theory and simulation) Alternative approach: select the most likely model using a classiﬁer and compute ABC approximation of the posterior predictive error rate Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

ABC for Model Comparison ABC for model comparison (Part I) Observe an empirical graph G Identify alternative possible generative network models M1 and M2 Draw model index from the model prior: τ1 = P(M = 1) = P(M = 2) = τ2 Draw parameter θ∗ from the prior p(θ|M) Simulate graph G∗ from the given generative network model using parameter θ∗ Accept θ∗ if ρ(S(G∗), S(G)) ≤ using any summaries S Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

ABC for Model Comparison ABC for model comparison (Part II) Accepted draws form the ABC approximation of the joint posterior p(θ, M|y) Generate n independent pseudo-data sets for each such draw (ABC approximation of the posterior predictive distribution) Compute posterior error rate using a random forest classiﬁer (i.e., how frequently it returns the true model index) Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Super Lerner for Model Selection Select model based on ABC training data with Super Learner (SL) SL = ensemble algorithm for prediction Combines a library of candidate algorithms Given loss function, SL aims for the lowest cross-validated risk Discrete SL minimizes over library of candidate algorithms Full SL minimizes over convex combinations of candidates algorithms Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Given bounded loss function, both version of SL have Oracle property The user is able to select: Loss function Candidate algorithms Predictors for each candidate algorithms This ﬂexibility is invaluable for models with intractable likelihood Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Procedure for Model Selection Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

We use as loss function = 1 − AUC AUC is the area under the receiver operating characteristic curve Choice of statistics to use for calibration and to use as predictors Unlikely to obtain suﬃciency given the nature of the likelihood Statistics for calibration: Need to characterize similarities between candidate models Ensure candidate models can plausibly generate the observed network Statistics as predictors: Need to characterize the diﬀerences between candidate models Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Model for Proof of Concept Model (2 mechanisms) for graphs with ﬁxed node and edge count 1 Pick two unconnected nodes uniformly at random 2 Determine probability to add edge based on number of closed triangles 3 Add edge based on determined probability 4 Repeat until requisite edge count is reached Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Simulation Studies Simulation for selection between: Full model with both mechanism Submodel with only ﬁrst mechanism 10000 networks generated from each as training data p0 = 0.3 and p1 = 0.1 for both candidates Edge count vary over 500, 1000, 2000 p2 for full model vary between 0.05, 0.03, 0.01, 0.005 Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Statistic for calibration: edge count Statistics as predictors: Triangle count Average local clustering coeﬃcient Quartiles of degree distribution Candidate algorithms for SL: Support vector machine k-nearest neighbors Random forest Performance will be evaluated on training data directly via cross-validation Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Conclusions ABC: very powerful methodology for sound statistical inference in LHD free settings Two distinct paradigms to the study of networked systems: Statistical modeling of networks (statistics) Network science (physics and applied mathematics) Statistical network science, a mixture of these two paradigms, appears potentially promising in the era of complex data Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

Further research lines Fast ABC inference via surrogate model for network Inference both on stochastic process (eg. spreading process) on a dynamic network Embed Super Learner in UQ framework Antonietta Mira / ICS and DISAT Approximate Bayesian Computation

QMC Program: Trends and Advances in Monte Carlo Sampling Algorithms Workshop, Approximate Bayesian Computation for Inference in Generative Models for Large-scale Network Data - Antonietta Mira, Dec 13, 2017

More Related Content

What's hot

Similar to QMC Program: Trends and Advances in Monte Carlo Sampling Algorithms Workshop, Approximate Bayesian Computation for Inference in Generative Models for Large-scale Network Data - Antonietta Mira, Dec 13, 2017

More from The Statistical and Applied Mathematical Sciences Institute

Recently uploaded

QMC Program: Trends and Advances in Monte Carlo Sampling Algorithms Workshop, Approximate Bayesian Computation for Inference in Generative Models for Large-scale Network Data - Antonietta Mira, Dec 13, 2017