Bruno Gonçalves, profile picture
Uploaded byBruno Gonçalves
1,708 views

A practical Introduction to Machine(s) Learning

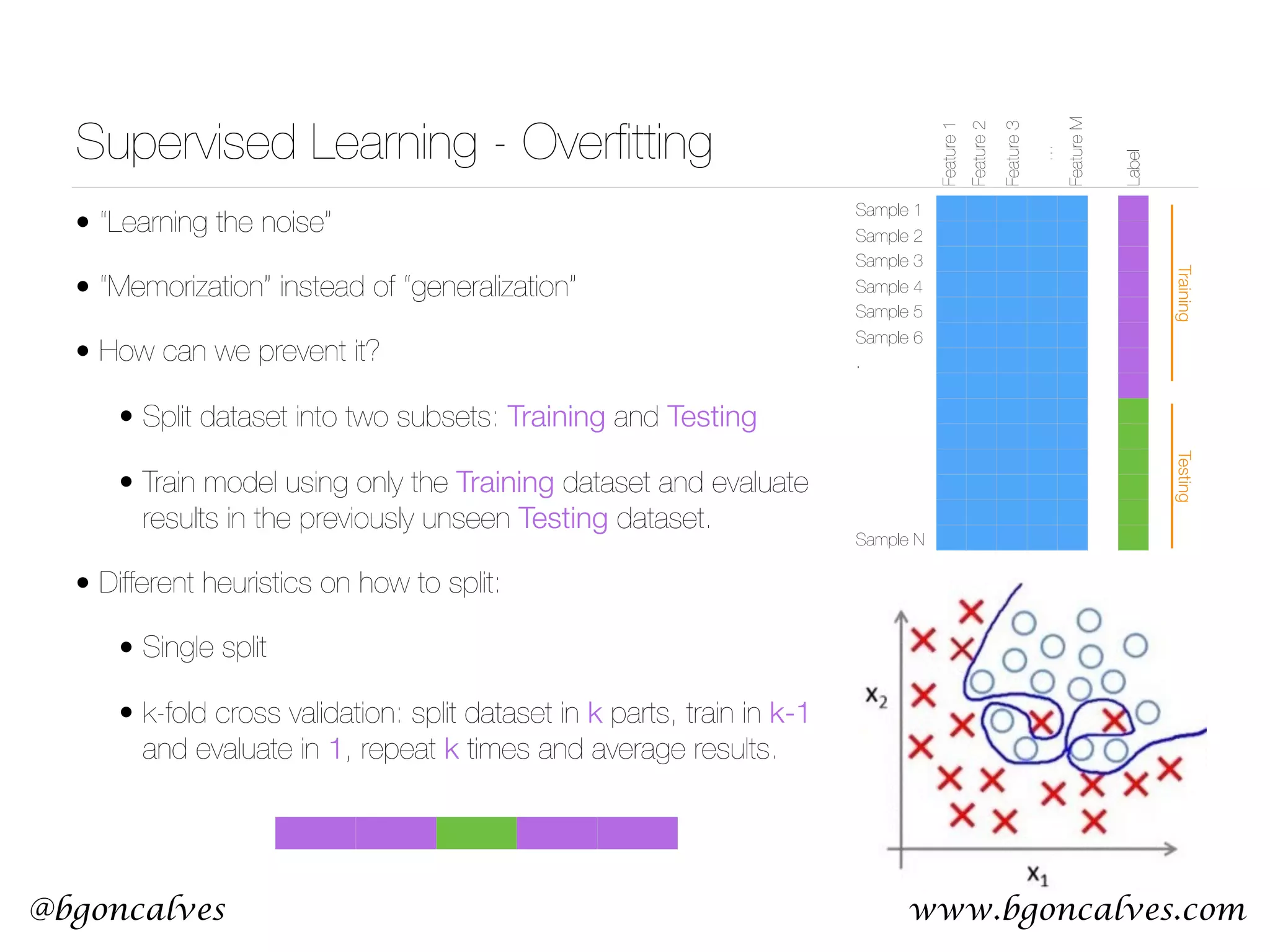
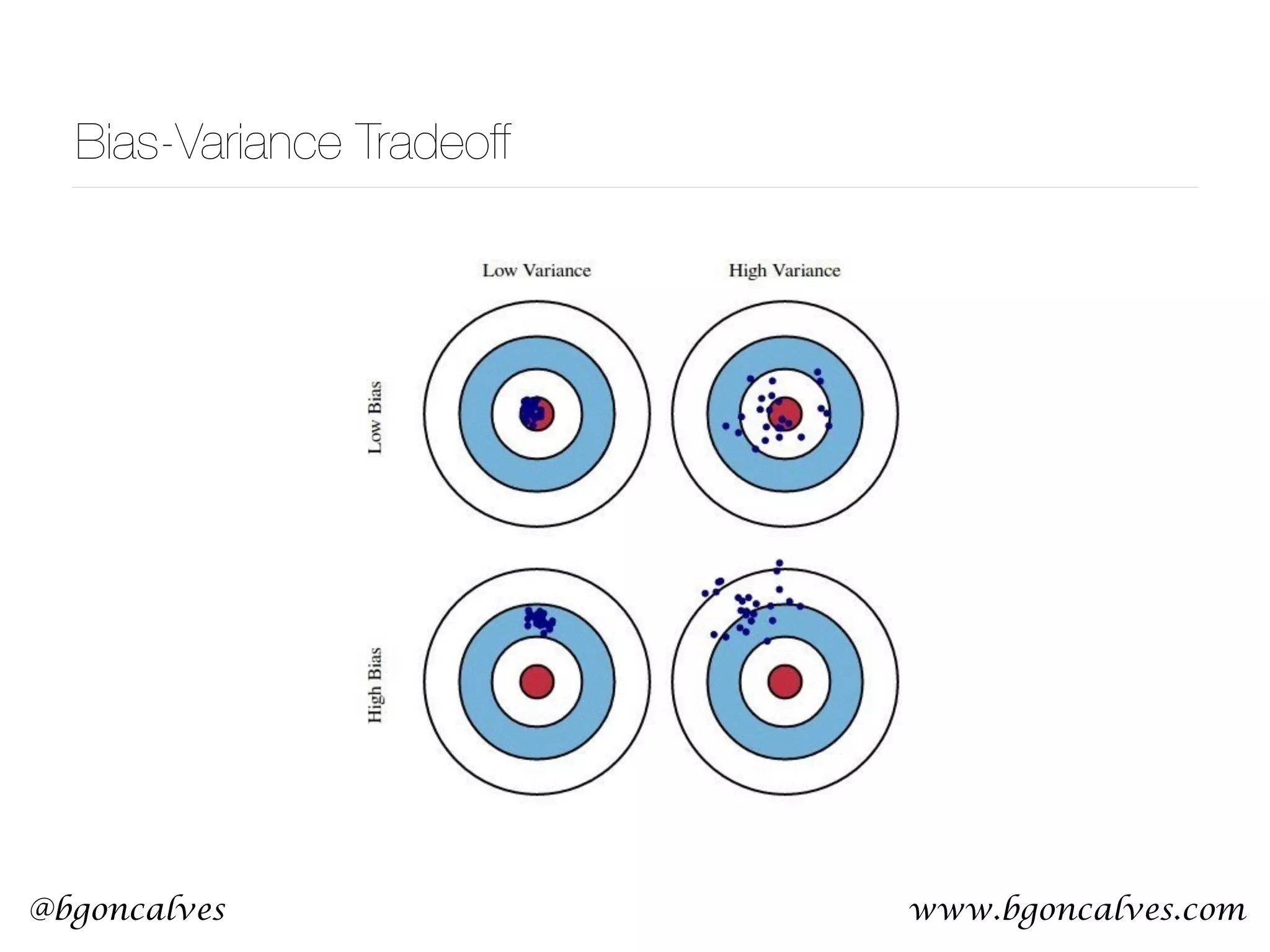
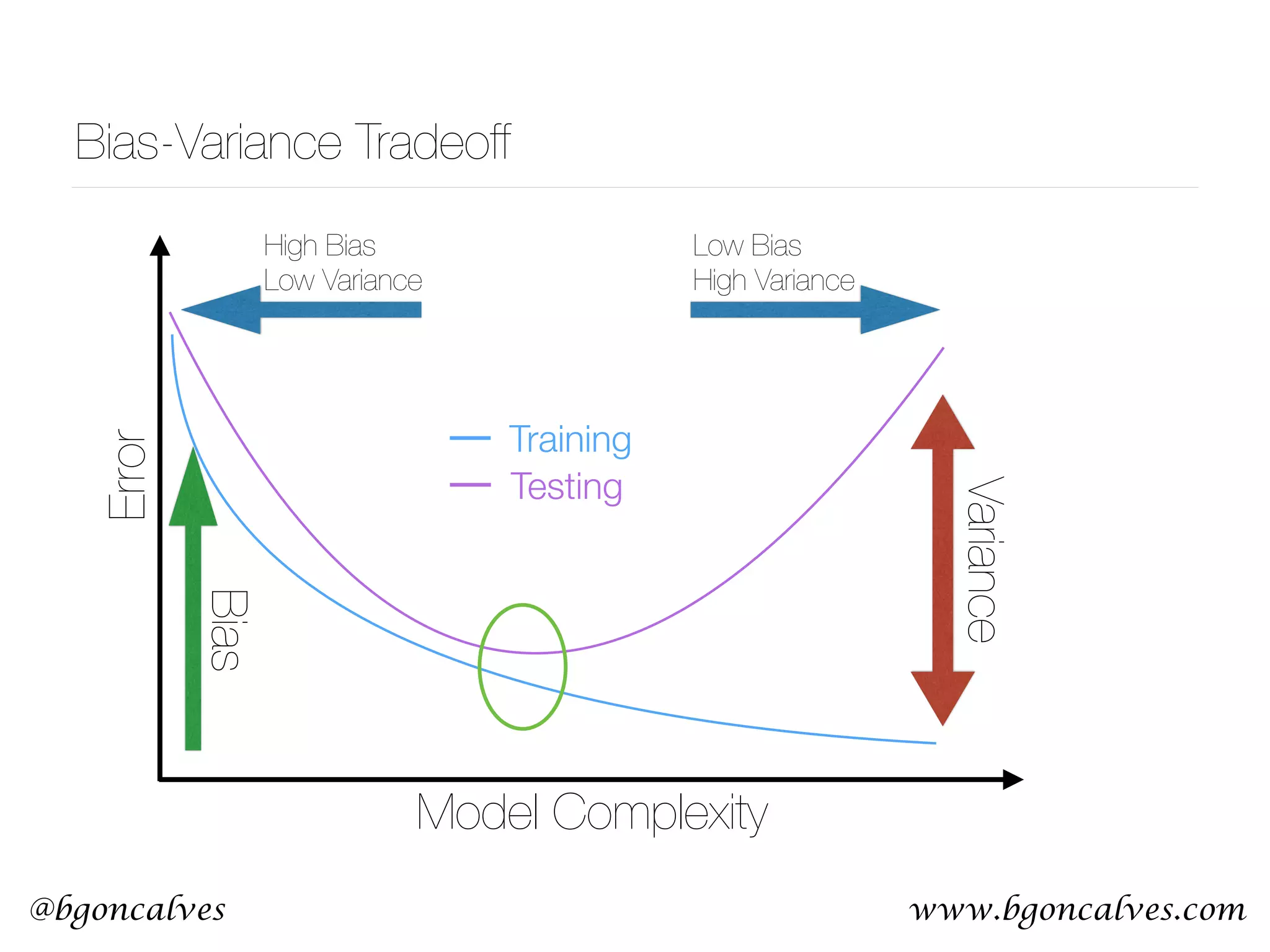
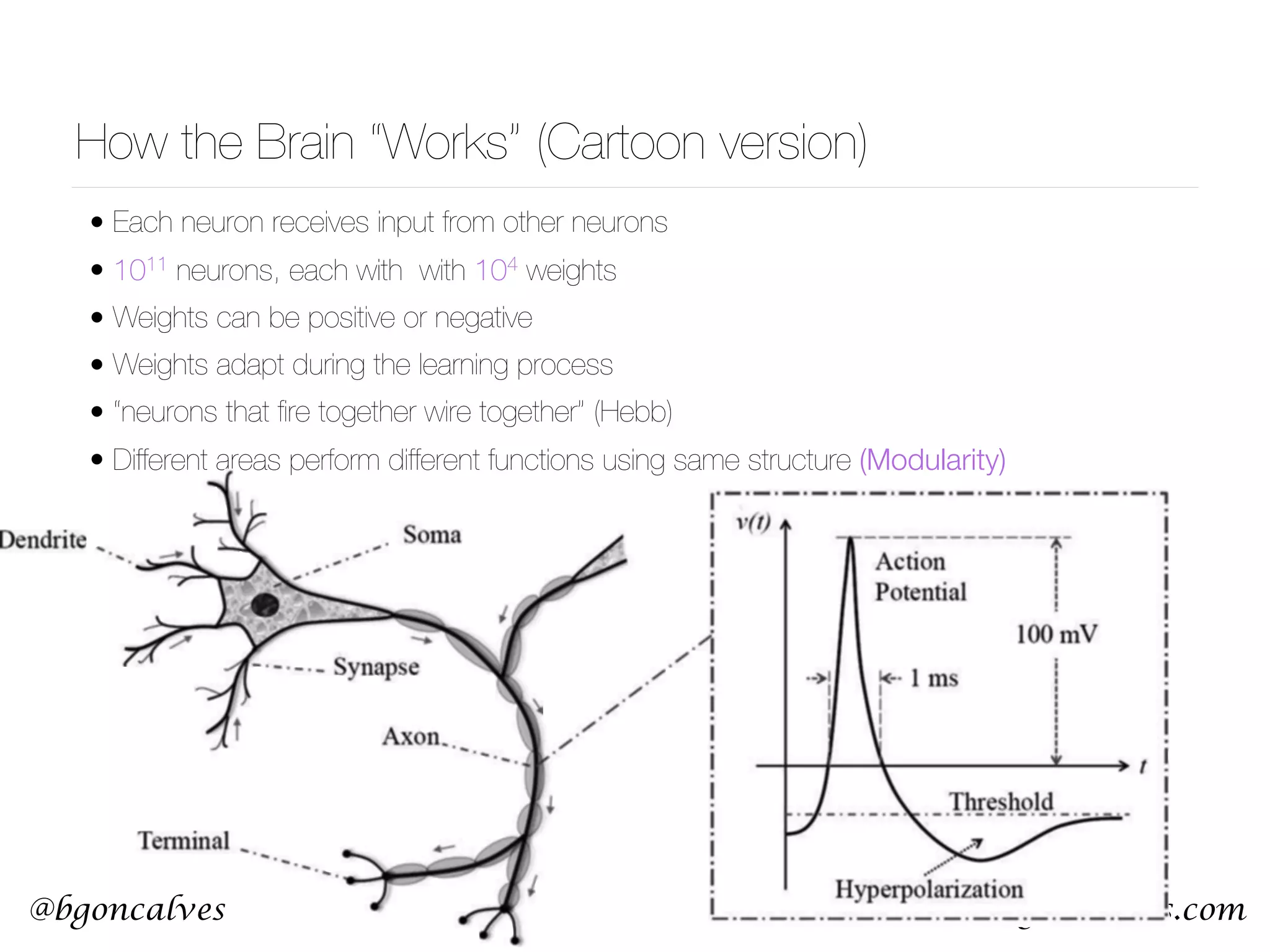
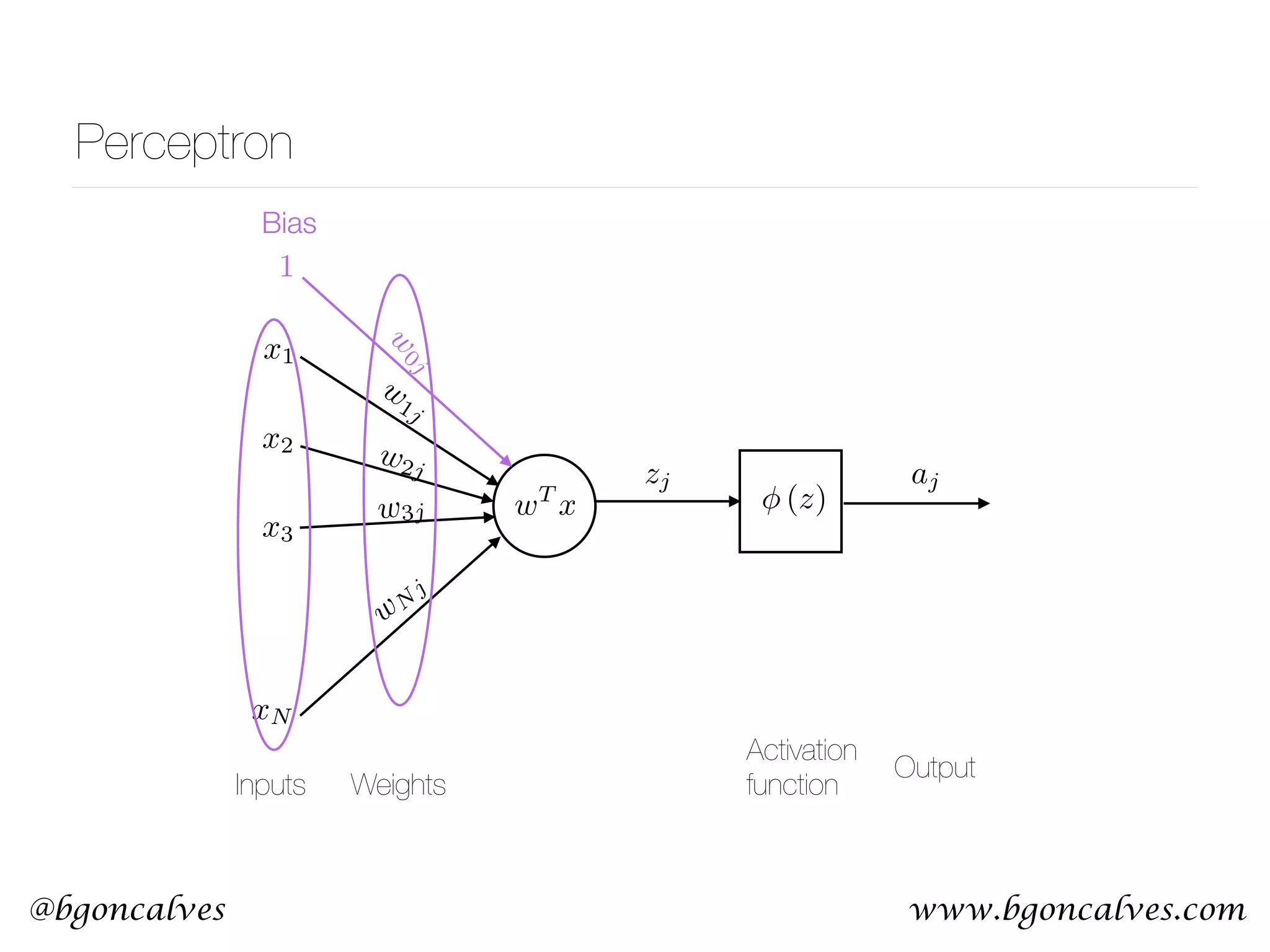
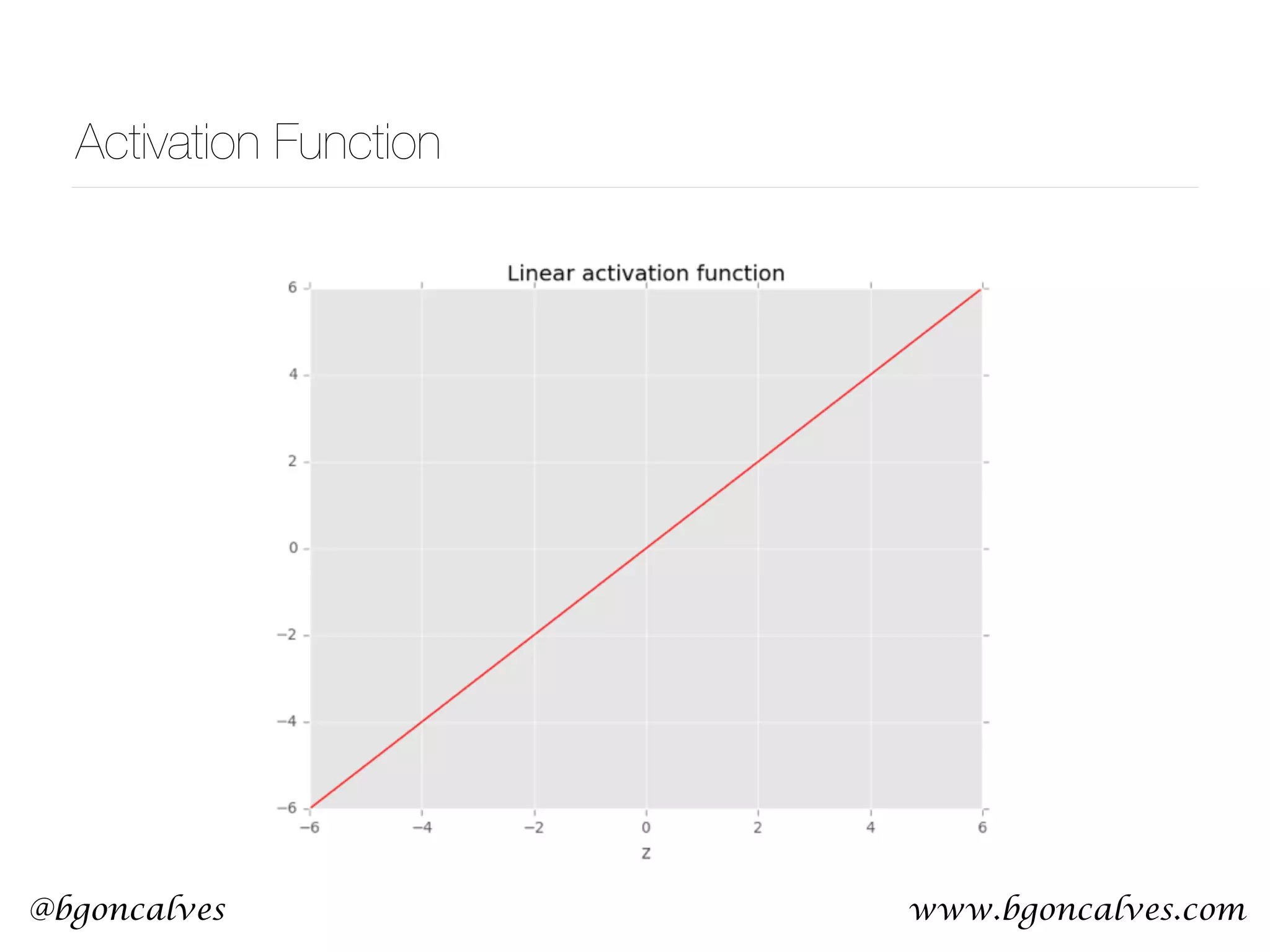
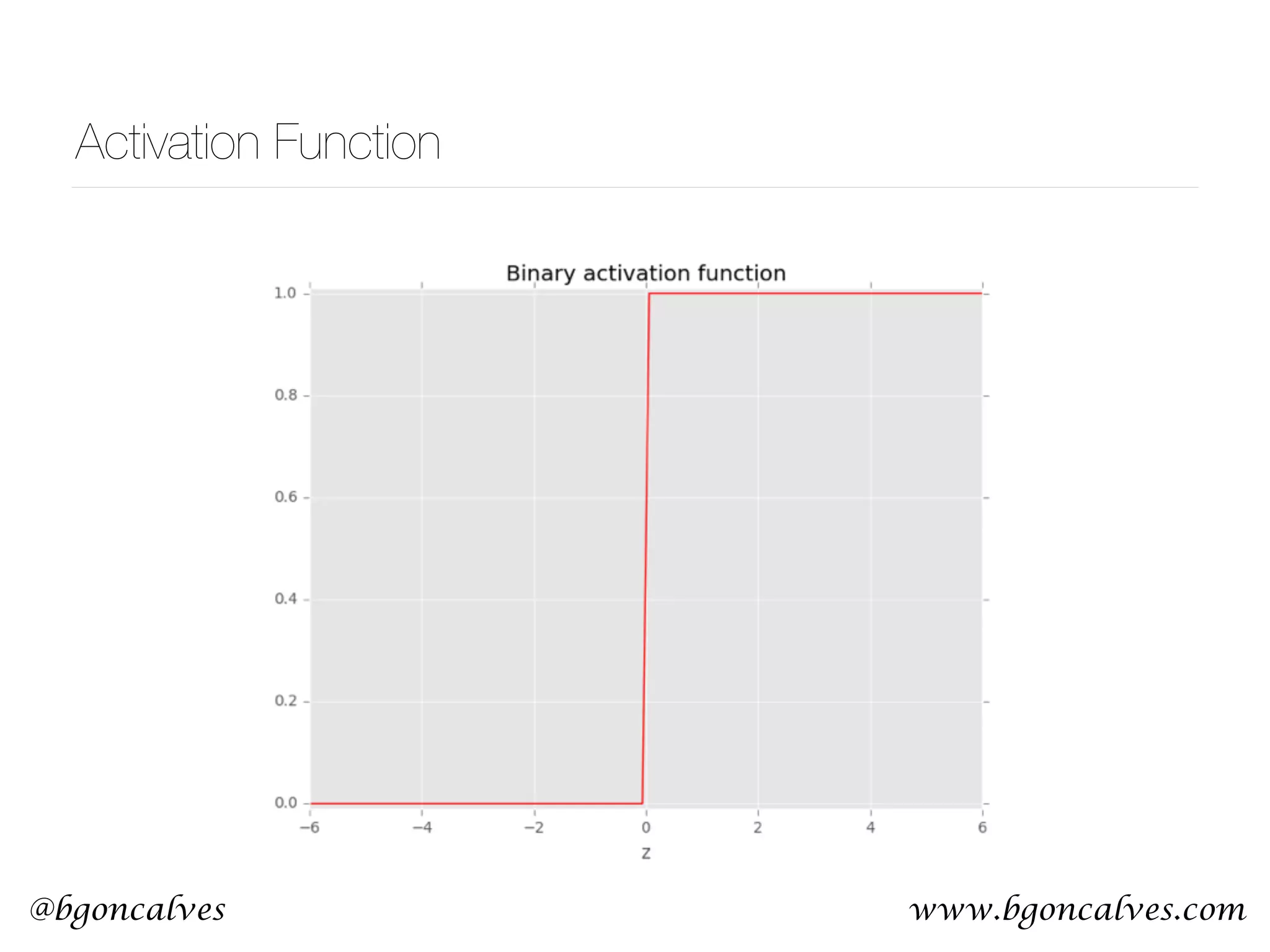
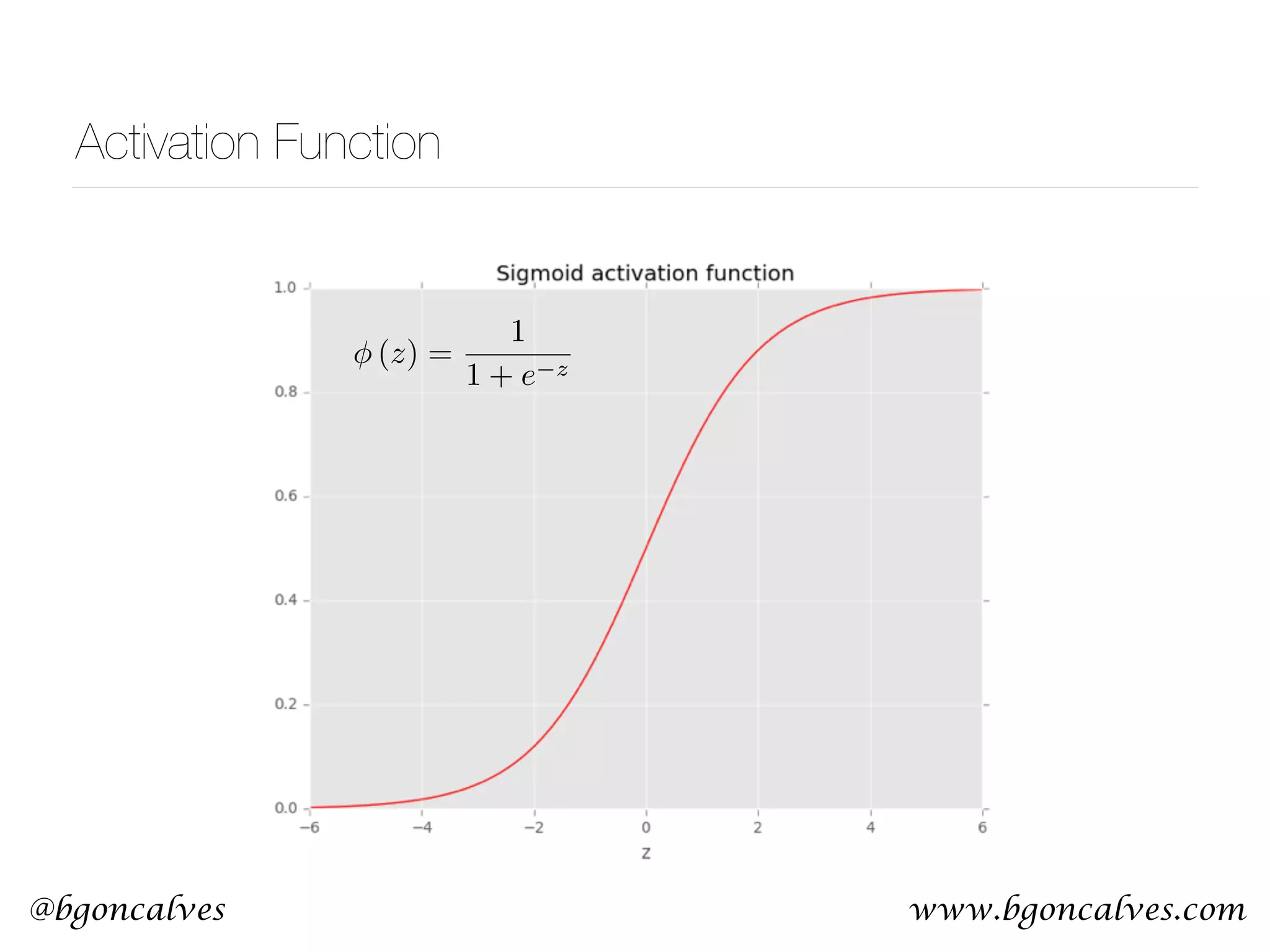
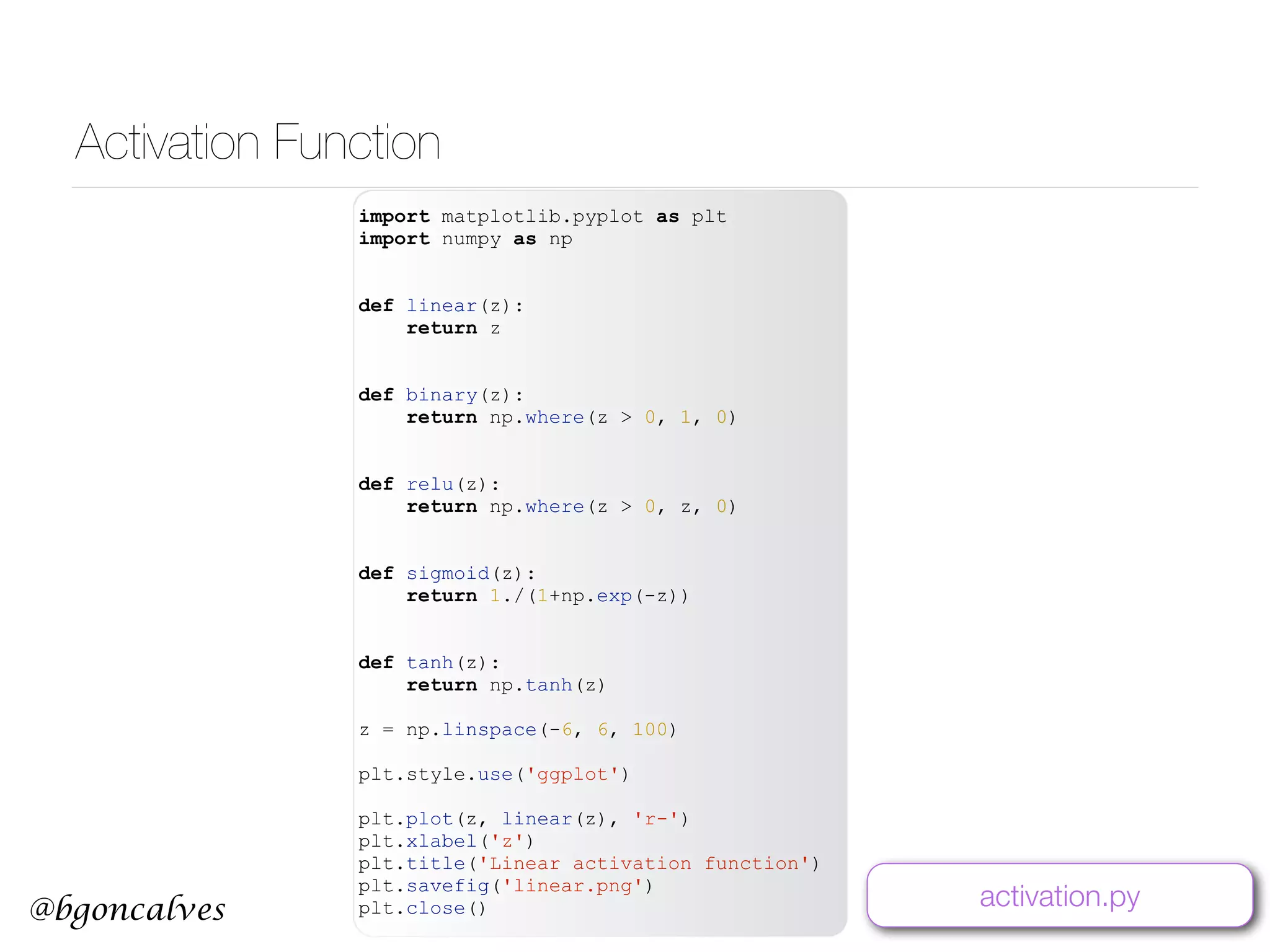
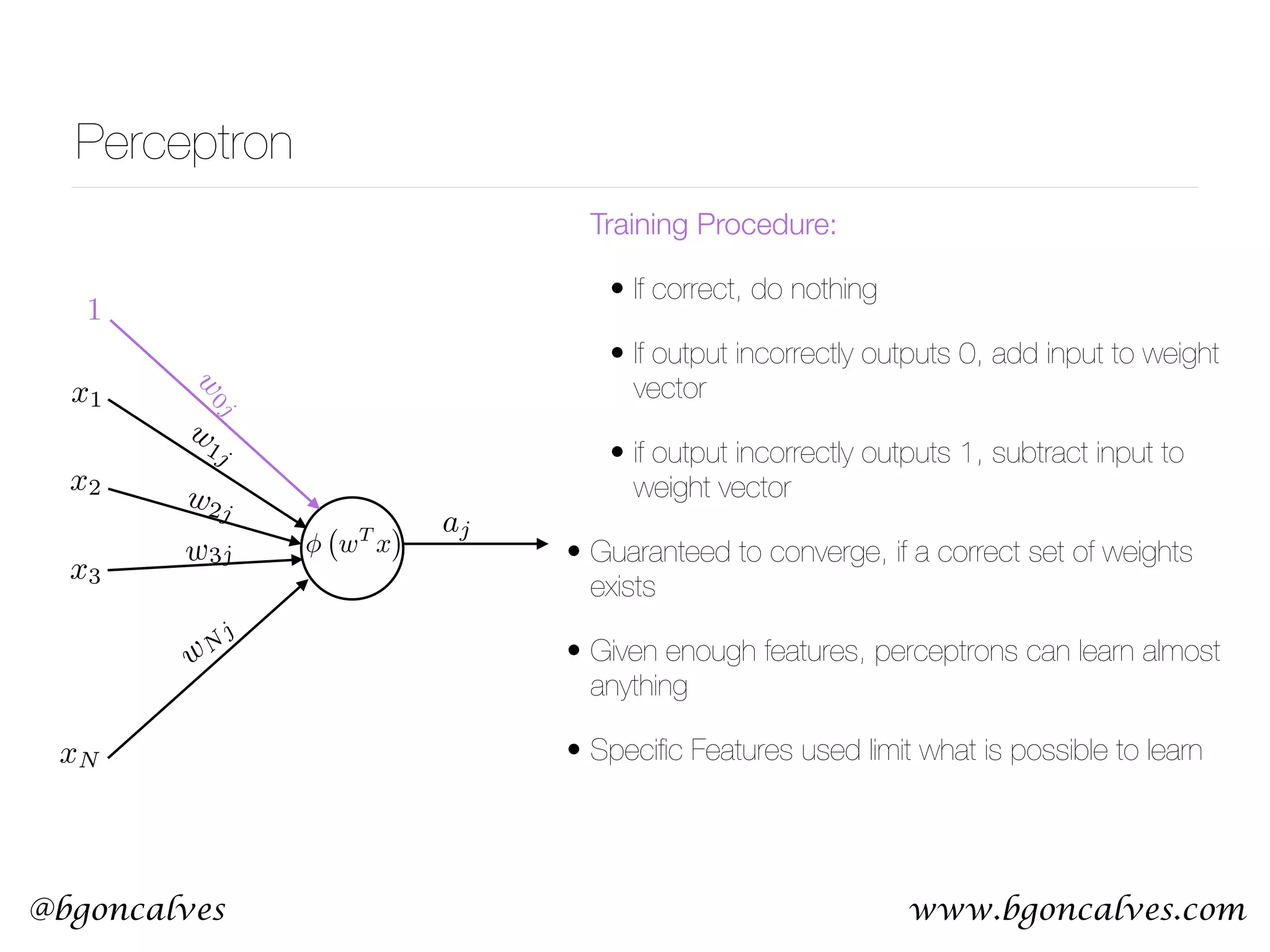
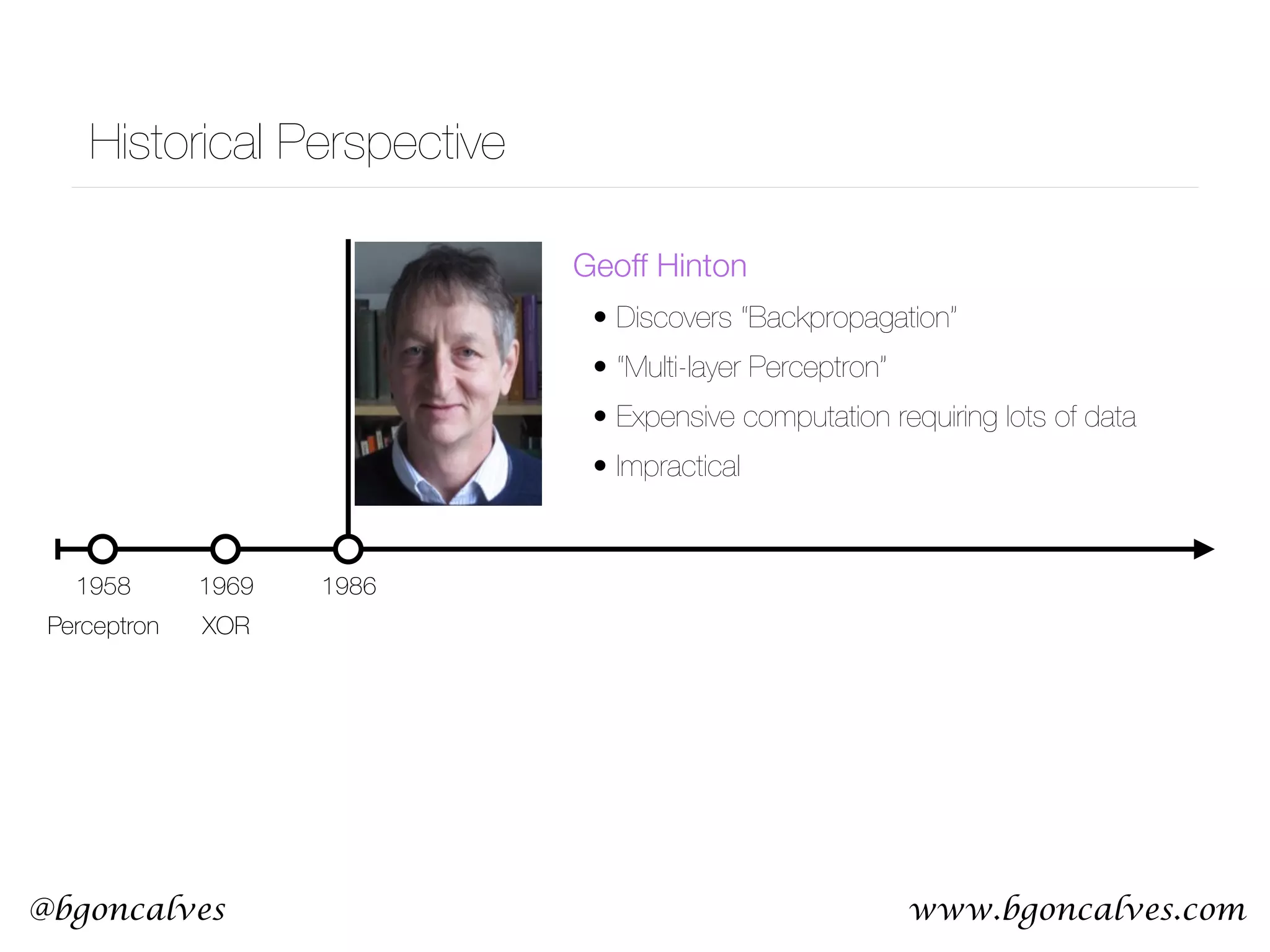
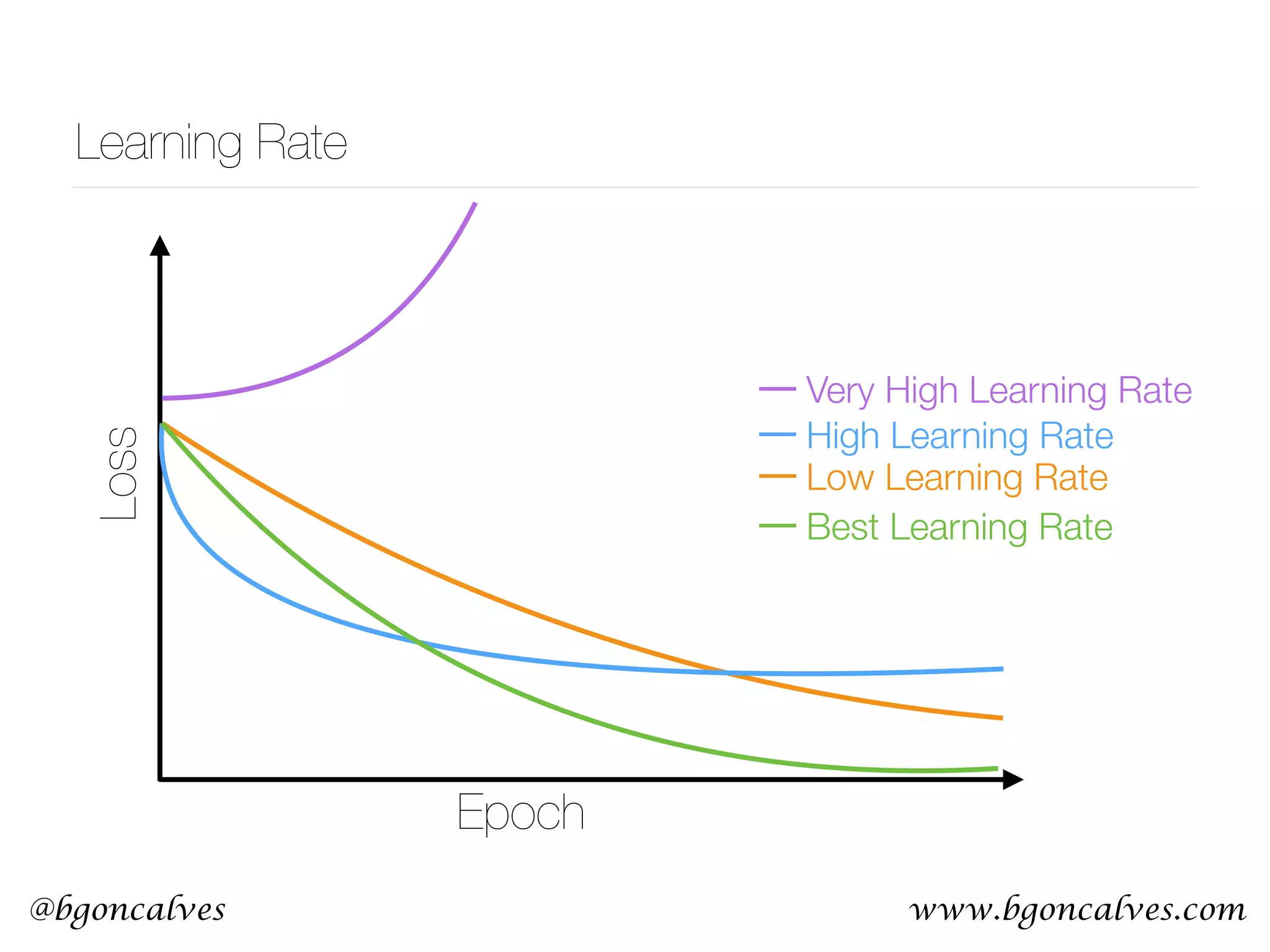
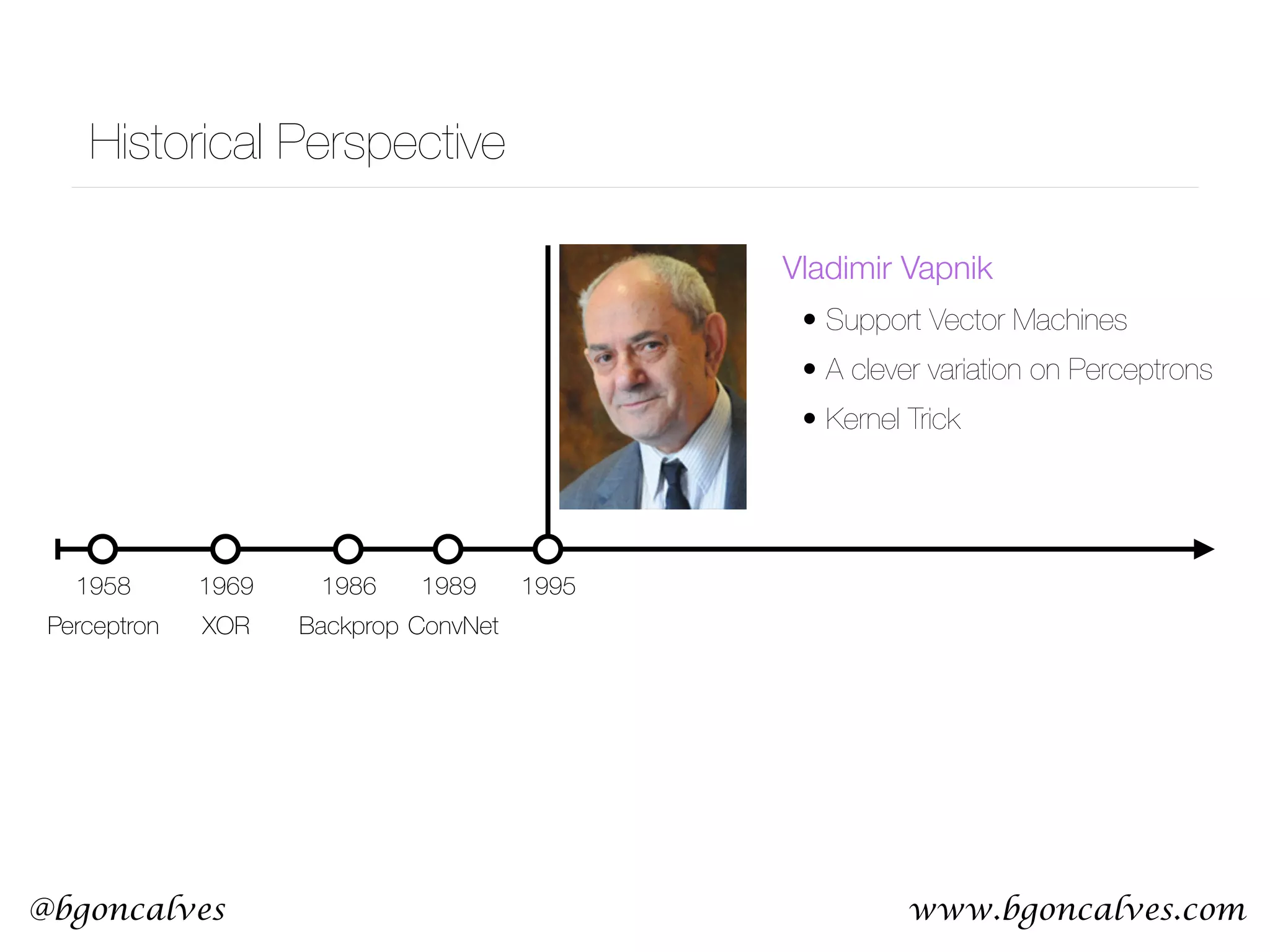
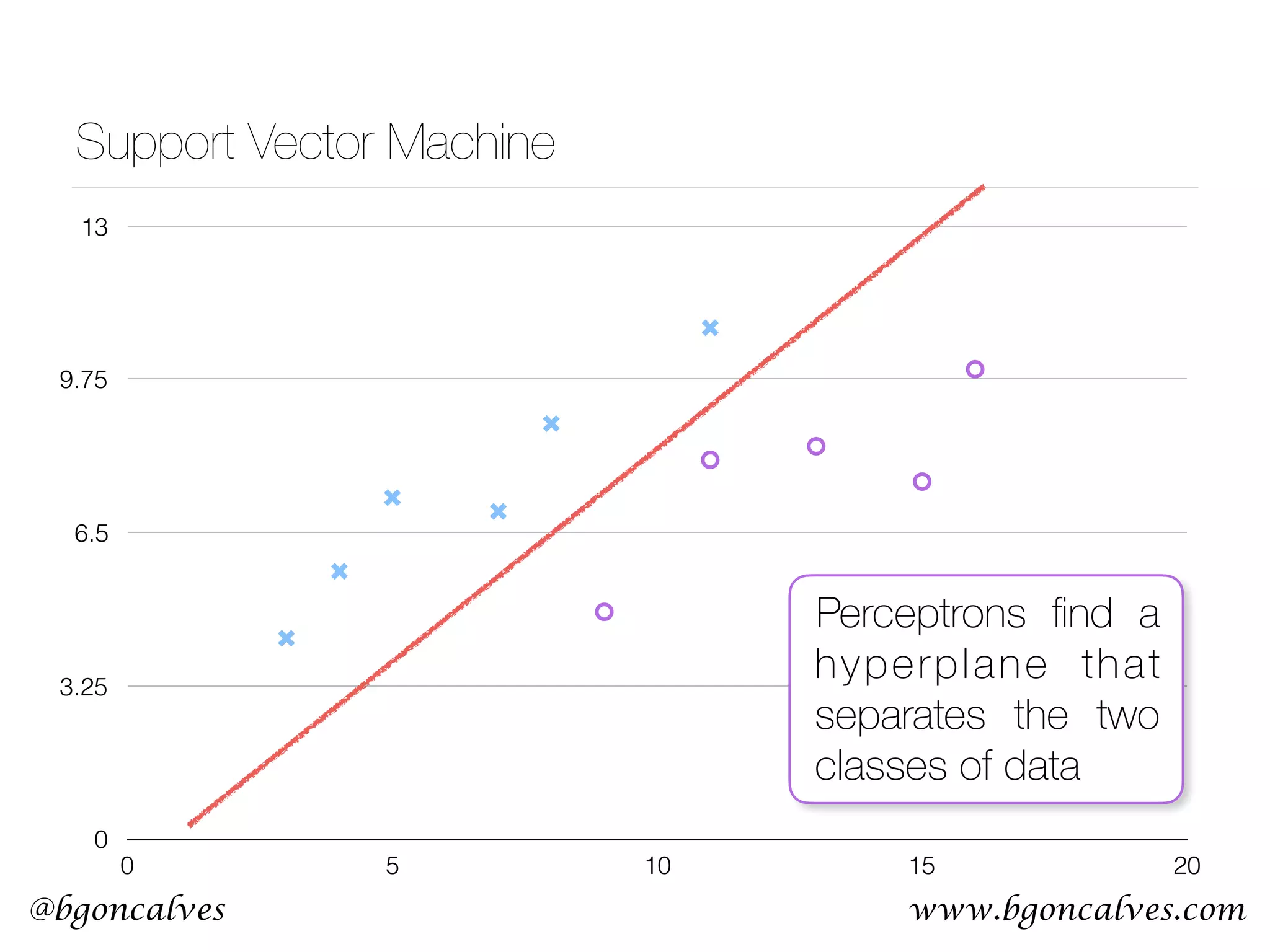
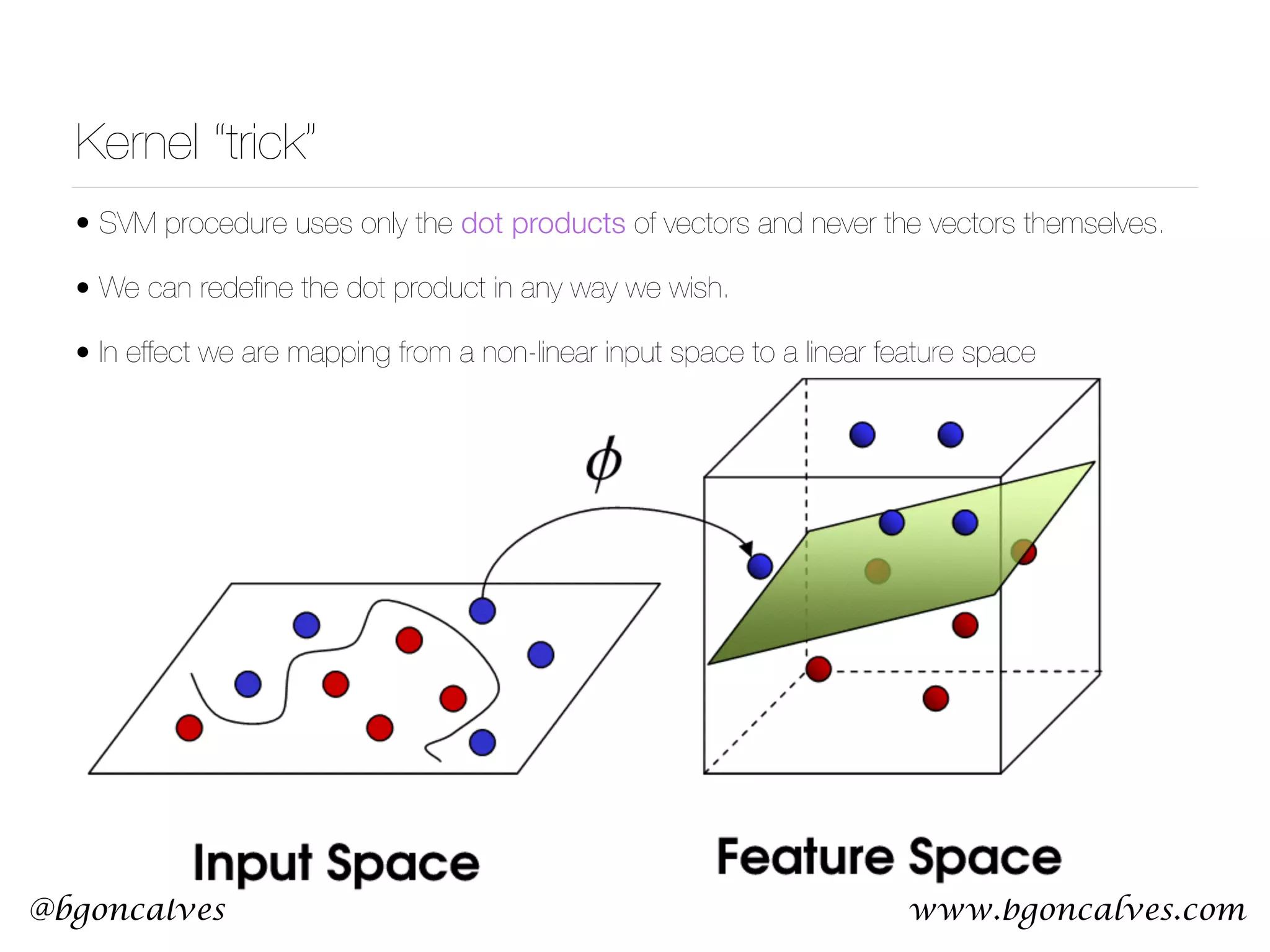
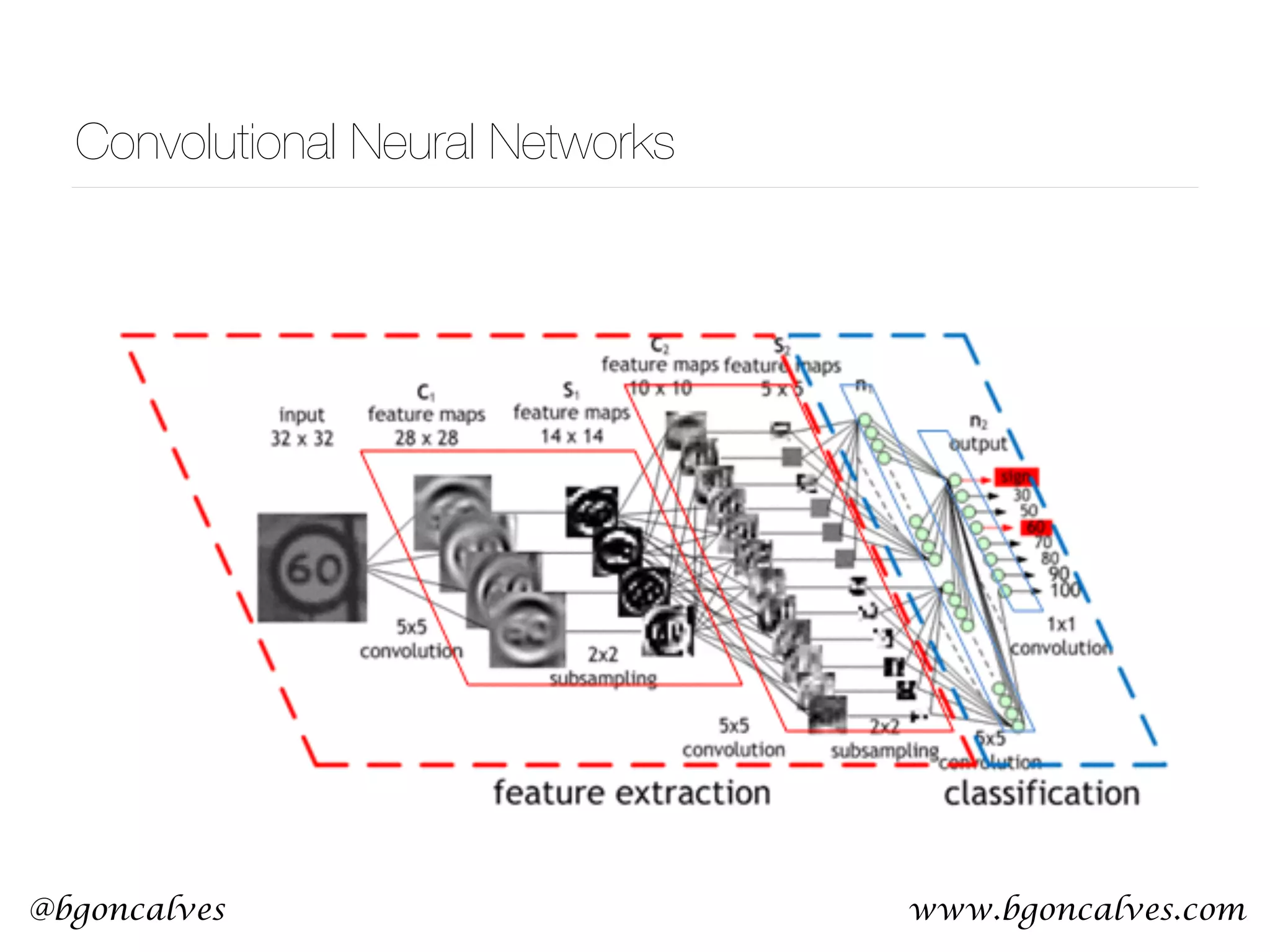
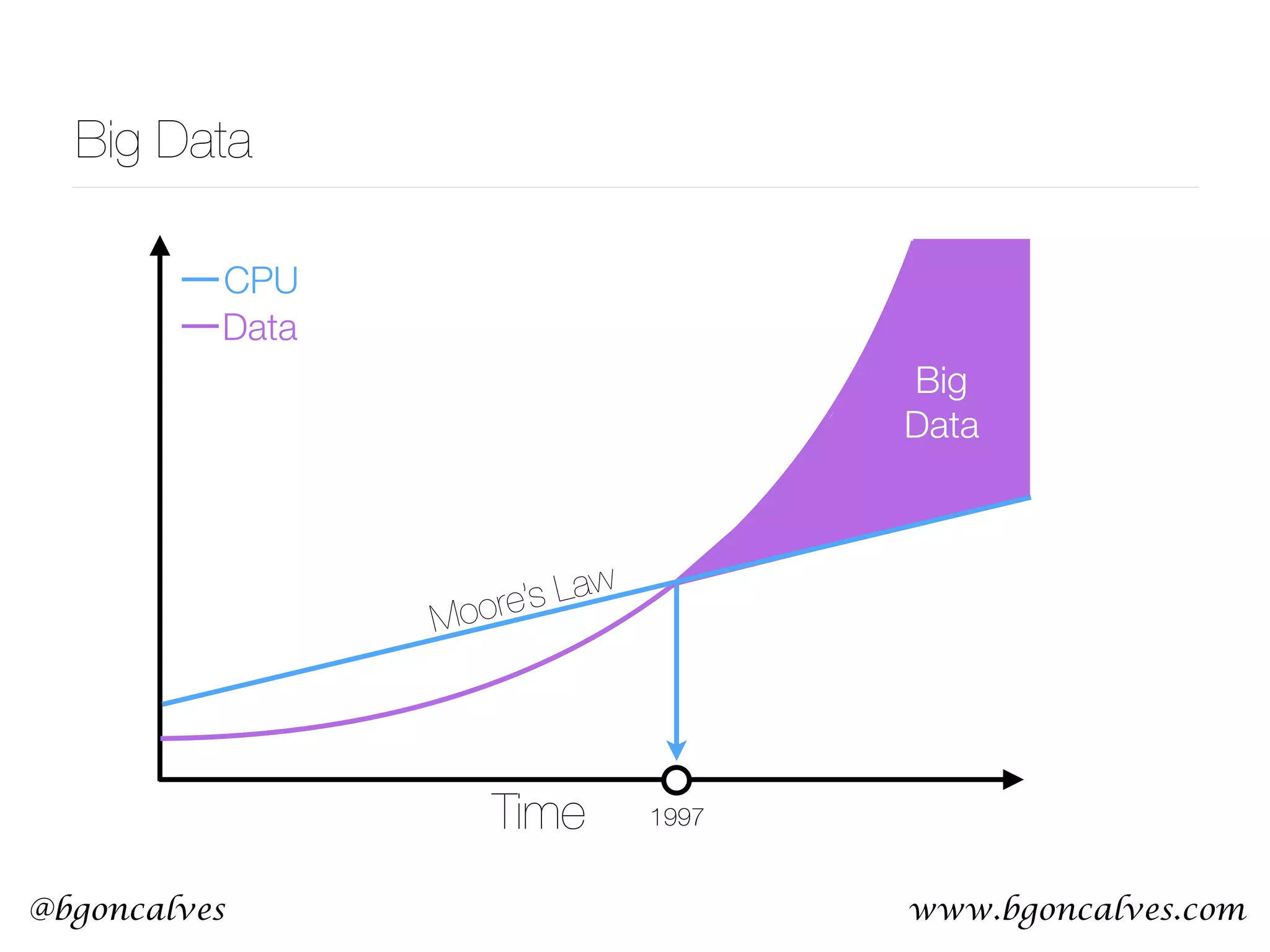
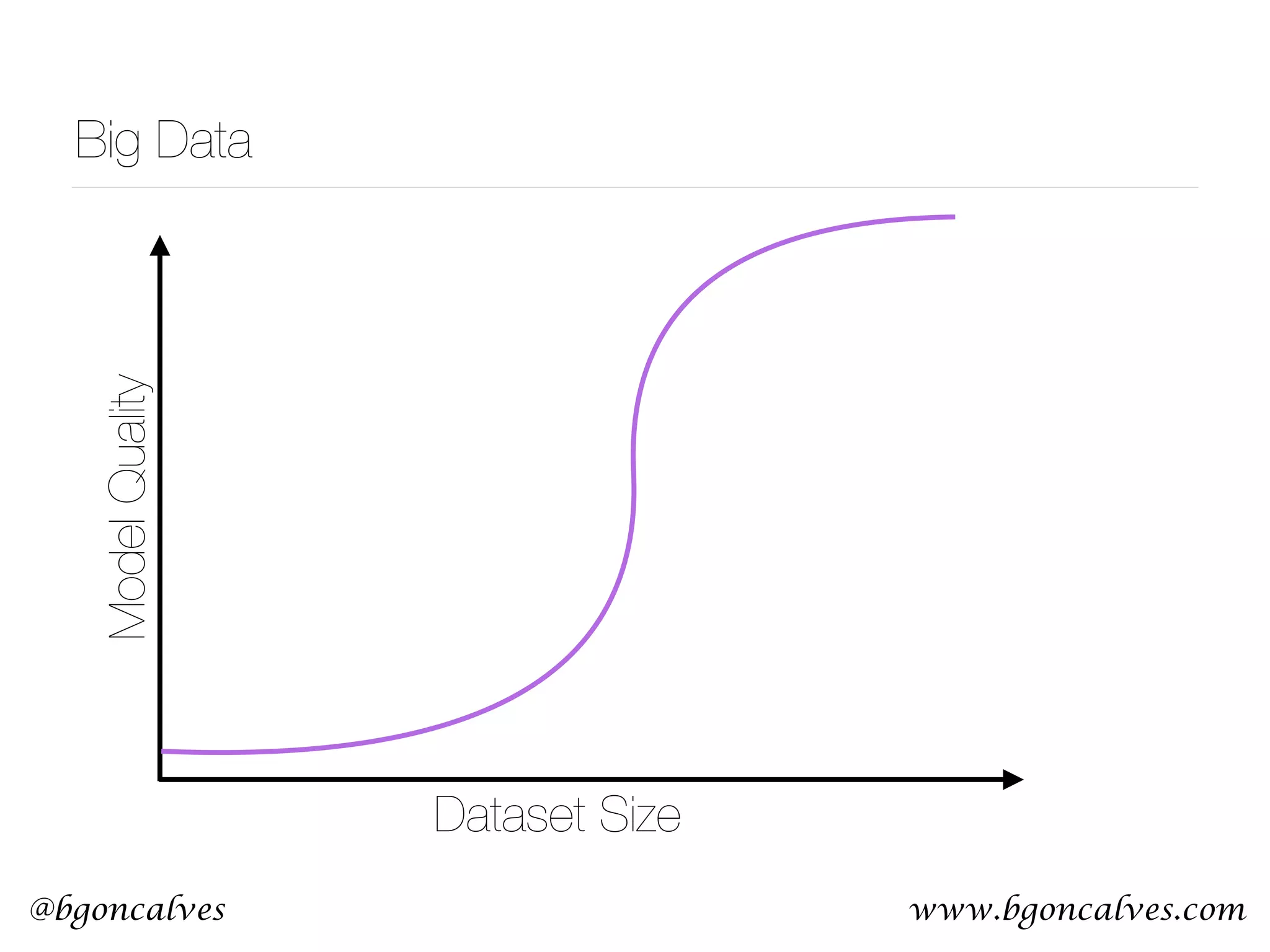
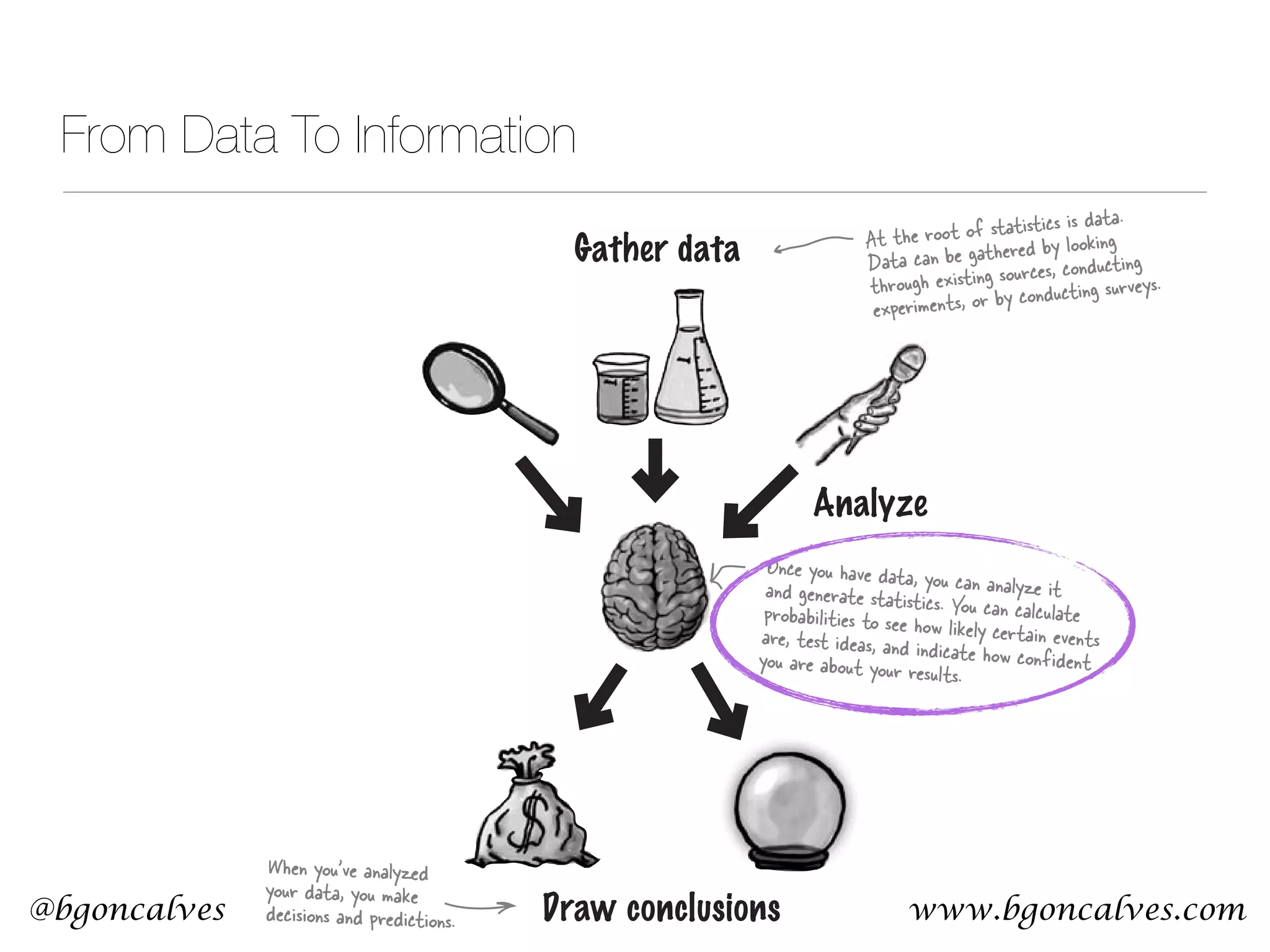
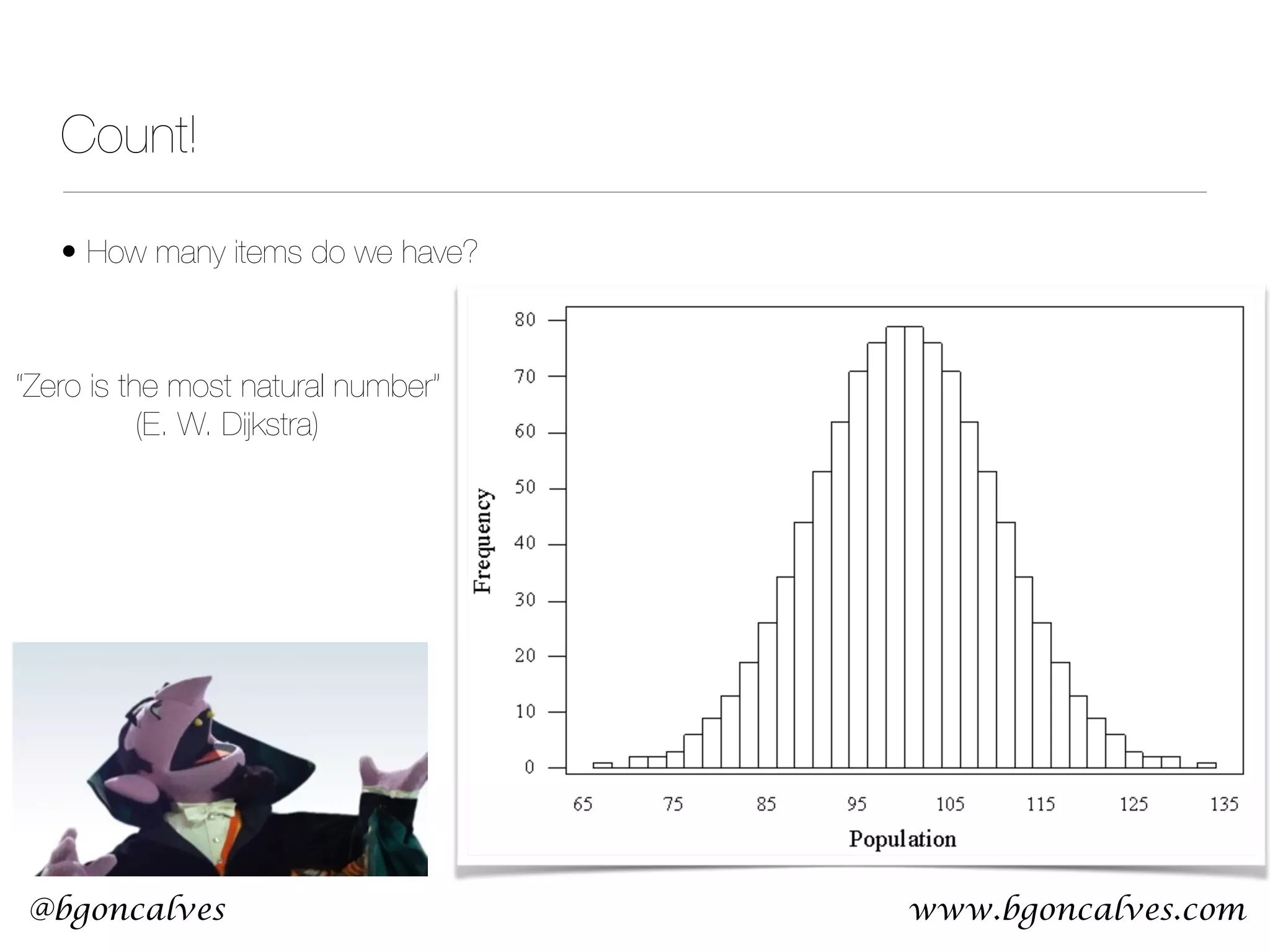
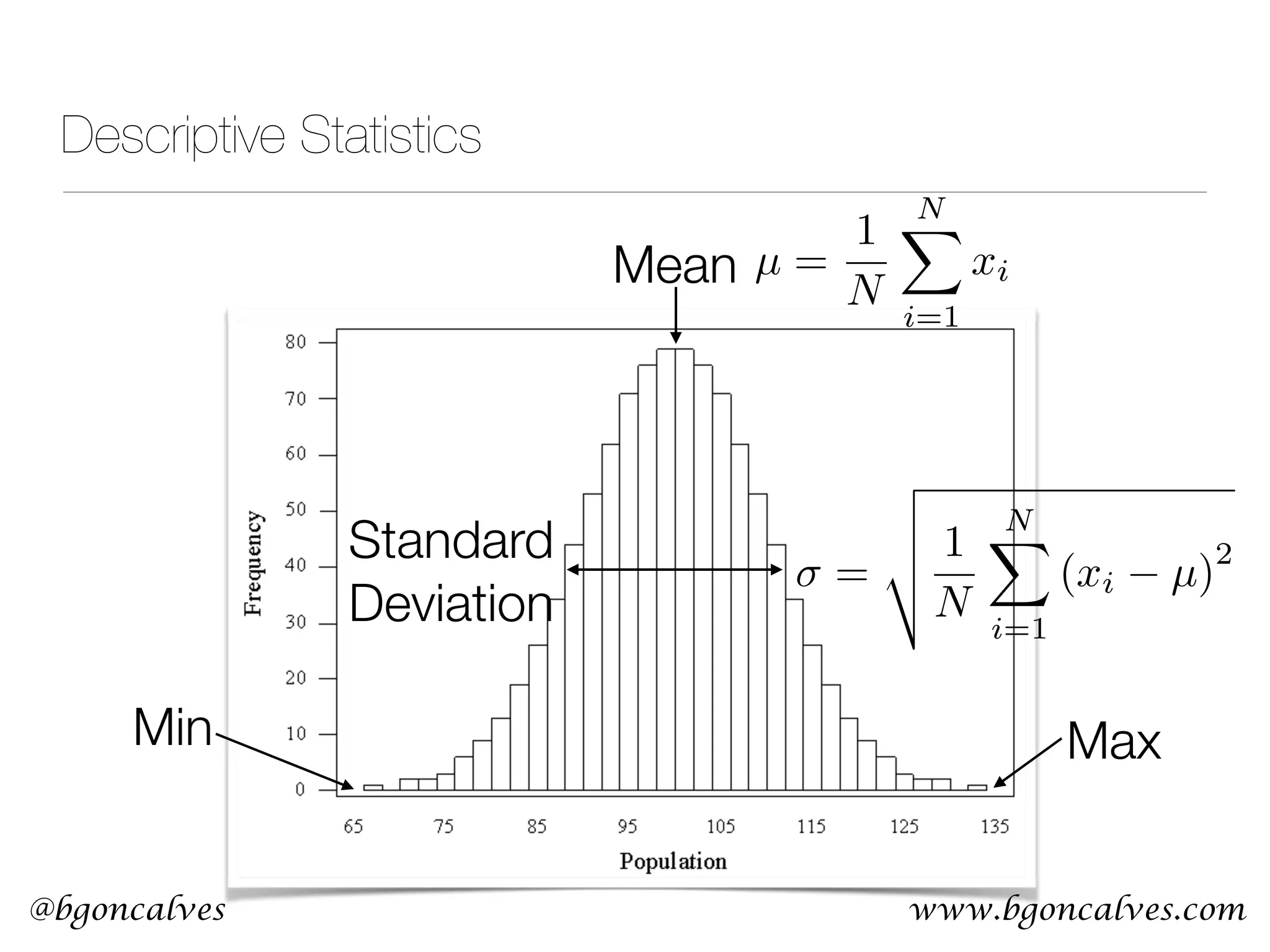
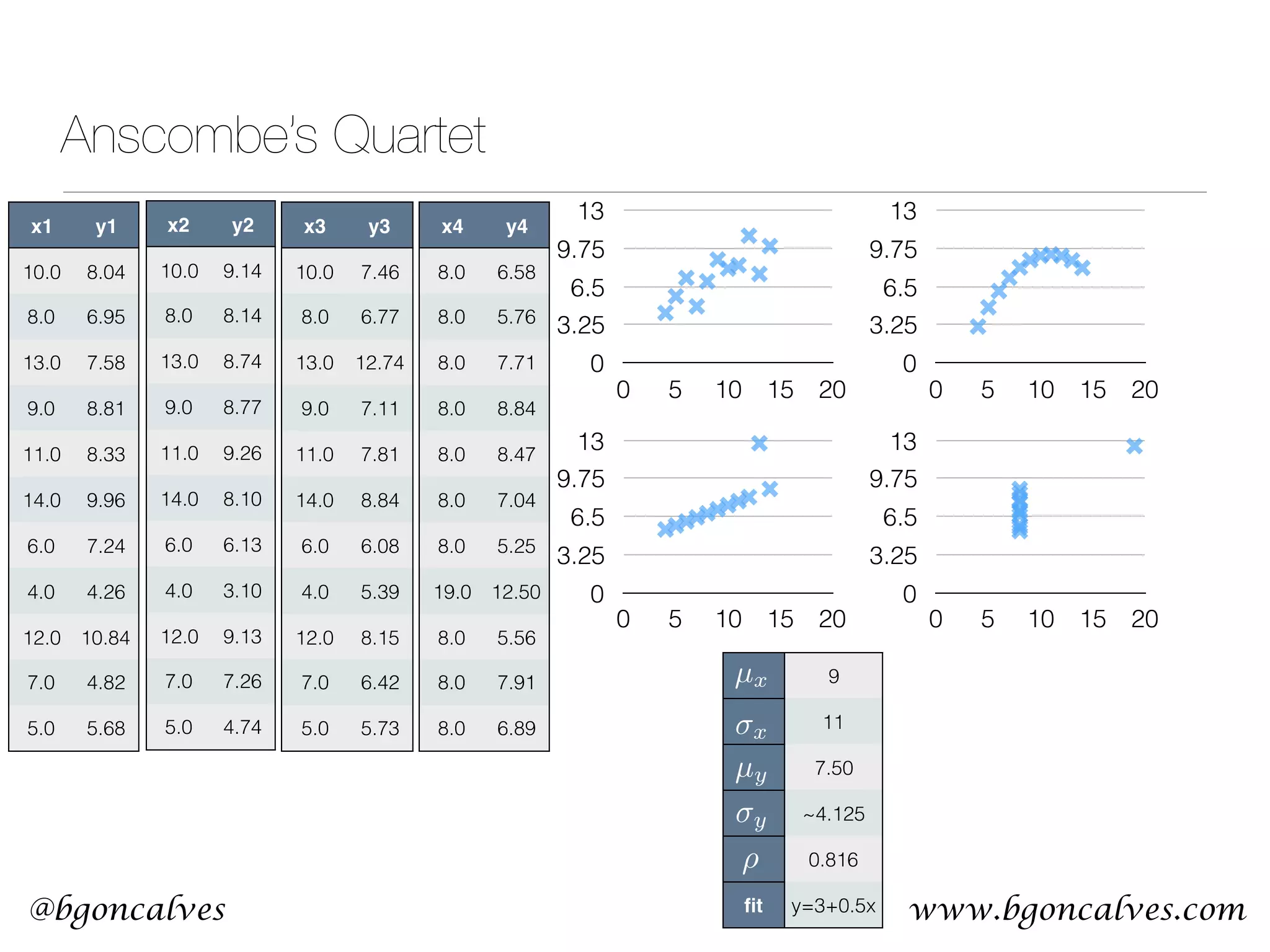
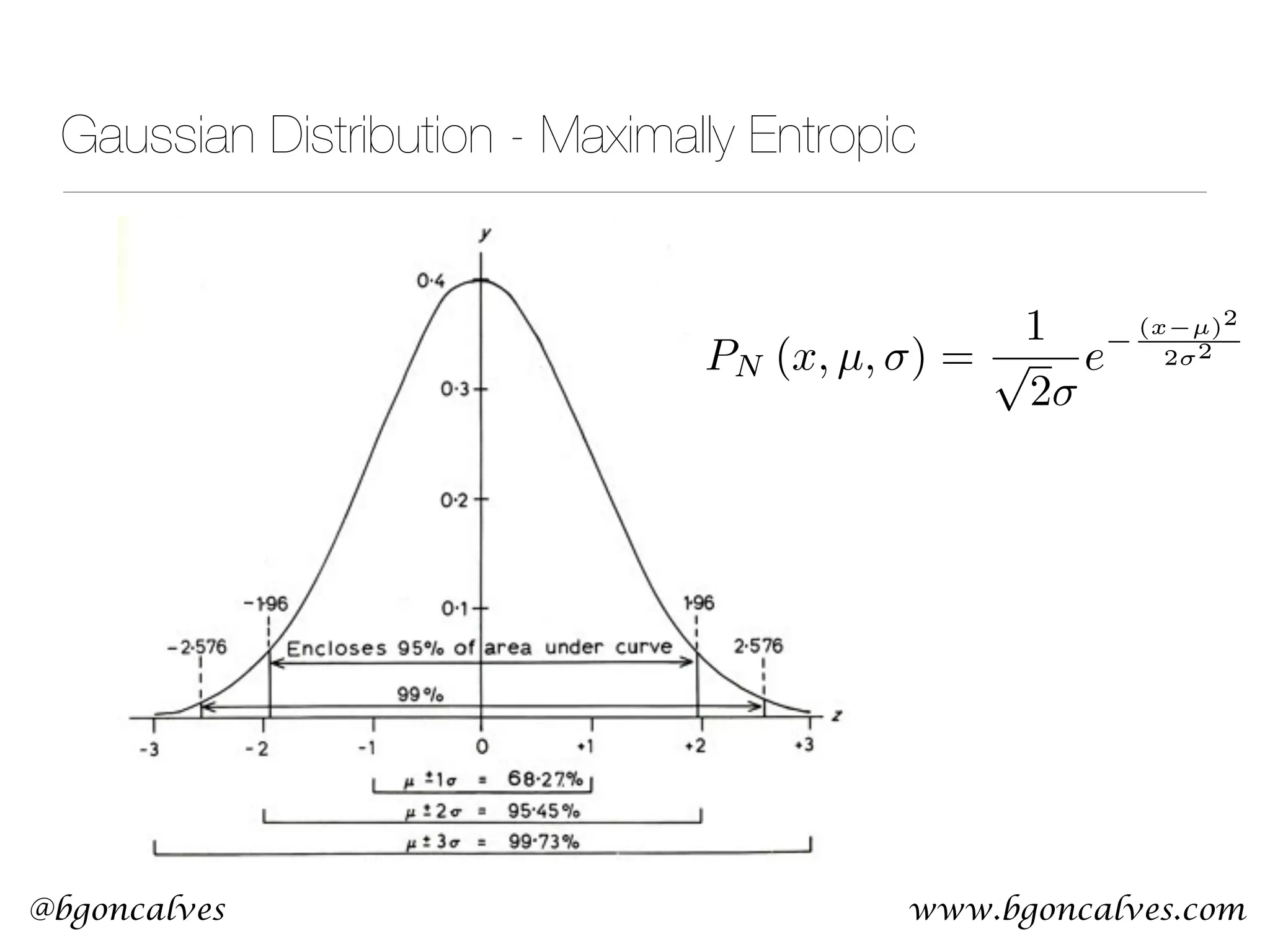
This document serves as a practical introduction to machine learning, covering essential statistical concepts, data analysis techniques, and various machine learning methods including supervised and unsupervised learning. Key topics discussed include the importance of data, statistical measures, clustering algorithms like k-means, and the basics of neural networks along with concepts such as bias-variance tradeoff. Additional emphasis is placed on understanding and minimizing errors in model fitting and the significance of generalization in machine learning.

Downloaded 53 times
A practical Introduction to Machine(s) Learning 
 www.bgoncalves.com
www.bgoncalves.com@bgoncalves
www.bgoncalves.com@bgoncalves Time CPU Data Big
 Data Moore’s Law Big Data 1997
www.bgoncalves.com@bgoncalves http://static.googleusercontent.com/media/research.google.com/en//pubs/archive/35179.pdf E X P E R T O P I N I O N Contact Editor: Brian Brannon, bbrannon@computer.org behavior. So, this corpus could serve as the basis of a complete model for certain tasks—if only we knew how to extract the model from the data. E ugene Wigner’s article “The Unreasonable Ef- fectiveness of Mathematics in the Natural Sci- ences”1 examines why so much of physics can be Alon Halevy, Peter Norvig, and Fernando Pereira, Google The Unreasonable Effectiveness of Data Big Data
www.bgoncalves.com@bgoncalves Dataset Size ModelQualityBig Data
www.bgoncalves.com@bgoncalves Big Data https://www.wired.com/2008/06/pb-theory/
www.bgoncalves.com@bgoncalves From Data To Information Statistics are numbers that summarize raw facts and figures in some meaningful way. They present key ideas that may not be immediately apparent by just looking at the raw data, and by data, we mean facts or figures from which we can draw conclusions. As an example, you don’t have to wade through lots of football scores when all you want to know is the league position of your favorite team. You need a statistic to quickly give you the information you need. The study of statistics covers where statistics come from, how to calculate them, and how you can use them effectively. Gather data Analyze Draw conclusions When you’ve analyzed your data, you make decisions and predictions. Once you have data, you can analyze itand generate statistics. You can calculateprobabilities to see how likely certain eventsare, test ideas, and indicate how confidentyou are about your results. At the root of statistics is data. Data can be gathered by looking through existing sources, conducting experiments, or by conducting surveys.
www.bgoncalves.com@bgoncalves “Zero is the most natural number”
 (E. W. Dijkstra) Count! • How many items do we have?
www.bgoncalves.com@bgoncalves Descriptive Statistics Min Max Mean µ = 1 N NX i=1 xi = v u u t 1 N NX i=1 (xi µ) 2Standard
 Deviation
www.bgoncalves.com@bgoncalves Anscombe’s Quartet x1 y1 10.0 8.04 8.0 6.95 13.0 7.58 9.0 8.81 11.0 8.33 14.0 9.96 6.0 7.24 4.0 4.26 12.0 10.84 7.0 4.82 5.0 5.68 x2 y2 10.0 9.14 8.0 8.14 13.0 8.74 9.0 8.77 11.0 9.26 14.0 8.10 6.0 6.13 4.0 3.10 12.0 9.13 7.0 7.26 5.0 4.74 x3 y3 10.0 7.46 8.0 6.77 13.0 12.74 9.0 7.11 11.0 7.81 14.0 8.84 6.0 6.08 4.0 5.39 12.0 8.15 7.0 6.42 5.0 5.73 x4 y4 8.0 6.58 8.0 5.76 8.0 7.71 8.0 8.84 8.0 8.47 8.0 7.04 8.0 5.25 19.0 12.50 8.0 5.56 8.0 7.91 8.0 6.89 9 11 7.50 ~4.125 0.816 fit y=3+0.5x µx µy y x ⇢ 0 3.25 6.5 9.75 13 0 5 10 15 20 0 3.25 6.5 9.75 13 0 5 10 15 20 0 3.25 6.5 9.75 13 0 5 10 15 20 0 3.25 6.5 9.75 13 0 5 10 15 20
www.bgoncalves.com@bgoncalves Central Limit Theorem • As the random variables: • with: • converge to a normal distribution: • after some manipulations, we find: n ! 1 Sn = 1 n X i xi N 0, 2 p n (Sn µ) Sn ⇠ µ + N 0, 2 p n The estimation of the mean converges to the true mean with the square root of the number of samples ! SE = p n
www.bgoncalves.com@bgoncalves Gaussian Distribution - Maximally Entropic PN (x, µ, ) = 1 p 2 e (x µ)2 2 2
www.bgoncalves.com@bgoncalves Experimental Measurements • Experimental errors commonly assumed gaussian distributed • Many experimental measurements are actually averages: • Instruments have a finite response time and the quantity of interest varies quickly over time • Stochastic Environmental factors • Etc
www.bgoncalves.com@bgoncalves • In an experimental measurement, we expect (CLT) the experimental values to be normally distributed around the theoretical value with a certain variance. Mathematically, this means:
 • where are the experimental values and the theoretical ones. The likelihood is then:
 • Where we see that to maximize the likelihood we must minimize the sum of squares MLE - Fitting a theoretical function to experimental data y f (x) ⇡ 1 p 2 2 exp " (y f (x)) 2 2 2 # y f (x) Least Squares Fitting L = N 2 log ⇥ 2 2 ⇤ X i " (yi f (xi)) 2 2 2 #
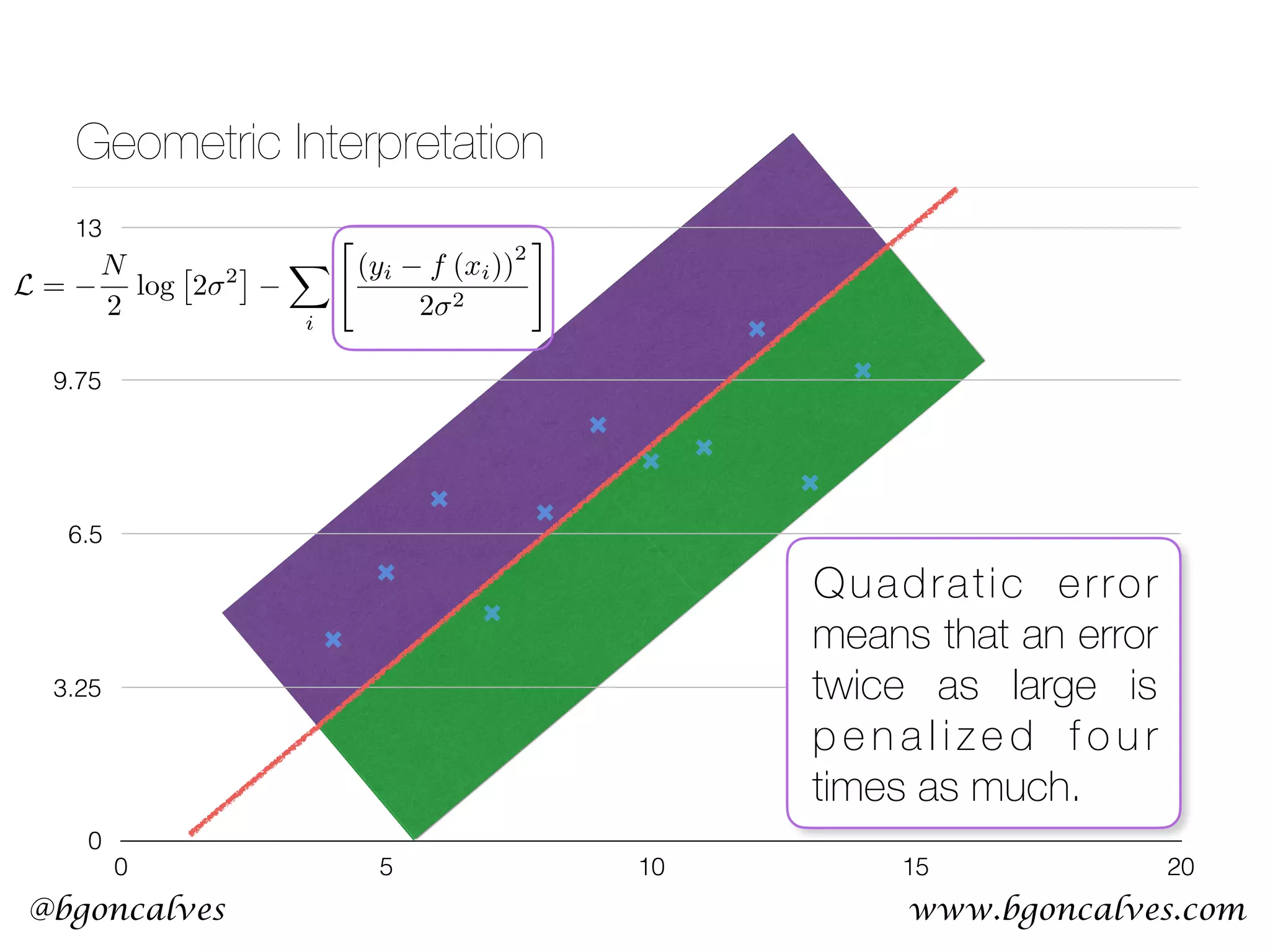
www.bgoncalves.com@bgoncalves MLE - Linear Regression • Let’s say we want to fit a straight line to a set of points: • The Likelihood function then becomes:
 • With partial derivatives:
 
 
 
 • Setting to zero and solving for and : y = w · x + b L = N 2 log ⇥ 2 2 ⇤ X i " (yi w · xi b) 2 2 2 # @L @w = X i [2xi (yi w · xi b)] @L @b = X i [(yi w · xi b)] ˆw = P i (xi hxi) (yi hyi) P i (xi hxi) 2 ˆb = hyi ˆwhxi ˆw ˆb
@bgoncalves MLE for Linear Regression from __future__ import print_function import sys import numpy as np from scipy import optimize data = np.loadtxt(sys.argv[1]) x = data.T[0] y = data.T[1] meanx = np.mean(x) meany = np.mean(y) w = np.sum((x-meanx)*(y-meany))/np.sum((x-meanx)**2) b = meany-w*meanx print(w, b) #We can also optimize the Likelihood expression directly def likelihood(w): global x, y sigma = 1.0 w, b = w return np.sum((y-w*x-b)**2)/(2*sigma) w, b = optimize.fmin_bfgs(likelihood, [1.0, 1.0]) print(w, b) MLElinear.py
www.bgoncalves.com@bgoncalves Geometric Interpretation 0 3.25 6.5 9.75 13 0 5 10 15 20 L = N 2 log ⇥ 2 2 ⇤ X i " (yi f (xi)) 2 2 2 # Quadratic error means that an error twice as large is p e n a l i ze d f o u r times as much.
www.bgoncalves.com@bgoncalves ` 0 3.25 6.5 9.75 13 0 5 10 15 20 2D y = !0 + !1x1 3D y = !0 + !1x1 + !2x2 Geometric Interpretation nD y = ~!T ~x
www.bgoncalves.com@bgoncalves How do Machines Learn?
www.bgoncalves.com@bgoncalves 3 Types of Machine Learning • Unsupervised Learning • Autonomously learn an good representation of the dataset • Find clusters in input • Supervised Learning • Predict output given input • Training set of known inputs and outputs is provided • Reinforcement Learning • Learn sequence of actions to maximize payoff • Discount factor for delayed rewards
www.bgoncalves.com@bgoncalves Unsupervised Learning • Extracting patters from data • K-Means • PCA
www.bgoncalves.com@bgoncalves Clustering
www.bgoncalves.com@bgoncalves K-Means • Choose k randomly chosen points to be the centroid of each cluster • Assign each point to belong the cluster whose centroid is closest • Recompute the centroid positions (mean cluster position) • Repeat until convergence
www.bgoncalves.com@bgoncalves K-Means: Structure Voronoi Tesselation
www.bgoncalves.com@bgoncalves K-Means: Convergence • How to quantify the “quality” of the solution found at each iteration, ? • Measure the “Inertia”, the square intra-cluster distance:
 
 
 
 where are the coordinates of the centroid of the cluster to which is assigned. • Smaller values are better • Can stop when the relative variation is smaller than some value µi xi In+1 In In < tol In = NX i=0 kxi µik 2 n
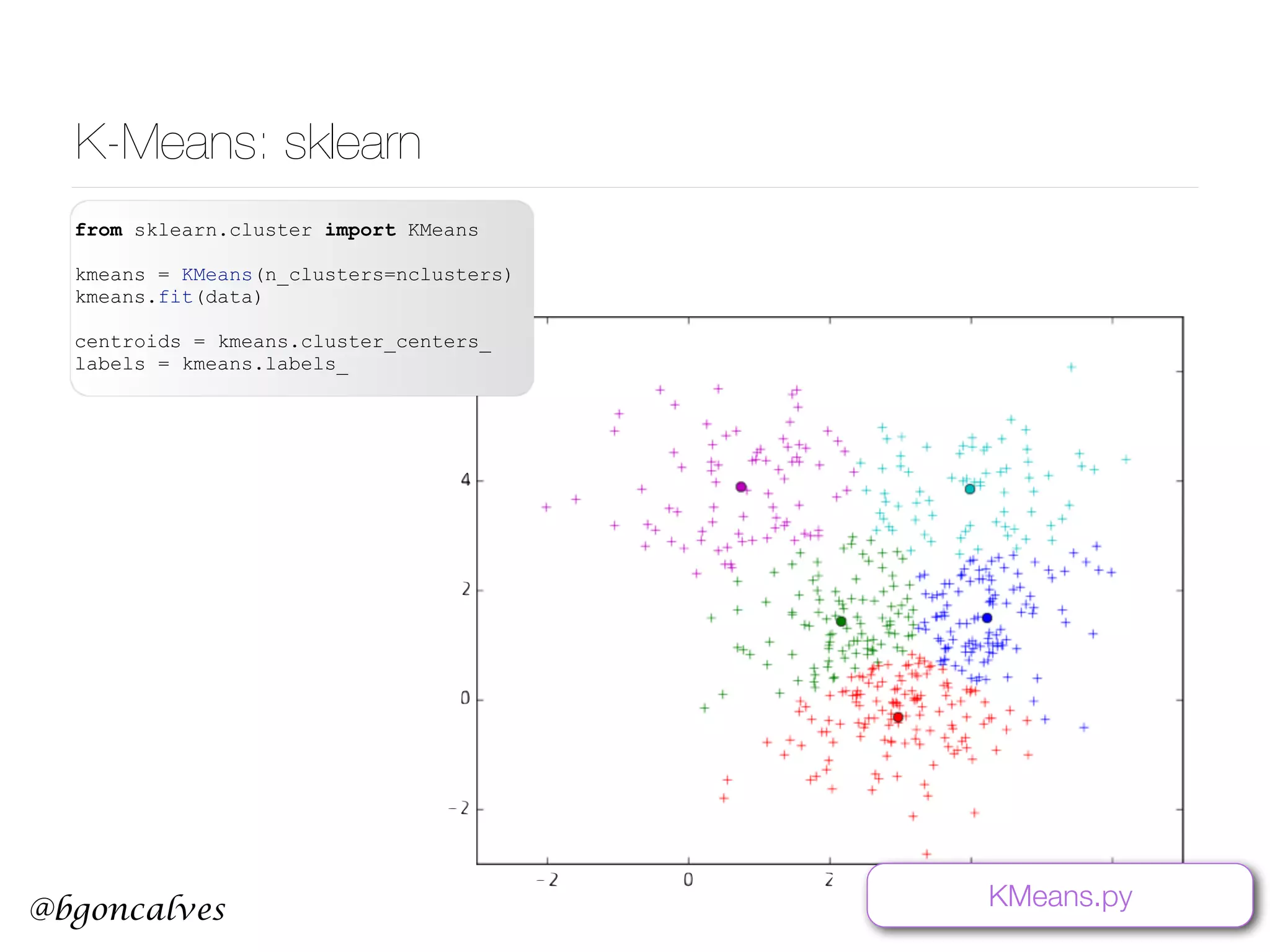
@bgoncalves K-Means: sklearn from sklearn.cluster import KMeans kmeans = KMeans(n_clusters=nclusters) kmeans.fit(data) centroids = kmeans.cluster_centers_ labels = kmeans.labels_ KMeans.py
www.bgoncalves.com@bgoncalves K-Means: Limitations
www.bgoncalves.com@bgoncalves K-Means: Limitations • No guarantees about Finding “Best” solution
 • Each run can find different solution
 • No clear way to determine “k”
www.bgoncalves.com@bgoncalves Silhouettes • For each point define as:
 
 
 
 the average distance between point and every other point within cluster . • Let be:
 
 the minimum value of excluding • The silhouette of is then: ac (xi) ac (xi) = 1 Nc X j2c kxi xjk b (xi) = min c6=ci ac (xi) s (xi) = b (xi) aci (xi) max {b (xi) , aci (xi)} xi xi c b (xi) ciac (xi) xi
www.bgoncalves.com@bgoncalves Silhouettes http://scikit-learn.org/stable/auto_examples/cluster/plot_kmeans_silhouette_analysis.html
www.bgoncalves.com@bgoncalves Silhouettes http://scikit-learn.org/stable/auto_examples/cluster/plot_kmeans_silhouette_analysis.html
www.bgoncalves.com@bgoncalves Silhouettes http://scikit-learn.org/stable/auto_examples/cluster/plot_kmeans_silhouette_analysis.html
www.bgoncalves.com@bgoncalves Silhouettes http://scikit-learn.org/stable/auto_examples/cluster/plot_kmeans_silhouette_analysis.html
www.bgoncalves.com@bgoncalves Silhouettes http://scikit-learn.org/stable/auto_examples/cluster/plot_kmeans_silhouette_analysis.html
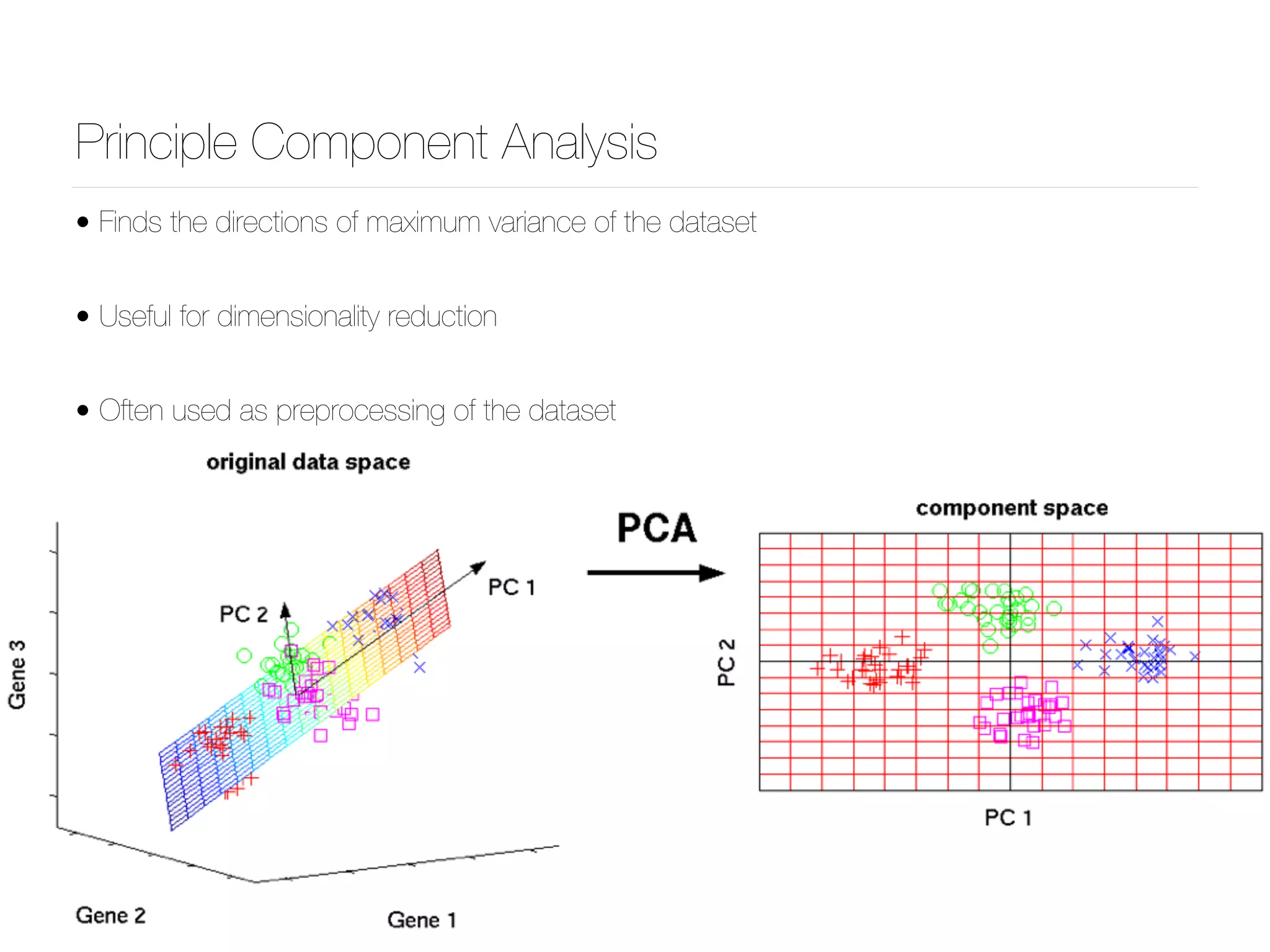
www.bgoncalves.com@bgoncalves Principle Component Analysis • Finds the directions of maximum variance of the dataset • Useful for dimensionality reduction • Often used as preprocessing of the dataset
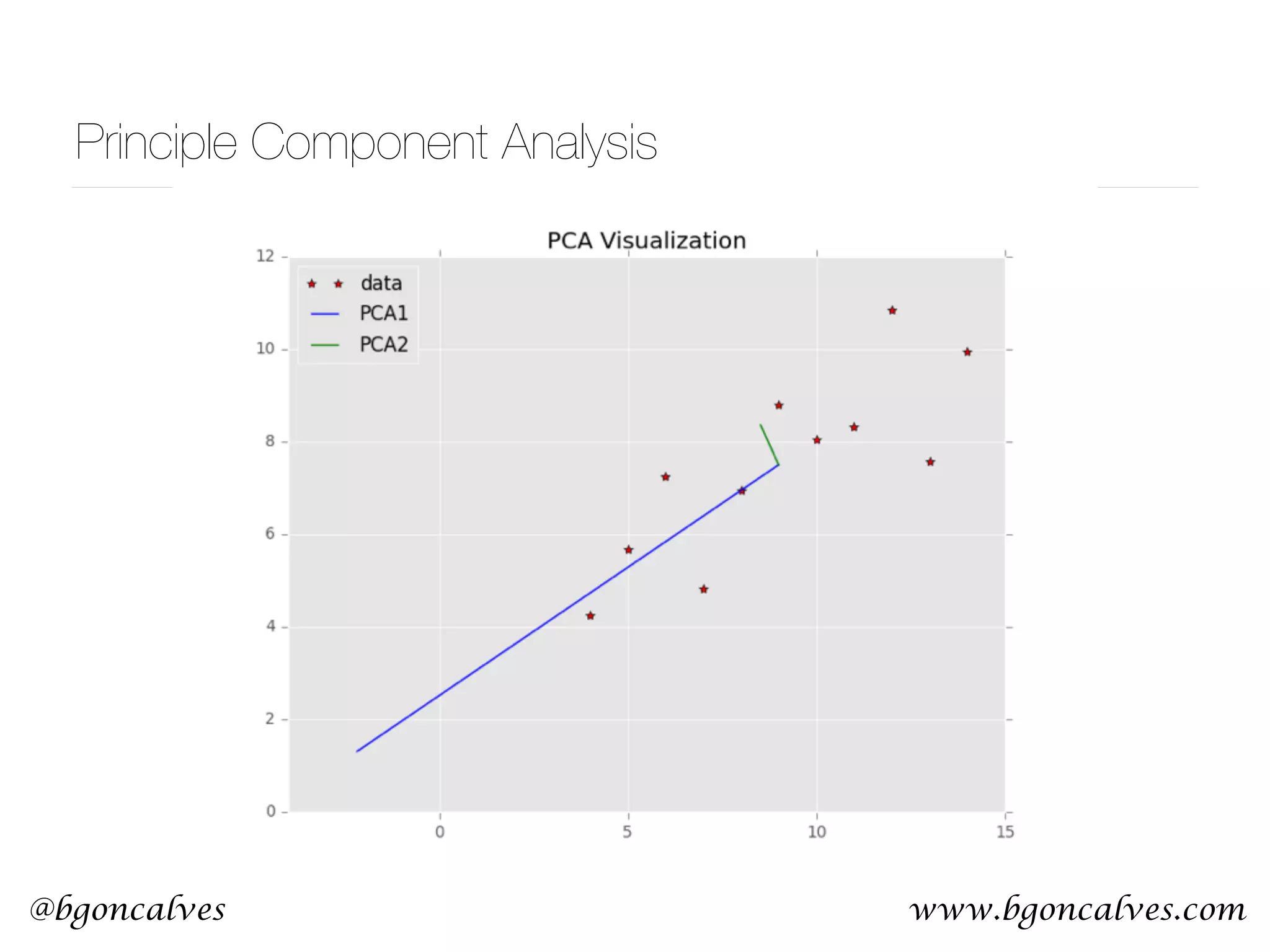
www.bgoncalves.com@bgoncalves Principle Component Analysis • The Principle Component projection, T, of a matrix A is defined as: • where W is the eigenvector matrix of: • and corresponds to the right singular vectors of A obtained by Singular Value Decomposition (SVD): • So we can write:
 • Showing that the Principle Component projection corresponds to the left singular vectors of A scaled by the respective singular values • Columns of T are ordered in order of decreasing variance. T = AW AT A T = U⌃WT W ⌘ U⌃ A = U⌃WT Generalization of Eigenvalue/ Eigenvector decomposition for non-square matrices. ⌃
@bgoncalves Principle Component Analysis from __future__ import print_function import sys from sklearn.decomposition import PCA import numpy as np import matplotlib.pyplot as plt data = np.loadtxt(sys.argv[1]) x = data.T[0] y = data.T[1] pca = PCA() pca.fit(data) meanX = np.mean(x) meanY = np.mean(y) plt.style.use('ggplot') plt.plot(x, y, 'r*') plt.plot([meanX, meanX+pca.components_[0][0]*pca.explained_variance_[0]], [meanY, meanY+pca.components_[0][1]*pca.explained_variance_[0]], 'b-') plt.plot([meanX, meanX+pca.components_[1][0]*pca.explained_variance_[1]], [meanY, meanY+pca.components_[1][1]*pca.explained_variance_[1]], 'g-') plt.title('PCA Visualization') plt.legend(['data', 'PCA1', 'PCA2'], loc=2) plt.savefig('PCA.png') PCA.py
www.bgoncalves.com@bgoncalves Principle Component Analysis
www.bgoncalves.com@bgoncalves Supervised Learning
www.bgoncalves.com@bgoncalves Supervised Learning - Classification Sample 1 Sample 2 Sample 3 Sample 4 Sample 5 Sample 6 . Sample N Feature1 Feature3 Feature2 … Label FeatureM • Dataset formatted as an NxM matrix of N samples and M features • Each sample belongs to a specific class or has a specific label. • The goal of classification is to predict to which class a previously unseen sample belongs to by learning defining regularities of each class • K-Nearest Neighbor • Support Vector Machine • Neural Networks • Two fundamental types of problems: • Classification • Regression (see Linear Regression above)
www.bgoncalves.com@bgoncalves Supervised Learning - Overfitting Sample 1 Sample 2 Sample 3 Sample 4 Sample 5 Sample 6 . Sample N Feature1 Feature3 Feature2 … Label FeatureM • “Learning the noise” • “Memorization” instead of “generalization” • How can we prevent it? • Split dataset into two subsets: Training and Testing • Train model using only the Training dataset and evaluate results in the previously unseen Testing dataset. • Different heuristics on how to split: • Single split • k-fold cross validation: split dataset in k parts, train in k-1 and evaluate in 1, repeat k times and average results. TrainingTesting
www.bgoncalves.com@bgoncalves Supervised Learning - Overfitting Sample 1 Sample 2 Sample 3 Sample 4 Sample 5 Sample 6 . Sample N Feature1 Feature3 Feature2 … Label FeatureM • “Learning the noise” • “Memorization” instead of “generalization” • How can we prevent it? • Split dataset into two subsets: Training and Testing • Train model using only the Training dataset and evaluate results in the previously unseen Testing dataset. • Different heuristics on how to split: • Single split • k-fold cross validation: split dataset in k parts, train in k-1 and evaluate in 1, repeat k times and average results. TrainingTesting
www.bgoncalves.com@bgoncalves Bias-Variance Tradeoff
www.bgoncalves.com@bgoncalves Bias-Variance Tradeoff Model Complexity Error Training Testing Variance Bias High Bias Low Variance Low Bias High Variance
www.bgoncalves.com@bgoncalves K-nearest neighbors • Perhaps the simplest of supervised learning algorithms • Effectively memorizes all previously seen data • Intuitively takes advantage of natural data clustering • Define that the class of any datapoint is given by the plurality of it’s k nearest neighbors • It’s not obvious how to find the right value of k
www.bgoncalves.com@bgoncalves K-nearest neighbors
www.bgoncalves.com@bgoncalves Biological Neuron What about Neurons?
www.bgoncalves.com@bgoncalves How the Brain “Works” (Cartoon version)
www.bgoncalves.com@bgoncalves How the Brain “Works” (Cartoon version) • Each neuron receives input from other neurons • 1011 neurons, each with with 104 weights • Weights can be positive or negative • Weights adapt during the learning process • “neurons that fire together wire together” (Hebb) • Different areas perform different functions using same structure (Modularity)
www.bgoncalves.com@bgoncalves How the Brain “Works” (Cartoon version) Inputs Outputf(Inputs)
www.bgoncalves.com@bgoncalves Historical Perspective 1958 Perceptron • Popularized by F. Rosenblatt who wrote “Principles of Neurodynamics" • Still used today • Simple but limited training procedure • Single Layer
www.bgoncalves.com@bgoncalves Perceptron x1 x2 x3 xN w 1j w2j w3j wN j zj wT x aj (z) w 0j 1 Inputs Weights Output Activation function Bias
www.bgoncalves.com@bgoncalves Activation Function
www.bgoncalves.com@bgoncalves Activation Function
www.bgoncalves.com@bgoncalves Activation Function
www.bgoncalves.com@bgoncalves Activation Function (z) = 1 1 + e z
www.bgoncalves.com@bgoncalves Activation Function (z) = ez e z ez + e z
@bgoncalves Activation Function import matplotlib.pyplot as plt import numpy as np def linear(z): return z def binary(z): return np.where(z > 0, 1, 0) def relu(z): return np.where(z > 0, z, 0) def sigmoid(z): return 1./(1+np.exp(-z)) def tanh(z): return np.tanh(z) z = np.linspace(-6, 6, 100) plt.style.use('ggplot') plt.plot(z, linear(z), 'r-') plt.xlabel('z') plt.title('Linear activation function') plt.savefig('linear.png') plt.close() activation.py
www.bgoncalves.com@bgoncalves Perceptron x1 x2 x3 xN w 1j w2j w3j wN j aj w 0j 1 wT x Training Procedure: • If correct, do nothing • If output incorrectly outputs 0, add input to weight vector • if output incorrectly outputs 1, subtract input to weight vector • Guaranteed to converge, if a correct set of weights exists • Given enough features, perceptrons can learn almost anything • Specific Features used limit what is possible to learn
www.bgoncalves.com@bgoncalves Historical Perspective 1958 Marvin Minsky • Co-authors “Perceptrons” with Seymour Papert • XOR Problem • Perceptrons can’t learn non-linearly separable functions • The first “AI Winter” Perceptron 1969
www.bgoncalves.com@bgoncalves Historical Perspective 1958 Perceptron 1969 XOR 1986 Geoff Hinton • Discovers “Backpropagation” • “Multi-layer Perceptron” • Expensive computation requiring lots of data • Impractical
www.bgoncalves.com@bgoncalves Forward Propagation • The output of a perceptron is determined by a sequence of steps: • obtain the inputs • multiply the inputs by the respective weights • calculate output using the activation function • To create a multi-layer perceptron, you can simply use the output of one layer as the input to the next one.
 • But how can we propagate back the errors and update the weights? x1 x2 x3 xN w 1j w2j w3j wN j aj w 0j 1 wT x 1 w 0k w 1k w2k w3k wNk ak wT a a1 a2 aN
www.bgoncalves.com@bgoncalves Backward Propagation of Errors (BackProp) • BackProp operates in two phases: • Forward propagate the inputs and calculate the deltas • Update the weights • The error at the output is the squared difference between predicted output and the observed one: • Where is the real output and is the predicted one. • For inner layers there is no “real output”! t E = (t y) 2 y
www.bgoncalves.com@bgoncalves Chain-rule • From the forward propagation described above, we know that the output of a neuron is: • But how can we calculate how to modify the weights ? • We take the derivative of the error with respect to the weights!
 • Using the chain rule:
 • And finally we can update each weight in the previous layer:
 • where is the learning rate yj = wT x @E @wij = @E @yj @yj @wij wij @E @wij wij wij ↵ @E @wij yj ↵
www.bgoncalves.com@bgoncalves Learning Rate Epoch High Learning Rate Very High Learning Rate Loss Low Learning Rate Best Learning Rate
www.bgoncalves.com@bgoncalves Backprop • Back propagation solved the fundamental problem underlying neural networks • Unfortunately, computers were still too slow for large networks to be trained successfully • Also, in many cases, there wasn’t enough available data
www.bgoncalves.com@bgoncalves Historical Perspective 1958 Perceptron 1969 XOR 1986 Yann LeCun • Starts working on Convolutional Neural Networks • (Eventually) develops the first practical application of image recognition Backprop 1989
www.bgoncalves.com@bgoncalves Historical Perspective 1958 Perceptron 1969 XOR 1986 Vladimir Vapnik • Support Vector Machines • A clever variation on Perceptrons • Kernel Trick Backprop 1989 ConvNet 1995
www.bgoncalves.com@bgoncalves Support Vector Machine 0 3.25 6.5 9.75 13 0 5 10 15 20 Perceptrons find a hyperplane that separates the two classes of data
www.bgoncalves.com@bgoncalves Support Vector Machine 0 3.25 6.5 9.75 13 0 5 10 15 20 But how can we find the hyperplane w i t h t h e b e s t separation of the data?
www.bgoncalves.com@bgoncalves Support Vector Machines • Decision plane has the form: • We want for points in the “positive” class and for points in the negative class. Where the “margin” is as large as possible. • Normalize such that and solve the optimization problem:
 
 
 subject to: • The margin is: wT x = 0 wT x b wT x  b 2b min w ||w||2 yi wT x > 1 2 ||w|| b = 1
www.bgoncalves.com@bgoncalves Kernel “trick” • SVM procedure uses only the dot products of vectors and never the vectors themselves. • We can redefine the dot product in any way we wish. • In effect we are mapping from a non-linear input space to a linear feature space
www.bgoncalves.com@bgoncalves Historical Perspective 1958 Perceptron 1969 XOR 1986 Backprop 1989 ConvNet 1995 SVM Geoff Hinton • Deep Neural Networks • Combines backprop 
 with faster machines and larger datasets 2006
www.bgoncalves.com@bgoncalves Neural Network Architectures
www.bgoncalves.com@bgoncalves Convolutional Neural Networks
www.bgoncalves.com@bgoncalves Interpretability
www.bgoncalves.com@bgoncalves “Deep” learning

More Related Content

PDF
Photo-realistic Single Image Super-resolution using a Generative Adversarial ...
byHansol Kang
 
PDF
Machine(s) Learning with Neural Networks
byBruno Gonçalves
 
PDF
Word2vec in Theory Practice with TensorFlow
byBruno Gonçalves
 
PDF
It Probably Works - QCon 2015
byFastly
 
PDF
Scaling Deep Learning with MXNet
byAI Frontiers
 
PDF
딥러닝 중급 - AlexNet과 VggNet (Basic of DCNN : AlexNet and VggNet)
byHansol Kang
 
PDF
Real Time Big Data Management
byAlbert Bifet
 
PDF
Lecture 5: Neural Networks II
bySang Jun Lee
 
Photo-realistic Single Image Super-resolution using a Generative Adversarial ...
byHansol Kang
 
Machine(s) Learning with Neural Networks
byBruno Gonçalves
 
Word2vec in Theory Practice with TensorFlow
byBruno Gonçalves
 
It Probably Works - QCon 2015
byFastly
 
Scaling Deep Learning with MXNet
byAI Frontiers
 
딥러닝 중급 - AlexNet과 VggNet (Basic of DCNN : AlexNet and VggNet)
byHansol Kang
 
Real Time Big Data Management
byAlbert Bifet
 
Lecture 5: Neural Networks II
bySang Jun Lee
 

What's hot

PDF
Introduction to Big Data Science
byAlbert Bifet
 
PDF
Internet of Things Data Science
byAlbert Bifet
 
PDF
Graph convolutional networks in apache spark
byEmiliano Martinez Sanchez
 
PDF
Network Analysis with networkX : Real-World Example-1
byKyunghoon Kim
 
PDF
Generative adversarial networks
by남주 김
 
DOCX
Study material ip class 12th
byanimesh dwivedi
 
KEY
Modern Algorithms and Data Structures - 1. Bloom Filters, Merkle Trees
byLorenzo Alberton
 
PDF
[232]mist 고성능 iot 스트림 처리 시스템
byNAVER D2
 
PDF
Mastering the game of Go with deep neural networks and tree search (article o...
byIlya Kuzovkin
 
PDF
Deep Convolutional GANs - meaning of latent space
byHansol Kang
 
PPTX
Class 26: Objectifying Objects
byDavid Evans
 
PPT
Bloom filter
bywang ping
 
PDF
2013 open analytics_countingv3
byabramsm
 
PDF
Hyperparameter optimization with approximate gradient
byFabian Pedregosa
 
PDF
Real-Time Big Data Stream Analytics
byAlbert Bifet
 
PDF
PyTorch 튜토리얼 (Touch to PyTorch)
byHansol Kang
 
PDF
Simple representations for learning: factorizations and similarities
byGael Varoquaux
 
PPTX
Quantum Computing for app programmer
byKyunam Cho
 
PDF
Polyglot Persistence in the Real World: Cassandra + S3 + MapReduce
bythumbtacktech
 
Introduction to Big Data Science
byAlbert Bifet
 
Internet of Things Data Science
byAlbert Bifet
 
Graph convolutional networks in apache spark
byEmiliano Martinez Sanchez
 
Network Analysis with networkX : Real-World Example-1
byKyunghoon Kim
 
Generative adversarial networks
by남주 김
 
Study material ip class 12th
byanimesh dwivedi
 
Modern Algorithms and Data Structures - 1. Bloom Filters, Merkle Trees
byLorenzo Alberton
 
[232]mist 고성능 iot 스트림 처리 시스템
byNAVER D2
 
Mastering the game of Go with deep neural networks and tree search (article o...
byIlya Kuzovkin
 
Deep Convolutional GANs - meaning of latent space
byHansol Kang
 
Class 26: Objectifying Objects
byDavid Evans
 
Bloom filter
bywang ping
 
2013 open analytics_countingv3
byabramsm
 
Hyperparameter optimization with approximate gradient
byFabian Pedregosa
 
Real-Time Big Data Stream Analytics
byAlbert Bifet
 
PyTorch 튜토리얼 (Touch to PyTorch)
byHansol Kang
 
Simple representations for learning: factorizations and similarities
byGael Varoquaux
 
Quantum Computing for app programmer
byKyunam Cho
 
Polyglot Persistence in the Real World: Cassandra + S3 + MapReduce
bythumbtacktech
 

Viewers also liked

PDF
Word2vec and Friends
byBruno Gonçalves
 
PDF
Twitterology - The Science of Twitter
byBruno Gonçalves
 
PDF
Mining Geo-referenced Data: Location-based Services and the Sharing Economy
bytnoulas
 
PDF
Human Mobility (with Mobile Devices)
byBruno Gonçalves
 
PDF
Complenet 2017
bytnoulas
 
PDF
Mining Georeferenced Data
byBruno Gonçalves
 
PDF
Making Sense of Data Big and Small
byBruno Gonçalves
 
Word2vec and Friends
byBruno Gonçalves
 
Twitterology - The Science of Twitter
byBruno Gonçalves
 
Mining Geo-referenced Data: Location-based Services and the Sharing Economy
bytnoulas
 
Human Mobility (with Mobile Devices)
byBruno Gonçalves
 
Complenet 2017
bytnoulas
 
Mining Georeferenced Data
byBruno Gonçalves
 
Making Sense of Data Big and Small
byBruno Gonçalves
 

Similar to A practical Introduction to Machine(s) Learning

PPT
Introduction to Machine Learning STUDENTS.ppt
byRafaelCorrea542592
 
PPT
Machine Learning and Statistical Analysis
bybutest
 
PPT
Machine Learning and Statistical Analysis
bybutest
 
PPT
Machine Learning and Statistical Analysis
bybutest
 
PPT
Machine Learning and Statistical Analysis
bybutest
 
PPT
Machine Learning and Statistical Analysis
bybutest
 
PPT
Machine Learning and Statistical Analysis
bybutest
 
PPT
Machine Learning and Statistical Analysis
bybutest
 
PPTX
Lecture 8 about data mining and how to use it.pptx
byHedraAtif
 
PPTX
Anomaly detection using deep one class classifier
by홍배 김
 
PPTX
DataAnalysis in machine learning using different techniques
bymtwnc202302
 
PDF
Machine Learning With MapReduce, K-Means, MLE
byJason J Pulikkottil
 
PPTX
Deep Learning: Introduction & Chapter 5 Machine Learning Basics
byJason Tsai
 
PDF
Explore ml day 2
bypreetikumara
 
PPTX
Data Mining Lecture_10(b).pptx
bySubrata Kumer Paul
 
PPT
Introduction
bybutest
 
PPTX
The world of loss function
by홍배 김
 
PDF
On learning statistical mixtures maximizing the complete likelihood
byFrank Nielsen
 
PDF
Data Science Cheatsheet.pdf
byqawali1
 
PDF
MLHEP 2015: Introductory Lecture #1
byarogozhnikov
 
Introduction to Machine Learning STUDENTS.ppt
byRafaelCorrea542592
 
Machine Learning and Statistical Analysis
bybutest
 
Machine Learning and Statistical Analysis
bybutest
 
Machine Learning and Statistical Analysis
bybutest
 
Machine Learning and Statistical Analysis
bybutest
 
Machine Learning and Statistical Analysis
bybutest
 
Machine Learning and Statistical Analysis
bybutest
 
Machine Learning and Statistical Analysis
bybutest
 
Lecture 8 about data mining and how to use it.pptx
byHedraAtif
 
Anomaly detection using deep one class classifier
by홍배 김
 
DataAnalysis in machine learning using different techniques
bymtwnc202302
 
Machine Learning With MapReduce, K-Means, MLE
byJason J Pulikkottil
 
Deep Learning: Introduction & Chapter 5 Machine Learning Basics
byJason Tsai
 
Explore ml day 2
bypreetikumara
 
Data Mining Lecture_10(b).pptx
bySubrata Kumer Paul
 
Introduction
bybutest
 
The world of loss function
by홍배 김
 
On learning statistical mixtures maximizing the complete likelihood
byFrank Nielsen
 
Data Science Cheatsheet.pdf
byqawali1
 
MLHEP 2015: Introductory Lecture #1
byarogozhnikov
 

Recently uploaded

PPTX
[DSC DACH 25] Jacqueline Berger - Beyond the Hype: The Real Story of Building...
byDataScienceConferenc1
 
PDF
FNB58-_MjrjejejddbbjznkwkJwnajwanual.pdf
byAhmedAli23521
 
PDF
The AI Singularity: Are We Heading for Salvation or Collapse? By Olumisimi Ak...
byTheta Prime Institute, Cheyenne, Wyoming, USA.
 
PDF
From Data to Insights: Turning Network Data into Community Impact with PARTNE...
byalexmderr
 
PDF
Comparative Analysis of Digital Maturity Models.pdf
byRawan Alharbi
 
PPTX
[DSC DACH 25] Dr. Jochen Kokemueller.pptx
byDataScienceConferenc1
 
PPTX
[DSC DACH 25] AI in Action_ From Industrial Data to Sustainable Impact_Ashraf...
byDataScienceConferenc1
 
PPTX
PR1Q3W1-LESSON.pptx PR1Q3W1-LESSON.pptx PR1Q3W1-LESSON.pptx
byVenomousCabbage
 
PDF
Google Search Console: The SEO power tool you're probably misusing
byMartin Hayman
 
PPTX
Linux chapter one Lesson 1.pptxLinux chapter one Lesson 1.pptx
byMAHERMOHAMED27
 
PPTX
Lecture 3 - Array Operations in C++ including all concepts of arrays in data ...
byvanizahz
 
PDF
[DSC DACH 25] Yudan Lin_The Human - AI Paradox and Effective Fix.pdf
byDataScienceConferenc1
 
PDF
POWER POINT.pdfaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
byMaCristinaDelacruz7
 
PPTX
Ppt experimental research_20251027_120924_0000.pptx
bysulfiaanggraini5
 
PPTX
Group project mgtkspgo gj a akf alkn mkla.pptx
bymadaminbekmahmudov02
 
PPTX
Hastings_County_Finaldsdffxgfxtr_v1.pptx
byrishitasetia1
 
PPTX
ACEH TAMIANG TO OPEN DEFECATION FREE AWARDS in HKN.pptx
byacumustakim
 
PDF
Can AI Write Better SQL Than You? Longhorn PHP 2025
byDave Stokes
 
PPTX
SQL Database Design For Developers at Longhorn PHP 2025
byScott Keck-Warren
 
PDF
ethicoder registration data analytics methods
byaabera884
 
[DSC DACH 25] Jacqueline Berger - Beyond the Hype: The Real Story of Building...
byDataScienceConferenc1
 
FNB58-_MjrjejejddbbjznkwkJwnajwanual.pdf
byAhmedAli23521
 
The AI Singularity: Are We Heading for Salvation or Collapse? By Olumisimi Ak...
byTheta Prime Institute, Cheyenne, Wyoming, USA.
 
From Data to Insights: Turning Network Data into Community Impact with PARTNE...
byalexmderr
 
Comparative Analysis of Digital Maturity Models.pdf
byRawan Alharbi
 
[DSC DACH 25] Dr. Jochen Kokemueller.pptx
byDataScienceConferenc1
 
[DSC DACH 25] AI in Action_ From Industrial Data to Sustainable Impact_Ashraf...
byDataScienceConferenc1
 
PR1Q3W1-LESSON.pptx PR1Q3W1-LESSON.pptx PR1Q3W1-LESSON.pptx
byVenomousCabbage
 
Google Search Console: The SEO power tool you're probably misusing
byMartin Hayman
 
Linux chapter one Lesson 1.pptxLinux chapter one Lesson 1.pptx
byMAHERMOHAMED27
 
Lecture 3 - Array Operations in C++ including all concepts of arrays in data ...
byvanizahz
 
[DSC DACH 25] Yudan Lin_The Human - AI Paradox and Effective Fix.pdf
byDataScienceConferenc1
 
POWER POINT.pdfaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
byMaCristinaDelacruz7
 
Ppt experimental research_20251027_120924_0000.pptx
bysulfiaanggraini5
 
Group project mgtkspgo gj a akf alkn mkla.pptx
bymadaminbekmahmudov02
 
Hastings_County_Finaldsdffxgfxtr_v1.pptx
byrishitasetia1
 
ACEH TAMIANG TO OPEN DEFECATION FREE AWARDS in HKN.pptx
byacumustakim
 
Can AI Write Better SQL Than You? Longhorn PHP 2025
byDave Stokes
 
SQL Database Design For Developers at Longhorn PHP 2025
byScott Keck-Warren
 
ethicoder registration data analytics methods
byaabera884
 

A practical Introduction to Machine(s) Learning