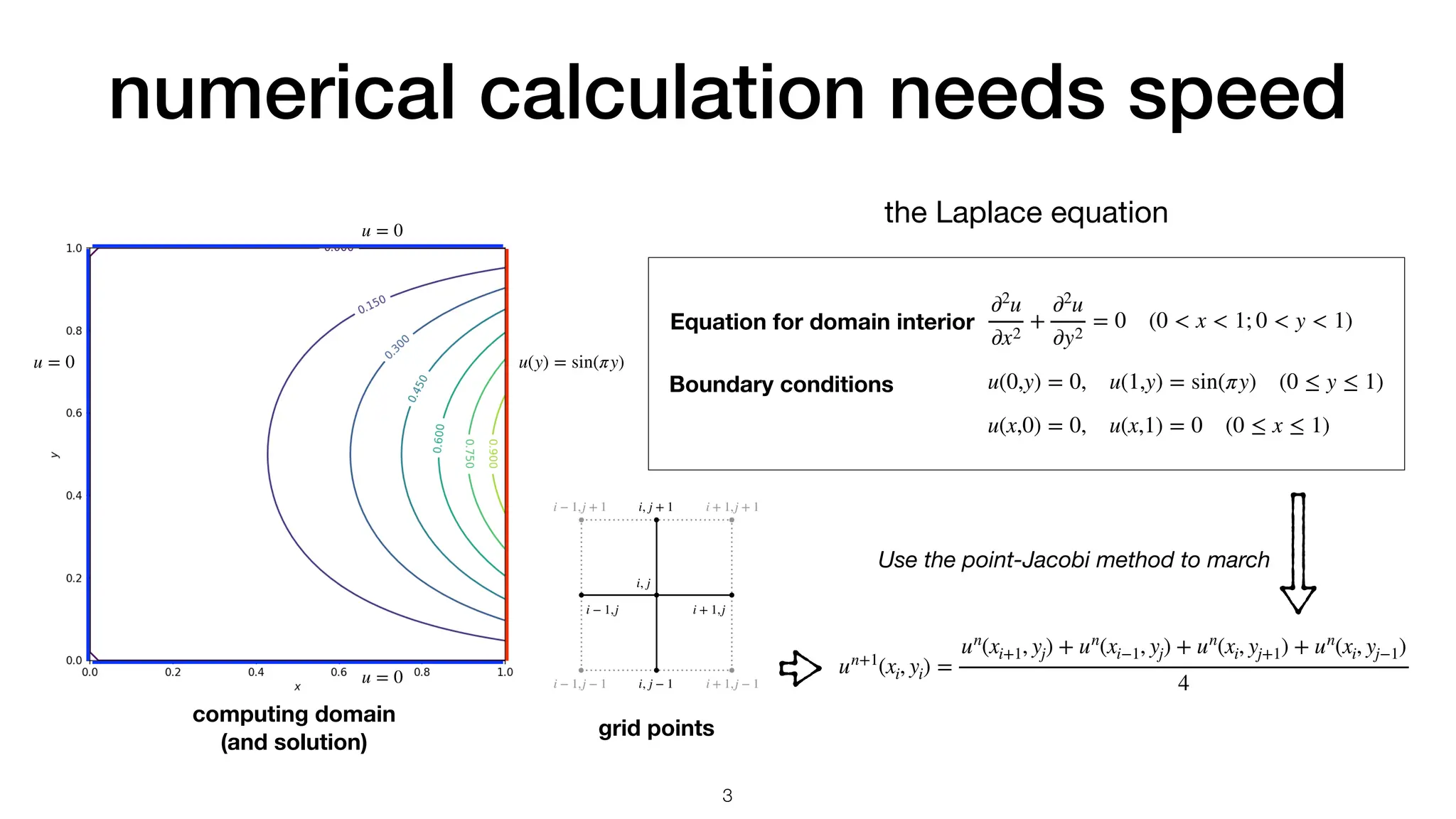
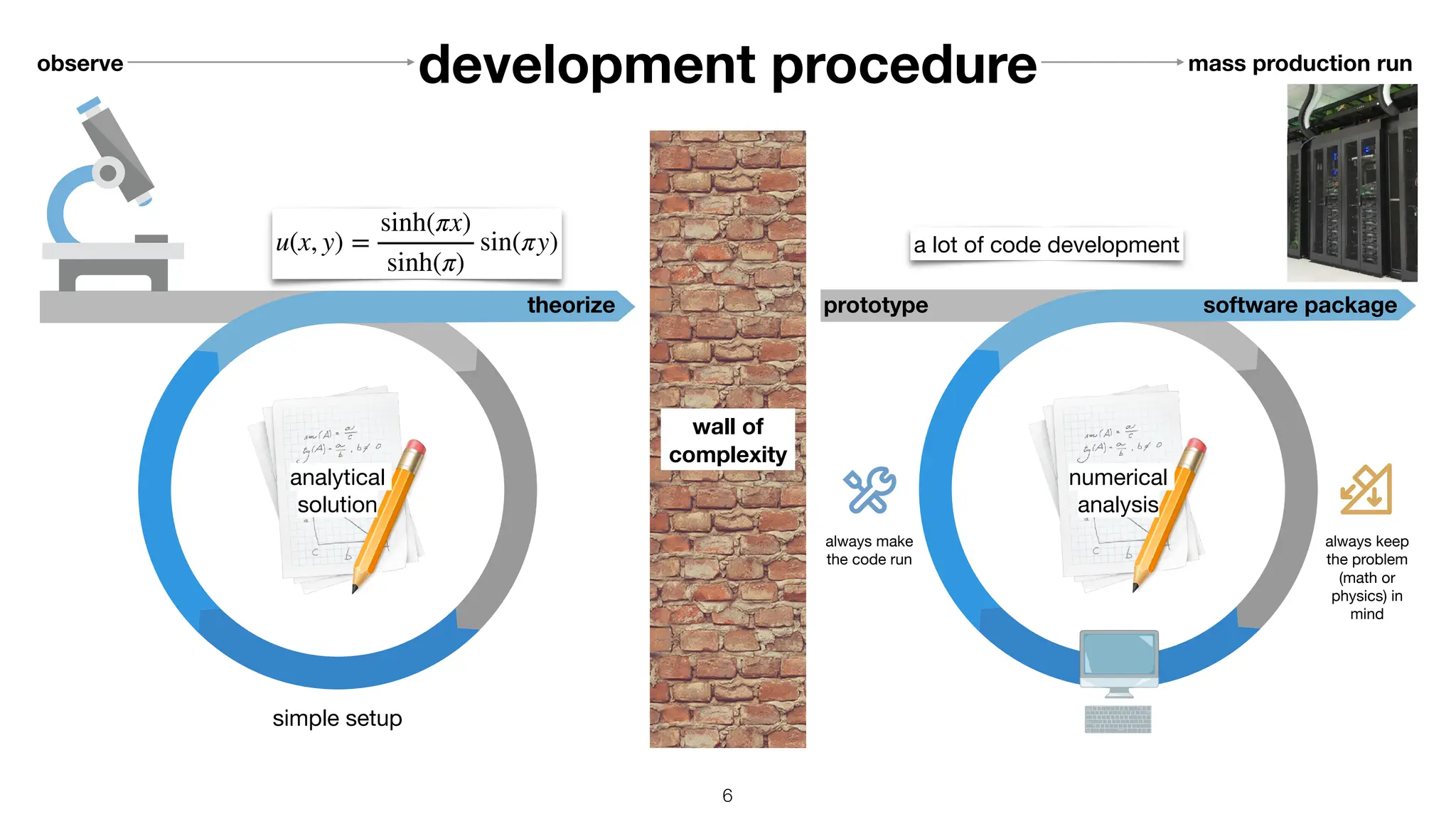
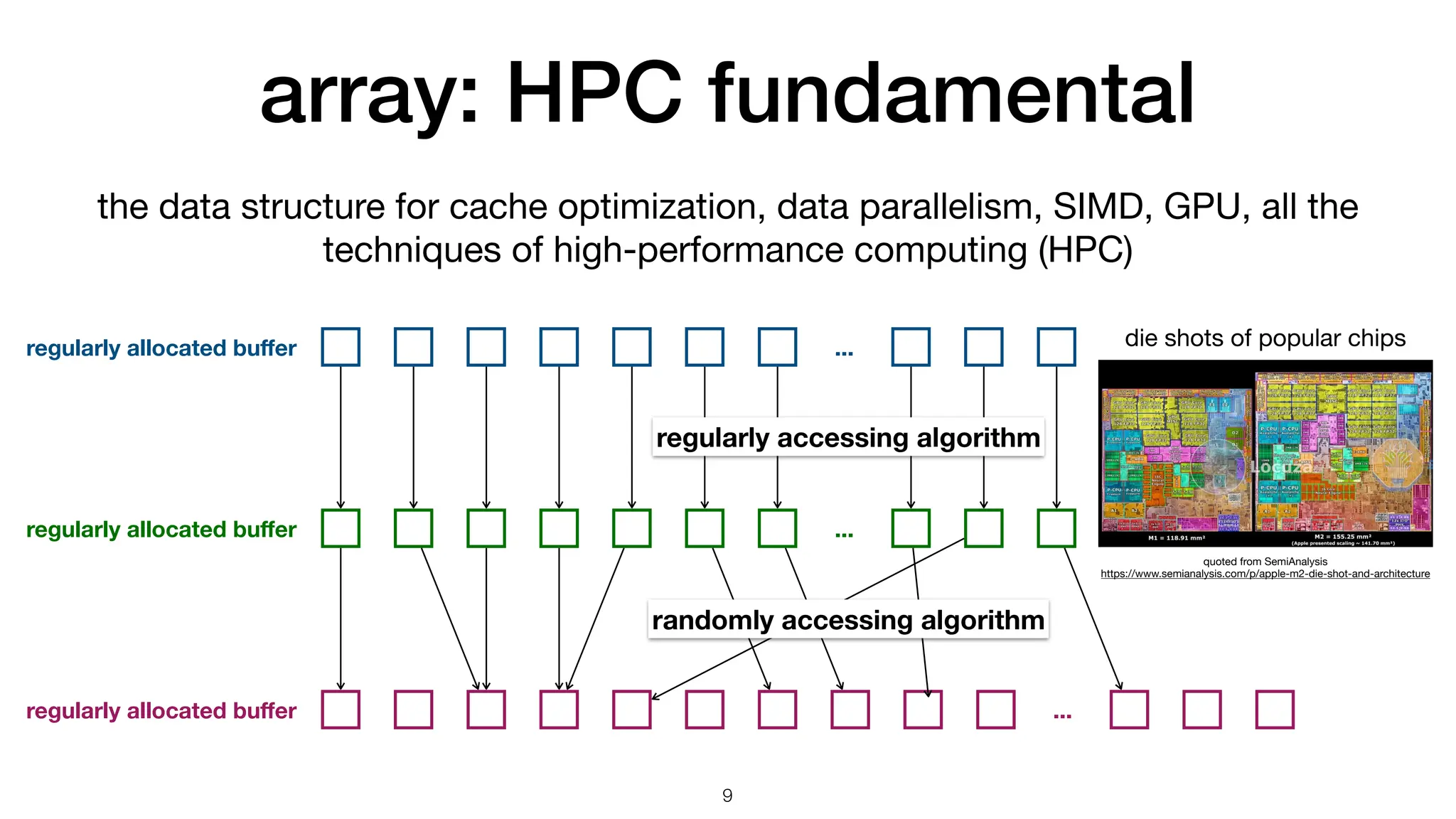
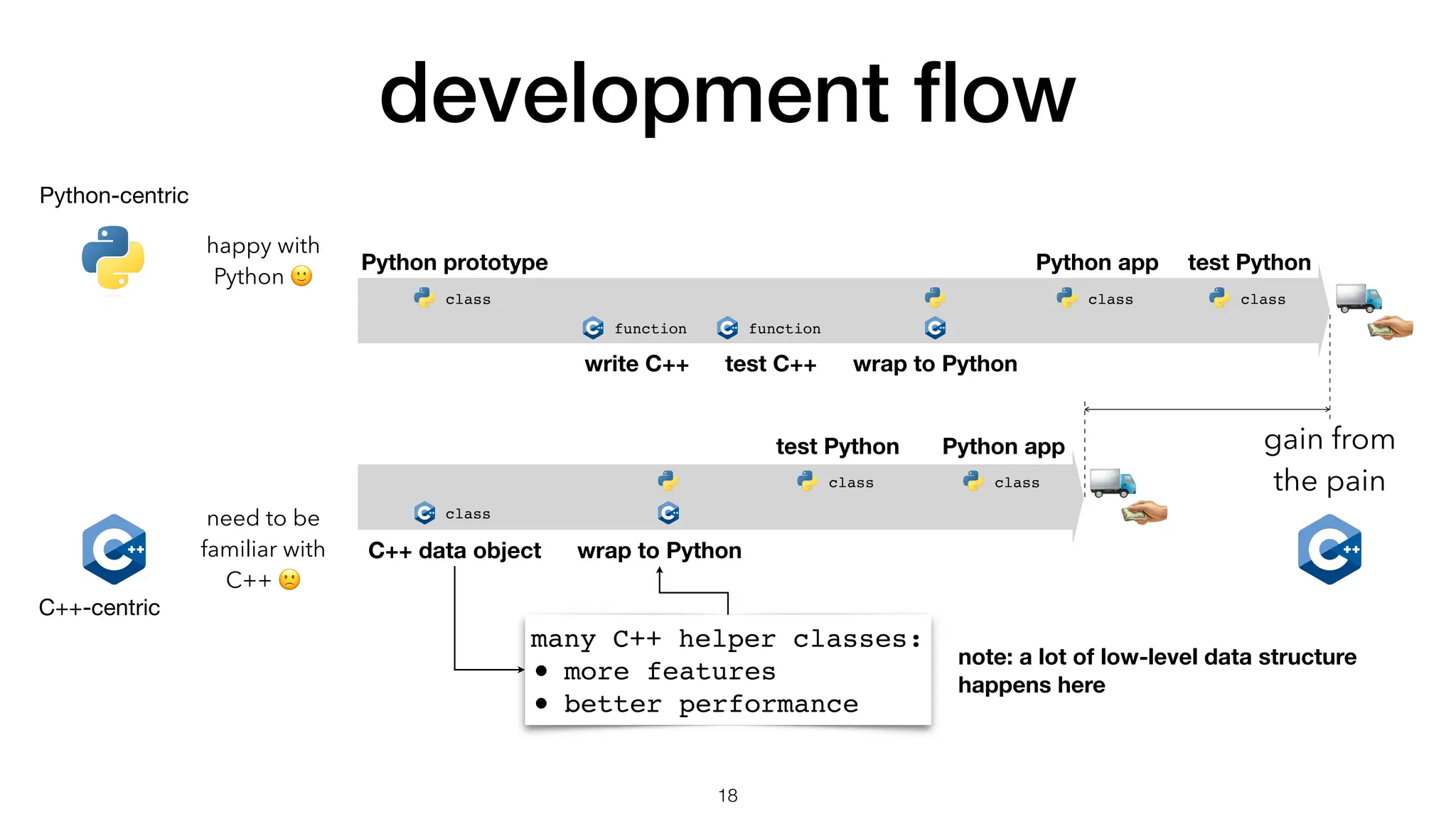
The document discusses the importance of speed in computational methods, particularly in relation to high-speed rail and numerical calculations. It provides an overview of the Point-Jacobi method for solving the Laplace equation, comparing the performance of Python and C++ implementations. It highlights the need for hybrid programming approaches that leverage Python for ease of use while utilizing C++ for performance-critical tasks in high-performance computing.


![Python is slow for it in range(1, nx-1): for jt in range(1, nx-1): un[it,jt] = (u[it+1,jt] + u[it-1,jt] + u[it,jt+1] + u[it,jt-1]) / 4 un[1:nx-1,1:nx-1] = (u[2:nx,1:nx-1] + u[0:nx-2,1:nx-1] + u[1:nx-1,2:nx] + u[1:nx-1,0:nx-2]) / 4 for (size_t it=1; it<nx-1; ++it) { for (size_t jt=1; jt<nx-1; ++jt) { un(it,jt) = (u(it+1,jt) + u(it-1,jt) + u(it,jt+1) + u(it,jt-1)) / 4; } } Point-Jacobi method Python nested loop Numpy array C++ nested loop 4.797s (1x) 0.055s (87x) 0.025s (192x) un+1 (xi, yi) = un (xi+1, yj) + un (xi−1, yj) + un (xi, yj+1) + un (xi, yj−1) 4 4](https://image.slidesharecdn.com/writepythonforspeedpyconapac20231027-231028212349-d3988144/75/Write-Python-for-Speed-4-2048.jpg)

![machine determines speed void calc_distance( size_t const n , double const * x , double const * y , double * r) { for (size_t i = 0 ; i < n ; ++i) { r[i] = std::sqrt(x[i]*x[i] + y[i]*y[i]); } } vmovupd ymm0, ymmword [rsi + r9*8] vmulpd ymm0, ymm0, ymm0 vmovupd ymm1, ymmword [rdx + r9*8] vmulpd ymm1, ymm1, ymm1 vaddpd ymm0, ymm0, ymm1 vsqrtpd ymm0, ymm0 movupd xmm0, xmmword [rsi + r8*8] mulpd xmm0, xmm0 movupd xmm1, xmmword [rdx + r8*8] mulpd xmm1, xmm1 addpd xmm1, xmm0 sqrtpd xmm0, xmm1 AVX: 256-bit-wide vectorization SSE: 128-bit-wide vectorization C++ code 8](https://image.slidesharecdn.com/writepythonforspeedpyconapac20231027-231028212349-d3988144/75/Write-Python-for-Speed-8-2048.jpg)
![quick prototype in Python: something new and fragile • thread pool for I/O? certainly Python • certainly not want to write complicated C++ to prototype • 64 threads on 32-core servers? • consider to move it to C++ • data-parallel code on top of the thread pool? • time to go with TBB (thread- building block) C++ library from _thread import allocate_lock, start_new_thread class ThreadPool(object): """Python prototype for I/O thread pool""" def __init__(self, nthread): # Worker callback self.func = None # Placeholders for managing data self.__threadids = [None] * nthread self.__threads = [None] * nthread self.__returns = [None] * nthread # Initialize thread managing data for it in range(nthread): mlck = allocate_lock(); mlck.acquire() wlck = allocate_lock(); wlck.acquire() tdata = [mlck, wlck, None, None] self.__threads[it] = tdata tid = start_new_thread(self.eventloop, (tdata,)) self.__threadids[it] = tid 11](https://image.slidesharecdn.com/writepythonforspeedpyconapac20231027-231028212349-d3988144/75/Write-Python-for-Speed-11-2048.jpg)
![quick prototype in Python: something complex i, j i, j + 1 i, j − 1 i + 1,j i − 1,j i + 1,j + 1 i + 1,j − 1 i − 1,j + 1 i − 1,j − 1 di ff erence equation def solve_python_loop(): u = uoriginal.copy() # Input from outer scope un = u.copy() # Create the buffer for the next time step converged = False step = 0 # Outer loop. while not converged: step += 1 # Inner loops. One for x and the other for y. for it in range(1, nx-1): for jt in range(1, nx-1): un[it,jt] = (u[it+1,jt] + u[it-1,jt] + u[it,jt+1] + u[it,jt-1]) / 4 norm = np.abs(un-u).max() u[...] = un[...] converged = True if norm < 1.e-5 else False return u, step, norm 12 grid points python nested loop implementing point-Jacobi method u(xi, yj) = u(xi+1, yj) + u(xi−1, yj) + u(xi, yj+1) + u(xi, yj−1) 4 point-Jacobi method un+1 (xi, yi) = un (xi+1, yj) + un (xi−1, yj) + un (xi, yj+1) + un (xi, yj−1) 4](https://image.slidesharecdn.com/writepythonforspeedpyconapac20231027-231028212349-d3988144/75/Write-Python-for-Speed-12-2048.jpg)
![production: many data many ways 13 fi t scattered points to a polynomial f(x) = a3x3 + a2x2 + a1x + a0 test many (like 1,000+) such data sets: def plot_poly_fitted(i): slct = (xdata>=i)&(xdata<(i+1)) sub_x = xdata[slct] sub_y = ydata[slct] poly = data_prep.fit_poly(sub_x, sub_y, 3) print(poly) poly = np.poly1d(poly) xp = np.linspace(sub_x.min(), sub_x.max(), 100) plt.plot(sub_x, sub_y, '.', xp, poly(xp), '-') plot_poly_fitted(10) (yeah, the data points seem to be too random to be represented by a polynomial) // The rank of the linear map is (order+1). modmesh::SimpleArray<double> matrix(std::vector<size_t>{order+1, order+1}); // Use the x coordinates to build the linear map for least-square // regression. for (size_t it=0; it<order+1; ++it) { for (size_t jt=0; jt<order+1; ++jt) { double & val = matrix(it, jt); val = 0; for (size_t kt=start; kt<stop; ++kt) { val += pow(xarr[kt], it+jt); } } } >>> with Timer(): >>> # Do the calculation for the 1000 groups of points. >>> polygroup = np.empty((1000, 3), dtype='float64') >>> for i in range(1000): >>> # Use numpy to build the point group. >>> slct = (xdata>=i)&(xdata<(i+1)) >>> sub_x = xdata[slct] >>> sub_y = ydata[slct] >>> polygroup[i,:] = data_prep.fit_poly(sub_x, sub_y, 2) >>> with Timer(): >>> # Using numpy to build the point groups takes a lot of time. >>> data_groups = [] >>> for i in range(1000): >>> slct = (xdata>=i)&(xdata<(i+1)) >>> data_groups.append((xdata[slct], ydata[slct])) >>> with Timer(): >>> # Fitting helper runtime is much less than building the point groups. >>> polygroup = np.empty((1000, 3), dtype='float64') >>> for it, (sub_x, sub_y) in enumerate(data_groups): >>> polygroup[it,:] = data_prep.fit_poly(sub_x, sub_y, 2) Wall time: 1.49671 s Wall time: 1.24653 s Wall time: 0.215859 s prepare data fi t polynomials](https://image.slidesharecdn.com/writepythonforspeedpyconapac20231027-231028212349-d3988144/75/Write-Python-for-Speed-13-2048.jpg)
![problem of speedup 14 >>> with Timer(): >>> # Using numpy to build the point groups takes a lot of time. >>> data_groups = [] >>> for i in range(1000): >>> slct = (xdata>=i)&(xdata<(i+1)) >>> data_groups.append((xdata[slct], ydata[slct])) Wall time: 1.24653 s >>> with Timer(): >>> # Fitting helper runtime is much less than building the point groups. >>> polygroup = np.empty((1000, 3), dtype='float64') >>> for it, (sub_x, sub_y) in enumerate(data_groups): >>> polygroup[it,:] = data_prep.fit_poly(sub_x, sub_y, 2) Wall time: 0.215859 s >>> with Timer(): >>> rbatch = data_prep.fit_polys(xdata, ydata, 2) Wall time: 0.21058 s /** * This function calculates the least-square regression of multiple sets of * point clouds to the corresponding polynomial functions of a given order. */ modmesh::SimpleArray<double> fit_polys ( modmesh::SimpleArray<double> const & xarr , modmesh::SimpleArray<double> const & yarr , size_t order ) { size_t xmin = std::floor(*std::min_element(xarr.begin(), xarr.end())); size_t xmax = std::ceil(*std::max_element(xarr.begin(), xarr.end())); size_t ninterval = xmax - xmin; modmesh::SimpleArray<double> lhs(std::vector<size_t>{ninterval, order+1}); std::fill(lhs.begin(), lhs.end(), 0); // sentinel. size_t start=0; for (size_t it=0; it<xmax; ++it) { // NOTE: We take advantage of the intrinsic features of the input data // to determine the grouping. This is ad hoc and hard to maintain. We // play this trick to demonstrate a hackish way of performing numerical // calculation. size_t stop; for (stop=start; stop<xarr.size(); ++stop) { if (xarr[stop]>=it+1) { break; } } // Use the single polynomial helper function. auto sub_lhs = fit_poly(xarr, yarr, start, stop, order); for (size_t jt=0; jt<order+1; ++jt) { lhs(it, jt) = sub_lhs[jt]; } start = stop; } return lhs; } prepare data and loop in Python: prepare data and loop in C++: C++ wins so much, but we lose fl exibility! // NOTE: We take advantage of the intrinsic features of the input data // to determine the grouping. This is ad hoc and hard to maintain. We // play this trick to demonstrate a hackish way of performing numerical // calculation.](https://image.slidesharecdn.com/writepythonforspeedpyconapac20231027-231028212349-d3988144/75/Write-Python-for-Speed-14-2048.jpg)

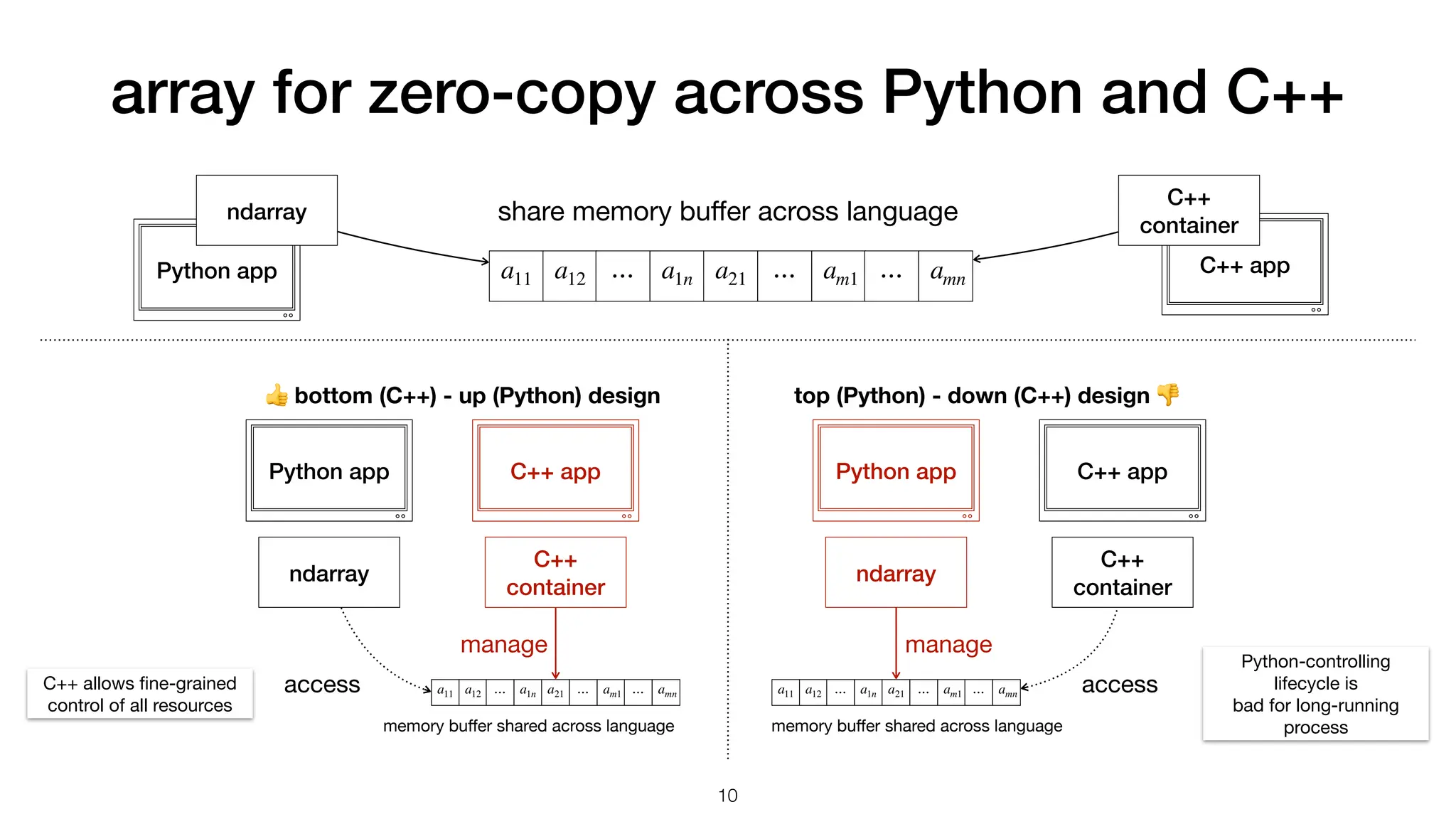
 -> decltype(auto) { return self.NAME(); }) (*this) // geometry arrays MM_DECL_ARRAY(ndcrd) MM_DECL_ARRAY(fccnd) MM_DECL_ARRAY(fcnml) MM_DECL_ARRAY(fcara) MM_DECL_ARRAY(clcnd) MM_DECL_ARRAY(clvol) // meta arrays MM_DECL_ARRAY(fctpn) MM_DECL_ARRAY(cltpn) MM_DECL_ARRAY(clgrp) // connectivity arrays MM_DECL_ARRAY(fcnds) MM_DECL_ARRAY(fccls) MM_DECL_ARRAY(clnds) MM_DECL_ARRAY(clfcs) MM_DECL_ARRAY(ednds); #undef MM_DECL_ARRAY # Construct the data object mh = modmesh.StaticMesh( ndim=3, nnode=4, nface=4, ncell=1) # Set the data mh.ndcrd.ndarray[:, :] = (0, 0, 0), (0, 1, 0), (-1, 1, 0), (0, 1, 1) mh.cltpn.ndarray[:] = modmesh.StaticMesh.TETRAHEDRON mh.clnds.ndarray[:, :5] = [(4, 0, 1, 2, 3)] # Calculate internal by the input data # to build up the object mh.build_interior() np.testing.assert_almost_equal( mh.fccnd, [[-0.3333333, 0.6666667, 0. ], [ 0. , 0.6666667, 0.3333333], [-0.3333333, 0.6666667, 0.3333333], [-0.3333333, 1. , 0.3333333]]) mesh shape information data arrays data arrays will be very large: gigabytes in memory use data in python C++ library pybind11 wrapper 16](https://image.slidesharecdn.com/writepythonforspeedpyconapac20231027-231028212349-d3988144/75/Write-Python-for-Speed-16-2048.jpg)
![test in Python def test_2d_trivial_triangles(self): mh = modmesh.StaticMesh(ndim=2, nnode=4, nface=0, ncell=3) mh.ndcrd.ndarray[:, :] = (0, 0), (-1, -1), (1, -1), (0, 1) mh.cltpn.ndarray[:] = modmesh.StaticMesh.TRIANGLE mh.clnds.ndarray[:, :4] = (3, 0, 1, 2), (3, 0, 2, 3), (3, 0, 3, 1) self._check_shape(mh, ndim=2, nnode=4, nface=0, ncell=3, nbound=0, ngstnode=0, ngstface=0, ngstcell=0, nedge=0) # Test build interior data. mh.build_interior(_do_metric=False, _build_edge=False) self._check_shape(mh, ndim=2, nnode=4, nface=6, ncell=3, nbound=0, ngstnode=0, ngstface=0, ngstcell=0, nedge=0) mh.build_interior() # _do_metric=True, _build_edge=True self._check_shape(mh, ndim=2, nnode=4, nface=6, ncell=3, nbound=0, ngstnode=0, ngstface=0, ngstcell=0, nedge=6) np.testing.assert_almost_equal( mh.fccnd, [[-0.5, -0.5], [0.0, -1.0], [0.5, -0.5], [0.5, 0.0], [0.0, 0.5], [-0.5, 0.0]]) np.testing.assert_almost_equal( mh.fcnml, [[-0.7071068, 0.7071068], [0.0, -1.0], [0.7071068, 0.7071068], [0.8944272, 0.4472136], [-1.0, -0.0], [-0.8944272, 0.4472136]]) np.testing.assert_almost_equal( mh.fcara, [1.4142136, 2.0, 1.4142136, 2.236068, 1.0, 2.236068]) np.testing.assert_almost_equal( mh.clcnd, [[0.0, -0.6666667], [0.3333333, 0.0], [-0.3333333, 0.0]]) np.testing.assert_almost_equal( mh.clvol, [1.0, 0.5, 0.5]) 17 namespace py = pybind11; (*this) // shape data .def_property_readonly("ndim", &wrapped_type::ndim) .def_property_readonly("nnode", &wrapped_type::nnode) .def_property_readonly("nface", &wrapped_type::nface) .def_property_readonly("ncell", &wrapped_type::ncell) .def_property_readonly("nbound", &wrapped_type::nbound) .def_property_readonly("ngstnode", &wrapped_type::ngstnode) .def_property_readonly("ngstface", &wrapped_type::ngstface) .def_property_readonly("ngstcell", &wrapped_type::ngstcell) #define MM_DECL_ARRAY(NAME) .expose_SimpleArray( #NAME, [](wrapped_type & self) -> decltype(auto){ return self.NAME(); }) (*this) // geometry arrays MM_DECL_ARRAY(ndcrd) MM_DECL_ARRAY(fccnd) MM_DECL_ARRAY(fcnml) MM_DECL_ARRAY(fcara) MM_DECL_ARRAY(clcnd) MM_DECL_ARRAY(clvol) // meta arrays MM_DECL_ARRAY(fctpn) MM_DECL_ARRAY(cltpn) MM_DECL_ARRAY(clgrp) // connectivity arrays MM_DECL_ARRAY(fcnds) MM_DECL_ARRAY(fccls) MM_DECL_ARRAY(clnds) MM_DECL_ARRAY(clfcs) MM_DECL_ARRAY(ednds); #undef MM_DECL_ARRAY wrapping to Python enables fast testing development may be done as writing tests! # Construct the data object mh = modmesh.StaticMesh( ndim=3, nnode=4, nface=4, ncell=1) # Set the data mh.ndcrd.ndarray[:, :] = (0, 0, 0), (0, 1, 0), (-1, 1, 0), (0, 1, 1) mh.cltpn.ndarray[:] = modmesh.StaticMesh.TETRAHEDRON mh.clnds.ndarray[:, :5] = [(4, 0, 1, 2, 3)] # Calculate internal by the input data # to build up the object mh.build_interior() np.testing.assert_almost_equal( mh.fccnd, [[-0.3333333, 0.6666667, 0. ], [ 0. , 0.6666667, 0.3333333], [-0.3333333, 0.6666667, 0.3333333], [-0.3333333, 1. , 0.3333333]])](https://image.slidesharecdn.com/writepythonforspeedpyconapac20231027-231028212349-d3988144/75/Write-Python-for-Speed-17-2048.jpg)
![develop SimpleArray in C++ SimpleArray std::vector SimpleArray is fi xed size 👍 • only allocate memory on construction std::vector is variable size 👎 • bu ff er may be invalidated • implicit memory allocation (reallocation) multi-dimensional access 👍 operator() one-dimensional access 👎 operator[] 19 C++ container ndarray manage access a11 a12 ⋯ a1n a21 ⋯ am1 ⋯ amn memory bu ff er make it yourself get it free from STL](https://image.slidesharecdn.com/writepythonforspeedpyconapac20231027-231028212349-d3988144/75/Write-Python-for-Speed-19-2048.jpg)