Understanding Autoencoder (Deep Learning Book, Chapter 14)

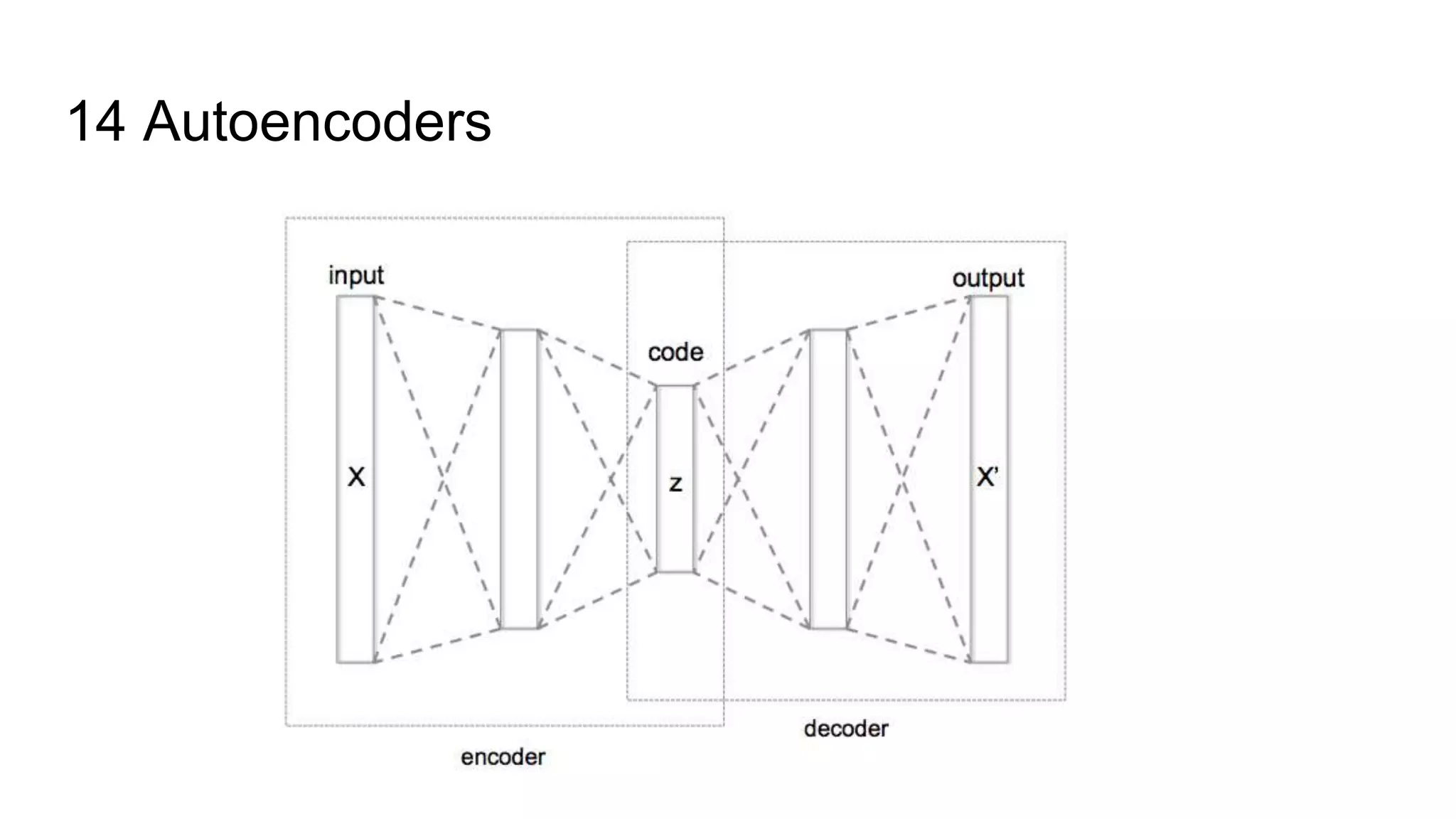
Deep Learning Chapter 14 - Auto Encoders Ashish Kumar Twitter: @ashish_fagna LinkedIn: https://www.linkedin.com/in/ashkmr1

Using presentation by Ike Okonkwo - @ikeondata

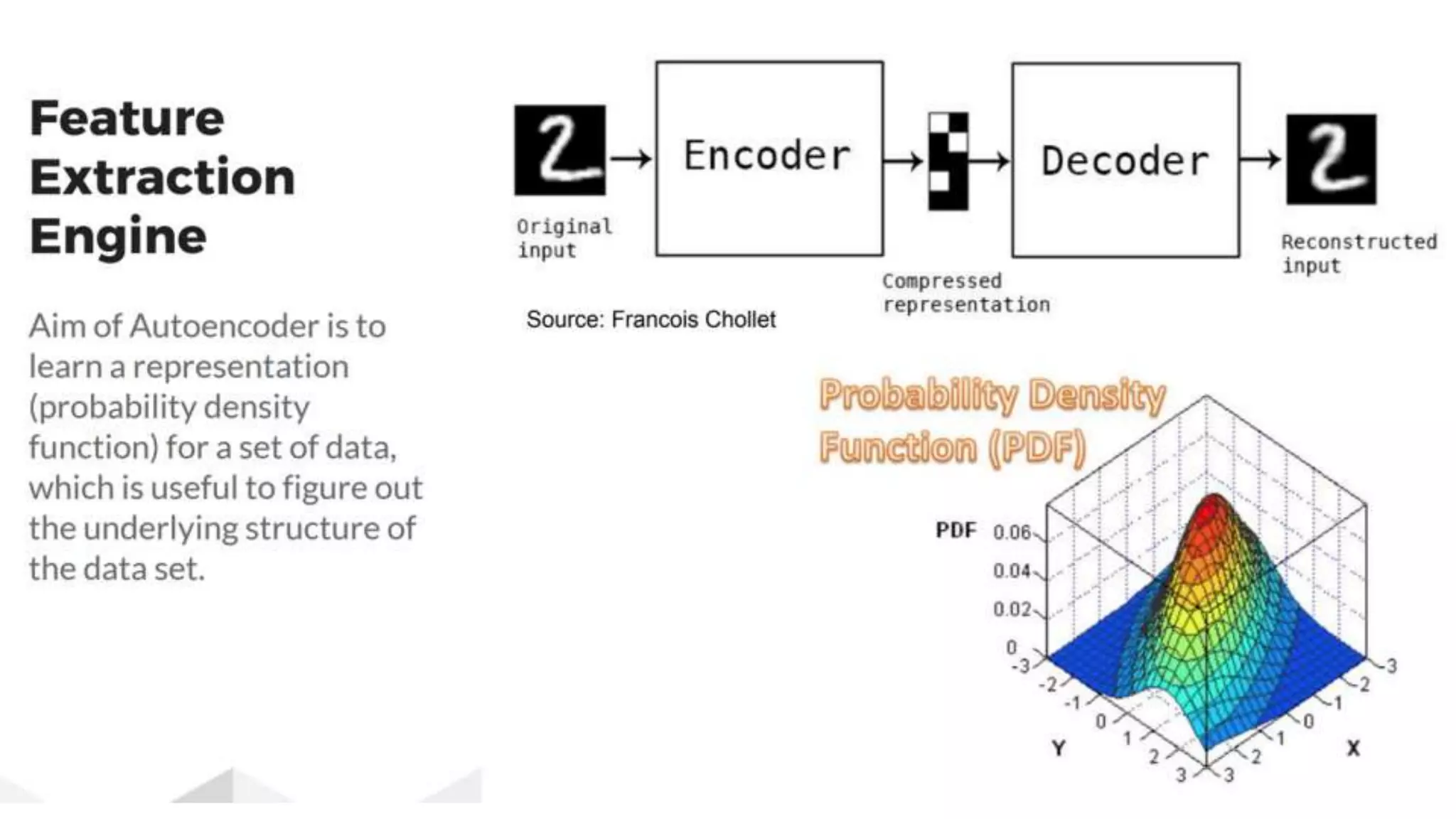
14 Autoencoders AE is neural network that is trained to attempt to copy its input to its output It has a hidden layer [h] that encodes the input [x]. H = f(wx + bias) and also a decoder AE are restricted in ways that allow them to copy the inputs only approximately and so it is forced to prioritize which aspects of the input should be copied which can be great for feature extraction AE traditionally used for dimensionality reduction or feature learning AE can be considered a special case of feedforward networks and can be trained with similar techniques - - MiniBatch GD. They’re also trained by recirculation

14.1 Undercomplete Autoencoders Undercomplete AE is one in which the dimension of Hidden layer [h] is less than the dimensions of Input layer [x]. We are typically not interested in the AE output but the hidden layer [h] [h] is typically constrained to smaller dimension than [x] which is called Undercomplete. This forces an AE to capture only the salient features If the AE is allowed too much capacity, then it just learn to copy the inputs with extracting useful information about the distribution of the data

14.2 Regularized Autoencoders AE with hidden layers with dimensions equal to or greater than the input are called Overcomplete. Regularized autoencoders provide the ability train a architecture of autoencoder successfully, choosing the code dimension and the capacity of the encoder and decoder based on the complexity of distribution to be modeled. Rather than limiting the model capacity by keeping the encoder and decoder shallow and the code size small, regularized autoencoders use a loss function that encourages the model to have other properties besides the ability to copy its input to its output. These other properties include sparsity of the representation, smallness of the derivative of the representation, and robustness to noise or to missing inputs. A regularized autoencoder can be nonlinear and overcomplete but still learn something useful about the data distribution, even if the model capacity is great enough to learn a identity function.

14.2.1 Sparse Autoencoders We can also think of the penalty as a regularizer term added to a feedforward network whose main task is to copy inputs to outputs and perform some supervised tasks Generative models are used in machine learning for either modeling data directly (i.e., modeling observations drawn from a probability density function), or as an intermediate step to forming a conditional probability density function. Another way to think about sparse AE framework is approximating maximum likelihood of a generative model* with latent variables

14.2.2 Denoising Autoencoders A denoising AE (DAE) is an AE that receives a corrupted input [x^hat ] and then try to reconstruct the original inputs We use a corruption process C ( x^hat | x) which represents a conditional distribution over the corrupted samples x^hat given the original input [x]. The AE then learn a reconstruction distribution p (x | x^hat) for training pairs (x | x^hat) Typically, we can perform gradient based optimization and as long as the encoder is deterministic, the denoising AE is a feed forward network and can be trained with the same techniques as other similar networks Denoising AE shows how useful byproducts emerge by just reducing the reconstruction error. They also show how high capacity models may be used as autoencoders and still learn useful features without learning the identity function

14.2.3 Regularizing by Penalizing Derivatives Another strategy for regularizing autoencoders is to use a penalty gamma, as in sparse autoencoders but with a different form . This forces the model to be invariant to slight changes in the input vector [x]. Since this is only applies to training examples, it forces the AE to capture useful information about the training distribution This is called a contractive AE

14.3 Representational Power, Layer Size and Depth AE are usually trained using single layer encoders and decoders but we can also make the hidden layer [h] deep Since the encoder and decoder are both feed forward networks, they both benefit from deep architectures. The major advantage of deep architectures for feed forward neural networks is that they can represent an approximation of any function to an arbitrary degree of accuracy A deep encoder can also approximate any mapping from the input [x] to hidden layer [h] given enough hidden units. Depth exponentially reduces training cost and amount of training data needed and achieves better compression.

14.4 Stochastic Encoders and Decoders AEs are essentially feed forward neural networks For a stochastic AE, the encoder and decoder are not just simple functions but sampled from a distribution. p(h | x) for the encoder and p (x | h) for the decoder

14.5.1 Estimating the Score Score matching is an alternative to maximum likelihood and provides an alternative to probability distribution by encouraging the model to have the same score as the data distribution at every training point in [x] For AEs, learning the gradient field is one way of learning the structure of p(data) Denoising training of a specific kind of AE (sigmoid hidden units , linear reconstruction units) is equivalent to training an RBM (restricted Boltzmann machine , basic neural network) with Gaussian visible units .

14.5.1 Estimating the Score Score matching applied to RBMs yields a cost function that is identical to the reconstruction error combined with a regularization term similar to the contractive penalty of the CAE

14.5.2 Historical Perspective The idea of using MLP (multilayer perceptron) to denoise goes back to the 80’s A multilayer perceptron (MLP) is a class of feedforward artificial neural network. An MLP consists of at least three layers of nodes. Except for the input nodes, each node is a neuron that uses a nonlinear activation function. MLP utilizes a supervised learning technique called backpropagation for training Denoising encoders are in some MLP trained to denoise. But the term “Denoising AE” refers to a model that learn not only to denoise its inputs but also learn a good internal representation (useful features) The learned representation can be used to pretrain a deeper unsupervised / supervised network The motivation for Denoising AE was to allow the learning of a very high capacity encoder while preventing the encoder / decoder from learning an identity function

14.6 Learning Manifolds with Autoencoders Most learning algorithms including AE exploit the idea that data concentrates around a low dimension manifold or learning surface. AEs aims to learn the structure of this manifold All AE training procedure involve a compromise between two forces - Learning a representation [h] of a training example [x] such that [x] can be reconstructed via [h] through a decoder - Satisfying the constraint of regularization penalty. This is usually an architectural constraint that limits the capacity of the AE These technique prefer methods that are less sensitive to the input The two forces force the hidden representation to capture information about the structure of the data generating distribution

14.6 Learning Manifolds with Autoencoders The AE can afford to represent only the variations needed for reconstruction The manifold captures a local coordinate system if the generating distribution concentrates near a low dimensional manifold. Hence the encoder learns a mapping from [x] to representative space that is only sensitive to changes along the manifold and not changes orthogonal to the manifold. The AE recovers the manifold structure if the reconstruction function is insensitive to the perturbation in the input -see example Most of the ML research of learning nonlinear manifolds has focused on non parametric methods based on the nearest-neighbour graph

14.6 Learning Manifolds with Autoencoders - Discuss locally linear Gaussian patches AI problems can usually have very complicated structures or manifolds that can be difficult to capture from local interpolation

14.7 Contractive Autoencoders The contractive AE introduces a regularizer on the [h] , the hidden layer There is a connection between Denoising AE and Contractive AE. In the limit of small Gaussian input noise the denoising reconstruction error is equivalent to the contractive penalty on the reconstruction function. That is Denoising AEs make the reconstruction function resist small but finite perturbations of the input while contractive AEs make the feature extraction function resist small perturbations to the input The CAE maps a neighborhood of input points to smaller neighborhood of output points,hence contracting the input.

14.7 Contractive Autoencoders Regularized AE learn manifolds by balancing opposing forces. For CAEs these are reconstruction error and the contractive penalty. Reconstruction error alone would allow the CAE to learn an identity function and contractive penalty alone will allow the CAE to learn features that are constant wrt [x] A good strategy to train AEs is to train a series of single layer AEs each trained to reconstruct the previous AEs hidden layer. The composition of these AEs forms a deep AE. Because each layer was separately trained to be contractive , the deep AE is contractive as well which is different from training the full AE with penalty The contractive penalty can also obtain useless results unless corrective action is taken

14.8 Predictive Sparse Decomposition PSD is hybrid model of sparse coding and parametric AE. A parametric AE is trained to predict the output of iterative inference and have been applied to unsupervised feature learning for object recognition in images/ video and audio PSD consists an encoder / decoder which are both parametric. The training algorithm alternates between minimizing wrt [h] and minimizing wrt to the model parameters PSD regularizes the decoder to use parameters for f(x) can infer good values For PSD the parametric encoder [f] is used to compute the learned features when the model is deployed. Evaluating [f] is computationally inexpensive vs inferring [h] via gradient descent. PSDs can be stacked and used to initialize a deep network

14.9 Applications of Autoencoders AE have successfully applied to recommendation systems, dimensionality reduction and information retrieval. The learned representation in [h] were qualitatively easier to interpret and relate to the underlying categories, with those categories manifesting as clusters Lower dimensional representation can improve performance on classification tasks since they consume less memory cheaper to run One task that benefits greatly from dimensionality reduction is information retrieval since search can become extremely efficient in low dimension spaces.

14.9 Applications of Autoencoders We can use DR (dimensional reduction) to produce [h] that is low dimension and binary and then store the entries in database mapping binary code vectors to entries (lookup) Searching of the hash table is very efficient. This approach to IR (Information Retrieval) via DM (data mining) and binarization is called semantic hashing. To produce binary codes for semantic hashing, we typically use an encoder with sigmoids (as activation function) on the final layer.

Thanks Special thanks to Laura Montoya and Accel.ai ! Ashish Kumar ashish.fagna@gmail.com Twitter: @ashish_fagna LinkedIn: https://www.linkedin.com/in/ashkmr1

Understanding Autoencoder (Deep Learning Book, Chapter 14)

In this document

More Related Content

What's hot

Similar to Understanding Autoencoder (Deep Learning Book, Chapter 14)

More from Entrepreneur / Startup

Recently uploaded

Understanding Autoencoder (Deep Learning Book, Chapter 14)