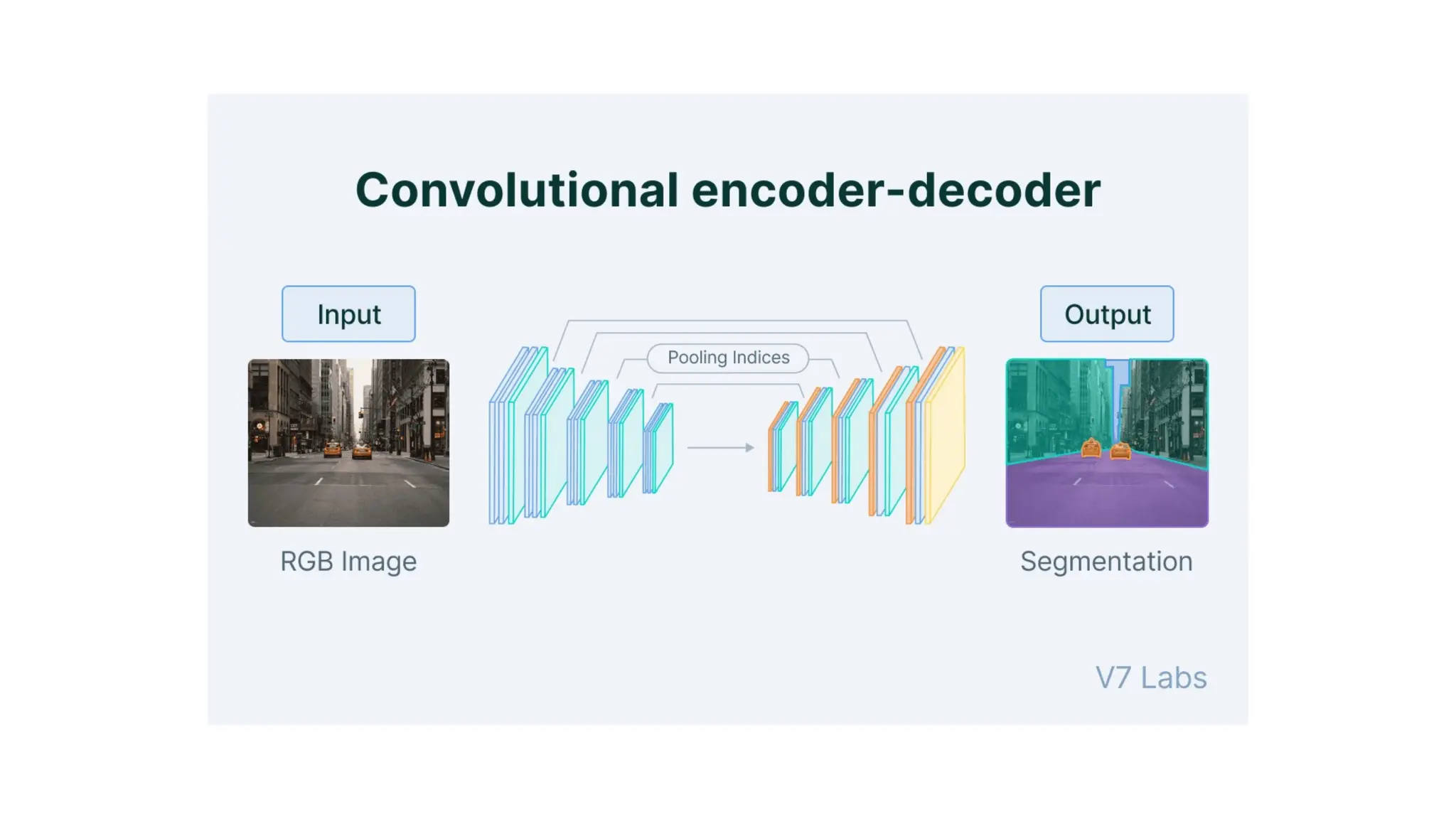
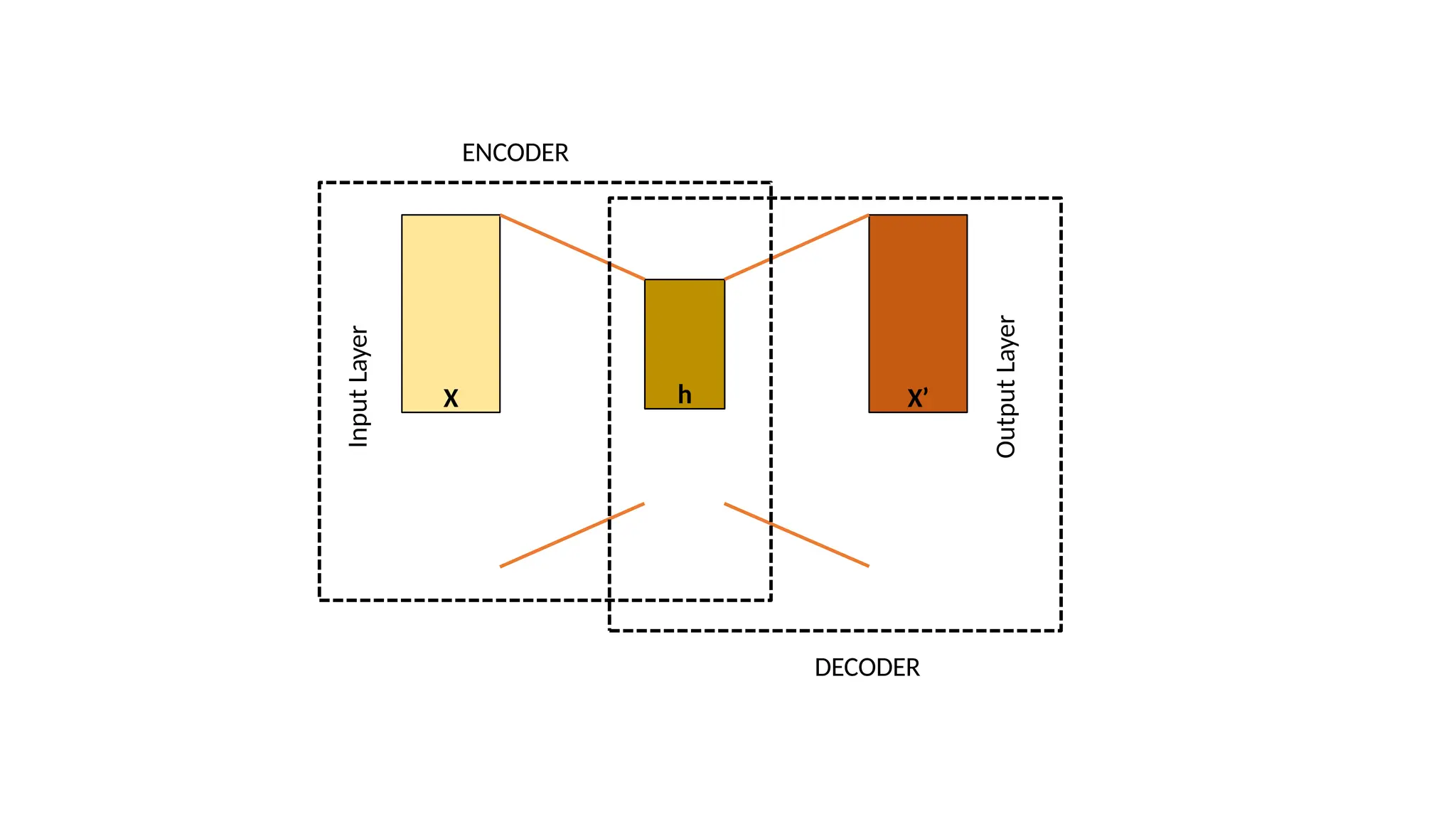
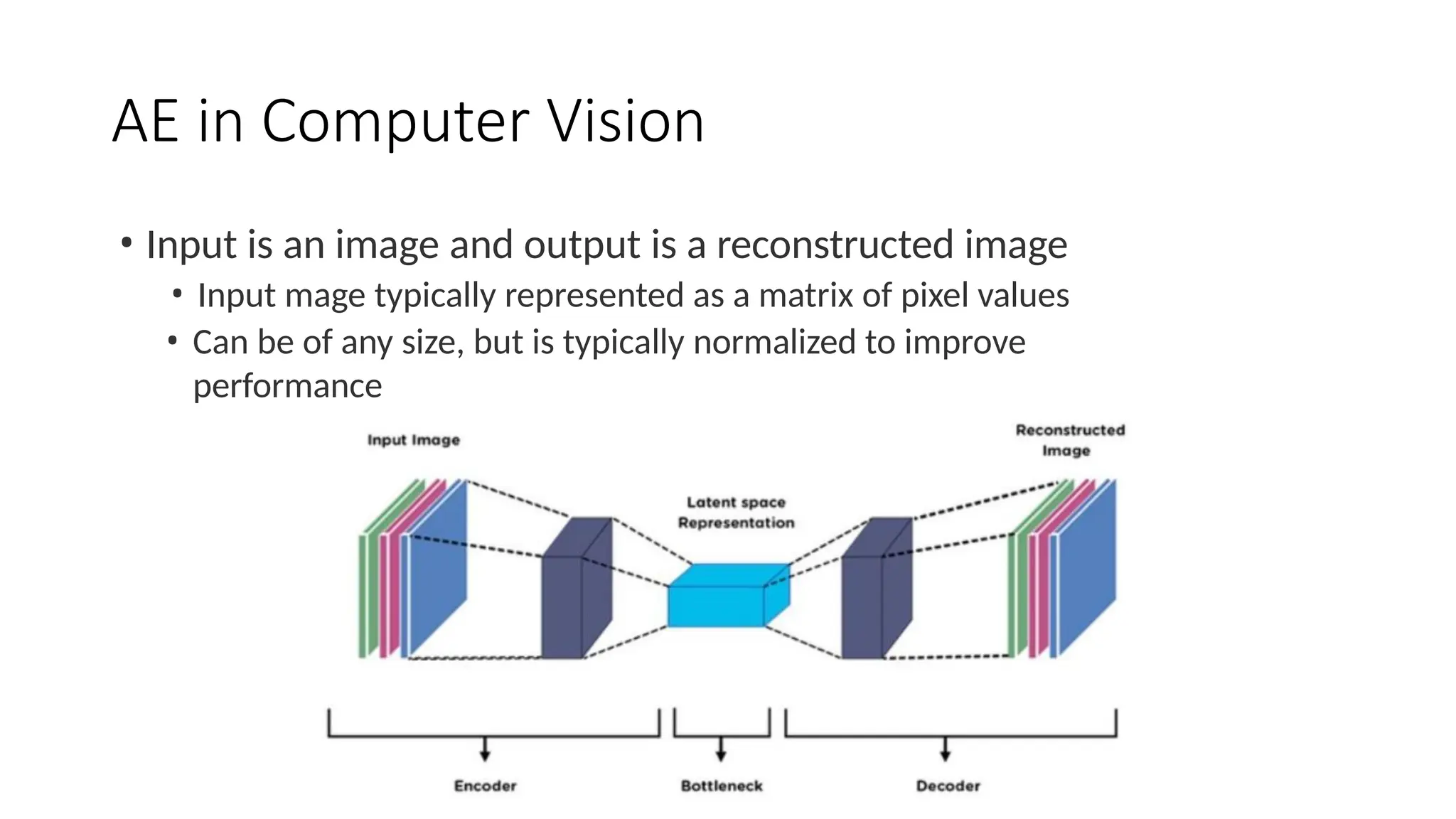
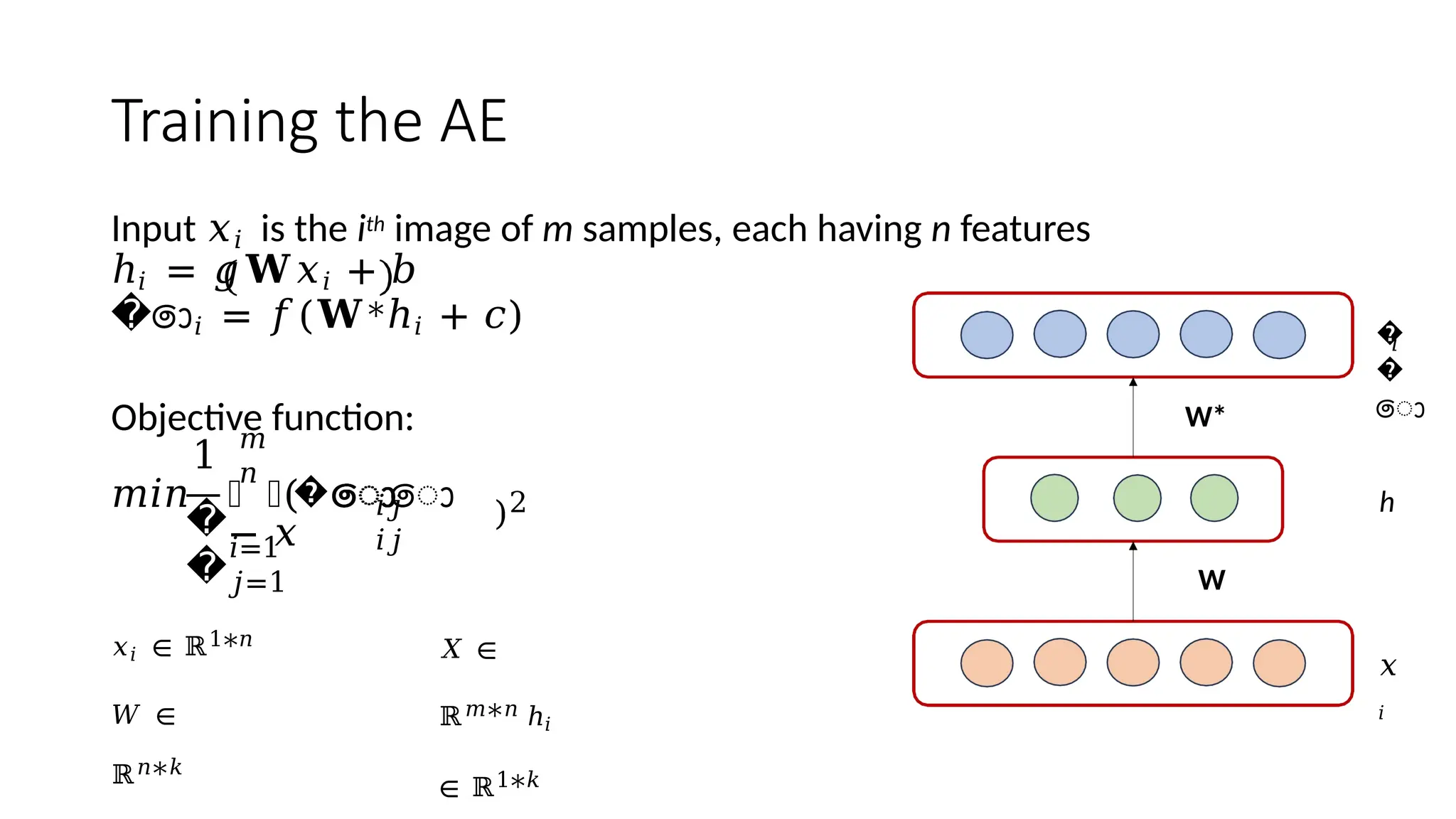
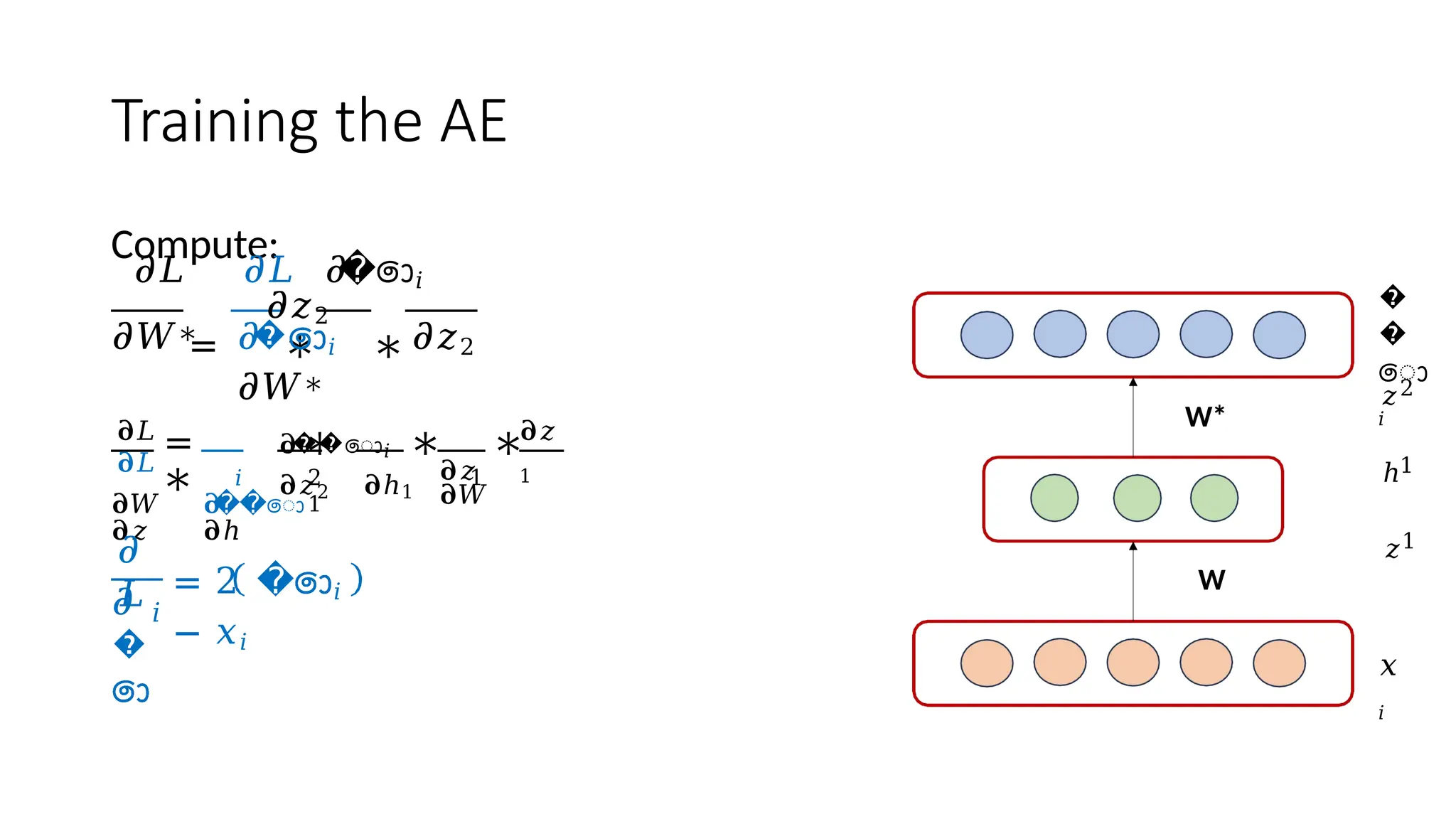
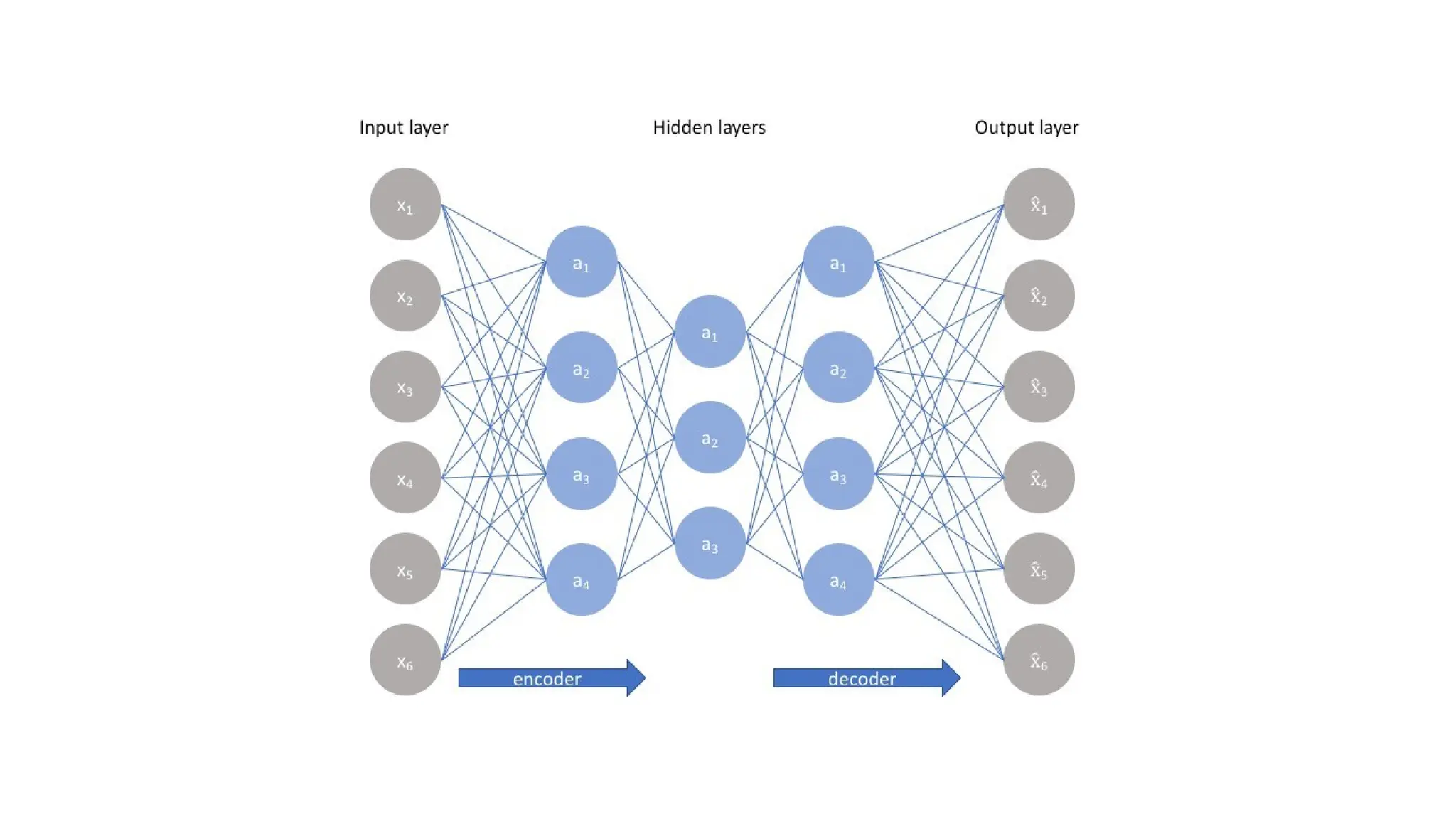
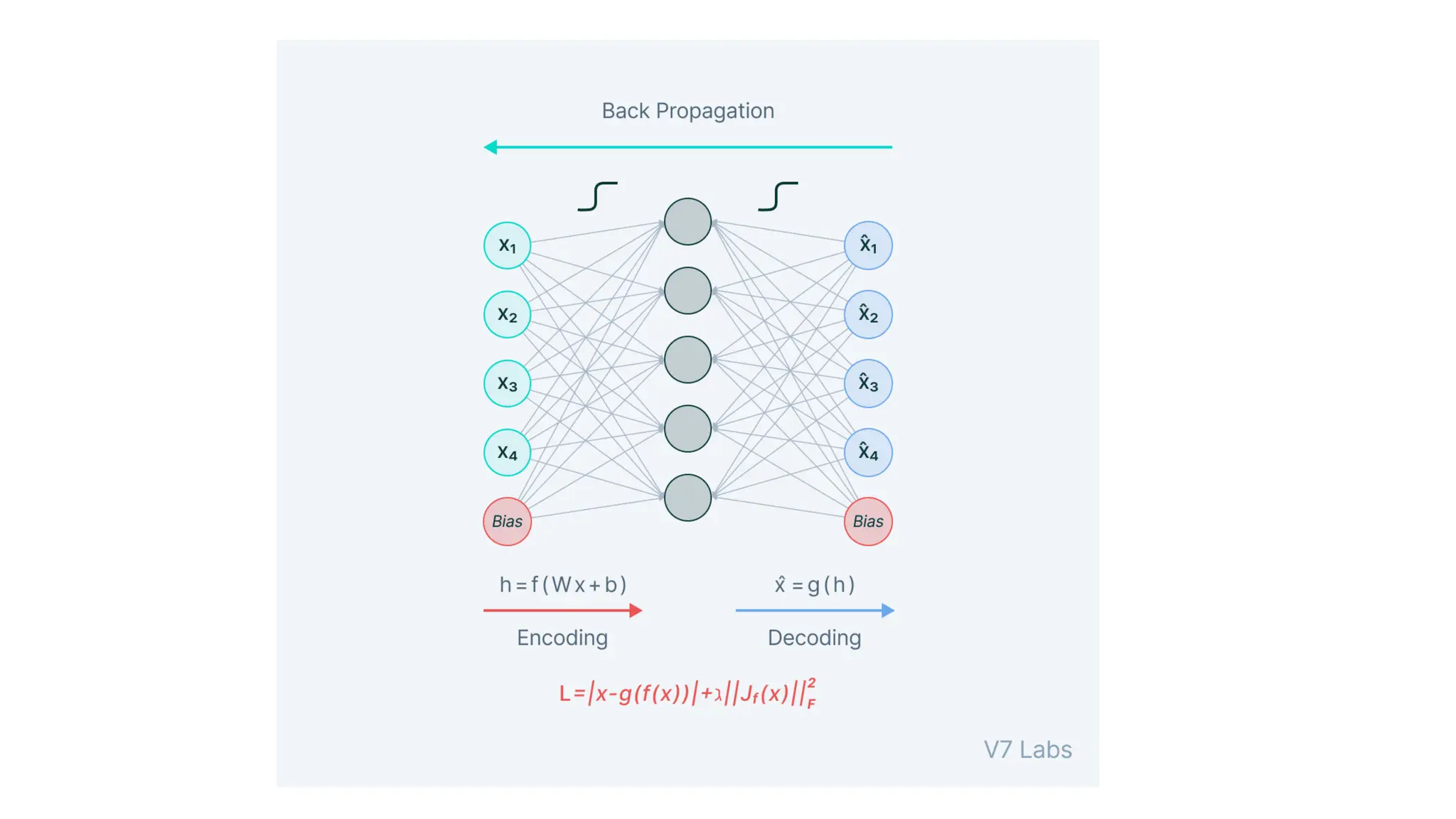
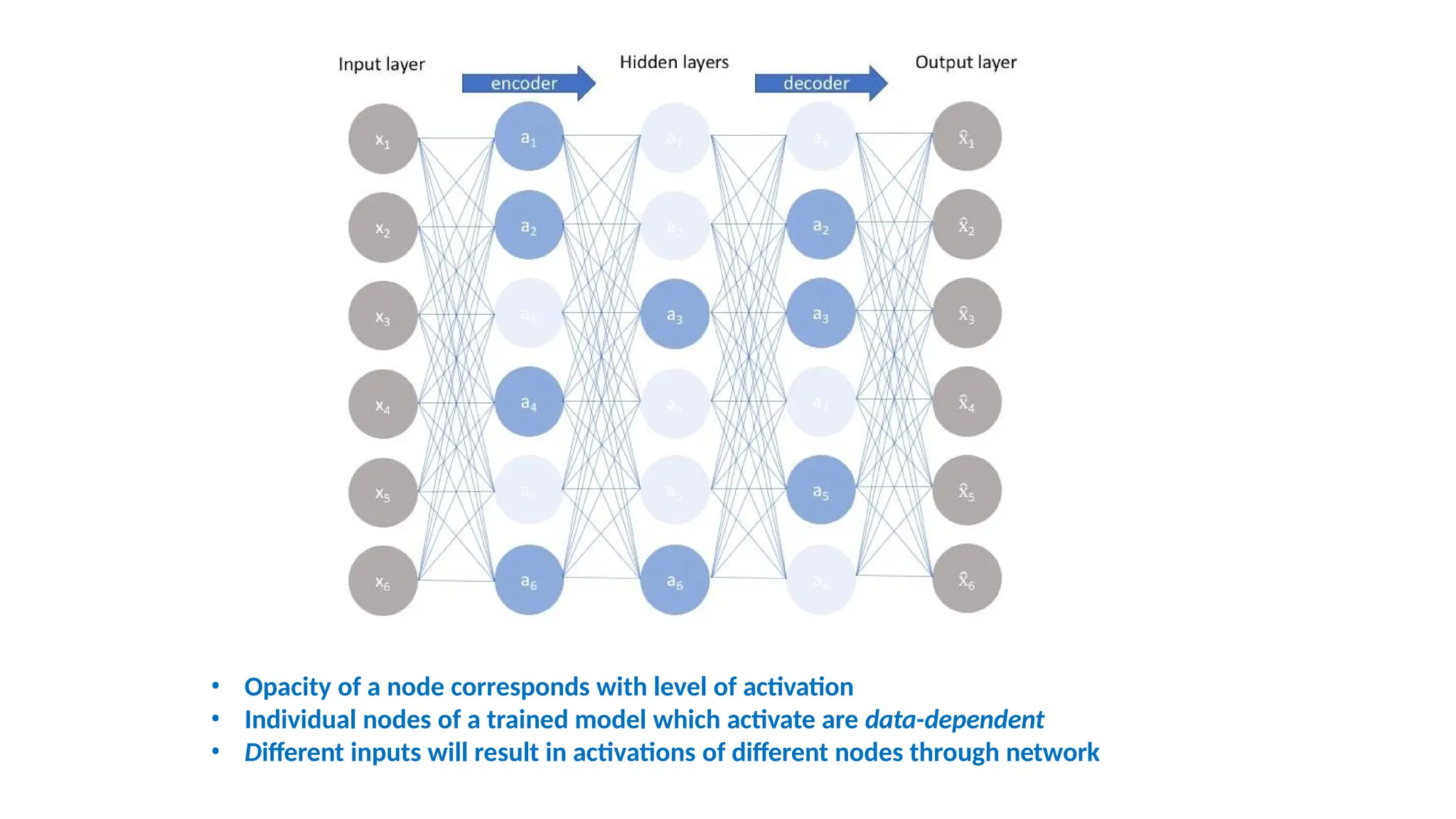
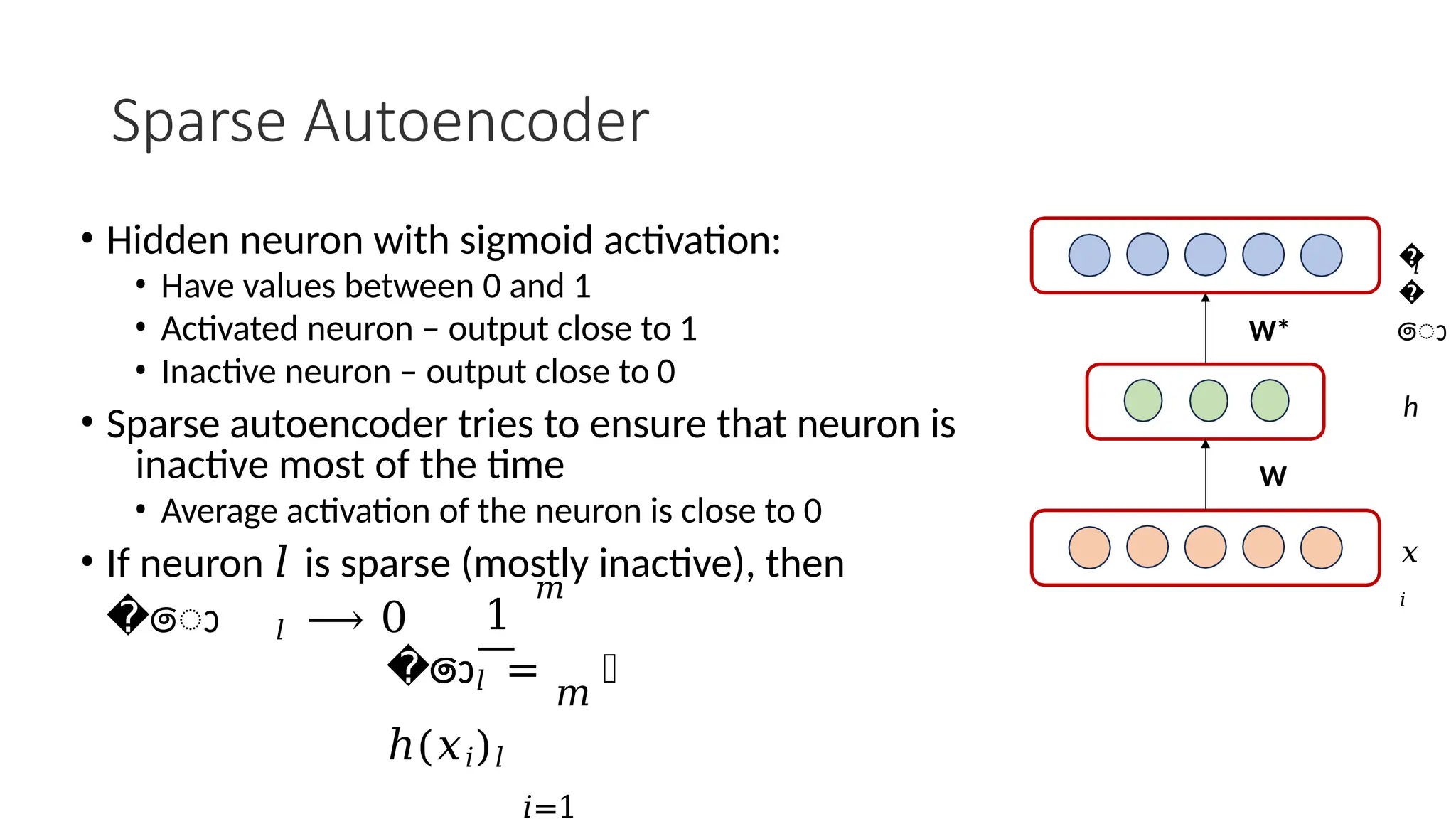
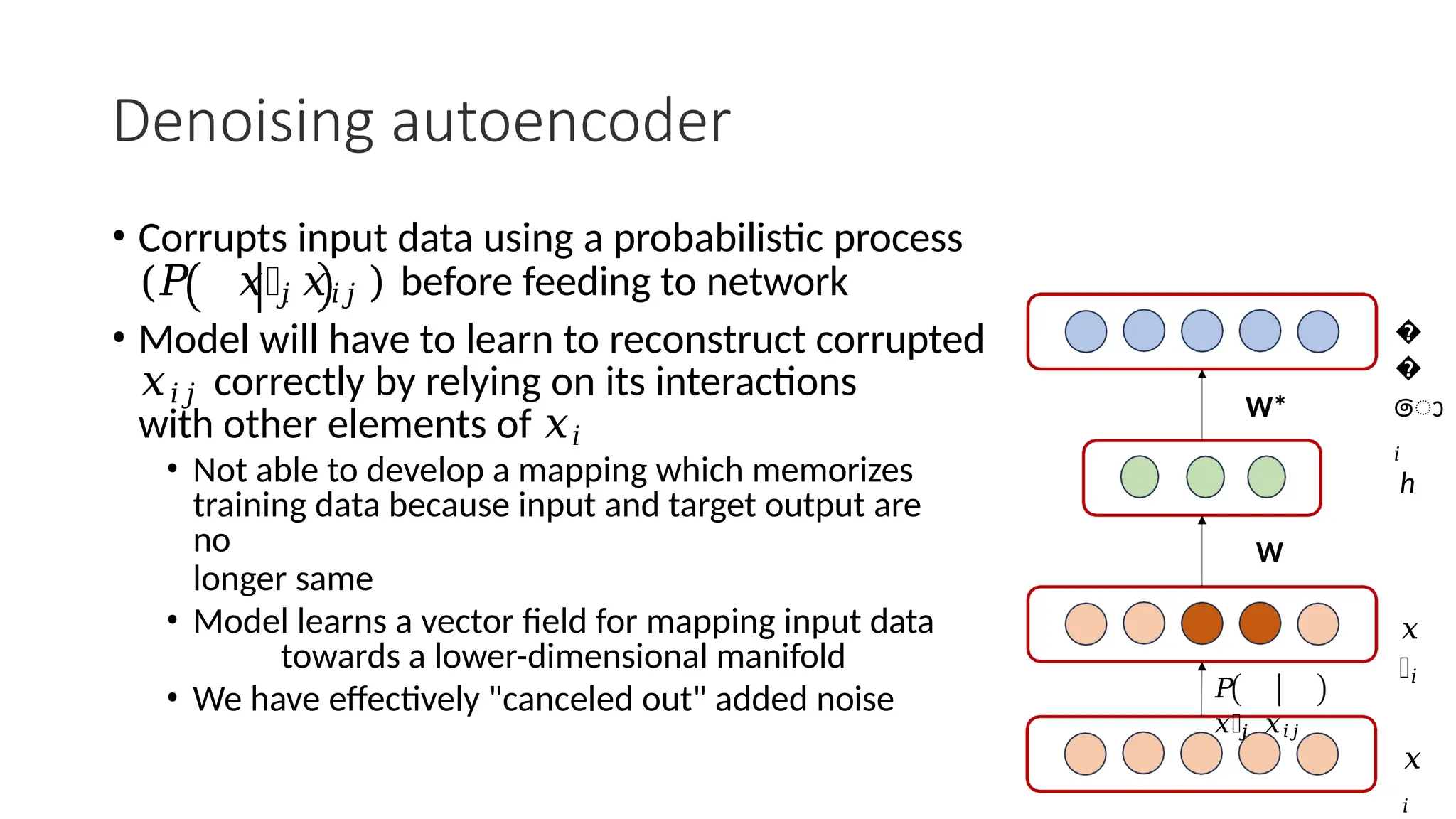
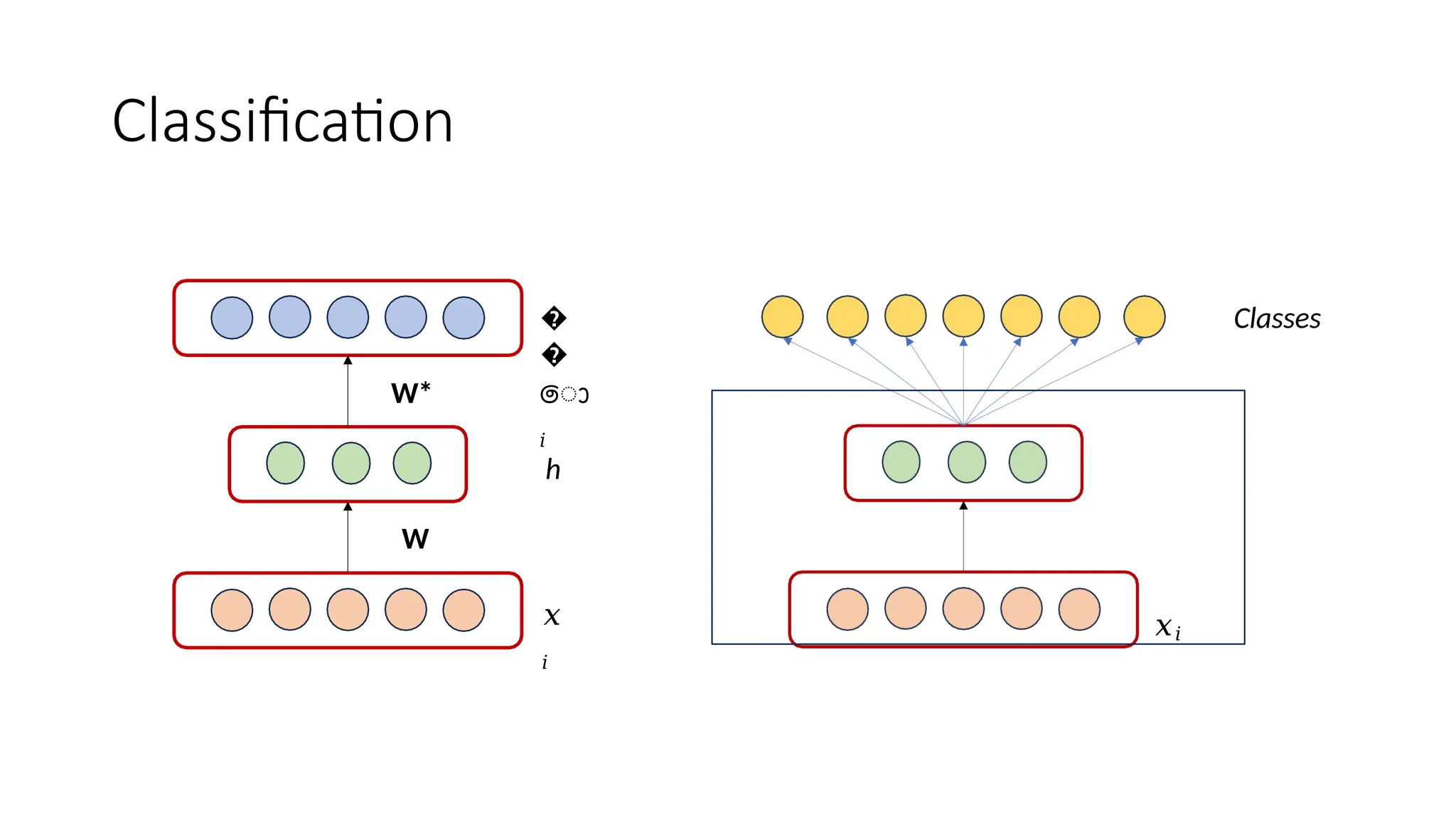
The encoder-decoder architecture is a fundamental framework in deep learning, commonly used in tasks such as sequence-to-sequence modeling, machine translation, and image generation. The encoder processes the input data into a compact representation, capturing essential features, while the decoder reconstructs the output from this encoded representation. This structure enables efficient learning of complex transformations and is widely applied in natural language processing (NLP), computer vision, and generative models.