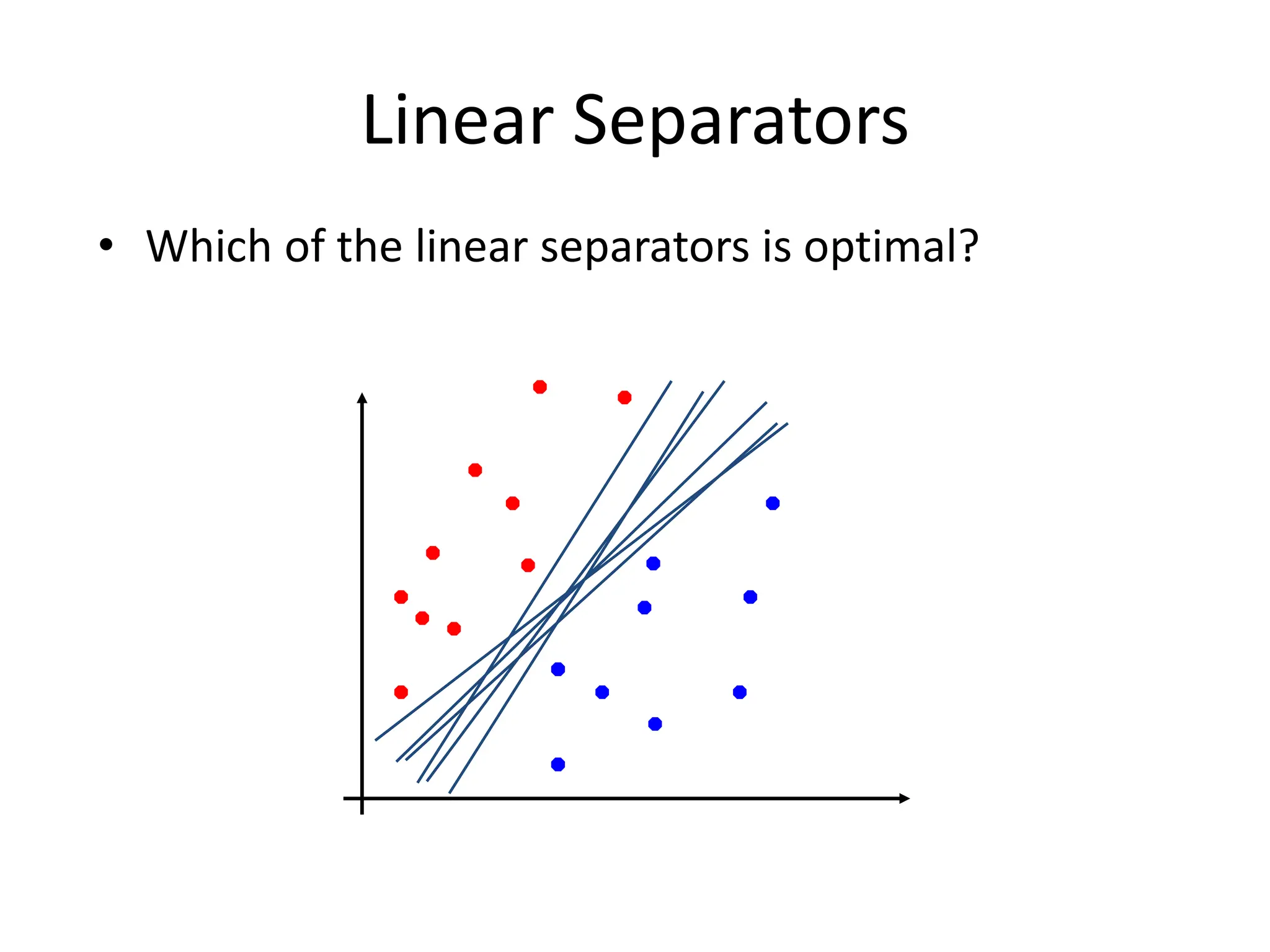
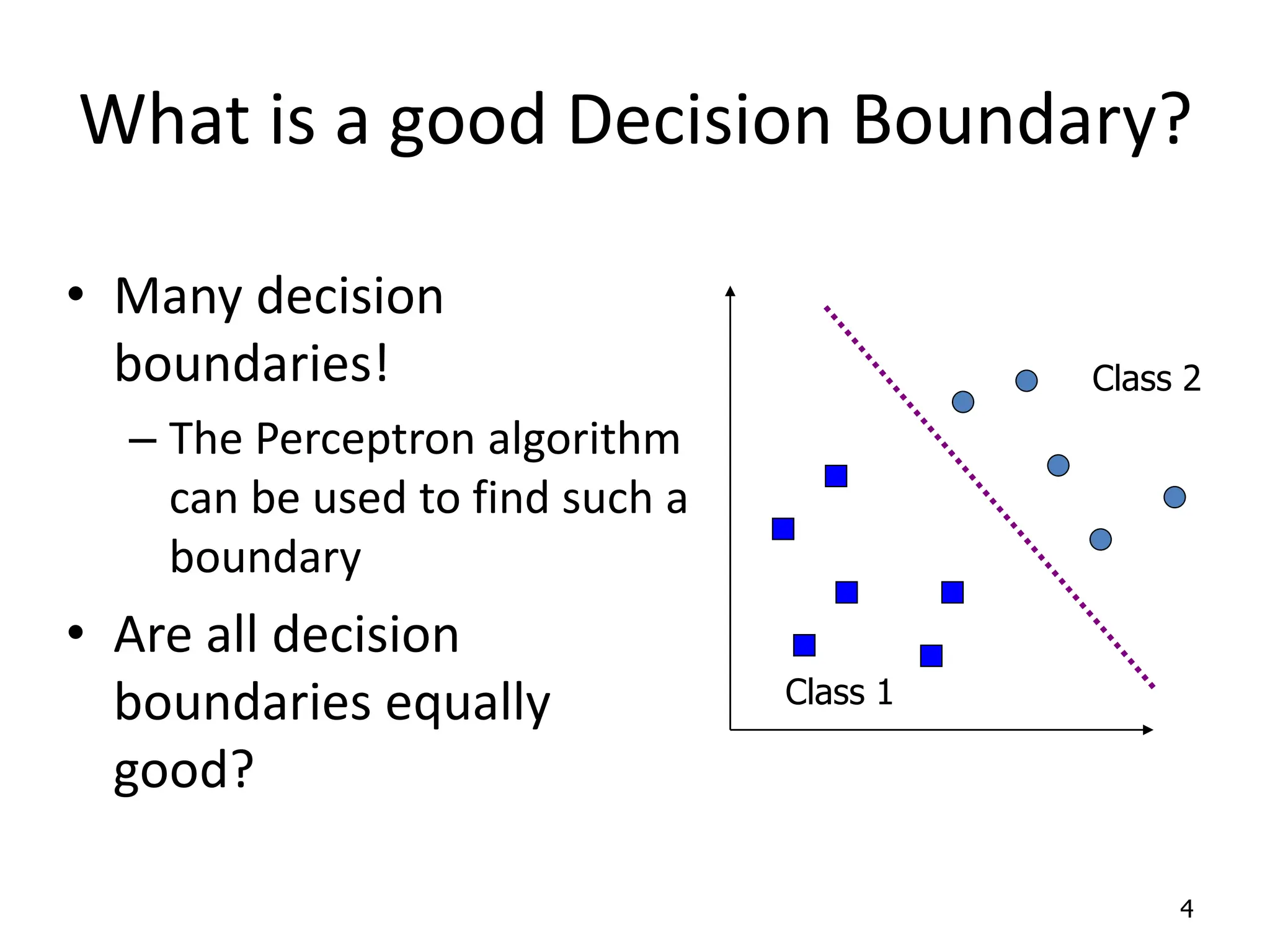
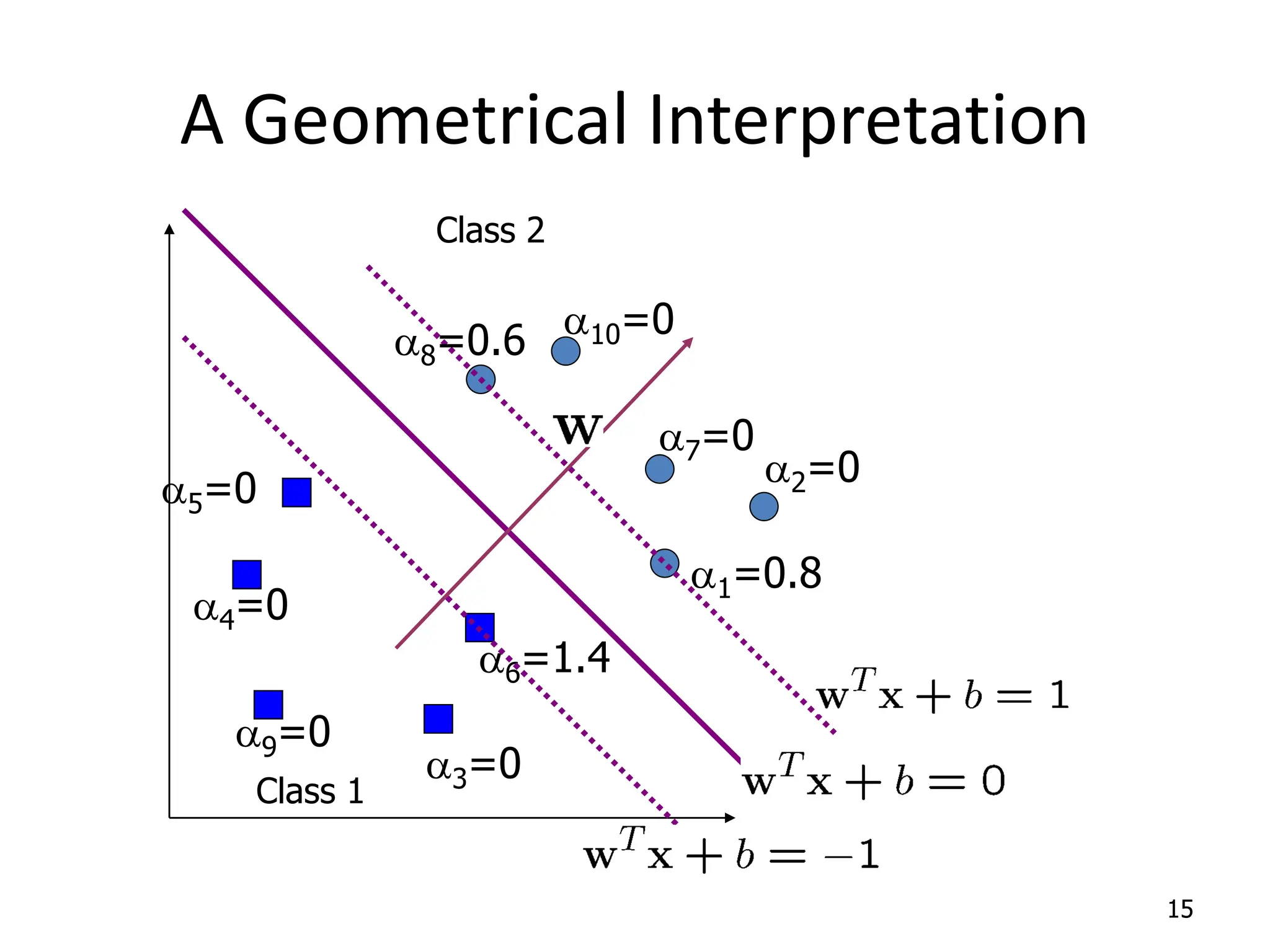
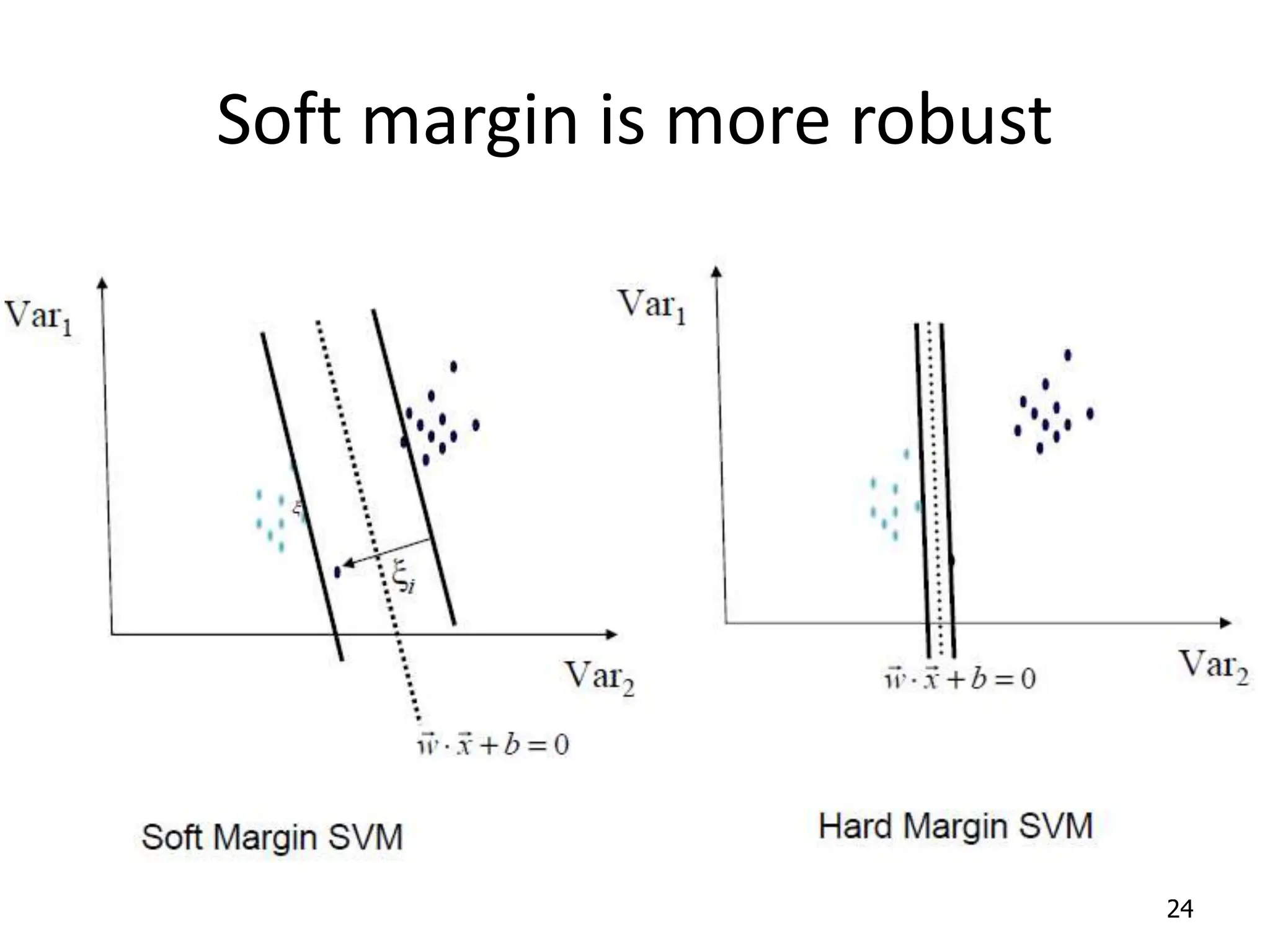
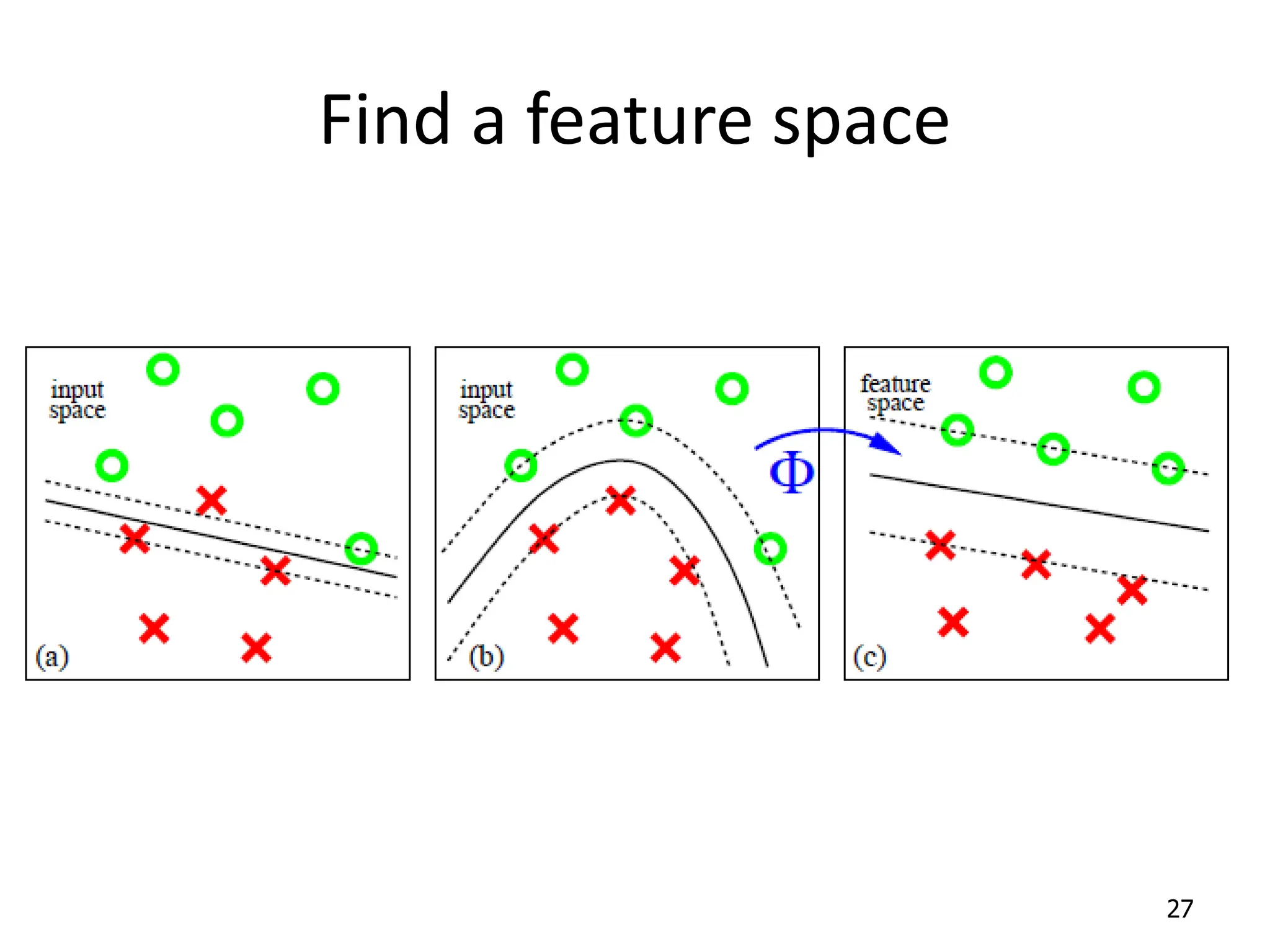
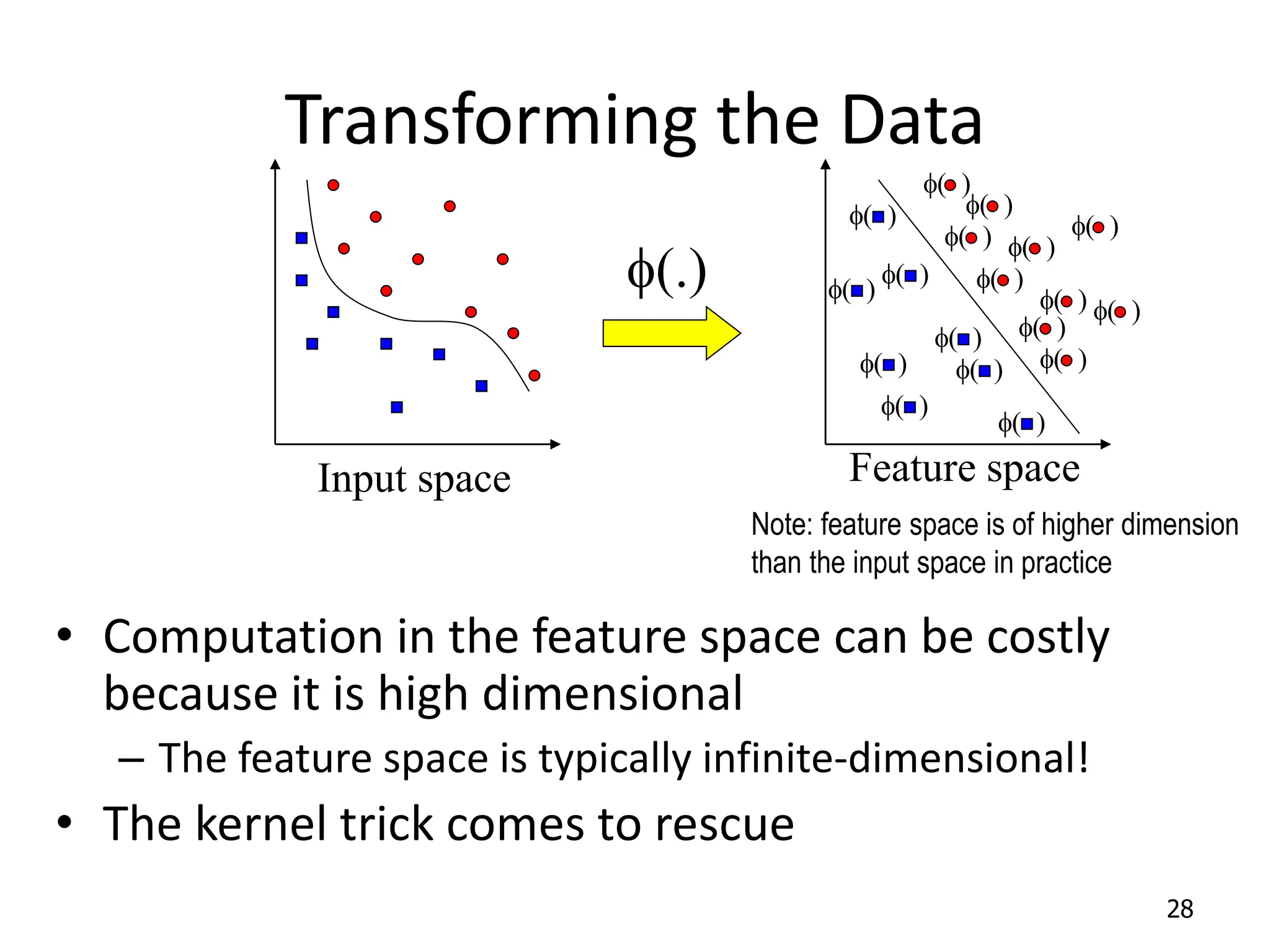
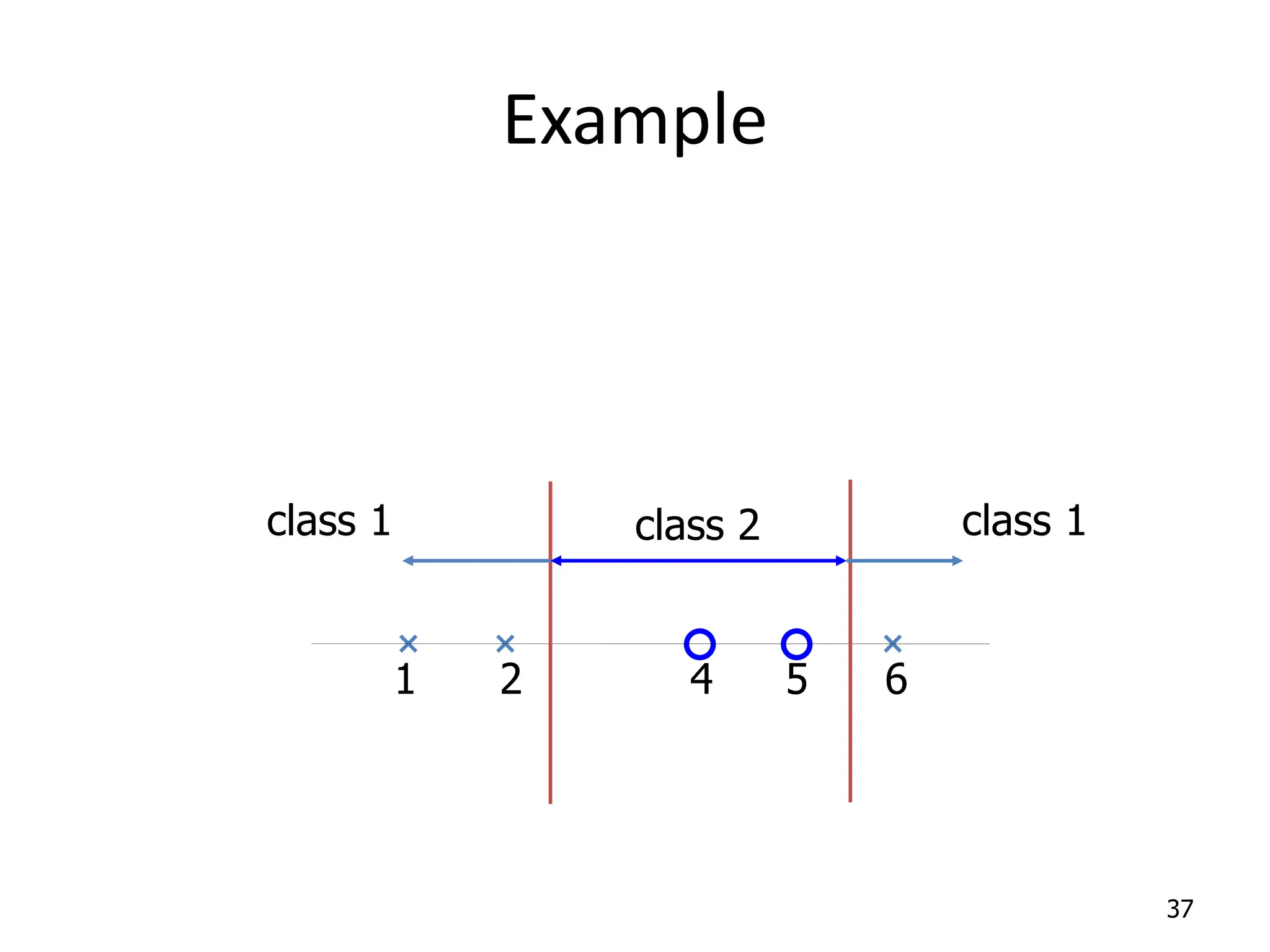
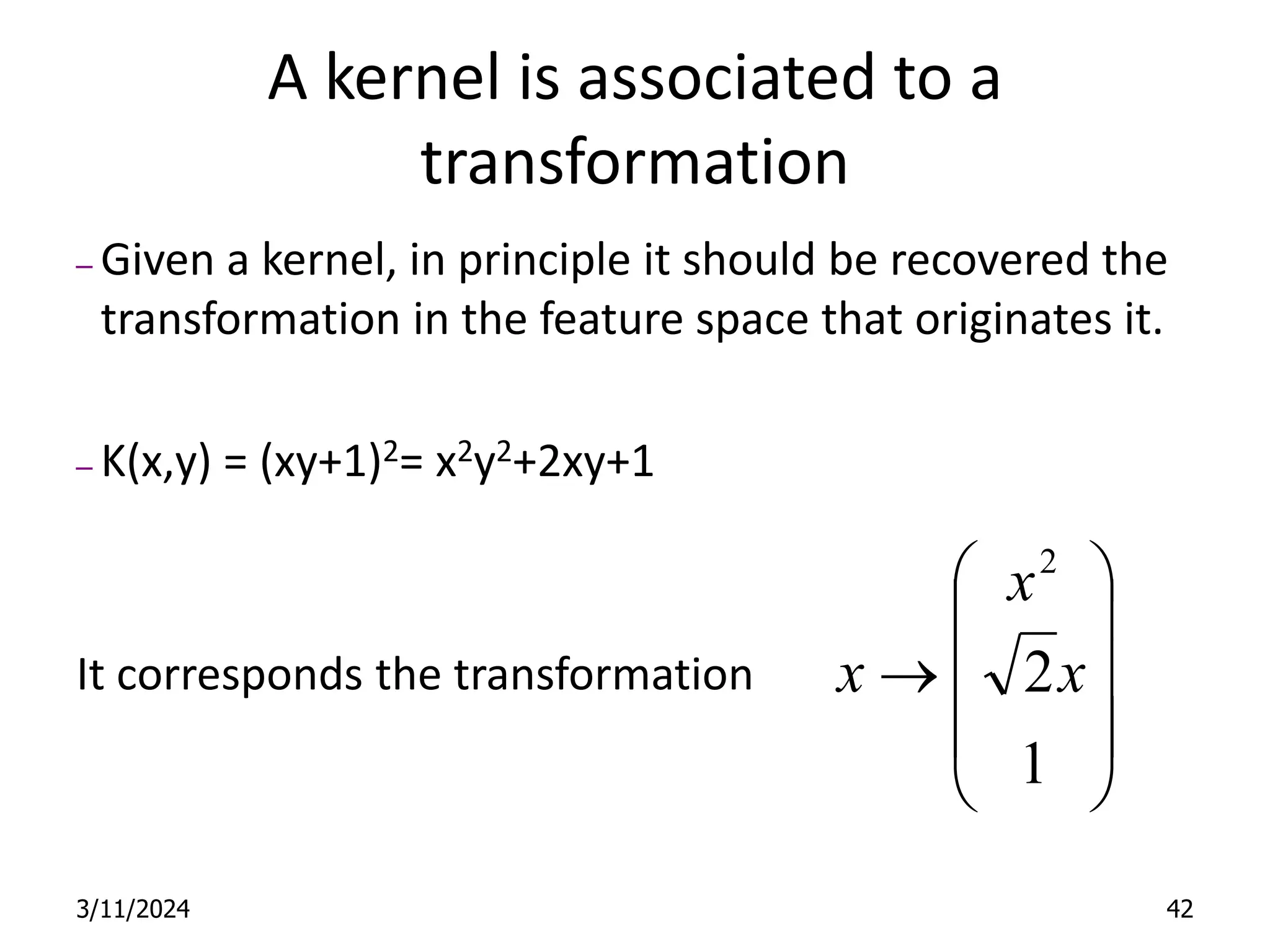
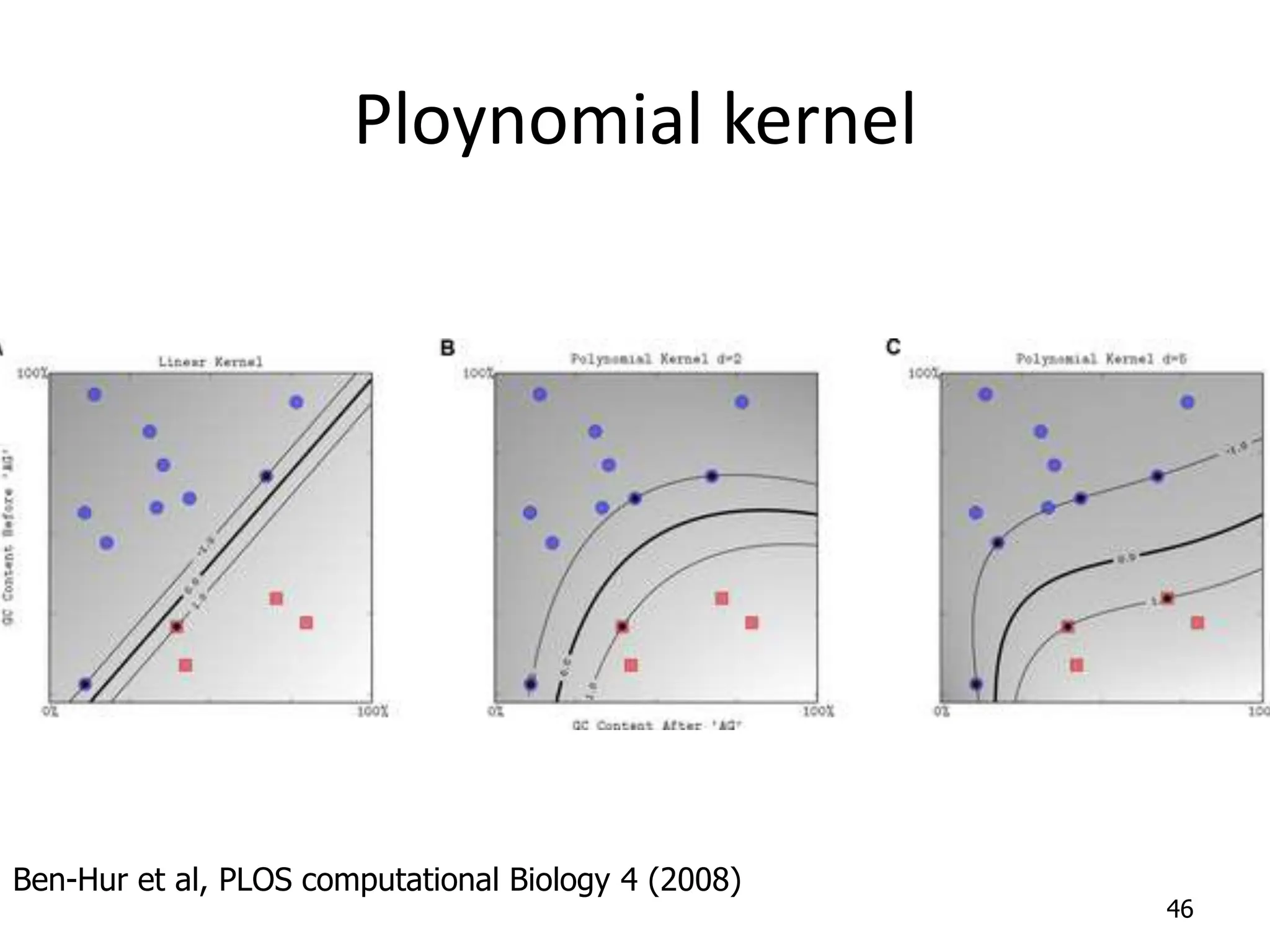
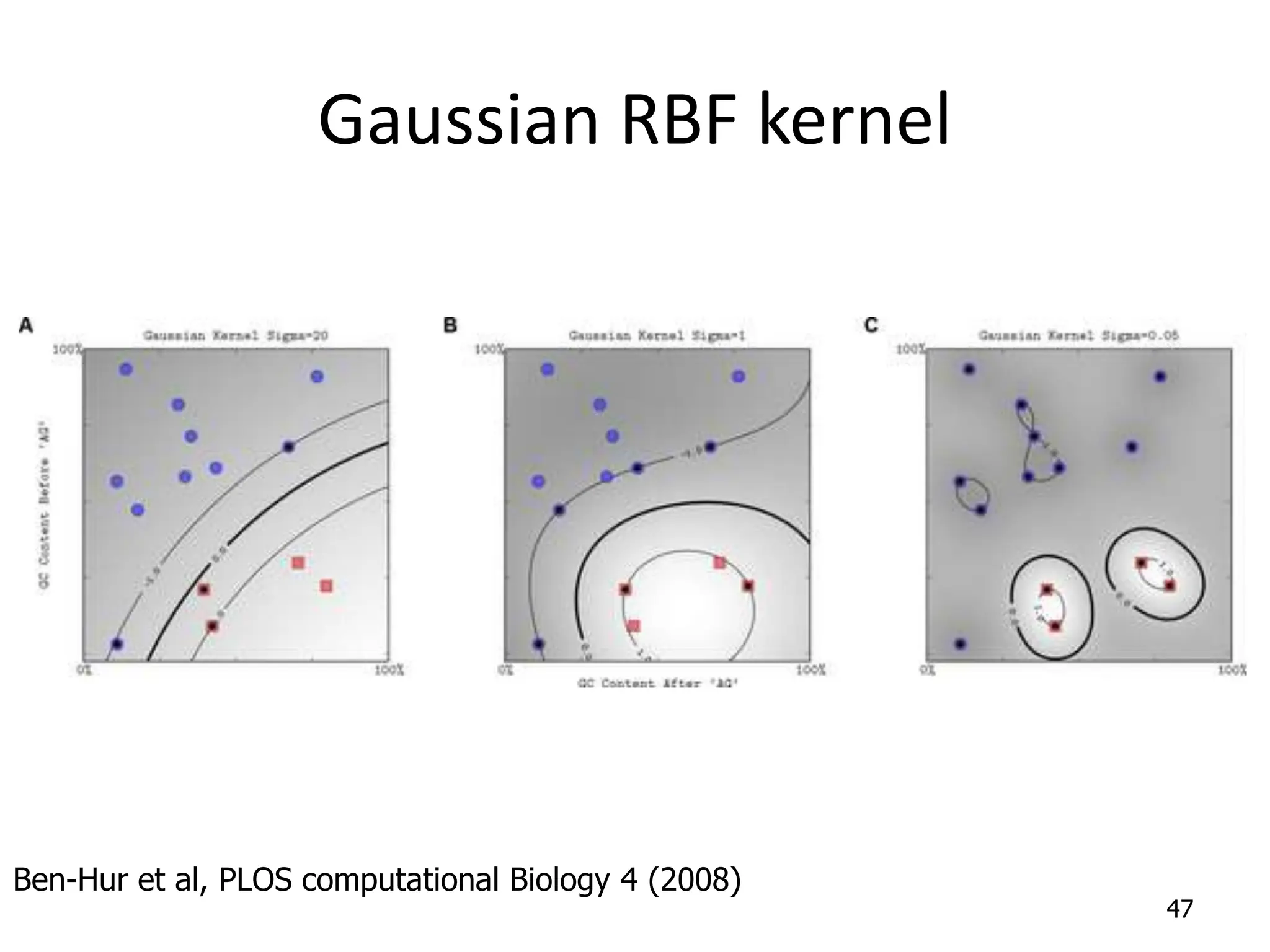
Support Vector Machines aim to find an optimal decision boundary that maximizes the margin between different classes of data points. This is achieved by formulating the problem as a constrained optimization problem that seeks to minimize training error while maximizing the margin. The dual formulation results in a quadratic programming problem that can be solved using algorithms like sequential minimal optimization. Kernels allow the data to be implicitly mapped to a higher dimensional feature space, enabling non-linear decision boundaries to be learned. This "kernel trick" avoids explicitly computing coordinates in the higher dimensional space.