Speech signal compression and encryption based on sudoku, fuzzy C-means and threefish cipher

Speech signal compression and encryption based on sudoku, fuzzy C-means and threefish cipher

• 1.
  International Journal ofElectrical and Computer Engineering (IJECE) Vol. 11, No. 6, December 2021, pp. 5049~5059 ISSN: 2088-8708, DOI: 10.11591/ijece.v11i6.pp5049-5059  5049 Journal homepage: http://ijece.iaescore.com Speech signal compression and encryption based on sudoku, fuzzy C-means and threefish cipher Iman Qays Abduljaleel, Amal Hameed Khaleel Department of Computer Science, Basrah University, Iraq Article Info ABSTRACT Article history: Received Oct 19, 2020 Revised May 12, 2021 Accepted May 23, 2021 Compression and encryption of speech signals are essential multimedia technologies. In the field of speech, these technologies are needed to meet the security and confidentiality of information requirements for transferring huge speech signals via a network, and for decreasing storage space for rapid retrieval. In this paper, we propose an algorithm that includes hybrid transformation in order to analyses the speech signal frequencies. The speech signal is then compressed, after removing low and less intense frequencies, to produce a well compressed speech signal and ensure the quality of the speech. The resulting compressed speech is then used as an input in a scrambling algorithm that was proposed on two levels. One of these is an external scramble that works on mixing up the segments of speech that were divided using Fuzzy C-Means and changing their locations. The internal scramble scatters the values of each block internally based on the pattern of a Sudoku puzzle and quadratic map so that the resulting speech is an input to a proposed encryption algorithm using the threefish algorithm. The proposed algorithm proved to be highly efficient in the compression and encryption of the speech signal based on approved statistical measures. Keywords: Encryption Fuzzy C-means Scrambling Speech compression Sudoku puzzle This is an open access article under the CC BY-SA license. Corresponding Author: Amal Hameed Khaleel Department of Computer Science Basrah University Basrah, Iraq Email: amal_albahrany@yahoo.com 1. INTRODUCTION Transferring multimedia files, such as audio, is a common information security problem. Encryption and compression technologies are, therefore, needed to overcome difficulties in handling huge amounts of data that need to be stored and transferred [1]. Speech-based communication has developed in numerous applications such as teleconferencing, the military, e-learning, and other sectors [2]. Speech is a fundamental way in which humans communicate information to each other. The major objective of speech encryption is to provide a high degree of security for the transfer of speech. Encryption can convert the data into unreadable forms so that only the intended receiver can read and alter the message. The major objective of speech compression is to represent signals with a smaller number of bits and remove redundancy between neighbouring samples. The reduction of data should be done in such a way that there is an acceptable loss of quality [3]. There are two main techniques used to compress the data: lossless compression and lossy compression [4]. Compression of speech is achieved by neglecting and discarding small and lesser coefficients and data and then using quantizing and encryption techniques without significant loss of speech intelligibility [3, 5]. Lossless compression reversibly encodes data, while lossy compression removes perceptually less significant information [6].
• 2.
   ISSN: 2088-8708 IntJ Elec & Comp Eng, Vol. 11, No. 6, December 2021 : 5049 - 5059 5050 In the last few years, numerous different performance methods have been used. The most common techniques in signal compression are: Bousselmi et al. [7], present a simulation algorithm of an audio compression scheme based on the fast Hartley transforms that offer a higher compression ratio in combination with a newly modified run-length encoding. Hassan et al. [8] suggest the JPEG scheme algorithm, commonly used in digital image compression and digital voice signal compression. The method contains many steps to prepare the speech signal to make it more comparable to the original JPEG technique. Vig and Chauhan [5], use a hybrid multi-resolution wavelet for speech signals with variable duration for compression. This hybrid wavelet construction uses two transforms (discrete cosine transform-DCT and Walsh). Aloui et al. [9], suggest a speech signal compression algorithm based on the discrete Hartley transformation to ensure a low bit rate and achieve high speaking compression efficiency. Currently, the studies concentrate on the mixing between compression and encryption. For example Al-Azawi and Gaze [10], explain the method for speech signal encryption and compression in a single-step. Compressive sensing theory ensures that compression and encryption occur in a single-step; in addition, the contourlet transformation is applied to ensure the basic principle of compressive sensing and is used as the base encryption. Hameed et al. [11], propose a lightweight system model to process ECG signals efficiently and securely, using buffer blocks and encryption of signal using the AES-CBC algorithm with 256-bit key size encryption. This paper explains a new method for speech signal compression and encryption to ensure the high quality and reliability of the reconstructed signal. Section 2 introduces proposed algorithms. The proposed system is discussed in section 3 while section 4 presents the experimental results and discussion related to the performance measurements used to assess the proposed system. Conclusions are summarized in section 5. 2. PROPOSED METHOD 2.1. Quantization Quantization is an essential phase in data compression, helping to make approximate mapping of the transform coefficient values to limit the length of binary representation of integer values [9, 12]. Uniform quantization is applied in this work to compress the speech signals. The value of the step size is calculated in (1): (1) Where: = The step size, 𝑚𝑚𝑘𝑘= Maximum value, 𝑚𝑚𝑜𝑜= Minimum value, L= The number of quantization levels. 2.2. Discrete cosine transform (DCT) Due to the high correlation within the adjacent coefficient, the DCT can be used for speech compression. This property helps in efficient data reduction. The discrete cosine transform concentrates the content of the information into relatively few coefficients of transformation because it identifies information pieces that can be effectively disposed of without seriously reducing the quality of the signal [13]. The DCT of 1-D sequence X is calculated by [3]: (2) (3) (4) where N= Length X= Discrete cosine transform = Inverse discrete cosine transform (IDCT)
• 3.
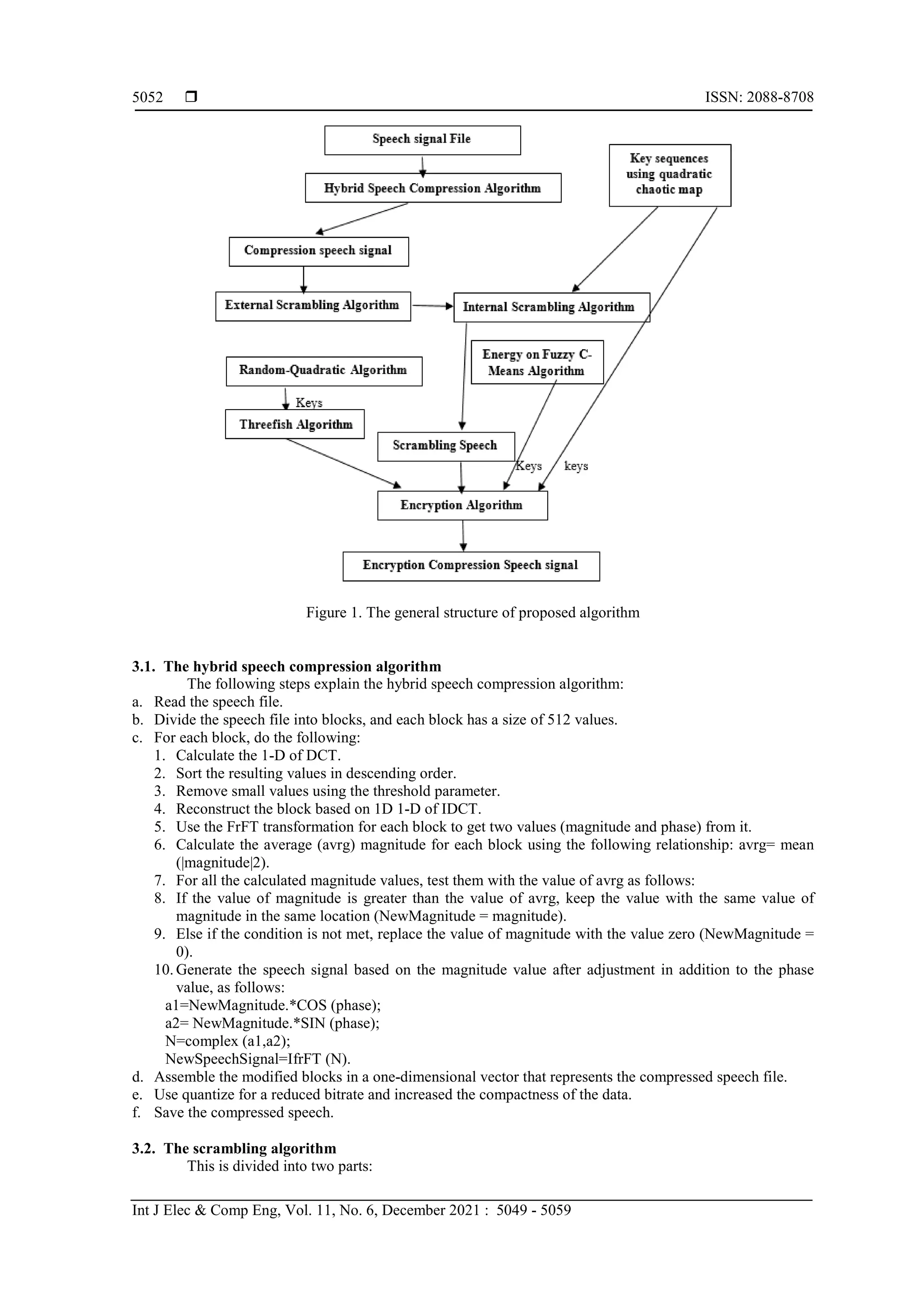
  Int J Elec& Comp Eng ISSN: 2088-8708  Speech signal compression and encryption based on sudoku, fuzzy C-means… (Iman Qays Abduljaleel) 5051 2.3. Fractional fourier transform (FrFT) FrFT is a generalized Fourier transform, and is also known as angular Fourier transform [14]. FrFT is a linear operator with angle (α) and signal (f (t)) according to (5) [15]: (5) (6) (7) where δ(t) = Represents the dirac function, α: represents the angle of rotation (α = α π /2), ƒˊ(t) = The inverse fractional fourier transform. 2.4. Quadratic map The quadratic map is a basic example of a Quadratic Chaotic, one-dimensional, and nonlinear. The quadratic map equation can be defined as [16, 17], (8) where the initial conditions specify that r is the chaotic behaviour parameter and n is the number of iterations. c=1.95 and x0=0.1 [18]. 2.5. Sudoku puzzles Sudoku puzzles are generated by removing some elements from the sudoku matrix but keeping some hints for a unique solution [19]. The central idea of the Sudoku solution is to change the pixel pairs selected in the cover signal using an index matrix [20]. 2.6. Short-term energy (en) The voice and the silence are separated by the thresholds of en(i). The en(i) formulae is as [21]: (9) 2.7. Fuzzy C-means The clustering technique is one of the most important techniques used in data mining. Clustering algorithms are useful in dealing with signal similitude and uncertainty. Fuzzy C-means (FCM) is a fuzzy theory-based algorithm that enables the element to belong to multiple classes with varying memberships. Details of fuzzy C-means algorithm can be found in [22]. 2.8. Threefish algorithm Threefish is a tweakable block cipher (i.e. three parameters are required as the key input, a tweak value, and a message block). Three types of keys inputted as 256, 512, and 1024 bits, are used by the threefish algorithm, and their block size is the same as the key size. Threefish's design philosophy is that a greater number of simple rounds is safer than fewer complex rounds [23]. Threefish comprises three operations: rotation of bits to the left, bitwise exclusive OR (⊕), and modulo 264 addition ( ). Details of the threefish algorithm can be found in [24]. 3. PROPOSED ALGORITHMS In this study, the compressed speech file was encrypted after scrambling it, and thus this work consists of, compression, scrambling, and encryption algorithms, in addition to two secondary algorithms for generating the three keys. The proposed algorithm is shown in Figure 1.
• 4.
   ISSN: 2088-8708 IntJ Elec & Comp Eng, Vol. 11, No. 6, December 2021 : 5049 - 5059 5052 Figure 1. The general structure of proposed algorithm 3.1. The hybrid speech compression algorithm The following steps explain the hybrid speech compression algorithm: a. Read the speech file. b. Divide the speech file into blocks, and each block has a size of 512 values. c. For each block, do the following: 1. Calculate the 1-D of DCT. 2. Sort the resulting values in descending order. 3. Remove small values using the threshold parameter. 4. Reconstruct the block based on 1D 1-D of IDCT. 5. Use the FrFT transformation for each block to get two values (magnitude and phase) from it. 6. Calculate the average (avrg) magnitude for each block using the following relationship: avrg= mean (|magnitude|2). 7. For all the calculated magnitude values, test them with the value of avrg as follows: 8. If the value of magnitude is greater than the value of avrg, keep the value with the same value of magnitude in the same location (NewMagnitude = magnitude). 9. Else if the condition is not met, replace the value of magnitude with the value zero (NewMagnitude = 0). 10. Generate the speech signal based on the magnitude value after adjustment in addition to the phase value, as follows: a1=NewMagnitude.*COS (phase); a2= NewMagnitude.*SIN (phase); N=complex (a1,a2); NewSpeechSignal=IfrFT (N). d. Assemble the modified blocks in a one-dimensional vector that represents the compressed speech file. e. Use quantize for a reduced bitrate and increased the compactness of the data. f. Save the compressed speech. 3.2. The scrambling algorithm This is divided into two parts:
• 5.
  Int J Elec& Comp Eng ISSN: 2088-8708  Speech signal compression and encryption based on sudoku, fuzzy C-means… (Iman Qays Abduljaleel) 5053 3.2.1. External scrambling (to change the blocks sequences) The external scrambling procedure is explained in the following steps: a. Read the compressed speech file. b. Divide the speech signal into blocks, each segment of 81 value and keep the total number of blocks, c. Divide the total number of blocks into three equal parts, and adding the fractional surplus specifically to the end of the third part. d. Read the block value indicator from each part until the end of the three parts as follows: 1. Read the index of the block from the end of the third segment and save it in the new vector. 2. Read the index of the block from the beginning of the first part and save it in the new vector. 3. Read the index of the block from the beginning of the second part and save it in the new vector. 4. After the end of the first and second parts, and in the event of a surplus in the third part, add the remaining unaddressed to the end of the new vector. e. Use the new vector for the locations of the blocks after replacing them to change the locations of their contents in the original speech signal and get the first stage of the scrambling. 3.2.2. An internal scrambling (to change the sequence of data within blocks) The internal scrambling procedure is explained in the following steps: a. Generate a key sequence of eight non-repeating keys for each block of the speech signal, using the random-quadratic algorithm. b. For each successive two blocks of the speech signal, do the following: 1. Generate a Sudoku puzzle of size 9 × 9 equal to the number of values of each block (i.e. 81 values) using eight non-repeating random-quadratic keys. 2. Convert the resulting vector from each block into a 9 × 9 matrix. 3. Use the values in the Sudoku puzzle to change the values in each row according to the new locations in it. 4. Use the values in the Sudoku puzzle to change the values in each column according to the new locations in it. 5. Swap the odd rows between the two matrices of the two consecutive blocks (i.e. the rows to be swapped are 1, 3, 5, 7, and 9) to create more complexity by mixing internally between values. c. If there is an excess block, repeat steps (a – d) for the excess block. d. Convert the matrices resulting from each block to a one-dimensional vector. e. Combine the resultant one-dimensional vectors of all the blocks to get the new speech signal after the internal scrambling. 3.3. Encryption algorithm 3.3.1. Keys of the encryption algorithm Three keys were used in the encryption algorithm as follows: a. Random-quadratic algorithm (to generate keys used in the threefish algorithm) The keyT generation process is described in the steps below: 1. For each speech block, generate eight of keys based on quadratic map equations. 2. Test the generated values as they should be positive, non-repeating and between 1- 9. 3. Use the values that meet the above test to create the eight keys. 4. Repeat steps 1-3 to generate eight new keys (KeyT) until blocks of keys are generated equal to the specified number of speech blocks. b. The energy on fuzzy C-means algorithm (to generate the third key) The key3 generation process is described in the steps below: 1. Divide the original sign into blocks, with each block containing 256 values. 2. Calculate the short time energy value for each block. 3. Find the 16 blocks with the highest values of short-time energy and convert each block into a 16×16 binary matrix. 4. Use the fuzzy c-means algorithm on binary arrays to get a 16-bit binary key. 5. Repeat steps 2-4 on 16 blocks to get 256 values representing 32 symbols, which is the third key (key3). 3.3.2. Encryption algorithm The following steps explain the encryption algorithm: a. Input the two keys (key1 and key2) with a size of 32 characters. b. Generate a third key (key3) using the energy on fuzzy C-means algorithm. c. Use the XOR function between the first key and the third key to getting a new key xoredkey1.
• 6.
   ISSN: 2088-8708 IntJ Elec & Comp Eng, Vol. 11, No. 6, December 2021 : 5049 - 5059 5054 d. Set the value of a tweak value with the size of 16 characters. e. Set the constant value C240 by 8 characters (i.e. 64 bits). f. Divide the speech signal into several blocks (i.e. 16 values for each block). g. Use the random-quadratic algorithm to generate a series of keys (KeyT) equal to the number of blocks at this stage. h. For each block, test value from the generated keychain as follows: 1. If the key value in the keychain (KeyT) is divisible by 2 (i.e. the key value is even) then encode the block values based on the threefish algorithm and xoredkey1 as the primary key. 2. If the key value in the keychain (KeyT) is not divisible by 2 (i.e. the key value is odd), encode the block values based on the threefish algorithm and key2 as the primary key. i. Repeat step 8 until all of the speech signal blocks are finished. j. Merge the blocks into one audio vector and save it to a wav speech file. 4. RESULTS AND DISCUSSION This work was conducted using the R2018b MATLAB programme. Equipment included a Core i7 PC with Intel Processor, 2.60 GHz CPU, and 6.00 GB RAM. The tested speech file was loaded from the "NOIZEUS" database produced by male and female speakers. Two different "16 KHZ" frequency messages were used from the database, one of which included only vowels (voiced) speech, and the other included voiced and voiceless continuous speech. The statistical measures used to assess the performance of the system in the encryption and decryption processes included (SNR, SNRseg, fwSNRseg, CC, LLR) [25], [26], [27], the statistical measures in compression used included (CR, SNR, SSSNR, PSNR, MSE). The equations of these measures were [2], [9], [10], [28]: a. Signal-to-noise-ratio (SNR) (10) b. Segmental signal-to-noise-ratio (SNRseg) (11) c. frequency-weighed signal-to-noise ratio (fwSNRseg) (12) d. Correlation coefficient (CC):rxy (13) (14) e. Log-likelihood ratio (LLR) (15) f. Segmental spectral signal to noise ratio (SSSNR) (16)
• 7.
  Int J Elec& Comp Eng ISSN: 2088-8708  Speech signal compression and encryption based on sudoku, fuzzy C-means… (Iman Qays Abduljaleel) 5055 g. Peak signal to noise ratio (PSNR) (17) h. Mean square error (MSE) (18) i. Compression ratio (CR) (19) (20) Where: X and y = block samples of the original and encrypted speech signal, respectively M = the number of frames in the signal of speech L = the number of samples in the speech signal K = the number of sub-bands in the speech signal W (j, m) = Weight in an mth frame on the jth sub-band X (j, m) and X̃ (j, m) = the spectrum magnitude of the original and distorted speech signal, respectively a0 and ac = the original LPC and cipher speech signal vectors, respectively, aT = transform R0= the automatic correlation matrix of the original speech signals s, r = the original and the reconstructed speech signal, respectively. n = the reconstructed audio signal length. Table 1 shows that the (PSNR) values are high, as are the (SNR and SSSNR) values, while the (MSE) values are lower. The compression ratio is generally good, as shown in Figure 2, because the audio signal data is characterized by building the sound at its high and low frequencies. Therefore, frequencies that represent noise that can be dispensed with by converting their values to zero values were looked for, so as to ensure that the file was reduced without losing important data. Table 1. Speech signals compression measurements Speech File Length Compession Ratio CR % SNR (dB) SSSNR (dB) PSNR MSE Signal1 2 2.0100 50.2483 12.299 -14.790 41.368 7.2978E-05 Signal2 2 2.0028 50.0695 11.842 -16.606 41.632 6.8680E-05 Signal3 2 2.0012 50.0295 11.958 -15.931 42.063 6.2188E-05 Signal4 3 2.0285 50.7014 11.657 -15.864 40.557 8.7965E-05 Signal5 3 2.0071 50.1763 12.553 -14.340 41.813 6.5874E-05 Signal6 3 1.9993 49.9813 12.575 -15.132 40.987 7.9679E-05 The conversions (DCT and FrFT) were used because the (DCT) one has the ability to display frequency and to remove low frequencies that are lower than the threshold value we identify based on the experience. Meanwhile, (FrFT) was used to deconstruct the signal for its frequencies and compare it with the total energy value of each block to which the signal was divided. In this way, transforms are conducted sequentially to zero and the signal reconstructed to ensure that the largest number of iterations of the zero values are obtained and to ensure firm pressure without losing any important value. See Table 2 for the results of the proposed encryption method. In this table, the values (SNR, SNRseg, and fwSNRseg) are clearly low. The measure (CC) values are also very small, while the (LLR) value is high, thus showing a big difference between the original signal and the coded signal, and low residual intelligibility. This indicates that the encryption quality introduced by the proposed method is high. In Table 3, the values of (SNR and SNRseg) are obviously high whereas the values of (fwSNRseg and LLR) are low. As for measure (CC) values, they are close to one, indicating the intelligibility of the signal. This means the quality of decryption of the compressed signal introduced through the study’s method is high.
• 8.
   ISSN: 2088-8708 IntJ Elec & Comp Eng, Vol. 11, No. 6, December 2021 : 5049 - 5059 5056 Figure 2. Original and Compressed speech signal with CR=50% Table 2. Speech signal encryption Speech File Length (ms) SNR SNRseg fwSNRseg CC LLR Signal1 2 -24.2149 -30.8442 -24.1010 -0.0033 11.643 Signal2 2 -24.9066 -31.8127 -24.5255 -0.0019 11.305 Signal3 2 -25.2374 -31.3639 -24.4974 0.0032 11.608 Signal4 3 -24.2528 -31.3048 -23.1309 -0.0029 11.810 Signal5 3 -24.5107 -30.8492 -24.1927 -0.0004 11.915 Signal6 3 -23.6707 -30.5503 -23. 0611 0.0026 11.732 Table 3. Speech signal decryption Speech File Length (ms) SNR SNRseg fwSNRseg CC LLR Signal1 2 170.7144 161.522 0.000002 0.9999 2.911E-14 Signal2 2 169.2952 158.098 0.000002 0.9999 3.354E-14 Signal3 2 168.7221 157.875 0.000003 0.9999 3.271E-14 Signal4 3 170.7142 161.519 0.000002 0.9999 2.909E-14 Signal5 3 171.7090 162.246 0.000002 0.9999 2.691E-14 Signal6 3 172.1243 162.919 0.000002 0.9999 2.682E-14 In Tables 4 and 5, transformations (DCT and FrFT) were both used separately to assess the efficiency of the algorithm and to evaluate the effect of the combination of both, as shown in Table 4, whereas the (SNR, PSNR, and MSE) values were better in Table 5. This means that the (FrFT) conversion preserves important frequency values, even if they are very small. It was therefore used after converting the (DCT) to remove the low frequencies individually while keeping them if they were within the specified mass energy range. The results of using both (DCT and FrFT) transformations shown in Table 1 of the proposed method. Figure 3 illustrates how, by comparing Figures 3(a) and 3(b), the compression maintains high and low signal frequencies, meaning that the speech signal remains understood. The scrambling methods (external and internal) are very effective when compared to Figures 3(a), (3(c), and 3(d)). Table 4. Compression measurements using DCT only Speech File Length Compession Ratio CR % SNR (dB) SSSNR (dB) PSNR MSE Signal1 2 1.1060 9.5841 9.3841 -4.0845 37.1877 1.9109e-04 Signal2 2 1.1026 9.3053 11.034 -3.5951 39.4358 1.1387e-04 Signal3 2 1.1019 9.2477 9.9516 2.7511 37.1468 1.9289e-04 Signal4 3 1.1005 9.1322 11.098 4.1698 38.6680 1.3589e-04 Signal5 3 1.1150 10.313 10.649 4.2098 38.4895 1.4160e-04 Signal6 3 1.1043 9.4449 11.122 6.3955 39.6179 1.0920e-04
• 9.
  Int J Elec& Comp Eng ISSN: 2088-8708  Speech signal compression and encryption based on sudoku, fuzzy C-means… (Iman Qays Abduljaleel) 5057 Table 5. Compression measurements using FrFT only Speech File Length Compession Ratio CR % SNR (dB) SSSNR (dB) PSNR MSE Signal1 2 1.7350 42.3631 -3.8010 -4.2846 25.0240 0.0031 Signal2 2 1.8201 45.0580 -3.8062 -4.9822 25.7154 0.0027 Signal3 2 1.7812 43.8581 -4.7720 -5.0119 25.0686 0.0031 Signal4 3 1.9829 49.5688 -3.4913 -6.4298 24.6873 0.0034 Signal5 3 1.8110 44.7819 -3.4585 -3.3707 25.5687 0.0028 Signal6 3 1.5022 33.4310 -3.5961 -3.6306 25.0242 0.0031 Furthermore, as shown in Figure 3, by comparing Figures 3(a) and 3(e), the encrypted waveform of the speech signal is unintelligible, and completely uniform which indicates a significant deviation from the acquired speech signal. Thus, by comparing Figures 3(a) and 3(f), it can be seen that the waveforms of the obtained and decrypted signals are identical, implying better accuracy and quality of the reconstructed signal. (a) (b) (c) (d) (e) (f) Figure 3. The stages of the proposed working method, a) original signal 1, b) compressed signal 1, c) scrambling1 of compressed signal 1, d) scrambling2 of compressed signal1, e) encrypted signal1, f) decrypted signal1
• 10.
   ISSN: 2088-8708 IntJ Elec & Comp Eng, Vol. 11, No. 6, December 2021 : 5049 - 5059 5058 5. CONCLUSION There is always a demand for compressed audio data with high cybersecurity. By encrypting the compressed speech, we get fast speech data transmission after compressing it because it is smaller in size and simultaneously secure. This study consists of three basic algorithms: hybrid compression, scrambling and encryption algorithms, where scrambling consists of both external and internal scrambling algorithms, in addition to two secondary algorithms to generate the keys, depending on fuzzy C-means and quadratic map techniques. The purpose of this work is to shrink large speech signal files before encrypting them to provide sufficient space during correspondence, in addition to transmission speed, as well as adding a complexity to any attempt to penetrate because there are several stages before the encryption process. This experiment has demonstrated that the proposed method outperforms other current techniques. REFERENCES [1] X. Wang and Y. Su, “An Audio Encryption Algorithm Based on DNA Coding and Chaotic System,” IEEE Access, vol. 8, pp. 9260–9270, 2020, doi: 10.1109/ACCESS.2019.2963329. [2] O. A. Imran, S. F. Yousif, I. S. Hameed, W. N. Al-Din Abed, and A. T. Hammid, “Implementation of El-Gamal algorithm for speech signals encryption and decryption,” Procedia Comput. Sci., vol. 167, no. Iccids 2019, pp. 1028–1037, 2020, doi: 10.1016/j.procs.2020.03.402. [3] S. S. M. V. Patil, A. Gupta, and A. Varma, “Audio and Speech Compression Using DCT and DWT Techniques,” Int. J. Innov. Res. Sci. Eng. Technol., vol. 2, no. 5, pp. 1712–1719, 2013. [4] A. Tsegaye and G. Tariku, “Audio Compression Using DWT and RLE Techniques,” Am. J. Electr. Electron. Eng., vol. 7, no. 1, pp. 14–17, 2019, doi: 10.12691/ajeee-7-1-3. [5] R. Vig and S. S. Chauhan, “Speech Compression using Multi-Resolution Hybrid Wavelet using DCT and Walsh Transforms,” Procedia Comput. Sci., vol. 132, pp. 1404–1411, 2018, doi: 10.1016/j.procs.2018.05.070. [6] B. Kim and Z. Rafii, “Lossy audio compression identification,” Eur. Signal Process. Conf., vol. 2018, 2018, pp. 2459–2463, doi: 10.23919/EUSIPCO.2018.8553611. [7] S. Bousselmi, N. Aloui, and A. Cherif, “DSP Real-Time Implementation of an Audio Compression Algorithm by using the Fast Hartley Transform,” Int. J. Adv. Comput. Sci. Appl., vol. 8, no. 4, 2017, doi: 10.14569/ijacsa.2017.080462. [8] T. A. Hassan, R. H. Al-Hashemy, and R. I. Ajel, “Speech Signal Compression Algorithm Based on the JPEG Technique,” J. Intell. Syst., vol. 29, no. 1, pp. 554–564, 2020, doi: 10.1515/jisys-2018-0127. [9] N. Aloui, S. Bousselmi, and A. Cherif, “New algorithm for speech compression based on discrete hartley transform,” Int. Arab J. Inf. Technol., vol. 16, no. 1, pp. 156–162, 2019. [10] M. K. M. Al-Azawi and A. M. Gaze, “Combined speech compression and encryption using chaotic compressive sensing with large key size,” IET Signal Process., vol. 12, no. 2, pp. 214–218, 2018, doi: 10.1049/iet-spr.2016.0708. [11] M. E. Hameed, M. M. Ibrahim, and N. A. Manap, “Compression and encryption for ECG biomedical signal in healthcare system,” Telkomnika Telecommunication Comput. Electron. Control., vol. 17, no. 6, pp. 2826–2833, 2019, doi: 10.12928/TELKOMNIKA.v17i6.13240. [12] P. K. R. Manohar, M. Pratyusha, R. Satheesh, S. Geetanjali, and N. Rajasekhar, “Audio Compression Using Daubechie Wavelet,” IOSR J. Electron. Commun. Eng. Ver. III, vol. 10, no. 2, pp. 2278–2834, 2015, doi: 10.9790/2834-10234144. [13] Z. T. Drweesh and L. E. George, “Audio Compression Based on Discrete Cosine Transform, Run Length and High Order Shift Encoding,” International Journal of Engineering and Innovative Technology (IJEIT), vol. 4, no. 1, pp. 45–51, 2014. [14] K. Pramila R. and G. Shital S., “A Survey Paper on Different Speech Compression Techniques,” IJARIIE, vol. 2, no. 5, pp. 736–741, 2016. [15] B. T. Krishna, “Fractional Fourier transform: A survey,” ACM Int. Conf. Proceeding Ser., 2012, pp. 751–757, doi: 10.1145/2345396.2345519. [16] C. R. Revanna and C. Keshavamurthy, “A new selective document image encryption using GMM-EM and mixed chaotic system,” Int. J. Appl. Eng. Res., vol. 12, no. 19, pp. 8854–8865, 2017. [17] C. R. Revanna and C. Keshavamurthy, “A novel priority based document image encryption with mixed chaotic systems using machine learning approach,” Facta Univ. - Ser. Electron. Energ., vol. 32, no. 1, pp. 147–177, 2019, doi: 10.2298/fuee1901147r. [18] N. Ramadan, H. E. H. Ahmed, S. E. Elkhamy, and F. E. A. El-samie, “Chaos-Based Image Encryption Using an Improved Quadratic Chaotic Map,” Am. J. Signal Process., vol. 6, no. 1, pp. 1–13, 2016, doi: 10.5923/j.ajsp.20160601.01. [19] Y. Wu, Y. Zhou, J. P. Noonan, K. Panetta, and S. Agaian, “Image encryption using the Sudoku matrix,” Mob. Multimedia/Image Process. Secur. Appl., vol. 7708, Art. No. 77080P, 2010, doi: 10.1117/12.853197. [20] S. Ijeri, S. Pujeri, S. B, and U. B A, “Image Steganography using Sudoku Puzzle for Secured Data Transmission,” Int. J. Comput. Appl., vol. 48, no. 17, pp. 31–35, 2012, doi: 10.5120/7443-0460. [21] Y. Zhang, D. Xiao, Q. Ren, S. Guo, and F. Mo, “An effective speech compression based on syllable division,” Proc. Meet. Acoust., vol. 29, no. 1, Art. no. 055002, 2016, doi: 10.1121/2.0000480.
• 11.
  Int J Elec& Comp Eng ISSN: 2088-8708  Speech signal compression and encryption based on sudoku, fuzzy C-means… (Iman Qays Abduljaleel) 5059 [22] J. Kong, J. Hou, M. Jiang, and J. Sun, “A novel image segmentation method based on improved intuitionistic fuzzy C-Means clustering algorithm,” KSII Trans. Internet Inf. Syst., vol. 13, no. 6, pp. 3121–3143, 2019, doi: 10.3837/tiis.2019.06.020. [23] M. Usman et al., “A Comprehensive Comparison of Symmetric Cryptographic Algorithms by Using Multiple Types of Parameters,” International Journal Of Computer Science And Network Security, vol. 18, no. 12, pp. 131–137, 2018. [24] P. G. Ayathri, K. U. N. A. S. Ateesh, and C. H. N. Avya, “High-Throughput Hardware Implementation of Three Fish Block Cipher Encryption and Decryption on FPGA,” International Journal of VLSI System Design And Communication Systems, vol. 03, no. 08, pp. 1325–1329, 2015. [25] S. F. Yousif, “Speech Encryption Based on Zaslavsky Map,” J. Eng. Appl. Sci., vol. 14, no. 17, pp. 6392–6399, 2019, doi: 10.36478/jeasci.2019.6392.6399. [26] E. Hato and D. Shihab, “Lorenz and Rossler Chaotic System for Speech Signal Encryption,” Int. J. Comput. Appl., vol. 128, no. 11, pp. 25–33, 2015, doi: 10.5120/ijca2015906670. [27] A. H. Khaleel and I. Q. Abduljaleel, “A novel technique for speech encryption based on k-means clustering and quantum chaotic map,” Bulletin of Electrical Engineering and Informatics (BEEI), vol. 10, no. 1, pp. 160–170, 2021, doi: 10.11591/eei.v10i1.2405. [28] A. H. Khaleel and I. Q. Abduljaleel, “Secure image hiding in speech signal by steganography-mining and encryption,” Indonesian Journal of Electrical Engineering and Computer Science (IJEECS), vol. 21, no. 3, pp. 1692–1703, 2021, doi: 10.11591/ijeecs.v21.i3.pp1692-1703.