SPACE TIME ADAPTIVE PROCESSING FOR CLUTTER SUPPRESSION IN RADAR USING SUBSPACE BASED TECHNIQUE

SPACE TIME ADAPTIVE PROCESSING FOR CLUTTER SUPPRESSION IN RADAR USING SUBSPACE BASED TECHNIQUE

• 1.
  International Journal ofTechnical Research and Applications e-ISSN: 2320-8163, www.ijtra.com Volume 2, Issue 3 (May-June 2014), PP. 163-168 163 | P a g e SPACE TIME ADAPTIVE PROCESSING FOR CLUTTER SUPPRESSION IN RADAR USING SUBSPACE BASED TECHNIQUE Elza Baby, Ashish.A.Bhargave Dept of Electronics and Telecommunication K. K. Wagh IEER Nasik ,India Abstract— Space-time adaptive processing (STAP) is a signal processing technique most commonly used in radar systems where interference is a problem. The radar signal processor is used to remove the unintentional cluttering effects caused by ground reflections and echoes due to sea, desert, forest, etc. and intentional jamming and make the received signal useful. In this paper a new approach to STAP based on subspace projection has been described in detail. According to linear algebra and three dimensional geometry, if we project a range space on to a subspace spanned by linearly independent vectors, we can suppress data which is perpendicular to that subspace. In subspace based technique, the received data is projected on to a subspace which is orthogonal to clutter subspace to remove the clutter. The probability of target detection can be find out in order to analyse the performance of the proposed algorithm. Two existing algorithms, SMI and DPCA are chosen to do the comparison. while plotting the detection Probability against SINR , the results obtained are better for subspace technique than DPCA and SMI. We got the SINR improved for subspace based technique for same detection probability. The effect of subspace rank on SINR was also analysed for understanding the computational load caused by the technique. We also analysed the convergence of the algorithm by taking plots of SINR against range snapshots. Keywords—STAP, Clutter suppression, Clutter subspace, Jammer subspace, Subspace Projection I. INTRODUCTION Space-time adaptive processing (STAP) is a popular radar signal processing technique to detect slow-moving targets in the presence of a strong interference background. The space dimension arises from the use of an array of N antenna elements and the time dimension from the use of a coherent train of M pulses. The power of STAP comes from the joint processing along the space and time dimensions. The data collected by STAP radars are a sequence of N × M arrays, one at each range. These arrays are typically treated as NM × 1 vectors. These arrays or vectors are called ‘snapshots.’ The calculation of the optimum processor generally involves the inversion of the ‘interference + noise (I + N)’ covariance matrix of each snapshot. This matrix is generally estimated using snapshots at neighbouring ranges. A general assumption is that the snapshots used for estimation are statistically independent, have identical probability density functions (PDF) and obey a Gaussian distribution. A very important, practical issue in fielding a STAP-based system concerns accurately estimating the interference covariance matrix and then computing an improved adaptive weight vector. For an optimum system large sample support is required. There are different approaches for STAP depending upon the interference is homogenous or non-homogenous. The paper describes a homogenous clutter suppression technique which is based on subspace projection. The whole of the interference matrix are formed by two subspaces, the clutter subspace and jammer subspace. The received data which contains the target response as well as the interference is projected on to the subspace orthogonal to clutter subspace so as to remove the clutter. A. Motivation For The study Of STAP STAP is used for processing the radar data against strong interference. The whole process consists of different steps in which clutter suppression is the first objective. In a practical environment the clutter need not be uniform, that means it is non homogenous in nature. Therefore for effective filtering the weight should be adjustable. The adaptive filters are used for suppressing these non-uniform clutters. By comparing the performance we can select some particular algorithm for filtering. We should be concerned about the minimization of computational load, that is, the convergence rate of the algorithm selected. Once the
• 2.
  International Journal ofTechnical Research and Applications e-ISSN: 2320-8163, www.ijtra.com Volume 2, Issue 3 (May-June 2014), PP. 163-168 164 | P a g e algorithm is selected, the whole step by step processing can be avoided by downloading the algorithm into a processor. This can be inserted into the system for using a particular technique. The embedded signal processing systems used for radar data processing contains many of these processor cards, which varies according to the processing steps needed to extract the required data. In a radar system, where, real time operation is important, such an embedded processor is really useful. This will increase the computational complexity as well as increase the accuracy. II. STAP BACKGROUND STAP stands for Space Time Adaptive Processing which is a signal processing technique most commonly used in radar systems. It involves adaptive array processing algorithms to aid in target detection. Radar signal processing benefits from STAP in areas where interference is a problem (ground clutter, jamming).A space-time snapshot was defined to be the slice of the data cube corresponding to a single range gate as shown in Figure 1. This data may contain a target component as well as undesired components due to noise, jamming, and clutter. The target signal is modelled as a random amplitude times a space-time steering vector that has the target's angle and Doppler. The undesired signal components are modelled as random processes and expressions for their covariance matrices are derived. Fig 1: Radar CPI Data cube A Problem Description The radar antenna is a uniformly spaced linear array antenna consisting of N elements. Radar returns are collected in a coherent processing interval (CPI), which is referred to as the 3-D radar data cube shown in Figure. 1, where L denotes the number of samples collected to cover the range interval. The data is then processed at one range of interest, which corresponds to a slice of the CPI data cube. This slice is an M × N matrix which consists of N × spatial snapshots for M pulses at the range of interest. It is convenient to stack the matrix column-wise to form the J × ,J MN vector ri , termed a space-time snapshot [1],[2]. The function of radar is to ascertain whether targets are present in the data. The vector ru is used to estimate the interference covariance matrix Ru which consists of the summation of clutter matrix Rc, jammer matrix Rj, and thermal noise matrix Rn.Thus, the J × J covariance matrix Ru of the undesired clutter-plus-jammer-plus-noise component can be modelled as Ru =E{ruru H } = Rc + Rj + Rn (1) Where H represents Hermitian transpose, Rc where H represents Hermitian transpose, Rc = E{rcrc H },Rj =E{rjrj H } and Rn =E{rnrn H } denote clutter, jamming and noise covariance matrix respectively. In practice, the interference-plus-noise covariance matrix Ru is typically unknown. The common approach is to estimate it from the secondary data set which does not contain the signal of interest (r = ru). In this context, we can refer the interference-plus-noise covariance matrix Ru as R. In practice, since R is unknown, the processor substitutes an estimation of R for to arrive at the adaptive weight ω. It is most common to compute the covariance matrix estimate as = . This approach is known as sample matrix inversion (SMI). Another conventional method for suppressing clutter is the DPCA method. The displaced phase centre antenna (DPCA) algorithm is often considered to be the first STAP algorithm. This algorithm uses the shifted aperture to compensate for the platform motion so that the clutter return does not change from pulse to pulse. Thus, this algorithm can remove the clutter via a simple subtraction of two consecutive pulses. B Literature Survey Research has focused on the use of space-time adaptive processing (STAP) fix interference cancellation in airborne radar systems since 1970’s. The theory of adaptive radar [1] have been explained by L. E. Brennan and L. S. Reed. After that some conventional methods were developed to estimate the adaptive weights for filtering out the clutters [2, 3]. Then methods based on Eigen values and Eigen vectors were used to estimate the weight vectors [4, 5, 6, 7] by scientists A. M. Haimovich and Y. Bar-Ness. This method is based on the fact that the highest power is concentrated on the Eigen values of a matrix. These
• 3.
  International Journal ofTechnical Research and Applications e-ISSN: 2320-8163, www.ijtra.com Volume 2, Issue 3 (May-June 2014), PP. 163-168 165 | P a g e methods were simple to perform but the accuracy was not always good due to insufficient data for estimating the interference matrix. Some STAP approaches used circular arrays [8,9] of antennas for the purpose. For non- homogenous clutter suppression different techniques were found out based non statistical estimation of the weight vector [10, 11]. Many scientists like T. K. Sarkar, S. Park, J. Koh, and R. A. Schneible worked on this area and contributed their ideas. Studies based on Subspace approach for clutter suppression [12, 13, 14] started in 1990’s and they are found to be easier to implement. Recent studies are based on improving the performance of the technique by reducing the rank of the subspace. III. SUBSPACE APPROACH IN STAP In this section we describe a technique based on subspace projection which is used to suppress the homogenous clutter. This uses an observation that the clutter returns are range dependant, because it exists at all ranges of interest, to obtain an improved estimate of the covariance matrix R(u) from measured data x(r). The subspace technique is based on the theory of subspace projection in three dimensional geometry. Consider a point P(x, y, z) in XYZ space. If this point is projected on to an orthogonal plane, say XY plane the z co-ordinate will be eliminated. This means that this is another form of representing the point P(x, y, z) using different basis vectors. Same is the case with received data, which is a three dimensional matrix which contains clutters, jammers, and target data. The clutter subspace and jammer subspace are orthogonal to each other because they are independent vectors and satisfy the properties of orthogonality. Therefore if the received data is firstly projected on to a subspace orthogonal to clutter subspace that is jammer subspace then the clutters can be eliminated. And the jammer can be easily nulled out from the resulting signal to make it a useful signal. The whole algorithm is based on the matrix operation called projection, which is actually representation of same data using different basis vectors. Here we need to know more about clutter and jammer subspaces to understand the process well. A. Clutter and Jammer Subspaces The clutter subspace Sc can be described as the subspace spanned by the array response vectors with Doppler combinations corresponding to clutter patches. The remaining vectors U span s subspace orthogonal to Sc, which we denote as Sc┴. For notational convenience both Sc and Sc┴ are assumed to matrices with orthonormal columns. R{Sc(r)}≈R{[Vst(ϕ,f1;r),.....Vst(ϕ,fN;r)]} (2) Where R{A} denotes the range space of matrix A. For a jammer component rj, the vector exists in a relatively low dimensional subspace. This subspace can be found out by singular value decomposition of Rj. The jammer subspace Sj is spanned by the array response vectors corresponding to the jammer azimuth and all possible Doppler frequencies. R{Sj(r)}≈ R{[Vst(ϕj,f1;r),.....Vst(ϕj,fN;r)]} (3) Projecting the data on to the columns of Sc ┴, we can remove the clutter component because (Sc┴)H r(r)=(Sc┴)H rc(r)+ (Sc┴)H rj(r)+(Sc┴)H rn(r) (4) ≈ (Sc┴)H rj(r) + (Sc┴)H rn(r) The degree to which the clutter can be removed depends upon the quality of the subspace chosen. By knowing the array response and the platform position relative to ground, we can compute Sc┴ without requiring any measured data. Thus the process of clutter removal can be accomplished without the potentially estimation of the covariance matrix .however to complete the space time processing we have to compute the jammer covariance matrix. In practice, the accurate estimation of the clutter subspace requires a more sophisticated and detailed local earth model, rather than relatively simple model chosen here. The sensitivity to the clutter model can be reduced by increasing the dimension of the clutter subspace or equivalently reducing the dimension of Sc┴. Estimating the jammer signal from receive only data does have some drawbacks that is they reduce the time for active radar operation and there is always a chance that the jammer may change after it was measured. IV. SIMULATIONS AND ANALYSIS For simulations we use the Monte Carlo simulations for randomly generating the signal and noise based on statistic. The 8 element ULA is defined and element
• 4.
  International Journal ofTechnical Research and Applications e-ISSN: 2320-8163, www.ijtra.com Volume 2, Issue 3 (May-June 2014), PP. 163-168 166 | P a g e spacing is selected as λ/2, where λ is the wavelength of the signal. The system is mounted on a plane at 1000m high and radar platform is moving with same velocity as of the flight. The target is a non-fluctuating target and of radar cross section 1 square metre. The jammer signal with 100 W radiated power is defined. The next interference to be defined is the clutter. A clutter with γ value 15 dB is selected which is the γ value often selected for a terrain of woods. The clutter will contribute to the received signal as patches for each range bin. Platform direction is through 0 to 90 degrees as the antenna array is back baffled. Maximum range is selected as 5000 metres. Then a two way free space propagation path for the signal is created. The received signals in the first pulse interval is plotted as in the Fig. 2 and used for studying the nature of received signal. We found that the clutter is masking the target which is plotted as the blue vertical line. We have to do further processing to remove or suppress the clutter for making the received signal more useful. Now we can examine how the conventional method s like Displaced Phase Centred Antenna (DPCA) and Sample Matrix Inversion (SMI) are used to suppress the clutter in the received signal. Fig. 2: Received signal during the first pulse interval. After that we used subspace projection based algorithm to remove the clutter. The clutter suppressed signal using subspace based algorithm is shown in Fig.3. First we applied the theoretical algorithm which says that if the received signal is projected on a subspace other than clutter subspace, we can suppress the clutter. Here we assume that both of these subspaces are orthogonal to each other. But in the practical case it is very difficult to estimate the subspace other than clutter from the received signal which is a mixture of target, clutter and jammer responses. Practically two approaches can be used, either we can make the radar into receiver only mode and collect the jammer signals or we can use historical data for the projection purpose. Fig.3. Clutter Suppressed signal using Subspace Based technique Next we analysed the probability of detection of all the for algorithms and then SINR and plotted them compare the goodness of the algorithms which is shown in Fig. 4. The results obtained from theoretical subspace projection are found to be really good. There are some difference in practical case and theoretical case but can be resolved in the future research so as to get a good technique for clutter suppression. Although the results obtained by DPCA are very good, the radar platform has to satisfy very strict requirements in its movement to use this technique. Fig.4 Probability of Detection v/s SINR Plots Then SINR is plotted against the rank of the subspace which shows that better SINR is obtained at higher ranks. Fig.5 shows the result.
• 5.
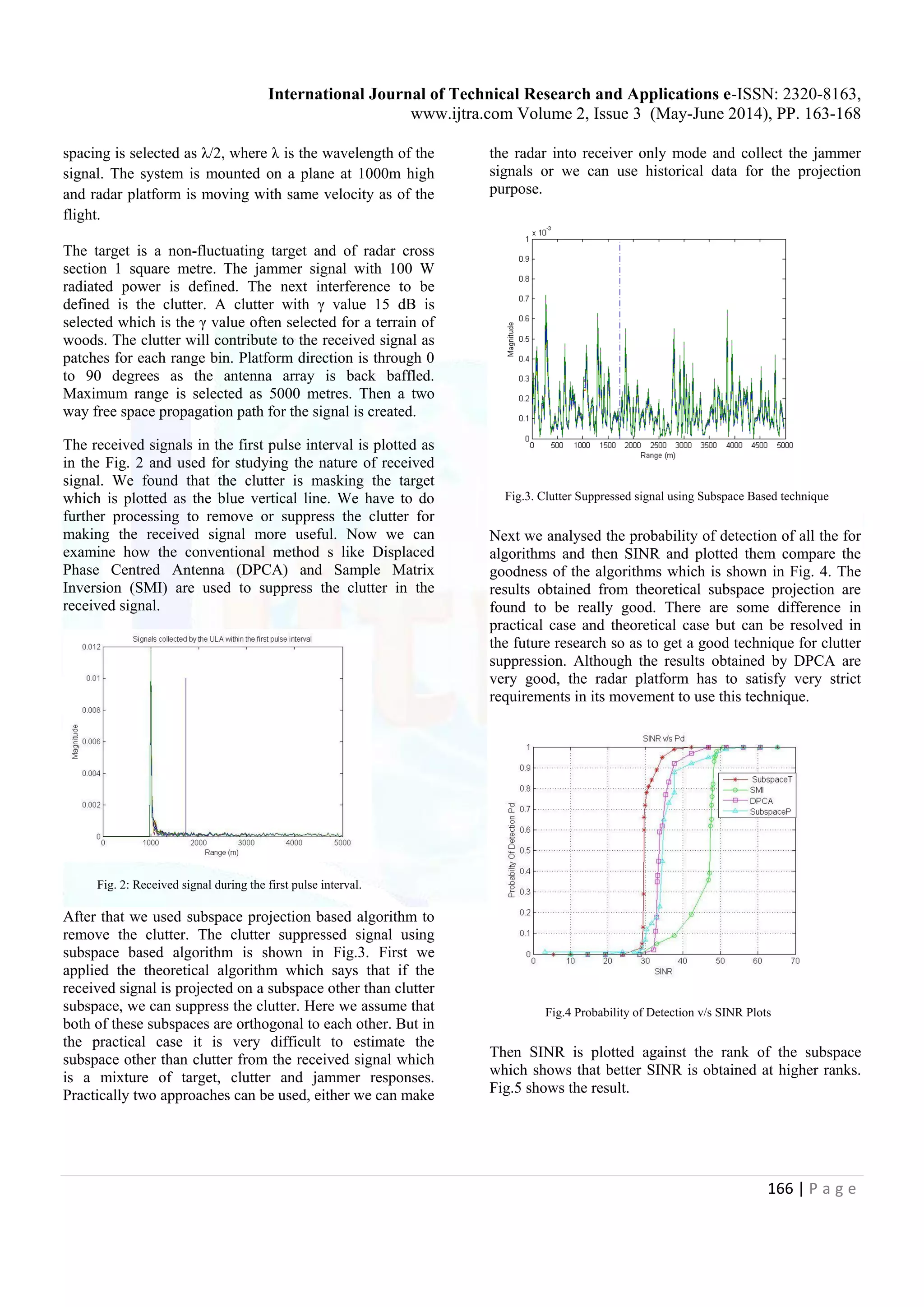
  International Journal ofTechnical Research and Applications e-ISSN: 2320-8163, www.ijtra.com Volume 2, Issue 3 (May-June 2014), PP. 163-168 167 | P a g e Fig. 5 SINR v/s Rank of the subspace The SINR is also plotted against the no: of range gates and found that higher ranges results are good. The result is shown in Fig.6. Fig. 6 SINR v/s Range Snapshots V. CONCLUSION The ground moving target surveillance is a very important application of radars as always. But usually airborne radars used for the purpose are faced with objections caused by the interference. STAP has been a best option for suppressing the clutters and make targets detectable. The subspace based technique for clutter suppression is based on matrix operations and are easy to apply. The subspace can be chosen by measuring the orthogonality between the received signal space and the subspace in which the data is to be projected. This method consumes less time to perform the operation and does not have any hardware issues like DPCA algorithm. The probability of detection against SINR is found to be the best for Subspace projection based technique. The future works can find a more effective practically possible subspace and eliminate the parity between both cases. If the rank of the subspace we can improve the performance of the algorithm, but this will increase the computational load. So we always try to keep a compromise between rank and Signal strength. ACKNOWLEDGMENT I express my heart filled gratitude to Prof. Dinesh M Chandwadkar, HOD, Department of Electronics and Communication, KKWIEER for giving me the opportunity to carry out this project. I profusely thank Prof. Dr. Ashish.A.Bhargave, my guide and mentor who helped me in every step of the project, patiently clearing out my incessant doubts. His technical competence is far beyond imagination. Both as a person and guide he has lead me into a realm of professionalism. I would also like to thank my teachers and friends who have helped me to do the work successfully. REFERENCES [1] L. E. Brennan and L. S. Reed, “Theory of adaptive radar”, Aerospaceand Electronic Systems, IEEE Transactions on, vol. AES-9, no. 2, pp.237–252, 1973. [2] J. Ward, “Space-Time Adaptive Processing for Airborne Radar”, Technical Report 1015, MIT Lincoln Laboratory, Lexington, MA, USA, 1994 (available: http://handle.dtic.mil/100.2/ADA293032) [3] D. Rabideau and A. Steinhardt, “Improved Adaptive Clutter Cancellation through Data-Adaptive Training”, IEEE Transactions on Aerospace and Electronic Systems, vol. 35, no. 3 (1999), pp. 879-891 [4] A. M. Haimovich and Y. Bar-Ness, “An Eigen analysis interference canceller”, Signal Processing, IEEE Transactions on, vol. 39, no. 1,pp. 76–84, 1991. [5] A. Haimovich, “The Eigen canceller: adaptive radar by Eigen analysis methods”, Aerospace and Electronic Systems, IEEE Transactions on,vol. 32, no. 2, pp. 532–542, 1996. [6] A. M. Haimovich and M. Berin, “Eigen analysis-based space- time adaptive radar: performance analysis”, Aerospace and Electronic Systems,IEEE Transactions on, vol. 33, no. 4, pp. 1170–1179, 1997. [7] BARBAROSSA,S., and FARINA,A,:”Space time frequency processing of synthetic aperture radar signals”,IEEE TRANS. Aerosp.Electron.syst,1994,30,pp 341-358 [8] Zatman, M “Circular array STAP”.IEEE Transactions on Aerospace and Electronic Systems,36, 2 (Apr. 2000), 510-517. [9] Tapan K. Sarkar and RavirajAdve “Space-Time Adaptive Processing Using Circular Arrays” IEEE Antennas and Propagation Magazine, Vol. 43, No. 1, February 2001 pp.138 - 143 [10] T. K. Sarkar, S. Park, J. Koh, and R. A. Schneible, “A deterministic least square approach to adaptive antennas,” Digital Signal Processing— Rev.J., vol. 6, pp. 185–194, 1996.
• 6.
  International Journal ofTechnical Research and Applications e-ISSN: 2320-8163, www.ijtra.com Volume 2, Issue 3 (May-June 2014), PP. 163-168 168 | P a g e [11] T. K. Sarkar, H. Waiig, S. Park, R. Adve, J. Koh, Y. Zhang, M.C. Wicks, and R. D. Brown, “A Deterministic Least Squares Approach to Space-Time Adaptive Processing (STAP),” IEEE Transactions on Antennas am1 Propagation, Dec 2000 [12] B. Friedlander, "A Subspace Method for Space Time Adaptive Processing,"IEEE Trans. Sig. Proc. pp. 74-82, Jan. 2005. [13] J. S. Goldstein and I. S. Reed, “Subspace selection for partially adaptive sensor array processing”, Aerospace and Electronic Systems, IEEE Transactions on, vol. 33, no. 2, pp. 539–544, 1997. [14] Samira Dib1 , Mourad Barkat, Jean-Marie Nicolas, Morad Grimes “A Reduced Rank STAP and Staggered PRF for Multiple Target Situations” International Journal on New Computer Architectures and Their Applications (IJNCAA) 2(1): 52-69 The Society of Digital Information and Wireless Communications, 2012 (ISSN: 2220-9085