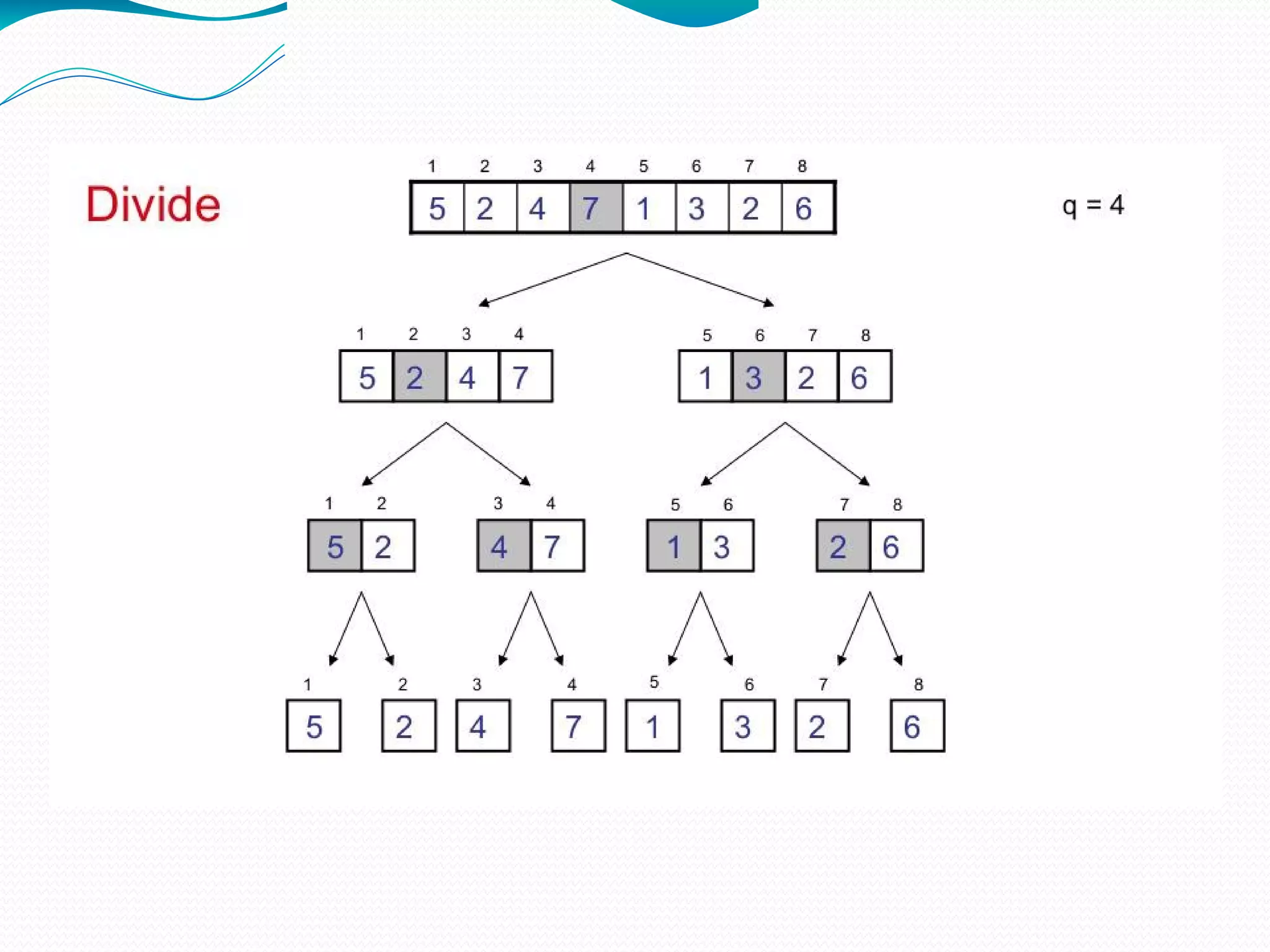
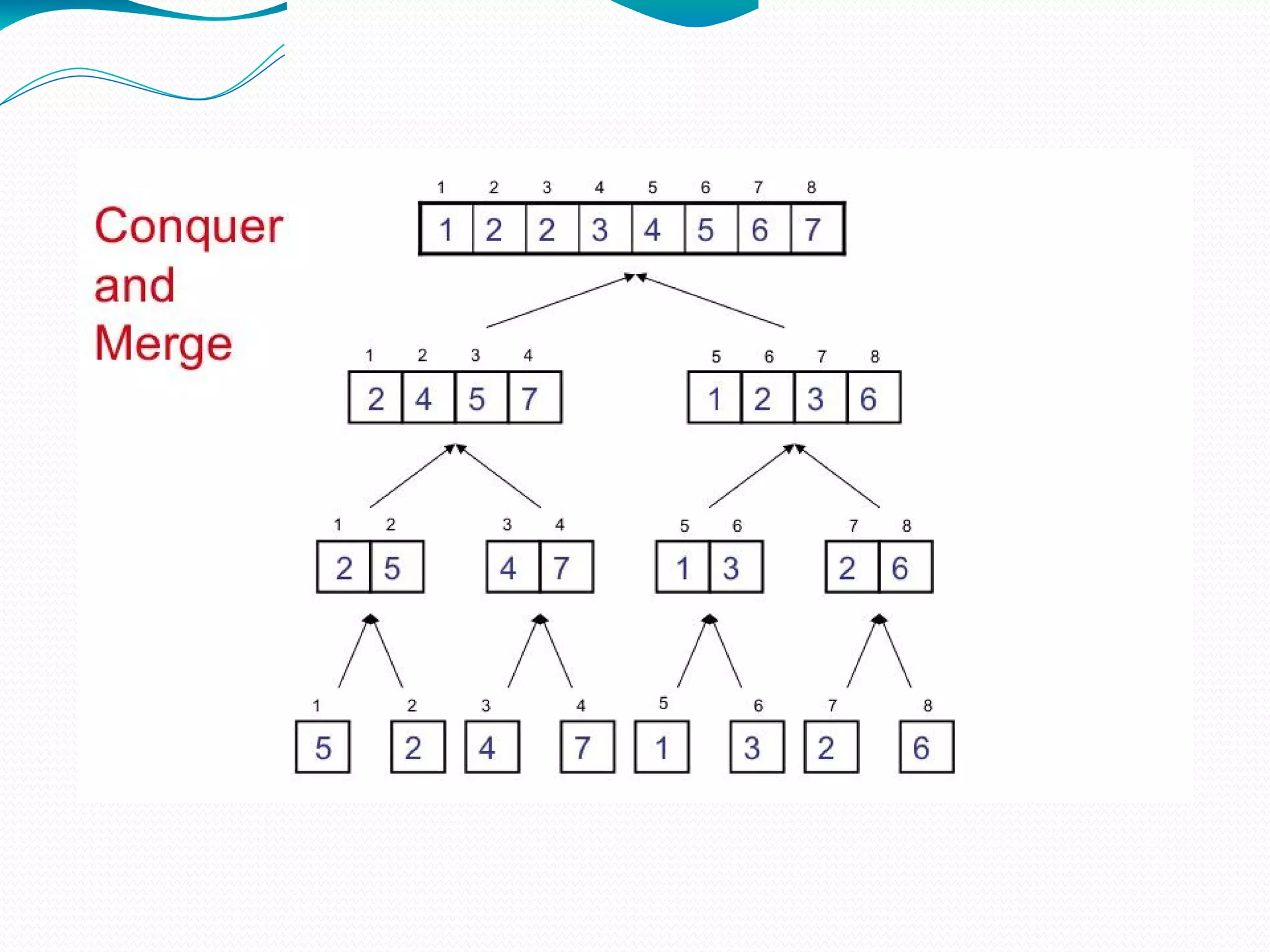
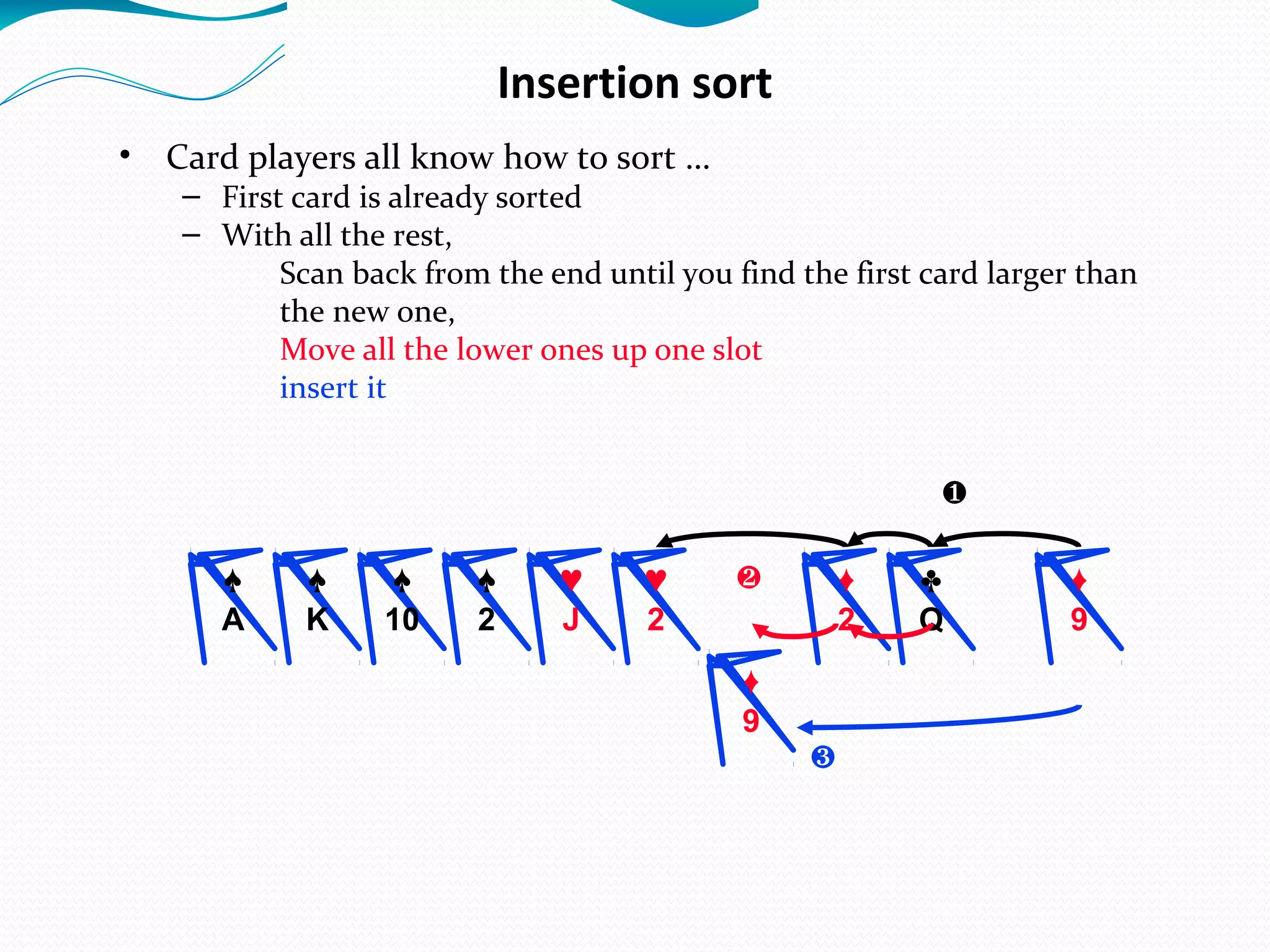
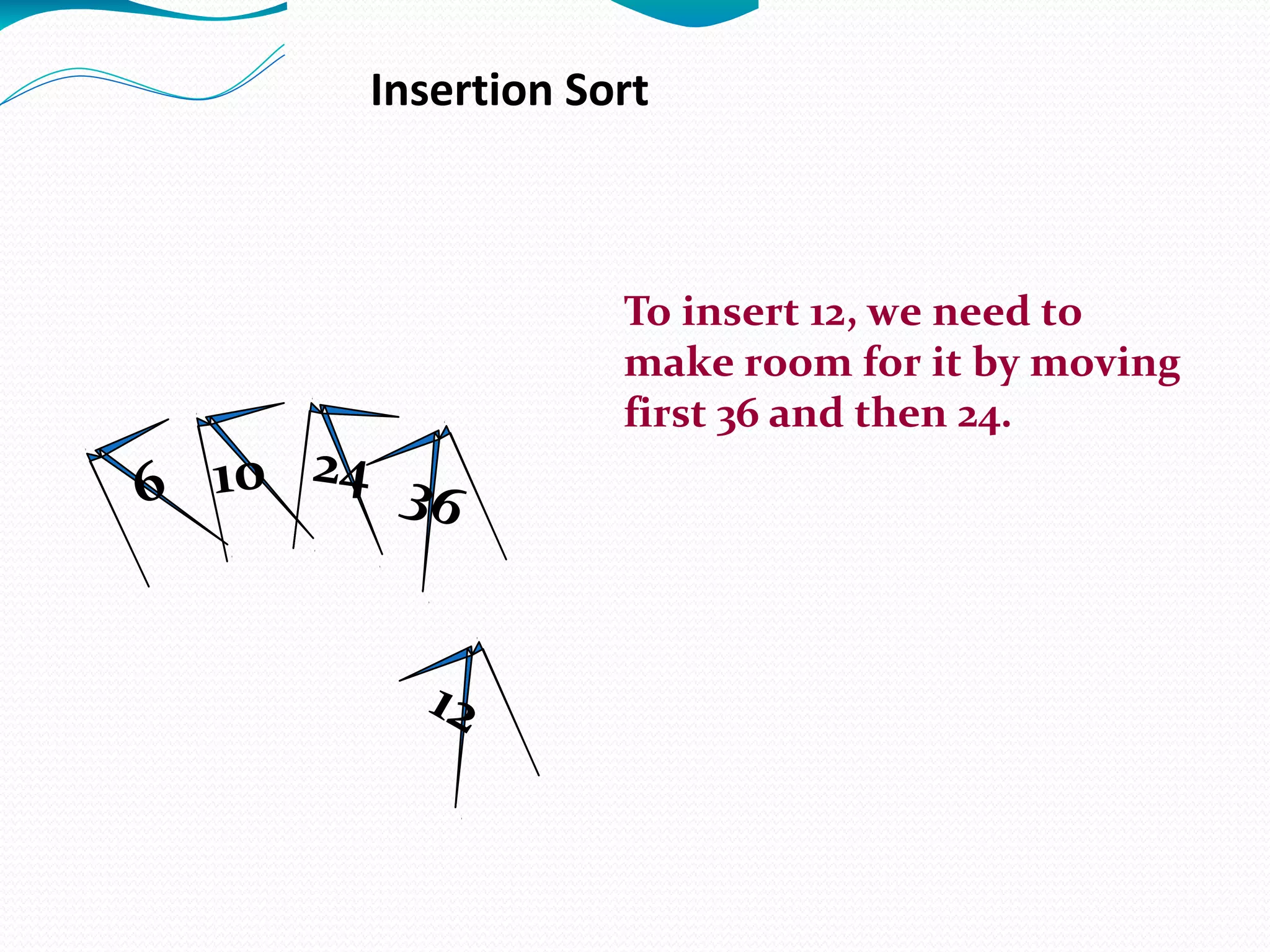
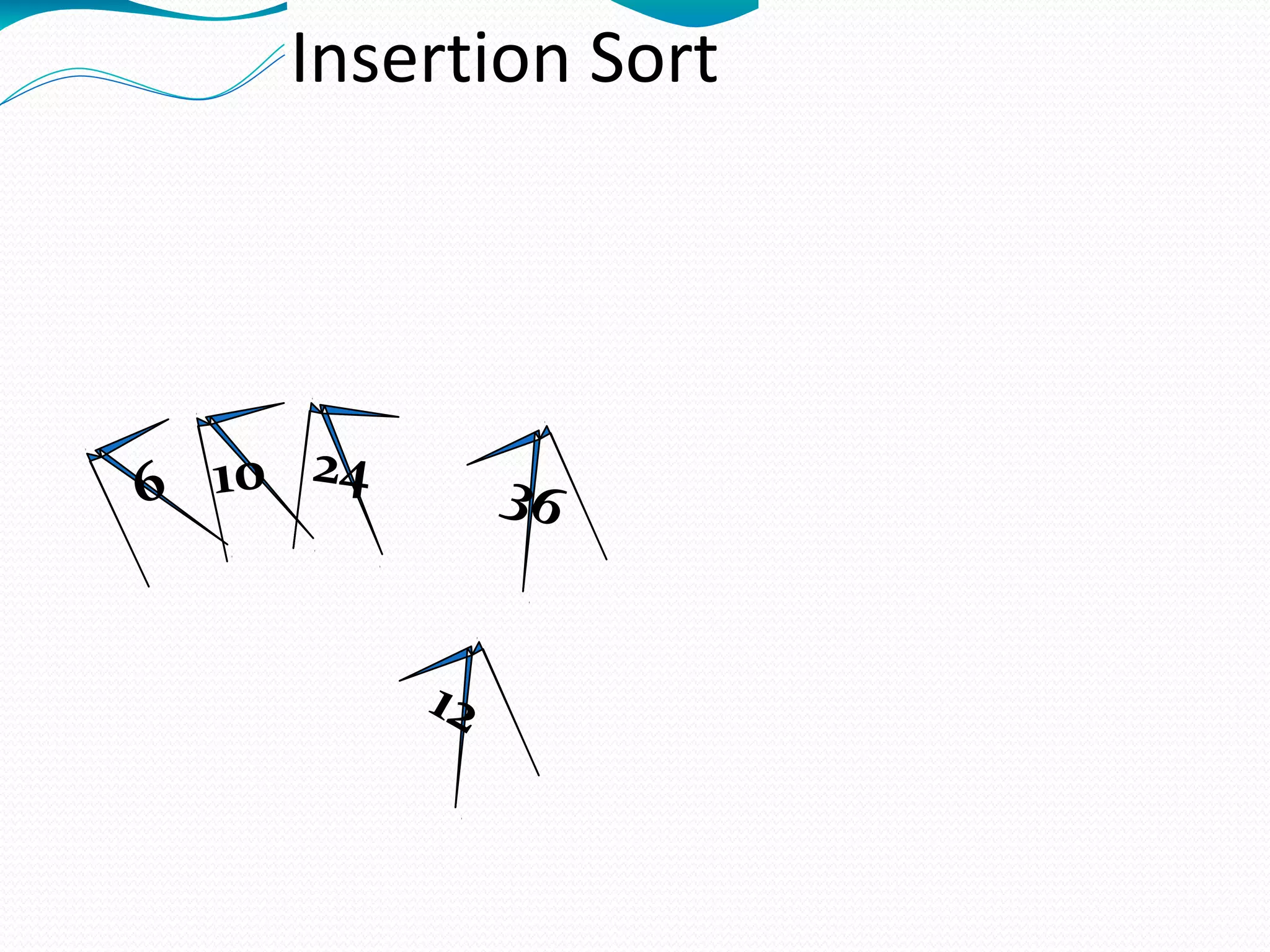
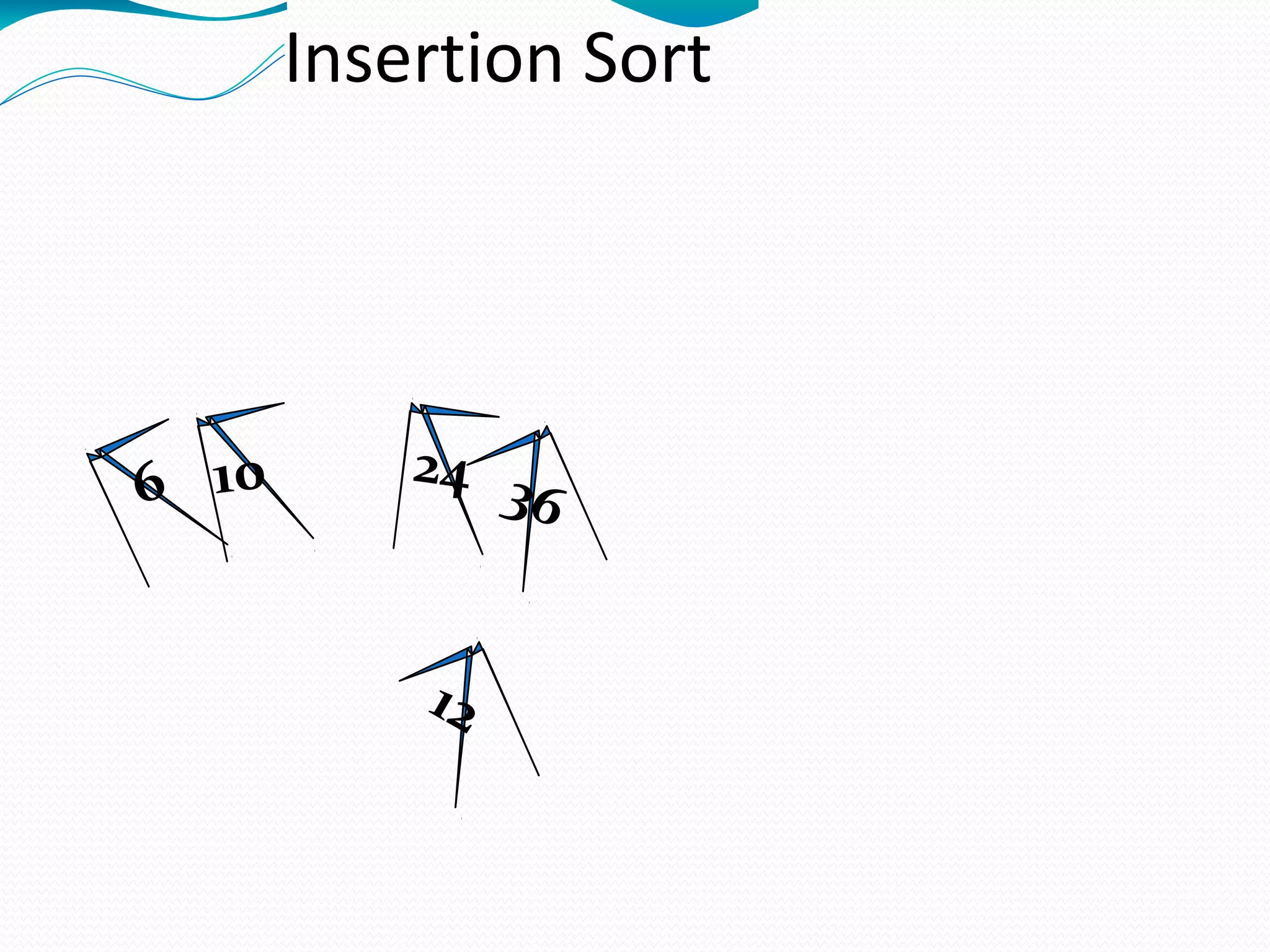
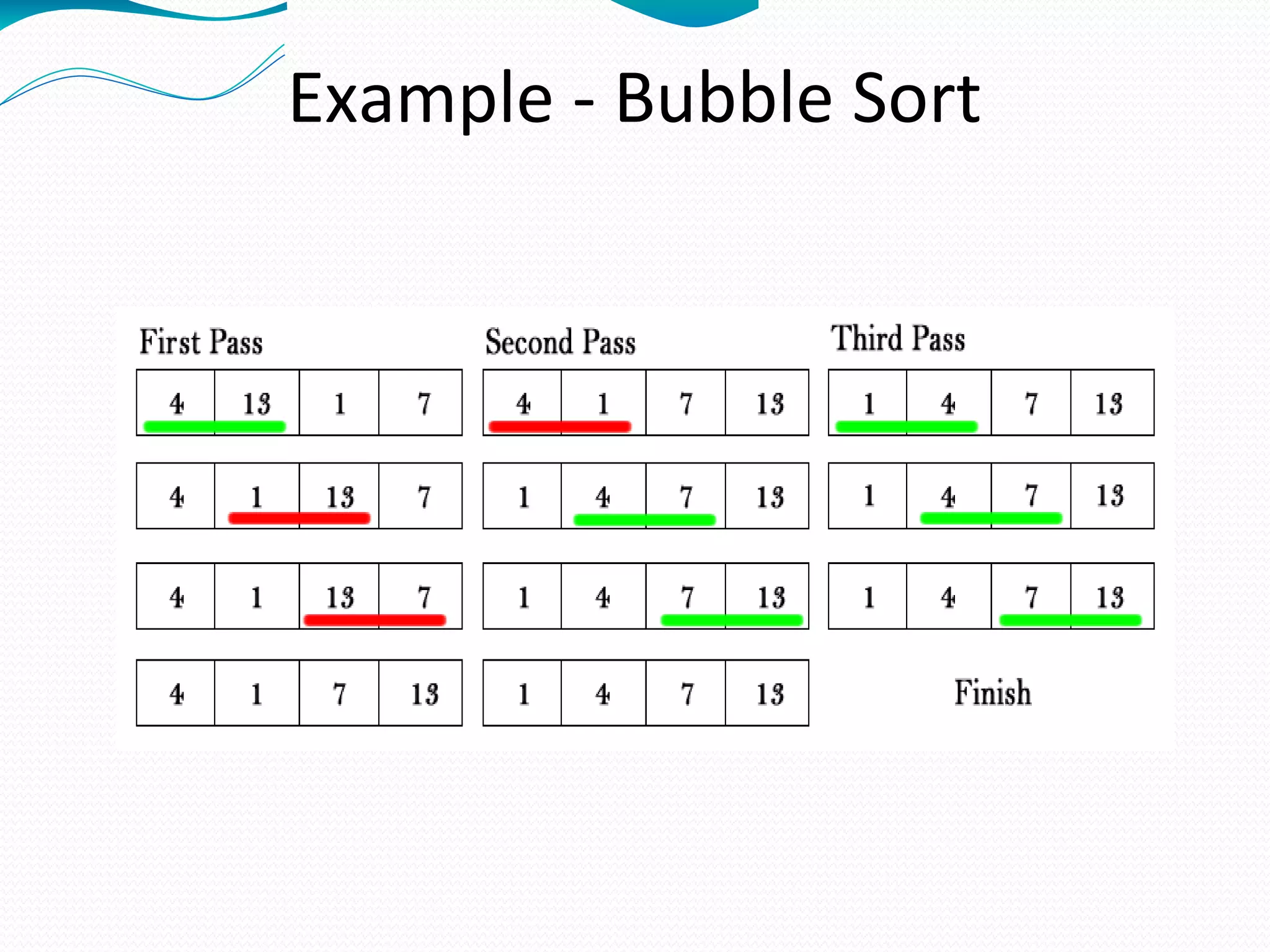
The document discusses several sorting algorithms: insertion sort, selection sort, bubble sort, and merge sort. It provides descriptions of how each algorithm works and comparisons of their time complexities. For insertion sort, it notes its advantage for nearly sorted data but quadratic worst-case time. Selection sort runs in quadratic time with little advantage for ordered data. Bubble sort is easy to implement but slower than insertion sort. Merge sort works by recursively dividing the array into halves and then merging the sorted halves.










![Bubble Sort Alg.: BUBBLESORT(A) for i ← 1 to length[A] do for j ← length[A] downto i + 1 do if A[j] < A[j -1] then exchange A[j] ↔ A[j-1] 1329648 i = 1 j i](https://image.slidesharecdn.com/algorithm-161124202203/75/Sorting-Algorithm-16-2048.jpg)