Downloaded 84 times
![Bubble Sort Algorithm in Java void bubbleSort(int List[]){ int temp; int size = List.length; for (i = 0; i < size - 1; i++) for (j = 0; j < size – (i + 1); j++){ if (List[j] > List[j+1]){ temp = List[j]; List[j] = List[j+1]; List[j+1] = temp; } } } } Time complexity of the Bubble Sort algorithm is O(n2). Think why?](https://image.slidesharecdn.com/part4basicsortingalgorithms-140828232256-phpapp01/75/Data-Structures-Part4-basic-sorting-algorithms-13-2048.jpg)
![Selection Sort Algorithm in Java void selectionSort(int List[]){ int temp, min; int size = List.length; for (i = 0; i < size; i++){ min = i; for (j = i + 1; j < size; j++){ if (List[j] < List[min]){ min = j; } } temp = List[min]; List[min] = List[i]; List[i] = temp; } } Time complexity of the Selection Sort algorithm is O(n2). Think why?](https://image.slidesharecdn.com/part4basicsortingalgorithms-140828232256-phpapp01/75/Data-Structures-Part4-basic-sorting-algorithms-18-2048.jpg)
![Insertion Sort Algorithm in Java void insertionSort(int List[]){ int temp; int size = List.length; for (int i = 1; i < size; i++){ int j = i; temp = List[i]; while (j > 0 && temp < List[j - 1]){ List[j] = List[j - 1]; // right shifting j--; } List[j] = temp; } } Time complexity of the Insertion Sort algorithm is O(n2). Think why?](https://image.slidesharecdn.com/part4basicsortingalgorithms-140828232256-phpapp01/75/Data-Structures-Part4-basic-sorting-algorithms-25-2048.jpg)
Uploaded byAbdullah Al-hazmy
Data Structures- Part4 basic sorting algorithms
The document discusses various sorting algorithms. It begins by explaining the motivation for sorting and providing examples. It then lists some common sorting algorithms like bubble sort, selection sort, and insertion sort. For each algorithm, it provides an informal description, works through examples to show how it sorts a list, and includes Java code implementations. It compares the time complexity of these algorithms, which is O(n2) for bubble sort, selection sort, and insertion sort, and explains why. The document aims to introduce fundamental sorting algorithms and their workings.
Data Structures- Part4 basic sorting algorithms
- 1. Data Structures I(CPCS-204) Week # 4: Sorting Algorithms
- 2. Sorting Motivation Generally, to arrange a list of elements in some order List of numbers 10 20 50 30 40 60 25 (Unsorted list) 10 20 25 30 40 50 60 (Sorted list, ascending) 60 50 40 30 25 20 10 (Sorted list, descending) List of alphabets P A K I S T A N (Unsorted list) A A I K N P S T (Sorted list, ascending) T S P N K I A A (Sorted list, descending)
- 3. Sorting Algorithms 1.Bubble Sort 2. Selection Sort 3. Insertion Sort 4. Quick Sort 5. Merge Sort There are few more sorting algorithms; you can find them in a book on data structures and algorithms (or on the Web)
- 4. Bubble Sort Algorithm:Informal Repeatedly compare the elements at consecutive locations in a given list, and do the following until the elements are in required order: If elements are not in the required order, swap them (change their position) Otherwise do nothing
- 5. Bubble Sort inAction: Phase 1 3 15 45 40 8 12 5 22 14 3 15 45 40 8 12 5 22 14 3 15 45 40 22 8 12 5 14 3 15 45 40 22 8 12 5 14 3 15 45 40 8 12 22 5 14 3 15 45 40 8 22 12 5 14 3 15 45 40 22 8 12 5 14 3 45 15 40 22 8 12 5 14 45 3 15 40 22 8 12 5 14 8 c o mpari s o ns
- 6. 45 3 15 40 22 8 12 5 14 Bubble Sort in Action: Phase 2 45 3 15 40 22 14 8 12 5 45 3 15 40 22 14 8 12 5 45 3 15 40 22 8 12 14 5 45 3 15 40 22 8 14 12 5 45 3 15 40 22 14 8 12 5 45 3 40 15 22 14 8 12 5 45 40 3 15 22 14 8 12 5 7 c o mpari s o ns
- 7. Bubble Sort inAction: Phase 3 45 40 3 15 22 14 12 8 5 45 40 3 15 22 14 12 8 5 45 40 3 15 22 14 8 12 5 45 40 3 15 22 14 8 12 5 45 40 3 15 22 14 12 8 5 45 40 3 22 15 14 12 8 5 45 40 22 3 15 14 12 8 5 6 c o mpari s o ns
- 8. Bubble Sort inAction: Phase 4 45 40 22 3 15 14 12 8 5 45 40 22 3 15 14 12 8 5 45 40 22 3 15 14 12 8 5 45 40 22 3 15 14 12 8 5 45 40 22 3 15 14 12 8 5 45 40 22 15 3 14 12 8 5 5 c o mpari s o ns
- 9. Bubble Sort inAction: Phase 5 45 40 22 15 3 14 12 8 5 4 c o mpari s o ns 45 40 22 15 3 14 12 8 5 45 40 22 15 3 14 12 8 5 45 40 22 15 3 14 12 8 5 45 40 22 15 14 3 12 8 5
- 10. Bubble Sort inAction: Phase 6 3 c o mpari s o ns 45 40 22 15 14 3 12 8 5 45 40 22 15 14 3 12 8 5 45 40 22 15 14 3 12 8 5 45 40 22 15 14 12 3 8 5
- 11. Bubble Sort inAction: Phase 7 2 c o mpari s o ns 45 40 22 15 14 12 3 8 5 45 40 22 15 14 12 3 8 5 45 40 22 15 14 12 8 3 5
- 12. Bubble Sort inAction: Phase 8 1 c o mpari s o n 45 40 22 15 14 12 8 3 5 45 40 22 15 14 12 8 5 3
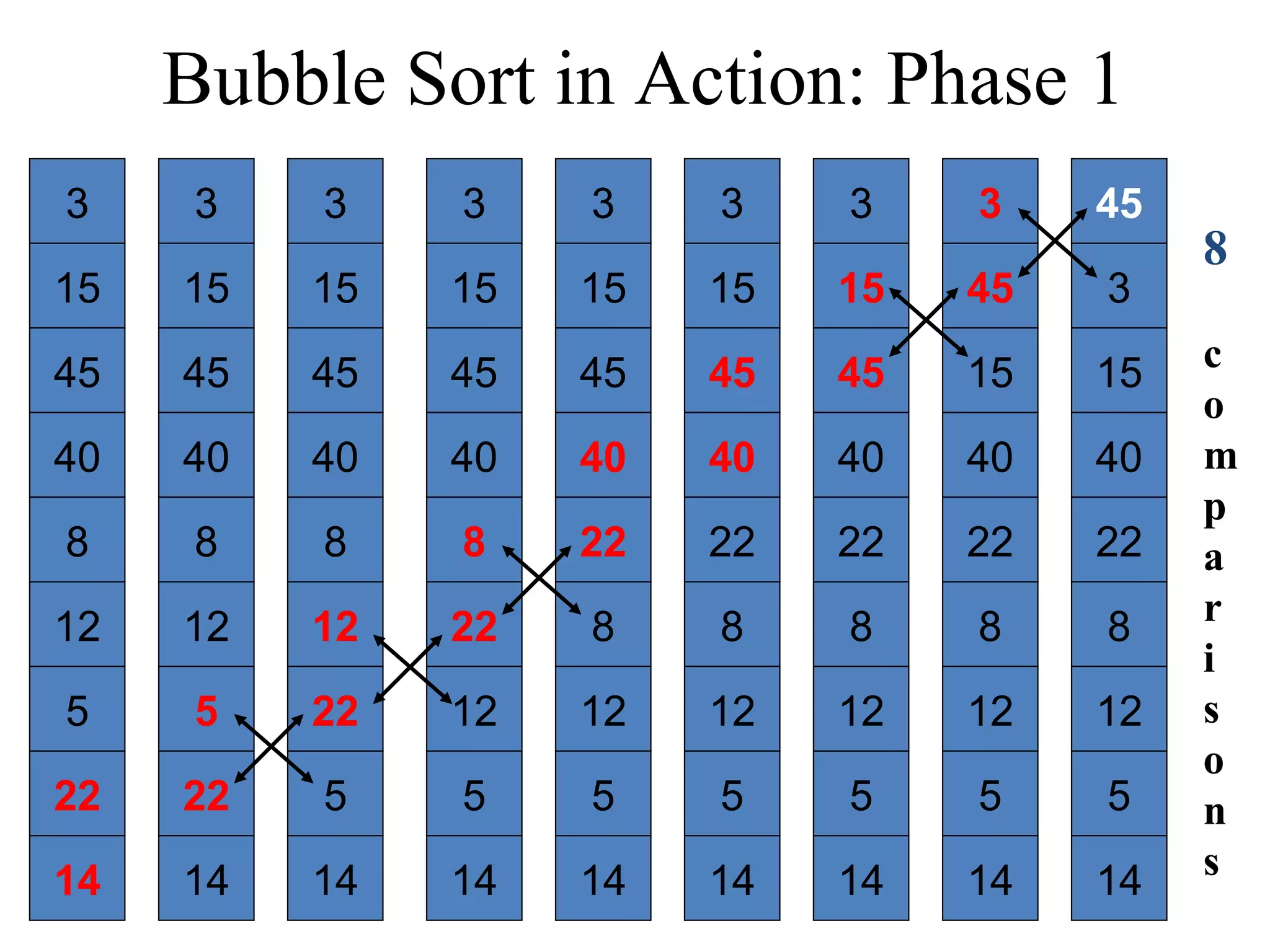
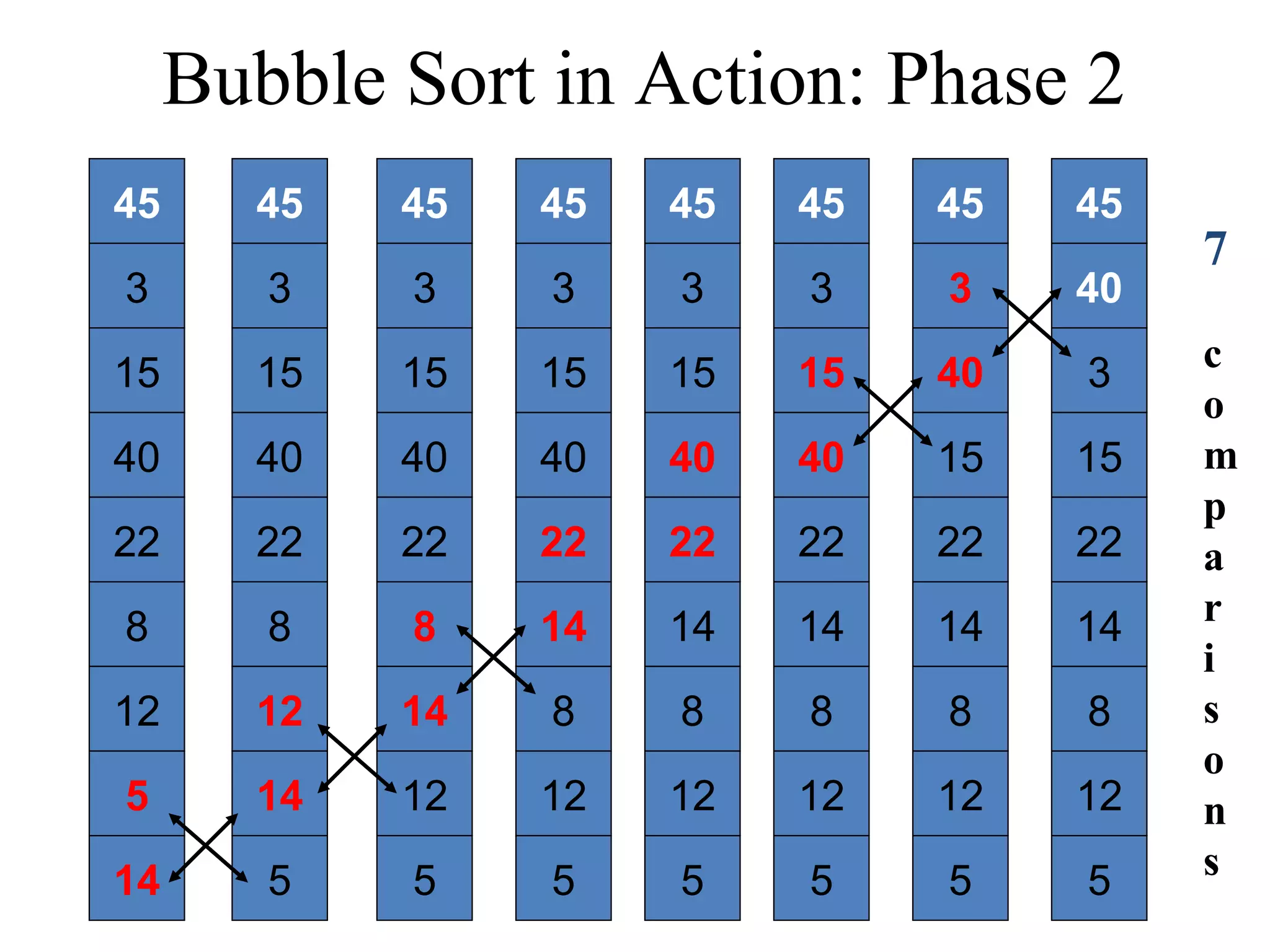
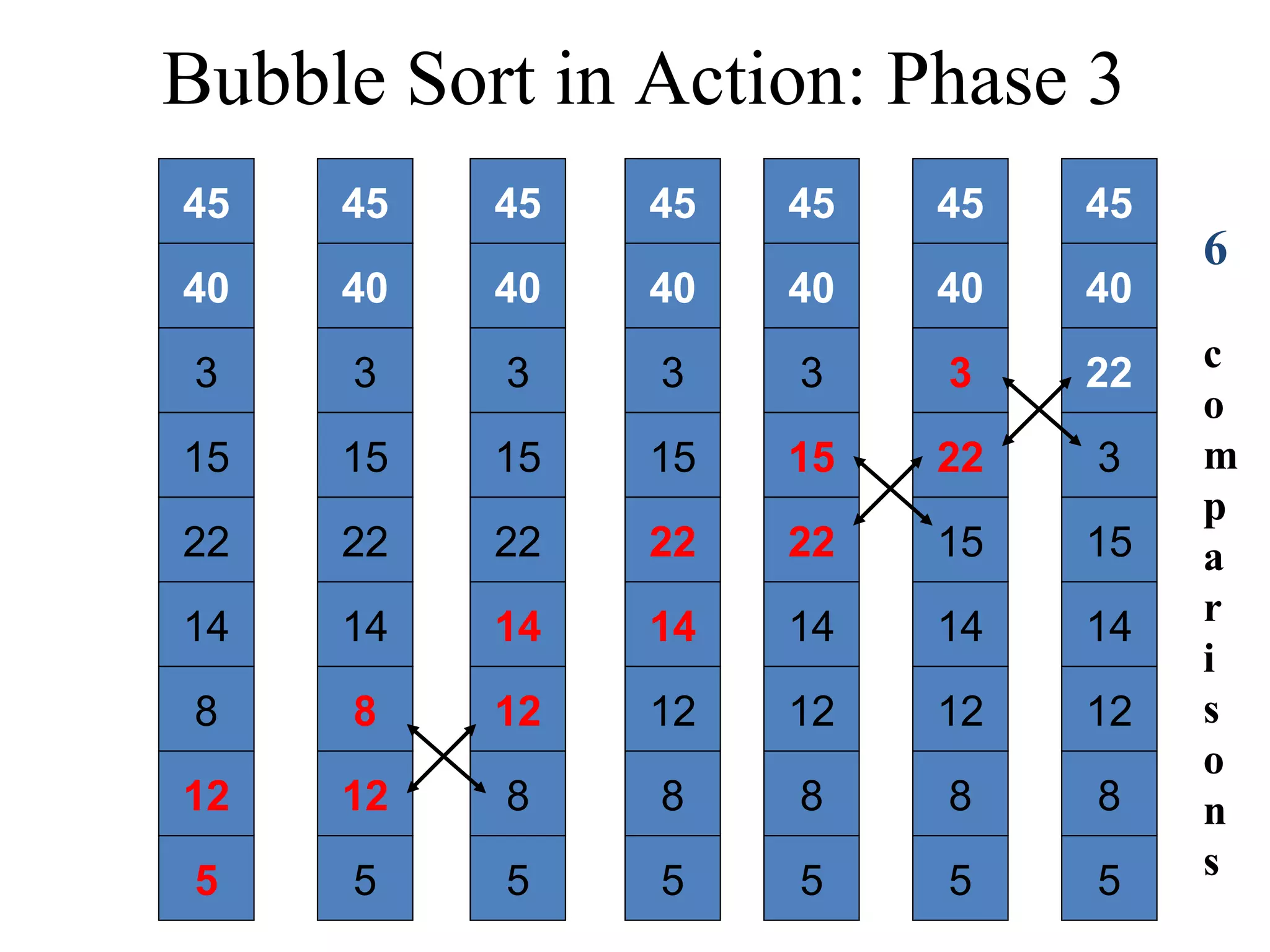
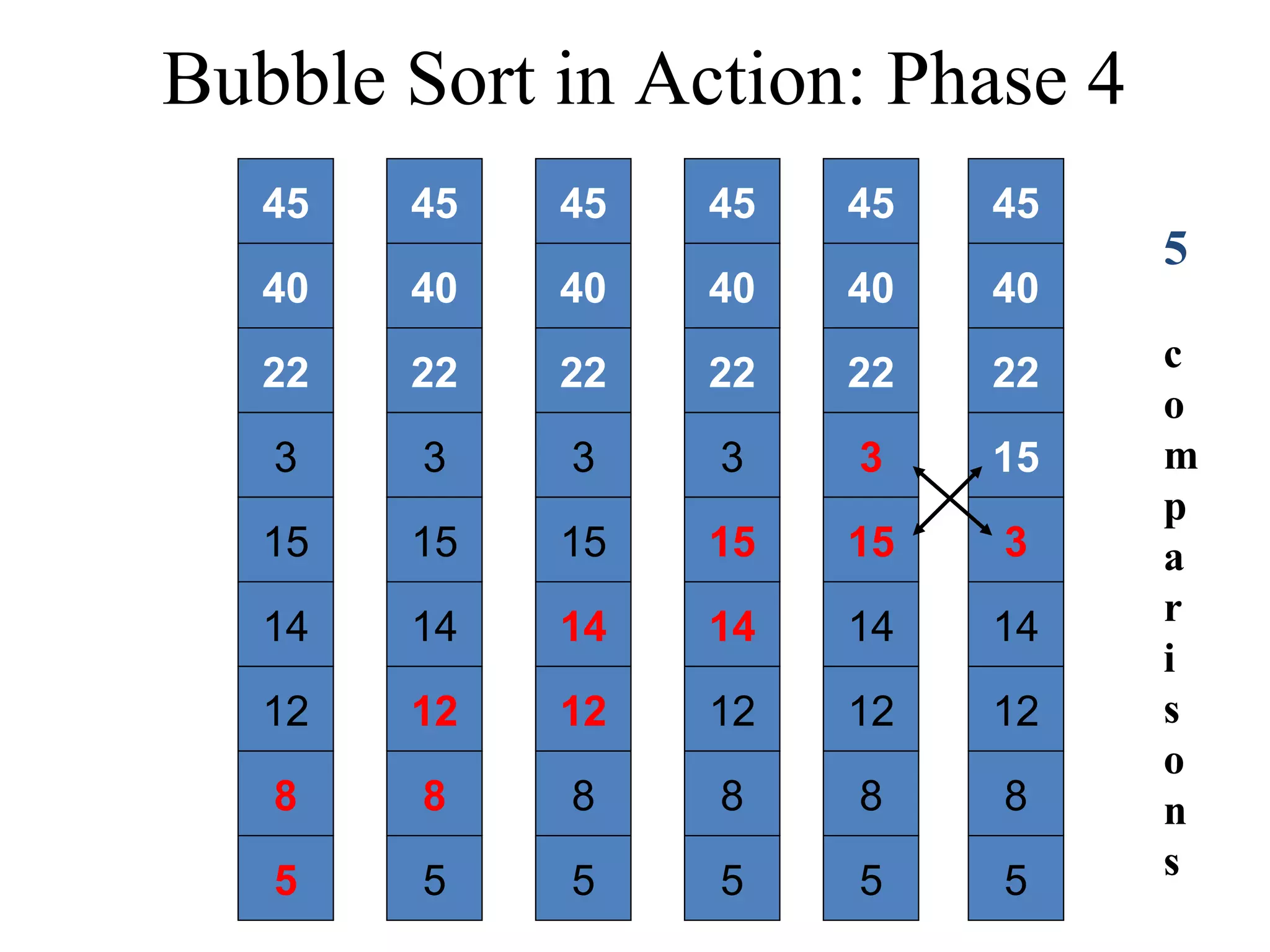
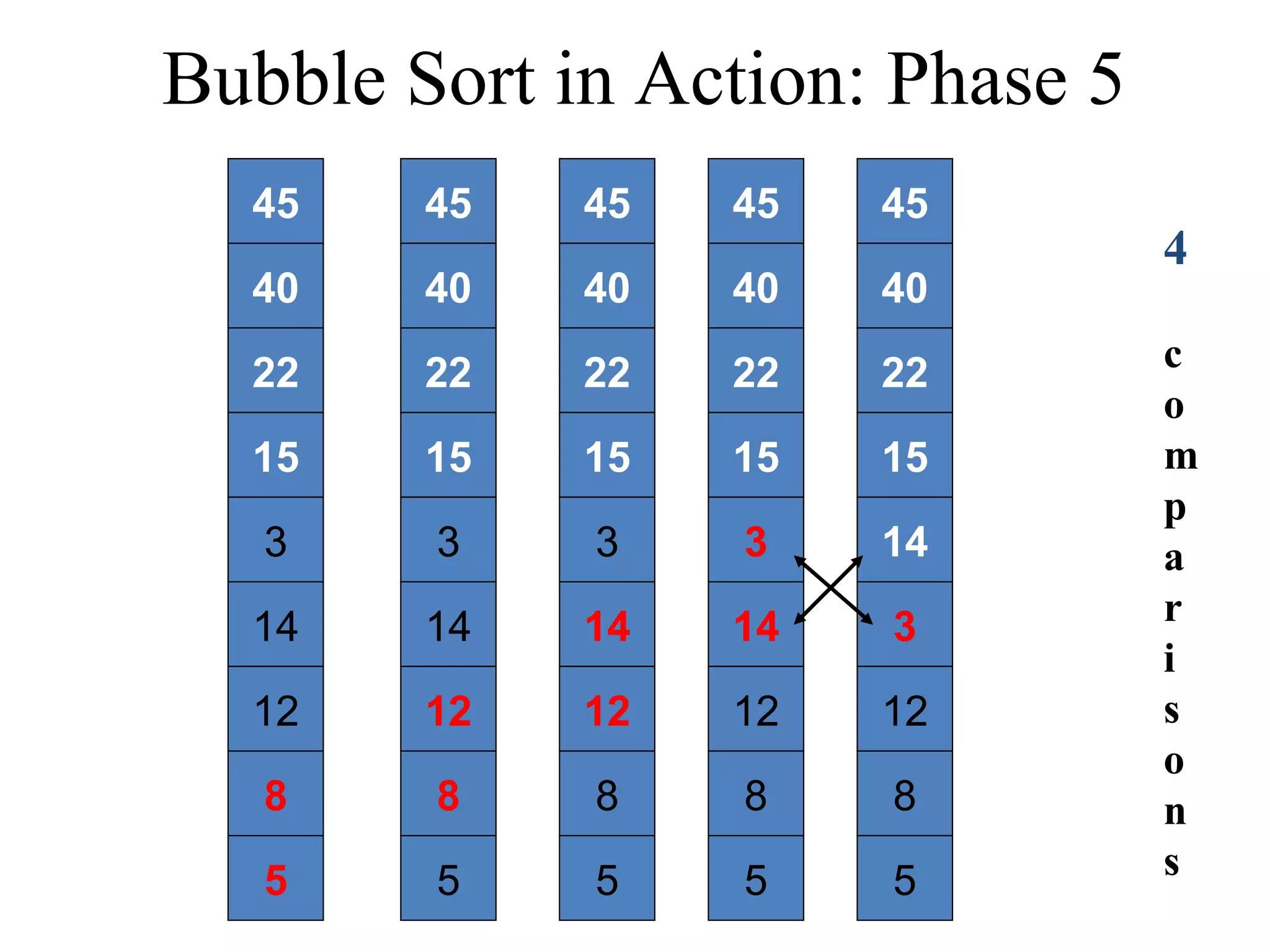
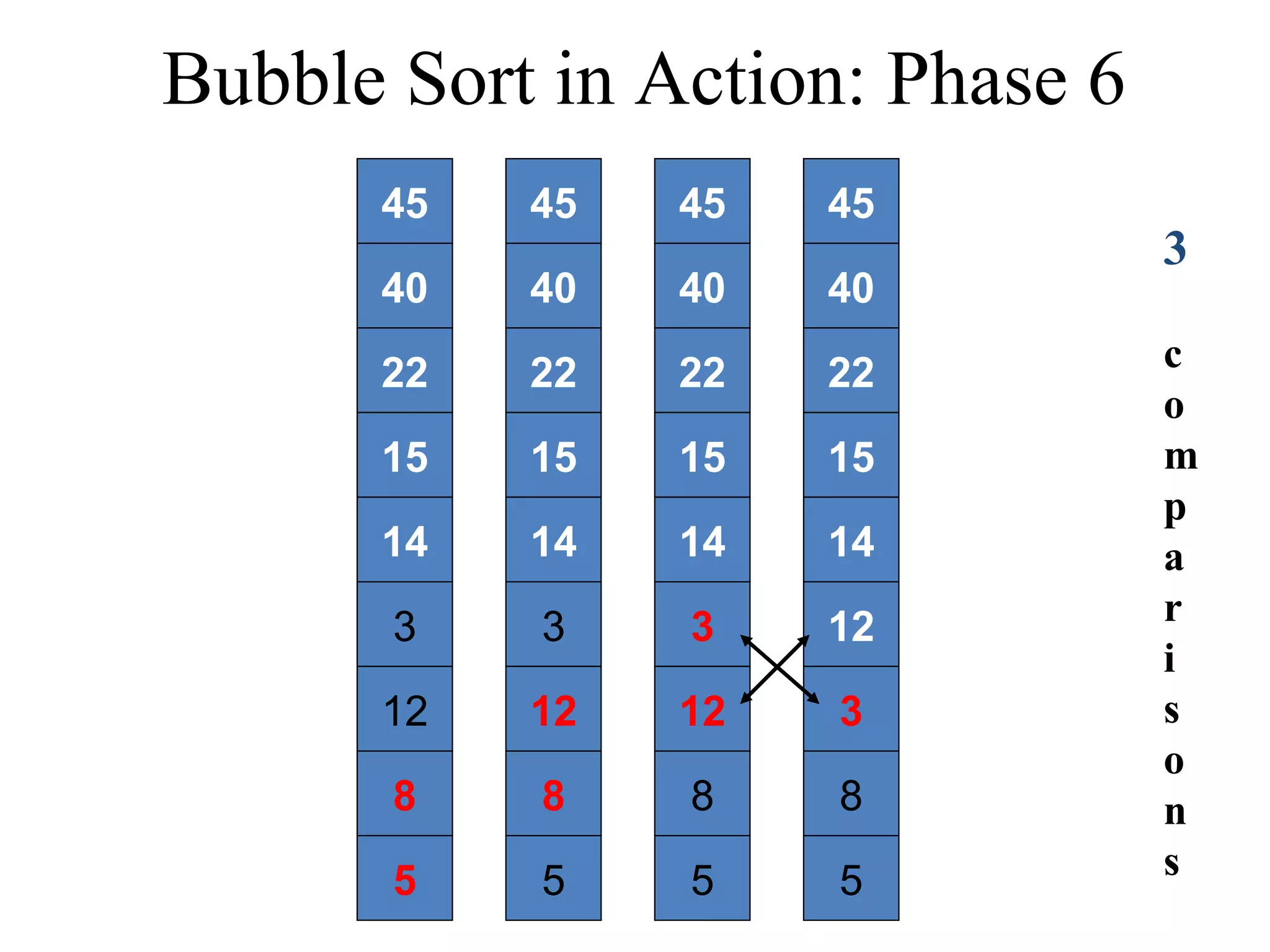
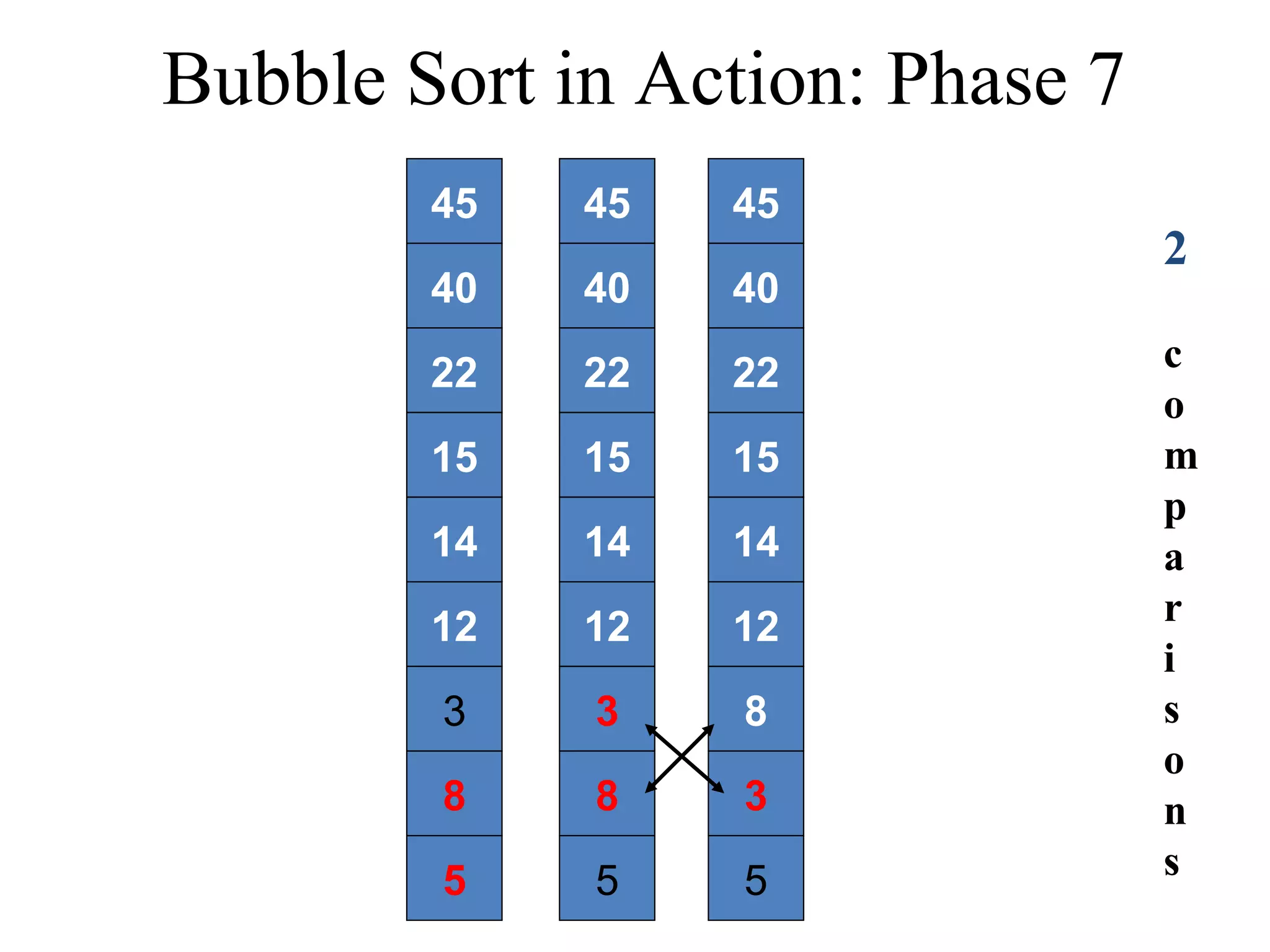
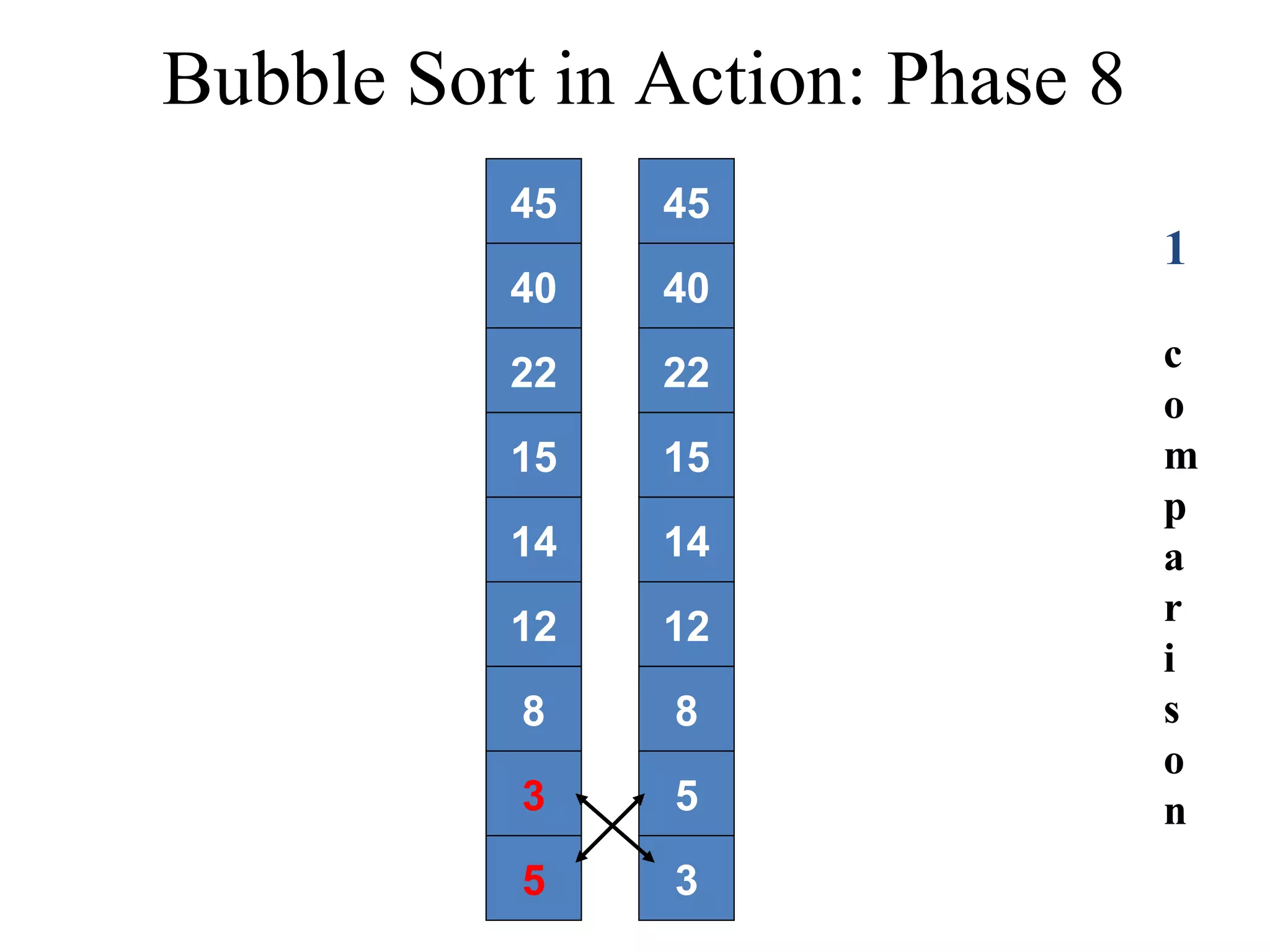
- 13. Bubble Sort Algorithmin Java void bubbleSort(int List[]){ int temp; int size = List.length; for (i = 0; i < size - 1; i++) for (j = 0; j < size – (i + 1); j++){ if (List[j] > List[j+1]){ temp = List[j]; List[j] = List[j+1]; List[j+1] = temp; } } } } Time complexity of the Bubble Sort algorithm is O(n2). Think why?
- 14. Selection Sort: Informal Suppose we want to sort an array in ascending order: Locate the smallest element in the array; swap it with element at index 0 Then, locate the next smallest element in the array; swap it with element at index 1. Continue until all elements are arranged in order
- 15. 14 15 45 40 22 12 8 5 3 14 15 45 40 8 12 22 5 3 14 15 45 40 8 12 5 22 3 3 15 45 40 8 12 5 22 14 Selection Sort in Action
- 16. Selection Sort inAction 22 15 45 40 14 12 8 5 3 14 15 45 40 22 12 8 5 3 14 15 45 40 22 12 8 5 3 22 40 45 15 14 12 8 5 3
- 17. Selection Sort inAction 22 45 45 40 40 40 45 22 22 15 15 15 14 14 14 12 12 12 8 8 8 5 5 5 3 3 3 45 40 22 15 14 12 8 5 3
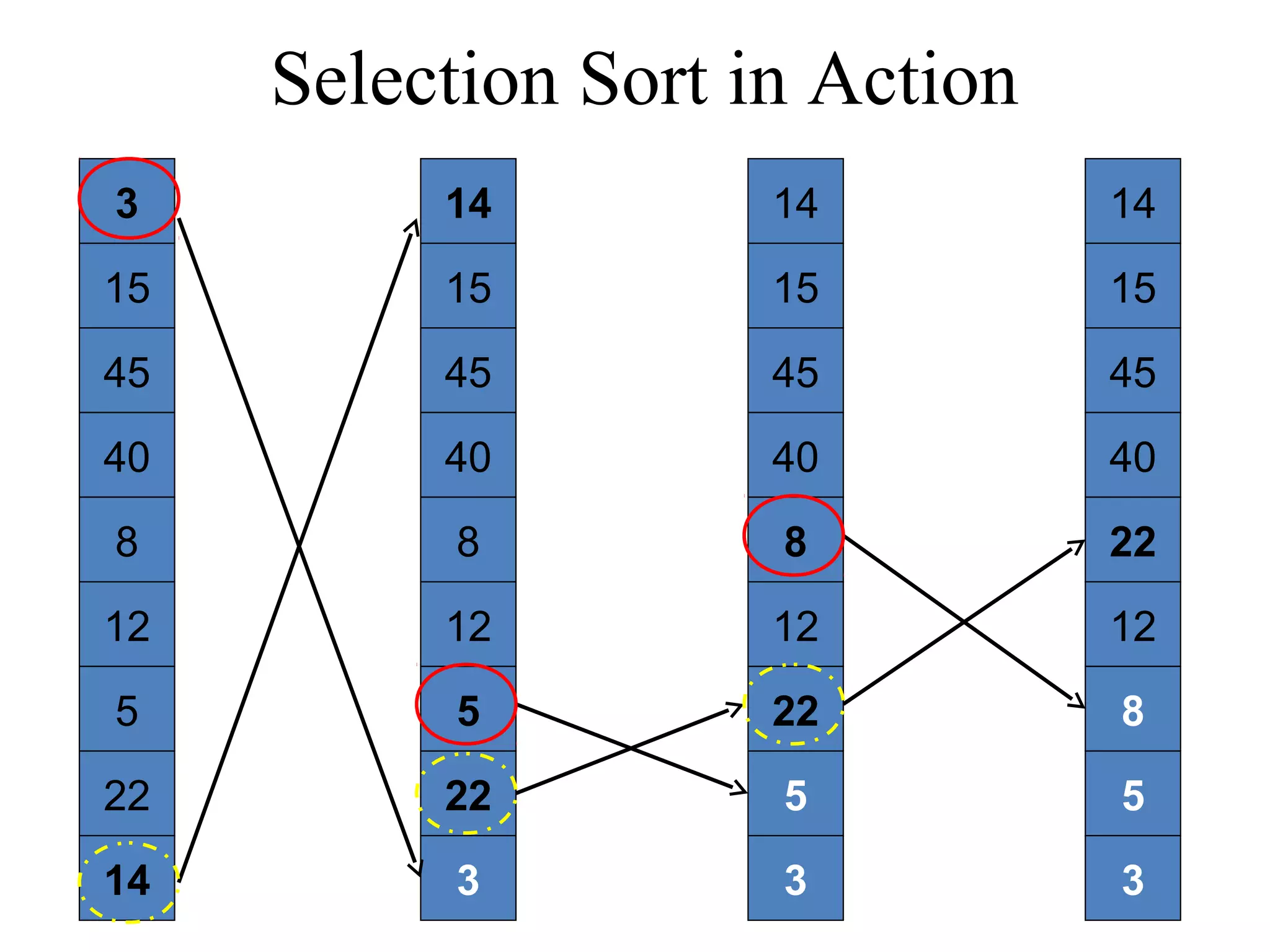
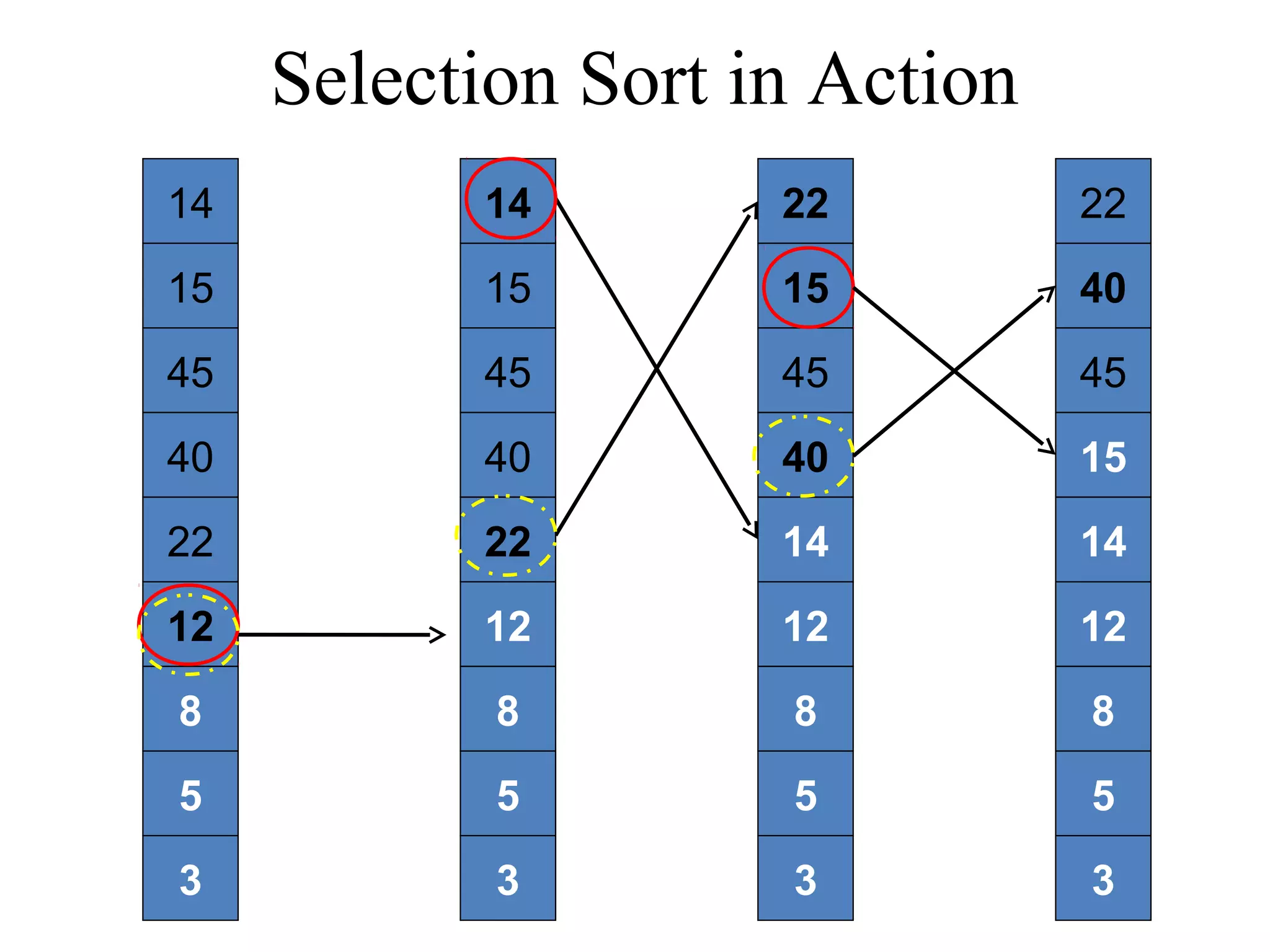
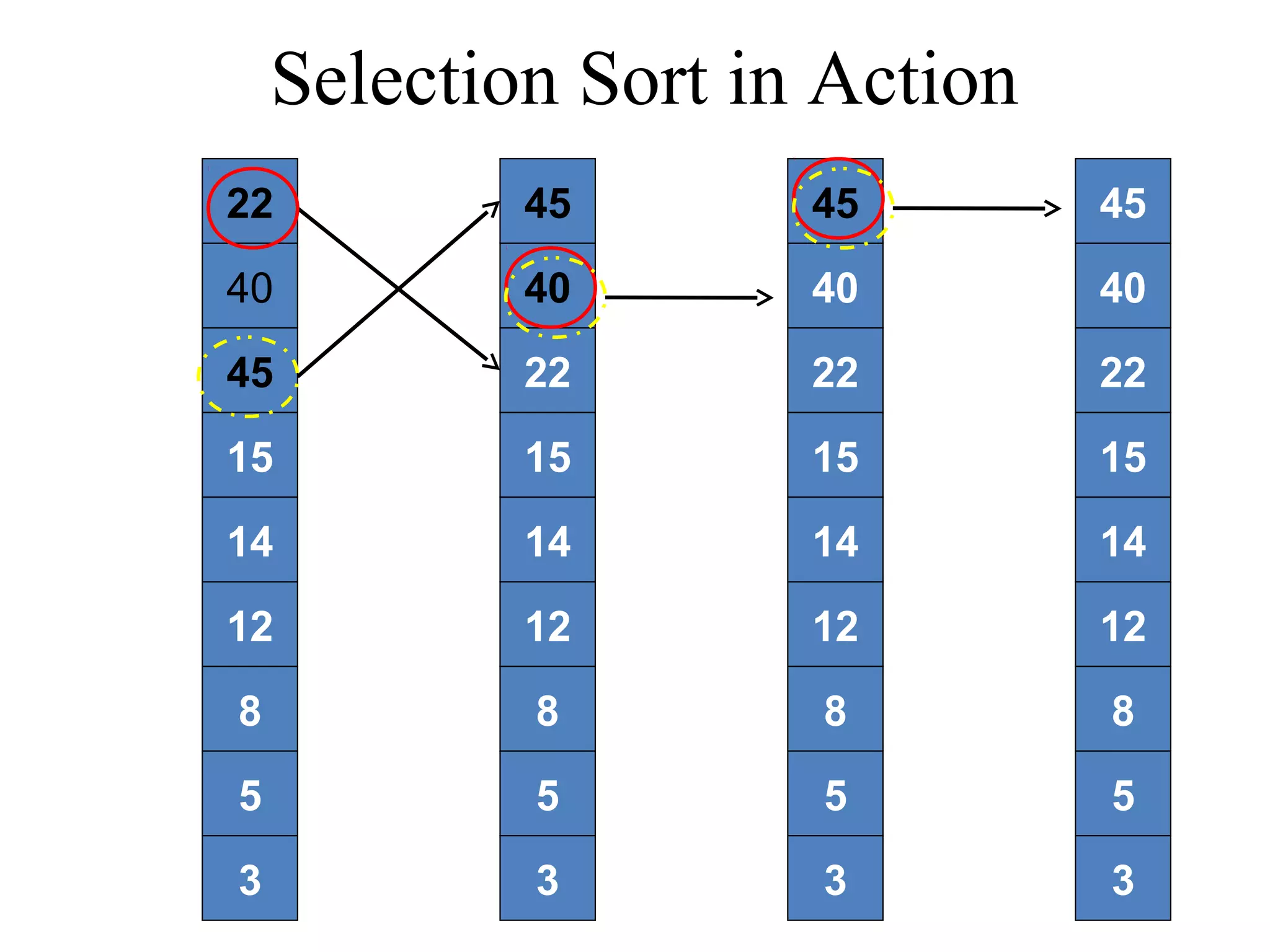
- 18. Selection Sort Algorithmin Java void selectionSort(int List[]){ int temp, min; int size = List.length; for (i = 0; i < size; i++){ min = i; for (j = i + 1; j < size; j++){ if (List[j] < List[min]){ min = j; } } temp = List[min]; List[min] = List[i]; List[i] = temp; } } Time complexity of the Selection Sort algorithm is O(n2). Think why?
- 19. Bubble Sort vs.Selection Sort Selection Sort is more efficient than Bubble Sort, because of fewer exchanges in the former Both Bubble Sort and Selection Sort belong to the same (quadratic) complexity class (O(n2)) Bubble Sort may be easy to understand as compared to Selection Sort – What do you think?
- 20. Insertion Sort Workslike someone who inserts one more card at a time into a hand of cards that are already sorted To insert 12, we need to make room for it … 6 10 24 36 12 20
- 21. 21 6 1024 … by shifting first 36 towards right… 36 12 21 Insertion Sort
- 22. … and thenshifting 24 towards right 6 10 24 36 12 22 Insertion Sort
- 23. Once room isavailable, insert the element (12 in this case) 6 10 12 24 36 23 Insertion Sort
- 24. Insertion Sort: Informal We divide the list into two parts: Sorted and Unsorted parts Initially o the sorted part contains the first element (at index 0) o the unsorted part contains the elements from index 1 to N-1 Then, we move element from index 1 to an appropriate position in the sorted part, keeping order intact Then, we move element from index 2 to an appropriate position in the sorted part, keeping order intact ... Finally, we move element from index N-1 to an appropriate position in the sorted part, keeping order intact
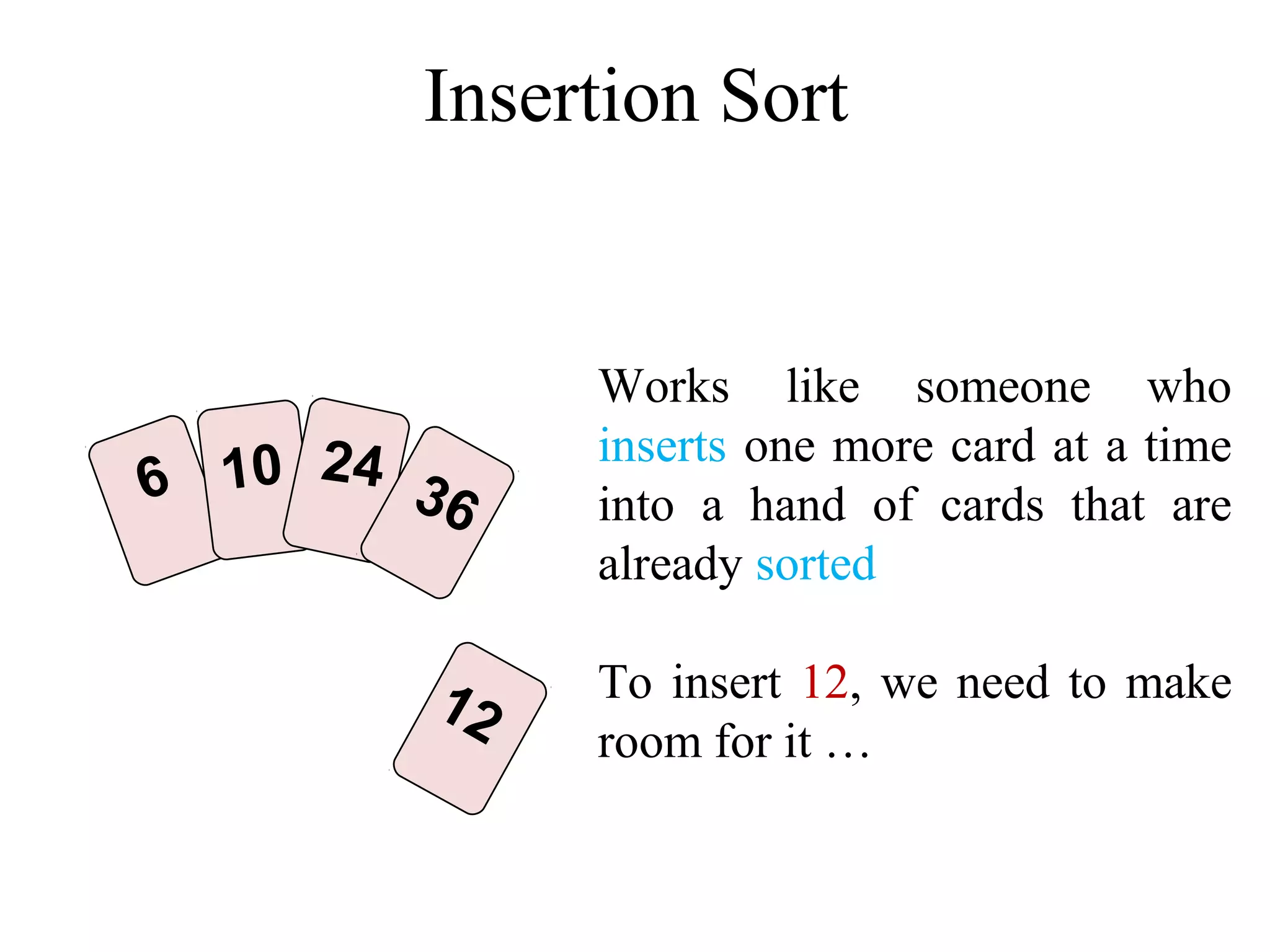
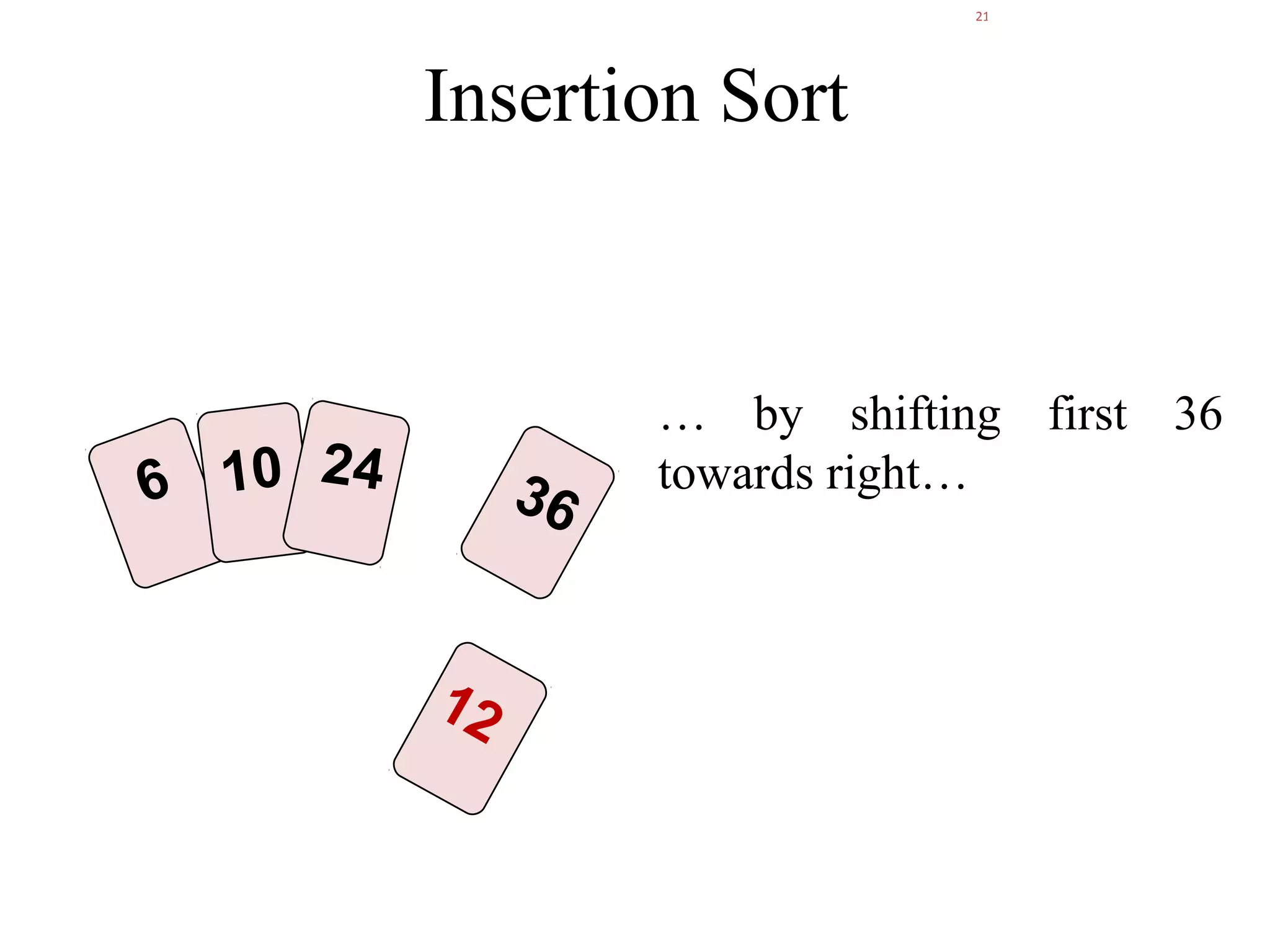
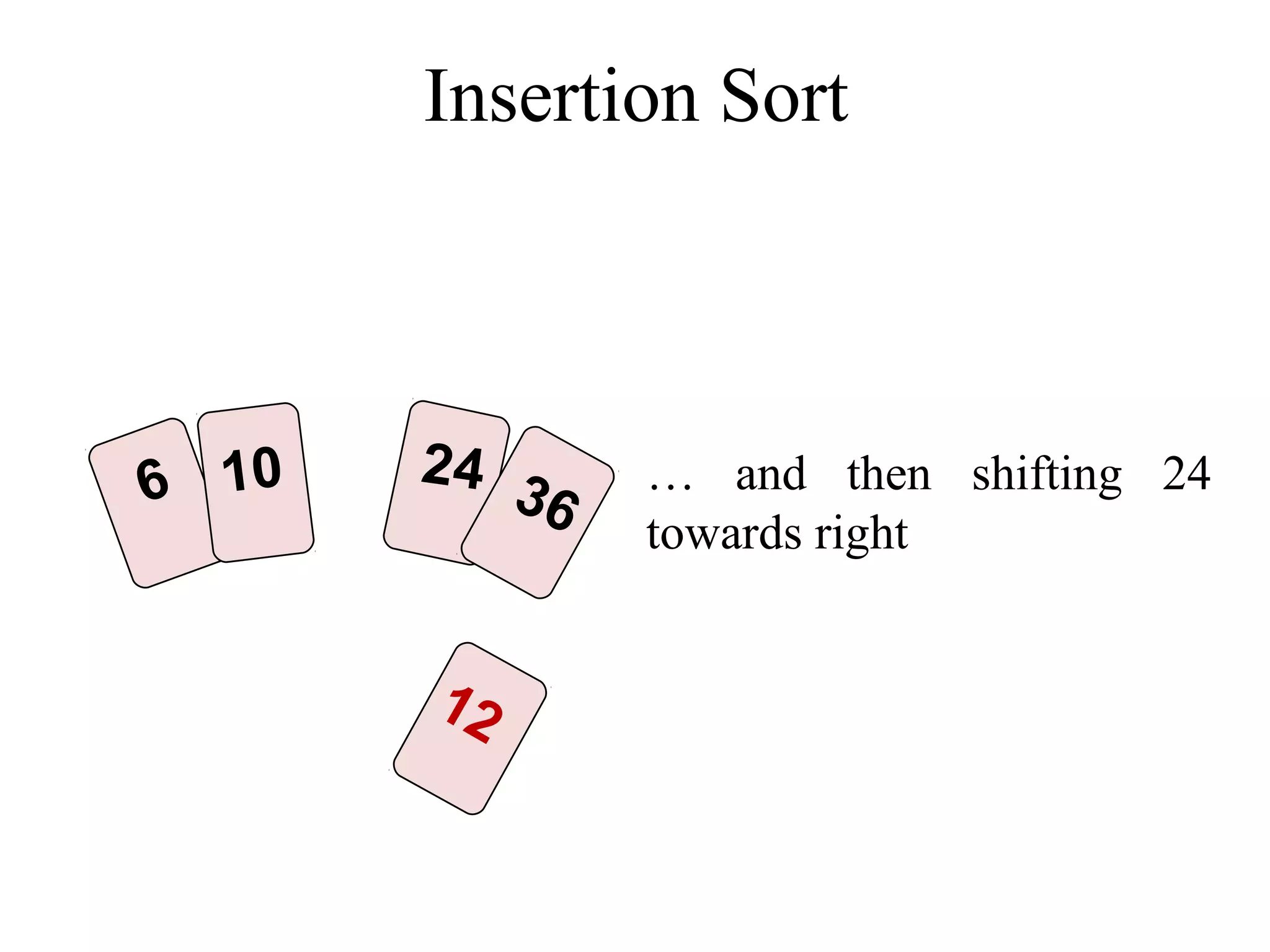
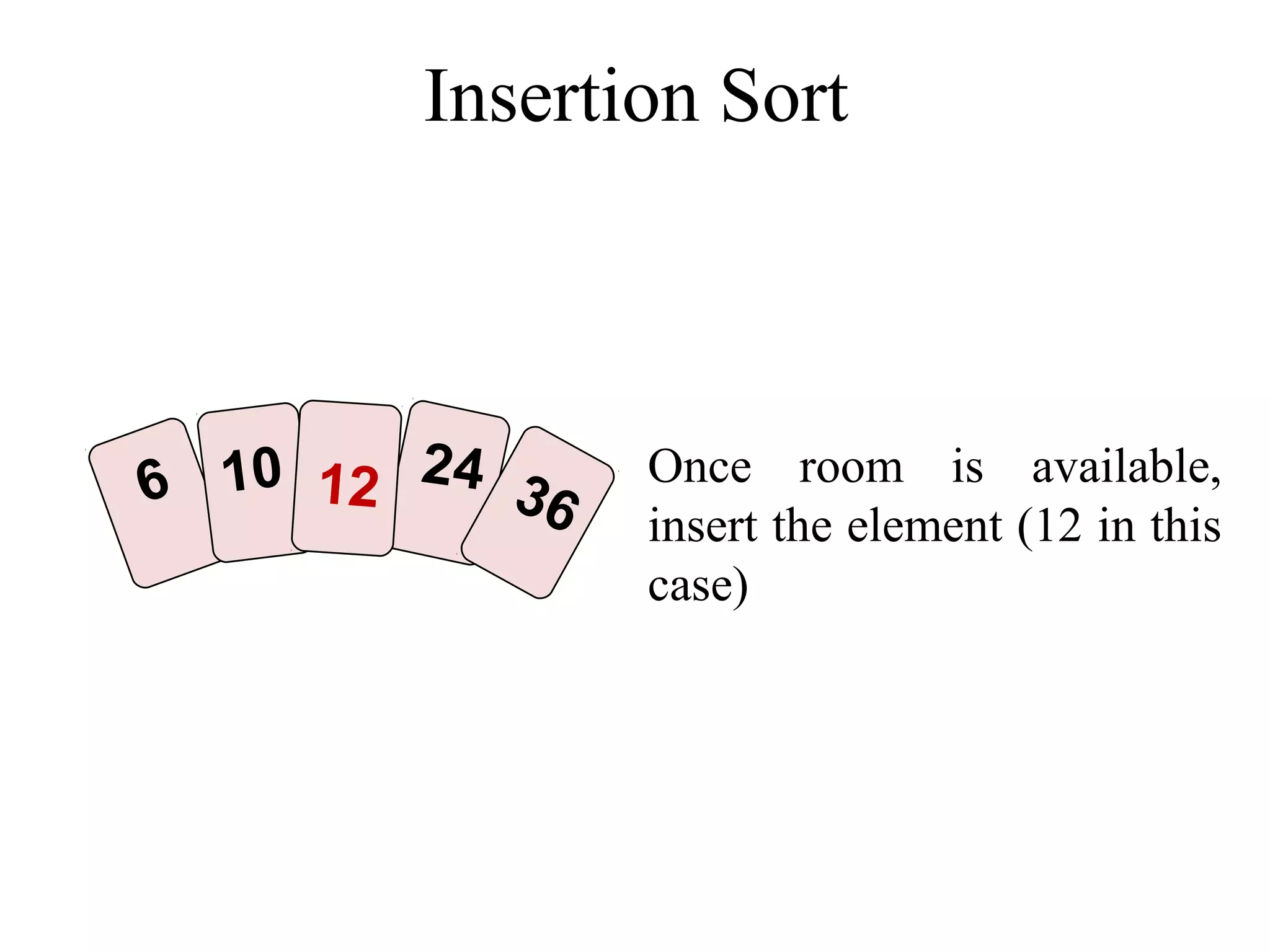
- 25. Insertion Sort Algorithmin Java void insertionSort(int List[]){ int temp; int size = List.length; for (int i = 1; i < size; i++){ int j = i; temp = List[i]; while (j > 0 && temp < List[j - 1]){ List[j] = List[j - 1]; // right shifting j--; } List[j] = temp; } } Time complexity of the Insertion Sort algorithm is O(n2). Think why?
- 26. Outlook Next week,we’ll discuss recursion