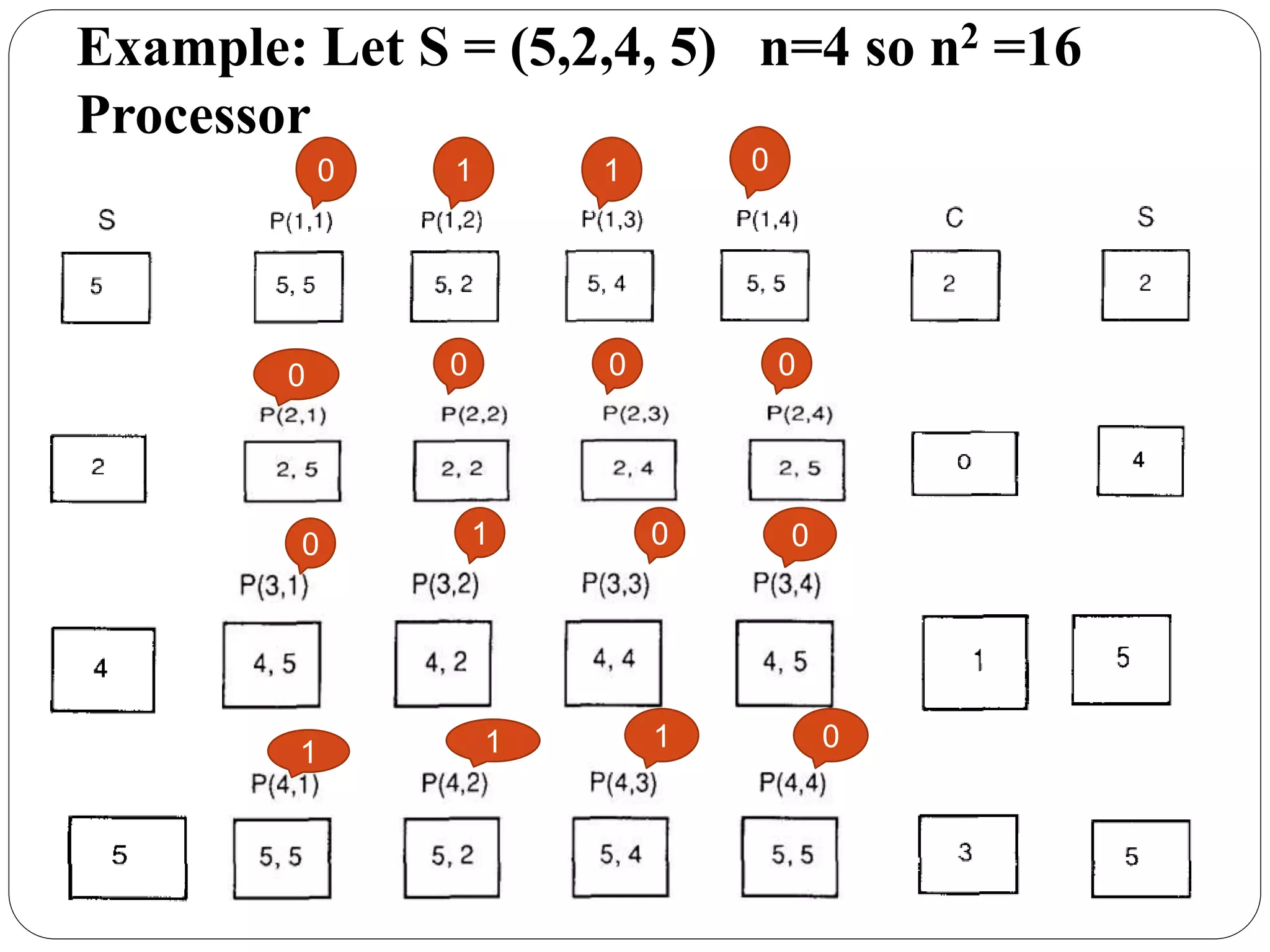
This document discusses parallel algorithms for sorting. It begins by defining parallel algorithms and explaining that the lower bound for comparison-based sorting of n elements is Θ(n log n). It then discusses several parallel sorting algorithms: odd-even transposition sort on a linear array, quicksort, and sorting networks. It also covers sorting on different parallel models like CRCW, CREW, and EREW. An example is provided of applying an EREW sorting algorithm to a sample data set by recursively dividing it into subsequences until single elements remain to be sorted locally.












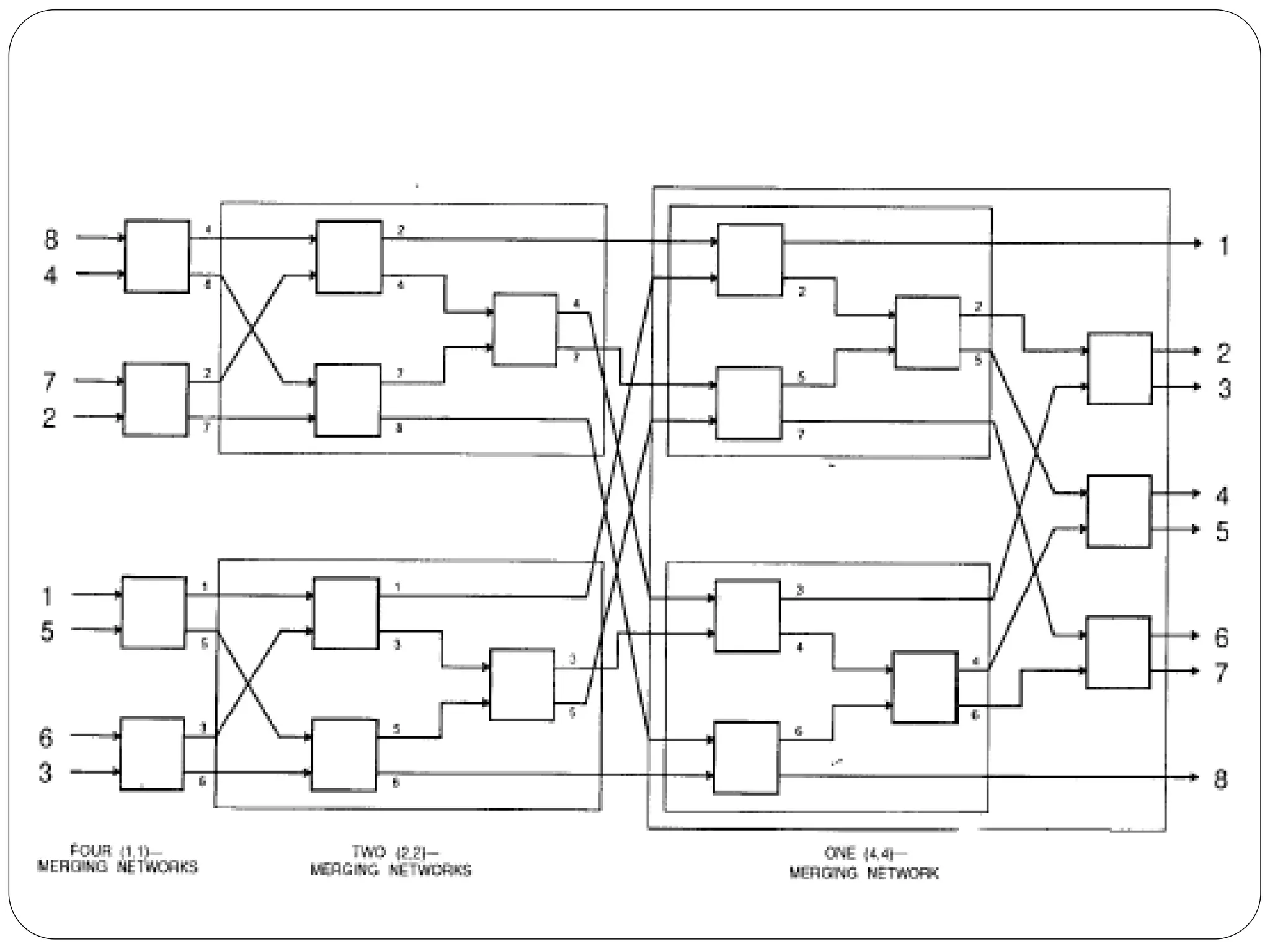
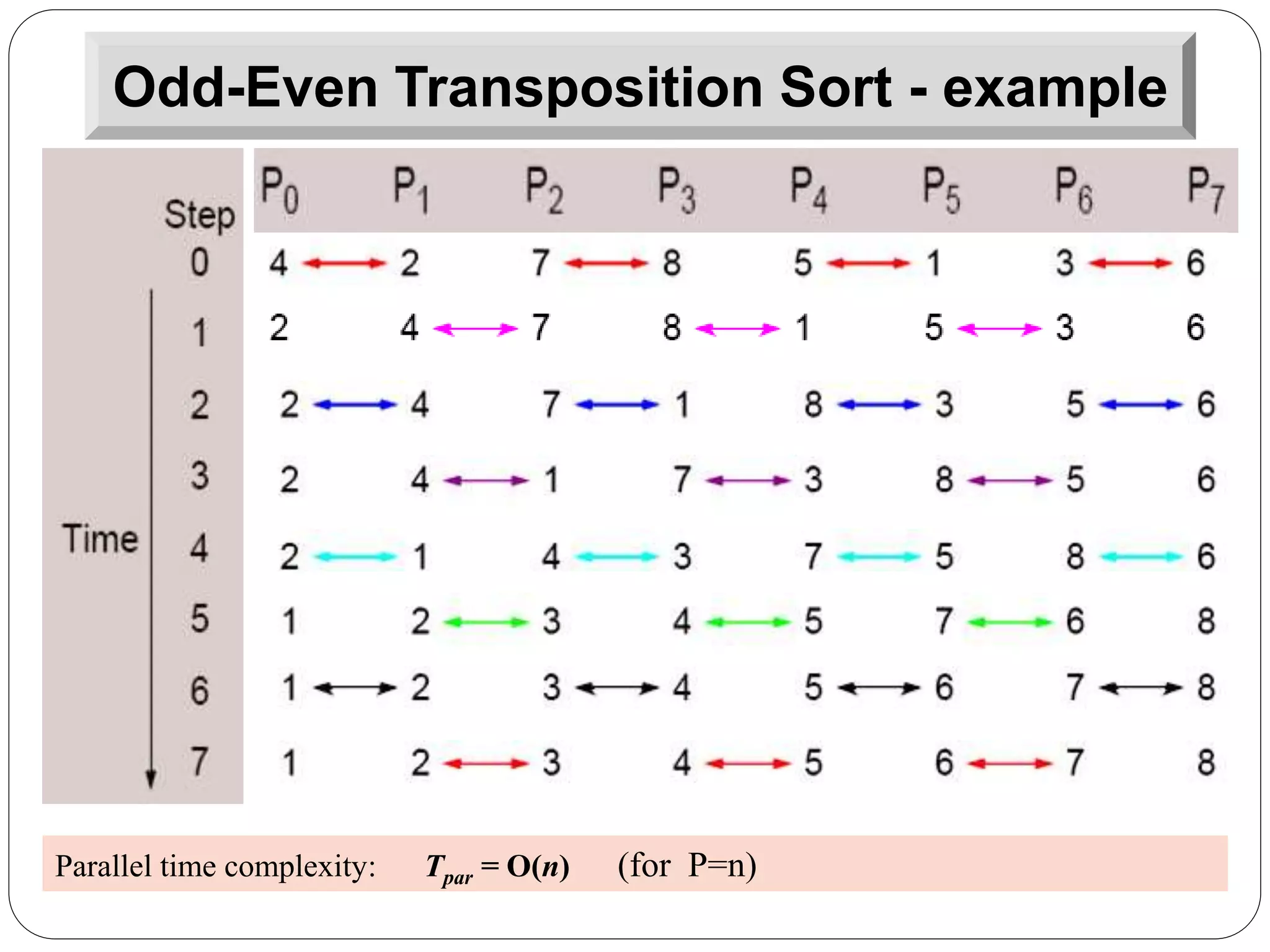
![The odd-even sorting network is impractical for large input sequences : (i) The network is extremely fast. It can sort a sequence of length 2^20 within, on the order of, (20)2 time units. This is to be contrasted with the time required by procedure QUICKSORT, which would be in excess of 20 million time units.[(log n)^2] (ii) The number of comparators is too high. Again for n = 2^20, the network would need on the order of 400 million comparators.[n (log n)^2] (iii) The architecture is highly irregular and the wires linking the comparators have lengths that vary with n.](https://image.slidesharecdn.com/parallelsortingalgo-150220012432-conversion-gate01/75/Parallel-sorting-algorithm-14-2048.jpg)


















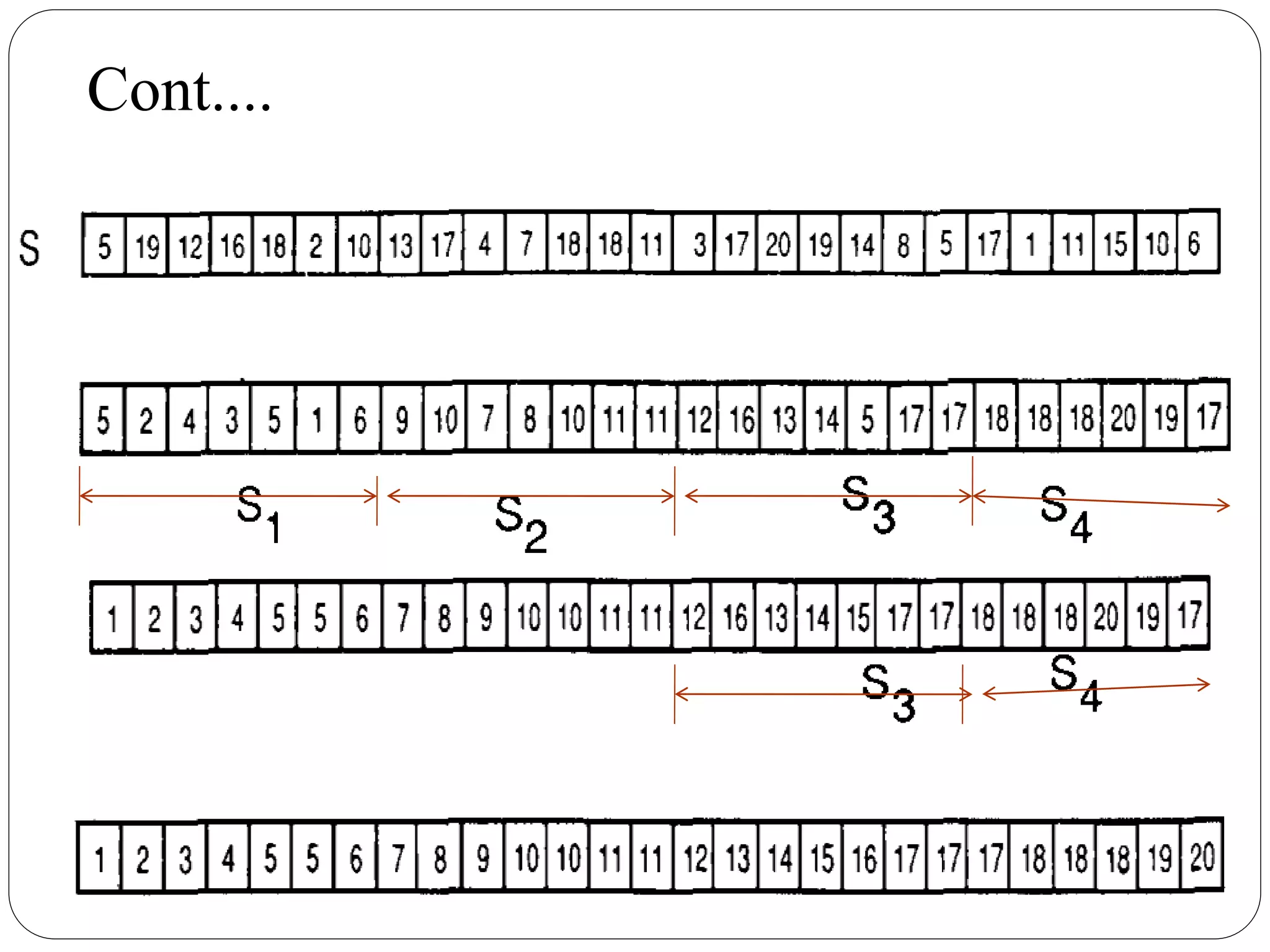
![Cont…. since N < n, N=n1-x where 0<x<1. Now mi =[ i(n/21/x)], for 1<=i<=21/x-1 . The mi can be used to divide S into 21/x subsequence of size n/21/x . These subsequences, denoted by S1,S2,..., Sj, Sj+1,........S2j, where j =2(1/x)-1 Every subdivision process can now be applied recursively to each of the subsequences Si until the entire sequence S is sorted in nondecreasing order. K= 2(1/x)](https://image.slidesharecdn.com/parallelsortingalgo-150220012432-conversion-gate01/75/Parallel-sorting-algorithm-35-2048.jpg)
![Algorithm:- procedure EREW SORT (S) Step1 if |S| < k then QUICKSORT (S) else (1) for i = 1 to k - 1 do PARALLEL SELECT (S, |i |s|/k|) [obtain mi] end for (2) Si = (s E S: s<=mi ) (3) for i = 2 to k - 1 do Si ={s E S : mi-1<=s <=mi } end for](https://image.slidesharecdn.com/parallelsortingalgo-150220012432-conversion-gate01/75/Parallel-sorting-algorithm-36-2048.jpg)