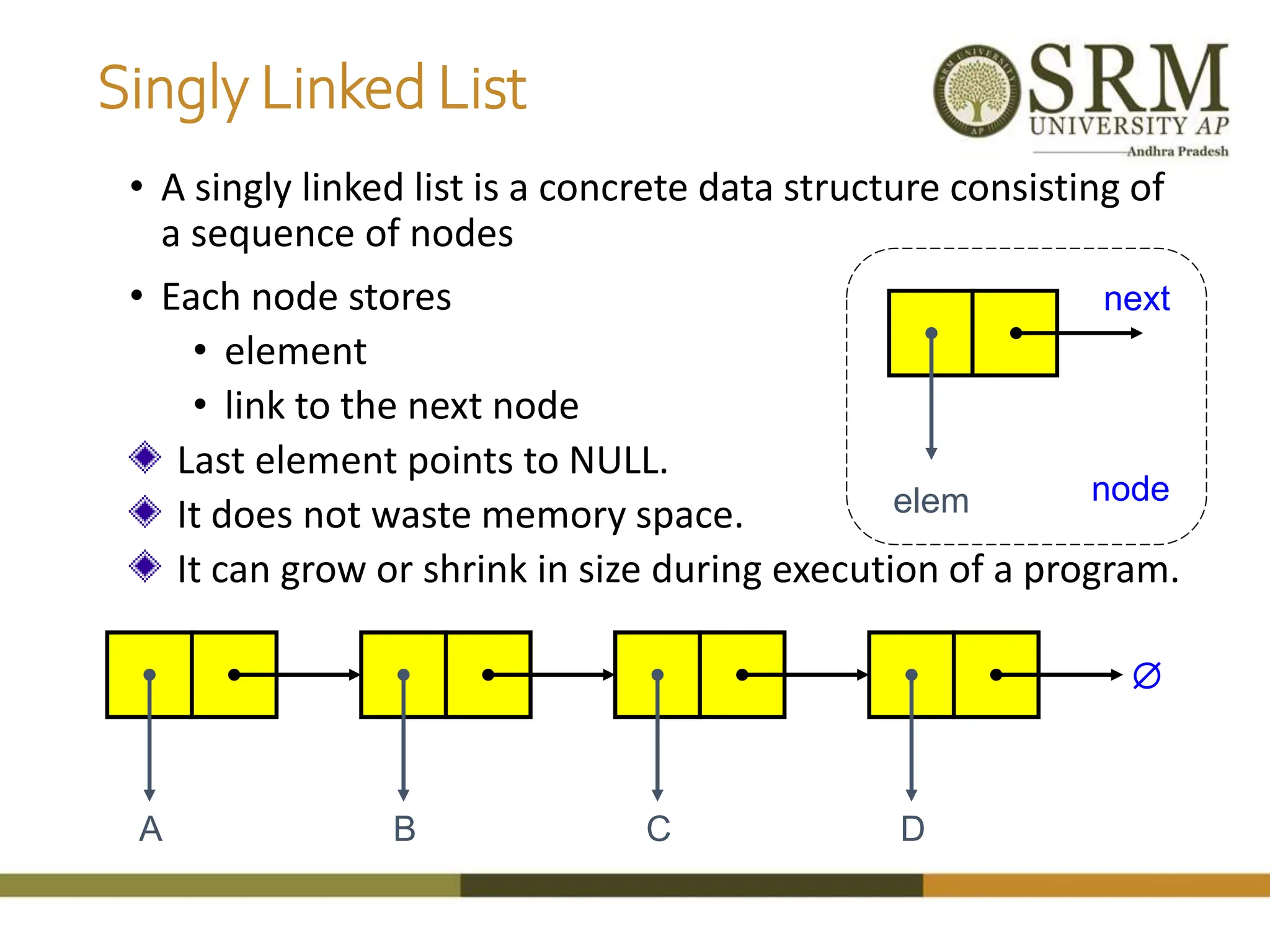
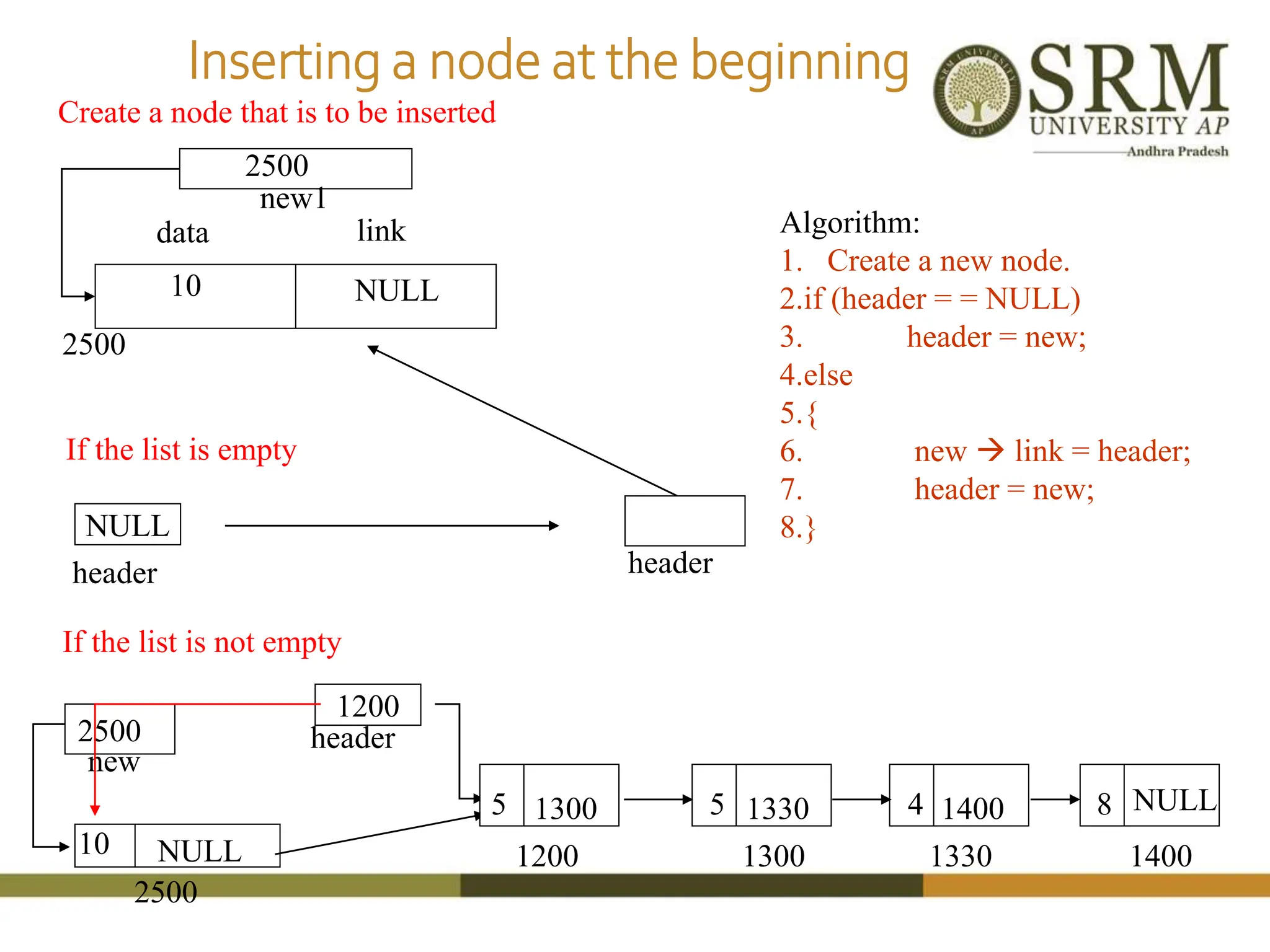
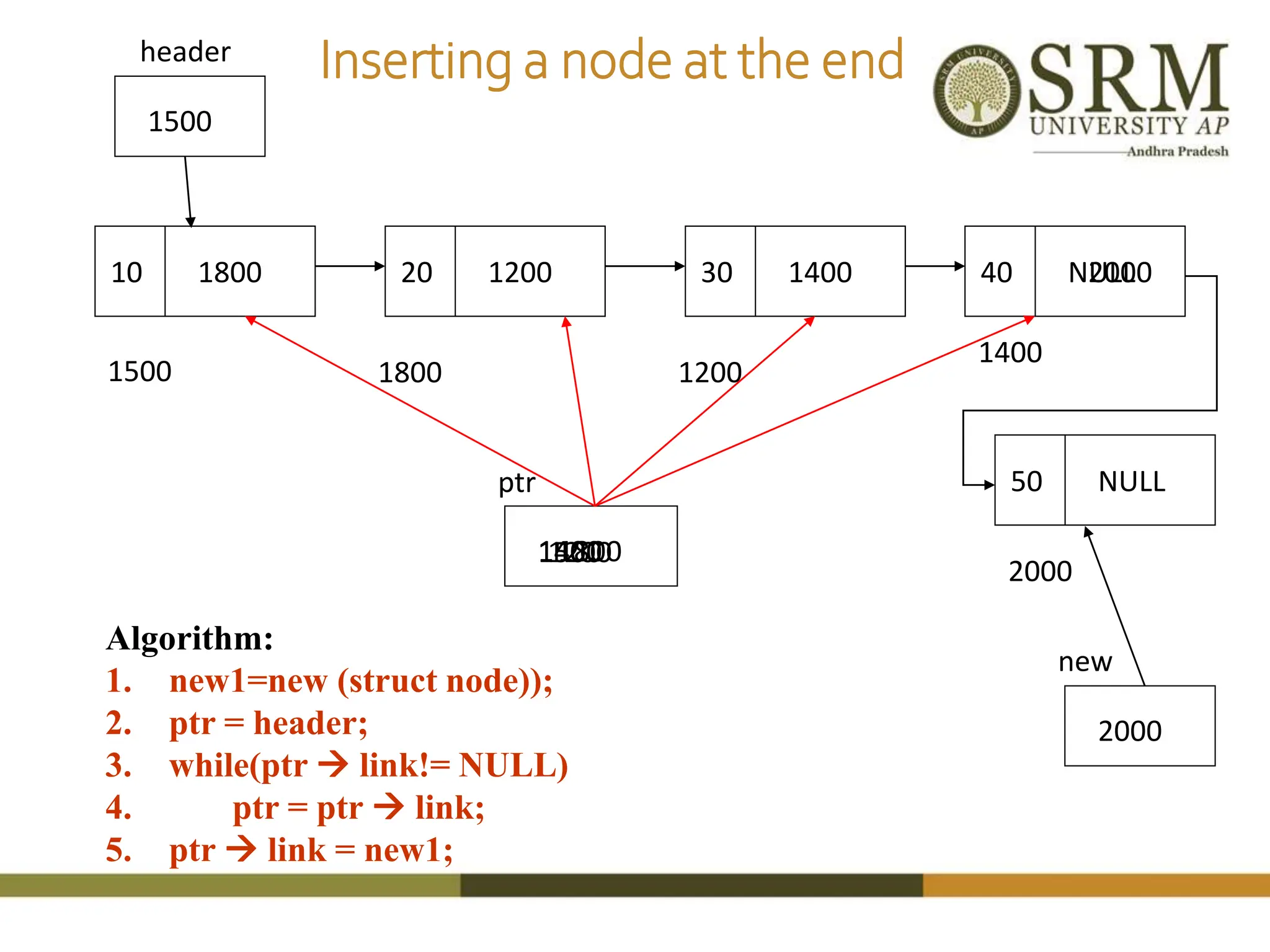
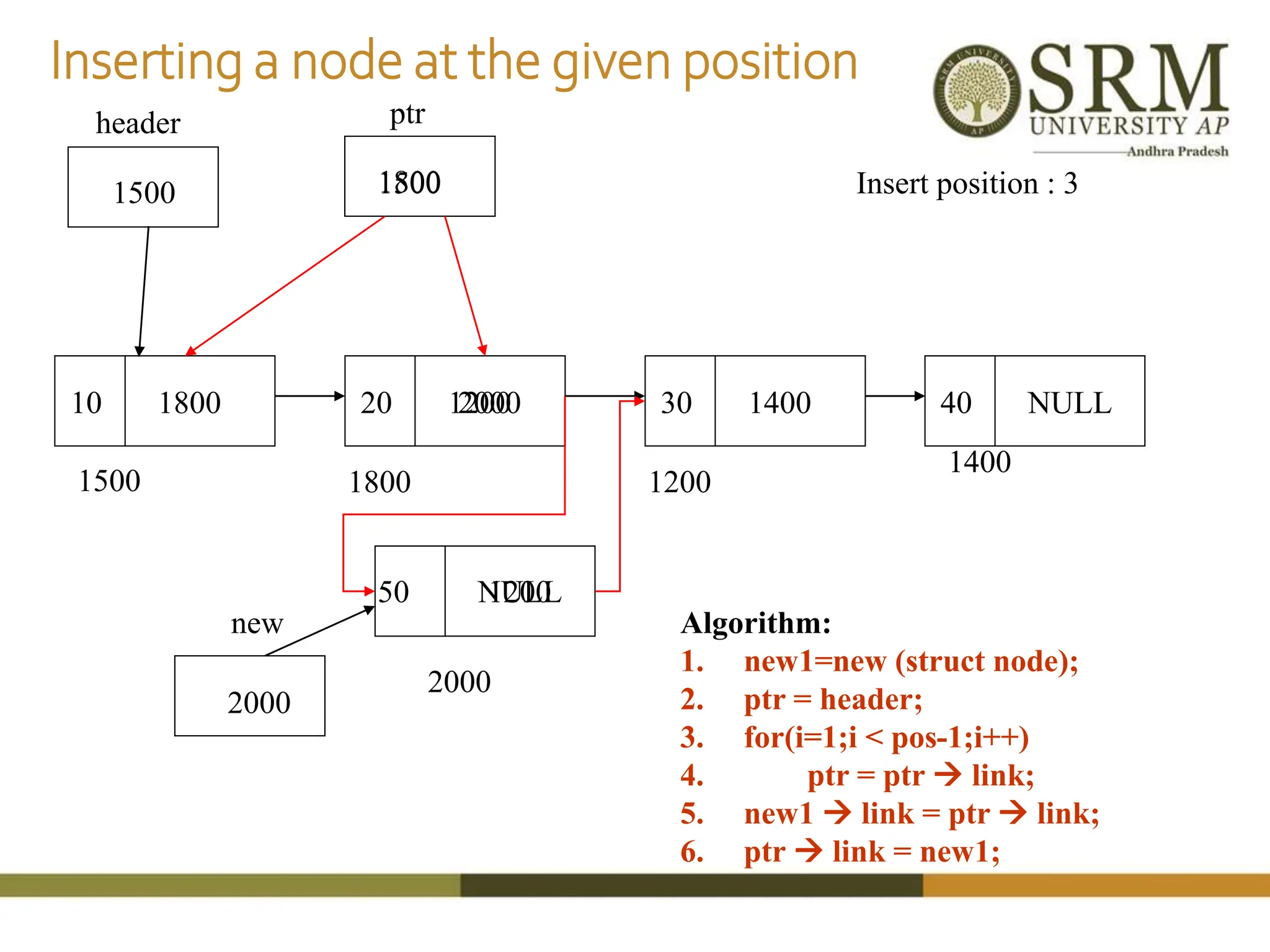
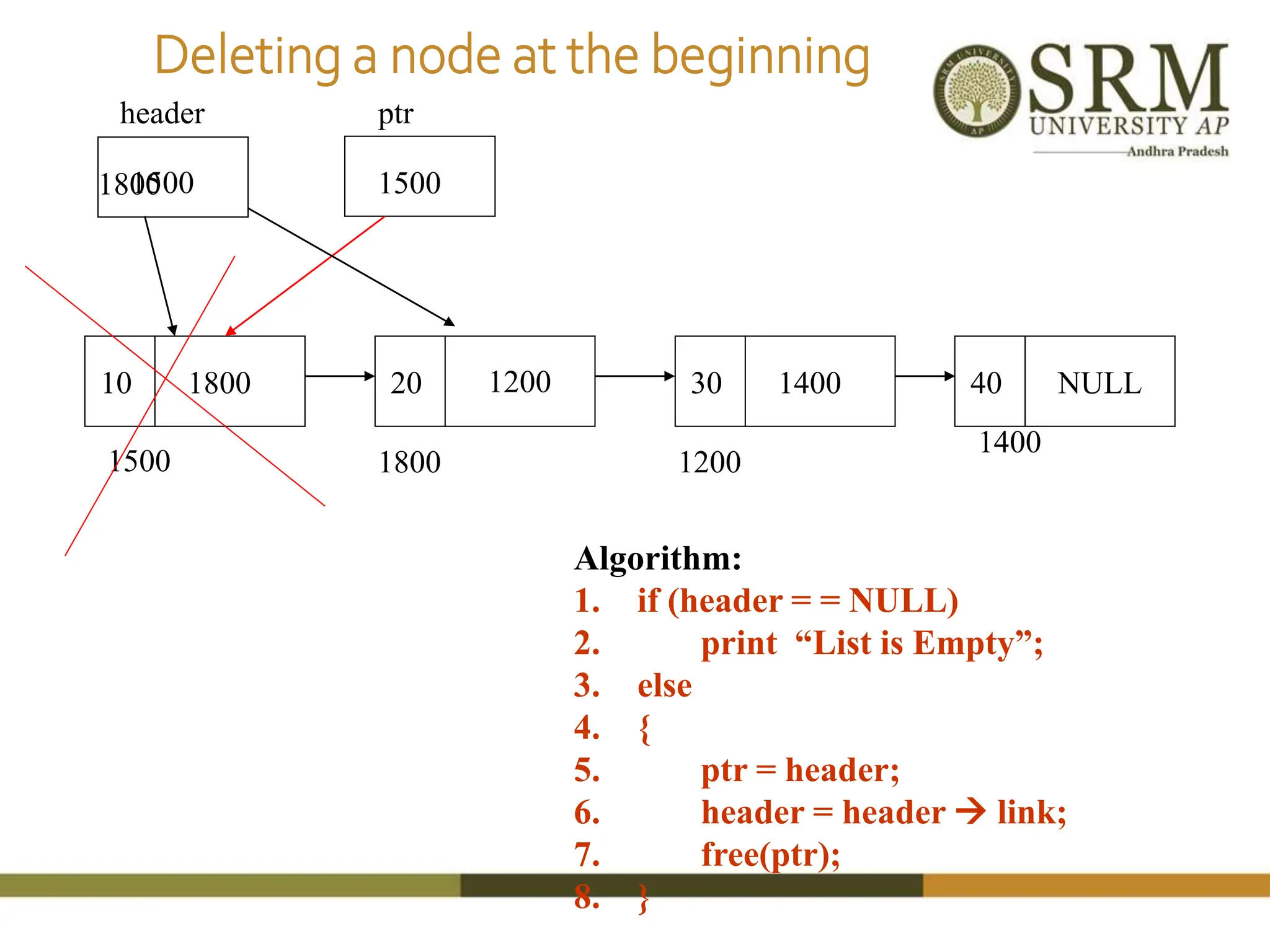
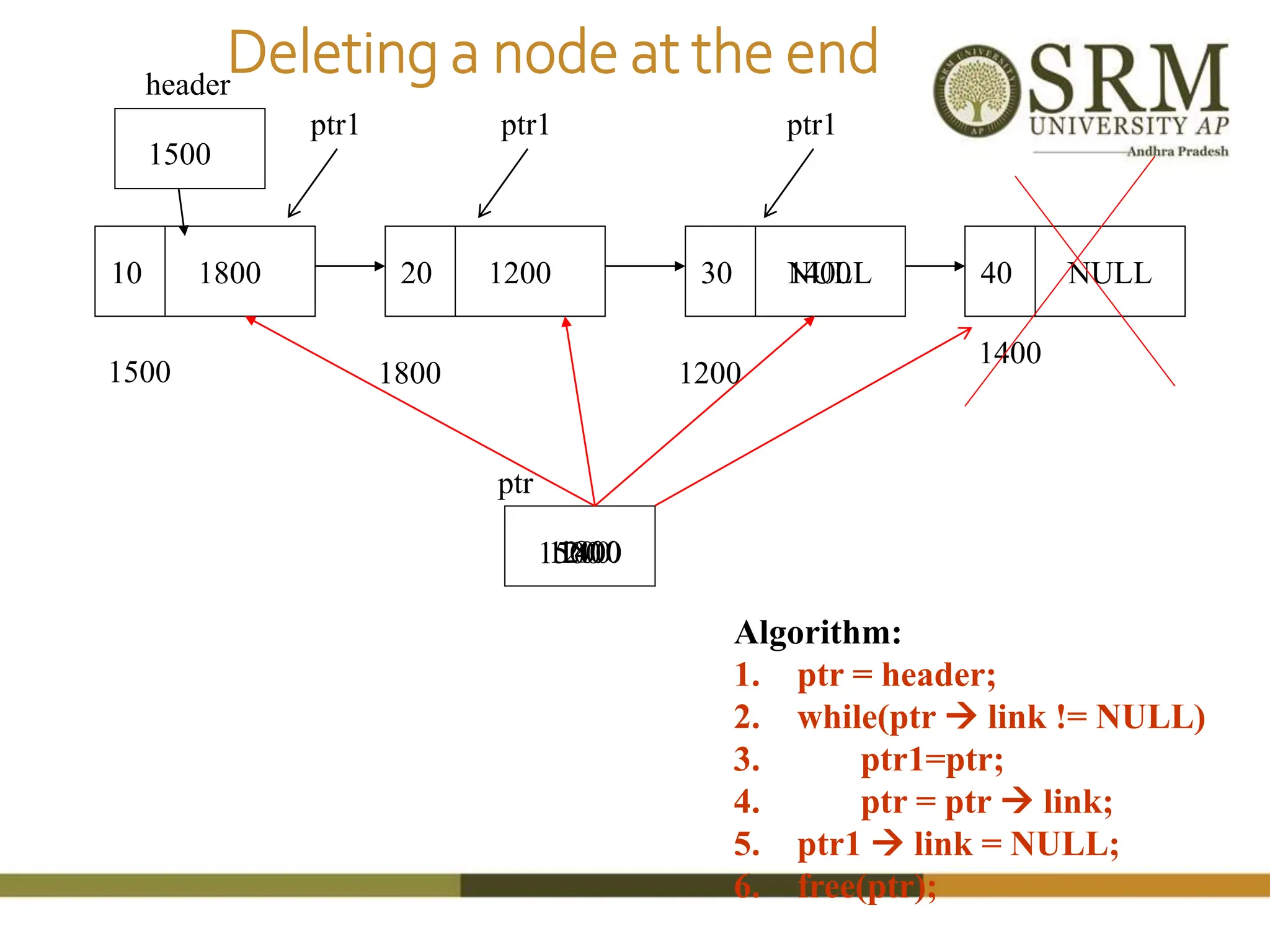
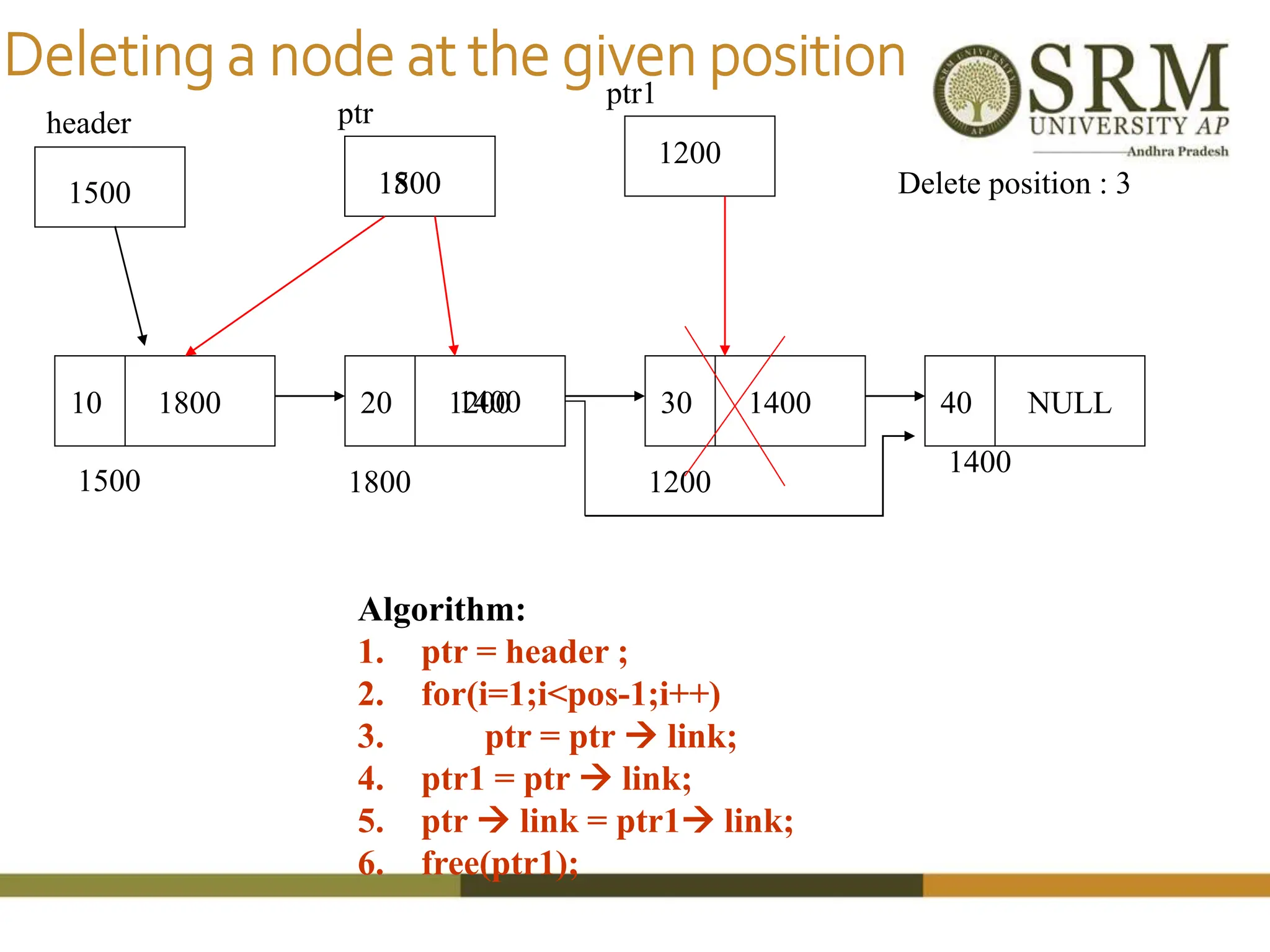
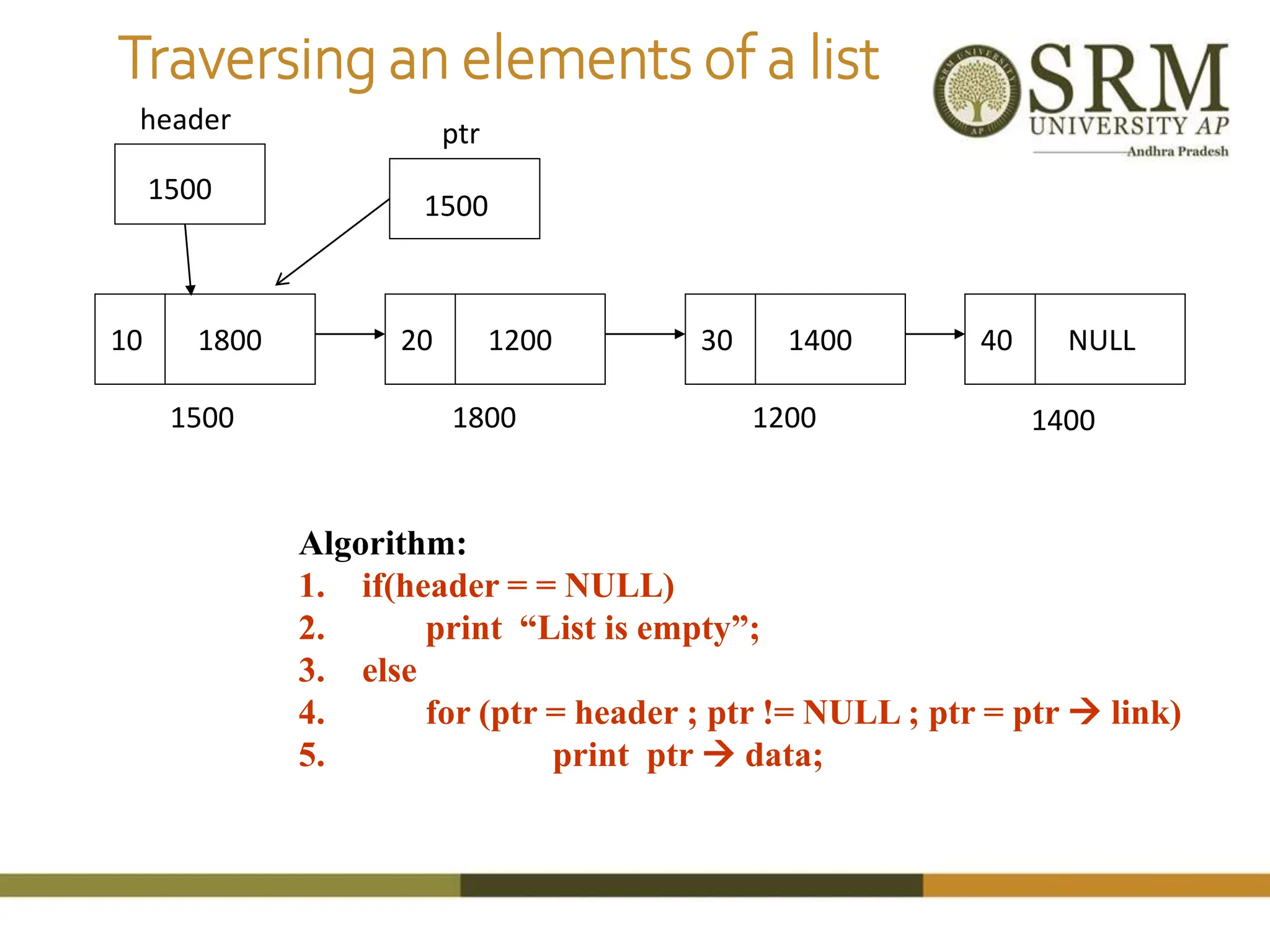
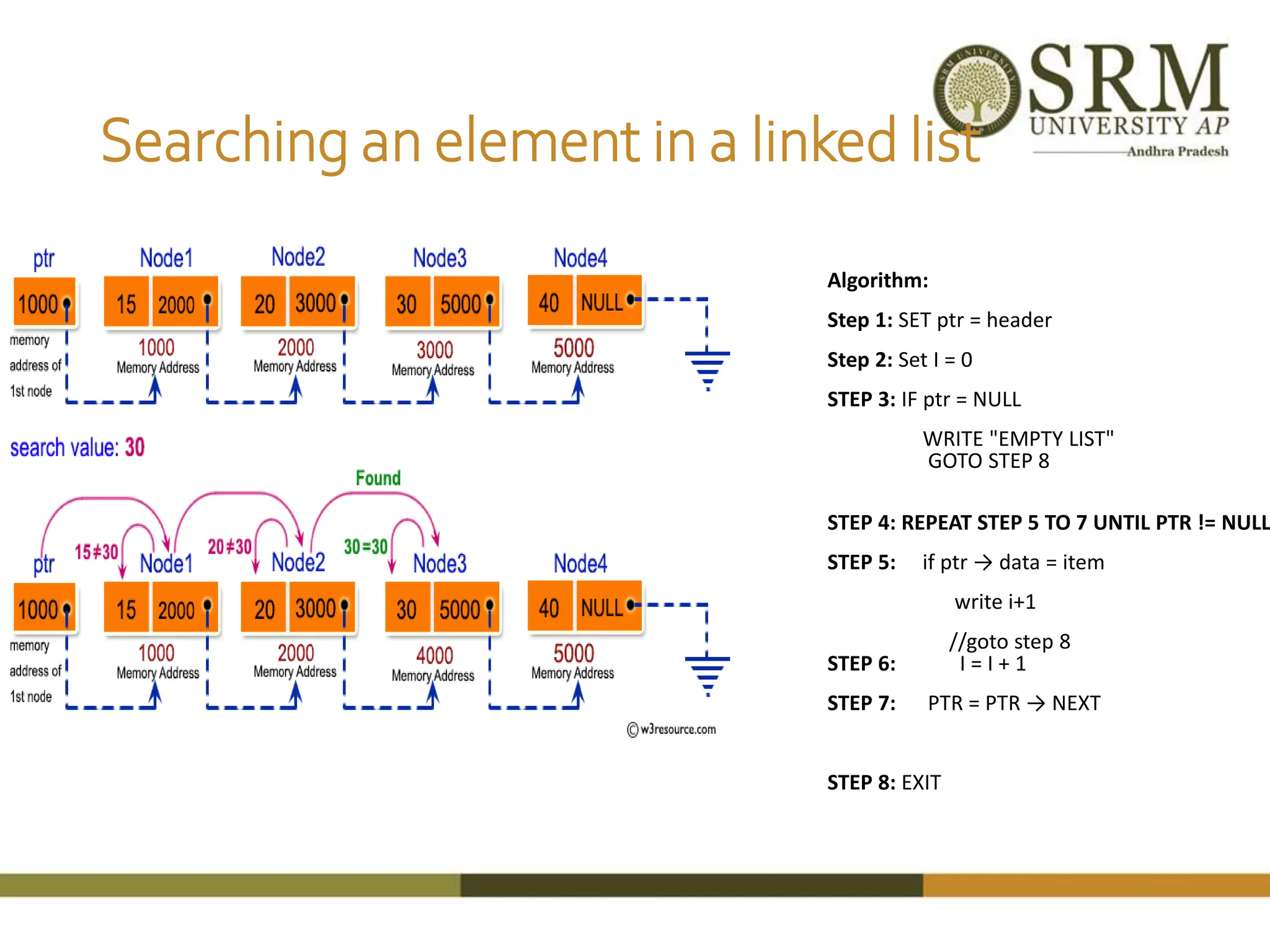
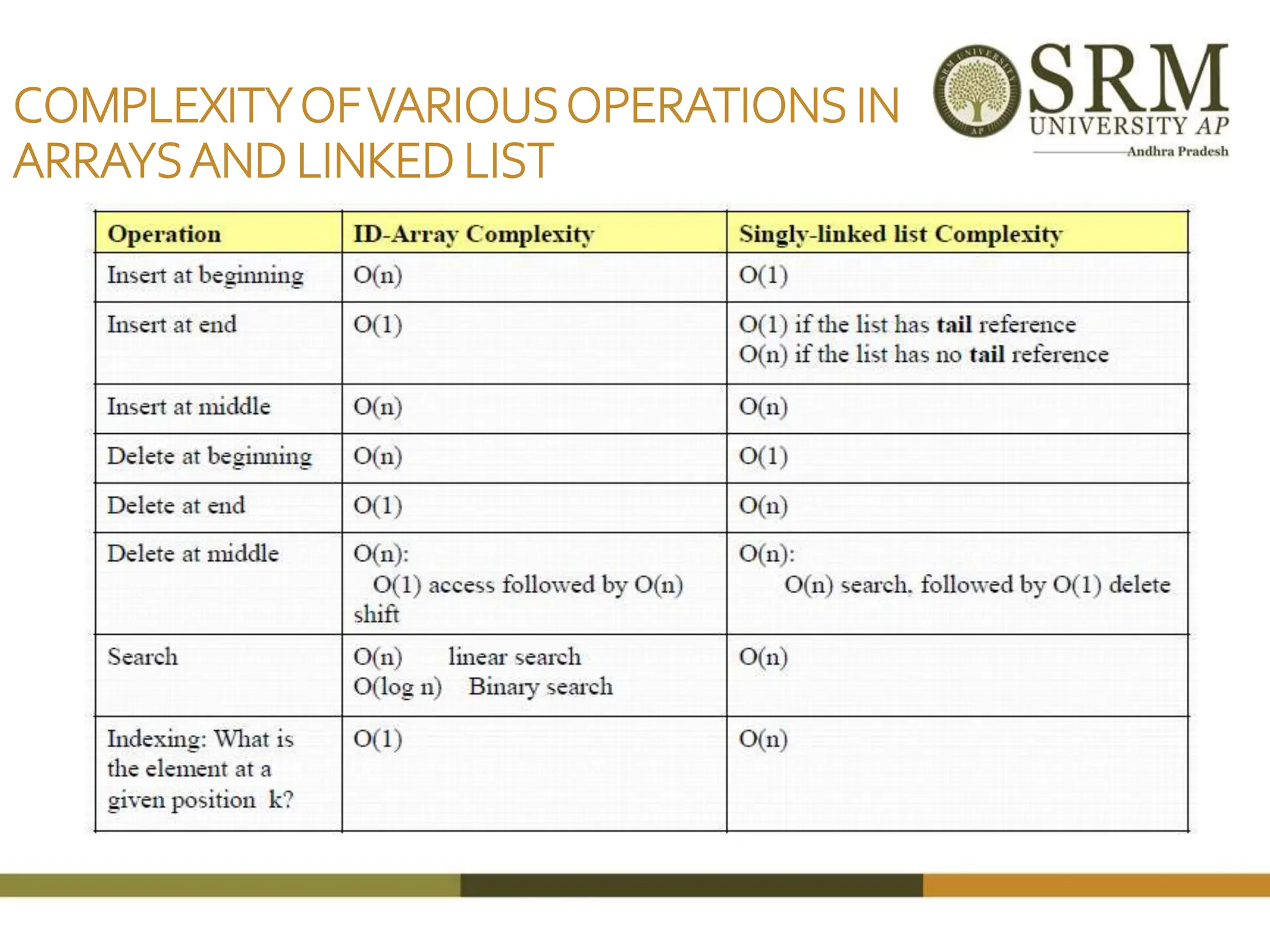
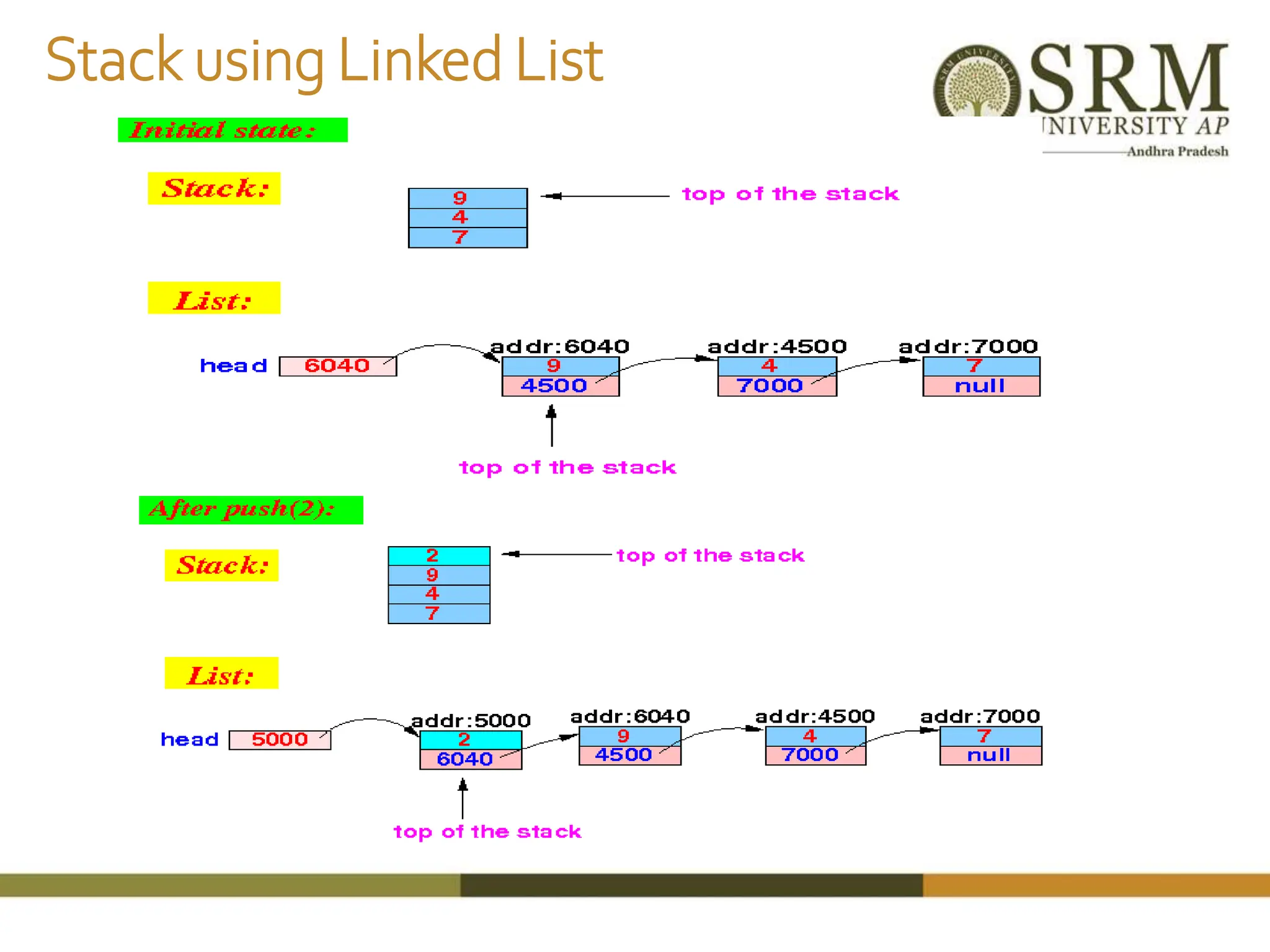
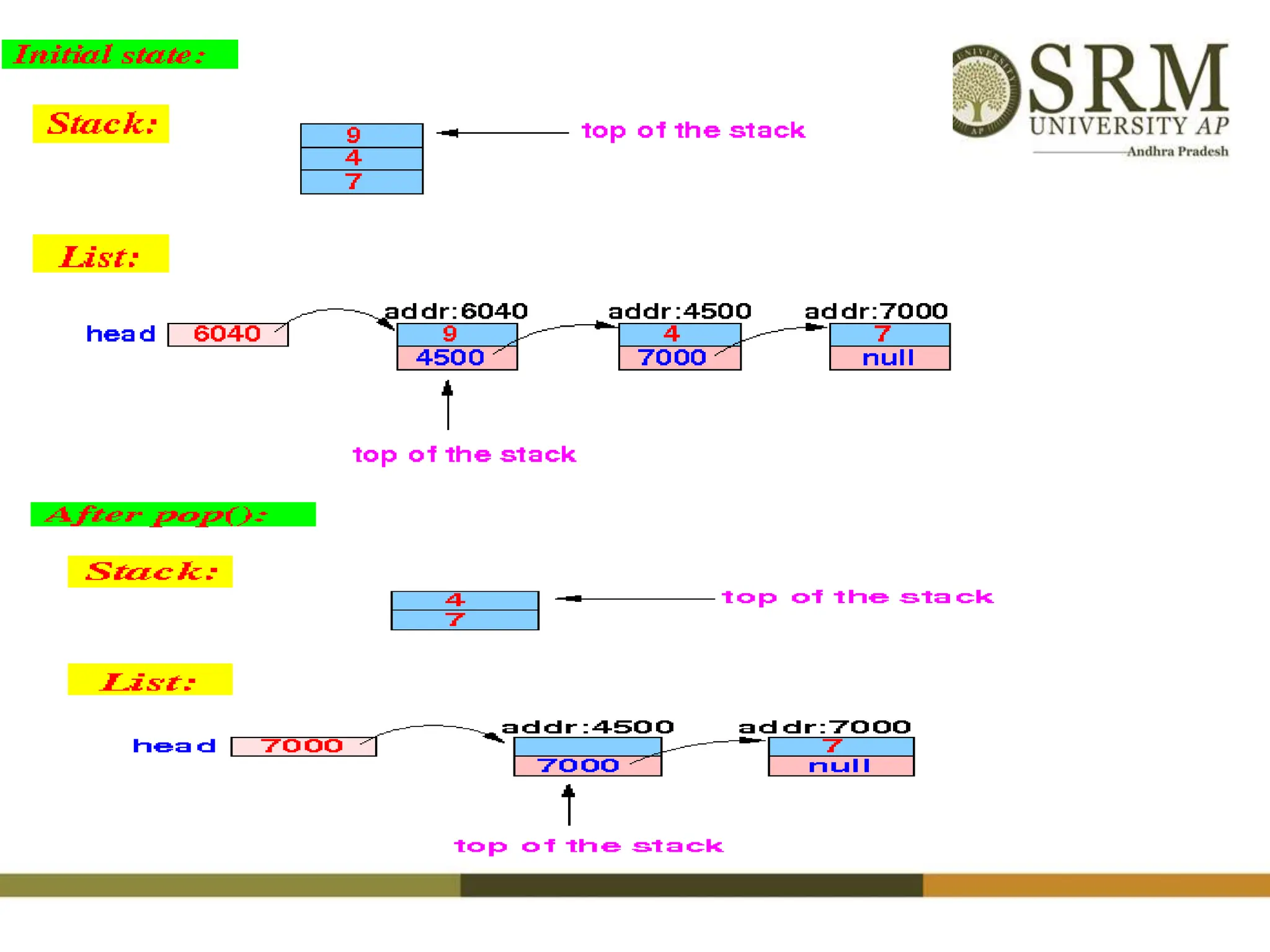
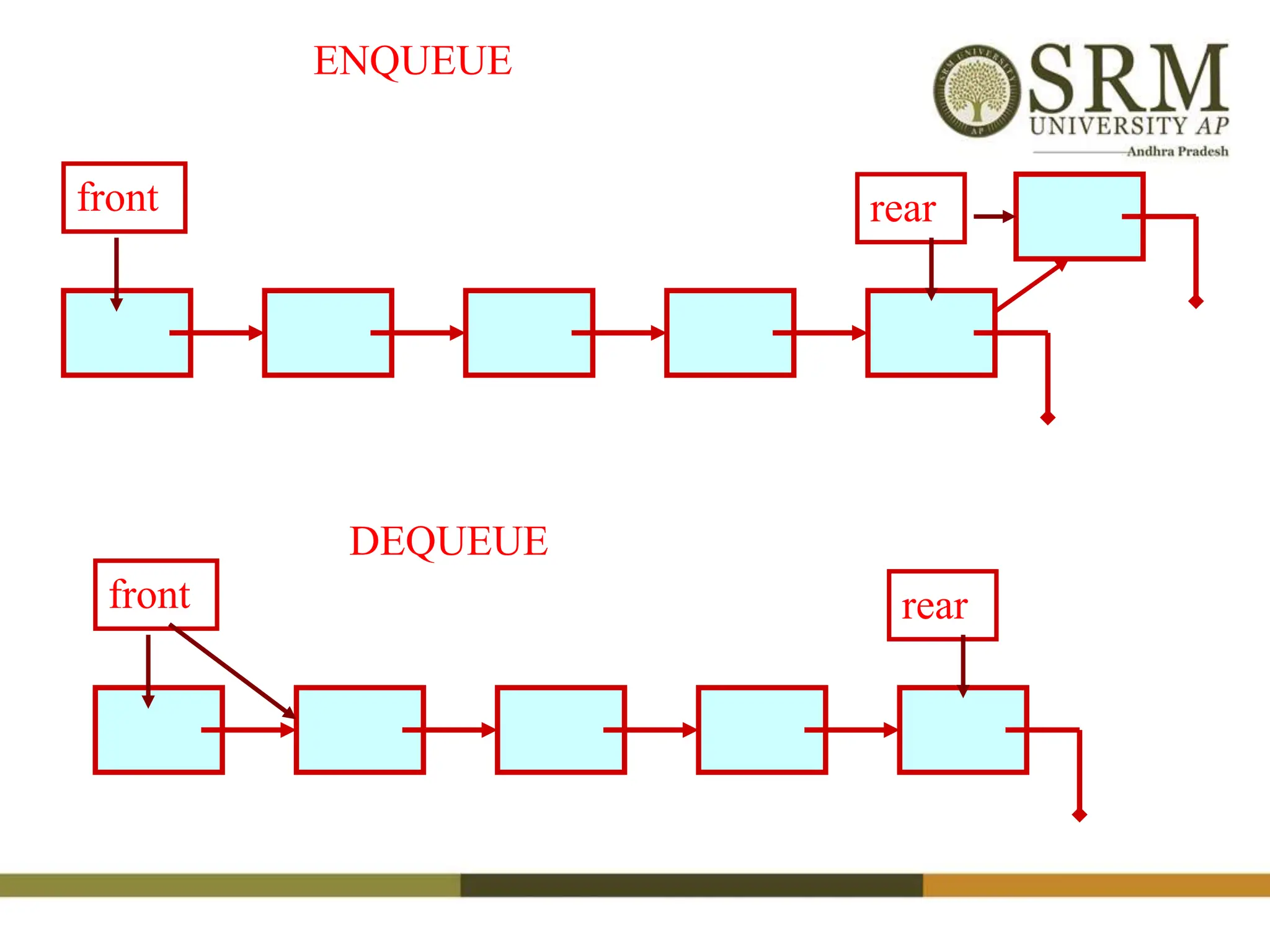
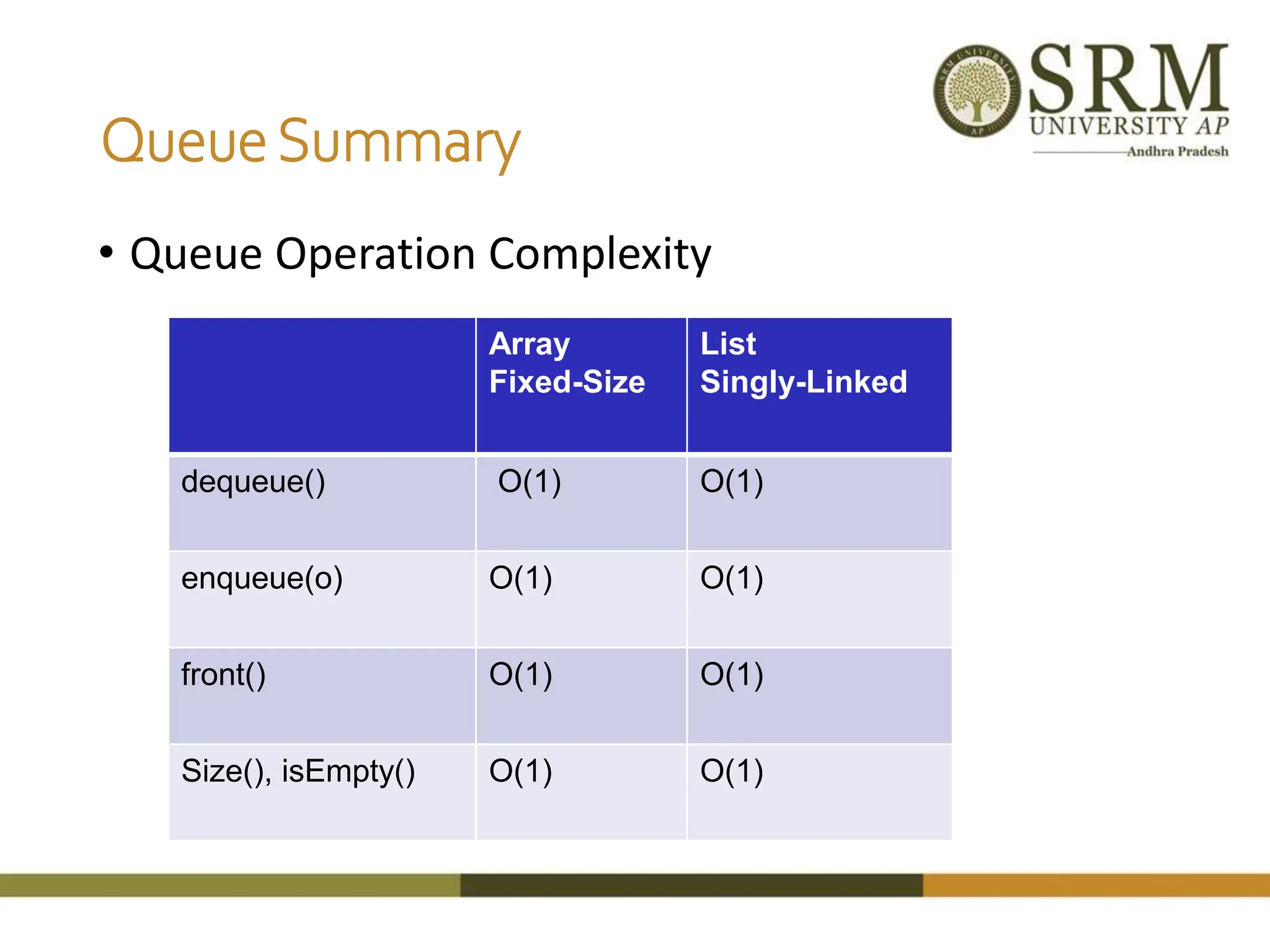
This document discusses various data structures including arrays, stacks, queues, and linked lists. It provides code examples for creating and manipulating each type of data structure. Specifically, it shows code for inserting and deleting elements from arrays and linked lists. It also includes algorithms and code for common stack and queue operations like push, pop, enqueue, and dequeue. The document provides a detailed overview of linear and non-linear data structures.





![#include<iostream> using namespace std; int main() { int i,a[50],no,pos,size; cout<<"Enter array size( Max:50 ) :: "; cin>>size; cout<<"nEnter array elements :: n"; for(i=0; i<size; i++) { cout<<"nEnter arr["<<i<<"] Element :: "; cin>>a[i]; } cout<<"nStored Data in Array :: nn"; for(i=0;i<size;i++) { cout<<" "<<a[i]<<" "; } cout<<"nnEnter position to insert number :: "; cin>>pos; if(pos>size) { cout<<"nThis is out of range.n"; } else { cout<<"nEnter number to be inserted :: "; cin>>no; --pos; for(i=size;i>=pos;i--) { a[i+1]=a[i]; } a[pos]=no; cout<<"nNew Array is :: nn"; for(i=0;i<size+1;i++) { cout<<" "<<a[i]<<" "; } } cout<<"n"; return 0; }](https://image.slidesharecdn.com/1-240222043734-16d8326a/75/Revisiting-a-data-structures-in-detail-with-linked-list-stack-and-queue-6-2048.jpg)

![#include<iostream> #include<conio> void main() { int arr[50], size, i, del, count=0; cout<<"Enter array size : "; cin>>size; cout<<"Enter array elements : "; for(i=0; i<size; i++) { cin>>arr[i]; } cout<<"Enter element to be delete : "; cin>>del; for(i=0; i<size; i++) { if(arr[i]==del) { for(int j=i; j<(size-1); j++) { arr[j]=arr[j+1]; } count++; break; } } if(count==0) { cout<<"Element not found..!!"; } else { cout<<"Element deleted successfully..!!n"; cout<<"Now the new array is :n"; for(i=0; i<(size-1); i++) { cout<<arr[i]<<" "; } } getch(); }](https://image.slidesharecdn.com/1-240222043734-16d8326a/75/Revisiting-a-data-structures-in-detail-with-linked-list-stack-and-queue-8-2048.jpg)


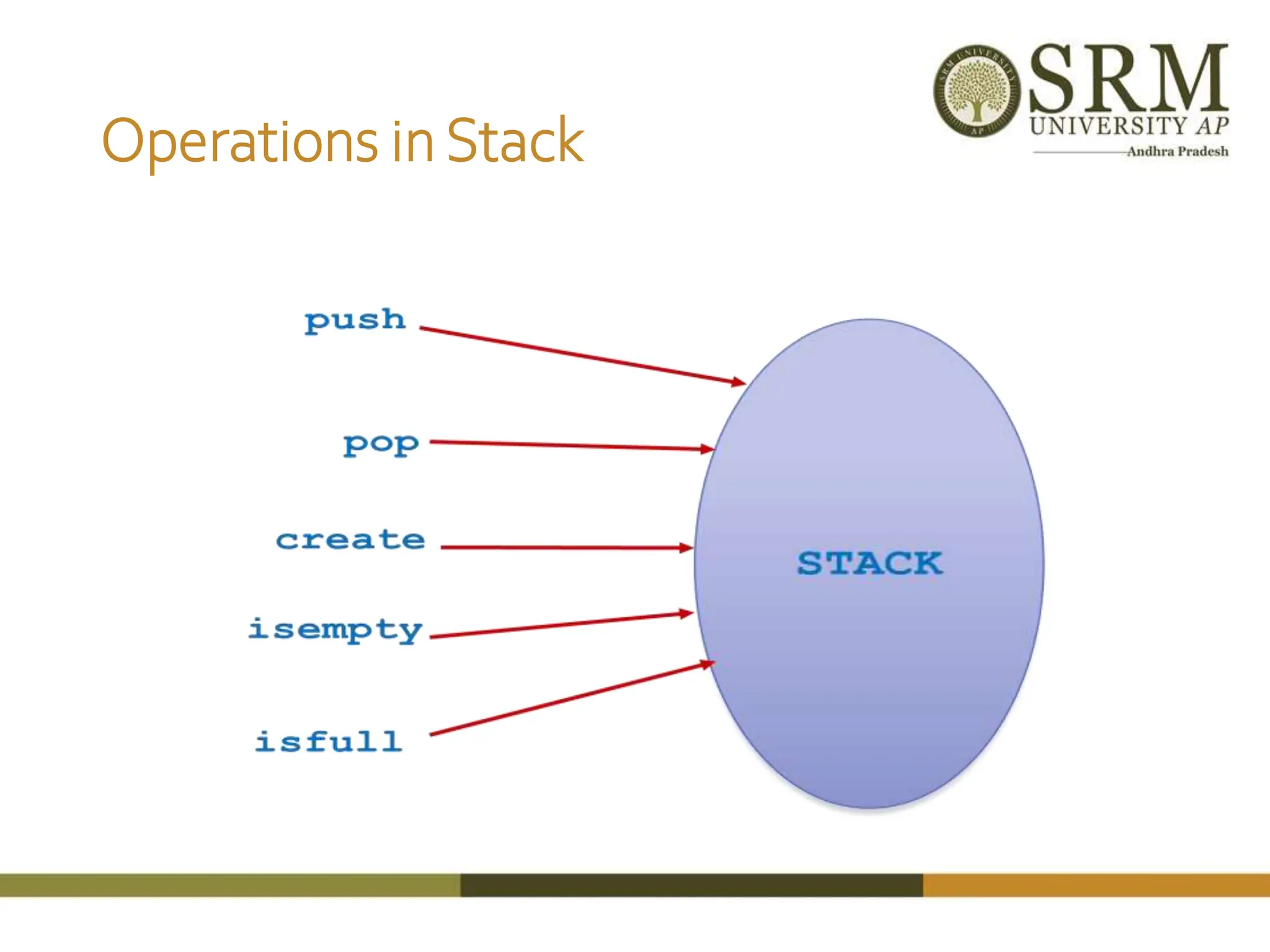
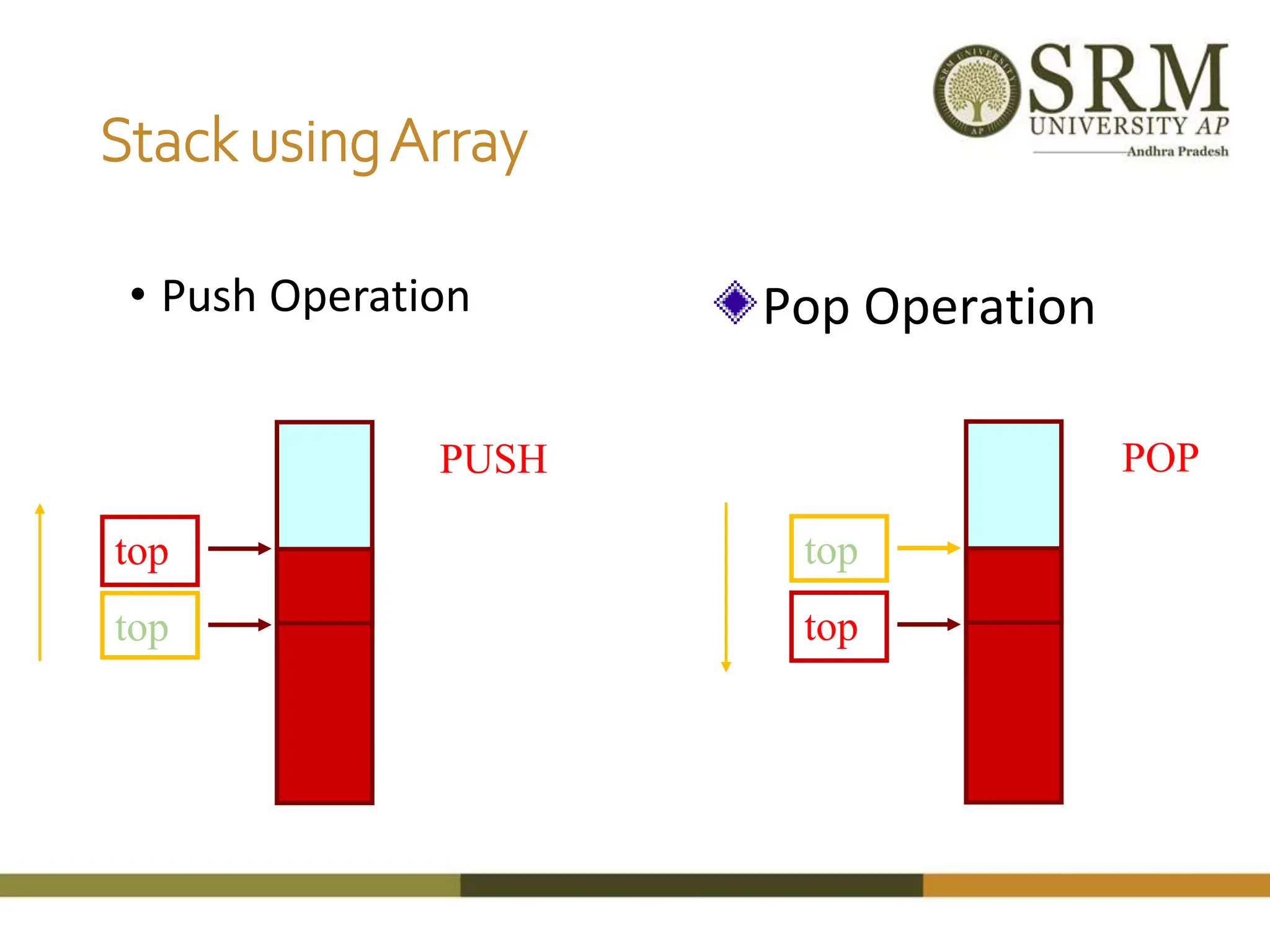
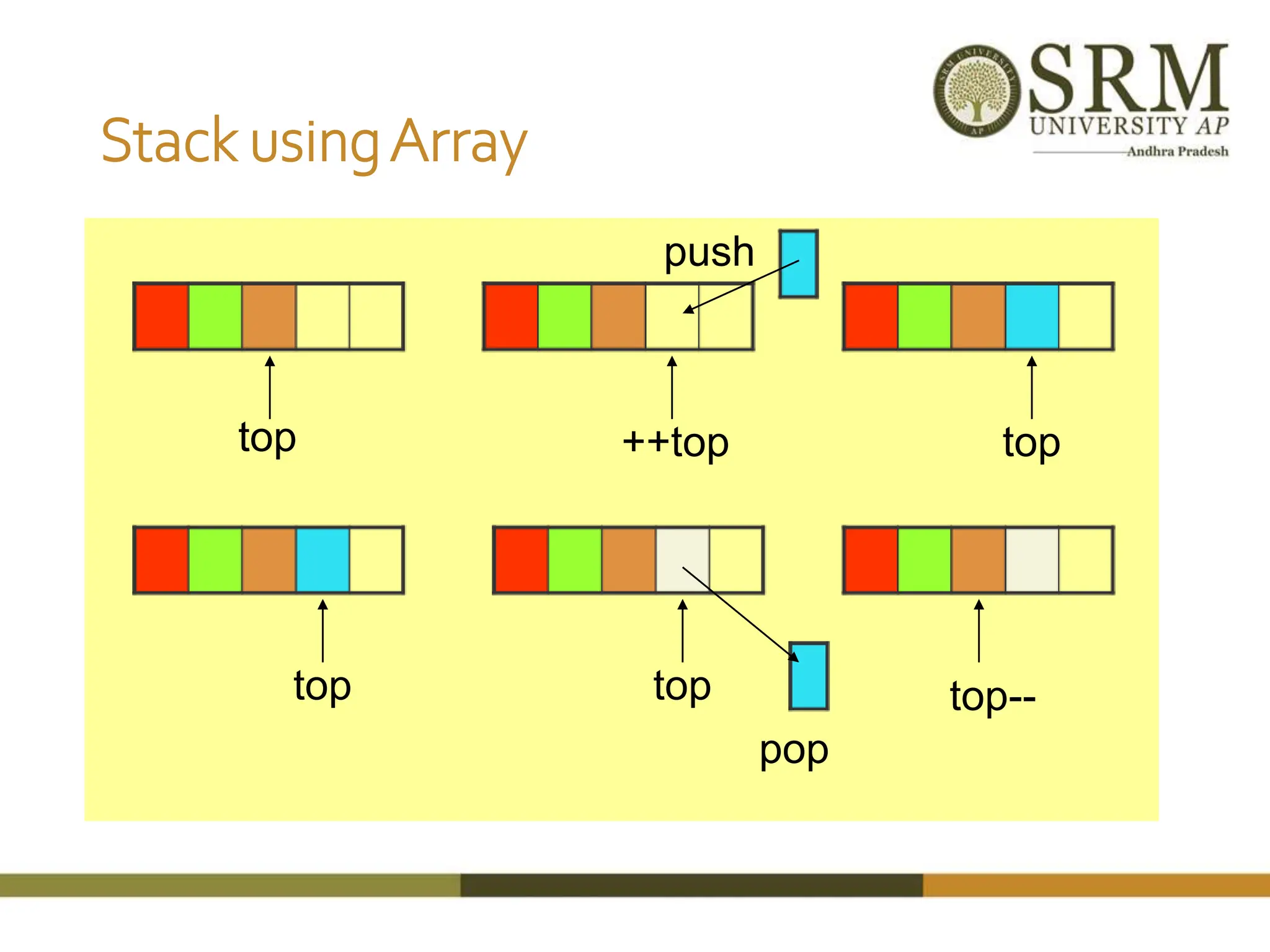
![StackAlgorithms Algorithm size() return top +1 Algorithm pop(S[],top,item) if top=-1 then print “ stack is underflow” else top top - 1 return S[top+1] Algorithm push(S[],item, max, top) if top = max-1 then print “ stack is full” else top top + 1 S[top] item](https://image.slidesharecdn.com/1-240222043734-16d8326a/75/Revisiting-a-data-structures-in-detail-with-linked-list-stack-and-queue-14-2048.jpg)


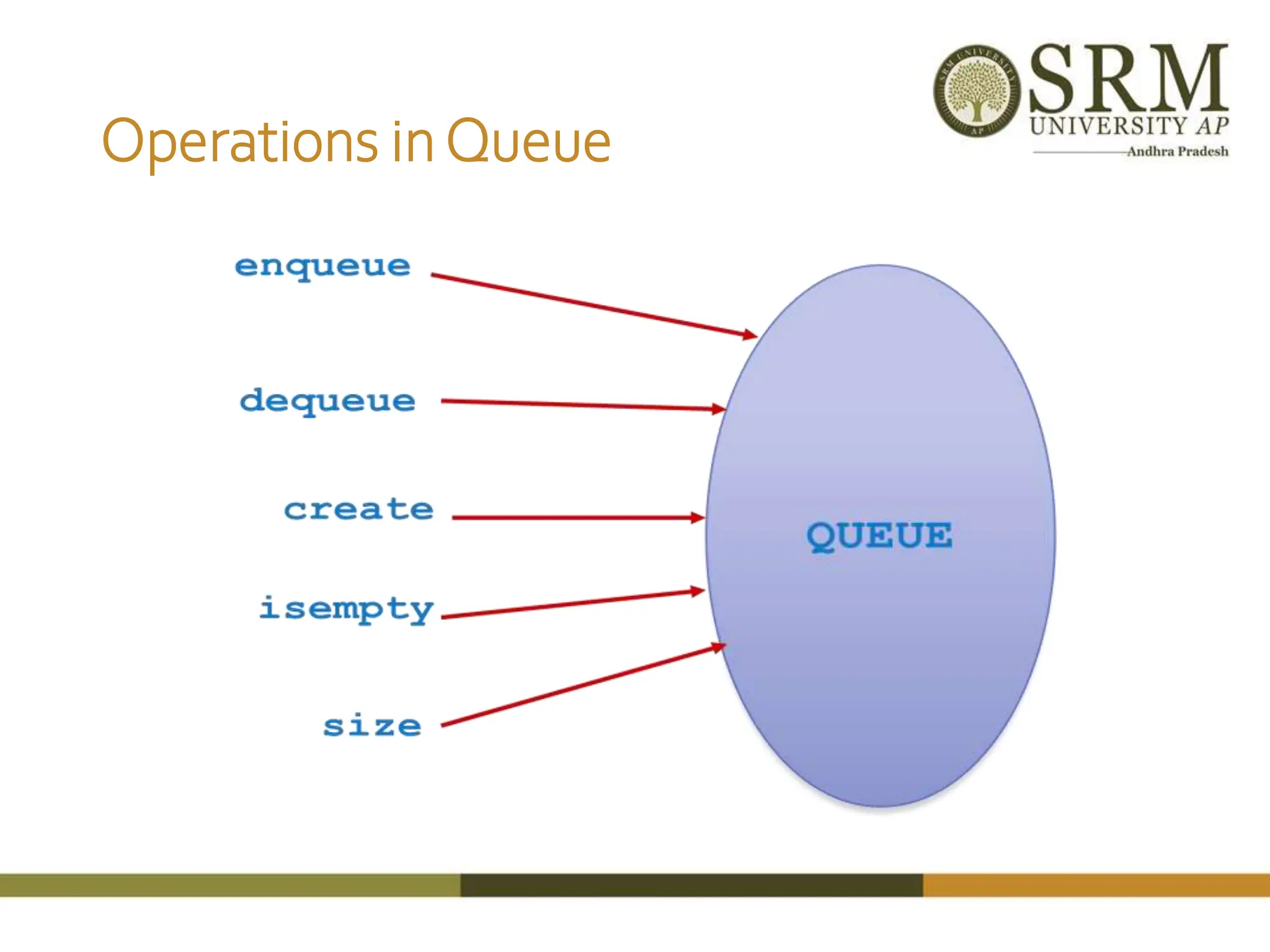
![Algorithm enqueue(o) if rear = N-1 then print “queue full error” else if(front =-1) front=0 r (f + sz) mod N Q[r] o sz (sz + 1) Algorithm isfull() return sz=N Algorithm size() return sz Algorithm isEmpty() return (sz ==0) Algorithm dequeue() if front=rear then print “ Queue is empty” else o Q[f] f (f + 1) mod N sz (sz - 1) if (front==rear) front=rear=-1 return o](https://image.slidesharecdn.com/1-240222043734-16d8326a/75/Revisiting-a-data-structures-in-detail-with-linked-list-stack-and-queue-18-2048.jpg)