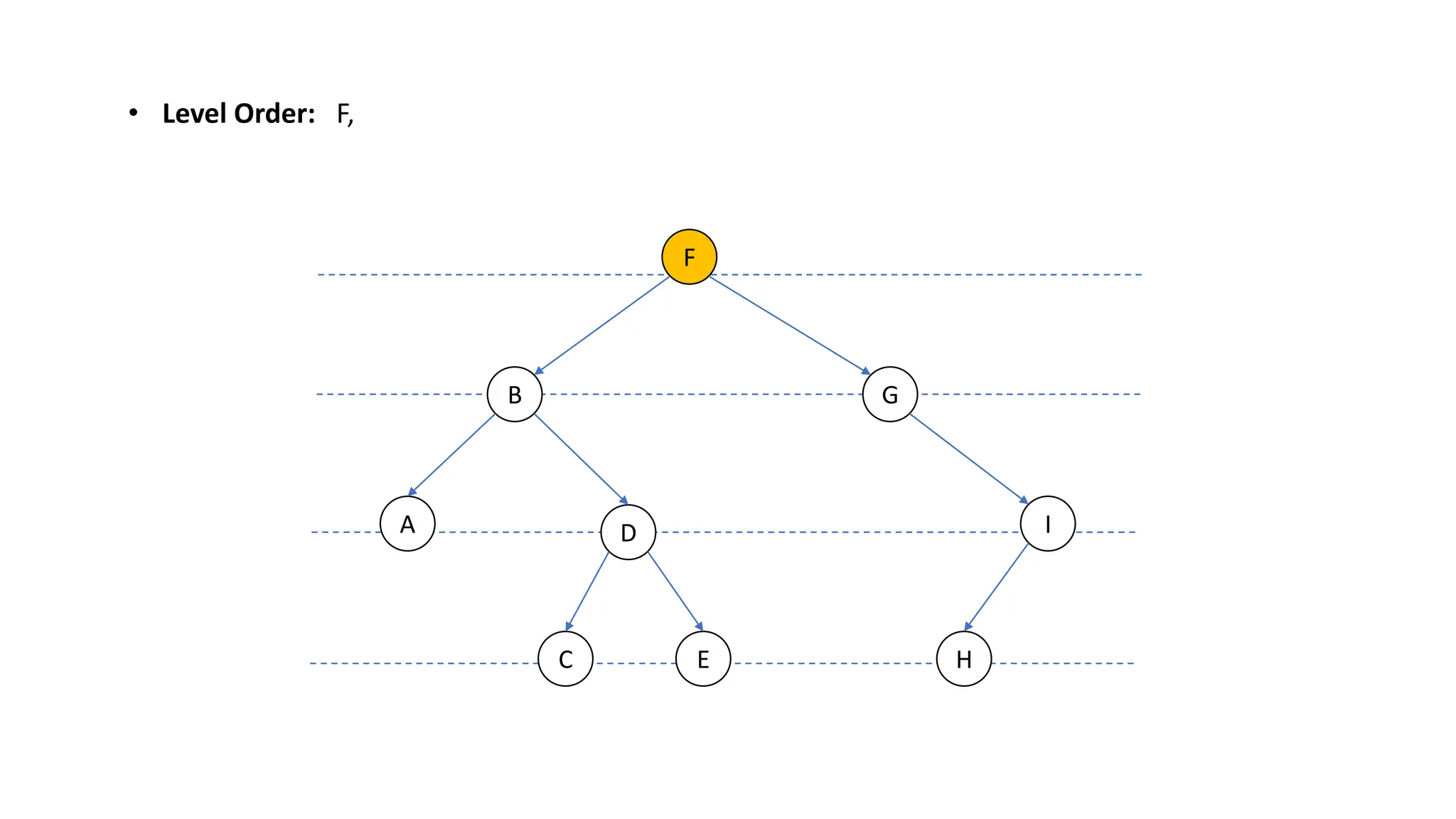
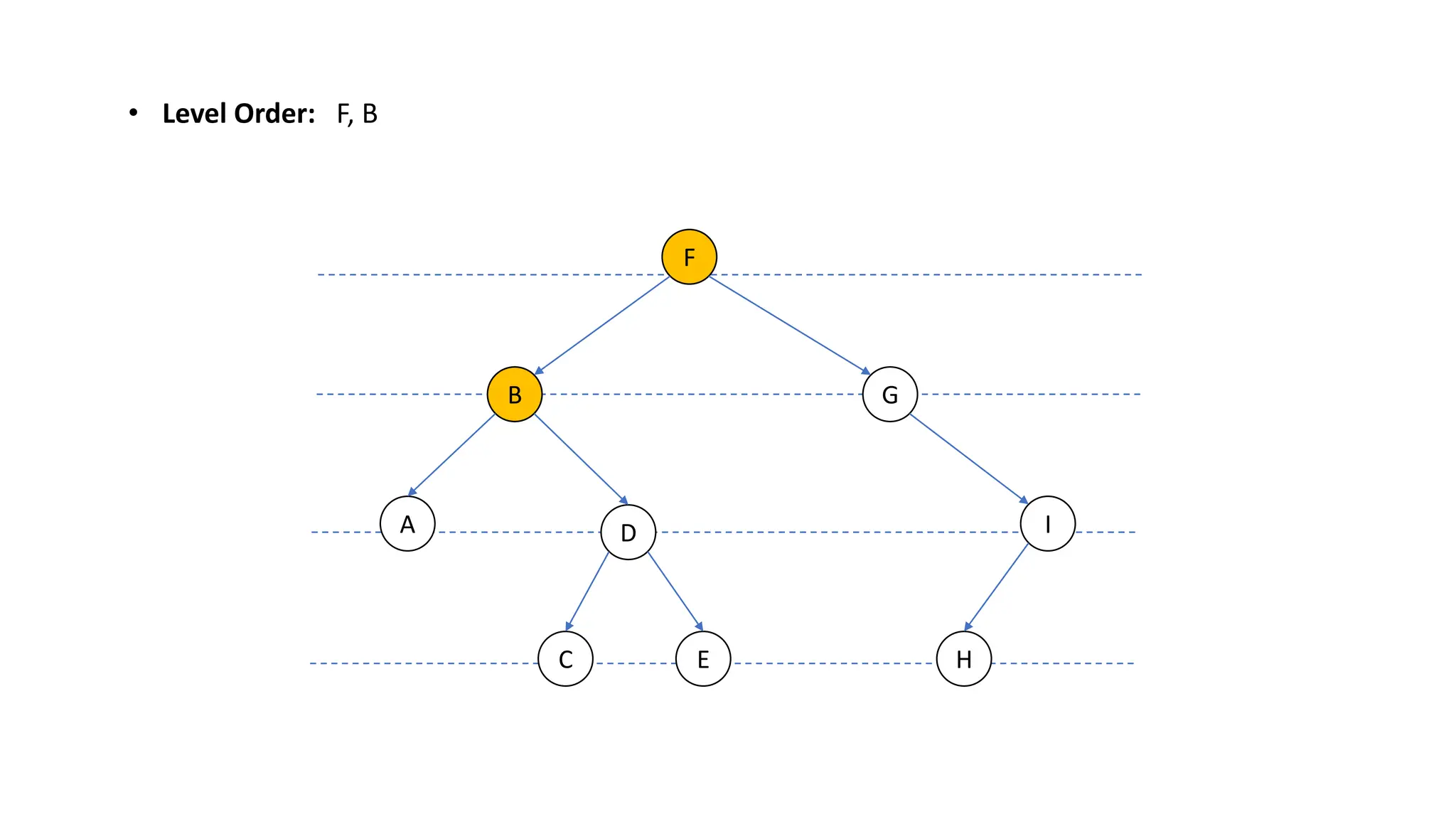
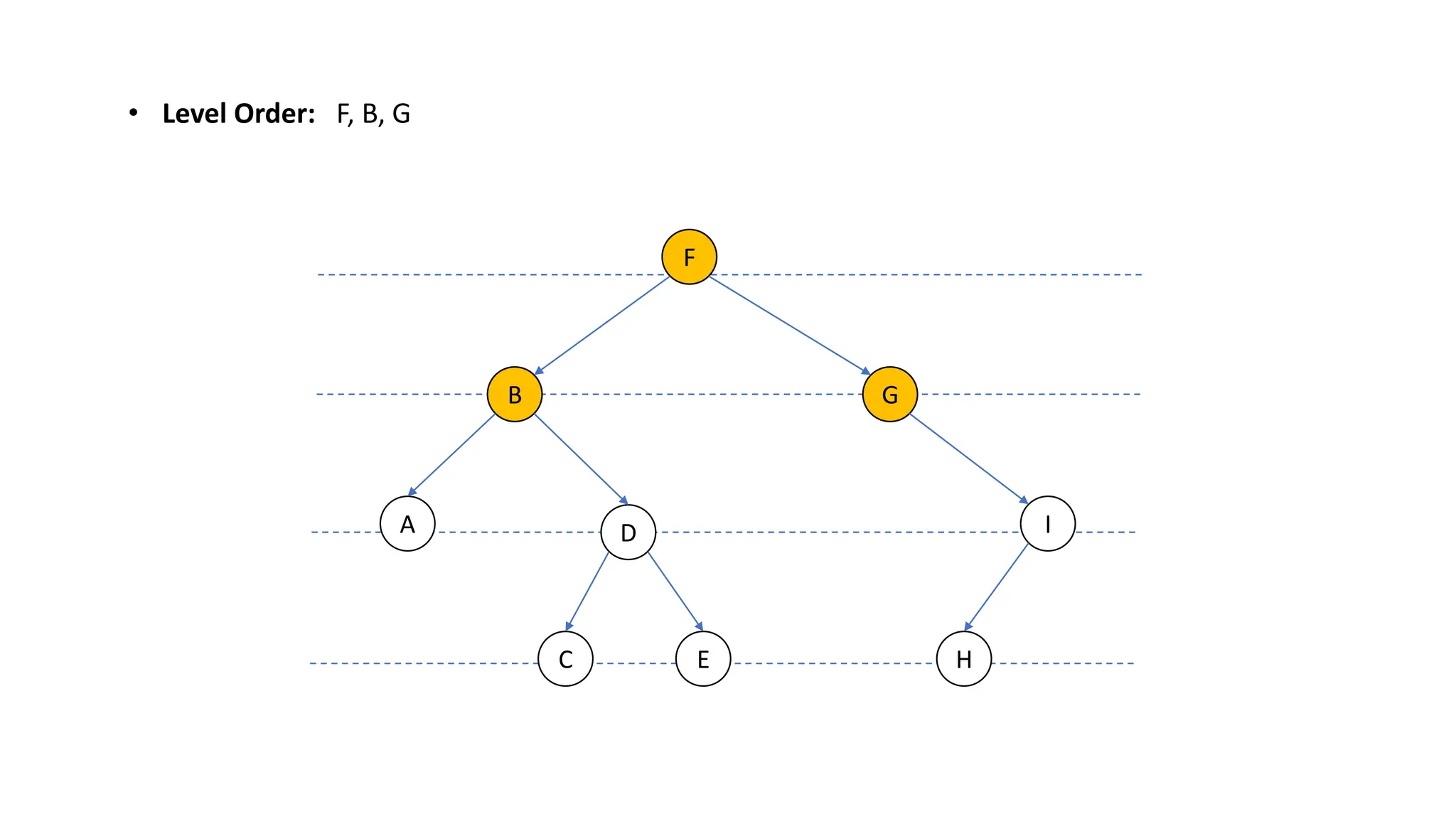
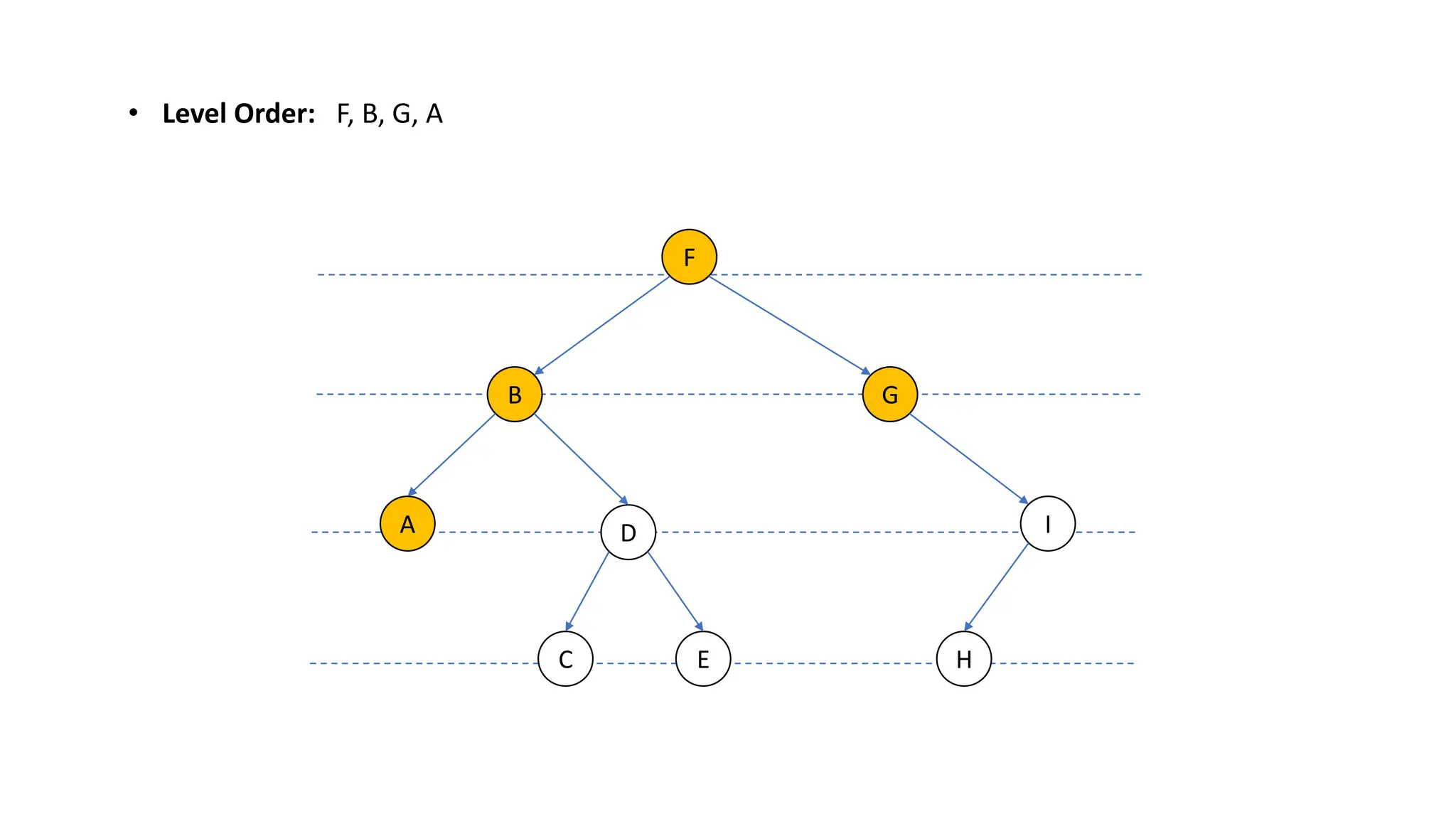
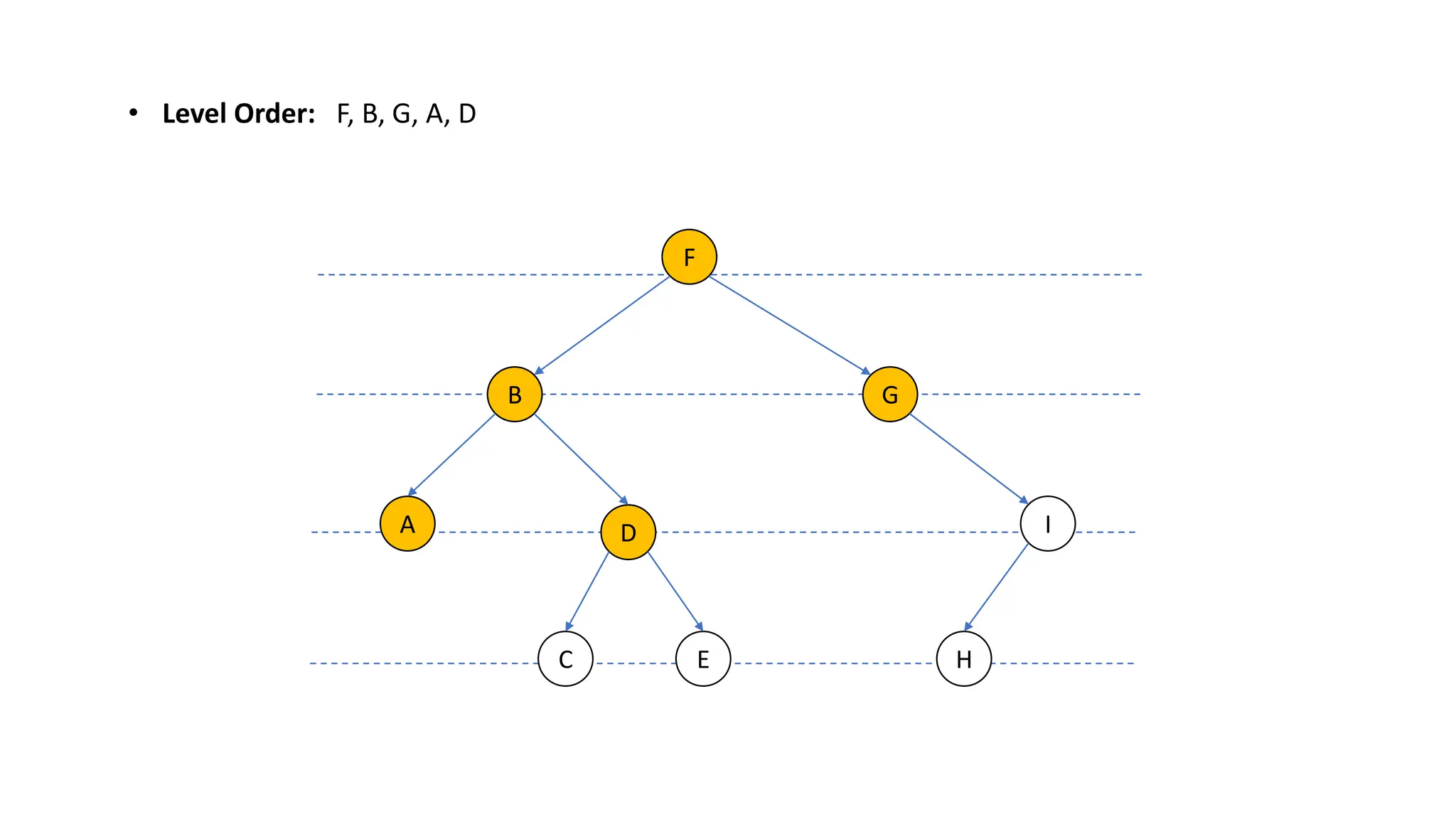
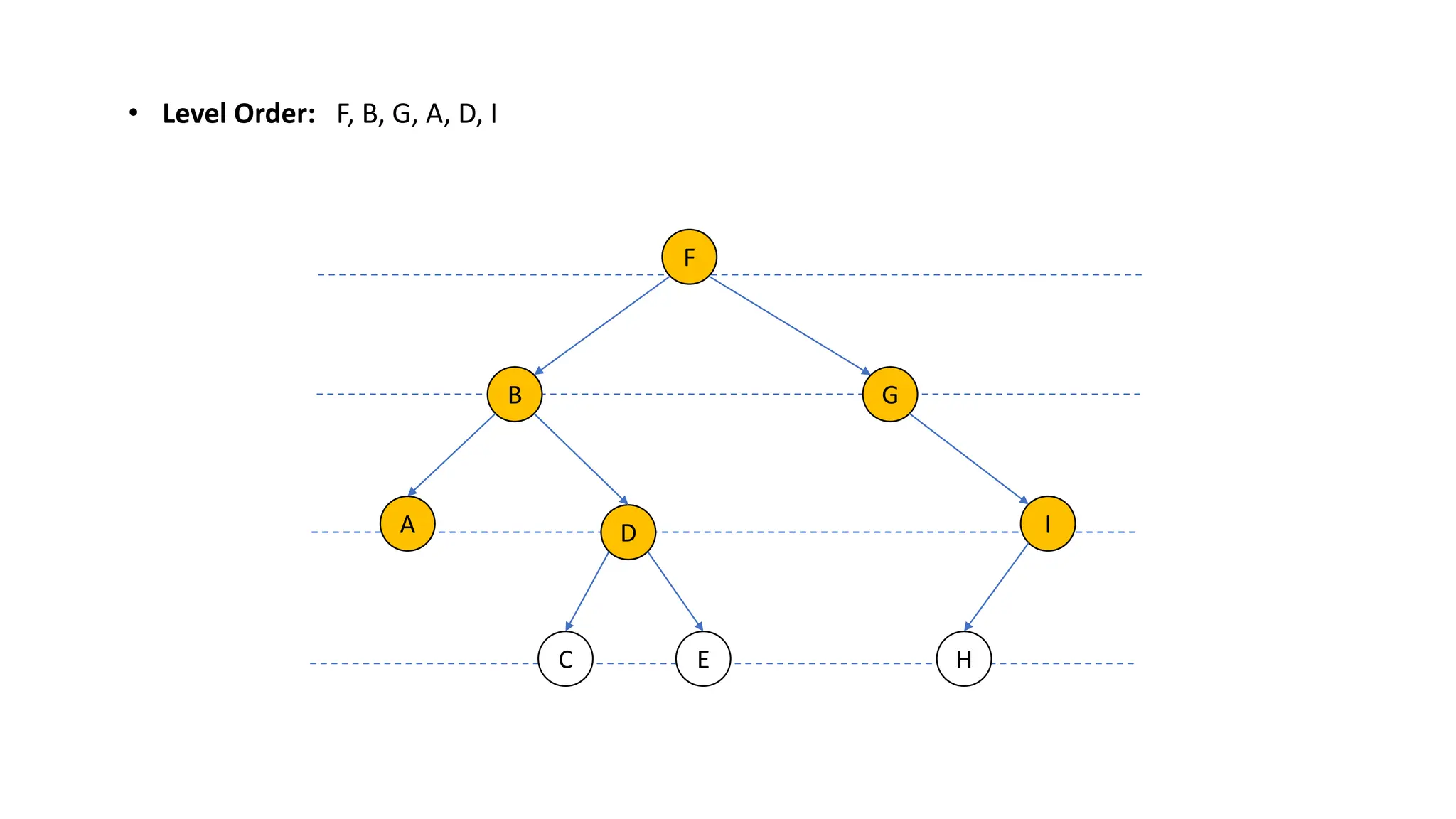
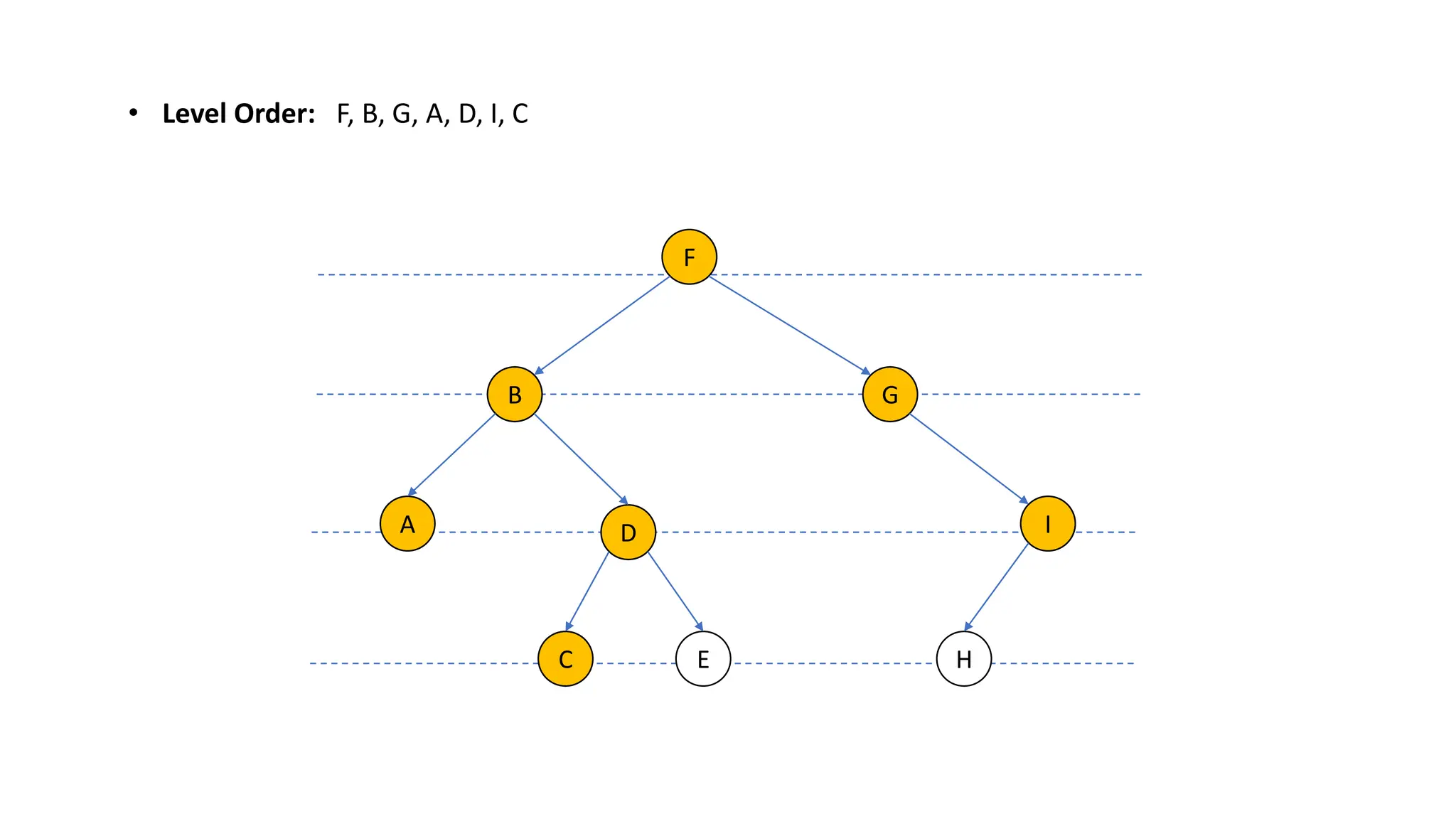
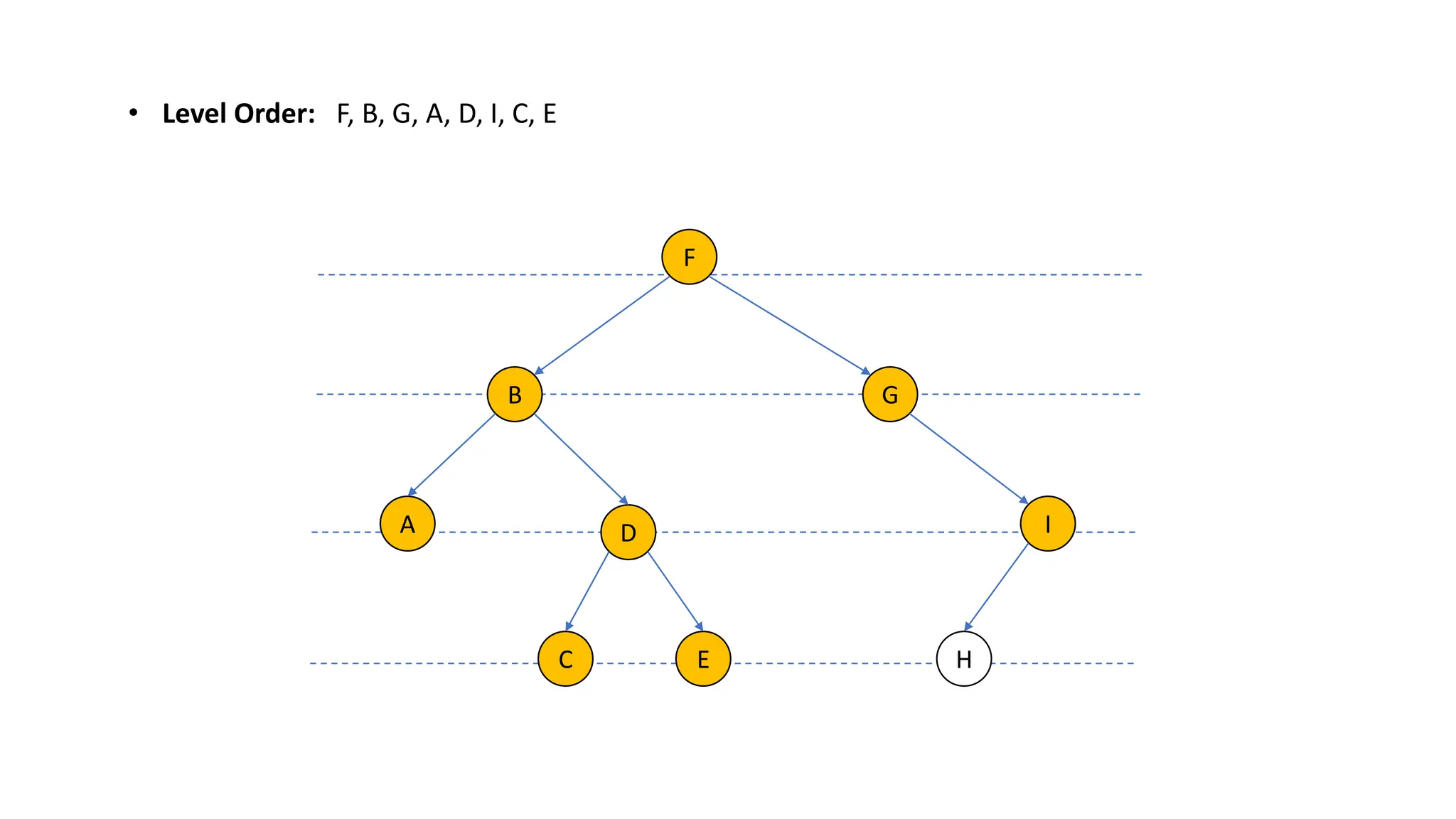
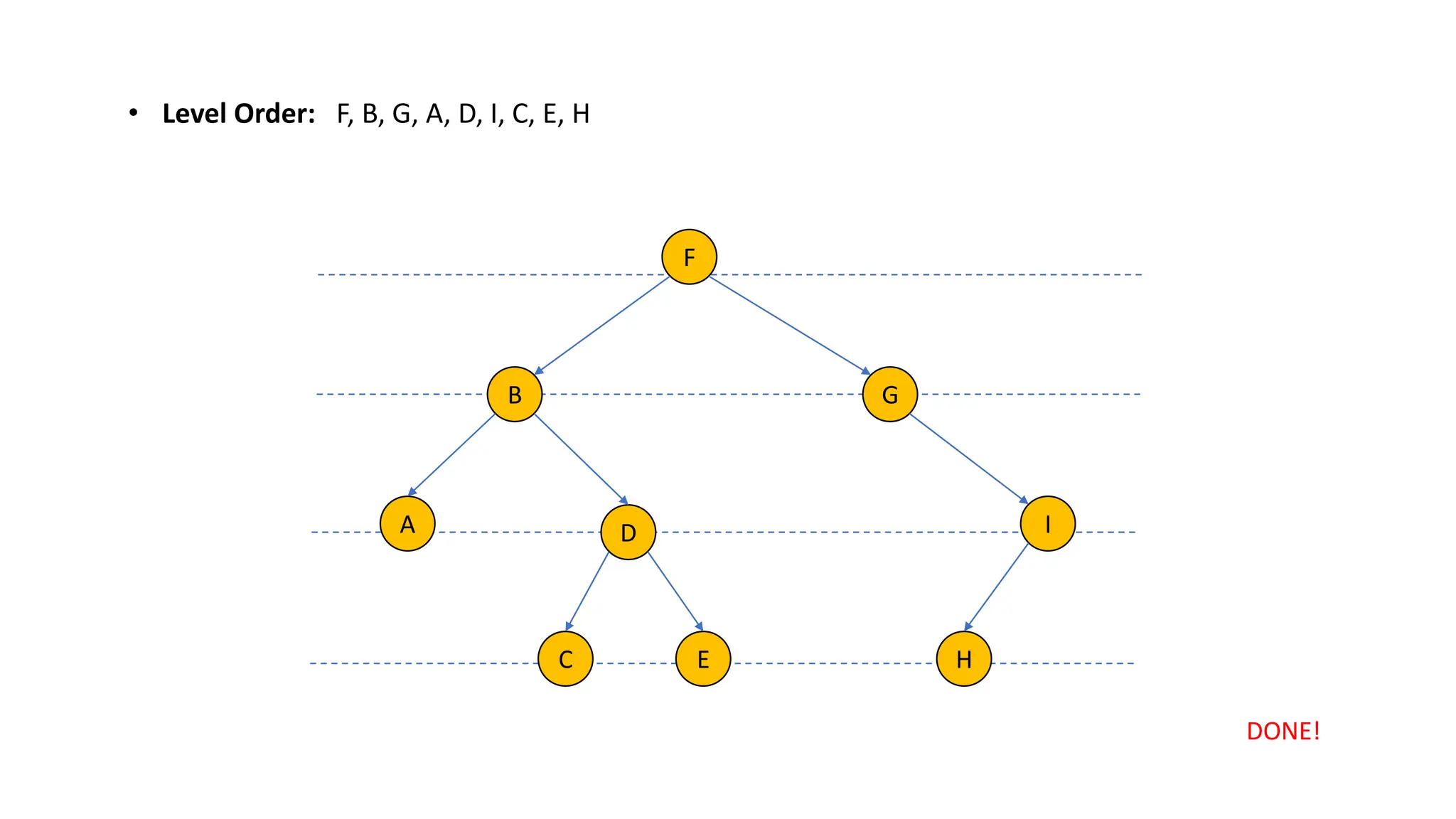
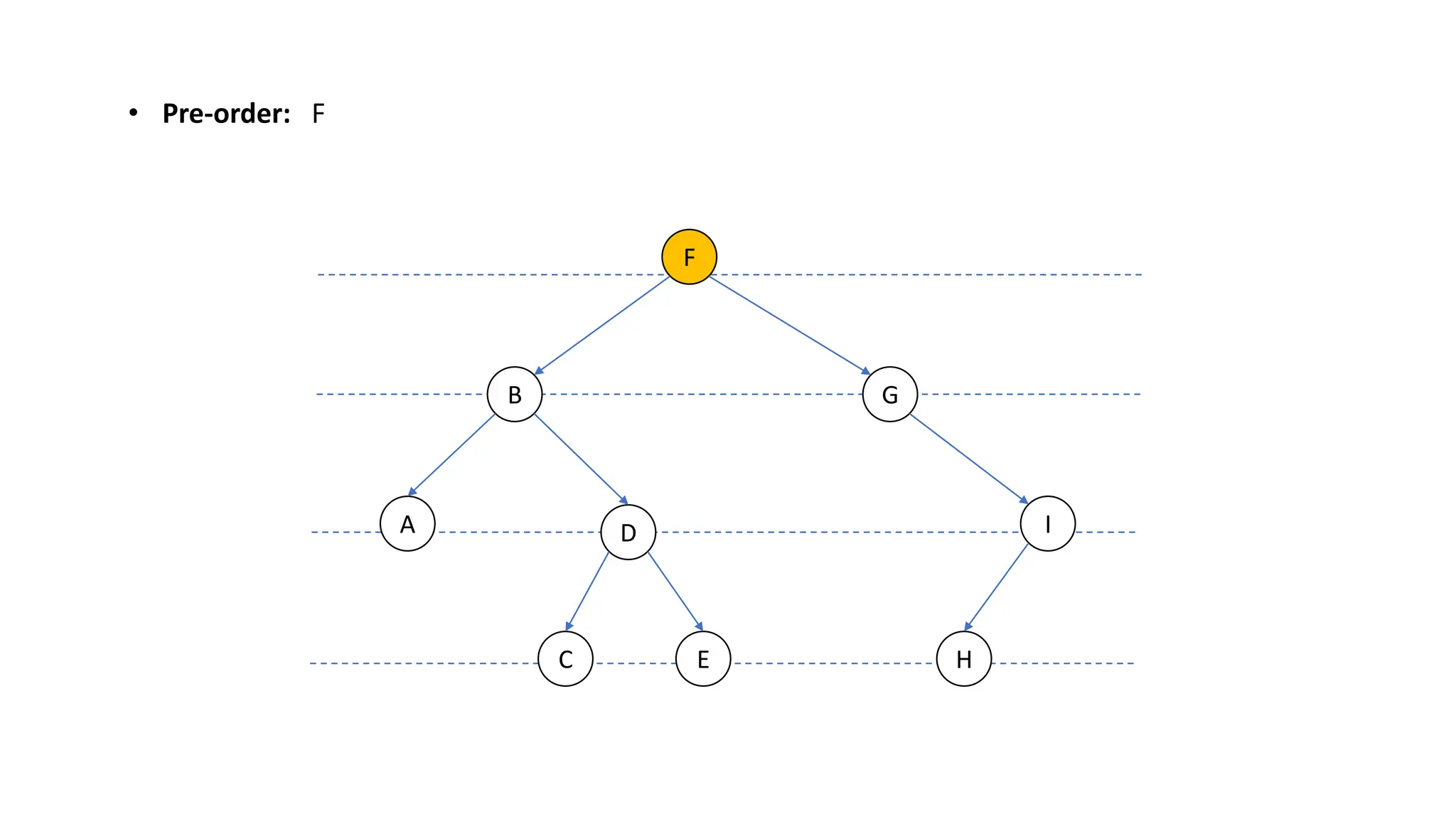
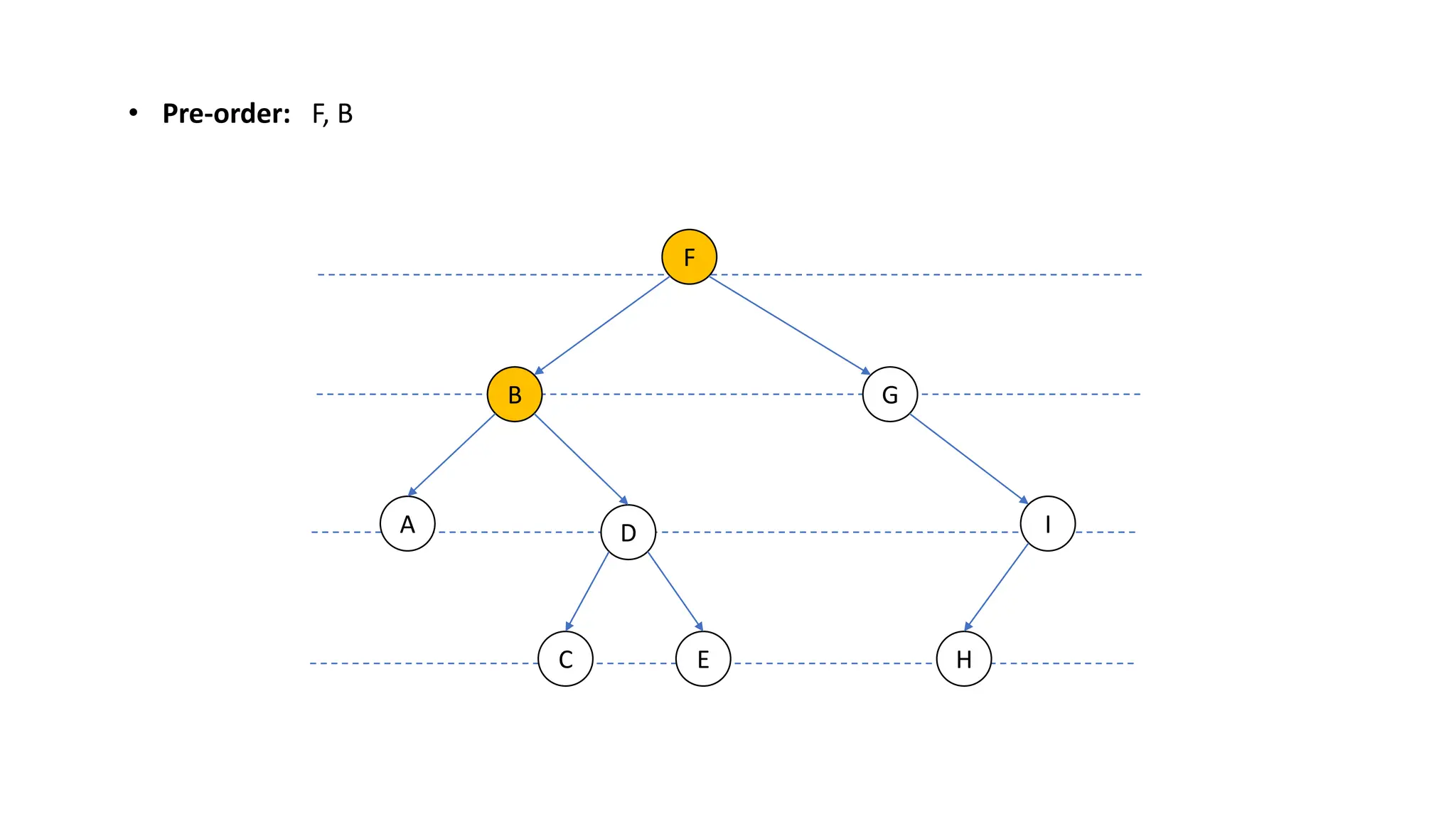
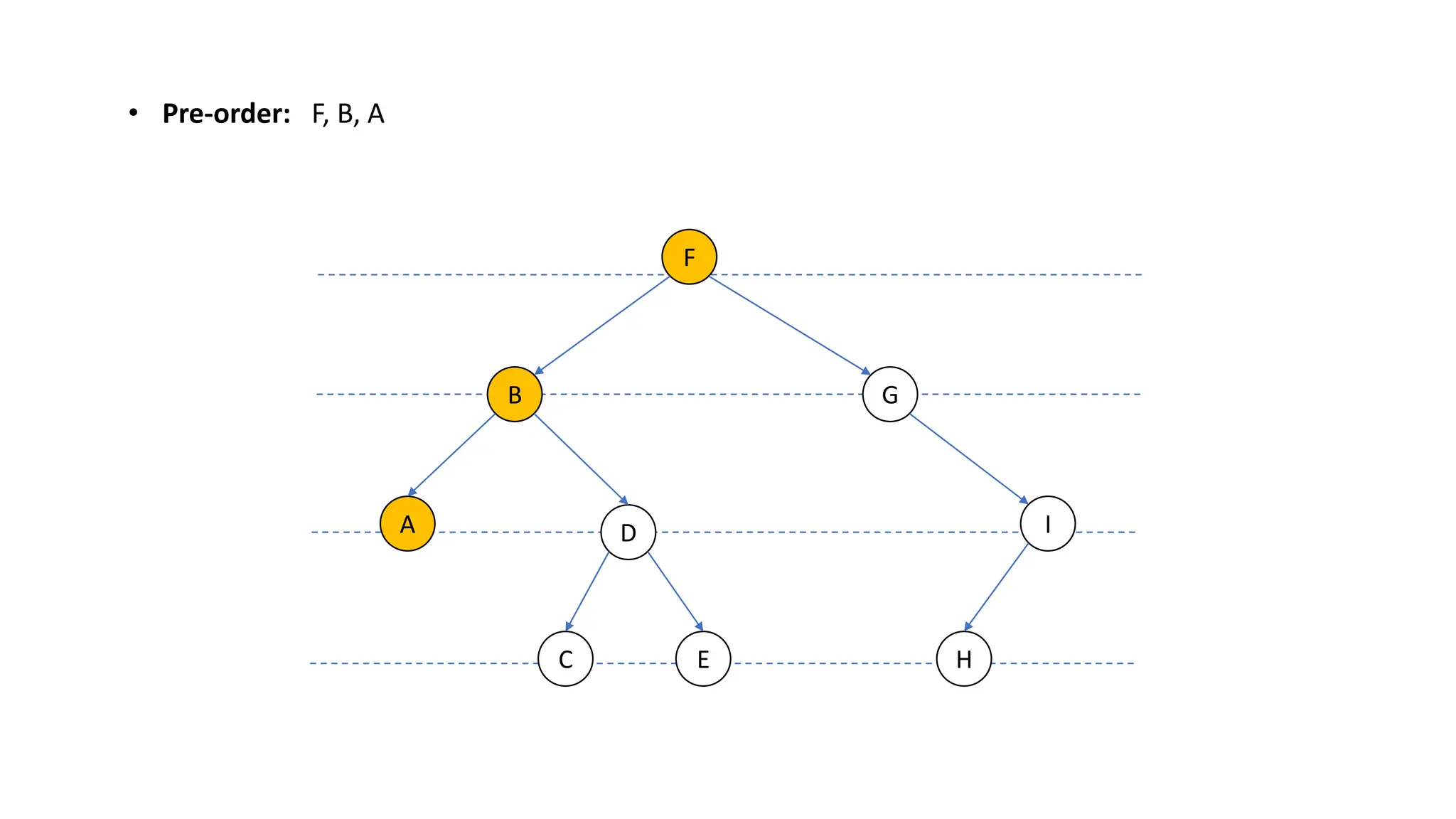
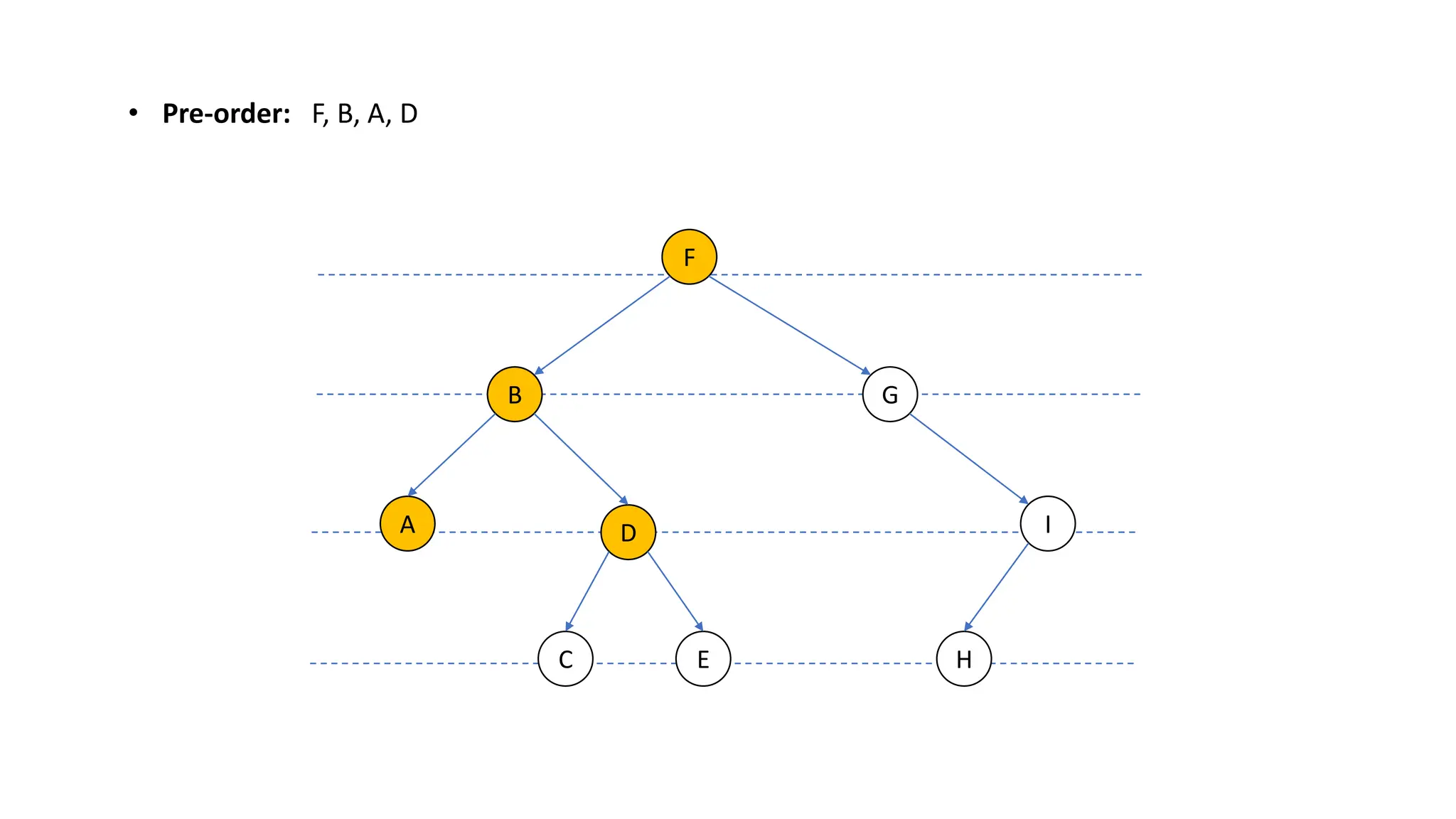
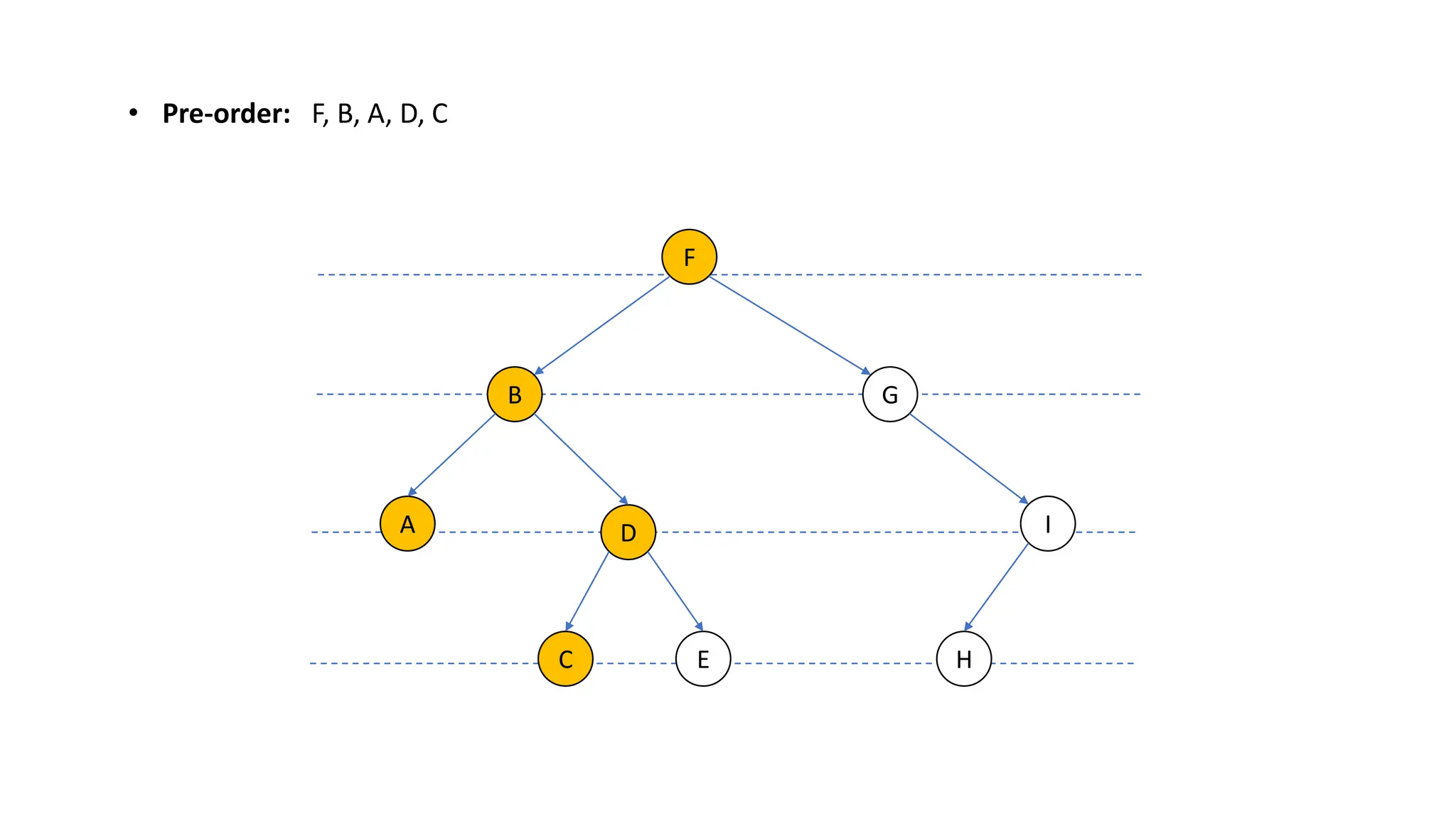
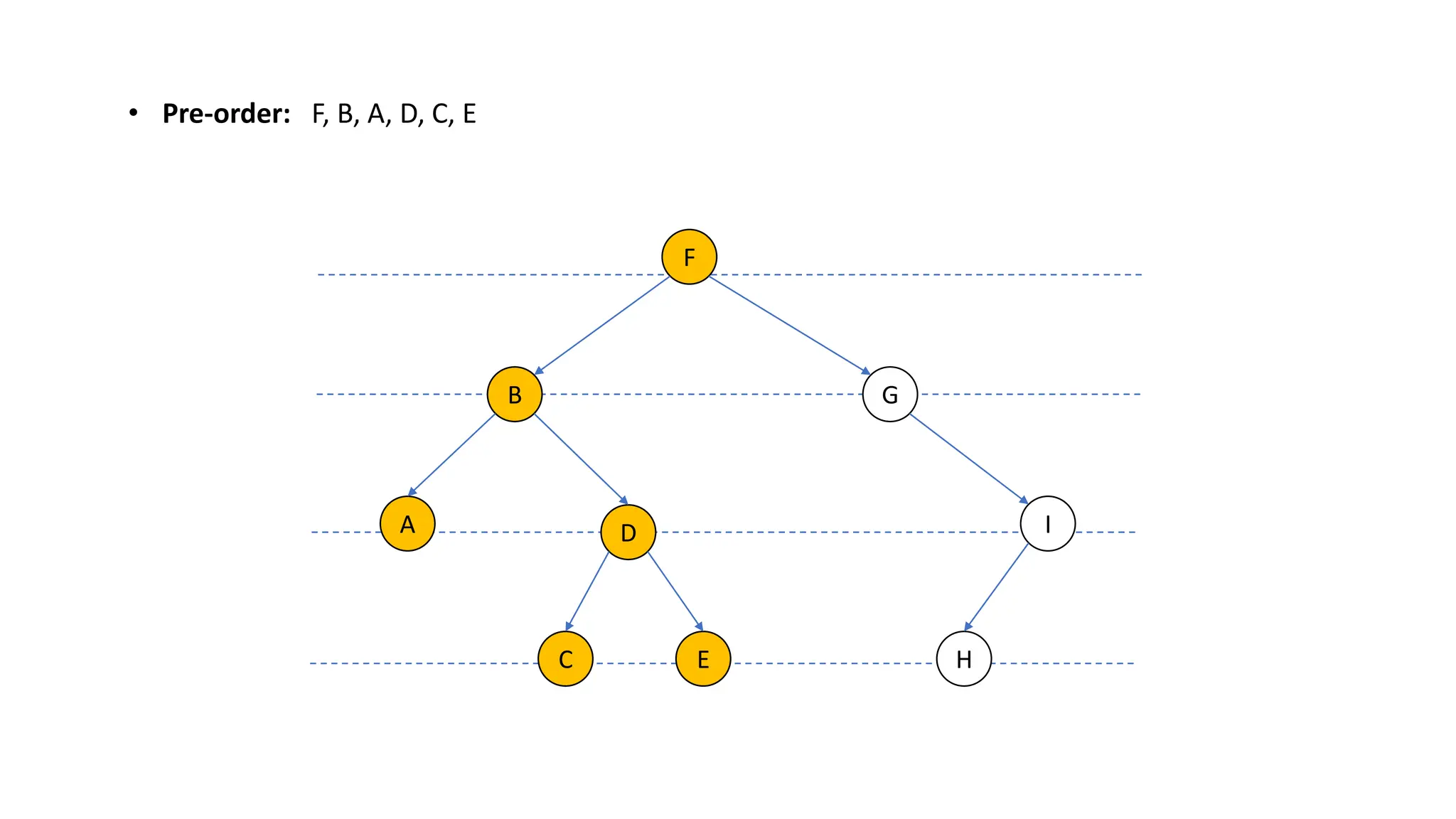
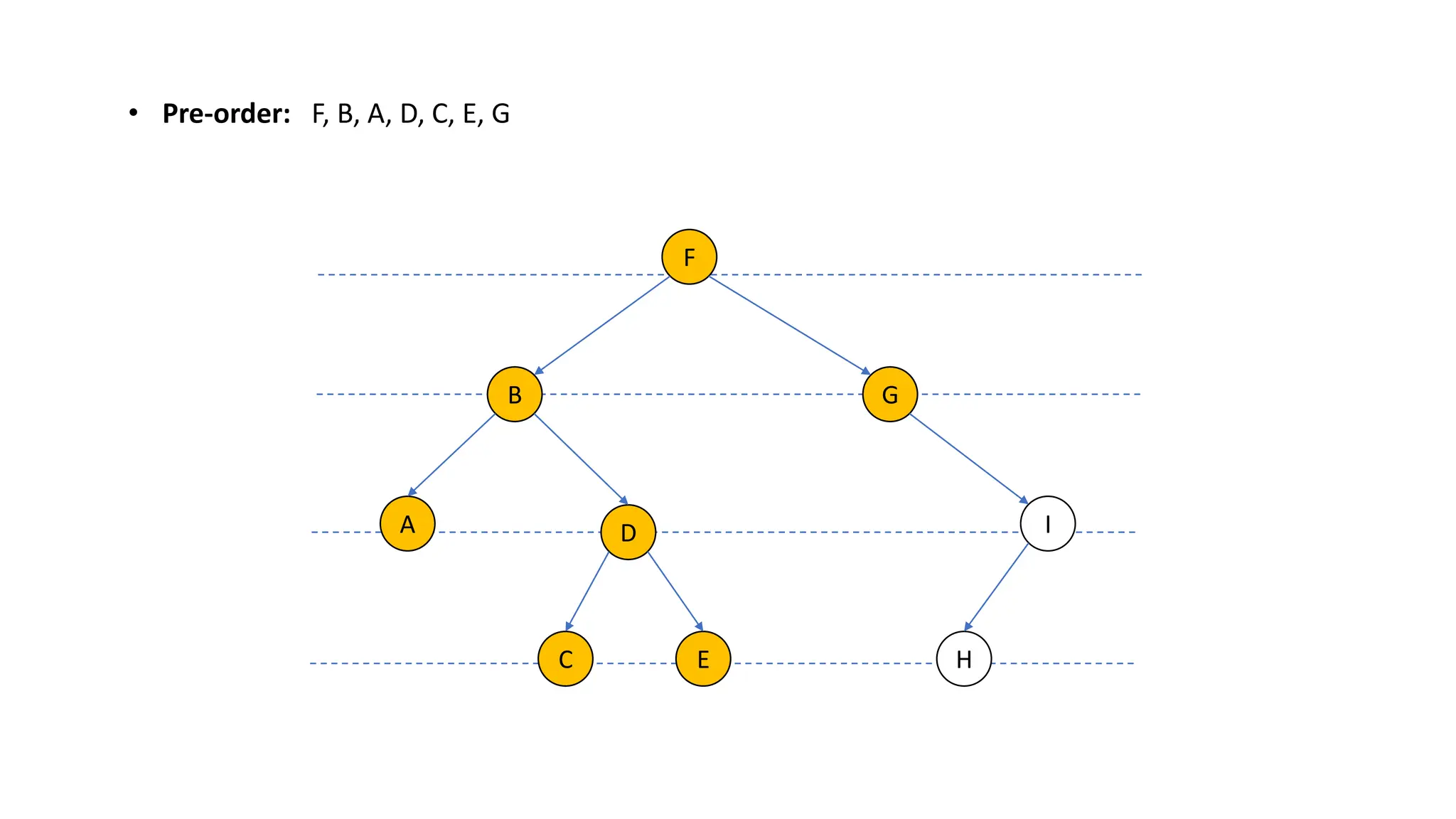
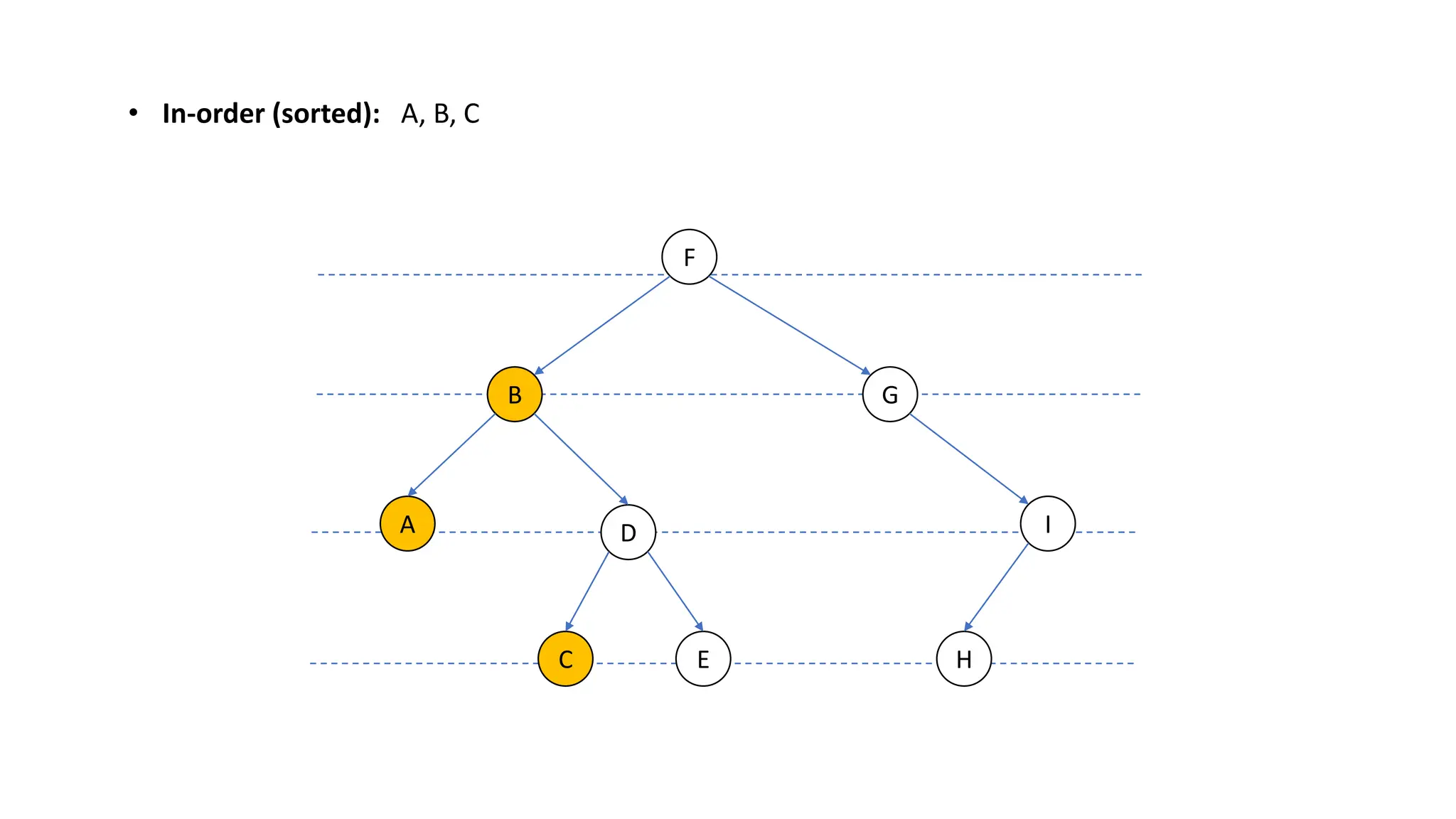
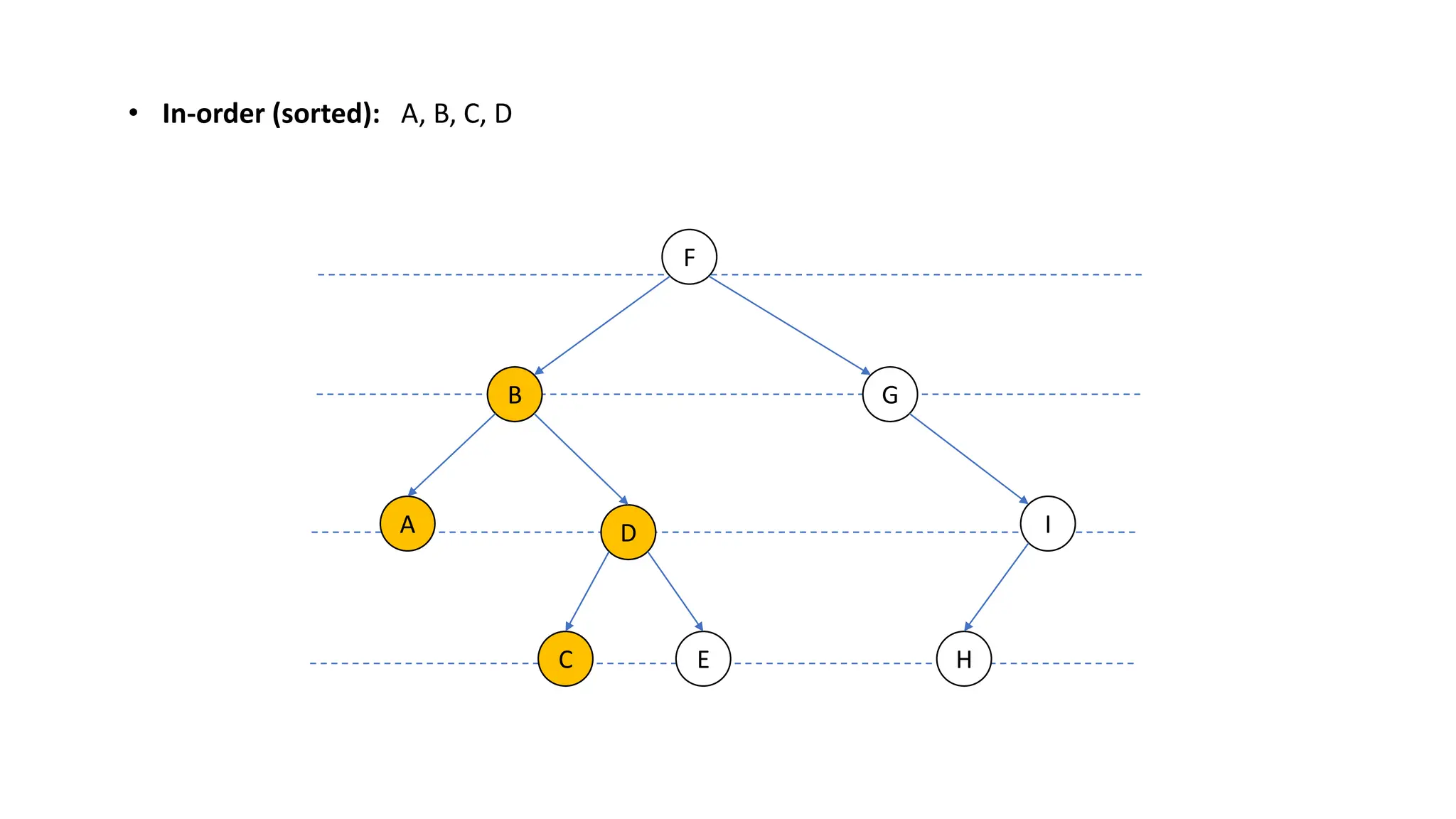
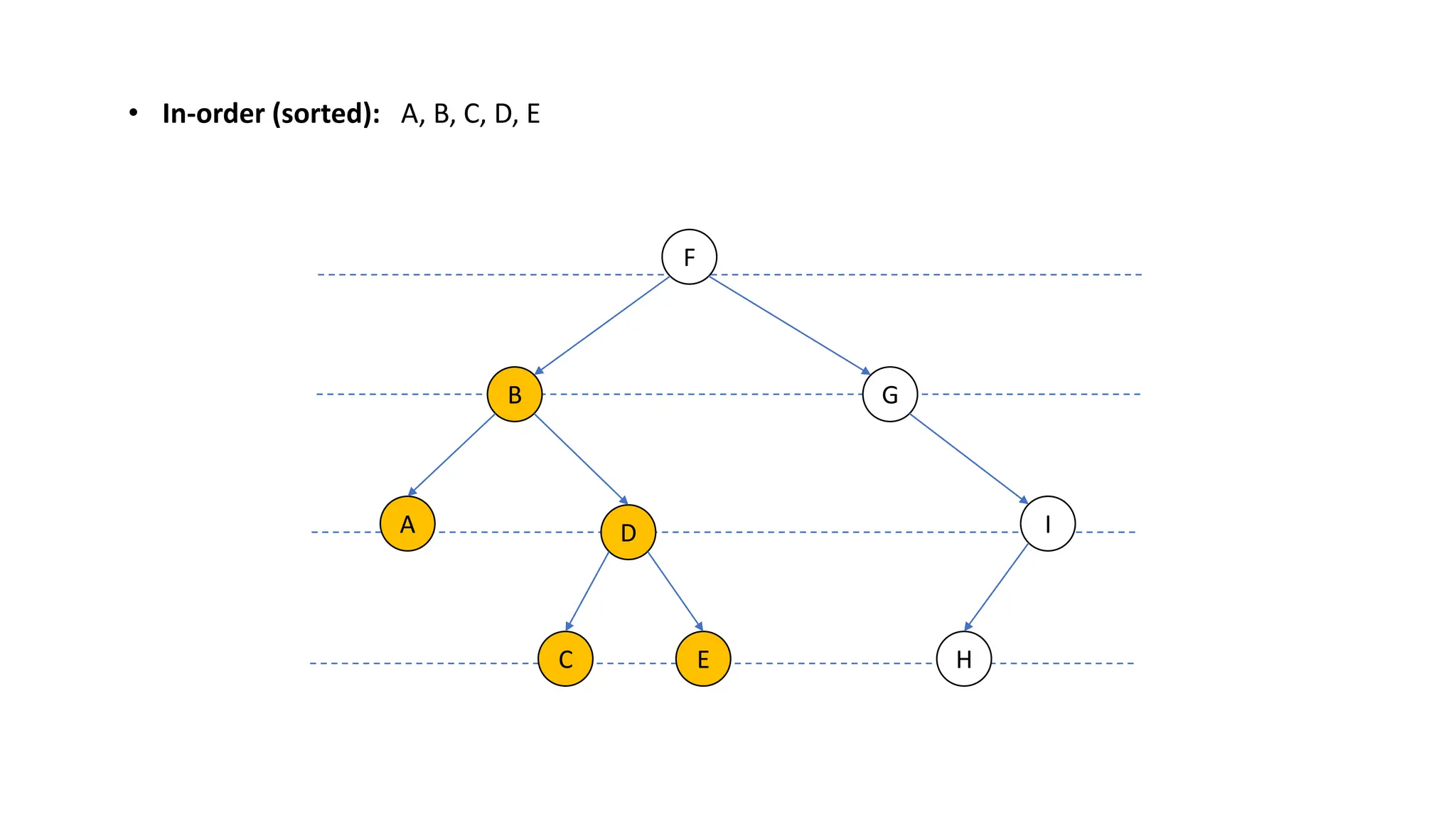
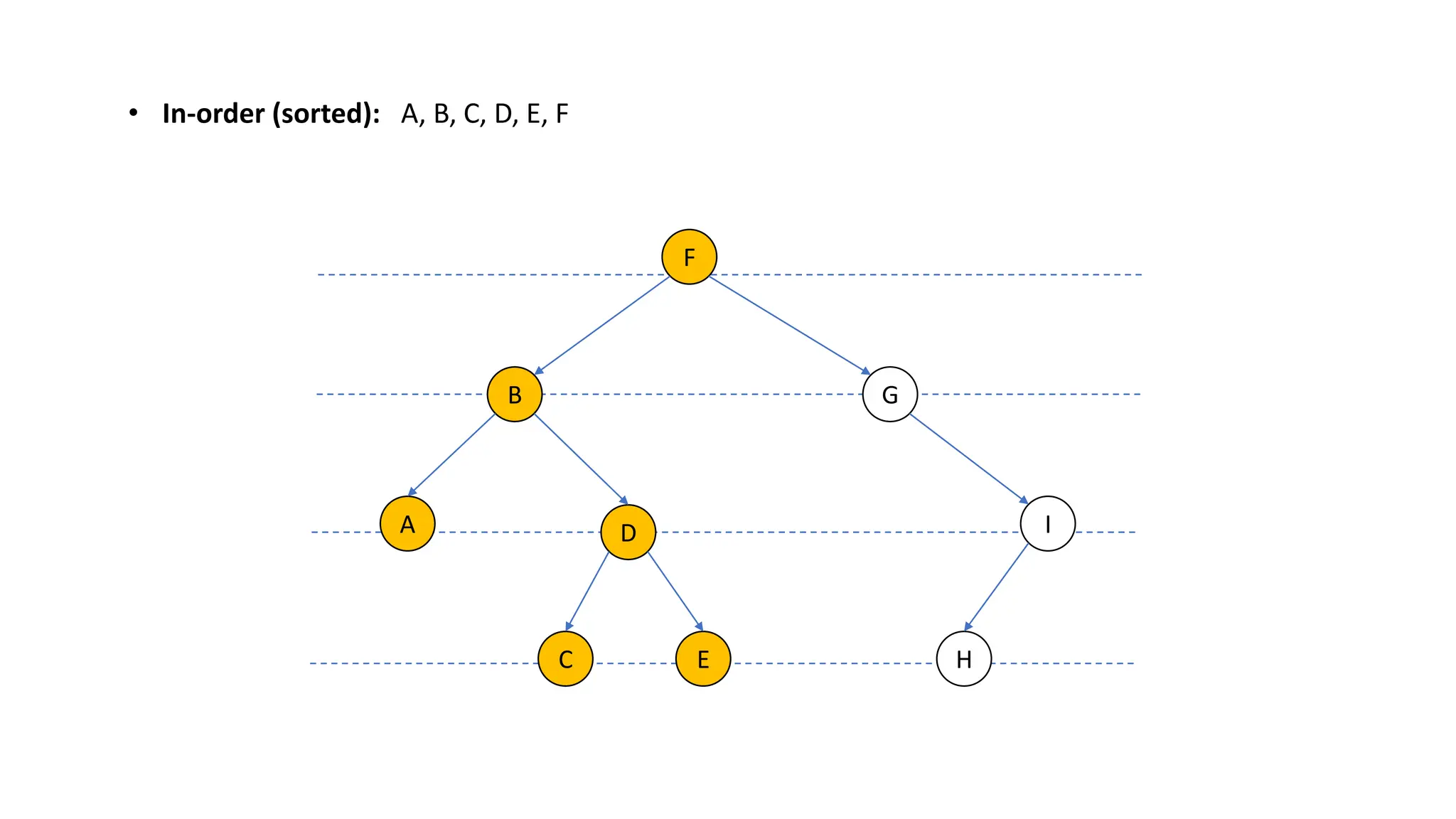
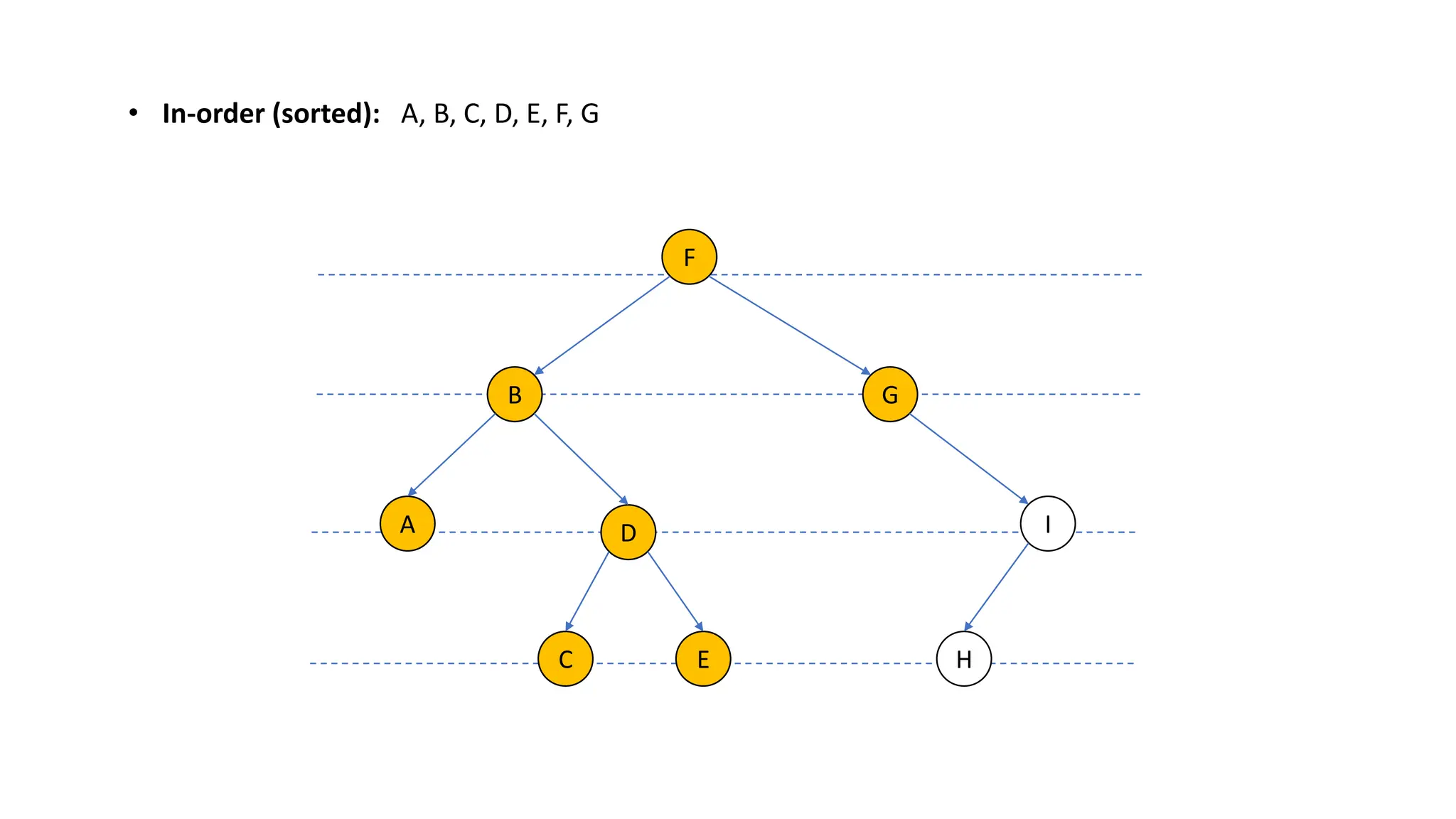
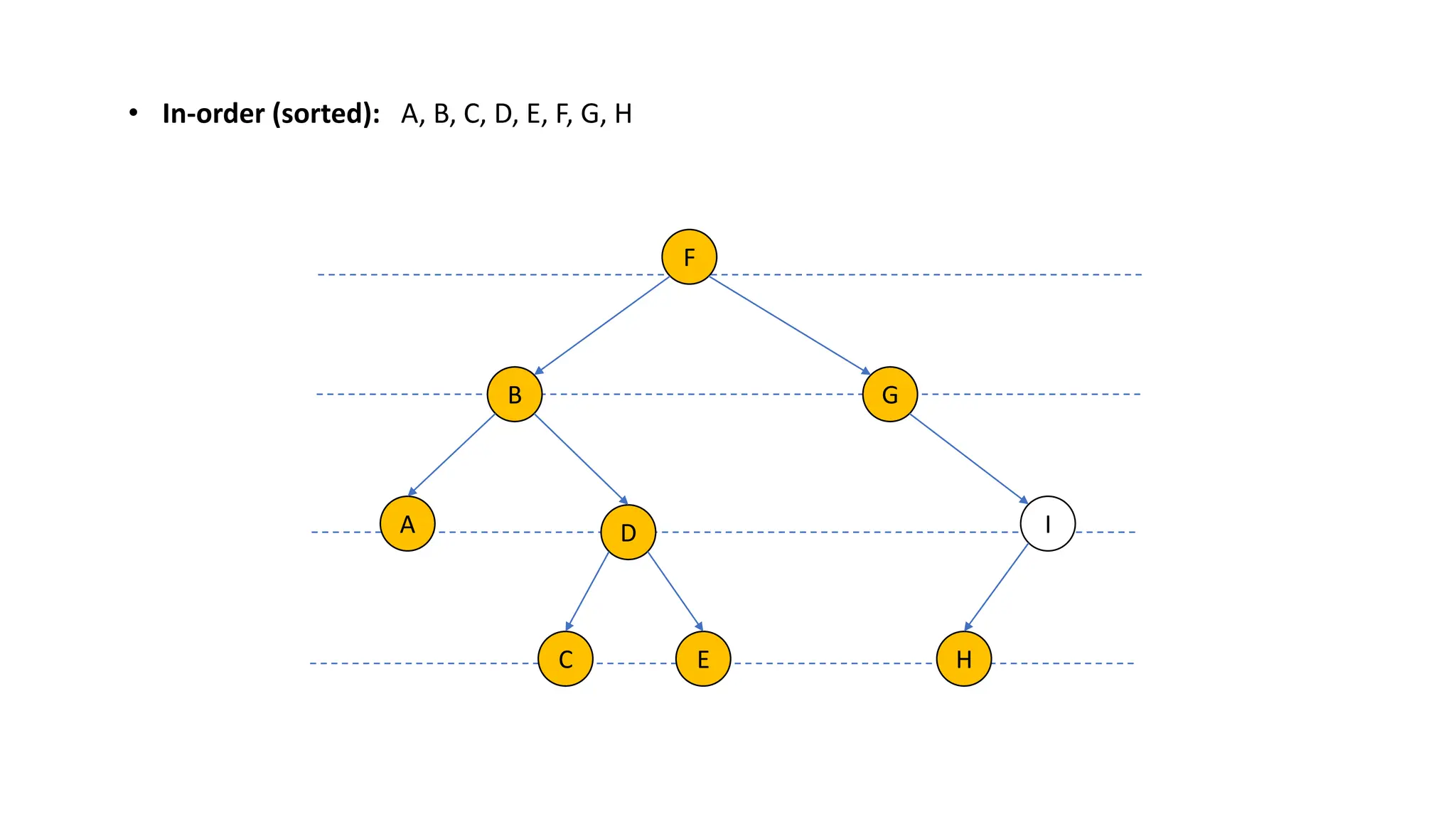
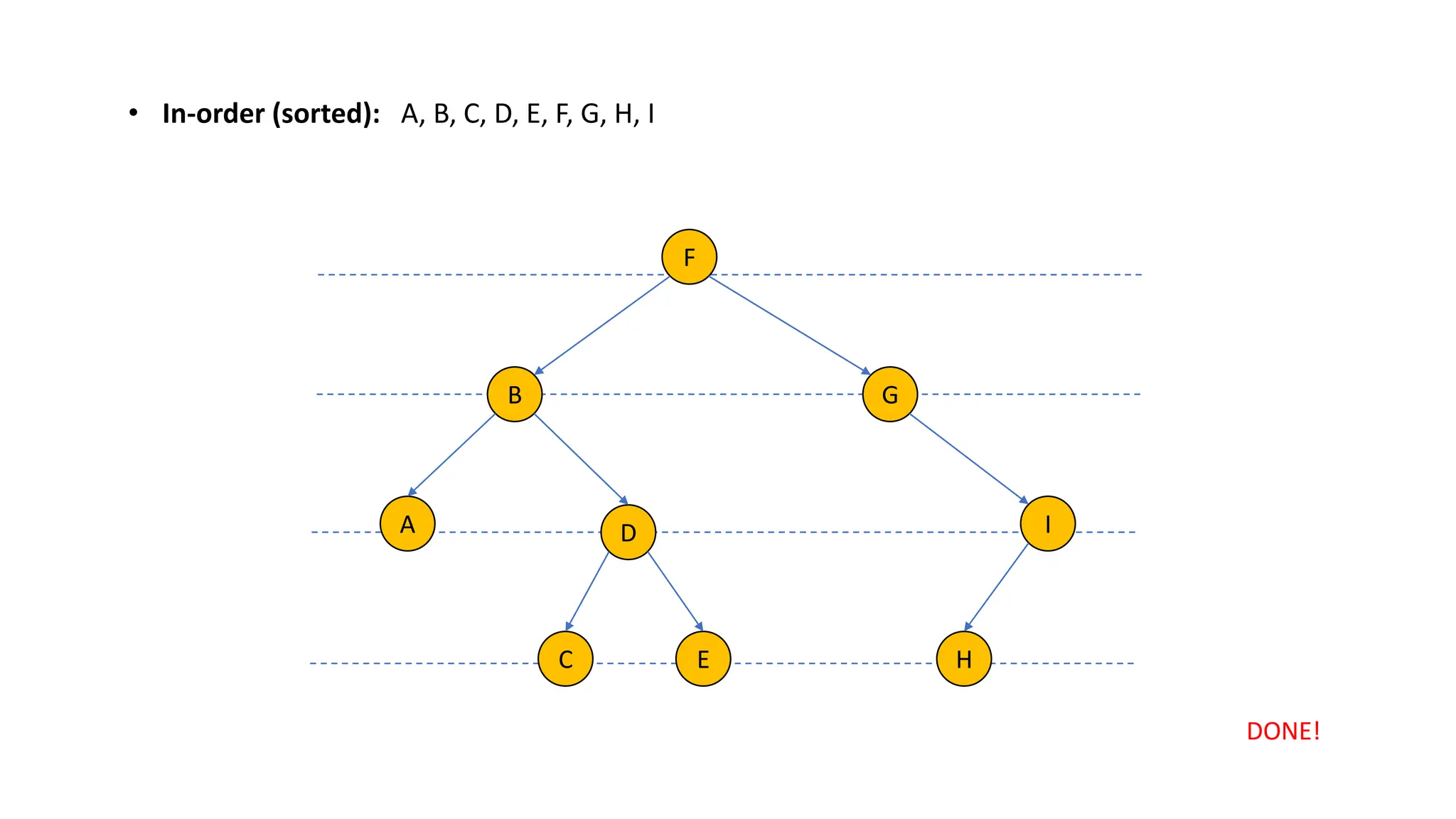
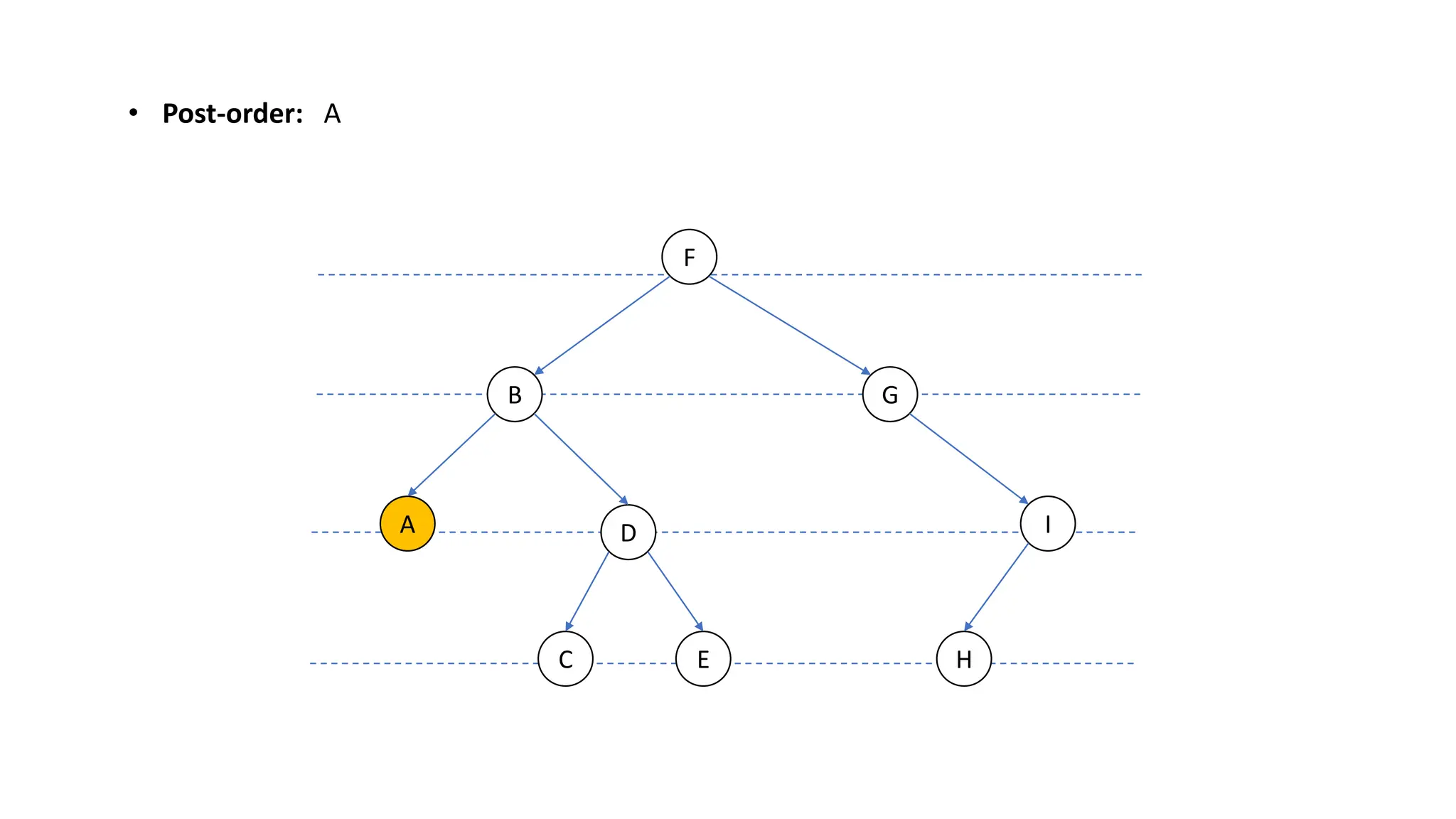
The document provides an overview of data structures and algorithms focusing on lists and their implementations in C++. It discusses various types of lists including simple arrays, linked lists, doubly linked lists, and the operations associated with them, such as insertion and deletion. Performance considerations are addressed, indicating the suitability of different list structures based on usage scenarios.






![const int n = 7; int arr[n] = { 1, 2, 3, 4, 5, 7, 7 }; 1 2 3 4 5 6 7 0 1 2 3 4 5 6 List const int n = 7; int *arr = new int[n]; // allocate memory for (int i = 0; i < n; i++) arr[i] = i + 1; delete[] arr; // free memory](https://image.slidesharecdn.com/datastructuresandalgorithms-lecture3-240909222602-b0822a03/75/Data-Structures-Algorithms-Lecture-3-8-2048.jpg)
![#include <iostream> using namespace std; class ArrayList { private: int *arr; int capacity; int size; // Helper function to resize the array when needed void resize() { capacity *= 2; int *newArr = new int[capacity]; for (int i = 0; i < size; i++) { newArr[i] = arr[i]; } delete[] arr; arr = newArr; delete[] newArr; } public: // Constructor ArrayList(int cap = 10) { capacity = cap; size = 0; arr = new int[capacity]; } // Destructor ~ArrayList() { delete[] arr; // free memory } // Print the list void printList() { for (int i = 0; i < size; i++) cout << arr[i] << " "; cout << endl; } // Find the element at the kth position int findKth(int k) { if (k < 0 || k >= size) { throw out_of_range("Index out of range"); } return arr[k]; } // Insert an element at the specified position void insert(int element, int position) { if (position < 0 || position > size) { throw out_of_range("Index out of range"); } if (size == capacity) { // If the array is full, resize it resize(); } // Shift elements to the right for (int i = size; i > position; i--) { arr[i] = arr[i - 1]; } arr[position] = element; size++; } // Check if the list is empty bool isEmpty() { return size == 0; } // Remove the first occurrence of the specified element void remove(int element) { int position = -1; for (int i = 0; i < size; i++) { if (arr[i] == element) { position = i; break; } } if (position == -1) { cout << "Element not found" << endl; return; } for (int i = position; i < size - 1; i++) { arr[i] = arr[i + 1]; } size--; } }; int main() { ArrayList list; // { 34, 12, 52, 16, 12, 7 } list.insert(34, 0); list.insert(12, 1); list.insert(52, 2); list.insert(16, 3); list.insert(12, 4); list.insert(7, 5); cout << "List after insertion: "; list.printList(); cout << "Element at position 2: " << list.findKth(2) << endl; list.remove(52); cout << "List after removing 52: "; list.printList(); return 0; } Array List C++ implementation](https://image.slidesharecdn.com/datastructuresandalgorithms-lecture3-240909222602-b0822a03/75/Data-Structures-Algorithms-Lecture-3-9-2048.jpg)











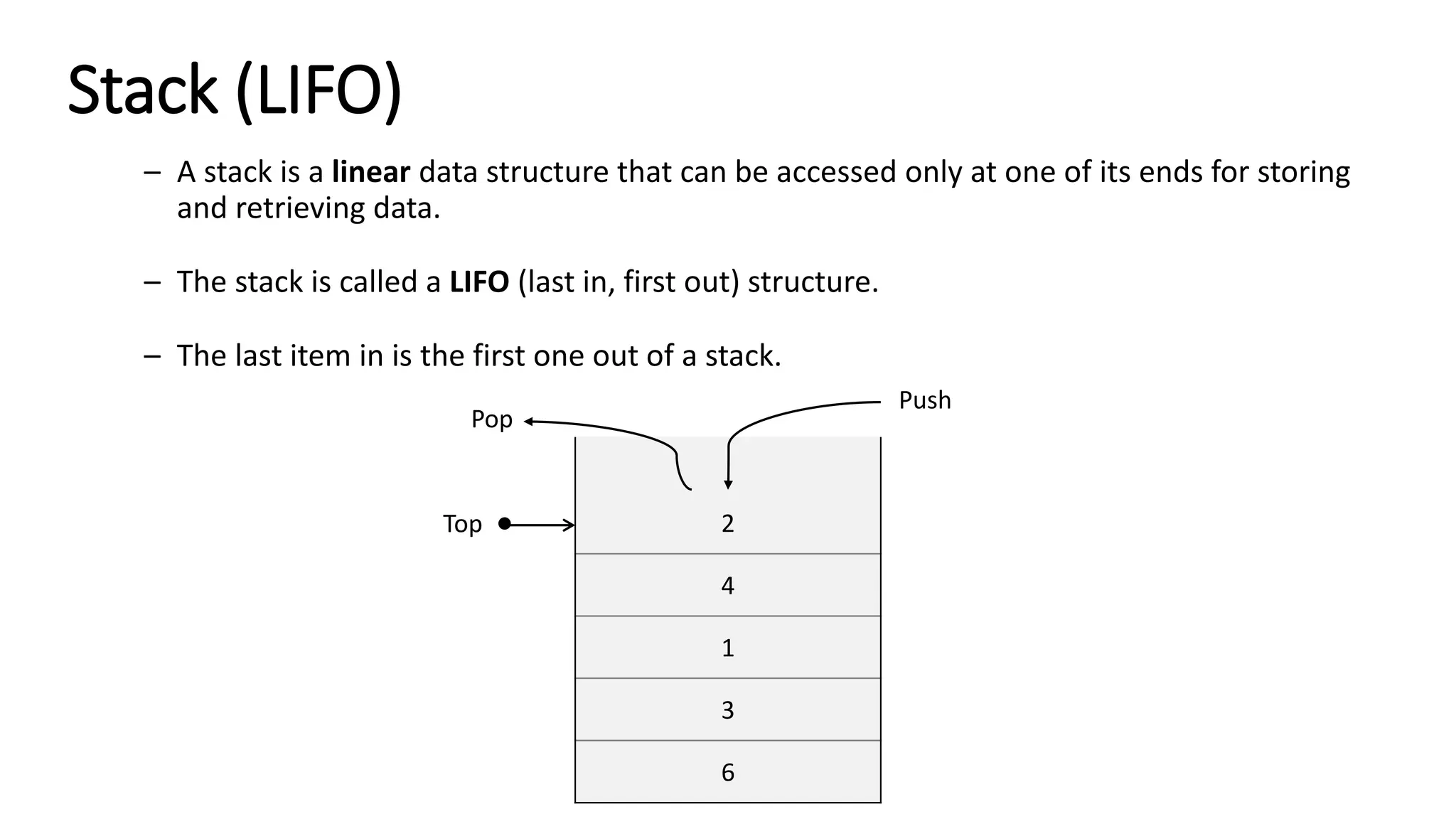
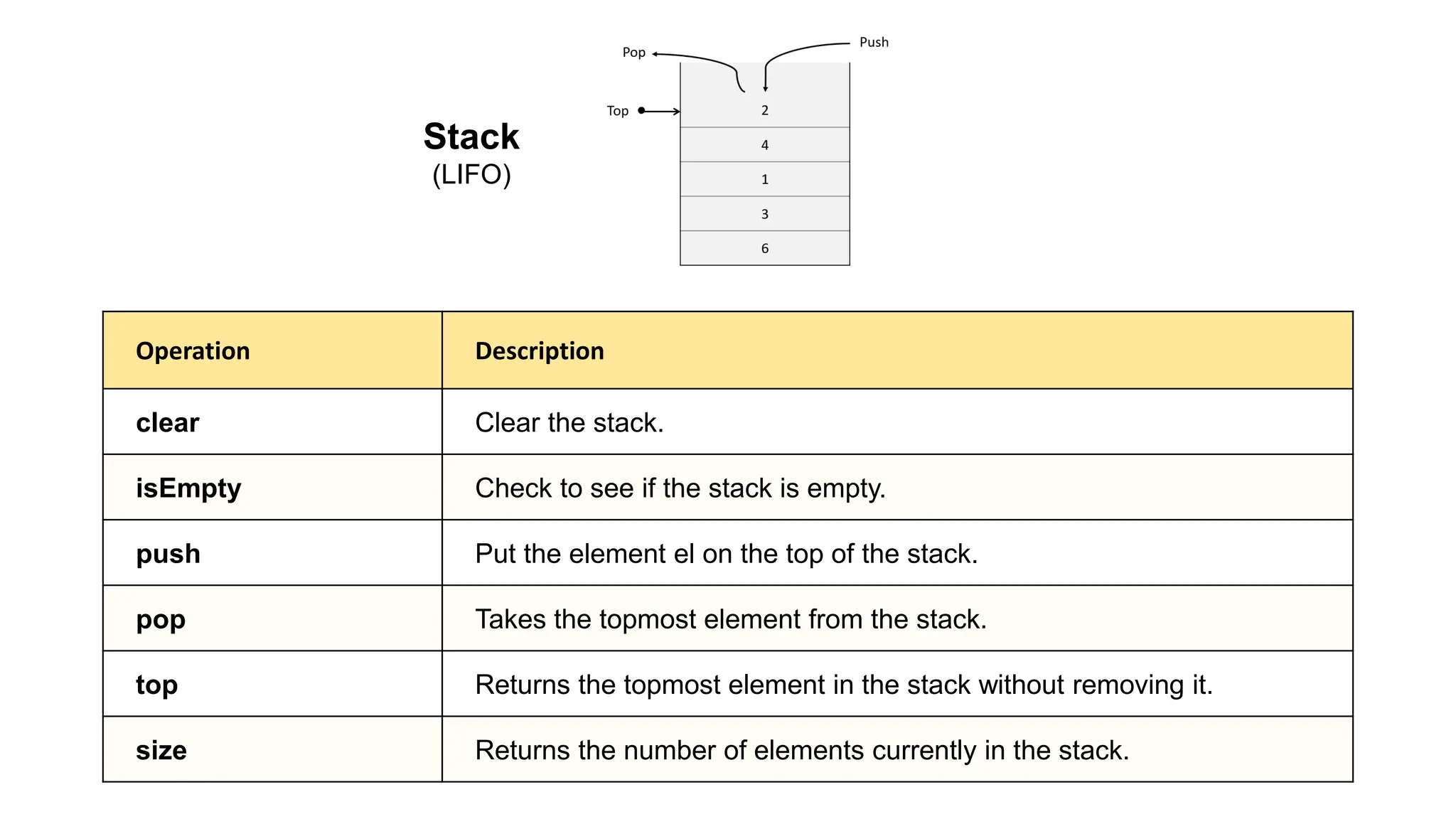

![2 + 3 * 4 – 6 = 8 { [ ( ) ] }](https://image.slidesharecdn.com/datastructuresandalgorithms-lecture3-240909222602-b0822a03/75/Data-Structures-Algorithms-Lecture-3-31-2048.jpg)
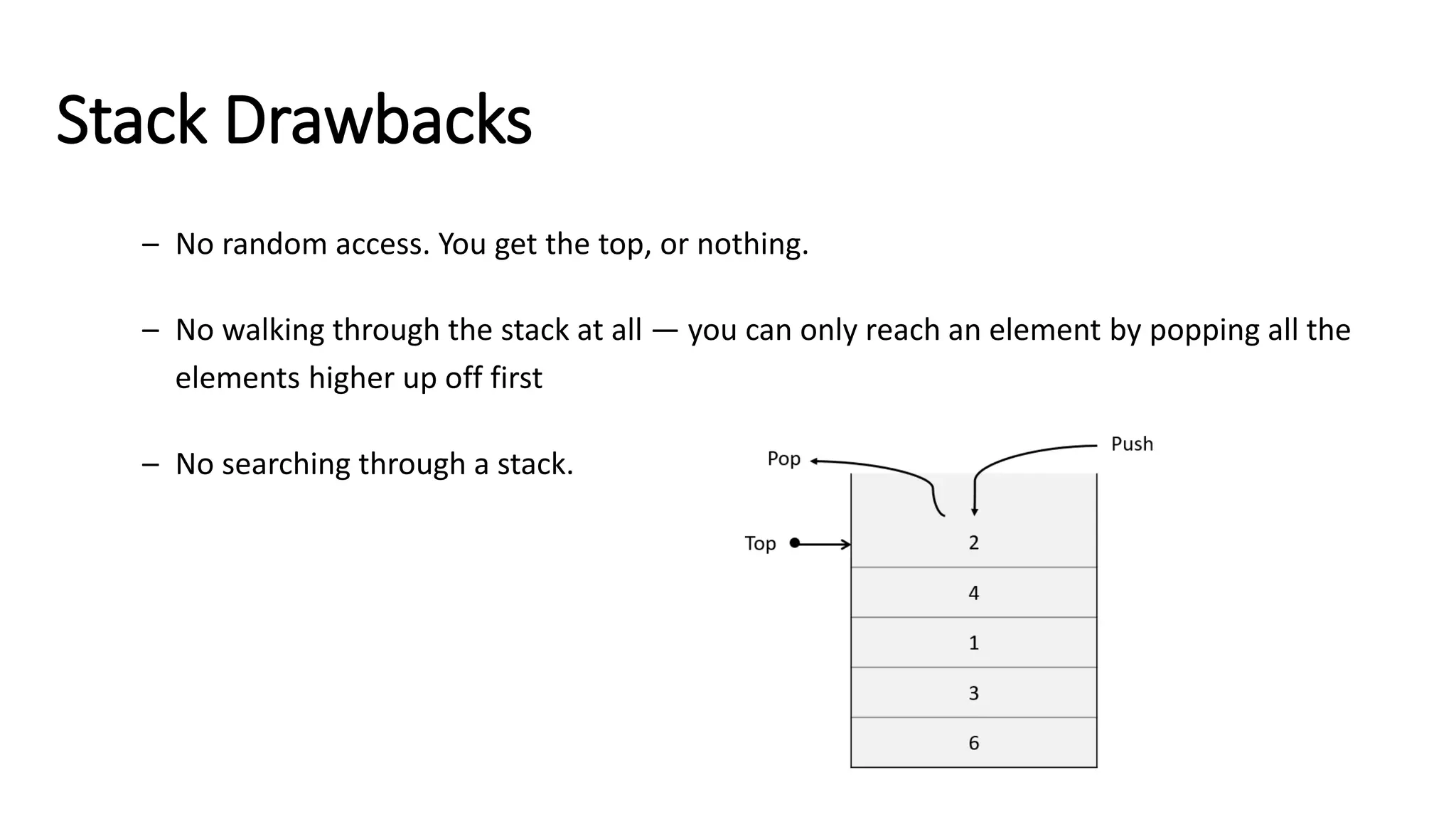
![#include <iostream> using namespace std; class Stack { private: static const int MAX_SIZE = 100; int arr[MAX_SIZE]; int topIndex; public: // Constructor Stack() : topIndex(-1) {} // Removes all elements from the stack void clear() { topIndex = -1; } // Checks if the stack is empty bool isEmpty() const { return topIndex == -1; } // Adds an element to the top of the stack void push(int value) { if (topIndex >= MAX_SIZE - 1) throw overflow_error("Stack overflow"); arr[++topIndex] = value; } // Removes and returns the top element of the stack int pop() { if (isEmpty()) throw underflow_error("Stack underflow"); return arr[topIndex--]; } // Returns the top element of the stack without removing it int top() const { if (isEmpty()) throw underflow_error("Stack is empty"); return arr[topIndex]; } // Returns the number of elements in the stack int size() const { return topIndex + 1; } // Prints all elements of the stack void printStack() const { for (int i = topIndex; i >= 0; i--) cout << arr[i] << endl; cout << endl; } }; int main() { Stack stack; stack.push(10); stack.push(20); stack.push(30); cout << "Stack elements:" << endl; stack.printStack(); // Should print 30, 20, 10 cout << "Top element: " << stack.top() << endl; // Should print 30 cout << "Stack size: " << stack.size() << endl; // Should print 3 cout << "Popped element: " << stack.pop() << endl; // Should print 30 cout << "Top element after pop: " << stack.top() << endl; // Should print 20 cout << "Stack size after pop: " << stack.size() << endl; // Should print 2 stack.clear(); cout << "Stack size after clear: " << stack.size() << endl; // Should print 0 cout << "Is stack empty: " << (stack.isEmpty() ? "Yes" : "No") << endl; // Should print Yes return 0; } Stack (LIFO) C++ implementation](https://image.slidesharecdn.com/datastructuresandalgorithms-lecture3-240909222602-b0822a03/75/Data-Structures-Algorithms-Lecture-3-33-2048.jpg)



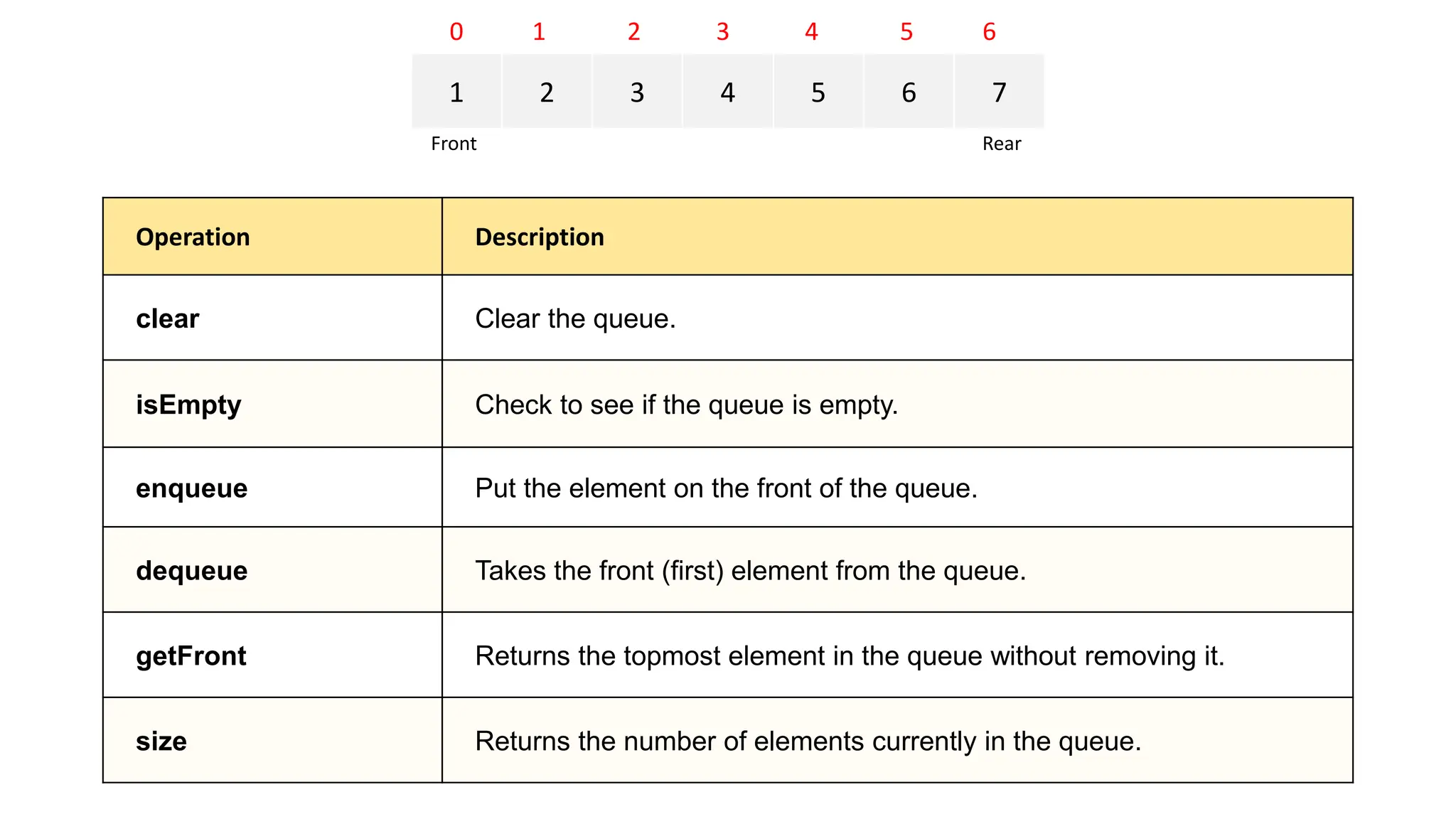

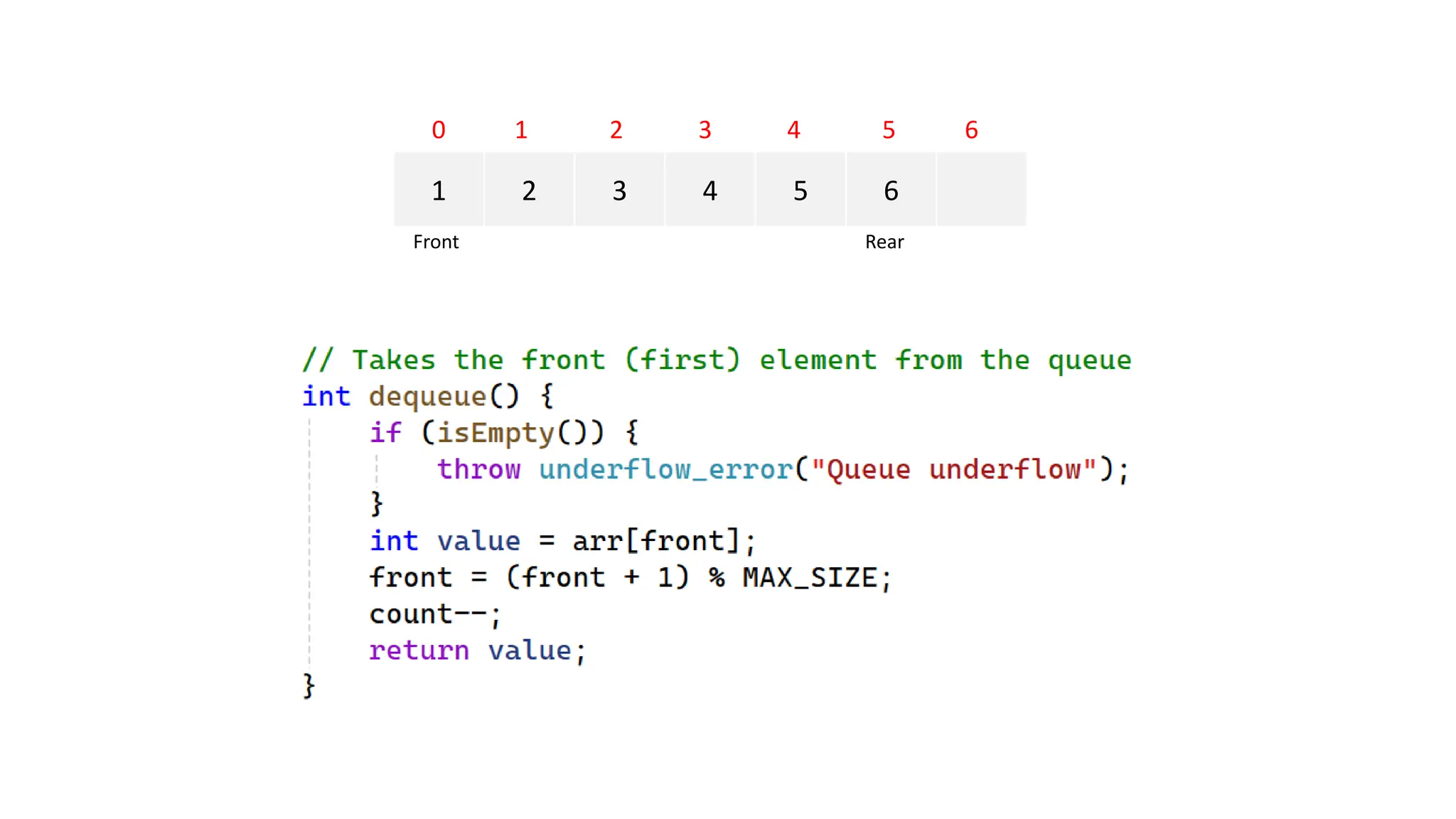
![#include <iostream> #include <stdexcept> using namespace std; class LinearQueue { private: static const int MAX_SIZE = 100; // Maximum size of the queue int arr[MAX_SIZE]; // Array to store queue elements int front; // Index of the front element int rear; // Index of the rear element int count; // Number of elements in the queue public: // Constructor LinearQueue() : front(0), rear(-1), count(0) {} // Clear the queue void clear() { front = 0; rear = -1; count = 0; } // Check to see if the queue is empty bool isEmpty() const { return count == 0; } // Put the element on the front of the queue void enqueue(int value) { if (count == MAX_SIZE) { throw overflow_error("Queue overflow"); } rear = (rear + 1) % MAX_SIZE; arr[rear] = value; count++; } // Takes the front (first) element from the queue int dequeue() { if (isEmpty()) { throw underflow_error("Queue underflow"); } int value = arr[front]; front = (front + 1) % MAX_SIZE; count--; return value; } // Returns the topmost element in the queue without removing it int getFront() const { if (isEmpty()) { throw underflow_error("Queue is empty"); } return arr[front]; } // Returns the number of elements currently in the queue int size() const { return count; } }; int main() { LinearQueue queue; queue.enqueue(10); queue.enqueue(20); queue.enqueue(30); cout << "Front element: " << queue.getFront() << endl; // Should print 10 cout << "Queue size: " << queue.size() << endl; // Should print 3 cout << "Dequeued element: " << queue.dequeue() << endl; // Should print 10 cout << "Front element after dequeue: " << queue.getFront() << endl; // Should print 20 cout << "Queue size after dequeue: " << queue.size() << endl; // Should print 2 queue.clear(); cout << "Queue size after clear: " << queue.size() << endl; // Should print 0 cout << "Is queue empty: " << (queue.isEmpty() ? "Yes" : "No") << endl; // Should print Yes return 0; } Linear Queue C++ implementation](https://image.slidesharecdn.com/datastructuresandalgorithms-lecture3-240909222602-b0822a03/75/Data-Structures-Algorithms-Lecture-3-40-2048.jpg)
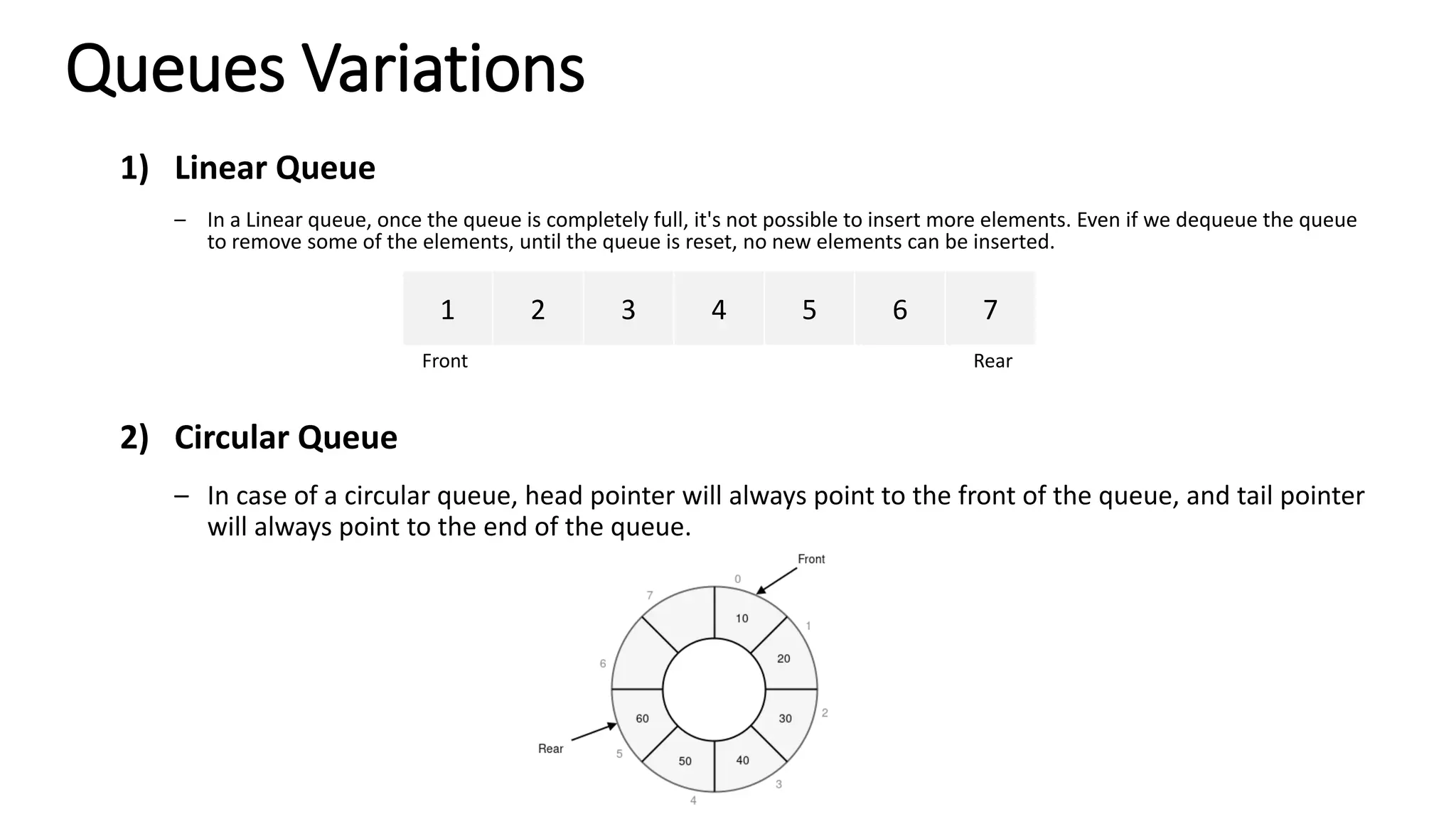
![#include <iostream> #include <stdexcept> using namespace std; class CircularQueue { private: static const int MAX_SIZE = 100; // Maximum size of the queue int arr[MAX_SIZE]; // Array to store queue elements int front; // Index of the front element int rear; // Index of the rear element int count; // Number of elements in the queue public: // Constructor CircularQueue() : front(0), rear(0), count(0) {} // Clear the queue void clear() { front = 0; rear = 0; count = 0; } // Check to see if the queue is empty bool isEmpty() const { return count == 0; } // Put the element at the rear of the queue void enqueue(int value) { if (count == MAX_SIZE) { throw overflow_error("Queue overflow"); } arr[rear] = value; rear = (rear + 1) % MAX_SIZE; count++; } // Takes the front (first) element from the queue int dequeue() { if (isEmpty()) { throw underflow_error("Queue underflow"); } int value = arr[front]; front = (front + 1) % MAX_SIZE; count--; return value; } // Returns the front element in the queue without removing it int getFront() const { if (isEmpty()) { throw underflow_error("Queue is empty"); } return arr[front]; } // Returns the number of elements currently in the queue int size() const { return count; } }; int main() { CircularQueue queue; queue.enqueue(10); queue.enqueue(20); queue.enqueue(30); cout << "Front element: " << queue.getFront() << endl; // Should print 10 cout << "Queue size: " << queue.size() << endl; // Should print 3 cout << "Dequeued element: " << queue.dequeue() << endl; // Should print 10 cout << "Front element after dequeue: " << queue.getFront() << endl; // Should print 20 cout << "Queue size after dequeue: " << queue.size() << endl; // Should print 2 queue.clear(); cout << "Queue size after clear: " << queue.size() << endl; // Should print 0 cout << "Is queue empty: " << (queue.isEmpty() ? "Yes" : "No") << endl; // Should print Yes return 0; } Circular Queue C++ implementation](https://image.slidesharecdn.com/datastructuresandalgorithms-lecture3-240909222602-b0822a03/75/Data-Structures-Algorithms-Lecture-3-42-2048.jpg)



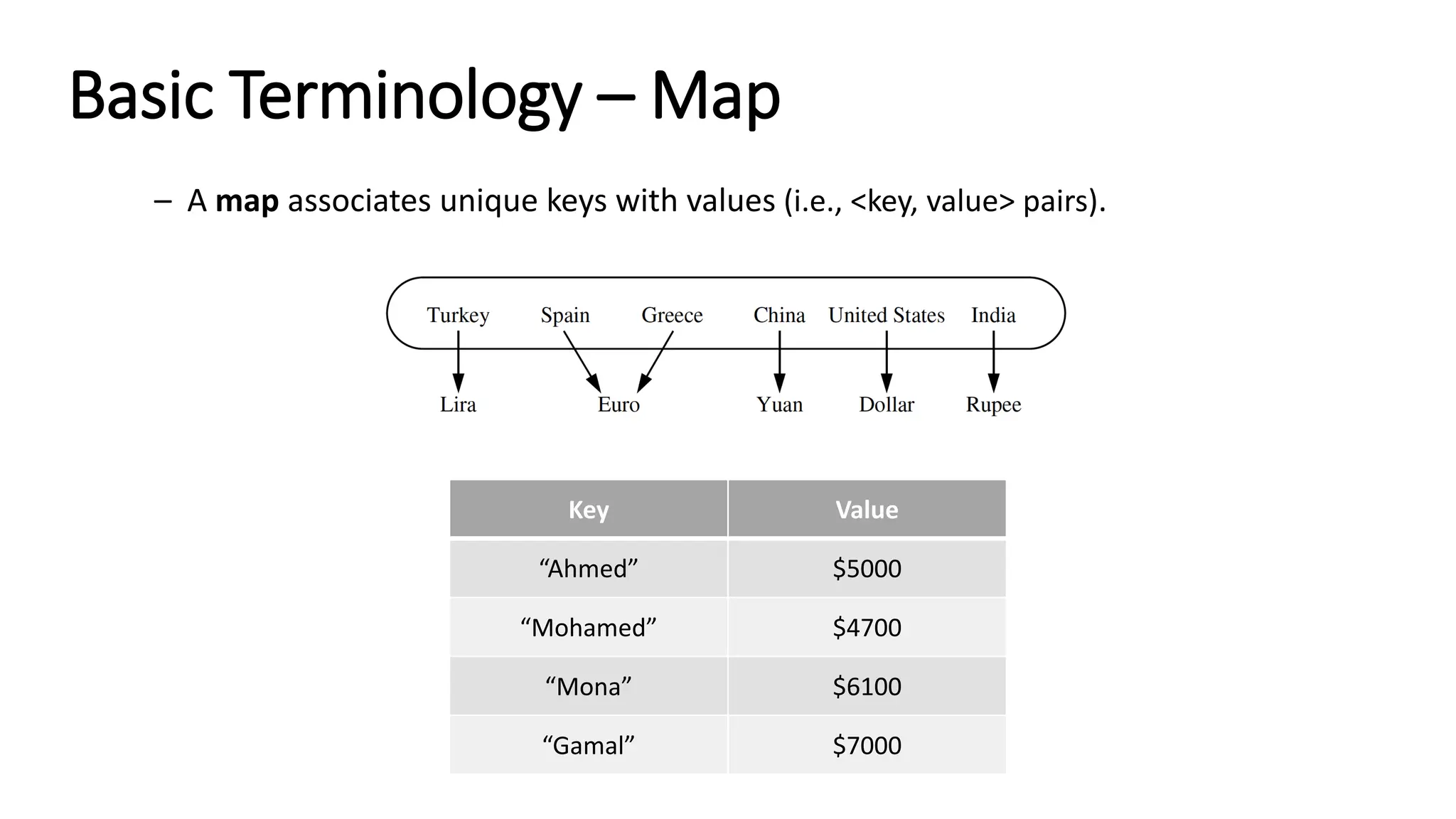
![#include <iostream> #include <string> using namespace std; template <typename K, typename V> class Map { private: K* keys; V* values; int size; int capacity; void expand() { capacity *= 2; K* newKeys = new K[capacity]; V* newValues = new V[capacity]; for (int i = 0; i < size; i++) { newKeys[i] = keys[i]; newValues[i] = values[i]; } delete[] keys; delete[] values; keys = newKeys; values = newValues; } public: Map() : size(0), capacity(10) { keys = new K[capacity]; values = new V[capacity]; } ~Map() { delete[] keys; delete[] values; } void add(const K& key, const V& value) { if (size == capacity) expand(); keys[size] = key; values[size] = value; size++; } bool isEmpty() const { return size == 0; } V& operator[](const K& key) { for (int i = 0; i < size; i++) if (keys[i] == key) return values[i]; // If key is not found, add it with a default value if (size == capacity) expand(); keys[size] = key; values[size] = V(); // Default value for type V size++; return values[size - 1]; } void deleteKey(const K& key) { for (int i = 0; i < size; i++) { if (keys[i] == key) { for (int j = i; j < size - 1; j++) { keys[j] = keys[j + 1]; values[j] = values[j + 1]; } size--; return; } } } void print() const { for (int i = 0; i < size; i++) cout << "<" << keys[i] << "," << values[i] << ">" << endl; } }; int main(void) { Map<string, int> salaries; salaries["Ahmed"] = 5000; salaries["Mohamed"] = 4700; salaries["Mona"] = 6100; salaries["Gamal"] = 7000; salaries.print(); return 0; } Map C++ implementation Method #1](https://image.slidesharecdn.com/datastructuresandalgorithms-lecture3-240909222602-b0822a03/75/Data-Structures-Algorithms-Lecture-3-47-2048.jpg)
![#include <iostream> #include <map> #include <string> using namespace std; int main() { // map<key_type, value_type> map_name; map<string, int> salaries = { {"Ahmed", 5000}, {"Mohamed", 4700}, {"Mona", 6100}, {"Gamal", 7000} }; // Add new element salaries["Ali"] = 5500; // Iterator to the first element map<string, int>::iterator it = salaries.begin(); // Iterate over the map while (it != salaries.end()) { cout << "Key: " << it->first << ",t Value: " << it->second << endl; it++; } return 0; } Map C++ implementation Method 2](https://image.slidesharecdn.com/datastructuresandalgorithms-lecture3-240909222602-b0822a03/75/Data-Structures-Algorithms-Lecture-3-48-2048.jpg)
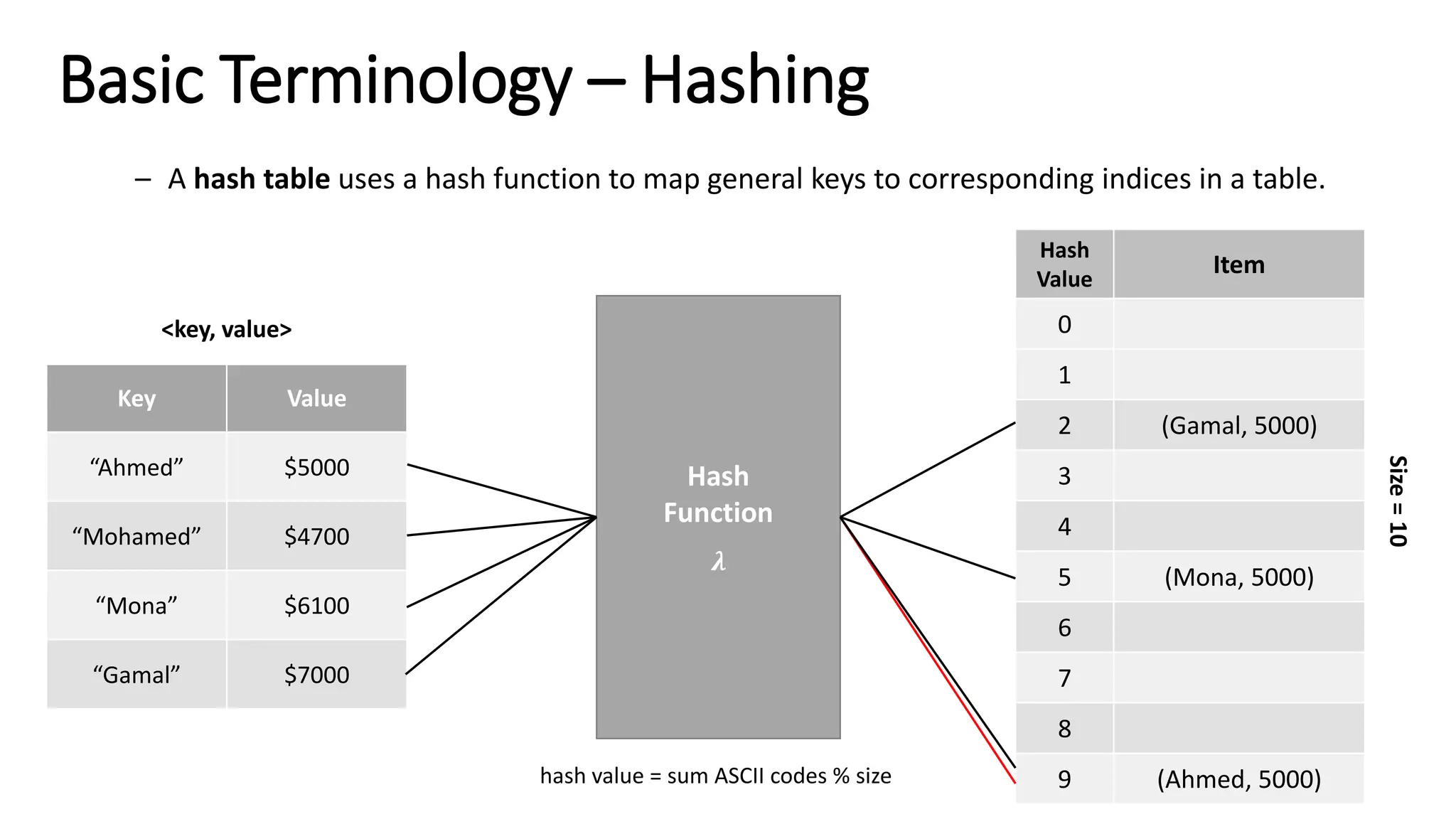

![#include <iostream> #include <string> using namespace std; int hashFunction(string name) { int ascii_sum = 0; for (int i = 0; i < name.size(); i++) ascii_sum += int(name[i]); return (ascii_sum % 10); } int main(void) { string name = "Ahmed"; cout << "Hash value for " << name << " is " << hashFunction(name) << endl; return 0; } Hash Function](https://image.slidesharecdn.com/datastructuresandalgorithms-lecture3-240909222602-b0822a03/75/Data-Structures-Algorithms-Lecture-3-51-2048.jpg)
![class Hashing { private: Map<string, int> hashTable[10]; int hashFunction(string name) { int ascii_sum = 0; for (int i = 0; i < name.size(); i++) ascii_sum += int(name[i]); return (ascii_sum % 10); } public: void add(const string& key, const int& value) { int hashValue = hashFunction(key); hashTable[hashValue][key] = value; } int get(const string& key) { int hashValue = hashFunction(key); return hashTable[hashValue][key]; } void remove(const string& key) { int hashValue = hashFunction(key); hashTable[hashValue].deleteKey(key); } void print() { for (int i = 0; i < 10; i++) { if (hashTable[i].isEmpty()) continue; cout << "Hash value " << i << ": "; hashTable[i].print(); } } }; Hashing Class C++ implementation](https://image.slidesharecdn.com/datastructuresandalgorithms-lecture3-240909222602-b0822a03/75/Data-Structures-Algorithms-Lecture-3-52-2048.jpg)
![#include <iostream> #include <string> using namespace std; template <typename K, typename V> class Map { private: K* keys; V* values; int size; int capacity; void expand() { capacity *= 2; K* newKeys = new K[capacity]; V* newValues = new V[capacity]; for (int i = 0; i < size; i++) { newKeys[i] = keys[i]; newValues[i] = values[i]; } delete[] keys; delete[] values; keys = newKeys; values = newValues; } public: Map() : size(0), capacity(10) { keys = new K[capacity]; values = new V[capacity]; } ~Map() { delete[] keys; delete[] values; } void add(const K& key, const V& value) { if (size == capacity) expand(); keys[size] = key; values[size] = value; size++; } bool isEmpty() const { return size == 0; } V& operator[](const K& key) { for (int i = 0; i < size; i++) if (keys[i] == key) return values[i]; // If key is not found, add it with a default value if (size == capacity) expand(); keys[size] = key; values[size] = V(); // Default value for type V size++; return values[size - 1]; } void deleteKey(const K& key) { for (int i = 0; i < size; i++) { if (keys[i] == key) { for (int j = i; j < size - 1; j++) { keys[j] = keys[j + 1]; values[j] = values[j + 1]; } size--; return; } } } void print() const { for (int i = 0; i < size; i++) cout << "<" << keys[i] << "," << values[i] << ">" << endl; } }; class Hashing { private: Map<string, int> hashTable[10]; int hashFunction(string name) { int ascii_sum = 0; for (int i = 0; i < name.size(); i++) ascii_sum += int(name[i]); return (ascii_sum % 10); } public: void add(const string& key, const int& value) { int hashValue = hashFunction(key); hashTable[hashValue][key] = value; } void remove(const string& key) { int hashValue = hashFunction(key); hashTable[hashValue].deleteKey(key); } int get(const string& key) { int hashValue = hashFunction(key); return hashTable[hashValue][key]; } void print() { for (int i = 0; i < 10; i++) { if (hashTable[i].isEmpty()) continue; cout << "Hash value " << i << ": "; hashTable[i].print(); } } }; int main() { Hashing hashing; hashing.add("Ahmed", 5000); hashing.add("Mohamed", 4700); hashing.add("Mona", 6100); hashing.add("Gamal", 7000); hashing.print(); cout << "Ahmed's salary is " << hashing.get("Ahmed") << endl; return 0; } All put together C++ implementation](https://image.slidesharecdn.com/datastructuresandalgorithms-lecture3-240909222602-b0822a03/75/Data-Structures-Algorithms-Lecture-3-53-2048.jpg)