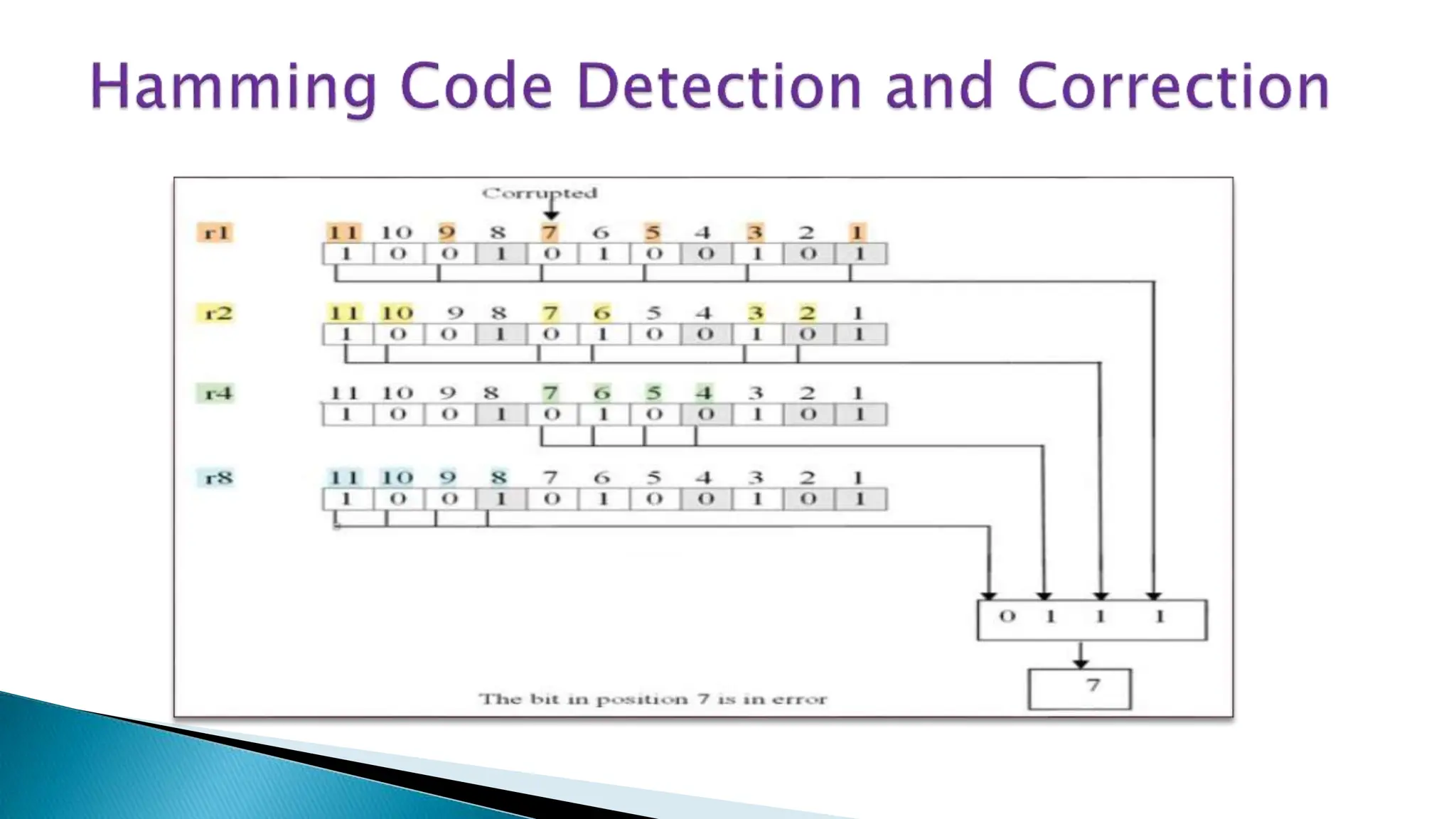
This document presents an overview of Hamming code and its implementation using Verilog. It discusses Hamming code, which can detect single and double bit errors and correct single bit errors. It also provides the block diagram and specifications of an (11,7,1) Hamming encoder and decoder developed using Verilog, including the encoder converting 7-bit data to 11-bit codewords and decoder converting codewords back to 7 bits. The design fits well on FPGAs and ASICs and is suited for communication applications requiring error control. In conclusion, Hamming code allows for higher data transmission speeds by enabling error correction without retransmission.












![ [1] Brajesh Kumar Gupta, Rajeshwar Lal Dua, “30 bit Hamming code for Error Detection and correction using VHDL” National Journal of Engineering Science And Management (ISSN : 2249-0264) volume number I issue II . [2]. Data communication and networking , Behrouz A. Forouzan , 2nd edition Tata McGraw Hill publication [3]. http://www.pragsoft.com/books/CommNetwork.pdf [4]. http://www.eng.uwaterloo.ca/~tnaqvi/downloads/DOC/sd192/ISE8_1i_manuals.pdf [5]. http://www.xilinx.com/training/xilinx-training-courses.pdf [6]. http://www.xilinx.com/itp/xilinx10/books/docs/qst/qst.pdf [7]. http://en.wikipedia.org/wiki/VHDL [8]. http://www.doulos.com/knowhow/vhdl_designers_guide/ [9]. Digital Logic Design with VHDL , Stephen Brown & Zvonko Vranesic , 2 nd edition TMH publication [10]. Hamming r.w error detection and correction code, bell sys. Tech. J.29:147-60 1950 bell telefone laboratories ,murray hill [11].Http://www.britannica.com/ebchecked/topic/585799/telecommunication/76275/repetition- codes#ref608200- [12]. Http://www.britannica.com/ebchecked/topic/253662/richard-wesley-hamming#ref1073410 [13] ISE 10.1 Quick Start Tutorial, available at http://www.xilinx.com/itp/xilinx10/books/docs/qst/qst.pdf [14] VHDL (VHSIC hardware description language): http://en.wikipedia.org/wiki/VHDL](https://image.slidesharecdn.com/presentation1-240303144442-911ccc4e/75/Presentation-for-the-Project-on-VLSI-and-Embedded-14-2048.jpg)