Particle Swarm Optimization based Network Reconfiguration in Distribution System with Distributed Generation and Capacitor Placement

Particle Swarm Optimization based Network Reconfiguration in Distribution System with Distributed Generation and Capacitor Placement

• 1.
  The International JournalOf Engineering And Science (IJES) || Volume || 3 || Issue || 12 || December - 2014 || Pages || 55-60|| ISSN (e): 2319 – 1813 ISSN (p): 2319 – 1805 www.theijes.com The IJES Page 55 Particle Swarm Optimization based Network Reconfiguration in Distribution System with Distributed Generation and Capacitor Placement 1, G. Balakrishna , 2, Dr. Ch. Sai Babu 1, Associate Professor, Department of Electrical and Electronics Engg., Intell Engineering Collge, Anantapur(AP), INDIA 2, Professor, Department of Electrical and Electronics Engg., JNTU College of Engg., Kakinada(AP), INDIA -----------------------------------------------------ABSTRACT----------------------------------------------------- This paper proposes an algorithm based on Particle Swarm Optimization (PSO) for optimal network reconfiguration of a distribution system in the presence of Distributed Generators (DGs) and Shunt Capacitor Banks to balance the feeder loads and to eliminate overloading conditions. The system Load Balancing Index (LBI) is used to represent the loading conditions and maximum system loading capacity. This index value should be low in the optimal network reconfiguration for load balancing. A 69-node system with DG units and Capacitor units are considered for verifying the effectiveness of PSO algorithm and results are presented. The simulation results shows that by operating the on/off patterns of proper tie switches and normally closed switches betters the load balancing in the system and also improves the voltage profile. KEYWORDS: Capacitor Placement, Distribution systems, Distributed Generators, Load Balancing Index(LBI), Network Reconfiguration -------------------------------------------------------------------------------------------------------------------------------------- Date of Submission: 25 December 2014 Date of Accepted: 10 January 2015 ------------------------------------------------------------------------------------------------------------------------------------- I. INTRODUCTION: The typical electrical power distribution system generally composed of group of interconnected radial networks and have to function subjected to some constraints like radial configuration, all the loads served, coordinated operation of protective devices, and voltage magnitude limits etc. Generally the distribution system feeds mixture of different loads against different daily load patterns. There are different operational schemes in the distribution systems; one of the most important of them is „network reconfiguration‟. Distribution systems consist of two types of switches viz., normally closed sectionalizing switches and normally opened tie switches [1], [2]. By the selection of operation of these switches the topological structure of the distribution system can be modified accordingly we can modify the power flow and hence one can obtain better voltage profile as well as good efficiency of the system. Therefore network reconfiguration is of very important operation of distribution system and always aims the good voltage profile and minimization of losses. Generally distribution network reconfiguration provides services to as many consumers as possible following fault coding and during planned outage for maintenance purpose with loss minimization and load balancing of the network [3]. The problem of network reconfiguration is a complex non-linear combinatorial problem due to non- differential status of switches and normally opened tie switches determined to meet the system requirements. From optimization point of view the reconfiguration method have been used for loss reduction using different techniques on the other hand from service restoration point of view, the reconfiguration allows to relocate loads by using an appropriate sequence of switching operations with operating constraints taken into account [4]. By moving the loads from heavily loaded feeders to the lightly loaded feeders, the network reconfiguration can balance the feeder loads and avoids the overloading condition [5]. There are many existing algorithms to find the optimal network reconfiguration. [6] uses the Artificial neural network approach based on the mapping capability to determine network reconfiguration. An expert system using heuristic rules to decrease the search space for reducing the computational time is presented in [7]. An algorithm called „distance measurement technique‟ (DMT) that found a loop first and then a switching operation to improve the load balancing was proposed in [8]. Aoki et al. formulated the load balancing and service restoration problem by taking capacity and voltage constraints as a mixed integer non-linear optimization problem and converted into a set of quadratic programming sub programs [9]. Baran formulated the problem of minimization of loss and load balancing as integer programming problem [10]. H.D. Chiang et al. [11] proposed a constrained multi objective and non differentiable optimization problem.
• 2.
  Particle Swarm OptimizationBased Network Reconfiguration… www.theijes.com The IJES Page 56 G. Peponis et al. [12] proposes an improved switch exchange procedure for load balancing problem using switch exchange operations. [13] proposed a new load balancing index and applied it to the network for load balancing. In [14] a new load balancing and unbalanced algorithm in distribution system for loss reduction. This paper emphasizes the importance of optimal network reconfiguration to the electric power distribution system that is equipped with Distributed Generator units and shunt capacitor banks for load balancing and node voltage improvement. The application of PSO is applied to obtain the optimal on/off status of the switches to minimize the load balancing index subject to system constraints. II. PROBLEM FORMULATION The aim of this work is to minimize the Loading Balance Index (LBI) that represents the degree of non- uniformity of loading among the feeders, mathematically LBI can be written as [12]; ….(1) Where B is the list of branches that forms the loops Lk is the length of the line branch ‘k’ Ik,t is the current though of branch ‘k’ for feeder reconfiguration pattern ‘t’ Ik max is the maximum current carrying capacity of branch ‘k’ The above objective function is subjected to following constraints: Power flow equations : Power flow in electrical power distribution network can be described by a set of recursive equations called distribution flow branch equations that uses the real and reactive power and voltage at the sending end of a branch to express the same quantities at the receiving end of the branch [3]. A simple radial distribution network is shown in fig. 1. Fig.1: Sample Distribution system main feeder The real and reactive power flow in the line between i+1 and nth buses are ; ….(2) ….(3) The magnitude of the voltage at bus ‘i+1’ can be calculated as; ….(4) The power loss of the line section connecting buses i and i+1 may be determined as; ….(5) Where Pi is the active power at bus ‘i’ Qi is the reactive power at bus ‘i’ Ri,i+1 is the resistance of line section between buses ‘i’ and i+1 Xi,i+1 is the reactance of line section between buses ‘i’ and i+1 Vi is the voltage at bus ‘i’ Bus voltage Constraint: The voltage magnitude constraint i.e the voltage at each and every bus should be within the specified minimum and maximum limits mathematically ….(6) Where Vmin and Vmax are the minimum and maximum allowable voltages.
• 3.
  Particle Swarm OptimizationBased Network Reconfiguration… www.theijes.com The IJES Page 57 2.3. Feeder capability constraint: The magnitude of the current through all the line sections should be within the tolerable limits of the respective section i.e. ….(7) Where is maximum current capability of branch k For each possible network reconfiguration condition and DG placement the voltages at all the nodes and currents through all the line section are calculated by using forward/backward sweep load flow technique. Radial configuration format: In a practical distribution network when we increase the number of switches then the number of possible switching operations will be numerous. Consequently selecting the proper switches for network reconfiguration will become a tedious decision making and time consuming procedure for system engineers. Furthermore network reconfiguration problem will be more difficult task as the electrical distribution systems are mostly configured in radial for proper relay coordination and protection. III. PSO ALGORITHM: The individual particle in this case is composed of set of tie switches that are to be opened in operating the distribution system in radial configuration only. The size of the particle is equal to number of tie switches in a system. Therefore individual i‟s position in 0th iteration can be represented as a vector Xi 0 =(TS1,TS2,TS3……TSn) where ‘n’ is the number of tie switches for a given radial distribution system. The velocity of individual ‘i’ i.e., Vi 0 = (Vil, …, Vin) represents the switch number updating quantity covering all tie lines and maneuver lines. The position and velocity of each element of a particle in this case is mere integer number. Here it is very important to note that while creating the individual particles it is very much essential to check for the radial nature of the network. To do this the below procedure is used to generate the particles at random. Step 1 : Set i=1 Step 2 : Set j=1 Step 3 : Select an element (i.e switch number) of an individual particle at random Step 4 : Choose the value of an element from a list of tie switches and sectionalizing switches that satisfies the radial nature of the network Step 5 : go for the next element i.e., j=j+1. Step 6 : Choose the next element from a list of all the tie switches and sectionalizing switches excluding the elements (switch numbers) already chosen. Step 7 : repeat step 4 to step 6 until j=N where N is the number of switches to be opened. Step 8 : increment the particle number i.e., i=i+1 Step 9 : If all particles are generated stop the initialization process otherwise go to step 2. The element of individual particles as created above is taken as the initial position of the elements. The initial velocity of the elements for all particles is taken as zero. PROPOSED PSO ALGORITHM: Step1. Initialization-initialize all particles as per the above algorithm Step2. Set iteration count=0 Step3. Evaluate the fitness function i.e. the Load Balancing Index for the each particle and fix the individual LBI to Pbest and from LBI of all the particles find the minimum LBI the fix it as Gbest for this iteration Step4. Evaluate the velocity of each population by using the equation ….(8) Step5. Update the position of each population by using the equation ….(9) Step6. Find the new values of fitness function (LBI) for all the population and replace it with Pbest if it less than the former value and also fix the least value of Pbest among all the population to Gbest Step7. Increase the iteration count by 1
• 4.
  Particle Swarm OptimizationBased Network Reconfiguration… www.theijes.com The IJES Page 58 Step8. Check the stopping criterion, if not satisfied go to step3 Finally the optimum solution can be obtained through „Gbest‟ IV. RESULTS AND ANALYSIS The effectiveness of the proposed PSO algorithm for network reconfiguration of a distribution system with DG units and shunt capacitors is verified on IEEE-69 systems. The initial statuses of all the sectionalizing switches are closed while all the tie-switches are open. The total loads for this test system are 3,801.89 kW and 2,694.10 kVAr. For this test system five cases are considered: Case-1: Original configuration of the system without DG Case-2: Optimal Configuration of the system without DG units and shunt capacitors Case-3: Optimal configuration with DG units and without shunt capacitors Case-4: Optimal configuration without DG units and with shunt capacitors Case-5: Optimal configuration with DG units and shunt capacitors In case-1 the original system has been considered without reconfiguration, without capacitors and without DG units. For this case the simulation results are given in Table 1. Table 1: Simulation results for base case Aspect Case-1 Sectionalizing Switches to be open --- Tie-Switches to be closed --- Load Balancing Index(LBI) 2.949 Minimum Voltage (p.u.) 0.909 Total power loss (kW) 224.68 In case-2 the proposed algorithm is used to find the optimal network reconfiguration that gives us the sectionalizing lines to be opened and tie-lines to be closed in the distribution system without using DG units and shunt capacitor banks. Simulation results of PSO are compared with the existing method and are given in Table 2. Table 2: Simulation Results of PSO and comparison with existing method for case-2 Aspect By Tabu Search By proposed PSO Sectionalizing Switches to be open 13, 20, 58, 63 13, 20, 56, 26 Tie-Switches to be closed 70, 71, 72, 73 70, 71, 72, 73 Load Balancing Index(LBI) 2.197 2.147 Minimum Voltage (p.u.) 0.948 0.9512 Total power loss (kW) 105.65 104.84 In case-3 the PSO is used determine the optimal network reconfiguration of the system in the presence of DG units without using shunt capacitors. In this case four DGs are assumed to be installed at bus numbers 14, 35, 46 and 53 with the capacities of 300, 200, 100 and 400 kW respectively. Table 3 gives the simulation results of PSO and is compared with the existing method for this case. Table 3: Simulation Results of PSO and comparison with existing method for case-3 Aspect By Tabu Search By proposed PSO Sectionalizing Switches to be open 14, 20, 52, 61 13, 20, 58, 64 Tie-Switches to be closed 70, 71, 72, 73 70, 71, 72, 73 Load Balancing Index(LBI) 1.685 1.592 Minimum Voltage (p.u.) 0.955 0.9612 Total power loss (kW) 84.38 82.47
• 5.
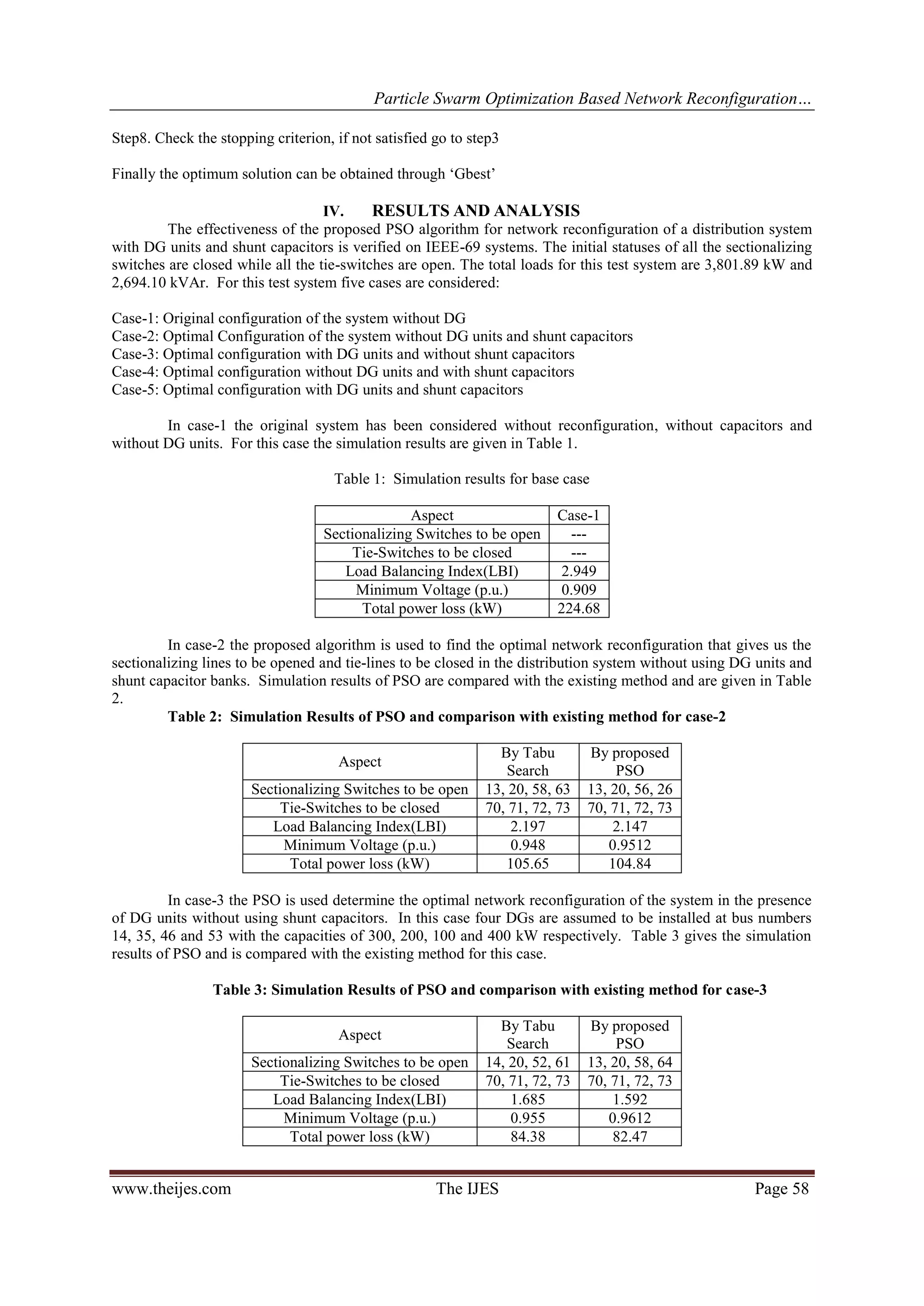
  Particle Swarm OptimizationBased Network Reconfiguration… www.theijes.com The IJES Page 59 In case-4 the PSO algorithm is used determine the optimal network reconfiguration of the system in the presence of Shunt capacitor bank units without using DG units. In this case four capacitor banks are assumed to be installed at bus numbers 24, 45, 49 and 61 of capacities of 100, 200, 300 and 400 kVar respectively. Table 4 gives the simulation results of PSO and is compared with the existing method for this case. Table 4: Simulation Results of PSO and comparison with existing method for case-4 Aspect By Tabu Search By proposed PSO Sectionalizing Switches to be open 14, 20, 52, 61 14, 19, 58, 63 Tie-Switches to be closed 70, 71, 72, 73 70, 71, 72, 73 Load Balancing Index(LBI) 1.796 1.728 Minimum Voltage (p.u.) 0.956 0.9641 Total power loss (kW) 108.94 102.47 In case-5 the PSO algorithm is used determine the optimal network reconfiguration of the system in the presence of Shunt capacitor bank units with DG units. In this case four capacitor banks are assumed to be installed at bus numbers 24, 45, 49 and 61 of capacities of 100, 200, 300 and 400 kVar respectively and four DG units of sizes 300, 200, 100 and 400kW are already installed at bus numbers 14, 35, 46 and 53. Table 5 gives the simulation results of PSO and is compared with the existing method for this case. Table 5: Simulation Results of PSO and comparison with existing method for case-5 Aspect By Tabu Search By proposed PSO Normal lines to be open 14, 20, 53, 62 14, 18, 55, 63 Tie-lines to be closed 70, 71, 72, 73 70, 71, 72, 73 Load Balancing Index(LBI) 1.442 1.441 Minimum Voltage (p.u.) 0.955 0.9668 Total power loss (kW) 77.604 74.324 From the above simulation results it is observed that from case-1 to case-5 the Load balancing index has reduced and except for case -4, the minimum voltage has increased to from 0.909p.u. to 0.9668 p.u. and at the same time the losses are also reduced from to 224.68 kW to 74.324 kW. All these results are better when compared to existing Tabu Search method. V. CONCLUSIONS: In this paper, a Particle Swarm Optimization algorithm has been proposed to find the optimal network reconfiguration of a distribution network in the presence of DG units and capacitor banks. The problem here is formulated as a non-linear optimization problem with an objective function of minimizing the Load Balancing Index (LBI) subject to a set of constraints. Test results has been presented, which shows that using PSO the optimal network reconfiguration problem with DG units and shunt capacitor banks can be solved effectively when compared to existing algorithm. REFERENCES [1] D. Das, “A fuzzy multi objective approach for network reconfiguration of distribution systems,” IEEE Trans Power Delivery, vol. 21, no 1, pp. 1401-1407, Jan. 2006. [2] P. Ravibabu, K. Venkatesh, and C. S. Kumar, “Implementation of genetic algorithm for optimal network reconfiguration in distribution systems for load balancing,” in Proc Conf. Computation Technology in Electrical and Electronics Engineering, Novosibirsk, 2008, pp.124-128. [3] C. T. Su, and C. S. Lee, “Network reconfiguration of distribution systems using improved mixed-integer hybrid differential evolution,” IEEE Trans. Power Delivery, vol. 18, no. 3, pp. 1022-1027, July 2003. [4] Y. K. Wu, and et al., “Study of Reconfiguration for the distribution system with distributed generators,” IEEE Trans. Power Delivery, vol. 25, no. 3, pp. 1678-1685, July 2010. [5] E. Carpaneto, G. Chicco, and J. S. Akilimali, “Branch current decomposition method for loss allocation in radial distribution systems with distributed generation,” IEEE Trans. Power Systems, vol. 21, no. 3, pp. 1170-1179, Aug. 2006. [6] H. Kim, Y. ko, and K. H. Jung, “Artificial neural network based feeder reconfiguration for loss reduction in distribution systems,” IEEE Trans Power Delivery, vol. 8, no. 3, pp. 1356-1366, July 1993.
• 6.
  Particle Swarm OptimizationBased Network Reconfiguration… www.theijes.com The IJES Page 60 [7] T. Taylor, and D. Lubkeman, “Implementation of heuristic search strategies for distribution feeder reconfiguration,” IEEE Trans Power Delivery, vol. 5, no. 1, pp.239-246, Jan. 1990. [8] M. A. Kashem, V. Ganapathy, and G. B. Jasmon, “Network reconfiguration for load balancing in distribution networks,” IEE Proc. Gener. Transm. Distrib., vol. 146, no. 6, pp. 563-567, Nov. 1999. [9] K. Aoki, and et al., “An efficient algorithm for load balancing of transformers and feeders,” IEEE Trans. Power Delivery, vol. 3, no. 4, pp. 1865-1872, Oct. 1988. [10] M. E. Baran, and F. F. Wu, “Network reconfiguration in distribution systems for loss reduction and load balancing,” IEEE Trans. Power Delivery, vol. 4, no. 2, pp. 1401-1407, Apr. 1989. [11] H. D. Chiang, and R.J Jumeau, “Optimal network reconfigurations in distribution systems: Part 1: A new formulation and a solution methodology,” IEEE Trans. Power Delivery, vol. 5, no. 4, pp. 1902- 1909, Nov. 1990. [12] G. Pepionis, and M. Papadopoulos, “Reconfiguration of radial distribution networks: application of heuristic methods on large scale networks, ”IEE Proc., Gener., Transm. Distrib, vol. 142, no. 6, pp. 631 – 638, Nov. 1995. [13] Mukwanga and et al., “Reconfiguration and load balancing in the LV and MV distribution networks for optimal performance,” IEEE Trans. on Power Delivery, vol. 22, no. 4, pp. 2534-1407, Oct. 2007. [14] G. K. V. Raju, and P.R. Bijwe, “Efficient reconfiguration of balanced and unbalanced distribution systems for loss minimization,” IEE Proc. Gener. Transm. Distrib., vol. 2, no. 1, pp. 7-12, Jan. 2008.