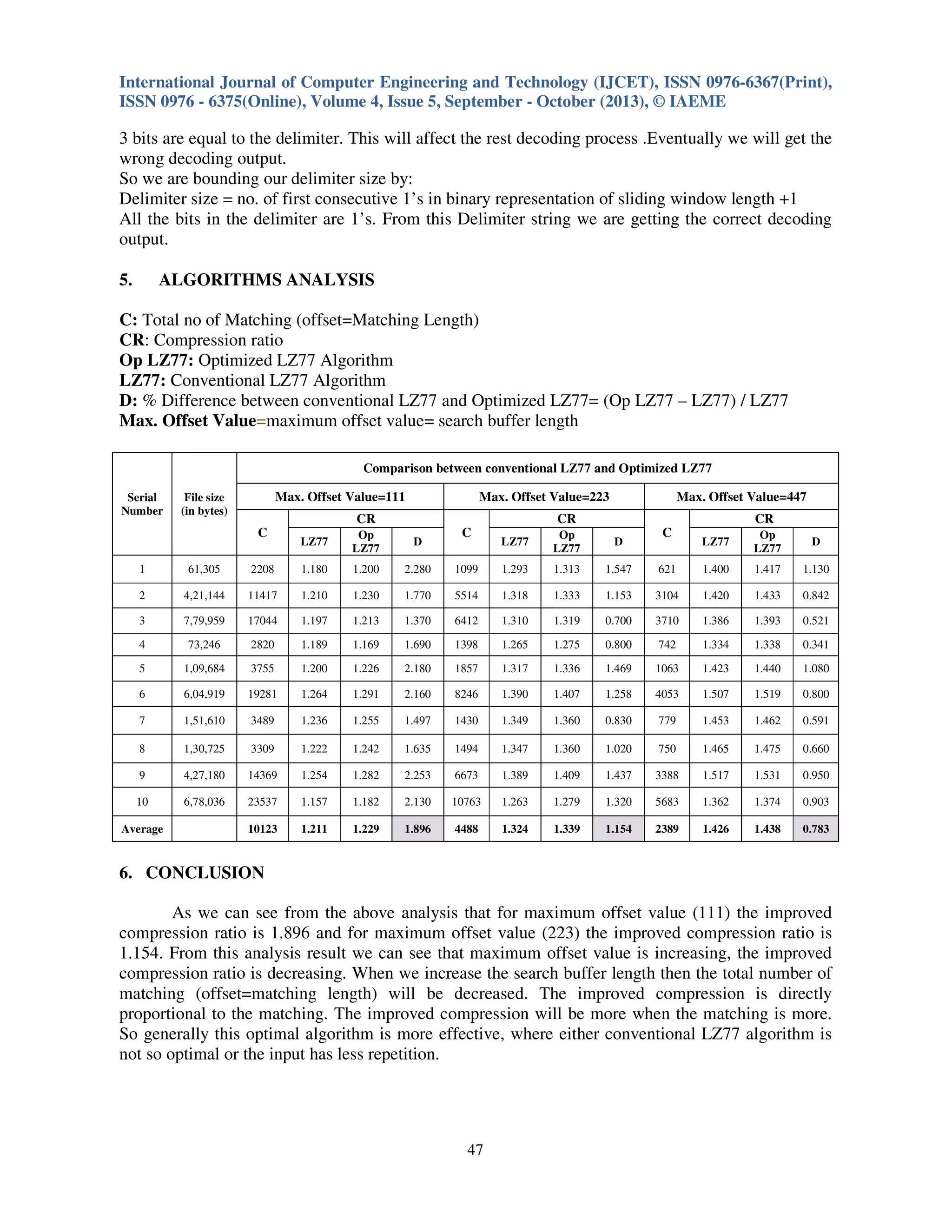
The document discusses the optimization of the LZ77 data compression algorithm, focusing on reducing unnecessary information conveyed during encoding by implementing variable triplet sizes. It introduces a new structure called 'doublet' to replace triplets when the offset equals the matching length, improving compression ratios through experiments. The analysis demonstrates that the optimized algorithm achieves better compression efficiency compared to the conventional LZ77 algorithm, particularly under conditions of increased data repetition.

![International Journal of Computer Engineering and Technology (IJCET), ISSN 0976-6367(Print), ISSN 0976 - 6375(Online), Volume 4, Issue 5, September - October (2013), © IAEME 43 1. INTRODUCTION LZ77 algorithm achieves compression by replacing repeated occurrences of data with references to a single copy of that data existing earlier in the input (uncompressed) data stream. A match is encoded by a pair of numbers called a length-distance pair. Some common convention and definition of the words that we are using in this paper. 2. CONVENTIONAL LZ77 ALGORITHM LZ77 compression algorithm exploits the fact that words and phrases within a text file are likely to be repeated. When there is repetition, they can be encoded as a pointer to an earlier occurrence, with the pointer accompanied by the number of characters to be matched. It is a very simple adaptive scheme that requires no prior knowledge of the source and seems to require no assumptions about the characteristics of the source. In the LZ77 approach the dictionary is simply a portion of the previously encoded sequence. The encoder examines the input sequence through a sliding window which consists of two parts: a search buffer that contains a portion of the recently encoded sequence and a look ahead buffer that contains the next portion of the sequence to be encoded. The algorithm searches the sliding window for the longest match with the beginning of the look-ahead buffer and outputs a reference (a pointer) to that match. It is possible that there is no match at all, so the output cannot contain just pointers. In LZ77 the reference is always represented as a triplet<o,l,c>, where ‘o’ is an offset to the match, ‘l’ is length of the match and ‘c’ is the next symbol after the match. If there is no match, the algorithm outputs a null-pointer (both the offset and the match length equal to 0) and the first symbol in the look-ahead buffer. The values of an offset to a match and length must be limited to some maximum constant. For this algorithm we have to define the length of the look-ahead buffer, search buffer. The symbol is usually encoded in 8 bit. More over the compression performance of LZ77 mainly depends on these values. Generally the search buffer length is more than the look-ahead-buffer size. So the total triplet size: While ( look-ahead Buffer not empty) { get a reference (position, length) to longest match; if (length > 0) { output (position, length, next symbol); shift the window length+1 positions along; } else { output (0, 0, first symbol in the look-ahead buffer); shift the window 1 character along; } } ST= [⌈log2(search buffer length)⌉] +[⌈log2(look-ahead buffer length)⌉]+8](https://image.slidesharecdn.com/lz77datacompressionalgoimprovement-140521022004-phpapp01/75/OPTIMIZATION-OF-LZ77-DATA-COMPRESSION-ALGORITHM-2-2048.jpg)
![International Journal of Computer Engineering and Technology (IJCET), ISSN 0976-6367(Print), ISSN 0976 - 6375(Online), Volume 4, Issue 5, September - October (2013), © IAEME 44 We can have better understanding with an example- “aacaacabcabaaac” For this example the size of look-ahead buffer is 6 and search buffer is 4. Triple Binary -- <0, 0, a> 00000011000001 -- <1, 1, c> 00100111000011 -- < 3, 4, b> 01110011000010 --< 3, 3, a> 01101111000001 -- <1, 2, c> 00101011000011 Sliding window( Size: 6 ) Longest match Next Character The triplet length for this example is 14(3+3+8). So here the encoded binary string of this example. 0000001100000100100111000011011100110000100110111100000100101011000011 triplet triplet triplet triplet triplet -------------------|-------------------|-----------------------|----------------------|--------------------| The decoding is much faster than the encoding in this process because we have to move our pointer with fixed length (triple length-14 for this example) and it is one of the important features of this process. From this way we get the triplets .Now we can easily decode to original data by reversing the encoding process. 3. OPTIMIZATION OF LZ77 As we have described earlier the triplets of LZ77 algorithm have fix size. In the case, when offset is equal to the matching length we can modify the structure of triplets and represent it with the new structure that have only <l,c> where l is the matching length and ‘c’ is the next symbol after the match .We called this new structure as “doublet” in this paper .All the things are same as the conventional LZ77 algorithm except replacing the triplet with doublet in the case of matching length equal to offset length. ࡿࡰ= log2(look-ahead buffer length)⌉] + 8 By replacing the triplet with doublet we are saving [⌈log2(search buffer length)⌉] number of bits per matching case. The exact algorithms is described in the block a a c a a c a b c a b a a a c a a c a a c a b c a b a a a c a a c a a c a b c a b a a a c a a c a a c a b c a b a a a c a a c a a c a b c a b a a a c](https://image.slidesharecdn.com/lz77datacompressionalgoimprovement-140521022004-phpapp01/75/OPTIMIZATION-OF-LZ77-DATA-COMPRESSION-ALGORITHM-3-2048.jpg)


![International Journal of Computer Engineering and Technology (IJCET), ISSN 0976-6367(Print), ISSN 0976 - 6375(Online), Volume 4, Issue 5, September - October (2013), © IAEME 48 REFERENCES [1] IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. IT-23, NO. 3, MAY 1977 337A Universal Algorithm for Sequential Data Compression [2] International Symposium on Information Theory and its Applications, ISITA2006 Seoul, Korea, October 29–November 1, 2006 Improving LZ77 Data Compression using Bit Recycling [3] International Journal of Wisdom Based Computing, Vol. 1 (3), December 2011 68 A Comparative Study Of Text Compression Algorithms [4] Northwestern University Department of Electrical and Computer Engineering ECE 428: Information Theory Spring 2004 [5] http://www.stringology.org/DataCompression/lz77/index_en.html [6] http://www.zlib.net/feldspar.html • Links of the text files used in Analysis are given below (sorted by the index of the table) 1. http://www.gutenberg.org/cache/epub/28466/pg28466.txt 2. http://www.gutenberg.org/cache/epub/16728/pg16728.txt 3. http://www.gutenberg.org/cache/epub/9173/pg9173.txt 4. http://www.gutenberg.org/cache/epub/32482/pg32482.txt 5. http://www.gutenberg.org/files/25731/25731-0.txt 6. http://www.gutenberg.org/cache/epub/26598/pg26598.txt 7. http://www.gutenberg.org/cache/epub/28569/pg28569.txt 8. http://www.gutenberg.org/cache/epub/32962/pg32962.txt 9. http://www.gutenberg.org/cache/epub/23319/pg23319.txt 10. http://www.gutenberg.org/cache/epub/101/pg101.txt](https://image.slidesharecdn.com/lz77datacompressionalgoimprovement-140521022004-phpapp01/75/OPTIMIZATION-OF-LZ77-DATA-COMPRESSION-ALGORITHM-7-2048.jpg)