Download to read offline
Uploaded bybabuece
PPTX, PDF3,594 views
Modified booths algorithm part 1
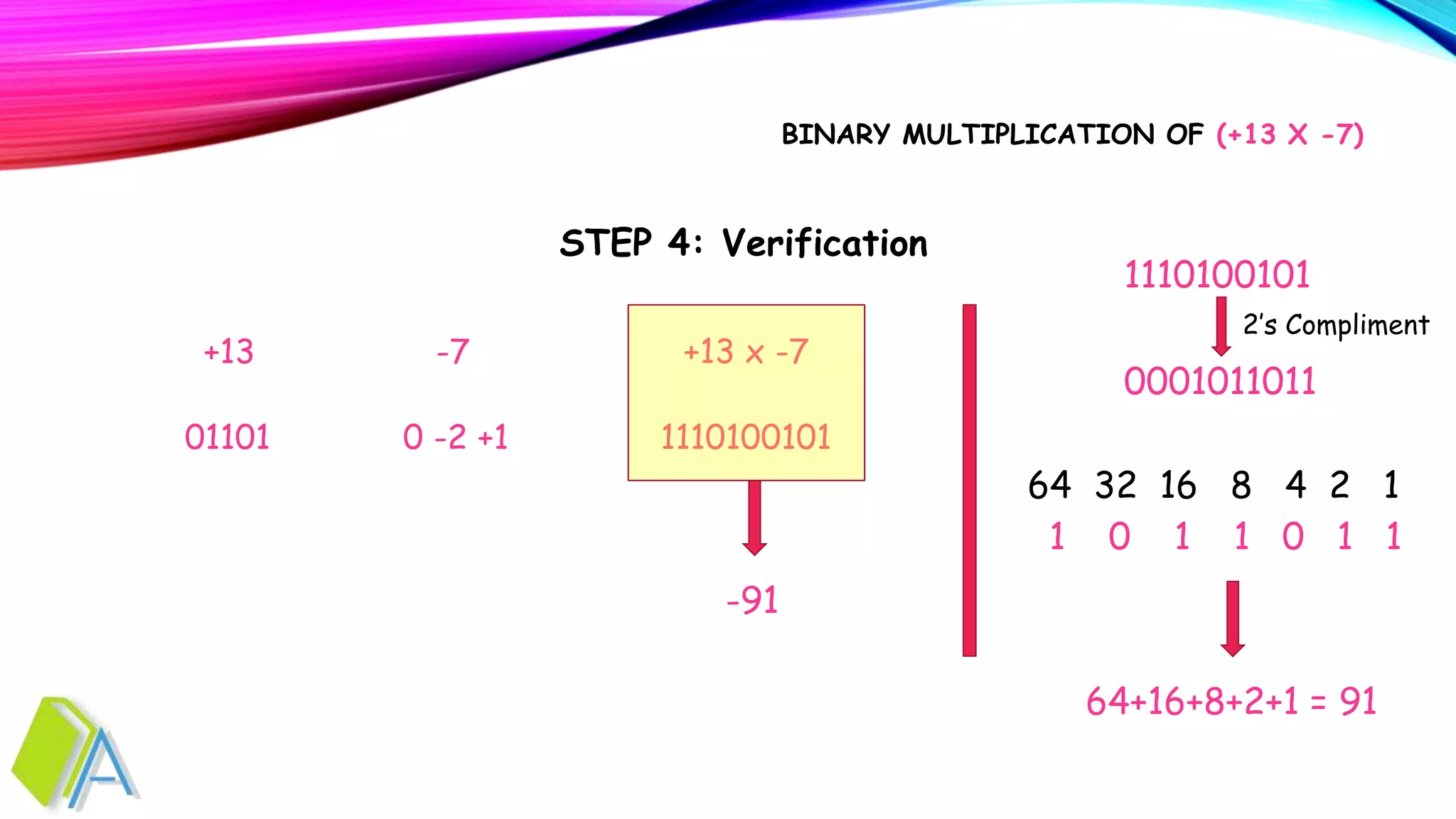
This document explains the modified Booth's radix-4 bit pair recoding algorithm for signed binary multiplication, using the example of multiplying +13 by -7. It details the steps including number representation, bit pair recoding, and the multiplication process with specific calculations and transformations. The document concludes with a verification of the resulting product.
Modified booths algorithm part 1
- 1. MODIFIED BOOTH’S ALGORITHM RADIX– 4 / BIT PAIR RECODING ALGORITHM Signed Binary Multiplication Algorithm E.g.: Binary Multiplication of Positive Multiplicand & Negative Multiplier (+13 X -7)
- 2. EXPLANATION Binary Multiplication of(+13 X -7) STEP 1: Number Representation Multiplicand +13 Multiplier -7 1101 1110 0 1 Binary Representation 2’s Compliment Representation 01101 11001
- 3. BINARY MULTIPLICATION OF(+13 X -7) STEP 2: Bit Pair Recoding of the Multiplier Multiplier -7 11001 1 1 0 0 1 Recoded Multiplier Multiplier Multiplicand selected Bit i+1 Bit i Bit i-1 0 0 0 0 X Multiplicand 0 0 1 +1 X Multiplicand 0 1 0 +1 X Multiplicand 0 1 1 +2 X Multiplicand 1 0 0 -2 X Multiplicand 1 0 1 -1 X Multiplicand 1 1 0 -1 X Multiplicand 1 1 1 0 X Multiplicand Modified Booth’s Recoding Table i 0 i-1 +1 i+1i i-1i+1 -2 i i-1i+1 0 1
- 4. BINARY MULTIPLICATION OF(+13 X -7) STEP 3: Multiplication Multiplicand 01101 Recoded Multiplier 0 -2 +1 Note: 1. Multiplication with 0 – 0 (00000) 2. Multiplication with +1 – Multiplicand (01101) 3. Multiplication with -1 – 2’s compliment of Multiplicand (10011) 4. Multiplication with +2 – Shift Multiplicand left by 1 bit (011010) 5. Multiplication with -2 – 2’s compliment of Shifted Multiplicand (100110) 0 1 1 0 1 0 -2 +1 0 1 1 0 10 0 0 0 0 1 0 0 1 1 01 1 0 0 0 0 00 1010010111 11
- 5. BINARY MULTIPLICATION OF(+13 X -7) 1110100101 +13 -7 01101 0 -2 +1 +13 x -7 1 0 1 1 0 1 1 64 32 16 8 4 2 1 64+16+8+2+1 = 91 -91 STEP 4: Verification 1110100101 0001011011 2’s Compliment